数据分析实验报告(主成分分析)
主成分分析报告

主成分分析报告第一点:主成分分析的定义与重要性主成分分析(Principal Component Analysis,PCA)是一种统计方法,它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量,这组变量称为主成分。
这种方法在多变量数据分析中至关重要,尤其是在数据的降维和可视化方面。
在实际应用中,数据往往包含多个变量,这些变量可能存在一定的相关性。
这样的数据集很难直接进行分析和理解。
主成分分析通过提取数据中的主要特征,将原始的多维数据转化为少数几个互相独立的主成分,使得我们能够更加清晰地看到数据背后的结构和模式。
主成分分析的重要性体现在以下几个方面:1.降维:在数据集中存在大量变量时,通过PCA可以减少数据的维度,简化模型的复杂性,从而降低计算成本,并提高模型的预测速度。
2.去除相关性:PCA能够帮助我们识别和去除变量间的线性相关性,使得我们分析的是更加纯净的独立信息。
3.数据可视化:通过将多维数据映射到二维或三维空间中,PCA使得数据的可视化成为可能,有助于我们直观地理解数据的结构和模式。
4.特征提取:在机器学习中,PCA可以作为一种特征提取工具,提高模型的性能和泛化能力。
第二点:主成分分析的应用案例主成分分析在各个领域都有广泛的应用,下面列举几个典型的案例:1.图像处理:在图像处理领域,PCA被用于图像压缩和特征提取。
通过将图像转换到主成分空间,可以大幅度减少数据的存储空间,同时保留图像的主要信息。
2.金融市场分析:在金融领域,PCA可以用来分析股票或证券的价格动向,通过识别影响市场变化的主要因素,帮助投资者做出更明智的投资决策。
3.基因数据分析:在生物信息学领域,PCA被用于基因表达数据的分析。
通过识别和解释基因间的相关性,PCA有助于揭示生物过程中的关键基因和分子机制。
4.客户细分:在市场营销中,PCA可以用来分析客户的购买行为和偏好,通过识别不同客户群的主要特征,企业可以更有效地制定市场策略和个性化推荐。
主成分分析

主成分分析法实验报告一、实验名称:主成分分析二、实验目的:利用计算机实现主成分分析,完成综合评价。
三、实验原理:四、实验过程:(一)数据录入:将相关指标数据录入如下表(二)数据标准化:为避免不同量纲引起的大数吃小数问题,我们对相关数据进行标准化,结果如下:表1:标准化后的数据录入表表2:描述统计量表表1是标准化后的相关数据,表2给出了标准化过程中涉及到的均值、标准差等数值。
(三)分析表3:公因子方差表表3给出了该次分析从每个原始变量中提取的信息,表格下的表注表明,该次分析使用主成分分析完成的。
可以看出除百元销售收入实现利税信息损失较大外,主成分几乎包含了各个原始变量至少85%的信息。
表4:相关矩阵表4为各指标因素量化后的相关矩阵。
表5:解释的总方差表由输出结果表5可以看出,前两个主成分y1,y2的方差和占全部方差的的比例为84.7%。
我们就选取y1为第一主成分,y2为第二主成分,且这两个主成分的方差和占全部方差的84.7%,即基本上保留了原来的指标的信息,这样由原来的9个指标转化为2个新指标,起到了降维的作用。
表6:因子载荷矩阵因子载荷矩阵(表6)是主成分和变量间的因子负荷量,即相关系数,代表相关度。
并非主成分的系数;所以我们要通过该成分矩阵计算出主成分的系数,计算结果如表7:表7:主成分系数表7中,a1代表第一主成分与各变量间的因子负荷量,a2代表第二主成分与各变量间的因子负荷量;u1代表y1的系数,u2代表y2的相应系数。
由此可得到两个主成分y1、y2的线性组合。
(四)主成分得分及分类表8:主成分得分为了分析各样品在主成分所反映的经济意义方面的情况,还将标准化后的原始数据代入主成分表达式中计算出各样品的主成分得分,如表8,得到28个省的、直辖市、自治区的主成分的分。
将这28个样品在平面直角坐标系上描出来,进而得到样品分类,如下图所示:由上图可以看出,分布在第一象限的是上海、北京、天津、广西四个省区,这四个省区的经济效益在全国来说属于较好的,上海经济效益最好。
主成分分析报告

主成分分析报告在当今的数据驱动的世界中,我们经常面临着处理大量复杂数据的挑战。
如何从这些海量的数据中提取有价值的信息,简化数据结构,发现潜在的模式和趋势,成为了数据分析领域的重要课题。
主成分分析(Principal Component Analysis,简称 PCA)作为一种强大的数据分析工具,为我们提供了一种有效的解决方案。
主成分分析是一种多元统计分析方法,其主要目的是通过对原始变量的线性组合,构建一组新的不相关的综合变量,即主成分。
这些主成分能够尽可能多地保留原始数据的信息,同时实现数据的降维。
让我们先来了解一下主成分分析的基本原理。
假设我们有一组观测数据,每个观测包含多个变量。
主成分分析的核心思想是找到一组新的坐标轴,使得数据在这些坐标轴上的投影具有最大的方差。
第一个主成分就是数据在方差最大方向上的投影,第二个主成分则是在与第一个主成分正交的方向上,具有次大方差的投影,以此类推。
为什么要进行主成分分析呢?首先,它能够帮助我们简化数据结构。
当我们面对众多相关的变量时,通过主成分分析可以将其归结为少数几个综合变量,从而减少数据的复杂性,便于后续的分析和处理。
其次,主成分分析可以去除数据中的噪声和冗余信息,突出数据的主要特征,有助于发现数据中的隐藏模式和关系。
此外,它还可以用于数据压缩和可视化,使得我们能够更直观地理解数据。
在实际应用中,主成分分析有着广泛的用途。
在图像处理领域,它可以用于图像压缩和特征提取,减少图像数据的存储空间,同时保留图像的主要特征。
在金融领域,主成分分析可以用于构建投资组合,通过对多个金融资产的分析,找出主要的影响因素,从而优化投资组合。
在生物学研究中,主成分分析可以用于分析基因表达数据,发现不同样本之间的差异和相似性。
接下来,我们来看看如何进行主成分分析。
首先,需要对原始数据进行标准化处理,以消除量纲的影响。
然后,计算数据的协方差矩阵或相关矩阵。
接着,通过求解特征值和特征向量,确定主成分的方向和权重。
主成份分析实验报告
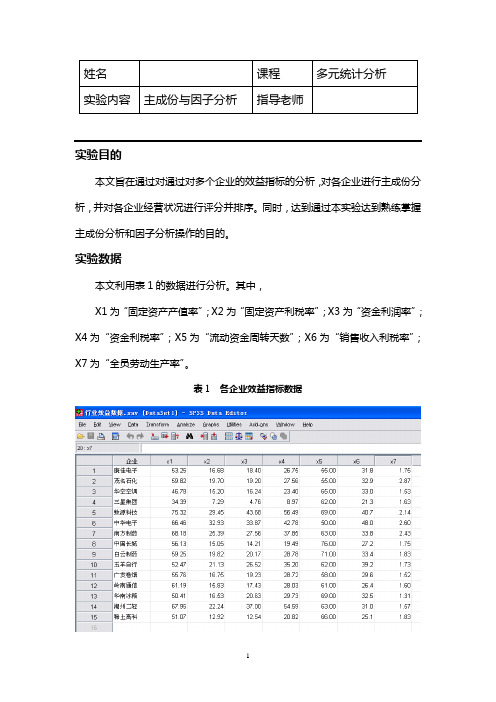
姓名课程多元统计分析实验内容主成份与因子分析指导老师实验目的本文旨在通过对通过对多个企业的效益指标的分析,对各企业进行主成份分析,并对各企业经营状况进行评分并排序。
同时,达到通过本实验达到熟练掌握主成份分析和因子分析操作的目的。
实验数据本文利用表1的数据进行分析。
其中,X1为“固定资产产值率”;X2为“固定资产利税率”;X3为“资金利润率”;X4为“资金利税率”;X5为“流动资金周转天数”;X6为“销售收入利税率”;X7为“全员劳动生产率”。
表1 各企业效益指标数据实验步骤选择【Analyze】-【Date Reduction】-【Factor】,如图2。
图2 主成份分析操作在主成份分析对话框中进行设置,将变量X1—X6选入Variables,如图3。
图3 主成份分析对话框选择【Descriptives】,弹出对话框如图4,保留默认设置。
图4 Descriptives对话框选择【Extraction】,弹出对话框如图5所示。
方法(method)默认为Principal components,即主成份分析,保留默认设置。
在提取Extract项下选Number of factors,填入6,即提取6个主成份。
图5 提取主成分设置选择【Rotation】,弹出对话框如图6所示,因子旋转采用Varimax方法,如图6所示。
图6 因子旋转对话框选择【Scores】,弹出对话框如图7所示。
选择将主成份保存成变量(Save as variables),方法(method)为回归(Regression)。
图7 主成份得分设置点击【OK】,即可得到主成份分析和因子分析结果。
实验结果表8为变量共同度,表中显示原始数据所有信息都被提取出来了。
表8 变量共同度CommunalitiesInitial Extraction固定资产产值率 1.000 1.000固定资产利税率 1.000 1.000资金利润率 1.000 1.000资金利税率 1.000 1.000流动资金周转天数 1.000 1.000销售收入利税率 1.000 1.000Extraction Method: Principal ComponentAnalysis.表9为各主成份特征根和累计贡献率。
主成分分析实验报告

一、实验目的本次实验旨在通过主成分分析(PCA)方法,对给定的数据集进行降维处理,从而简化数据结构,提高数据可解释性,并分析主成分对原始数据的代表性。
二、实验背景在许多实际问题中,数据集往往包含大量的变量,这些变量之间可能存在高度相关性,导致数据分析困难。
主成分分析(PCA)是一种常用的降维技术,通过提取原始数据中的主要特征,将数据投影到低维空间,从而简化数据结构。
三、实验数据本次实验采用的数据集为某电商平台用户购买行为的调查数据,包含用户年龄、性别、收入、职业、购买商品种类、购买次数等10个变量。
四、实验步骤1. 数据预处理首先,对数据进行标准化处理,消除不同变量之间的量纲影响。
然后,进行缺失值处理,删除含有缺失值的样本。
2. 计算协方差矩阵计算标准化后的数据集的协方差矩阵,以了解变量之间的相关性。
3. 计算特征值和特征向量求解协方差矩阵的特征值和特征向量,特征值表示对应特征向量的方差,特征向量表示数据在对应特征方向上的分布。
4. 选择主成分根据特征值的大小,选择前几个特征值对应特征向量作为主成分,通常选择特征值大于1的主成分。
5. 构建主成分空间将选定的主成分进行线性组合,构建主成分空间。
6. 降维与可视化将原始数据投影到主成分空间,得到降维后的数据,并进行可视化分析。
五、实验结果与分析1. 主成分分析结果根据特征值大小,选取前三个主成分,其累计贡献率达到85%,说明这三个主成分能够较好地反映原始数据的信息。
2. 主成分空间可视化将原始数据投影到主成分空间,绘制散点图,可以看出用户在主成分空间中的分布情况。
3. 主成分解释根据主成分的系数,可以解释主成分所代表的原始数据特征。
例如,第一个主成分可能主要反映了用户的购买次数和购买商品种类,第二个主成分可能反映了用户的年龄和性别,第三个主成分可能反映了用户的收入和职业。
六、实验结论通过本次实验,我们成功运用主成分分析(PCA)方法对数据进行了降维处理,提高了数据可解释性,并揭示了数据在主成分空间中的分布规律。
主成分分析、因子分析实验报告--SPSS

主成分分析、因子分析实验报告--SPSS主成分分析、因子分析实验报告SPSS一、实验目的主成分分析(Principal Component Analysis,PCA)和因子分析(Factor Analysis,FA)是多元统计分析中常用的两种方法,旨在简化数据结构、提取主要信息和解释变量之间的关系。
本次实验的目的是通过使用 SPSS 软件对给定的数据集进行主成分分析和因子分析,深入理解这两种方法的原理和应用,并比较它们的结果和差异。
二、实验原理(一)主成分分析主成分分析是一种通过线性变换将多个相关变量转换为一组较少的不相关综合变量(即主成分)的方法。
这些主成分是原始变量的线性组合,且按照方差递减的顺序排列。
主成分分析的主要目标是在保留尽可能多的数据信息的前提下,减少变量的数量,从而简化数据分析和解释。
(二)因子分析因子分析则是一种探索潜在结构的方法,它假设观测变量是由少数几个不可观测的公共因子和特殊因子线性组合而成。
公共因子解释了变量之间的相关性,而特殊因子则代表了每个变量特有的部分。
因子分析的目的是找出这些公共因子,并估计它们对观测变量的影响程度。
三、实验数据本次实验使用了一份包含多个变量的数据集,这些变量涵盖了不同的领域和特征。
数据集中的变量包括具体变量 1、具体变量 2、具体变量 3等,共X个观测样本。
四、实验步骤(一)主成分分析1、打开 SPSS 软件,导入数据集。
2、选择“分析”>“降维”>“主成分分析”。
3、将需要分析的变量选入“变量”框。
4、在“抽取”选项中,选择主成分的提取方法,如基于特征值大于1 或指定提取的主成分个数。
5、点击“确定”,运行主成分分析。
(二)因子分析1、同样在 SPSS 中,选择“分析”>“降维”>“因子分析”。
2、选入变量。
3、在“描述”选项中,选择相关统计量,如 KMO 检验和巴特利特球形检验。
4、在“抽取”选项中,选择因子提取方法,如主成分法或主轴因子法。
主成分分析报告

主成分分析报告1. 简介主成分分析(Principal Component Analysis, PCA)是一种常用的数据降维技术,用于将高维数据集映射到低维子空间。
主成分分析主要通过计算数据集中的主成分,来捕捉数据中的主要变化方向和模式。
本报告将介绍主成分分析的原理、应用、算法实现以及使用注意事项。
2. 主成分分析原理主成分分析旨在将高维数据投影到低维空间,并保留尽可能多的有用信息。
其基本思想是通过线性变换,将原始数据映射到新的坐标系中,其中新坐标系的轴是原始数据的主成分方向。
主成分分析的步骤如下:1.计算原始数据的协方差矩阵;2.对协方差矩阵进行特征值分解,得到特征向量和特征值;3.选择最大的k个特征值对应的特征向量,构成变换矩阵;4.将原始数据通过变换矩阵进行映射,得到降维后的数据。
3. 主成分分析的应用主成分分析在数据处理和分析中有很多应用,其中包括:1.数据降维:主成分分析可以将高维数据集投影到低维空间,从而减少数据的维度。
这对于处理大规模数据、可视化和提高计算效率都非常有用。
2.数据可视化:通过将高维数据映射到二维或三维空间,可以更直观地展示数据的结构和模式。
3.噪声过滤:主成分分析可以过滤掉数据中的噪声,保留主要的信号。
4.特征提取:通过提取数据的主成分,可以捕捉到数据的主要变化模式,便于后续分析。
4. 主成分分析算法实现以下是使用Python进行主成分分析的示例代码:import numpy as npfrom sklearn.decomposition import PCA# 创建一个样本矩阵X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 创建PCA对象并指定主成分的数量pca = PCA(n_components=2)# 执行主成分分析X_pca = pca.fit_transform(X)# 输出降维后的数据print(X_pca)在上述代码中,首先创建了一个样本矩阵X,然后创建了一个PCA对象,并指定要保留的主成分数量为2。
主成分分析实验报告剖析

一、引言主成分分析(PCA)是一种常用的数据降维方法,通过对原始数据进行线性变换,将高维数据投影到低维空间,从而简化数据结构,提高计算效率。
本文通过对主成分分析实验的剖析,详细介绍了PCA的基本原理、实验步骤以及在实际应用中的注意事项。
二、实验背景随着数据量的不断增长,高维数据在各个领域变得越来越普遍。
高维数据不仅增加了计算难度,还可能导致信息过载,影响模型的性能。
因此,数据降维成为数据分析和机器学习中的关键步骤。
PCA作为一种有效的降维方法,在众多领域得到了广泛应用。
三、实验目的1. 理解主成分分析的基本原理;2. 掌握PCA的实验步骤;3. 分析PCA在实际应用中的优缺点;4. 提高数据降维的技能。
四、实验原理主成分分析的基本原理是将原始数据投影到新的坐标系中,该坐标系由主成分构成。
主成分是原始数据中方差最大的方向,可以看作是数据的主要特征。
通过选择合适的主成分,可以将高维数据降维到低维空间,同时保留大部分信息。
五、实验步骤1. 数据准备:选择一个高维数据集,例如鸢尾花数据集。
2. 数据标准化:将数据集中的每个特征缩放到均值为0、标准差为1的范围,以便消除不同特征之间的尺度差异。
3. 计算协方差矩阵:计算标准化数据集的协方差矩阵,以衡量不同特征之间的相关性。
4. 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。
5. 选择主成分:根据特征值的大小选择前k个特征向量,这些向量对应的主成分代表数据的主要特征。
6. 数据投影:将原始数据投影到选择的主成分上,得到降维后的数据。
六、实验结果与分析1. 实验结果:通过实验,我们得到了降维后的数据集,并与原始数据集进行了比较。
结果表明,降维后的数据集保留了大部分原始数据的信息,同时降低了数据的维度。
2. 结果分析:实验结果表明,PCA在数据降维方面具有良好的效果。
然而,PCA也存在一些局限性,例如:(1)PCA假设数据服从正态分布,对于非正态分布的数据,PCA的效果可能不理想;(2)PCA降维后,部分信息可能丢失,尤其是在选择主成分时,需要权衡保留信息量和降低维度之间的关系;(3)PCA降维后的数据可能存在线性关系,导致模型难以捕捉数据中的非线性关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验八主成分分析一、实验目的和要求能利用原始数据与相关矩阵、协主差矩阵作主成分分析,并能理解标准化变量主成分与原始数据主成分的联系与区别;能根据SAS输出结果选出满足要求的几个主成分.实验要求:编写程序,结果分析.实验内容:书上4.5 4.64.5 data examp4_5;input id x1-x8;cards;1 8.35 23.53 7.51 8.62 17.42 10.00 1.04 11.212 9.25 23.75 6.61 9.19 17.77 10.48 1.72 10.513 8.19 30.50 4.72 9.78 16.28 7.60 2.52 10.324 7.73 29.20 5.42 9.43 19.29 8.49 2.52 10.005 9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.766 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.357 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.818 9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.659 9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.1710 8.70 28.12 7.21 10.53 19.45 13.30 1.6611.9611 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.6112 8.67 36.05 7.31 7.75 16.67 11.68 2.3812.8813 9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.6714 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.2315 8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.2816 7.67 35.71 8.04 8.31 15.13 7.76 1.41 13.2517 7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.2914.8019 8.82 33.70 7.59 10.98 18.82 14.73 1.78 10.1020 6.25 35.02 4.72 6.28 10.03 7.15 1.93 10.3921 10.60 52.41 7.70 9.98 12.53 11.70 2.31 14.6922 7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.5723 13.45 55.85 5.50 7.45 9.55 9.52 2.21 16.3024 10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.5725 7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.6926 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.8727 7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.6128 7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.9022.8930 12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.50;run;proc corr cov nosimple data=examp4_5;var x1-x8;run;proc princomp data=examp4_5 prefix=y out=bb; var x1-x8;run;proc plot data=bb;plot y2*y1 $ id='*';proc sort data=bb;by descending y1;run;proc print data=bb;var id y1 y2 x1-x8;run;输出结果:1、样本相关系数矩阵Correlation Matrixx1 x2 x3 x4 x5 x6 x7 x8x1 1.0000 0.3336 -.0545-.0613 -.2894 0.1988 0.34870.3187x2 0.3336 1.0000 -.02290.3989 -.1563 0.7111 0.41360.8350x3 -.0545 -.0229 1.00000.5333 0.4968 0.0328 -.1391-.2584x4 -.0613 0.3989 0.53331.0000 0.6984 0.4679 -.17130.3128x5 -.2894 -.1563 0.49680.6984 1.0000 0.2801 -.2083-.0812x6 0.1988 0.7111 0.03280.4679 0.2801 1.0000 0.41680.7016x7 0.3487 0.4136 -.1391-.1713 -.2083 0.4168 1.00000.3989x8 0.3187 0.8350 -.25840.3128 -.0812 0.7016 0.39891.00002、调用主成分分析的princomp过程,从相关系数矩阵出发进行主成分分析,输出集bbThe PRINCOMP ProcedureObservations 30Variables 8SimpleStatisticsx1 x2 x3 x4Mean 8.706666667 39.056000007.629000000 10.86566667StD 1.614728190 12.438758283.052716540 3.89495579SimpleStatisticsx5 x6x7 x8Mean 16.58900000 11.626000001.902000000 13.06100000StD 2.99785481 3.058108050.851576226 3.647070961)样本相关系数矩阵R的特征值、各主成分贡献率及累计贡献率Eigenvalues of theCorrelation Matrix特征值∧*λ Differencei贡献率% 累计贡献率%1 3.096288290.72906522 0.3870 0.38702 2.367223071.44723572 0.2959 0.6829已达68.29%3 0.919987350.21406199 0.1150 0.79794 0.705925360.20748303 0.0882 0.88625 0.498442330.26855403 0.0623 0.94856 0.229888310.09911254 0.0287 0.97727 0.130775770.07930623 0.0163 0.99368 0.05146954 0.0064 1.0000SAS 系统 14:09 Monday, October 22, 2001 22The PRINCOMP Procedure2)样本相关系数矩阵R特征值的正交化特征向量The SASSystem 17:30 Tuesday, October 26, 2012 4The PRINCOMP ProcedureEigenvectorsy1 y2 y3 y4 y5 y6 y7 y8x1 0.249607 -.241238 0.693918 -.3767700.502313 -.018418 -.036543 0.045052x2 0.519234 -.037607 -.071261 -.224871-.424453 0.001760 -.282467 0.642950x3 -.018480 0.475439 0.577819 0.032379 -.510472 -.173344 0.381416 -.050854x4 0.254092 0.538081 -.021777 -.231066 0.010358 0.399113 -.471680 -.458432x5 0.021695 0.575449 -.048087 0.285368 0.516270 0.146109 0.159192 0.520977x6 0.492663 0.134676 -.145348 0.224222 0.177156 -.754966 -.081452 -.244442x7 0.317147 -.260682 0.286391 0.768116 -.090759 0.355165 -.130720 -.089297x8 0.509332 -.087081 -.271279 -.176990 0.026015 0.304720 0.708416 -.1808213)按第一主成分对各省份进行排序The SAS System 17:30 Tuesday, October 26, 2012 6Obs id y1 y2 x1 x2 x3 x4 x5 x6 x7 x81 30 6.89591 -2.27833 12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.508.00 22.22 20.06 15.12 0.72 22.893 27 1.79214 2.88809 7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.614 26 1.51507 1.37353 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.875 23 1.40116 -3.17840 13.45 55.855.50 7.45 9.55 9.52 2.21 16.306 21 1.15390 -1.37420 10.60 52.417.70 9.98 12.53 11.70 2.31 14.697 22 1.05651 -1.23524 7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.578 24 0.43543 0.47409 10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.579 25 0.15329 0.11320 7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.6910 17 0.04520 0.98056 7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.2911 28 -0.13324 4.90844 7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.9012 18 -0.13489 0.34363 7.18 40.91 7.32 8.94 17.60 12.75 1.14 14.807.59 10.98 18.82 14.73 1.78 10.1014 12 -0.17044 -0.58962 8.67 36.05 7.31 7.75 16.67 11.68 2.38 12.8815 8 -0.39220 -0.29562 9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.6516 10 -0.43040 0.64570 8.70 28.12 7.21 10.53 19.45 13.30 1.66 11.9617 14 -0.51802 -0.55227 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.2318 9 -0.61274 -0.28257 9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.1719 13 -0.66670 -0.29548 9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.6720 11 -0.81850 -0.42128 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.6121 7 -1.11335 -0.01815 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.8122 15 -1.11496 -0.44043 8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.2823 6 -1.18223 -0.19296 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.356.61 9.19 17.77 10.48 1.72 10.5125 16 -1.25934 -0.42827 7.67 35.718.04 8.31 15.13 7.76 1.41 13.2526 3 -1.29370 -0.86033 8.19 30.504.72 9.78 16.28 7.60 2.52 10.3227 4 -1.32567 -0.10239 7.73 29.205.42 9.43 19.29 8.49 2.52 10.0028 5 -1.48595 -0.35156 9.42 27.938.20 8.14 16.17 9.42 1.55 9.7629 1 -1.68448 0.16743 8.35 23.537.51 8.62 17.42 10.00 1.04 11.2130 20 -1.96091 -2.10827 6.25 35.024.72 6.28 10.03 7.15 1.93 10.3 由输出结果可以看出:前两个主成分的累计贡献率已达68.29%,因此,取前两个主成分做进一步分析即可.给出了对应于∧*1λ和∧*2λ的正交单位化特征向量∧*1e 和∧*2e ,由此得到标准化指标的前两个样本主成分为11123456780249605092001840254100217049270317105093∧==+-+++++e x ***********........T y x x x x x x x x 为8个指标加权平均,反映各省份在生活基本消费的消费水平能力的综合指标.*1y 值大,则各省份的生活水平越低,21123456780241200376047540538005754013470360700871∧==--++++-+e x ***********........T y x x x x x x x x反映各省份在生活消费品德消费能力综合指标,2*y 值大,则各省份的消费水平越高。
