中南大学 最优化方法及控制应用1120-1
最优化方法及其应用 - 更多gbj149 相关pdf电子书下载
最优化方法及其应用作者：郭科出版社：高等教育出版社类别：不限出版日期：20070701最优化方法及其应用 的图书简介系统地介绍了最优化的理论和计算方法,由浅入深,突出方法的原则,对最优化技术的理论作丁适当深度的讨论,着重强调方法与应用的有机结合,包括最优化问题总论,线性规划及其对偶问题,常用无约束最优化方法,动态规划,现代优化算法简介,其中前八章为传统优化算法,最后一章还给出了部分优化问题的设计实例,也可供一般工科研究生以及数学建模竞赛参赛人员和工程技术人员参考,最优化方法及其应用 的pdf电子书下载最优化方法及其应用 的电子版预览第一章 最优化问题总论1.1 最优化问题数学模型1.2最优化问题的算法1.3 最优化算法分类1.4组合优化问題简卉习题一第二章 最优化问题的数学基础2.1二次型与正定矩阵2.2 方向导数与梯度2.3Hesse矩阵及泰勒展式2.4 极小点的判定条件2.5锥、凸集、凸锥2.6 凸函数2.7约束问题的最优性条件习题二第三章 线性规划及其对偶问题3.1线性规划数学模型基本原理3.2 线性规划迭代算法3.3对偶问题的基本原理3.4 线性规划问题的灵敏度习题三第四章一维搜索法4.1 搜索区间及其确定方法4.2 对分法4.3Newton切线法4.4 黄金分割法4.5 抛物线插值法习题四第五章常用无约束最优化方法5.1 最速下降法5.2 Newton法5.3修正Newton法5.4 共轭方向法5.5 共轭梯度法5.6 变尺度法5.7坐标轮换法5.8 单纯形法习題五第六章 常用约束最优化方法6.1外点罚函数法6.2 內点罚函数法6.3 混合罚函数法6.4约束坐标轮换法6.5 复合形法习题六第七章 动态规划7.1动态规划基本原理7.2 动态规划迭代算法7.3动态规划有关说明习题七第八章 多目标优化8.1多目标最优化问题的基本原理8.2 评价函数法8.3 分层求解法8.4目标规划法习题八第九章 现代优化算法简介9.1 模拟退火算法9.2遗传算法9.3 禁忌搜索算法9.4 人工神经网络第十章最优化问题程序设计方法10.1 最优化问题建模的一般步骤10.2常用最优化方法的特点及选用标准10.3最优化问题编程的一般过程10.4 优化问题设计实例参考文献更多 最优化方法及其应用 相关pdf电子书下载。
最优化方法及其应用PPT课件
一 最优化问题总论
如果是求一个约束的极小点，则每一次迭代的新点都应该在约束可 行域内，即 X k D，k 0，1，2，
下图为迭代过程
一 最优化问题总论
（二）收敛速度与计算终止准则
（1）收敛速度
作为一个算法A，能够收敛于问题的最优解当然
x1 x2
即求
2x，1 5x2 40
x1 0 ， x2 0
max f (x1, x2 ) x1 x2
2x1 5x2 40，
x1
0，x2
0．
一 最优化问题总论
最优化问题的数学模型包含有三个要求：即变
量（又称设计变量）、目标函数、约束条件．
一、变量 二、目标函数 三、约束条件 四、带约束条件的优化问题数学模型表示形式
t f (x1，x2 )
t c
L
L在 三维空间中曲面
与[平x1， 面x2 ]T 有一条交
线 ．交线在平面上的投影曲线是 ，可见曲线上的点到平
面
的高度都等于常数C，也即曲线上的的函数值都
具有相同的值．
一 最优化问题总论
当常数取不同的值时，重复 上面的讨论，在平面上得到一族 曲线——等高线.
等高线的形状完全由曲面的 形状所决定；反之，由等高线的 形状也可以推测出曲面的形状．
线（如图），不等式约束把坐标平面分成两部分当中的一部分 （如图）．
一 最优化问题总论
综上所述，当把约束条件中的每一个 等式所确定的曲线，以及每一个不等式所 确定的部分在坐标平面上画出之后，它 们相交的公共部分即为约束集合D．
一 最优化问题总论
例1.4 在坐标平面上画出约束集合
最优化算法分析及应用
最优化算法分析及应用最优化算法是一类用于求解最优问题的数学模型和算法。
最优问题是指在一定约束条件下，寻求使得目标函数取得最大或者最小值的问题。
最优化算法包括解析法和数值法两种方法。
解析法是通过对目标函数进行数学分析，利用导数、求极限等数学工具，从而找到最优解的一类算法。
其中最常用的方法是求解目标函数的一阶或者二阶偏导数，通过解方程求得目标函数的稳定点或是极值点，从而得到最优解。
解析法的优点是可以得到精确的最优解，其中最著名的算法是拉格朗日乘数法、KKT条件和牛顿法等。
这些方法在多种领域有着广泛的应用，比如经济学中的效用函数最大化问题、工程学中的最优设计问题等。
数值法是通过迭代计算的方式逼近最优解的一类算法。
与解析法不同，数值法不需要对目标函数进行精确的数学分析，而是通过给定初始点，通过一定规则进行迭代计算，从而逐步逼近最优解。
数值法的优点是可以处理复杂的非线性问题，也可以应用于高维问题或者没有解析解的问题。
常用的数值法有梯度下降法、共轭梯度法、模拟退火算法等等。
这些方法在机器学习、数据挖掘、图像处理等领域都有广泛的应用，比如利用梯度下降法进行参数优化，利用模拟退火算法求解旅行商问题等。
最优化算法在现实生活中有很多应用。
在工程领域，最优化算法被广泛应用于优化设计问题，比如在汽车工业中，通过最优化算法可以实现车辆的轻量化设计，从而降低燃料消耗和排放。
在物流领域，最优化算法可以帮助货物合理分配，提高物流效率，降低物流成本。
在电力系统中，最优化算法可以用于电力调度问题，从而实时调整发电机组的出力，保证电网的供需平衡。
在经济学中，最优化算法可以用来解决资源配置和决策问题，比如最大化收益、最小化成本等。
此外，最优化算法还可以应用于交通流量优化、医疗资源优化、网络传输优化等各个领域。
通过合理选择和应用最优化算法，可以提高效率，降低成本，优化资源配置，从而实现经济可持续发展和社会效益最大化。
总而言之，最优化算法是一类用于求解最优问题的数学模型和算法。
中南大学 最优化方法及控制应用11201
无约束优化问题
单变量优化问题
有约束优化问题 单目标优化问题
多变量优化问题
多目标优化问题
dgxu
28
目标函数的几何图形
一元函数
f(x)
二元函数
x
多元函数：“ 超曲面”
dgxu
29
等值线 ～ 等高线（测绘，地形图） ～由具有相同目标函数值的自变量点连成的曲线
f(x) f(x)
x2
x1
dgxu
30
通过观察等高线函数值的分布，可以初步确定最优点的搜索方向
a11 … a1n
… >0
an1 … ann
n阶矩阵A为负定的充要条件dgxu是–A为正定的。
27
§1.3.2 目标函数与等值线
目标函数——多方案选优中评价好坏的标准，性能指标 min f(x) 或 max f(x)
设计变量（决策变量） 静态优化问题：目标是参数的函数
动态优化问题：目标是函数的函数，即泛函数
f(x) = xTAx = [x1, x2]
5 -3 -3 5
[x1, x2]T
=5x12-6x1x2+5x22 =(x1+x2)2+4(x1-x2)2 >0
判定矩阵为正定或负定的Sylvester定理：
n阶矩阵A为正定的充要条件是A的各阶前主子式大于零，即
a11>0 ,
a11 a12
>0 , … a21 a22 …
4、有约束最优化问题的变分法
现代最优化技术 （20世纪50年代）
1、近代科学技术与工业生产的发展
需要
2、电子计算机的出现与发展
dgxu
可能
14
§1.2 工业过程领域中的应用
数学中的最优化方法
数学中的最优化方法数学是一门综合性强、应用广泛的学科，其中最优化方法是数学的一个重要分支。
最优化方法被广泛应用于各个领域，如经济学、物理学、计算机科学等等。
本文将从理论和应用两个角度探讨数学中的最优化方法。
一、最优化的基本概念最优化是在给定约束条件下，寻找使某个目标函数取得最大（或最小）值的问题。
在数学中，最优化可以分为无约束最优化和有约束最优化两种情况。
1. 无约束最优化无约束最优化是指在没有限制条件的情况下，寻找使目标函数取得最大（或最小）值的问题。
常见的无约束最优化方法包括一维搜索、牛顿法和梯度下降法等。
一维搜索方法主要用于寻找一元函数的极值点，通过逐步缩小搜索区间来逼近极值点。
牛顿法是一种迭代方法，通过利用函数的局部线性化近似来逐步逼近极值点。
梯度下降法则是利用函数的梯度信息来确定搜索方向，并根据梯度的反方向进行迭代，直至达到最优解。
2. 有约束最优化有约束最优化是指在存在限制条件的情况下，寻找使目标函数取得最大（或最小）值的问题。
在解决有约束最优化问题时，借助拉格朗日乘子法可以将问题转化为无约束最优化问题，进而使用相应的无约束最优化方法求解。
二、最优化方法的应用最优化方法在各个领域中都有广泛的应用。
以下将以几个典型的应用领域为例加以说明。
1. 经济学中的最优化在经济学中，最优化方法被广泛应用于经济决策、资源配置和生产计划等问题的求解。
例如，在生产计划中，可以使用线性规划方法来优化资源分配，使得总成本最小或总利润最大。
2. 物理学中的最优化最优化方法在物理学中也是常见的工具。
例如，在力学中，可以利用最大势能原理求解运动物体的最优路径；在电磁学中，可以使用变分法来求解电磁场的最优配置；在量子力学中，可以利用变分法来求解基态能量。
3. 计算机科学中的最优化在计算机科学中，最优化方法被广泛应用于图像处理、机器学习和数据挖掘等领域。
例如，在图像处理中，可以使用最小割算法来求解图像分割问题；在机器学习中，可以使用梯度下降法来求解模型参数的最优值。
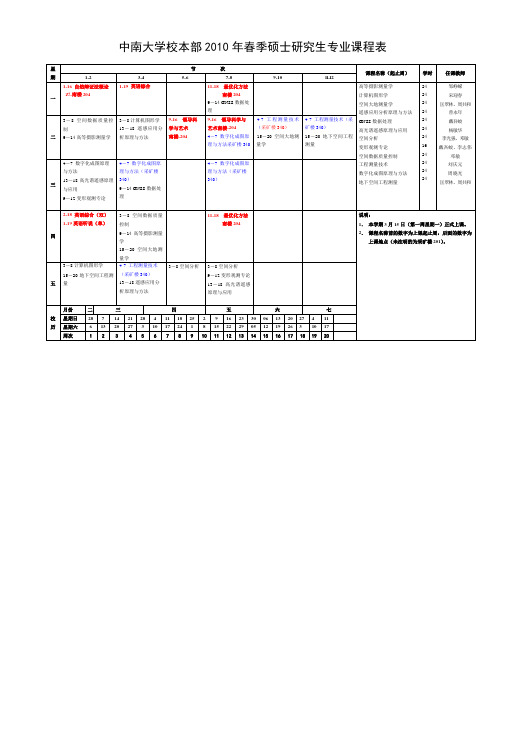
中南大学校本部2010年春季硕士研究生专业课程表
星期
节次
课程名称（起止周）
学时
任课教师
1-2
3-4
5-6
7-8
9-10
11-12
一
1-16自然辩证法概论
Z7-南楼204
1-19英语综合
11-18最优化方法
南楼204
9－14GNSS数据处理
高等摄影测量学
计算机图形学
空间大地测量学
遥感应用分析原理与方法
3－8计算机图形学
13－18遥感应用分析原理与方法
9-16领导科学与艺术
南楼-204
9-16领导科学与艺术南楼-204
4－7数字化成图原理与方法采矿楼340
4-7工程测量技术（采矿楼340）
15－20空间大地测量学
4-7工程测量技术（采矿楼340）
15－20地下空间工程测量
三
4－7数字化成图原理与方法
说明：
1．本学期3月15日（第一周星期一）正式上课。
2．课程名称前的数字为上课起止周，后面的数字为上课地点（未注明的为采矿楼201）。
五
3－8计算机图形学
15－20地下空间工程测量
4-7工程测量技术（采矿楼340）
13－18遥感应用分析原理与方法
3－8空间分析
3－8空间分析
9－12变形观测专论
13－18高光谱遥感原理与应用
GNSS数据处理
高光谱遥感原理与应用
空间分析
变形观测专论
空间数据质量控制
工程测量技术
数字化成图原理与方法
地下空间工程测量
24
24
24
24
24
24
24
最优化计算方法(工程优化)第1章
最优化在物质运输、自动控制、机械设计、采矿冶金、经 济管理等科学技术各领域中有广泛应用。下面举几个简单的实 例。
例1：把半径为1的实心金属球熔化后，铸成一个实心圆柱体， 问圆柱体取什么尺寸才能使它的表面积最小？
解：决定圆柱体表面积大小有两个决策变量：圆柱体底面半 径r、高h。
问题的约束条件是所铸圆柱体重量与球重相等。即
优化模型的分类
根据问题的不同特点分类
一般的约束优化问题
标准形式
min
xRn
f
x
s.t. gi x 0, i 1, 2, , m
1） gi x 0 -gi x 0
2）
hi
x
0
hi x 0
-hi
x
0
优化模型的分类
根据函数类型分类
线性规划：目标函数、约束条件都是线性的 非线性规划：目标函数、约束条件中的函数不全是线性
yi
a1
1
a3
ln 1
a2 exp
xi
a4 a5
最优化问题举例
例3已：知有从一v旅i 到行团v j从的v旅0费出为发要cij遍，游问城应市如何v1安, v排2 行,..程.,使vn总 ，
费用最小？
模型：
变量—是否从i第个城市到第j个城市
xij 1, 0;
约束—每个城市只能到达一次、离开一次
因此，我们在学习本课程时要尽可能了解如何 由实际问题形成最优化的数学模型。
数学模型: 对现实事物或问题的数学抽象或描述。
最优化问题的数学模型与分类
数学模型的建立
建立数学模型时要尽可能简单，而且要能完整地描 述所研究的系统。
过于简单的数学模型所得到的结果可能不符合实际情 况；而过于详细复杂的模型又给分析计算带来困难。
最优化与最优控制
0
)
2 f (X0)
2
f
(
X
0
)
x2x1
2 f (X0
)
xnx1
2 f (X0) x1x2
2 f (X0 x1xn)源自2 f (X0) x2 2
2 f (X0)
xn x2
2 f (X0)
x2xn
2 f (X0
)
xn 2
是f在点X 0处的Hesse矩阵
npjiangb@
npjiangb@
• 2.2 多元函数无约束的极小化 一、Hesse矩阵
设f
: Rn
R1 ,
X
0
Rn
, 如果f在点X
处对于自变量
0
X的各分量的二阶偏导数 2 f ( X 0 ) (i, j 1,2,, n) xix j
都存在，
则
称
函数f在
点X
处
0
二阶
可
导，
并且称矩阵
2
f (X x12
其中 N x * x x x * , 0 。 同样有：严格局部最优解。若 f x * f x
npjiangb@
定义 范数： 在 n 维实向量空间 R n 中，
定义实函数 x , 使其满足以下三个条件：
（１）对任意 x R n 有 x 0 , 当且仅当
dt
t0
• 五 终端控制问题
J Q[x(t f ), t f ]
• 六 非线性系统的最优控制
npjiangb@
• 1.5 最优化问题的解法
• 解析法：利用函数的解析性质去构造迭代公式使之收敛 到最优解
• 直接法：它对函数的解析性质没有要求，而是根据一定 的数学原理来确定
最优化方法及应用
最优化方法及应用最优化方法是一种数学领域的研究方法，旨在寻找最佳解决方案或最佳结果的方法。
最优化方法广泛应用于各个领域，如工程、经济、物流、管理等。
本文将介绍最优化方法的基本原理、常用模型和应用案例。
最优化方法的基本原理是通过建立数学模型，定义目标函数和约束条件，利用数学方法求得最佳解决方案。
最常见的最优化方法包括线性规划、非线性规划、动态规划、整数规划、模拟退火等。
线性规划是最常见的最优化方法之一，适用于目标函数和约束条件都是线性的问题。
线性规划通常使用单纯形法或内点法进行求解。
一个经典的应用案例是生产计划问题，通过最小化生产成本或最大化利润来确定最佳生产量和产品组合。
非线性规划是一个更一般的最优化方法，适用于目标函数和约束条件中包含非线性项的问题。
非线性规划可以使用梯度下降法、牛顿法等迭代算法进行求解。
一个典型的应用案例是参数估计问题，通过最小化误差函数来确定最佳参数值。
动态规划是一种适用于具有阶段性决策的问题的最优化方法。
动态规划通常将一个大问题划分为若干小问题，并通过递推的方式求解最优解。
一个常见的应用案例是背包问题，通过在每个阶段选择是否放入物品来最大化总价值。
整数规划是一种最优化方法，适用于目标函数和约束条件中包含整数变量的问题。
整数规划的求解比线性规划更困难，通常使用分支定界法等算法进行求解。
一个典型的应用案例是旅行商问题，通过确定一条最短路径来解决路线规划问题。
模拟退火是一种全局优化方法，通过模拟退火的过程来搜索最优解。
模拟退火可以应用于各种问题，如旅行商问题、机器学习算法优化等。
最优化方法在实际应用中具有广泛的应用场景。
在工程领域，最优化方法可以应用于产品设计、流程优化、资源调度等问题。
在经济领域，最优化方法可以应用于投资组合优化、货币政策制定等问题。
在物流领域，最优化方法可以应用于仓库位置选择、路径规划等问题。
在管理领域，最优化方法可以应用于员工排班、生产计划等问题。
总之，最优化方法是一种求解最佳解决方案或最佳结果的数学方法。
最优化方法解可新
最优化方法解可新最优化问题是数学建模中一个重要的问题类别，它的主要目标是在给定一些约束条件下找到一个使得目标函数取得最大或最小值的最优解。
最优化方法是解决这类问题的一种有效手段，通过对问题进行数学建模和算法求解，可以得到最优解或近似最优解。
最优化问题可以分为无约束优化和有约束优化两类。
在无约束优化问题中，目标函数的优化不受约束条件的限制；而在有约束优化问题中，目标函数的优化需要满足一定的约束条件。
下面将分别介绍无约束优化和有约束优化的最优化方法。
一、无约束优化的方法：1. 梯度下降法（Gradient Descent）：梯度下降法是最为常用的无约束优化方法之一。
它通过迭代的方式不断地沿着目标函数梯度的反方向更新参数，直至达到收敛条件。
梯度下降法的核心思想是利用函数的导数信息进行搜索，从而找到函数的最小值点。
2. 牛顿法（Newton Method）：牛顿法是一种基于函数局部二阶泰勒展开的优化方法。
它通过迭代的方式利用目标函数的一阶和二阶导数信息来求解最优解。
牛顿法在每次迭代时通过求解线性方程组来计算更新的步长，因此通常具有更快的收敛速度。
3. 拟牛顿法（Quasi-Newton Method）：拟牛顿法是对牛顿法的改进，它通过估计目标函数的二阶导数信息来近似求解最优解。
拟牛顿法不需要计算目标函数的二阶导数，而是通过迭代更新一个代表二阶导数信息的矩阵。
拟牛顿法比牛顿法更加稳定和易于实现，因此被广泛应用于实际问题中。
二、有约束优化的方法：1. 线性规划（Linear Programming）：线性规划是求解线性约束下的最优解的一种方法。
它的目标函数和约束条件均为线性函数，可以利用线性规划的特殊结构进行高效求解。
线性规划在工程、经济和管理等领域有广泛应用，如生产调度、资源分配等问题。
2. 非线性规划（Nonlinear Programming）：非线性规划是求解非线性约束下的最优解的方法。
它的目标函数和/或约束条件为非线性函数，常常需要使用数值优化方法进行求解。
《最优化方法》课程教学大纲
最优化方法》课程教学大纲课程编号：100004英文名称：Optimizatio n Methods一、课程说明1. 课程类别理工科学位基础课程2. 适应专业及课程性质理、工、经、管类各专业，必修文、法类各专业，选修3. 课程目的（1 ）使学生掌握最优化问题的建模、无约束最优化及约束最优化问题的理论和各种算法;（2）使学生了解二次规划与线性分式规划的一些特殊算法；（3）提高学生应用数学理论与方法分析、解决实际问题的能力以及计算机应用能力。
4. 学分与学时学分2,学时405. 建议先修课程微积分、线性代数、Matlab语言6. 推荐教材或参考书目推荐教材：（1）《非线性最优化》（第一版）.谢政、李建平、汤泽滢主编.国防科技大学出版社.2003年.孙（第一版）参考文瑜、徐成贤、朱德通主编.高等教育出版社.2004年（2）《最优化方法》书目：（第一版）.胡适耕、施保昌主编.华中理工大学出版社.2000年（1）《最优化原理》（2）《运筹学》》（修订版）.《运筹学》教材编写组主编.清华大学出版社.1990年7. 教学方法与手段（1）教学方法：启发式（2）教学手段：多媒体演示、演讲与板书相结合8. 考核及成绩评定考核方式：考试成绩评定：考试课（1）平时成绩占20%形式有：考勤、课堂测验、作业完成情况（2）考试成绩占80%形式有：笔试（开卷）。
9. 课外自学要求（1）课前预习；（2）课后复习；（3）多上机实现各种常用优化算法。
二、课程教学基本内容及要求第一章最优化问题与数学预备知识基本内容：（1 ）最优化的概念；（2）经典最优化中两种类型的问题--无约束极值问题、具有等式约束的极值问题的求解方法；（3）最优化问题的模型及分类；（4）向量函数微分学的有关知识；5）最优化的基本术语。
基本要求：（1）理解最优化的概念；（2）掌握经典最优化中两种类型的问题--无约束极值问题、具有等式约束的极值问题的求解方法；（3）了解最优化问题的模型及分类；（4）掌握向量函数微分学的有关知识；（5）了解最优化的基本术语。
最优化理论在智能决策与控制中应用
最优化理论在智能决策与控制中应用智能决策与控制是指利用人工智能和自动化技术，通过对大量数据的分析和处理，为问题的解决提供最佳化方案。
而最优化理论作为一种数学工具，可以有效地应用于智能决策与控制系统中，以提高系统的性能和效率。
本文将从最优控制、最优化算法和智能决策与控制系统中最优化应用三个方面探讨最优化理论在智能决策与控制中的应用。
一、最优控制最优控制是最优化理论在控制系统中的应用。
它通过数学模型和优化算法，寻找给定系统的最优控制策略，以最大程度地满足系统的性能要求。
最优控制的关键是确定目标函数和约束条件，以及选择适当的优化算法。
在智能决策与控制系统中，最优控制可以用来解决各种实际问题。
例如，在供应链管理中，可以利用最优控制模型来确定最佳的物流路线和配送策略，以降低成本和提高效率。
在机器人控制中，可以利用最优控制模型来规划机器人的运动轨迹和操作方式，以实现高效的任务执行。
在交通控制中，可以利用最优控制模型来调控交通信号和车流，以优化交通流量和减少拥堵。
二、最优化算法最优化算法是最优化理论的核心内容，它致力于寻找给定问题的最优解。
常见的最优化算法包括线性规划、非线性规划、整数规划、动态规划等。
在智能决策与控制系统中，最优化算法的应用非常广泛。
例如，在机器学习中，可以利用最优化算法来训练模型的参数，以使模型的预测误差最小化。
在数据挖掘中，可以利用最优化算法来发现大规模数据集中的隐藏模式和规律。
在优化调度中，可以利用最优化算法来分配资源和任务，以提高生产效率和降低成本。
三、智能决策与控制系统中的最优化应用智能决策与控制系统中的最优化应用主要涉及到决策和控制两个方面。
在决策方面，最优化可以帮助系统做出最佳的决策，以满足系统的目标和要求。
在控制方面，最优化可以帮助系统选择最佳的控制策略，以实现系统的稳定性和优化性能。
在智能决策中，最优化可以用来优化决策模型和评估指标。
例如，在股票投资中，可以利用最优化模型来确定最佳的投资组合，以实现最大的收益和最小的风险。
最优化方法 总结
最优化方法总结
最优化方法是一种用于求解最优化问题的数学工具和技术。
最优化问题是指在给定约束条件下寻找使得目标函数取得最大或最小值的变量取值。
最优化方法主要分为两类：无约束优化和约束优化。
在无约束优化中，最优化方法包括：
1. 梯度下降法：通过不断迭代来寻找函数的最小值点，在每一步迭代中通过计算函数的梯度来确定下降的方向和步长。
2. 牛顿法：使用函数的一阶和二阶导数来近似估计最小值点，通过迭代计算来逐步逼近最小值点。
3. 拟牛顿法：使用函数的梯度信息来估计牛顿法的一阶导数信息，以减少计算二阶导数的复杂性。
4. 共轭梯度法：通过迭代来求解线性最小二乘问题，可以高效地求解大规模问题。
在约束优化中，最优化方法包括：
1. 等式约束优化：利用拉格朗日乘数法将等式约束转化为无约束优化问题，并使用无约束优化方法求解。
2. 不等式约束优化：使用罚函数、投影法或者序列二次规划等方法将不等式约束转化为无约束优化问题，并使用无约束优化方法求解。
3. 信赖域方法：通过构造信赖域来限制搜索方向和步长，以保证在搜索过程中满足约束条件。
4. 内点法：通过转化为等式约束问题，并使用迭代法来逐步逼近约束边界。
总体来说，选择适当的最优化方法取决于问题的性质和约束条件的类型。
不同的最优化方法有不同的优缺点，适用于不同的问题，因此需要在具体应用中进行选择和调整。
《最优化方法》硕士研究生课程.
从而得到两杆桁架最优设计问题的数学模型：
min 2dB L2 h 2 2 2 p L h s.t. 0 dhB 2 E d 2 B 2 p L2 h 2 0 2 2 dhB 8 L h d max d d min h h h min max
这是作为系统决策变量的一个数学函数来衡量系统的 效率，即系统追求的目标。
§2 最优化问题
最优化在物质运输、自动控制、机械设计、采矿冶金、经济 管理等科学技术各领域中有广泛应用。下面举几个专业性不强 的实例。 例1.把半径为1的实心金属球熔化后，铸成一个实心圆柱体， 问圆柱体取什么尺寸才能使它的表面积最小？ 解：决定圆柱体表面积大小有两个决策变量：圆柱体底面半 径r、高h。 问题的约束条件是所铸圆柱体重量与球重相等。即
h 2r
2 2 3 r . h2 3 3
3
此时圆柱体的表面积为 例2.多参数曲线拟合问题
2 6 3
2 3
已知两个物理量x和y之间的依赖关系为: a2 y a1 x a4 1 a3 ln 1 exp a 5 a2 a3 a4 和 a5待定参数,为确定这些参数, 其中 a1
最优化原理与方法 第一章 最优化原理建模与数学预备知识
§1 引言
最优化技术是一门较新的学科分支。它是在本世纪五十年 代初在电子计算机广泛应用的推动下才得到迅速发展，并成为 一门直到目前仍然十分活跃的新兴学科。最优化所研究的问题 是在众多的可行方案中怎样选择最合理的一种以达到最优目标。 将达到最优目标的方案称为最优方案或最优决策，搜寻最 优方案的方法称为最优化方法，关于最优化方法的数学理论称 为最优化论。 最优化问题至少有两要素：一是可能的方案；二是要追求 的目标。后者是前者的函数。如果第一要素与时间无关就称为 静态最优化问题，否则称为动态最优化问题。 本科程专门讲授静态最优化问题。
最优化理论在智能决策与控制中应用
最优化理论在智能决策与控制中应用随着人工智能和自动化技术的不断发展，智能决策与控制在各个领域中扮演着越来越重要的角色。
而最优化理论作为一种数学方法，在智能决策与控制中得到了广泛应用。
本文将探讨最优化理论在智能决策与控制中的应用，并分析其对决策与控制效果的影响。
一、最优化理论概述最优化理论是一种数学方法，旨在寻找使某个目标函数取得最优值的决策变量。
最优化理论可以通过数学模型和算法来解决实际问题中的最优化问题。
常见的最优化方法包括线性规划、非线性规划、动态规划等。
二、最优化理论在智能决策中的应用1. 算法优化最优化理论在算法优化中发挥着重要的作用。
通过利用最优化方法对算法进行优化，可以提高算法的效率和准确性。
例如，在机器学习中，最优化理论可以用于调整模型参数以使损失函数最小化，从而提高模型的性能和泛化能力。
2. 资源分配智能决策涉及到对有限资源的分配和利用。
最优化理论可以通过优化资源分配方案，使得系统整体效益最大化。
例如，在供应链管理中，最优化理论可以用于确定最佳的供应链网络结构以及最优的物流路径，从而降低成本并提高运营效率。
3. 任务调度智能决策中的任务调度问题通常涉及到多个任务和多个资源之间的匹配与分配。
最优化理论可以用于确定最佳的任务调度方案，以实现任务的高效完成。
例如，在云计算中，最优化理论可以用于动态任务调度，将任务分配给最适合的云服务器，从而降低系统能耗和延迟。
三、最优化理论在智能控制中的应用1. 系统优化最优化理论在智能控制系统中的应用非常广泛。
通过构建数学模型和建立优化目标，最优化理论可以用于确定最佳控制策略，并对系统进行优化。
例如，在自动驾驶中，最优化理论可以用于确定最佳的车辆路径规划算法，以实现安全、高效的驾驶。
2. 参数优化智能控制系统中的参数选择对系统性能至关重要。
最优化理论可以应用于参数优化问题，通过寻找最佳参数配置，使得控制系统达到最优效果。
例如，在机器人控制中，最优化理论可以用于确定最佳的控制参数，以实现精确控制和优化运动路径规划。
数学中的控制论与最优化方法
数学中的控制论与最优化方法控制论是一种研究如何通过改变系统的某些变量来使系统达到预定目标的学科。
最优化方法是一种寻找最佳解决方案的数学方法。
在数学中，控制论和最优化方法是两个相互关联且互为补充的领域。
本文将探讨数学中的控制论和最优化方法，并介绍它们的应用。
一、控制论概述控制论是一门研究动力系统稳定性、稳定性判据、稳定性测试和控制器设计的学科。
它的主要目标是通过对系统进行监测和控制，使系统的输出达到期望的目标或稳定在某种状态。
控制论可以应用于各种领域，如工程、经济、生物学等。
控制论中的主要概念包括系统、输入、输出、状态和控制器。
系统是指被控制的对象，可以是物理系统、经济系统或生物系统等。
输入是指施加到系统中的控制信号，输出是系统响应的结果。
状态是系统在某一时刻的内部状态，它对系统的未来行为产生影响。
控制器是根据输出和期望输出之间的误差来调整输入信号的设备或算法。
控制论的数学模型主要基于差分方程和微分方程。
通过建立数学模型，可以分析系统的稳定性、性能和响应特性。
控制器的设计可以通过数学优化方法来获得最佳的控制策略。
二、最优化方法概述最优化方法是一种寻找最佳解决方案的数学方法。
它的主要目标是在给定约束条件下，找到使目标函数取得最大或最小值的变量值。
最优化方法可以应用于各种领域，如经济学、物理学、工程学等。
最优化问题有两种类型：无约束最优化和有约束最优化。
在无约束最优化问题中，目标函数的取值不受任何限制；而在有约束最优化问题中，目标函数的取值受到一定的约束条件限制。
最优化方法的常见算法有梯度下降法、牛顿法、拟牛顿法等。
这些算法可以通过计算目标函数的导数或近似导数来确定搜索方向，并通过迭代来不断优化解决方案。
三、控制论与最优化方法的关系控制论和最优化方法在数学上有着密切的联系和相互补充。
控制论关注如何通过调整系统的输入来实现系统的稳定性和性能要求，而最优化方法则提供了一种寻找最佳输入的数学工具。
在控制论中，最优化方法可以用于设计控制器。
最优化方法与最优控制课程设计
最优化方法与最优控制课程设计一、设计背景随着现代科技的迅猛发展和社会竞争的加剧，各领域都需要越来越高效、精确、优化的设计方法和控制策略。
其中，最优化方法和最优控制技术是目前工程和科学领域中广泛应用的重要工具。
为了培养具有创新、实际和实践能力的工科人才，本次课程设计旨在通过对最优化方法和最优控制的讲解和实践，让学生更好地掌握和应用相关知识和技能。
二、设计目标通过本次课程设计，学生将会达到以下目标：1.掌握最优化方法和最优控制技术的基本理论和基本方法。
2.学会使用常见的数学建模软件，如Matlab等进行系统建模和仿真分析。
3.能够独立和团队完成一个小型的最优化或最优控制项目，提高实践能力和工程实践能力。
三、设计内容本次课程设计包含以下主要内容：1. 最优化方法最优化问题是在已知约束和目标函数的情况下，寻找能够使目标函数达到最大值或最小值的决策变量。
本部分主要包括以下内容：1.1. 常见最优化方法：线性规划、非线性规划、整数规划等。
1.2. 最优化算法：梯度下降法、共轭梯度法、拟牛顿法、遗传算法等。
1.3. 最优化软件：Matlab、Gurobi、CPLEX等。
2. 最优控制方法最优控制是指将控制问题描述为寻求使性能指标最优的动态过程。
本部分主要包括以下内容：2.1. 常见最优控制方法：最优控制基本原理、极小值原理与动态规划、Pontryagin最小值原理、最优控制的数值方法等。
2.2. 最优控制软件：Matlab、Simulink、LabVIEW等。
3. 课程设计环节选做题目：利用所学知识设计一个最优化或最优控制的小型项目，完成以下步骤：3.1. 对所选项目进行问题陈述和问题定义，明确项目的目标和指标。
3.2. 采用合适的数学建模方法，将该项目建立为数学模型。
3.3. 选择相应的最优化或最优控制方法，探究寻找最优解的过程。
3.4. 采用合适的软件工具，在计算机上进行仿真分析和可视化呈现。
3.5. 编写实验报告，总结和分析实验结果，分享并展示项目成果。
最优化方法及应用
陆吾生教授是加拿大维多利亚大学电气与计算机工程系 (Dept. of Elect. and Comp. Eng. University of Victoria) 的正教授, 且为我校兼职教授，曾多次来我校数学系电子系讲学。
陆吾生教授的研究方向是：最优化理论和小波理论及其在1维和2维的数字信号处理、数字图像处理、控制系统优化方面的应用。
现陆吾生教授计划在 2007 年 10－11 月来校开设一门为期一个月的短期课程“最优化理论及其应用”（每周两次，每次两节课），对象是数学系、计算机系、电子系的教师、高年级本科生及研究生，以他在2006年出版的最优化理论的专著作为教材。
欢迎数学系、计算机系、电子系的研究生及高年级本科生选修该短期课程，修毕的研究生及本科生可给学分。
上课地点及时间：每周二及周四下午2:00开始，在闵行新校区第三教学楼326教室。
（自10月11日至11月8日）下面是此课程的内容介绍。
-----------------------------------最优化方法及应用I. 函数的最优化及应用1.1 无约束和有约束的函数优化问题1.2 有约束优化问题的Karush-Kuhn-Tucker条件1.3 凸集、凸函数和凸规划1.4 Wolfe对偶1.5 线性规划与二次规划1.6 半正定规划1.7 二次凸锥规划1.8 多项式规划1.9解最优化问题的计算机软件II 泛函的最优化及应用2.1 有界变差函数2.2 泛函的变分与泛函的极值问题2.3 Euler-Lagrange方程2.4 二维图像的Osher模型2.5 泛函最优化方法在图像处理中的应用2.5.1 噪声的消减2.5.2 De-Blurring2.5.3 Segmentation-----------------------------------------------注：这是一门约二十学时左右的短期课程，旨在介绍函数及泛函的最优化理论和方法，及其在信息处理中的应用。
最优控制经典方法
最优控制经典方法作者：边疆来源：《科技创新导报》 2014年第20期边疆(湖南省长沙市中南大学湖南长沙 410083)摘要：最优控制理论是现代控制理论中的经典。
该文论述了其中的基本支柱方法变分法和极小值原理。
两种方法都有自己独有的特性，优点缺点和适用范围，可分别用于求解不同种类的问题。
最优控制理论已经广泛地融入到了现代社会中，在将来仍有广阔的发展前景。
关键词：最优控制理论变分法极小值原理。
中图分类号：TP13 文献标识码：A 文章编号：1674-098X(2014)07(b)-0255-02早在20世纪50年代初，就开始了对最短时间控制问题的研究，形成了时间最优控制理论，其中包含著名的Bang-Bang控制理论；随后，由于空间技术的发展，导弹、卫星等复杂系统提出了消耗燃料要少，飞行速度要快，运行可靠性要高等严格的要求，在工程上刺激了最优控制理论的发展，逐步形成了一套较为完整的最优控制理论体系。
该文将介绍最优控制理论中的经典方法。
1 变分法一个经典的例子是，曲线上的最速降线问题，在重力作用下一个粒子沿着该路径可以在最短时间从点A到达不直接在它底下的一点B[1]。
任务是在所有可能的曲线中确定一条，使得下降的时间达到最小。
这是一个求取泛函极值的问题。
泛函取极值的必要条件是泛函的变分为零。
若连续可微，在点达到极值，则泛函在处的变分等于零。
极小值原理很好地扩大了变分法的适用范围。
不仅可以用来求解函数U(t)不受约束或只受开集性约束的最优控制问题，而且也可以用来求解控制函数U(t)受到闭集性约束条件的最优控制问题。
这就意味着极小值原理放宽了对控制函数U(t)的要求。
极小值原理可以求解带有闭域约束的更加一般的最优控制问题，如最短的时间，最快的速度，最佳的利用，最短的路径等等。
在没有闭域约束的最优控制问题中时，变分法，极小值原理是等价等效的。
4 结语最优控制理论已经潜移默化地深深融入到了现代社会的发展中，在不久的将来仍然有广阔的发展前景。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
或
min f(x)
s.t. gi (x) 0, i 1,,l
h j (x) 0, j 1,, m
模型的普遍意义
(1) max F(x) 令 f(x) = －F(x) 变为 min f(x)
xS
xS
(2) Gi(x)0
令 gi(x)=－Gi(x)0
(3) l, m 可以为0
4、有约束最优化问题的变分法
现代最优化技术 （20世纪50年代）
1、近代科学技术与工业生产的发展
需要
2、电子计算机的出现与发展
dgxu
可能
14
§1.2 工业过程领域中的应用
1、工程最优设计 2、操作分析与制定计划 3、工程分析与数据处理
静态优化 （参数优化）
4、过程动态特性与最优控制方案的研究
例：f(x1,x2)=60－10x1－4x2+x12+x22－x1x2
0≤x1≤6
0≤x2≤8
x2
f=20 f=11
8
f=8
(8,6)
0
0 dgxu
6
(6,5)
x1
31
§1.3.3 约束条件与可行域
约束条件：自变量取值范围的限制
(可用等式或不等式表示)
gi (x) 0,
i=1,…, l
内点
hj(x)=0 , j=1,…, m
可行点：满足约束条件的点 可行域: 可行点组成的集合
S={x| gi (x) 0, i=1,2,…, l; hj(x)=0, j=1,2,…, m}
若存在等式约束，则可行点均为边界点
dgxu
S
边界点 外点
32
§1.3.4 最优化问题的数学模型
min f(x) xS
S ={x | gi(x)0, i=1,…, l ; hj(x) = 0, j=1,…, m}
r2ex
p r2cal r2exp
2
21
§1.2.4 过程动态特性与最优控制方案的研究
例1.2.6 管式反应器中温度最优分布问题：要求B的产率最大
A
L
A，B，C
A B C
反应速率方程为
dxA (l) dl
k01
exp
E1 RT
xA
dgxu
33
min f x 目标函数
s.t.
g j x 0 不等式约束
hi x 0 等式约束
称满足所有约束条件的向量 x为容许解，或可行解，或可 行点，全体容许点的集合称为容许集或可行集，记为 D 。
D {x | hi x 0, i 1,2, m, g j x 0,
dgxu
4
第一章 概 述
• 最优化问题 • 发展中的最优化技术 • 最优化技术的应用 • 最优化技术的基本概念
要点：二次型函数、恒定矩阵、目标函数、等值线、 约束条件、可行域、优化问题的数学模型、算法
dgxu
5
最优化问题
按一定标准在多个候选方案中选优
项
候选方案1
目 或
候选方案2
min F 或 max F
dgxu
25
设A为n阶对称矩阵
若对Rn中任意非零向量x，恒有f(x)=xTAx＞0，则称 f(x)为正定二次型，A为正定对称矩阵，记为A＞0。
恒 若对Rn中任意非零向量x，恒有f(x)=xTAx≥0，则称f(x) 定 为半正定二次型，A为半正定对称矩阵，记为A≥0。
矩 阵
若－A＞0，则称f(x)＝xTAx为负定二次型，A为负定
......
dgxu
18
例1.2.3 生产计划的最优化问题
某工厂生产A和B两种产品，它们需要经过三种设备的加工， 其工时如下表所示。设备I、II和III每天可使用的时间分别不超 过12、10和8小时。产品A和B的利润随市场的需求有所波动，如 果预测未来某个时期内A和B的利润分别为 4千元／吨和 3千元／ 吨，问在那个时期内，每天应安排产品A、B各多少吨，才能使工 厂获利最大？
工 程
• •
最优化技术
最优方案
问
•
题
候选方案n
dgxu
6
最优化控制技术 研究和解决最优化问题的学科
建立数学模型
实际问题的近似与抽象
数学关系式
方程 不等式 逻辑关系式
求最优解
模型分析 选方法 编程序 运算 评价
dgxu
物理定律 市场约束 工艺关系 ……
最优控制器设定
7
Three-Tank Cyanidation Plant
dgxu
8
Optimal control
dgxu
9
复杂有色冶金过程
dgxu
10
优化控制方案
dgxu
11
广义过程优化控制
dgxu
12
考虑市场机制的多目标优化控制
dgxu
13
§1.1 发展简史
经典最优化技术
1、欧几里德命题（古希腊，前300年）:
周长L＝constant Max 面积S＝？ 2、最短路线问题：30个省会城市旅游 3、微积分求极值（17、18世纪）
工业过程最优化及控制方法
主讲人：徐德刚
信息科学与工程学院
2012.11.20
dgxu
1
课程简介
课程名称：工业过程最优化及控制方法 Optimal Control Methods of Industry Process
性质：专业选修课 课时：32学时（课堂28学时，实验4学时） 任课老师：徐德刚 联系方式：民主楼112 电子邮箱：dgxu@
对称矩阵，记为A＜0。
若－A≥0，则称f(x)＝xTAx为半负定二次型，A为半负 定对称矩阵，记为A≤0。x为
不定二次型，A为不定对称矩阵。
dgxu
26
例1.3.1 验证 A=
5 -3 -3 5
是正定对称矩阵.
因为对任意的 x =[x1, x2]T 0，有
例1.2.4 非线性曲线拟合
R-K方程：
P
RT V b
a T 1/ 2V (V
b)
2
min L(a,b)
8 i1
Pi
RTi Vi bdgxu
Ti1
/
2Vi
a (Vi
b)
20
例1.2.5 甲醇合成反应动力学模型参数估值
CO+2H2 CO2+3H2
CH3OH CH3OH+H2O
dgxu
2
考核方式： 包括论文或大作业成绩及平时成绩两大部分：
论文或大作业成绩：70%
平时成绩：30% (考勤，实验)
注：三次考勤不到者，平时成绩记0分
dgxu
3
参考书
1.实用最优化方法 R.Fleter著，游兆永等译 天津科技翻译出版公司 2.非线性规划数值方法 袁亚湘 上海科学技术出版社 1995 3.非线性最优方法 席少霖 高等教育出版社 4.最优化方法 解文新，韩立兴等 天津大学出版社 2001 5.最优化方法 施光燕，董加礼 高等教育出版社 2001 6.工程优化方法及其应用 张可村等 西安交大出版社 2007 7.工程优化方法 陈卫东等 哈尔滨工程大学出版社 2006 8.实用最优化方法 唐焕文等 大连理工大学社 2004
动态优化
（函数优化）
dgxu
15
§1.2.1 工程最优设计
化工单元、流程结构、工艺条件的最优设计； 过程最佳操作参数的确定； 工业设备结构与尺寸的最优设计； 能量系统（如热交换网络）的最优集成； 工业企业的总体最优设计；
......
dgxu
16
例1.2.1 在某个化学反应器内，原料经过加热与加压进行化
j 1, 2, p, x Rn} 若 hi (x), g j (x) 是连续函数，则 D是闭集。
dgxu
34
在容许集中找一点 x*，使目标函数 f x在该点取最小值，即
满足：f x* min f x . s.t. g j x* 0. hi x 0的过程即为
无约束优化问题
单变量优化问题
有约束优化问题 单目标优化问题
多变量优化问题
多目标优化问题
dgxu
28
目标函数的几何图形
一元函数
f(x)
二元函数
x
多元函数：“ 超曲面”
dgxu
29
等值线 ～ 等高线（测绘，地形图） ～由具有相同目标函数值的自变量点连成的曲线
f(x) f(x)
x2
x1
dgxu
30
通过观察等高线函数值的分布，可以初步确定最优点的搜索方向
(l
)
dxB (l) dl
k01
exp
E1 RT
dgxxuA
(l)
k02
exp
E2 RT
xB
(l
)
22
求使反应器出口处目的产物B产率Y 最大的轴向温度分布T(l),
即 max Y[T (l)] max L dxB(l)dl 0 dl
dxB (l) dl
I
II
III
利润
A(x1) B(x2)
最多工作
3小时/吨 4小时/吨
12小时
3小时/吨 3小时/吨
10小时
4 小时/吨 2 小时/吨
8小时
4千元/吨 3千元/吨
解：总利润 max f＝4x1+3x2 （千元）