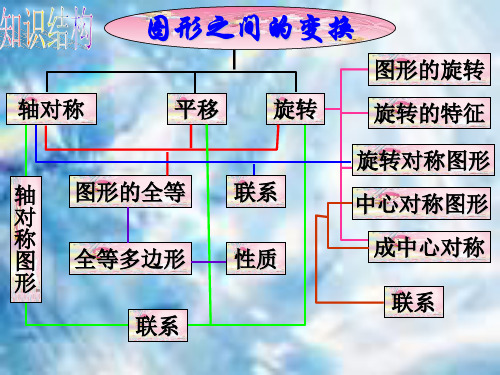
图形的构造
圆的构造及性质

圆的构造及性质圆是几何中常见且重要的图形之一,具有许多独特的性质和构造方法。
本文将介绍圆的构造及其性质,帮助读者更好地理解和应用圆形几何。
一、圆的构造方法1. 圆的定义:一个平面上的点到另一个固定点的距离保持不变,称这个固定距离为半径,将所有满足这个条件的点构成的图形称为圆。
2. 圆心和半径:在圆的构造中,首先需要确定圆心和半径。
圆心即为上述定义中提到的固定点,而半径则是指圆心到圆上任意一点的距离。
3. 圆的构造方法:- 利用半径和圆心:给定圆心和半径的情况下,可以使用直尺和圆规来画出一个确定的圆。
- 通过直径构造:直径是连接圆上任意两点并通过圆心的线段,利用直径可以轻松构造出一个圆。
- 切割法:利用圆规和直尺以及给定的弦长,可以逐步构造出一个圆。
二、圆的性质1. 圆心角和弧度:- 圆心角是指以圆心为顶点的角,其对应的弧度等于其所对应的弧长除以圆的半径。
- 圆心角的度数等于其对应的弧度乘以180°。
2. 弧和弧长:- 弧是圆上两点之间的曲线部分,可以通过两个端点来唯一确定。
- 弧长是指弧所对应的圆周上的长度,可以通过圆心角和半径来计算。
3. 切线和切点:- 切线是与圆相切且只有一个公共点的直线。
- 切点是切线与圆相交的点,切点与圆心之间的线段垂直于切线。
4. 弦和弦长:- 弦是圆上连接两点的线段。
- 弦长是指弦的长度,可以通过圆心角和半径来计算。
5. 正切线和切线长度:- 正切线是通过圆上一点并且垂直于半径的直线。
- 切线长度是正切线与圆的切点距离。
6. 同位角和异位角:- 同位角是指两个角分别位于两条平行线与一条直线所夹的锐角或钝角中,且两个角的位置相对应。
- 异位角是指两个角分别位于两条平行线与一条直线所夹的外角中,且两个角的位置相对应。
7. 弧的性质:- 同样弧长的圆心角相等。
- 弦长相等的弦对应的圆心角相等。
- 等弧长的弧所对应的圆心角相等。
8. 切线与半径的性质:- 切线与半径垂直于切点。
小学三年级数学---图形的构造
应角。
全等多边形的性质和判定
D
C D´ C´
A
A´
性质:
B
B´
全等多边形的对应边相等、对应角相等。
判定:
边、角分别相等的两个多边形全等。
注意:三角形是特殊的多边形。
把以上复习的内容抄写 一遍,少抄一个罚抄全 部内容10遍。
对折重合
直线方向、 对应线段平行 或在一条直线 按一定的角度、 对应点到对应 中心距离相等
旋转对称图形
定义:
一个图形绕着某一定 点旋转一定的角度 (00<旋转角<3600) 后能与自身重合,这 个图形就叫做旋转对 称图形。
这个点就叫做旋转中 心。
旋转的角度就叫旋转 角。
1
1
·
旋转对称图形是具有 旋转特征的特殊图形。
旋转对称图形不一定都是 轴对称图形,也不是所有 的轴对称图形都是旋转对 称图形。它们都是具有特 殊性质的图形。
一个图形绕着中心
点旋转1800后能与
11
自身重合,我们把这
11
种图形叫做中心对
·
·
称图形.这个点叫
做对称中心.
中心对称图形是旋转对称图形的一种特殊形式.
把一个图形绕着某一 点旋转1800,如果它 能够和另一个图形重 合,我们就说这两个
图形中每一点都绕着旋转
A 中心按同一旋转方向旋转 了同样大的角度,对应点
到旋转中心的距离相等,
B
对应线段相等,对应角相 等,图形的形状与大小都
没有发生变化。
轴对称、平移与旋转三种图形 变换的异同
相同点
不同点
轴对称 平移 旋转
1.对应线段 相等,对应角 相等,图形的 形状与大小 都没有发生 变化.
图案的构成形式

一、格律体构图 格律体构图是指以九宫格、米宇格或两种格子相结合作
骨式基础的构图。既具有结构严谨、和谐稳定的程式化特征 ,又具有骨式变化多样、不拘一格的情趣。
从二方连续的骨式结构我们可以看出,二方连续的基 本构成形式是线。无论是点、圆、长线、短线最终汇集而 成的都是带状的群线。群线的组合可聚集可分散,可交叉 可循环,这样才可以无限反复排列,形成带状图案。线的 魅力在于不论直线曲线都能给人的心理带来强烈的反应。 直线的干脆利落,曲线的波澜起伏都给人们带来视觉上的 享受。
图案的构成形式
单独纹样
对称纹样 均衡纹样
适合纹样
填充纹样 角隅纹样 边饰纹样
连续纹样
二方连续纹样 四方连续纹样
一、单独纹样
单独纹样是指没有外轮廓及骨格限制,可单独处理 、自由运用的一种装饰纹样。这种纹样的组织与周围其 他纹样无直接联系,但要注意外形完整、结构严谨,避 免松散零乱。单独纹样可以单独用作装饰,也可用作适 台纹样和连续纹样的单位纹样。作为图案的最基本形式 ,单独纹样从布局上分为对称式和均衡式两种形式。
二方连续的组织骨式变化极为丰富,一般可分为八种不 同的排列骨式.它的基本排列骨式可分为散点式、直立式、 倾斜式、波浪式、水平式、一整二破式、折线式、旋转式 等八种基本骨式。
设计过程中应注意其排列的韵律变化,疏密、大小、色 调等变化,期达到完整的视觉效果。
1、散点式 单位纹样一般是完整而独立的单独纹样.以散点的形式 分布开来,之间没有明显的连接物或连接线,简洁明快, 但易显呆板生硬。可以用两三个大小、繁简有别的单独纹 样组成单位纹样,产生一定的节奏感和韵律感,装饰效果 会更生动。
[小结] 1、图案的构成包括纹样组织和装饰构图两个部分。 2、图案的组织形式可分为单独纹样、适合纹样、连续纹样三大类。 3、单独纹样是指没有外轮廓及骨格限制,可单独处理、自由运用的一种 装饰纹样。 4、单独纹样从布局上分为对称式和均衡式两种形式。 5、对称式又称均齐式,可分为绝对对称和相对对称两种组织形式。 6、均衡式又称平衡式,它不受对称轴或对称点的限制,结构较自由。 7、适合纹样是将形态限制在一定形状的空间内,整体形象呈某种特定 轮廓的一种装饰纹样。 8、适合纹样从外形上可归纳为几何形、自然形和人造形三种形式。 9、适合纹样从内部布局上分对称和均衡两种形式, 10、适合纹样从组织类型应用上一般分为填充纹样、角隅纹样、边饰 纹样三种形式。
图形的初步认识知识点及线段习题

⎧⎨⎩⎧⎨⎩图形的初步认识一、本章的知识构造图一、立体图形与平面图形立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形平面图形:三角形、四边形、圆等。
主〔正〕视图---------从正面看2、几何体的三视图侧〔左、右〕视图-----从左〔右〕边看俯视图---------------从上面看〔1〕会判断简单物体〔直棱柱、圆柱、圆锥、球〕的三视图。
〔2〕能根据三视图描述根本几何体或实物原型。
3、立体图形的平面展开图〔1〕同一个立体图形按不同的方式展开,得到的平现图形不一样的。
〔2〕了解直棱柱、圆柱、圆锥、的平面展开图,能根据展开图判断和制作立体模型。
4、点、线、面、体〔1〕几何图形的组成点:线和线相交的地方是点,它是几何图形最根本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
〔2〕点动成线,线动成面,面动成体。
例1 〔1〕如图1所示,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的物体。
〔2〕如图2所示,写出图中各立体图形的名称。
图1图2解:〔1〕①与d类似,②与c类似,③与a类似,④与b类似。
〔2〕①圆柱,②五棱柱,③四棱锥,④长方体,⑤五棱锥。
例2 如图3所示,讲台上放着一本书,书上放着一个粉笔盒,指出右边三个平面图形分别是左边立体图形的哪个视图。
图3解:〔1〕左视图,〔2〕俯视图,〔3〕正视图练习1.以下图是一个由小立方体搭成的几何体由上而看得到的视图,小正方形中的数字表示该位置小立方块的个数,那么从正面看它的视图为〔〕3.如图,下面三个正方体的六个面按一样规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是〔〕A.蓝、绿、黑 B.绿、蓝、黑 C.绿、黑、蓝 D .蓝、黑、绿4.假设如下平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值。
5.一个物体从不同方向看的视图如下,画出该物体的立体图形。
例谈几何图形构造法

在几何中,构造法是使用规则或原则来绘制几何图形的方法。
下面是几个常见的构造法例子。
1 垂线构造法:在平面内给定一点和一条直线,从该点作垂线与该
直线的交点,就是所求的点。
2 垂足构造法:在平面内给定一点和一条直线,从该点作垂线与该
直线的交点,这个交点称作该点的垂足。
3 垂直平分线构造法:在平面内给定一点和一条直线,从该点作垂
线,并做该垂线的中垂线,这条中垂线称作该点的垂直平分线。
4 垂直于直线的平分线构造法:在平面内给定一点和一条直线,从
该点作垂线,并做该垂线的中垂线,这条中垂线垂直于给定的直线,称作该点的垂直于直线的平分线。
5 直线平分线构造法:在平面内给定一条直线和一个点,从该点作
该直线的平分线,并做该直线的中垂线,这条中垂线称作该点的直线平分线。
6 对称构造法:在平面内给定两点或两条直线,建立一条对称轴,
使得对称轴上的一侧和对称轴的对侧关于对称轴对称,这样就可以使用对称构造法来构造出许多几何图形。
7 图形复制构造法:在平面内给定一个图形,通过将图形复制并移
动到另一个位置来构造出新的图形。
8 线段构造法:在平面内给定两个点,连接这两个点就是所求的线
段。
9 圆构造法:在平面内给定一个点和一条直线,以该点为圆心,该
直线为圆的直径,连接两端点即为圆。
这些只是几何图形构造法的一小部分例子,在几何学中还有许多其他的构造法。
初中数学几何图形构造方法梳理

初中数学几何图形构造方法梳理几何图形构造方法梳理在初中数学学习中,几何图形构造是一个重要的部分,它涉及到直线、角度、三角形、四边形等各种图形的构造方法。
本文将梳理一些常见的初中数学几何图形构造方法,帮助学生更好地理解和掌握这些内容。
一、直线图形的构造方法1. 画线段:给定两个不同的点A和B,我们可以使用直尺在点A和B之间画一条直线段AB。
2. 画射线:给定一个起点A和一个方向,我们可以使用直尺在起点A开始,按照给定的方向延伸出一条射线。
3. 画平行线:给定一条直线L和一个点P,在点P处画一条与直线L平行的直线。
4. 画垂直线:给定一条直线L和一个点P,在点P处画一条与直线L垂直的直线。
二、角度的构造方法1. 画角:给定两条射线,将它们的起点重合,通过尺规作图的方法,可以构造出一个特定的角。
2. 以角的顶点为中心,以确定的角度为半径,画弧:给定一个角的顶点O和一个角度a,我们可以使用尺规作图的方法,在以O为中心,以a为半径的圆上选择一点P,然后连接OP,即可得到一个角为a的角。
3. 画平分线:给定一个角,我们可以使用尺规作图的方法,构造出这个角的平分线,即将这个角平分为两个相等的角。
4. 画垂线:给定一条直线L和一个点P,在点P处画一条与直线L垂直的直线。
三、三角形的构造方法1. 画等边三角形:给定一个边长,我们可以使用尺规作图的方法,构造一个边长相等的等边三角形。
2. 画等腰三角形:给定一个底边和两个底角,我们可以使用尺规作图的方法,构造一个具有底边和底角相等的等腰三角形。
3. 画直角三角形:给定一个直角,我们可以使用尺规作图的方法,在直角的一边上任选一点,然后以这个点为顶点,直角的两条边为另外两边,构造一个直角三角形。
4. 画任意三角形:给定三条边长a、b、c,我们可以使用尺规作图的方法,构造一个具有边长分别为a、b、c的任意三角形。
四、四边形的构造方法1. 画平行四边形:给定两条平行线L1和L2,以及一个点P,我们可以使用尺规作图的方法,在点P处作出一条与L1平行的线段,然后再以该线段为边作出一条与L2平行的线段,连接两个线段的两个端点,即可得到一个平行四边形。
巧妙构造图形解决数学问题

巧妙构造图形解决数学问题【摘要】在数学问题解决过程中,巧妙构造图形常常起着关键作用。
通过利用几何图形的特性,我们可以更轻松地解决复杂的数学难题。
形状的对称性可以帮助我们简化计算过程,提高解题效率。
通过观察图形的变换以及规律,我们能够更快地找出解题思路。
构造图形并用它们证明数学定理,不仅使证明过程更加清晰,也深化了我们对定理的理解。
通过图形解释抽象的数学概念,我们能够更直观地理解和应用这些概念。
巧妙构造图形可以帮助我们更好地理解和解决数学问题,是解决数学难题的有力工具。
在解决数学问题时,我们应该尝试从图形构造的角度入手,以提升解题效率和深化对数学问题的理解。
【关键词】巧妙构造图形解决数学问题、几何图形、对称性、图形变换、证明数学定理、抽象数学概念、直观理解、解决数学难题、工具、图形构造、数学问题、图形构造的角度。
1. 引言1.1 巧妙构造图形解决数学问题在数学领域,巧妙构造图形成为了一种常见的解决问题的方法。
通过利用几何图形的特性,我们可以更加直观地理解和解决数学难题。
图形在数学中扮演着重要的角色,它们能够帮助我们简化计算过程,找出规律,构造证明数学定理,解释抽象概念。
利用几何图形的特性解决数学难题是一种常见的方法。
在解决几何问题时,通过构造辅助图形,我们可以得到更多的信息,从而找到解题的突破口。
图形的直观性使得复杂的数学问题变得易于理解和解决。
利用形状的对称性也可以简化计算过程。
对称性是图形的重要特征,通过观察和利用图形的对称性,我们可以推导出一些结论,从而更快地解决数学问题。
利用图形的变换找出规律也是一种常见的方法。
通过对图形进行平移、旋转、反射等操作,我们可以发现一些隐藏的规律,从而推断出数学定理或结论。
巧妙构造图形可以帮助我们更直观地理解数学问题,图形构造是解决数学难题的有力工具。
在解决数学问题时,不妨尝试从图形构造的角度入手,这可能会为我们带来意想不到的启发和发现。
2. 正文2.1 利用几何图形的特性解决数学难题利用几何图形的特性解决数学难题是数学中常用的一种方法。
小学三年级数学---图形的构造
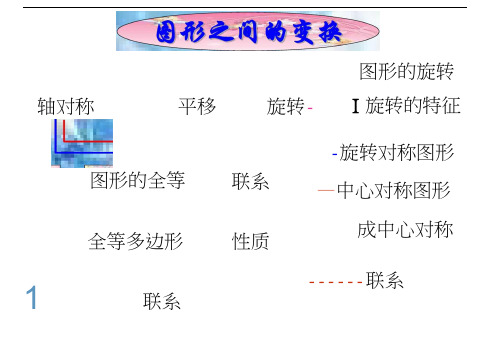
图形的旋转平移旋转-轴对称图形的全等联系I旋转的特征-旋转对称图形—中心对称图形全等多边形性质成中心对称------ 联系联系1把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,我们就说这两个图形关于这条直线对称。
如果一个图形能够沿着某一条直线对折重合,那么这个图形就叫轴对称图形。
轴对称图形是一个具有轴对称特征的图形。
o 1卜对应线段也可能在-条矽上, (如BB 中的B©与BC ) 对应点的连线埠可能在一条直线上。
(如圜中的BB 写CCJ <年卷罰特征:平移后的圏形与原来的圏形的对 相等 <对应角相等<与大"嘟没有发生变化。
注无圏形的形状 c当在一条直线上时,就不存在平行了。
在平面内,将一个图形绕一个定点-旋转一定的角度,这样的图形运动称为这个定点称为旋转中心,旋转的角度称为旋转角。
AA fB r图形中每一点都绕着旋转 A 中心按同一旋转方向旋转了同样大的角度,对应点 到旋转中心的距离相等. 对应线段相等,对应角相 等”图形的形状与大小都 没有发生变化@ 敎無的特征L T<ABBEE柚对稀、年卷鸟莪務三种樹形麦换的异同1 •对应线段檳等D阿JE箱相错图形的形状与大小都没有发生对折重合直线方向、对应线段平行或在一杂直经相同点■不同点是线-轴对称旋转对称图康F定心一个图形绕着某一定点旋转一定的角度(Q?v 旋转角<360°)%洁能与自身重合,这a个图形就叫做旋转对徹图形@这个点就叫做旋转中旋转对称图形是具有旋转的角度就叫旋转旋转特征的特殊图形。
旋角。
对称图形,也不是所有的轴对称图形都是旋转对称图形。
它们都是具有特殊性质的图形。
能与蠡齊们把迭談闕甌中心对葆图形点叫中心®[|中心对称图形是旋转对称图形的一种特殊形式. \- Hl fflll把一个图形绕着某一点旋转耀0叮如果它眞盘娜另一个图形重合:我们就说这两个IM形成中心对称。
这厂点叫做对称中心。
