统计学 第10章 方差分析与试验设计(2)
方差分析

第七章方差分析●了解方差分析的概念和作用;●掌握方差分析的基本原理和步骤;●掌握单向分组资料的方差分析;●掌握两向分组和系统分组资料的方差分析。
能力目标:●学会完全随机试验资料进行方差分析;●学会单向分组资料进行方差分析;●学会两向分组和系统分组资料进行方差分析。
对一个或两个样本进行平均数的假设测验,可以采用u测验或t测验来测定它们之间的差异显著性。
而当试验的样本数k≥3时,上述方法已不宜应用。
其原因是当k≥3时,就要进行k(k-1)/2次测验比较,不仅工作量大,而且精确度降低。
因此,对多个样本平均数的假设测验,需要采用一种更加适宜的统计方法,即方差分析法。
方差分析法是科学研究工作的一个十分重要的工具。
第一节方差分析基本原理方差分析(analysis of variance,ANOV A)就是将试验数据的总变异分解为来源于不同因素的相应变异,并作出数量估计,从而发现各个因素在总变异中所占的重要程度。
即将试验的总变异方差分解成各变因方差,并以其中误差方差作为和其他变因方差比较的标准,以推断其他变因所引起变异量是否真实的一种统计分析方法。
一、自由度与平方和分解方差是平方和除以自由度的商。
要将一个试验资料的总变异分解为各个变异来源的相应变异,首先将总平方和与总自由度分解为各个变异来源的相应部分。
因此,平方和与自由度的分解是方差分析的第一步骤。
下面以单因素完全随机试验设计的资料为例说起。
假设有k 个处理,每个处理有n 个观察值,则该试验资料共有nk 个观察值,其观察值的组成如表7-1。
表7-1中,i 代表资料中任一样本;j 代表样本中任一观测值;x ij 代表任一样本的任一观测值;T t 代表处理总和;t x 代表处理平均数;T 代表全部观测值总和;x 代表总平均数。
表7-1 每处理具n 个观测值的k 组数据的符号表处理观察值处理总和T t 处理平均t x 12 … j … n 1 x 11 x i 2 … x 1j … x 1n T t1 1t x 2 x 21 x i 2 … x 2j … x 2n T t2 2t x… … … … … … … … …i x i1 x i 2 … x ij … x in T ti ti x… … … … … … … … …kx k 1x k 2… x kj…x k nT tk tk xT =∑xx在表7-1中,总变异是nk 个观测值的变异,故其自由度v =nk -1,而其平方和SS T 则为: =T SS 221()nk ij x x x C -=-∑∑ (7-1)(7-1)式中的C 称为矫正数:22()x T C nknk==∑ (7-2) 产生总变异的原因可从两方面来分析:一是同一处理不同重复观测值的差异是由偶然因素影响造成的,即试验误差,又称组内变异;二是不同处理之间平均数的差异主要是由处理的不同效应所造成,称处理间变异,又称组间变异。
方差分析与试验设计

方差分析与试验设计方差分析是一种通过比较不同组之间的变差来判断均值差异是否显著的统计方法。
它通常用于试验设计中,用于分析不同处理组间的均值差异是否显著,从而评估不同处理的效果。
试验设计是科学研究中的一项重要工作,旨在通过科学的方法来验证研究假设。
试验设计涉及确定适当的样本大小、确定控制组和实验组、识别并控制潜在的影响因素等。
好的试验设计能够最大程度地减少偏差,提高实验的可靠性和准确性。
在方差分析中,我们通常将变量分为因素变量和响应变量。
因素变量是试验设置的处理组,例如不同的药物剂量或不同的施肥量。
响应变量是实验结果,可以是连续变量(如体重、收益等)或分类变量(如治疗成功与否)。
方差分析的基本原理是计算组内变差与组间变差之比,通过比较比值与理论的F分布来判断差异是否显著。
如果比值较大,则表明组间差异显著,即不同处理组的均值差异明显。
在进行方差分析时,我们需要满足一些前提条件,如独立性、正态性和方差齐性。
如果数据不符合这些条件,我们可以应用一些转换方法或进行非参数检验来处理。
完全随机设计是最简单的试验设计方法之一,它将实验对象随机分配到不同的处理组中。
这种设计方法适用于研究变量之间没有任何关系的情况,其优点是简单易行,但缺点是可能存在一些潜在的影响因素未被控制。
随机区组设计是一种常用的试验设计方法,它将实验对象分组后再随机分配到不同的处理组中。
这种设计方法能够控制部分潜在因素的影响,并提高实验的可靠性和准确性。
Latin square设计是一种更加复杂的试验设计方法,它在随机区组设计的基础上增加了均衡性。
Latin square设计通过交叉安排处理组和区块,使得每个处理出现在每个区块中,从而进一步控制潜在因素的影响。
除了上述常见的试验设计方法外,还有其他一些高级试验设计方法,如因子分析设计、回归分析设计等。
这些方法可以根据实验的具体要求来选择和应用。
综上所述,方差分析和试验设计是统计学中重要的概念和方法。
生物统计学习题集答案

.. 生物统计学习题集参考答案第一章概论一、填空1 变量按其性质可以分为 连续 变量和 非连续 变量。
2 样本统计数是总体 参数 的估计量。
3 生物统计学是研究生命过程中以样本来推断 总体 的一门学科。
4 生物统计学的基本内容包括_试验设置、统计分析_两大部分。
5 统计学的发展过程经历了 古典记录统计学、 近代描述统计学现代推断统计学 3个阶段。
6 生物学研究中,一般将样本容量 n大于等于 30称为大样本。
7 试验误差可以分为__随机误差 、系统误差 两类。
二、判断(-)1 对于有限总体不必用统计推断方法。
(-)2 资料的精确性高,其准确性也一定高。
(+) 3 在试验设计中,随机误差只能减少,而不可能完全消除。
(+)4 统计学上的试验误差,通常指随机误差。
三、名词解释样本:从总体中抽出的若干个体所构成的集合称为样本。
总体:具有相同的个体所构成的集合称为总体。
连续变量:是指在变量范围内可抽出某一范围的所有值。
非连续变量:也称离散型变量,表示变量数列中仅能取得固定数值并且通常是整数。
准确性:也称准确度指在调查或试验中某一试验指标或性状的观测值与真实值接近的程度。
精确性:也称精确度指在调查或试验中同一试验指标或性状的重复观测值彼此接近程度的大小。
第二章 试验资料的整理与特征数的计算一、填空1 1 资料按生物的性状特征可分为资料按生物的性状特征可分为资料按生物的性状特征可分为_________数量性状资料数量性状资料数量性状资料__变量和变量和______变量性变量性状资料状资料__变量。
2 2 直方图适合于表示直方图适合于表示直方图适合于表示______计量计量计量 、、 连续变量连续变量__资料的次数分布。
3 3 变量的分布具有两个明显基本特征,即变量的分布具有两个明显基本特征,即变量的分布具有两个明显基本特征,即__集中性集中性__和____离散性离散性离散性__。
4 4 反映变量集中性的特征数是反映变量集中性的特征数是反映变量集中性的特征数是______平均数平均数平均数______,反映变量离散性的特征,反映变量离散性的特征数是数是______变异数(标准差)变异数(标准差)变异数(标准差)__。
统计学习题及答案(完整) 2

第一部分计量资料的统计描述一、最佳选择题1、描述一组偏态分布资料的变异度,以()指标较好。
A、全距B、标准差C、变异系数D、四分位数间距E、方差2.用均数和标准差可以全面描述()资料的特征。
A.正偏态分布B.负偏态分布C.正态分布D.对称分布E.对数正态分布3.各观察值均加(或减)同一数后()。
A.均数不变,标准差改变B.均数改变,标准差不变C.两者均不变D.两者均改变E.以上都不对4.比较身高和体重两组数据变异度大小宜采用()。
A.变异系数B.方差C.极差D.标准差E.四分位数间距5.偏态分布宜用()描述其分布的集中趋势。
A.算术均数B.标准差C.中位数D.四分位数间距E.方差6.各观察值同乘以一个不等于0的常数后,()不变。
A.算术均数B.标准差C.几何均数D.中位数E.变异系数7.()分布的资料,均数等于中位数。
A.对数正态B.正偏态C.负偏态D.偏态E.正态8.对数正态分布是一种()分布。
(说明:设X变量经Y=lgX变换后服从正态分布,问X变量属何种分布?)A.正态B.近似正态C.左偏态D.右偏态E.对称9.最小组段无下限或最大组段无上限的频数分布资料,可用()描述其集中趋势。
A.均数B.标准差C.中位数D.四分位数间距E.几何均数10.血清学滴度资料最常用来表示其平均水平的指标是()。
A.算术平均数B.中位数C.几何均数D.变异系数E.标准差二、简答题1、对于一组近似正态分布的资料,除样本含量n 外,还可计算,S 和,问各说明什么?2、试述正态分布、标准正态分布及对数正态分布的某单位1999年正常成年女子血清联系和区别。
甘油三酯(mmol/L)测量结果3、说明频数分布表的用途。
4、变异系数的用途是什么?组段频数5、试述正态分布的面积分布规律。
0.6~ 10.7~ 3三、计算分析题0.8~ 91、根据1999年某地某单位的体检资料,116名正常0.9~ 13成年女子的血清甘油三酯(mmol/L)测量结果如右表, 1.0~ 19请据此资料: 1.1~ 25(1)描述集中趋势应选择何指标?并计算之。
医学统计学(方差分析)
各种变异的表示方法
04
列举存在的变异及意义
各种变异的表示方法
SS总 总 MS总
SS组内 组内 MS组内
SS组间 组间 MS组间
三者之间的关系: SS总= SS组内+ SS组间 总= 组内+ 组间
F=MS组间/MS组内
自由度: 组间=组数-1
组内=N-组数
通过这个公式计算出统计量F,查表求出对应的P值,与进行比较,以确定是否为小概率事件。
01
计算 C=(Σx) 2/N=(3309.5) 2/30=365093 SS总=Σx2-C=372974.87-365093=7881.87
α=0.05
02
SS组内=SS总-SS组间=7881.87-2384.026=5497.84
Ν总=N-1=29, Ν组间=k-1=2, Ν组内=N-k=30-3=27
159.0
111.0
115.0
合计Σxij
1160
921.5
1228
3309.5(Σx)
ni
11
9
10
30(N)
均数
105.45
102.39
122.80
110.32()
糖尿病
IGT
正常人
xij
106.5
Σ
Σxij2
123509.52
144.0
105.2
124.5
117.0
109.5
105.1
110.0
96.0
76.4
109.0
115.2
95.3
103.
95.3
第10章单因素方差分析

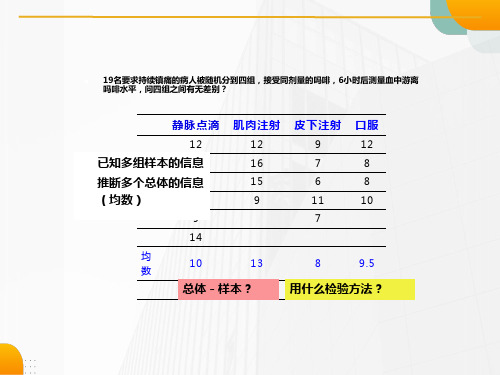
第10章单因素方差分析单因素方差分析(0ne-Way ANOV A),又称一维方差分析,它能够对单因素多个独立样本的均数进行比较,可以用10种检验方法对变量间的均数进行两两比较(即多重比较检验)并给出方差分析表,还可以作出5种类型图形(Type of plots)和2种均数图形(Means plot options)10.1 单因素方差分析的计量资料[例10—1] 某社区随机抽取了30名糖尿病患者、IGT异常人和正常人进行载脂蛋白(mg/dL)测定,结果示于表10—1。
试问3组人群的载脂蛋白测定结果含量是否相同?(倪宗瓒.卫生统计学.第4版,北京:人民卫生出版社,2001.50)本例是一个完全随机设计的单因素方差分析。
已建立SAS数据集文件并保存Sasuser.onewav4。
(1)进入SAS/Win(v8)系统,单击Solutions-Analysis-Analyst,得到分析家窗口。
(2)单击File-open By SAS Name—Sasuser-0neway4—0K,调入数据文件。
(3)在“分析家”窗口单击Statistics-ANOV A-One way ANOV A,得到图10—1所示对话框。
本例因变量(Dependent)为A(载脂蛋白),单击A—Dependent。
自变量(1ndependent):B(3种人的组别),单击B—Independent 。
图10.1 0ne—way ANOV A:0neway4(单因素方差分析)对话框(4)单击Tests按钮,得到图10—2所示对话框。
在此对话框的ANOV A(F—检验)选项中可进行如下设置。
Analysis of variance,方差分析。
Welch’s variance-weighted ANOV A,威尔奇方差—权重方差分析。
Tests for equal variance,相等方差检验,即方差齐性检验。
Barlett’s test,巴特尼特检验。
统计学第十章(方差分析)

第十章方差分析一、单项选择题:1.在方差分析中,( )反映的是样本数据与其组平均值的差异。
A.总离差平方和B.组间离差平方和C.抽样误差D.组内离差平方和2.∑∑=⎪⎪⎭⎫⎝⎛k1i 21-j ij n i i x x ——是( )。
A.组内平方和 B.组间平方和C.总离差平方和D.因素B 的离差平方和3.∑∑=⎪⎪⎭⎫⎝⎛k1i 21-j ij n i i x x ——是( )。
A.组内平方和 B.组间平方和 C.总离差平方和D.总方差4.单因素方差分析中,计算F 统计量,其分子与分母的自由度各位( )。
A.k ,nB.k ,n-kC.k-1,n-kD.n-k ,k-15.方差分析基本原理是( )首先提出的。
A.费雪B.皮尔逊C.泰勒D.凯特勒6.组间离差平方和反映的是( )。
A.抽样误差B.系统误差C.随机误差D.总误差7.组内离差平方和反映的是( )。
A.抽样误差B.系统误差C.随机误差D.总误差8.单因素方差分析的对立和假设是( )。
A.μμμk 21===B.差距不显著,,,μμμk 21C.不是全部相等,,,μμμk 21D.全部不相等,,,μμμk 219.单因素方差分析的零假设是( )。
A.μμμk 21===B.差距不显著,,,μμμk 21C.不是全部相等,,,μμμk 21D.全部不相等,,,μμμk 2110.在方差分析中,若F k -n 1,-k 05.0F )(>,则统计推论是( )。
A.各组间的总体均数不全相等B.各组间的总体均数都不相等C.各组间的样本均数都不相等D.各组间的总体方差不全相等11.为研究温度对菌种生产率的影响,将温度控制在三个水平上,则应该使用( )。
A.单因素方差分析B.双因素方差分析C.独立样本t 检验D.三因素方差分析12.为分析学历对收入的影响,调查了50个职工,按学历高低分成四组,使用单因素方差分析,则F 检验临界值为( )。
医学统计学:第十章 常用实验设计方法

分组结果 甲组:4、6、8、11、15号
乙组:3、5、9、12、14号
和检验、Ridit 分析、有序变量的 logistic 回归 模型和有序变量的对数线型模型等。 (2)若比较各样本不同等级构成情况,用 2 检验。
14
4.双向有序且属性不同资料的比较 (1)若分析两变量是否存在线性相关关系时,用 等级相关分析或 Pearson 列联系数。 (2)若分析两变量是否存在直线变化趋势时,用 线性趋势检验。 5.双向有序且属性相同资料的一致性检验,用
丙组:1、2、7、10、13号
10
11
(二)统计分析
数值变量资料
1.两样本比较 (1)小样本时 ①两样本来自正态分布总体且总 体方差相等时,用成组设计的两样本均数比较的
t 检验;②两样本来自非正态总体或总体方差不
等时,通过变量变换使数据呈正态或方差齐后,
再用成组设计的两样本均数比较的 t 检验;若仍 达不到 t 检验的应用条件时,可选用 t' 检验或成
18 1 10 13 17 2 0 3 8 15 7 4 19 12 5 14 9 11 6 16
动物编号 1 2 3 4 5 6 7 8 9 10 随机数字 1 2 0 3 8 7 4 5 9 6 组 别甲乙乙甲乙甲乙甲甲乙
分组结果 甲组:1、4、6、8、9号小鼠 乙组:2、3、5、7、10号小鼠
17
随机分组
1.1 2.1 3.1 4.1 5.1 6.1 7.1 8.1 9.1 10.1 小鼠编号
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.
考虑两个因子(可推广到多个因子 )的搭配实验设计称 为因子设计 该设计主要用于分析两个因子及其交互作用对实验结 果的影响 实验数据采用可重复双因子方差分析
� 可重复双因子方差分析
甲
因子设计 (例题分析)
实验空表:
乙
品种1
品种2
品种3
� 可重复双因子方差分析
甲 81 82 79 81 78 71 72 72 66 72 76 79 77 76 78
因子设计 因子设计
正交 设计 正交设计
可重复双因 可重复双因 素方差分析 素方差分析
多因素多水平极 多因素多水平极 差分析、方差分 差分析、方差分 析 析
10.4.1 实验设计的原则
1)随机原则: 2)对照原则 3)重复原则
应充分发挥具有各种知识结构和背景的人的作用, 群策群力,方可有效地提高实 验设计方案的均衡性。在实验设计的过程中要注意时间上的分配,只有在时间上 分配好了,才不会出现一段时间特别忙而一段时间特别闲的情况。 5) 弹性原则:所谓空格,指的是在时间分配图上留有空缺。适当的空缺 是非常必要的,只有这样才能富有弹性的实施实验计划,并不断地调整好自己的 实验进度。 6) 最经济原则: 不论什么实验,都有它的最优选择方案,这包括在资金 的使用上,也包括人力时间的损耗上,必要时可以预测一下自己实验的产出和投 入的比值,这个比值越大越好,当然是以你所拥有的实验条件作基础的。
(3) L12(211)
列号 1 试验号 1 2 3 4 5 6 7 8 9 10 11 12 1 1 1 1 1 1 2 2 2 2 2 2 1 1 1 2 2 2 1 1 1 2 2 2 1 1 2 1 2 2 2 2 1 2 1 1 1 1 2 2 1 2 2 1 2 1 2 1 1 1 2 2 2 1 1 2 2 1 1 2 2 3 4 5
2) 实验因素
�
3) 实验效应
�
10.4.2 完全随机化设计
) (completely randomized design design)
1.
“处理”被随机地指派给实验单元的一种设计
� �
“处理”是指可控制的因子的各个水平 )”是接受“处理”的 unit) “实验单元(experiment unit 对象或实体
全面试验设计的尴尬
�
多因素多水平若进行全面试验 ,则试验的规模将很 大 ,往往因试验条件的限制而难于实施 。
三因素三水平的试验,如果作全面试验,需作=27次。
正交试验设计就是安排多因素试验 、寻求最优 水平组合 的一种高效率试验设计方法。
正交试验设计是利用正交表来安排与分析多因素试验的 一种设计方法。
2.
3.
在实验性研究中,感兴趣的变量是明确规定 的,因此,研究中的一个或多个因子可以被控 制,使得数据可以按照因子如何影响变量来获 取 对完全随机化设计的数据采用 单因子方差分析
10.4.2 完全随机化设计
(例题分析)
�
【例】一家种业开发股份公司研究出3个新的小麦品 种:品种1、品种2、品种3。为分析不同品种对产量 的影响,需要选择一些地块,在每个地块种上不同品 种的小麦,然后获得产量数据进行分析。这一过程就 是实验设计的过程 这里的“小麦品种”就是实验因子或因子,品种1、 品种2、品种3就是因子的3个不同水平,称为处理
正交试验设计的基本特点
用部分试验来代替全面试验,通过对部 分试验结果的分析,了解全面试验的情 况。 � 它能通过部分试验找到最优水平组合 “均匀分散,齐整可比”
�
正交表
列号 试验号 1 2 3 4 1 1 1 2 2
“均匀分散,齐整可比”
ቤተ መጻሕፍቲ ባይዱ
正交表是正交试验设计的工具。 2 1 2 1 2 3 1 2 2 1
因子数 L4(23)
试验数
水平数
正交表
③
L4(23)表的效率
全因素全水平的实验做8次,正交实验做 4次.
L4(23)
实际试验次数
理论上全部试验的次数
正交表 (1)L4(23)
列号 1 试验号 1 2 3 4 1 1 2 2 1 2 1 2 1 2 2 1 2 3
正交表
(2) L8(27) 列号 1 试验号 1 2 3 4 5 6 7 8 1 1 1 1 2 2 2 2 2 1 1 2 2 1 1 2 2 3 1 1 2 2 2 2 1 1 4 1 2 1 2 1 2 1 2 5 1 2 1 2 2 1 2 1 6 1 2 2 1 1 2 2 1 7 1 2 2 1 2 1 1 2
完全随机化设计
(例题分析)
�
方差分析:
10.4.3 随机化区组设计
) (randomized block design design)
1.
2.
先按一定规则将实验单元划分为若干同质组,称 )” 为“区组(block block) 再将各种处理随机地指派给各个区组
�
�
3.
比如在上面的例子中,首先根据土壤的好坏分成几个 区组,假定分成4个区组:区组1、区组2、区组 3、 区组4,每个区组中有三个地块 在每个区组内的3个地块以抽签的方式决定所种的小 麦品种
第10章 方差分析与试验设计
10.1 方差分析引论 10.2 单因素方差分析 10.3 双因素方差分析
开课学院:机电工程学院 授课教师:何金成 联系方式: Stu_ex@
10.4 试验设计初步
学习目标
1. 2. 3. 4. 5. 6.
解释方差分析的概念 解释方差分析的基本思想和原理 掌握单因素方差分析的方法及应用 理解多重比较的意义 掌握双因素方差分析的方法及应用 掌握试验设计的基本原理和方法
10.4 试验设计初步
10.4.1 实验设计原则 10.4.2 完全随机化设计 10.4.3 随机化区组设计 10.4.4 因子设计 10.4.5 正交实验设计
试验设计与方差分析
试验设计 试验设计
完全 完全 随机化设计 随机化设计 单因素 单因素 方差分析 方差分析
随机化 随机化 区组设计 区组设计 无重复双因 无重复双因 素方差分析 素方差分析
正交表
2 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 3 1 2 3 4 2 1 4 3 3 4 1 2 4 3 2 1 4 1 2 3 4 3 4 1 2 4 3 2 1 2 1 4 3 5 1 2 3 4 4 3 2 1 2 1 4 3 3 4 1 2
(6)L25(56)
列号 1 试验号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5 2 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 3 1 2 3 4 5 2 3 4 5 1 3 4 5 1 2 4 5 1 2 3 5 1 2 3 4 4 1 2 3 4 5 3 4 5 1 2 5 1 2 3 4 2 3 4 5 1 4 5 1 2 3 5 1 2 3 4 5 4 5 1 2 3 2 3 4 5 1 5 1 2 3 4 3 4 5 1 2 6 1 2 3 4 5 5 1 2 3 4 4 5 1 2 3 3 4 5 1 2 2 3 4 5 1
(4)L9(34) 列号 1 试验号 1 2 3 4 5 6 7 8 9 1 1 1 2 2 2 3 3 3
正交表
2 1 2 3 1 2 3 1 2 3 3 1 2 3 2 3 1 3 1 2 4 1 2 3 3 1 2 2 3 1
(5) L16(45)
列号 试验号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4
�
最简单的正交表是L4(23),此外还有 L8(27) , L9(34) ,L16(45)等等。 L表示一张表,它的数字,有三层不 同的含义,以L4(23)为例加以说明。
正交表
①
L4(23)表的结构: 包括4行,3列,表中只出现1、2两个 反映水平的数字。
列数 L4(23)
行数
水平数
正交表
②
L4(23)表的用法 作4次试验,可以最多安排3个二水平 的因素(因子)
�
�
�
假定选取3个面积相同的地块,这里的 “地块”就是接受处 理的对象或实体,称为实验单元 将每个品种随机地指派给其中的一个地块,这一过程就 是随机化设计过程
完全随机化设计
(例题分析)
� 单因子方差分析
�
实验数据:
产量
小 麦 品 种 品种1 品种2 品种3 368 386 351 349 383 348 351 370 336 342 357 331
1.
感兴趣的因子有两个
�
如:小麦品种和施肥方式
�
假定有甲、乙两种施肥方式,这样 3 个小麦品种和两种施肥 方式的搭配共有 3×2=6种。如果我们选择 30 个地块进行实 验,每一种搭配可以做 5 次实验,也就是每个品种 ( 处理 ) 的 样本量为5,即相当于每个品种 (处理)重复做了5次实验
2.
3.
正交表
6 1 2 1 1 2 2 1 2 2 1 2 1 7 1 2 1 2 1 2 2 2 1 1 1 2 8 1 2 1 2 2 1 2 1 2 2 1 1 9 1 2 2 1 1 2 1 1 2 2 1 2 10 1 2 2 1 2 1 2 1 1 1 2 2 11 1 2 2 2 1 1 1 2 1 2 2 1
一、正交试验统计的基本思想
三因素三水平试验: 33 = 27
它是由试验因素的全部水平组合中,挑选部分有代表性的 水平组合进行试验的,通过对这部分试验结果的分析了解全面 试验的情况,找出最优的水平组合。 如果进行正交试验 设计,利用正交表 安排试验,对于三 因素三水平的试验 来说,需要作9次 试验,用“Δ”表 示,标在图中。 “均匀分散,齐整可比”
