趣味数学134：连续自然数立方和公式探源
立方和公式证明
立方和公式证明立方和公式是数学中一个很重要的公式，它表述为：$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$ 。
接下来，咱们就一起来证明这个公式。
咱们先从乘法运算开始，逐步推导。
\[\begin{align*}&(a + b)(a^2 - ab + b^2)\\=&a(a^2 - ab + b^2) + b(a^2 - ab + b^2)\\=&a^3 - a^2b + ab^2 + a^2b - ab^2 + b^3\\=&a^3 + b^3\end{align*}\]这样，就证明了立方和公式。
不过，这公式看起来简单，真要熟练掌握并且能灵活运用，那可得下一番功夫。
我想起之前教过的一个学生小明，那时候刚给他讲这个公式，他一脸迷茫，觉得这东西太抽象，怎么都理解不了。
我就给他举了个特别实在的例子。
我说：“小明啊，假设你有一堆边长为 a 的小正方体，你同桌有一堆边长为 b 的小正方体。
现在你们俩要把这些小正方体拼成一个大的长方体，那这个大长方体的体积怎么算呢？”小明皱着眉头想了半天，还是不太清楚。
我接着说：“那咱们就一步一步来，先看你这一堆小正方体，体积是不是$a^3$？你同桌那堆就是$b^3$，那把你们俩的合在一起，体积不就是$a^3 + b^3$嘛。
但换个角度想，把这两堆合起来，拼成的大长方体，长就是 a + b，宽是$a^2 - ab + b^2$，高是 1，那体积是不是就等于 (a + b)(a^2 - ab + b^2) ？所以，这两个式子肯定是相等的呀。
”小明听了，眼睛一下子亮了起来，好像突然开窍了，兴奋地说：“老师，我懂啦！”从那以后，小明对这个公式的理解特别深刻，做起相关的题目来也得心应手。
在数学的学习中，像立方和公式这样的知识点还有很多。
咱们不能死记硬背，得像这样通过具体的例子，真正理解公式背后的原理，这样才能举一反三，不管遇到什么样的题目，都能轻松应对。
自然数立方的规律研究
自然数立方的规律研究我喜欢数学，因为在数学王国里有许多有趣的规律。
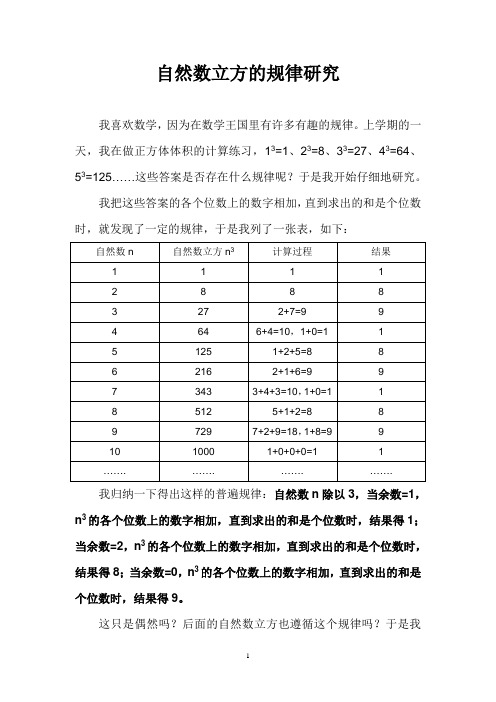
上学期的一天，我在做正方体体积的计算练习，13=1、23=8、33=27、43=64、53=125……这些答案是否存在什么规律呢？于是我开始仔细地研究。
我把这些答案的各个位数上的数字相加，直到求出的和是个位数时，就发现了一定的规律，于是我列了一张表，如下：我归纳一下得出这样的普遍规律：自然数n除以3，当余数=1，n3的各个位数上的数字相加，直到求出的和是个位数时，结果得1；当余数=2，n3的各个位数上的数字相加，直到求出的和是个位数时，结果得8；当余数=0，n3的各个位数上的数字相加，直到求出的和是个位数时，结果得9。
这只是偶然吗？后面的自然数立方也遵循这个规律吗？于是我开始验证我发现的规律。
验证结果让我太高兴了，我立刻把这个发现告诉全家人，大家纷纷拿笔来计算，最后也都符合我发现的这个规律。
我太自豪了，这可是我自己动脑筋思考和研究的结果，也许这还是个伟大的发现呢！妈妈笑着提醒我，“你再研究研究，为什么自然数立方会有这样的规律呢？”对呀，为什么呢？于是，我又进入了新一轮的苦思冥想，经过几番挫折，我都没有成功，后来我逐个突破，先从余数是0的开始，这个自然数n就是3的倍数，即n=3x（x=1，2，3，……），那么，n3=27x3=9×3x3，也就是说这类自然数的立方一定是9的倍数，9的倍数各个位数之和一定是9的倍数，所以将各个位数上的数字相加，直到求出的和是个位数时，结果一定是9。
啊哈，我越来越接近成功了！再来看，当余数是1时，这个自然数n就是3的倍数加1，即n=3x+1（x=0，1，2，3，……），那么，n3=（3x+1）3=27x3+27x2+9x+1=9（3x3+3x2+x）+1，也就是说这类自然数的立方一定是9的倍数再加1，那么结果一定是9+1=10，1+0=1，哈哈，第二关闯关成功！最后看，当余数是2时，这个自然数n就是3的倍数减1，即n=3x-1（x=1，2，3，……），那么，n3=（3x-1）3=27x3-27x2+9x-1=9（3x3-3x2+x）-1，也就是说这类自然数的立方一定是9的倍数再减1，那么结果一定是9-1=8，哈哈，第三关闯关成功！耶！我兴奋地大叫并跳了起来。
n个数立方和公式
n个数立方和公式在我们的数学世界里，有一个挺有意思的东西，叫做“n 个数立方和公式”。
这玩意儿听起来好像有点复杂，其实啊，要是搞明白了，还挺有趣的。
先来说说啥是立方。
一个数的立方，就是这个数自己乘自己两次。
比如说 2 的立方，那就是 2×2×2 = 8 。
那 n 个数的立方和公式到底是啥呢？它就是：1³ + 2³ + 3³ + …… + n³ = [n(n + 1) / 2]²。
咱们拿个具体的例子来瞅瞅。
比如说，咱们要算 1 到 5 这 5 个数的立方和。
那就是 1³ + 2³ + 3³ + 4³ + 5³。
按照公式来，先算 5×(5 + 1)÷ 2 = 15 ，15 的平方是 225 。
咱们再一个个算立方验证一下，1³ = 1 ，2³ = 8 ，3³ = 27 ，4³ = 64 ，5³ = 125 ，加起来 1 + 8 + 27 + 64 + 125 ，正好就是 225 ，你看，这公式准没错！我记得之前有一次，我给学生们讲这个公式。
有个小家伙，瞪着大眼睛，一脸迷茫地问我：“老师，这公式有啥用啊？”我笑了笑，跟他们说：“同学们，咱们来玩个游戏。
假设咱们要盖一个积木城堡，每一层的积木数量就按照这个立方和来，那咱们就能知道一共需要多少块积木啦。
”孩子们一听，来了兴趣，开始七嘴八舌地讨论起来。
有的说：“那要是盖个 10 层的城堡呢？”还有的说：“那要是 20 层呢？”我看着他们那积极的样子，心里特别欣慰。
然后带着他们一起用公式算了起来。
其实啊，这个公式在很多地方都能派上用场。
比如说在工程计算里，算一堆材料的体积；在物理问题中，计算一些有规律的物体的总量。
学习这个公式的过程，就像是在探索一个神秘的宝藏。
刚开始可能觉得有点难，但是一旦找到了窍门，那种成就感可太棒啦！希望同学们在今后的学习中，遇到类似的公式，别害怕，多琢磨琢磨，说不定就能发现其中的乐趣呢！总之，n 个数立方和公式虽然看起来有点复杂，但只要咱们用心去理解，多做几道题练练手，就能熟练掌握，让它成为我们解决数学问题的有力武器。
立方和公式及证明
⽴⽅和公式及证明⽴⽅和公式本⽂主要介绍了⽴⽅和公式的字母表达，语⾔表达，公式延伸，公式证明，⼏何验证等⽬录1字母表达2⽂字表达3公式证明4公式延伸5⼏何验证6关于因数展开1字母表达1.1⽴⽅和公式a^3+b^3 = (a+b) (a^2-ab+b^2）1.2⽴⽅差公式a^3-b^3=(a-b) (a^2+ab+b^2）a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)推导过程：a^3+b^3+c^3-3abc=(a^3+3a^2 b+3ab^2+b^3+c^3）-（3abc+3a^2 b+3ab^2）=[(a+b)^3+c^3]-3ab(a+b+c)=(a+b+c)(a^2+b^2+2ab-ac-bc+c^2）-3ab(a+b+c)=(a+b+c)(a^2+b^2+c^2+2ab-3ab-ac-bc)=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)2⽂字表达2.1⽴⽅和，差公式两数和（差），乘它们的平⽅和与它们的积的差（和），等于这两个数的⽴⽅和（差）2.23项⽴⽅和公式三数之和，乘它们的平⽅和与它们两两的积的差，等于这三个数的⽴⽅和减三数之积的三倍3公式证明⒈迭代法：我们知道：0次⽅和的求和公式ΣN^0=N 即1^0+2^0+...+n^0=n1次⽅和的求和公式ΣN^1=N(N+1）/2 即1^1+2^1+...+n^1=n(n+1）/22次⽅和的求和公式ΣN^2=N(N+1）（2N+1）/6 即1^2+2^2+…+n^2=n(n+1）（2n+1）/6——平⽅和公式，此公式可由同种⽅法得出，取公式（x+1）^3-x^3=3x^2+3x+1，迭代即得。
取公式：（X+1）^4-X^4=4×X^3+6×X^2+4×X+1系数可由杨辉三⾓形来确定那么就得出：（N+1）^4-N^4=4N^3+6N^2+4N+1…………⑴N^4-(N-1）^4=4(N-1）^3+6(N-1）^2+4(N-1）+1…………⑵（N-1）^4-(N-2）^4=4(N-2）^3+6(N-2）^2+4(N-2）+1…………⑶…………2^4-1^4=4×1^3+6×1^2+4×1+1…………（n).于是⑴+⑵+⑶+……+(n）有左边=(N+1）^4-1右边=4（1^3+2^3+3^3+……+N^3）+6（1^2+2^2+3^2+……+N^2）+4（1+2+3+……+N)+N所以呢把以上这已经证得的三个公式代⼊4（1^3+2^3+3^3+……+N^3）+6（1^2+2^2+3^2+……+N^2）+4（1+2+3+……+N)+ N=(N+1）^4-1得4（1^3+2^3+3^3+……+N^3）+N(N+1）（2N+1）+2N(N+1）+N=N^4+4N^3+6N^ 2+4N移项后得1^3+2^3+3^3+……+N^3=1/4 (N^4+4N^3+6N^2+4N-N-2N^2-2N-2N^3-3N^ 2-N)等号右侧合并同类项后得1^3+2^3+3^3+……+N^3=1/4 (N^4+2N^3+N^2）即1^3+2^3+3^3+……+N^3= 1/4 [N(N+1）]^2⼤功告成！⽴⽅和公式推导完毕1^3+2^3+3^3+……+N^3= 1/4 [N(N+1）]^22. 因式分解思想证明如下：a^3+b^3=a^3+a^2×b+b^3-a^2×b=a^2(a+b)-b(a^2-b^2）=a^2(a+b)-b(a+b)(a-b)=(a+b)[a^2-b(a-b)]=(a+b)(a^2-ab+b^2）4公式延伸正整数范围中1^3 + 2^3 + …… n^3 = [n (n+1）/ 2]^2=（1+2+……+n)^25⼏何验证透过绘⽴体的图像，也可验证⽴⽅和。
连数的奇妙世界找规律求和
连数的奇妙世界找规律求和连数的奇妙世界：找规律求和在数学的世界里，有许多有趣的数列，其中连数数列是一种非常特殊的数列。
所谓连数，就是从1开始，每一个数都比前一个数的立方大1。
下面，我们将一起探索连数数列的奇妙世界，并学会如何找到它的规律并求和。
1. 连数数列的前几项连数数列的前几项为：1, 2, 9, 28, 65, 126, ...2. 规律的发现我们首先可以观察到，连数数列的每一项都是前一项的立方再加1，即：第二项 = 1^3 + 1 = 2第三项 = 2^3 + 1 = 9第四项 = 3^3 + 1 = 28...这个规律可以用以下公式来表示：第n项 = (n-1)^3 + 13. 求和公式的推导现在我们来寻找连数数列的求和公式。
为了更好地理解，我们将连数数列的前几项相加，看看是否能够找到规律：1 +2 + 9 + 28 + 65 + 126 + ...我们可以将每一项拆分成一个立方数和一个常数的和：(1^3 + 1) + (2^3 + 1) + (3^3 + 1) + (4^3 + 1) + (5^3 + 1) + ...再将括号内的项展开：(1^3 + 2^3 + 3^3 + 4^3 + 5^3 + ...) + (1 + 1 + 1 + 1 + 1 + ...)我们可以发现，第一个括号内的部分就是立方数的求和公式，即：1^3 + 2^3 + 3^3 + 4^3 + 5^3 + ... = (1 + 2 + 3 + 4 + 5 + ...)^2而第二个括号内的部分，就是一个常数项与无限个1的和，它的值为无限大。
因此，连数数列的和可以表示为：1 +2 + 9 + 28 + 65 + 126 + ... = (1 + 2 +3 +4 +5 + ...)^2 + ∞从数学上来讲，无限大是无法精确表示的，但我们可以看出，连数数列的和是一个无限的值。
4. 结论通过以上的探索，我们可以总结出连数数列的规律和求和方式：规律：连数数列的每一项等于前一项的立方再加1。
连续自然数平方和公式推导
连续自然数平方和公式推导推导连续自然数数平方和公式有多种方法，今天我们主要用代数法和三角形数阵图法来推导连续自然数求和公式。
代数法推导过程：用代数法推导连续自然数求和公式，我们需要知道以下两个公式。
（1）连续自然数求和公式：这个公式很容易可以证明，就不再赘述。
(2)整数列项公式：对于这个公式，我们可以对每一项作如下拆分。
比如3✖️4=（3✖️4✖️5-2✖️3✖️4）➗33✖️4后面加一个因数5扩大5倍，前面加一个因数2扩大2倍，作减法后扩大3倍，因此后面除以3。
然后把每一项都作上述拆分并相加，相加后几乎所有项都可以抵消，只剩最小的第一项和最大的最后一项，因为第一项是0✖️1✖️2=0，因此省略。
得如上公式形式。
上述从1✖️2开始的整数列项如果用语言表述，就是最后一项后边添一项，然后再除以3.（3）推导过程：把每个平方数拆为两数相乘形式，并把其中一个因数写成一个数减1的形式，或一个数加1的形式。
比如3✖️3=3✖️（4-1）或3✖️3=3✖️（2+1）。
这两种形式选一种即可。
我们选择相减，拆分后如下。
1×(2-1)+2×(3-1)+3×(4-1)+…+n×[(n+1)-1]然后再把括号展开变为如下形式1×2+2×3+3×4+…+n(n+1)-(1+2+3+4+…+ n)然后按照上面所讲的整数裂项公式和连续自然数求和公式求得结果如下最后通分相减得出公式：这个就是连续自然数求和公式的结果数阵图法推导过程看如下三角形数阵图这个数阵图每一行的和刚好是该行数字的平方，比如倒数第2行，2个2就是2的平方。
因此这个数阵图的所有数字和就是从1开始的连续自然数平方和。
下面我们对数阵图进行变形这三个数阵图的数字一样，只是排列方式不一样，你会发现这三个数阵相同位置的三个数字和都是2n+1,因此这三个数阵图的所有数字和是：(1+2+3+…+n)×(2n+1)。
立方和与立方差公式的推导
立方和与立方差公式的推导立方和与立方差公式是数学中常见的两个公式，用于计算数的立方和和立方差。
它们在代数运算和数学推导中有着重要的应用。
我们来看立方和公式的推导。
假设有连续的n个数，分别为a, a+1, a+2, ..., a+(n-1)。
它们的立方和可以表示为S1= (a^3 + (a+1)^3 + (a+2)^3 + ... + (a+(n-1))^3)。
为了推导立方和公式，我们可以先观察前几个立方和的数列，然后找出其中的规律。
当n=1时，立方和为a^3；当n=2时，立方和为(a^3 + (a+1)^3)；当n=3时，立方和为(a^3 + (a+1)^3 + (a+2)^3)。
根据这个规律，我们可以猜测立方和公式的一般形式。
接下来，我们来进行数学归纳法证明，以验证我们的猜测。
首先，当n=1时，立方和为a^3，符合我们的猜测。
假设当n=k时，立方和公式成立，即S1= (a^3 + (a+1)^3 + (a+2)^3 + ... + (a+(k-1))^3)。
那么当n=k+1时，立方和为S2= (a^3 + (a+1)^3 + (a+2)^3 + ... + (a+(k-1))^3 + (a+k)^3)。
我们可以将S2拆分为S1和(a+k)^3两部分，即S2= S1 + (a+k)^3。
根据归纳假设，S1可以用立方和公式表示，所以我们只需要将(a+k)^3加到S1中即可。
我们展开(a+k)^3的式子，可以得到(a+k)^3=a^3 + 3a^2k + 3ak^2 + k^3。
将这个式子代入S2中，可以得到S2= (a^3 + (a+1)^3 + (a+2)^3 + ... + (a+(k-1))^3) +(a^3 + 3a^2k + 3ak^2 + k^3)。
通过整理和合并项，我们可以得到S2的简化形式，即S2= ((k+1)a^3 + 3a^2(k+1)(k/2) + 3a(k+1)(k/2)^2 + (k+1)^3(k/2)^3)。
自然数立方和公式的多种推导方法
自然数立方和公式的多种推导方法作者：刘东亮来源：《读写算·教研版》2014年第22期摘;;要：一题多解是培养学生发散思维的重要途径，能够很好地体现学习过程中的自主探究与合作学习过程，本文探究了自然数立方和公式的多种推导方法，从不同角度分析问题，找出事物间的内在本质和联系，从而提高学生分析问题、解决问题的能力。
关键词：自然数立方和;裂项法;倒序相加法;组合数;数列中图分类号：G658;;;;;;;;;;;;;;;;;;;文献标识码：B;;;;;;;;;;;;;;;文章编号：1002-7661（2014）22-109-02一、预备知识我们已经熟知公式如下：方法一、恒等式变形相消法上面各式相加，得方法二、配凑函数相消法上面各式相加，得方法三、奇数列分组法已知奇数列：1，3，5，7，9，11，13，15，17，……按如下方式分组（每行为一组）：13，57，9，1113，15，17，19……;;……;……方法四、倒序相加法设：（1）+（2）得，方法五、裂项相消法方法六、构造“三角”数列法的和。
按照每列一组的方式求和，得方法七、组合数配凑法先证明以下式子成立：三、结束语以上是给出了自然数立方和公式的7种推导方法，当然，我们还有更多的方法，比如图表法、数学归纳法、行列式法等。
自然数高次幂的求和问题是由著名的数学家雅克布.贝努利首先解决的。
我们有些方法可以推广到对自然数高次幂求和推导。
从不同的角度思考问题的本质，抓住事物的内在联系，从而对培养学生的发散思维有重大意义。
参考文献：[1];陈科钧.林;;雅，腾思媛.裂项法的运用探索[J].中国科技博览，2010（21）：213-214.[2];王;;媛.数列求和的常用方法.[J].读写算：教育教学研究.2011：（（4）：95-97.[3];袁;;桐.金立建.新编高中数学大观[M].南京：南京大学出版社.1995.[4];葛;;军.涂荣豹.初等数学研究教程[M].江苏教育出版社.2009.7.[5];王竹青。
推导立方和公式
推导立方和公式推导立方和公式在数学中，推导立方和公式是一种常见的数学方法，用于求解立方和的公式。
本文将针对这个话题进行详细介绍和解释。
立方和的定义首先，我们来回顾一下立方和的定义。
立方和指的是将一系列连续整数的立方相加的结果。
比如，1的立方加2的立方加3的立方，以此类推。
立方和的数学符号立方和的数学符号通常用大写字母Sigma（Σ）表示，下面是立方和的一般表示形式：Σn^3 = 1^3 + 2^3 + 3^3 + … + n^3其中，n表示整数的范围。
例如，当n为4时，立方和的公式可以表示为：Σn^3 = 1^3 + 2^3 + 3^3 + 4^3推导立方和的公式现在，我们来看一下推导立方和的公式的具体步骤。
步骤1：将立方和的公式展开，展开后的式子如下：Σn^3 = 1^3 + 2^3 + 3^3 + … + (n-1)^3 + n^3步骤2：利用立方的求和公式，将上述展开式化简为：Σn^3 = (n*(n+1)/2)^2这就是立方和的公式。
举例说明为了更好地理解立方和的公式，我们来举个具体的例子。
假设要计算1的立方加2的立方加3的立方的和，即Σn^3，其中n的范围为3。
按照立方和的公式，我们有：Σn^3 = (3*(3+1)/2)^2化简后，得到：Σn^3 = (3*4/2)^2 = 6^2 = 36所以，1的立方加2的立方加3的立方的和为36。
总结通过上述步骤，我们可以推导出立方和的公式，并且通过具体例子来说明。
推导立方和的公式在数学计算中非常常用，能够简化计算过程，提高效率。
希望本文能够帮助读者更好地理解和应用立方和的公式。
推导立方和的公式的证明在上一节中，我们介绍了推导立方和的公式的步骤和一个具体的例子。
在本节中，我们将给出推导立方和公式的证明过程。
证明：我们需要证明下面的等式成立：Σn^3 = (n*(n+1)/2)^2我们可以使用数学归纳法来证明这个等式。
假设对于任意正整数n，等式成立。
立方和公式和立方差公式记忆口诀
立方和公式和立方差公式记忆口诀立方和公式与立方差公式记忆口诀各位朋友，今天咱们来聊聊数学里的两个小宝贝——立方和公式和立方差公式。
这两个公式可是数学界的“老熟人”，但很多人可能还是一脸懵，不知道它们长啥样，更别提怎么用啦。
别急，跟着我一起，咱们轻松搞定这两个公式，让数学不再难！让我们来认识一下立方和公式。
这个公式就像是数学里的“万能钥匙”，无论遇到什么形状的箱子，都能轻松打开。
它告诉我们，当一个数的立方加或减另一个数的立方时，结果是多少呢？简单说，就是将两个数分别开立方后相加或相减。
举个例子，如果有一个数是2，还有一个数是3，那么2的立方加上3的立方等于多少呢？答案是17。
这是因为2的立方是8，3的立方是27，两者相加正好是35，也就是17。
是不是感觉一下子就明白了？接下来，我们来聊聊立方差公式。
这个公式就像是数学里的“隐形翅膀”，让我们在解决复杂问题时如鱼得水。
它告诉我们，当一个数的立方减去另一个数的立方时，结果是多少呢？同样地，我们可以用数字来举例说明。
比如说，如果有一个数是4，还有一个数是5，那么4的立方减去5的立方等于多少呢？答案是-1。
这是因为4的立方是64，5的立方是125，两者相减正好是-61，也就是-1。
是不是感觉像是在数星星一样，一清二楚？现在，咱们来点不一样的，用点俏皮话来记这些公式。
想象一下，你面前摆着一堆数学题，就像是一个迷宫，每个题目都像是一只怪兽，让你头疼不已。
但是，有了立方和公式和立方差公式这两个小助手，你就不再是那个孤军奋战的勇士了。
因为这两个公式就像是你的私人教练，随时为你排忧解难。
比如，当你遇到一个难题：“一个数的平方加上它的立方等于多少？”不用愁，告诉你吧，答案就是那个数。
因为一个数的平方就是它的平方根乘以它自己，而这个数的平方加上它的立方，就等于那个数的平方加上它的立方根再乘以它自己。
所以，只要你知道那个数的平方根是多少，就可以直接计算出来了。
是不是感觉就像是找到了宝藏一样，兴奋不已？还有啊，当你遇到一个难题：“一个数的立方减去它的平方等于多少？”不用怕，告诉你吧，答案也是那个数。
趣味数学134：连续自然数立方和公式探源
连续自然数立方和公式探源前面，在“有趣的图形数”和“求连续自然数立方和的公式”两篇文章中，曾经两次推导过求连续自然数立方和的公式：13＋23＋33＋…＋n3＝[n(n＋1)/2]2一次用的是“图形法”，一次用的是“列表法”。
其实，早在公元100年前后，毕达哥拉斯学派的继承人尼科马霍斯，在他的著作《算术入门》中就曾经用非常简单的方法推导过这个公式。
现在，让我们按照他的思路，重复一下这个公式的推导过程。
过程大体上是这样的：首先，从奇数列的一个性质入手。
奇数列1，3，5，7，9，11，13，…有一个性质，很容易验证：1＝133＋5＝237＋9＋11＝3313＋15＋17＋19＝4321＋23＋25＋27＋29＝53……请你自上而下仔细观察这一系列等式的左端：第1个等式左端，结束于第1个奇数；第2个等式左端，结束于第3个奇数；第3个等式左端，结束于第6个奇数；第4个等式左端，结束于第10个奇数；第5个等式左端，结束于第15个奇数；……结果发现，这些奇数的序数1，3，6，10，15，…原来是“三角形数”，它的每一项等于从1开始的连续自然数的和。
第1项是1，第2项是1＋2＝3，第3项是1＋2＋3＝6，第4项是1＋2＋3＋4＝10，第5项是1＋2＋3＋4＋5＝15，……第n项是1＋2＋3＋…＋n＝n(n＋1)/2。
即，第n个等式左端，结束于第n(n＋1)/2个奇数。
然后，对上面这一系列等式的左右两端，分别求和：右端是连续自然数的立方和13＋23＋33＋…＋n3。
左端是连续奇数的和。
我们知道，求连续奇数的和，求到第几个奇数，就等于第几个奇数的平方。
现在，求到第n(n＋1)/2个奇数，当然等于[n(n＋1)/2]2。
这样就得到求连续自然数立方和的公式：13＋23＋33＋…＋n3＝[n(n＋1)/2]2这种方法思路清晰论证简单。
尼科马霍斯之所以能够想到这个方法，显然跟毕达哥拉斯学派对图形数的宠爱有关。
图形数是自然数的形象化，自然数是众数之源，自然数真是一个取之不尽用之不竭的宝藏。
立方和公式和立方差公式记忆口诀
立方和公式和立方差公式记忆口诀你知道吗？在咱们的数学世界里，有些公式就像是老友一样，虽然不经常见面，但每次一见面总能给你惊喜。
比如那个立方和公式和立方差公式，它们就像是两个好朋友，总是在你最需要的时候出现。
首先来说说立方和公式吧。
这个公式就像是你的朋友突然问你：“我能不能和你一
起出去玩？”你说：“当然可以啊，但是我得先算出我们这次旅行要花多少钱。
”然后你就用立方和公式来算出了结果。
你知道这个公式怎么来的吗？其实就是把三个数加起来，然后除以2。
这样算出来的结果就是这三个数的平均值了。
再来说说立方差公式吧。
这个公式就像是你的朋友突然问你：“我最近有点烦心事，你能帮我分析一下吗？”你说：“当然可以，不过你得先告诉我具体是什么问题。
”然后你的朋友就用立方差公式来分析，最后得出了结论。
你知道这个公式是怎么来的吗？其实就是把三个数相减，然后除以3。
这样算出来的结果就是这三个数的差值了。
这两个公式在生活中的应用可是超级广泛呢！比如说，你在超市买东西时，想要知道买三样东西需要多少钱，你就可以用立方和公式来计算；或者你想知道你的朋友最近的心情如何，也可以用立方差公式来分析。
怎么才能记住这两个公式呢？其实很简单，只需要把它们编成一个口诀就可以了。
口诀是这样的：“立方和公式：三个数加在一起除以2，等于它们的平均数。
”而立方差
公式则是：“三个数相减再除以3，等于它们的差值。
”这样一来，你就能轻松地记住这
两个公式啦！
关于立方和公式和立方差公式的记忆口诀就介绍到这里啦。
希望这些小技巧能帮助你更好地掌握这两个公式哦！。
奥数立方和计算公式
奥数立方和计算公式在数学中，奥数立方和是一种常见的数学问题，它要求我们计算一系列连续整数的立方和。
这个问题既有一定的难度，又有一定的趣味性，因此备受学生和数学爱好者的喜爱。
在本文中，我们将介绍奥数立方和的计算公式，并通过实例演示如何应用这个公式来解决具体问题。
奥数立方和的计算公式可以用来求解一系列连续整数的立方和，其数学表达式为：S = (1^3 + 2^3 + 3^3 + ... + n^3) = (1 + 2 + 3 + ... + n)^2。
其中，S表示连续整数的立方和，n表示整数的个数。
这个公式的推导过程相对复杂，我们在这里不做详细展开，只需要记住这个公式即可。
接下来，我们通过一个具体的例子来演示如何应用这个公式来计算奥数立方和。
假设我们要计算前5个连续整数的立方和，即1^3 + 2^3 + 3^3 + 4^3 + 5^3。
根据奥数立方和的计算公式，我们可以将这个问题转化为计算前5个连续整数的和，然后再将结果的平方。
因此，我们首先计算前5个连续整数的和：1 +2 +3 +4 +5 = 15。
然后将结果的平方：15^2 = 225。
因此，前5个连续整数的立方和为225。
通过这个例子，我们可以看到奥数立方和的计算公式是非常简单有效的。
除了直接使用奥数立方和的计算公式外，我们还可以通过一些技巧来简化计算过程。
例如，我们可以利用数学归纳法来证明奥数立方和的计算公式，从而减少计算的复杂度。
此外，我们还可以利用数学软件来辅助计算，提高计算的效率和准确性。
总之，奥数立方和是一个非常有趣的数学问题，它不仅考验了我们的数学能力，还锻炼了我们的逻辑思维能力。
通过掌握奥数立方和的计算公式，并结合一些技巧和工具，我们可以更加轻松地解决这类问题。
希望本文对您有所帮助，谢谢阅读！。
立方和公式和立方差公式记忆口诀
立方和公式和立方差公式记忆口诀立方和公式和立方差公式，这两个听起来就让人头大的概念，其实是数学里最基础的运算之一。
不过别急，咱们今天就来聊聊怎么轻松记起来，让这两个公式在脑海中生根发芽。
首先得说，立方和公式嘛，就是求三个数相加或者相乘的结果是多少。
想象一下，如果你有三个苹果，再给你两个苹果，总共有几个？是不是直接加起来就是五个苹果了？这就像是“一加二等于三”，简单明了。
而立方和呢，就是“一个数的三次方加上另一个数的三次方等于第三个数的三次方”。
比如，2的三次方加上3的三次方，结果是10，也就是5的三次方。
这个记忆口诀可以变成：“一个数的三次方加另一个数的三次方，等于第三个数的三次方。
”再来说说立方差公式，这可是解决各种实际问题的小能手哦！它说的是两个数的三次方之差。
比如，4和5的三次方差是什么？就是(4^3 5^3) = (64 125) = -61。
这就像是你和朋友比赛跑步，你跑得快一点，他就跑慢一点，最后你们的差距就是61米。
这个记忆口诀可以变成：“两个数的三次方相减，结果就是第三个数的三次方。
”怎么样，是不是感觉一下子就记住了？其实，这些口诀都是用我们日常生活中的例子来形象地解释的，比如“一个数的三次方加另一个数的三次方，就等于第三个数的三次方”就像是两个人打架，一个人先动手，另一个人后动手，最后两个人打成平手，这就是“一个数的三次方加另一个数的三次方，就等于第三个数的三次方”。
所以啊，无论是立方和公式还是立方差公式，只要我们用心去记，再加上一些生活化的例子，就一定能够牢牢掌握住它们。
这样一来，不管是在学校考试还是工作中遇到难题，都能够迎刃而解了。
当然啦，除了口诀记忆法外，我们还可以通过做题、总结规律等方式来加深理解。
比如说，做多了练习题就会发现，当一个数是另一个数的三倍时，它们的立方和总是等于那个数的四次方。
这是因为任何数乘以自己一次，得到的是它本身；任何数乘以自己两次，得到的是它的平方；任何数乘以自己三次，得到的是它的立方。
立方累加求和公式
立方指数为3的乘方运算即表示三个相同数的乘积，也叫三次方。三个相同的数相乘，叫做这个数的立方。如5×5×5叫做5的立方，记做5。量词，用于体积，一般指立方米。在图形方面，立方是测量物体体积的，如立方米、立方分米、立方厘米等常用单位。
数学立方和公式
数学立方和公式在数学的广阔天地中，有许多奇妙而重要的公式，立方和公式便是其中之一。
它就像是一把神奇的钥匙，能够帮助我们打开解决一系列数学问题的大门。
首先，让我们来明确一下立方和公式到底是什么。
立方和公式表述为：＄a^3 ＋ b^3 ＝（a ＋ b)（a^2 ab ＋ b^2)＄。
为了更好地理解这个公式，我们不妨通过一些具体的例子来感受一下它的魅力。
假设我们要计算$2^3 ＋ 3^3$，按照常规方法，我们分别计算出$2^3 ＝ 8$，＄3^3 ＝ 27$，然后相加得到$8 ＋ 27 ＝ 35$。
但如果运用立方和公式，我们令$a ＝ 2$，＄b ＝ 3$，则：＼＼begin{align}2^3 ＋ 3^3&＝（2 ＋ 3)（2^2 2×3 ＋ 3^2)＼＼＆＝5×（4 6 ＋ 9)＼＼＆＝5×7\＼＆＝35＼end{align}＼可以看到，结果是一致的，而且使用公式计算有时会更加简便快捷。
那么，这个公式是怎么推导出来的呢？让我们一起来探究一下。
我们从乘法分配律开始：＼＼begin{align}（a ＋ b)（a^2 ab ＋ b^2)＆＝a×（a^2 ab ＋ b^2) ＋ b×（a^2 ab ＋b^2)＼＼＆＝a^3 a^2b ＋ ab^2 ＋ a^2b ab^2 ＋ b^3\＼＆＝a^3 ＋ b^3＼end{align}＼经过这样一步步的推导，立方和公式就清晰地呈现在我们面前了。
立方和公式在数学中的应用非常广泛。
在代数运算中，它可以帮助我们简化复杂的计算，提高解题的效率。
比如，当我们遇到形如$x^3＋ y^3$的式子时，就可以直接运用公式进行变形和计算。
在几何方面，立方和公式也有着重要的意义。
比如在计算立方体体积的组合问题时，它就能发挥很大的作用。
此外，立方和公式还是进一步学习更高深数学知识的基础。
比如在数学分析、高等代数等课程中，都会经常用到这个公式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
连续自然数立方和公式探源
前面，在“有趣的图形数”和“求连续自然数立方和的公式”两篇文章中，曾经两次推导过求连续自然数立方和的公式：
13＋23＋33＋…＋n3＝[n(n＋1)/2]2
一次用的是“图形法”，一次用的是“列表法”。
其实，早在公元100年前后，毕达哥拉斯学派的继承人尼科马霍斯，在他的著作《算术入门》中就曾经用非常简单的方法推导过这个公式。
现在，让我们按照他的思路，重复一下这个公式的推导过程。
过程大体上是这样的：
首先，从奇数列的一个性质入手。
奇数列1，3，5，7，9，11，13，…有一个性质，很容易验证：
1＝13
3＋5＝23
7＋9＋11＝33
13＋15＋17＋19＝43
21＋23＋25＋27＋29＝53
……
请你自上而下仔细观察这一系列等式的左端：
第1个等式左端，结束于第1个奇数；
第2个等式左端，结束于第3个奇数；
第3个等式左端，结束于第6个奇数；
第4个等式左端，结束于第10个奇数；
第5个等式左端，结束于第15个奇数；
……
结果发现，这些奇数的序数1，3，6，10，15，…原来是“三角形数”，它的每一项等于从1开始的连续自然数的和。
第1项是1，第2项是1＋2＝3，第3项是1＋2＋3＝6，第4项是1＋2＋3＋4＝10，第5项是1＋2＋3＋4＋5＝15，……第n项是1＋2＋3＋…＋n＝n(n＋1)/2。
即，第n个等式左端，结束于第n(n＋1)/2个奇数。
然后，对上面这一系列等式的左右两端，分别求和：
右端是连续自然数的立方和13＋23＋33＋…＋n3。
左端是连续奇数的和。
我们知道，求连续奇数的和，求到第几个奇数，就等于第几个奇数的平方。
现在，求到第n(n＋1)/2个奇数，当然等于[n(n＋1)/2]2。
这样就得到求连续自然数立方和的公式：
13＋23＋33＋…＋n3＝[n(n＋1)/2]2
这种方法思路清晰论证简单。
尼科马霍斯之所以能够想到这个方法，显然跟毕达哥拉斯学派对图形数的宠爱有关。
图形数是自然数的形象化，自然数是众数之源，自然数真是一个取之不尽用之不竭的宝藏。