08-09学年第二学期山东理工大学线性代数试题

合集下载

线性代数试题线性代数试卷及答案大全(173页大合集)

由，得的特征值，
属于对应的特征向量为，单位化：，
属于对应的特征向量为，单位化：，
取，则有。
八、（本题8分）证明：由
得的特征值，
，
故的最大特征值是。
试卷2
闭卷考试时间：100分钟
一、填空题（本题15分，每小题3分）
1、若n阶行列式零元素的个数超过n（n-1）个，则行列式为。
三、（本题8分）解：从第一行开始，每行乘后逐次往下一行加，再按最后一行展开得：
原式= 。
四、（本题12分）解：由，得：，
可逆，故；
由于，。
五、（本题14分）解：（1）令，，
则线性无关，故是向量组的一个极大无关组；
（2）由于4个3维向量线性相关，
若线性无关，则可由线性表示，与题设矛盾；
A:矩阵A必没有零行
B:矩阵A不一定是阶梯形矩阵
C:矩阵A必有零行
D:矩阵A的非零行中第一个不等于零的元素都是1
非齐次线性方程组Ax=b中，系数矩阵A和增广矩阵(A b)的秩都等于3，A是3×4矩阵，则▁▁▁。【A】
A:方程组有无穷多解
B:无法确定方程组是否有解
C:方程组有唯一解
D:方程组无解
试卷1
4、若阶实方阵，为阶单位矩阵，则（）。
（A）（B）
（C）（D）无法比较与的大小
5、设，，，，其中为任意常数，则下列向量组线性相关的为（）。
（A） ( B) (C) (D)
三、（10分）计算阶行列式，的主对角线上的元素都为，其余位置元素都为，且。
四、（10分）设3阶矩阵、满足关系：，且，求矩阵。
B:Ax=0的基础解系中的解向量的个数不可能为n-r

理工大往年线代期末考试试题(1)

0
0
0
2
故 r(1, 2, 3, 4 ) = r(1,2,3,4 ) = 4 ，即 1, 2 , 3, 4 线性无关。
2 1 −1 1
六、(本题10 分)
求向量组 1
=
1 4
,
2
=
1 2
,
3
=
−2 2
,
4
=
1 −2
的秩及其极大无关组。
3
0
−9
(C)、A −1 A−1 ；
注： A−1 = A −1 A ，即 A = A A−1 ，故 ( A )−1 = A −1 A 。
(D)、A A−1 。
( B ) 11、设 A, B Rnn ，则下面结论错误的是
(A)、r(AB) r(A) ；
(B)、r(A) r(A + B) ；
(C)、r( AB) = r(BT AT ) ；
( A)、相同的特征向量；
(B)、不同的特征向量；
(C)、相同的特征向值；
(D)、不同的特征值。
5、实二次型 f ( X ) = x12 + 5x22 + x32 − 4x1x2 − x2x3 为( B )
( A)、半正定；
(B)、正定；
(C)、负定；
(D)、不定。
244
《线性代数》历届试题详解
f (X ) = 2x12 + 3x22 + 3x32 + 4x2x3 = X T AX = Y T (PT AP)Y = 2y12 + 5y22 + y32 。
247
《线性代数》历届试题详解
2014～2017 年线性代数试题详解
一、单项选择题

2008-2009学年线性代数试卷A及答案

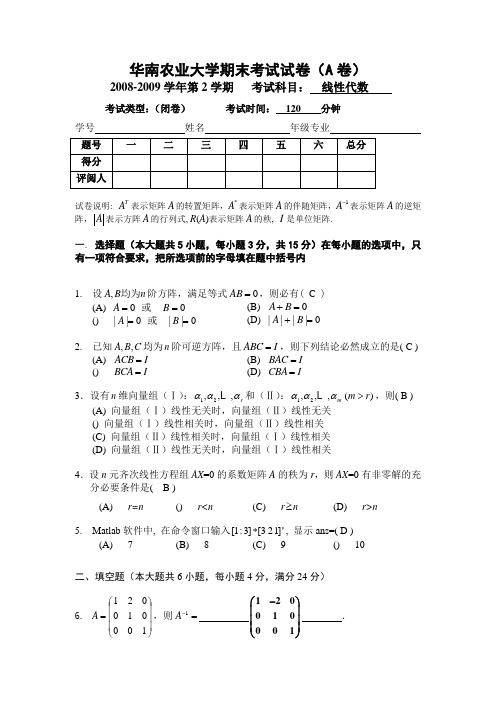
华南农业大学期末考试试卷（A 卷）2008-2009学年第2学期考试科目：线性代数考试类型：（闭卷）考试时间： 120 分钟学号姓名年级专业题号一二三四五六总分得分评阅人试卷说明: T A 表示矩阵A 的转置矩阵，*A 表示矩阵A 的伴随矩阵，1A -表示矩阵A 的逆矩阵，A 表示方阵A 的行列式, R (A )表示矩阵A 的秩, I 是单位矩阵.一. 选择题（本大题共5小题，每小题3分，共15分）在每小题的选项中，只有一项符合要求，把所选项前的字母填在题中括号内1. 设n B A 均为,阶方阵，满足等式0=AB ，则必有( C )(A) 0=A 或 0=B(B) 0=+B A () 0||=A 或 0||=B(D) 0||||=+B A2. 已知,,A B C 均为n 阶可逆方阵，且ABC I =，则下列结论必然成立的是( C )(A) ACB I = (B) BAC I = () BCA I = (D) CBA I =3．设有n 维向量组（Ⅰ）：12,,,r ααα 和（Ⅱ）：12,,,()m m r ααα> ，则( B )(A) 向量组（Ⅰ）线性无关时，向量组（Ⅱ）线性无关() 向量组（Ⅰ）线性相关时，向量组（Ⅱ）线性相关 (C) 向量组（Ⅱ）线性相关时，向量组（Ⅰ）线性相关 (D) 向量组（Ⅱ）线性无关时，向量组（Ⅰ）线性相关4．设n 元齐次线性方程组AX =0的系数矩阵A 的秩为r ，则AX =0有非零解的充分必要条件是( B )5. Matlab 软件中, 在命令窗口输入[1:3][321]'*, 显示ans=( D )二、填空题（本大题共6小题，每小题4分，满分24分）6. ⎪⎪⎪⎭⎫ ⎝⎛=100010021A ，则=-1A120010001-⎛⎫⎪ ⎪ ⎪⎝⎭． (A) r=n() r<n(C) r ≥n(D) r>n(A) 7 (B) 8 (C) 9 () 107. 设t ηηη,,,21 及t t ηληληλ+++ 2211都是非齐次线性方程组b A =X 的解向量，则=+++t λλλ 21______1__________.8. 矩阵20002023A a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与矩阵10002000B b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似, 则a b += . 9. 设123,1,1),0,2,3),1,0,1),k ααα===（（（则当k = 时，α1,α2,α3 线性相关.10.设A 为三阶方阵，其特征值2,1,3,- 则*A = ．11.已知二次型222123112132233(,,)2245f x x x x tx x x x x x x x =+-+++正定, 则t 的取值范围为．三、计算题12.(7分) 已知100110,021A ⎛⎫ ⎪=- ⎪ ⎪⎝⎭131011,002B ⎛⎫⎪=- ⎪ ⎪⎝⎭求:2T A AB +13.（8分）计算下列行列式3214214314324321四、解方程组14. (10分)求方程组123412341234311232x x x xx x x xx x x x⎧⎪--+=⎪-+-=⎨⎪⎪--+=-⎩的通解.五、解答题15.（10分）求下列向量组的秩，并求一个最大无关组：a1=(1, 2,-1, 4)T,a2=(9, 100, 10, 4)T, a3= (-2,-4, 2,-8)T．16. (8分) 已知1121 342 012A--⎛⎫⎪= ⎪⎪-⎝⎭，求A的伴随矩阵*A．17.(12分) 设212122221A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，求一个正交阵P ，使1P AP -=Λ为对角阵．六、证明题18.(6分) 设向量组322211,a a b a a b +=+= 433,a a b += 144,a a b +=, 证明向量组4321,,,b b b b 线性相关.2008—2009第二学期《线性代数》（A ）参考答案和评分标准一. 选择题（本大题共5小题，每小题3分，共15分）1. C2. C3. B4. B5. D二、填空题（本大题共6小题，每小题4分，满分24分）6. 120010001-⎛⎫⎪ ⎪⎪⎝⎭ 7. 18. 8 9. -1/2 10. 36 11. 405t -<<三、计算题12.T T A AB A E B 2(2)+=+=1001001001102010310021001112⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪-+⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦3分100300110330021114⎛⎫⎛⎫ ⎪⎪=- ⎪⎪ ⎪⎪-⎝⎭⎝⎭ 5分 300030754⎛⎫ ⎪= ⎪ ⎪⎝⎭7分 13.将行列式第2、3、4列加到第1列上，得3214214314324321=32110214101431043210=101110222031104321------ 4分=10400440311--- 6分=160 8分14.11110111101111011131002410024111231/200121/200000⎛⎫⎛⎫⎛⎫------ ⎪ ⎪ ⎪--→-→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭ 4分 x x x x x x 1234340241--+=⎧⎨-=⎩，x x x x x x x x 1324132431-=-⎧⎨+=++⎩， 5分取x x 2400⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，得*120120η⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭， 6分取x x 2410,01⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，x x 1311,02⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 8分得齐次方程组基础解系为121110,0201ξξ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 9分通解为x x k kx x 12123411120101022010⎛⎫⎪⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭10分 15. 192192192210040820010110201900004480320000A ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦6分rank(A)=2 7分所以向量组的秩为2． 8分 a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T 不成比例，所以 a 1，a 2为最大无关组. 10分16. 因为1*1,||A A A -=2分*1111||||A A AA A ---==4分 1||1A -=- 6分*1||1*A A -=-=121342012--⎛⎫ ⎪--- ⎪ ⎪-⎝⎭8分17.123(1)(1)(5),1,1,5A E λλλλλλλ-=-+--=-==， 3分对应于11λ=-，由 ()0A E x += 得111122ξ-⎛⎫ ⎪=- ⎪ ⎪⎝⎭，单位化，得111162p -⎛⎫ ⎪=- ⎪ ⎪⎝⎭； 6分对应于21λ=，由 ()0A E x -= 得2110ξ-⎛⎫ ⎪= ⎪ ⎪⎝⎭，单位化，得211120p -⎛⎫⎪= ⎪ ⎪⎝⎭ 8分对应于35λ=，由 (5)0A E x -= 得3111ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭，单位化，得311131p ⎛⎫⎪= ⎪ ⎪⎝⎭． 10分 11162311162321063P ⎛⎫-- ⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪⎝⎭，有1100010005TP AP P AP --⎛⎫⎪==Λ= ⎪ ⎪⎝⎭． 12分18. 设有4321,,,x x x x 使得044332211=+++b x b x b x b x即0)()()()(144433322211=+++++++a a x a a x a a x a a x 3分整理得 01100011000111001)(43214321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛x x x x a a a a 4分而011000110001110014321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛x x x x 有非零解，所以结论成立 6分。

线性代数考试试题

5 0 1 1、设 A= 0 1 0 ，则| A−1 |=_____ 3 0 1
1 1 2、设行列式 D = 2 4
1 0 5 3、设 A = 03 0 0 2 −4 4、设 A = 3 a 7 0
__。
1 0 1 5
3 0 0 1
共3页
第 2页
山东理工大学《山东理工大学《线性代数》试卷纸》
（A）卷 2007-2008 学年第二学期班级：姓名：学号： …………………………………装……………………………订…………………………线………….………………………………
2 六、（15 分）用正交变换化二次型 f = 4 x12 + 3x2 + 3 x32 + 2 x2 x3 成标准型。
四、（15 分）线性方程组为
x1 − x2 − x3 + x4 = 0 x1 − x2 + x3 − 3x4 = 1 ，求其通解。 1 x1 − x2 − 2 x3 + 3x4 = − 2
3 0 1 1 1 五、（10 分）设 AX = B ，且 A = 1 1 0 ， B = 0 1 求 X . −1 0 0 1 4
0 1 1
（1） D = 1 0 1 1 1 0
1 2 −1 3 0 1 (2) 1 −2 0 −2 −4 1
2 5 。 3 6
共3页
第1页
山东理工大学《山东理工大学《线性代数》试卷纸》
（A）卷 2008-2009 学年第二学期班级：姓名：学号： …………………………………装……………………………订…………………………线………….……………………………… 三、（10 分）求向量组 α1 = (1, 2, −1, 2)T ,α 2 = (3, −1, 4,6)T , α 3 = (−1,1,5,5)T α 4 = (1,3,0, 4)T 的秩，并求出一个最大线性无关组。

2198线性代数试题[精选5篇]

2198线性代数试题[精选5篇]第一篇：2198线性代数试题2008年4月高等教育自学考试全国统一命题考试线性代数试卷课程代码2198 说明：在本卷中，A表示矩阵A的转置矩阵，A*表示矩阵A 的伴随矩阵，E是单位矩阵，|A|表示方阵A的行列式.一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.设A为m×n矩阵，B为n×m矩阵，m≠n, 则下列矩阵中为n 阶矩阵的是（）A.BA C.ABAa11a12a22a32a13a33a11a31TTTB.AB D.BAB5a11+2a125a21+2a225a31+2a32a13a23，则D1的值为（）a33TT2.设行列式D=a21a31a23=3，D1=a21A.-15 B.-6 C.6 D.15 3.设A为n阶方阵，n≥2，则|-5A|=（）A.(-5)|A| C.5|A| 4.设A= A.-4 ⎛1⎝32⎫⎪,则|A*|=（）4⎪⎭nB.-5|A| D.5n|A|B.-2C.2D.4 5.向量组α1，α2…，αS（s>2）线性无关的充分必要条件是（）A.α1，α2，…，αS均不为零向量B.α1，α2，…，αS中任意两个向量不成比例C.α1，α2，…，αS 中任意s-1个向量线性无关D.α1，α2，…，αS中任意一个向量均不能由其余s-1个向量线性表示6.设3元线性方程组Ax=b，A的秩为2，η1，η2，η3为方程组的解，η1+η2=(2,0,4)T，η1+η3=（1，-2，1）TTT，则对任意常数k，方程组Ax=b的通解为（）B.(1,-2,1)T+k(2,0,4)T A.(1,0,2)+k(1,-2,1)C.(2,0,4)T+k(1,-2,1)TD.(1,0,2)T+k(1,2,3)T7.设3阶方阵A的特征值为1，-1，2，则下列矩阵中为可逆矩阵的是（）A.E-A B.-E-A C.2E-A D.-2E-A8.设λ=2是可逆矩阵A的一个特征值，则矩阵(A2)-1必有一个特征值等于（）A.14 B.C.2 D.49.设3阶方阵A的秩为2，则与A等价的矩阵为（）⎛1 A. 0 0⎝⎛1 C. 2 0⎝1001201⎫⎪0⎪0⎪⎭1⎫⎪2⎪0⎪⎭⎛1 B. 0 0⎝⎛1 D. 2 3⎝1101231⎫⎪1⎪0⎪⎭1⎫⎪2⎪3⎪⎭22210.二次型f(x1,x2,x3,x4,)=x12+x2+x3+x4+2x3x4的秩为（）A.1B.2C.3D.4二、填空题（本大题共10小题，每空2分，共20分）请在每小题的空格中填上正确答案。

2007-2008第二学期线性代数及答案工科36学时

武汉大学数学与统计学院2007－2008第二学期《线性代数D 》（A 卷，工科36学时）学院专业学号姓名注：所有答题均须有详细过程，内容必须写在答题纸上，凡写在其它地方一律无效。

一、(10分)设123,,ααα均为三维向量，记三阶矩阵123123123123(,,),(,24,39).A B αααααααααααα==++++++ 已知1A =，求B ．二、(10分) 设211120212-⎛⎫ ⎪= ⎪ ⎪⎝⎭A ,023214014-⎛⎫ ⎪=- ⎪ ⎪-⎝⎭B ，-=+AC E B C ,求矩阵C ．三、（15分）已知向量组123418210:2,4,1,53826A -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪===-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭ξξξξ求向量组A 的秩及一个最大无关组，并把其它的向量用最大无关组表示出来．四、(15分）设线性方程组为123123123(2)2212(5)4224(5)31x x x x x x x x x λλλλ++-=⎧⎪++-=⎨⎪--++=+⎩问λ为何值时，该方程组有唯一解、无解或有无穷多解？并在有无穷多解时求其解.五、(15分）已知1，1，－1是三阶实对称矩阵A 的三个特征值，向量T 1(1, 1, 1)α＝，T2(2, 2, 1)α＝是A 的对应于121λλ＝＝的特征向量，1）能否求得A 的属于31λ＝－的特征向量？若能，试求出该特征向量，若不能，则说明理由。

2）能否由此求得实对称阵A ？若能，试求之，若不能则说明理由。

六、(15分) 设A 是m n ⨯矩阵，B 是n m ⨯矩阵，E 是n 阶单位矩阵().n n ⨯已知,BA E = 试判断A的列向量组是否线性相关？为什么？七、(20分)设二次型的矩阵为5212233a b a b cc c --⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，,,a b c 为常数，则（1).写出二次型),,321x x x f （的具体形式；(2).求A 的全部特征值与特征向量；(3).求一个正交变换X PY =,把二次型f 化为标准形；(4).在1x =的条件下，求二次型f 的最大值和最小值。

2008-2009第二学期线性代数试卷及标答(B卷)

12n n n b b b ；12312⎛⎫ ⎪，2⎛武汉理工大学教务处试题标准答案及评分标准用纸课程名称:线性代数（ A 卷）一、填空题（每小题3分，共15分）1、2A E +；2、1；3、4；4、3；5、 0.二、选择题（每小题3分，共15分）1、C2、C3、A4、D 5 、B三、解答题（每小题7分，共35分）1、 2212111nn nn i i n b b a b b D a b b a b =+⎡⎤=+⎢⎥⎣⎦+∑ ………………………………………………………（3分） 11n i iaa b a =⎡⎤=+⎢⎥⎣⎦∑ ………………………………………………………………（6分）11n n i i a b a -=⎡⎤=+⎢⎥⎣⎦∑…………………………………………………………………………………（7分） 2、因为()123240,312402231024A B ⎛⎫ ⎪= ⎪ ⎪⎝⎭……………………………………………………………（2分） 553100444333010444131001222r r ⎛⎫- ⎪ ⎪ ⎪−−→−−→- ⎪ ⎪ ⎪- ⎪⎝⎭………………………………………………（6分）所以 X=55313334262-⎛⎫ ⎪- ⎪ ⎪-⎝⎭………………………………………………………………（7分） 3、因 22|3|3||T AA A =29||A = ……………………………………………………（5分）2229()a b =+。

……………………………………………………（7分）4、设10,T X α= 即123220x x x ++= ……………………………………… （2分）解得基础解系12221,001ηη--⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭。

……………………………………… （4分）Schmidt 正交化12,ηη，得到222132222252[,]41,[,]501ηααηαηααα⎛⎫- ⎪-⎛⎫ ⎪ ⎪ ⎪===-=- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭即为所求。

2008级《线性代数》考题(2009年12月25用)(1)

2008级《线性代数》考题（2009年12月用）(附答案)一. 填空题（每空3分，共15分）1. 设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333222111c b a c b a c b a A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333222111d b a d b a d b a B 且4=A ,1=B 则=+B A 20 2. 二次型233222213214),,(x x tx x x x x x f +-+=是正定的，则t 的取值范围是44 t -3. A 为3阶方阵，且21=A ，则=--*12)3(A A 2716-4. 设n 阶矩阵A 的元素全为1，则A 的n 个特征值是0,21====n n λλλ5. 设A 为n 阶方阵，n βββ ,,21为A 的n 个列向量，若方程组0=AX 只有零解，则向量组(n βββ ,,21)的秩为 n二. 选择题（每题3分，共15分）6. 设线性方程组⎪⎩⎪⎨⎧=+=+--=-0322313221ax cx bc bx cx ab ax bx ，则下列结论正确的是（A ） (A)当c b a ,,取任意实数时，方程组均有解 (B)当a ＝0时，方程组无解 (C) 当b ＝0时，方程组无解 (D)当c ＝0时，方程组无解 7. A.B 同为n 阶方阵，则（C ）成立(A) B A B A +=+ (B) BA AB =(C) BA AB = (D) 111)(---+=+B A B A8. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=331332123111131211232221a a a a a a a a a a a a B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100010101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1010100012P 则（C ）成立 (A)21P AP (B) 12P AP (C) A P P 21 (D) A P P 12 9. A ,B 均为n 阶可逆方阵，则AB 的伴随矩阵=*)(AB （D ） (A) **B A (B) 11--B A AB (C) 11--A B (D)**A B 10. 设A 为n n ⨯矩阵，r A r =)(＜n ，那么A 的n 个列向量中（B ）（A ）任意r 个列向量线性无关 (B) 必有某r 个列向量线性无关(C) 任意r 个列向量均构成极大线性无关组(D) 任意1个列向量均可由其余n －1个列向量线性表示三. 计算题（每题7分，共21分）11. 设⎪⎪⎪⎭⎫⎝⎛=300041003A 。

线性代数试题(济南大学2008～2009学年第二学期课程考试试卷(A卷))

济南大学2008～2009学年第二学期课程考试试卷（A 卷）一、选择题（每小题3分，共15分）1．D 2333231232221131211==a a a a a a a a a ，则333132312321222113111211322322322a a a a a a a a a a a a ---的值为 [ C ] (A ) 4; (B ) 6; (C ) 8; (D ) 10.2. 设n 阶方阵A ，B ，C ，满足ABC=E ，则必有 [ D ](A ) ACB=E ; (B ) CBA=E ; (C ) BAC=E ; (D ) BCA=E .二、填空题（每空3分，共24分）1. 行列式225144196151214111=_________.2. 设矩阵A ，⎥⎦⎤⎢⎣⎡=1102,230311⎥⎦⎤⎢⎣⎡-=B 则=B A T .6. 4阶行列式D 某一行的所有元素都相等且它们对应的余子式也相等，则D = 0 . 三、（本题满分10分）计算4阶行列式 b b a a -+-+1111111111111111.四、（本题满分12分）设矩阵A =⎪⎪⎪⎭⎫⎝⎛400021012，矩阵B 满足：AB=A+2B ，求矩阵B .五、（本题满分14分）试求b 为何值时, 线性方程组⎪⎪⎩⎪⎪⎨⎧=+++-=---=++=+++bx x x x x x x x x x x x x x 43214324324321223121220有解,并求其通解.一、选择题（每小题3分，共18分） 1．若622211211=a a a a ，则120020221221112--a a a a 的值为 [ A ] (A ) 12-; (B )12; (C ) 18; (D ) 0.3. 设n 元齐次线性方程组=Ax 0的系数矩阵的秩为r ，则方程组=Ax 0有非零解的充分必要条件是 [ D ] (A ) n r =； (B ) n r ≥； (C ) n r >； (D ) n r <. 5. 设n 阶方阵A ，B ，C 满足ABC=E ，则必有 [ B ](A ) ACB=E ; (B ) BCA =E ; (C ) BAC=E ; (D ) CBA =E .二、填空题（每空3分，共24分）1. 行列式222111c b a c b a=_________. 2. 设A ，B 均为3阶方阵,且A =2,21=B ，则12-A B T =_____ __.4. 非齐次线性方程组b Ax =有解的充分必要条件是 . 56. 设n 阶矩阵A 满足=-+E A A 102320，则1)2(--E A = .三、（本题满分10分）计算4阶行列式aa a a a a a a aa a a 0000. 四、（本题满分12分）设AX +B =X ，其中A =，⎪⎪⎪⎭⎫ ⎝⎛---101111010B =⎪⎪⎪⎭⎫ ⎝⎛3-5021-1，求矩阵X .五、（本题满分14分）试求a 为何值时, 线性方程组⎪⎩⎪⎨⎧-=++-=++-=++322321321321a x x ax x ax x ax x x有唯一解、无解、有无穷多解？并在无穷多解时求其通解.一、填空题（每小题3分，共18分）2. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100020101A ，则(A +3E )-1 (A 2-9E )=.3. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200031021A ，则A -1=.二、选择题（每小题3分，共18分）1. 若矩阵A 有一个r 阶子式不为零，则下列结论正确的是 [ ](A ) R (A )<r ； (B ) R (A )≤ r ； (C ) R (A )>r ； (D ) R (A )≥ r .2. 设A ，B 为同阶可逆矩阵，则下列结论一定成立的是 [ D ](A ) AB = BA ； (B ) 存在可逆矩阵P ，使P -1 AP =B ； (C ) 存在可逆矩阵C ，使C T AP =B ； (D ) 存在可逆矩阵P 和Q ，使P -AQ =B . 5. 矩阵方程AX =B 有解的充分必要条件是 [ C ](A ) R (A )= R (B )； (B ) R (B )=R (A , B )； (C ) R (A )=R (A , B )； (D ) R (A )<R (A , B ).6. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=133312321131131211232221333231232221131211,a a a a a a a a a a a a a a a a a a a a a B A ,,101010001,10000101021⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=P P 则[ D ](A ) B =P 1AP 2； (B ) B =P 2AP 1； (C ) B =A P 1P 2； (D ) B =P 1P 2A .三、计算题（第1、2题每小题10分，第3小题12分，共32分）1. 计算行列式3321322132113211111b a a a a b a a a a b a a a a +++.2. 求齐次线性方程组⎪⎩⎪⎨⎧=++=++=+++000224214324321x x x x x x x x x x 的全部解.3. 已知矩阵⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--=2001,1121B P 满足P -1AP=B ，计算： (1) |-A 5|； (2) A 3.济南大学2011～2012学年第二学期课程考试试卷（A 卷）课程线性代数考试时间 2012 年 7 月 2 日一、填空题（每小题3分，满分27分）1、设行列式==11110342226111304z y xzy x，则行列式_________. 4、设矩阵A =⎪⎪⎪⎪⎪⎭⎫⎝⎛1100120000120025，则A -1=________________. 6、三元线性方程x 1+ x 2+ x 3=1的全部解是_______________.三、计算题（每小题9分，满分18分）（1）D =cc b b a a ------1100110011001.（2）设矩阵A =⎪⎪⎪⎭⎫⎝⎛161020101,而X 满足AX +E =A 2+X ，求X .四、应用题（每小题10分，满分20分）（2）设A =⎪⎪⎪⎭⎫ ⎝⎛-1-11020011-λλλ, b =⎪⎪⎪⎭⎫⎝⎛11-a ，已知非齐次线性方程组Ax=b 存在两个不同的解，求（I ）a ，λ的值；（II ）Ax =b 的通解.。

08-09年第二学期《线性代数Ⅱ》课程考试试卷B答案

2008─2009学年第二学期《线性代数Ⅱ》课程考试试卷B 答案注意：1、本试卷共 3 页； 2、考试时间120分钟一、单选题 (每小题 2 分，共 20 分)1.设A 为n 阶方阵，且2,n ≥则5A -等于（ A ）；(A ) (5)n A -； (B ) 5A -； (C ) 5A ； (D ) 5nA .2.设,,A B C 为同阶方阵，则()T ABC 等于 ( B )；(A ) T T T A B C ； (B ) T T T C B A ； (C ) T T T C A B ； (D ) T T T A C B .3.设矩阵1122A ⎛⎫= ⎪⎝⎭，则和A 等价的矩阵是( B )；(A ) 1022A ⎛⎫= ⎪⎝⎭；(B ) 1313A ⎛⎫= ⎪⎝⎭；(C ) 111222A ⎛⎫= ⎪⎝⎭；(D ) 112222A ⎛⎫⎪= ⎪⎪⎝⎭. 4.若向量组s ααα,...,,21，(2s )线性无关的充要条件是（ D ）； (A ) s ααα,...,,21 均不为零向量；(B ) s ααα,...,,21中任意两个向量不成比例； (C ) s ααα,...,,21任意s-1个向量线性无关；(D ) s ααα,...,,21中任意一个向量均不能由其余s-1个向量线性表示.5.已知12,ββ为非齐次线性方程组Ax b =两个不同的解，12,αα为其导出组0Ax =的一个基础解系，12,c c 为任意常数，则Ax b =的通解可以表示为（ A ）；(A ) )()(212121121αααββ++++c c ；(B ) )()(212121121αααββ+++-c c ；(C ) )()(212121121ββαββ-+++c c ；(D ) )()(212121121ββαββ+++-c c . 6.设A 为n 阶方阵，且032=-+E A A则=+-1)2(E A （ A ）；(A ) E A -；(B ) E A +；(C ))(31E A -；（D ）)(31E A +. 7．设n 阶可逆方阵A 有一个特征值为3，对应的特征向量为x, 则下列等式中不正确的是（ B ）；()3A Ax x = 1()3B A x x -= 11()3C A x x -= 2()9D A x x =.8.写出二次型1231213(,,)22f x x x x x x x =+的规范形（ C ）；（A ）221222y y -；（B ）221222y y +；（C ）2212y y -；（D ）2212y y +. 9.设3阶矩阵A 与B 相似,A 的特征值为4,2,3. 则B 等于（ D ）；1()24A ； 1()9B ； ()9C ； ()24D .10.二次型212311323(,,)44f x x x x x x x x =++的矩阵为（ D ）；(A ) 104004440⎛⎫ ⎪ ⎪ ⎪⎝⎭；(B ) 1022002000⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭；(C ) 1002000220⎛⎫⎪⎪⎪ ⎪ ⎪⎝⎭；(D ) 102002220⎛⎫ ⎪ ⎪ ⎪⎝⎭.二、计算下列行列式 (每小题6分，共12分)1．123233249499367677=02．1115115115115111=512三峡大学试卷纸教学班号序号学号姓名…………………….………….………………试题不要超过密封线………….………………………………三、计算矩阵 (共20分)设111210101A -⎛⎫ ⎪=- ⎪ ⎪⎝⎭ ，123120001B ⎛⎫ ⎪= ⎪ ⎪⎝⎭求（1）A AB 23-；(5分) （2）B A T；（5分）（3）判断矩阵A 是否可逆？若可逆，求1-A .（10分）解：（1）242126124AB ⎛⎫⎪= ⎪ ⎪⎝⎭ (2)2421114108323126221018181241011610AB A -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=--=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (5)（2）12112336411012000310*******TA B ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=-= ⎪⎪ ⎪ ⎪⎪ ⎪----⎝⎭⎝⎭⎝⎭………10 （3）40A =-≠，故A 可逆，……………………13 并且**1111222, (17)113111111222444113111 (204)222113444A A A A ----⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭---⎛⎫⎛⎫⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭ ⎪===- ⎪- ⎪ ⎪-- ⎪⎝⎭四、(每小题4分，共16分)已知向量组13125α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭21112α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭32013α⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭41101α⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭(1)若123430αααβ+--=，求β；(2)求向量组的秩),,,(4321ααααR ；(3)求向量组4321,,,αααα的一个最大无关组； (4)将其余向量组用此最大无关组线性表示.解：（1）1135383193β⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ (4)（2）31211011110101122110000052310000A ⎛⎫⎛⎫⎪ ⎪---⎪ ⎪=→⎪ ⎪⎪ ⎪⎝⎭⎝⎭向量组的秩),,,(4321ααααR =2 (8)（3）向量组4321,,,αααα的一个最大无关组为12,αα (12)（4）312412,2αααααα=-=- (16)三峡大学试卷纸教学班号序号学号姓名…………………….………….………………试题不要超过密封线………….………………………………五、(共15分)求下列非齐次线性方程组的通解及对应的齐次方程组的基础解系：123451234523451234513235226254337x x x x x x x x x x x x x x x x x x x ++++=-⎧⎪+++-=-⎪⎨+++=⎪⎪+++-=-⎩ 解111111101153321135012262012262000000543317000000-----⎛⎫⎛⎫⎪⎪-- ⎪ ⎪→⎪ ⎪⎪⎪--⎝⎭⎝⎭因R(A)=R(A,b)=2 5.故有无穷解. (5)原方程组的同解方程组为13452345532262x x x x x x x x =++-⎧⎨=---+⎩ (7)特解*32,000η-⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ (9)齐次的基础解系123115226,,100010001ξξξ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (13)通解为*112233k k k ηηξξξ=+++(123,,k k k 为任意常数) (15)六、(共17分) 设矩阵100032023A ⎛⎫ ⎪= ⎪ ⎪⎝⎭.(1)求矩阵A 的特征值和特征向量；（2）求一正交矩阵P ，使得AP P 1-为对角矩阵.解：（1）10032(1)(1)(5)0023A E λλλλλλλ--=-=---=- 得A 的特征值为1231,5λλλ===……………4 对应121λλ==，解方程0)(=-x E A 得特征向量⎪⎪⎪⎭⎫ ⎝⎛-=1101ξ，⎪⎪⎪⎭⎫ ⎝⎛=0012ξ (8)1ξ，2ξ为对应于121λλ==的特征向量.对应53=λ，解方程0)5(=-x E A 得特征向量⎪⎪⎪⎭⎫ ⎝⎛=1103ξ (10)3ξ为对应于53=λ的特征向量.(2)将321,,ξξξ单位化有,11021,001,11021321⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-=P P P ......... (12)令),,(321P P P P =（不唯一）有⎪⎪⎪⎭⎫⎝⎛=-5000200011AP P (15)三峡大学试卷纸教学班号序号学号姓名…………………….………….………………试题不要超过密封线………….………………………………。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

08-09学年第二学期《线性代数》试题
一填空题（每小题2分，共20分）
1 若3阶矩阵),,(321ααα=A ，且3=A ，),3,2(321ααα=B 则
=B __________；
2已知B 为三阶可逆矩阵，R(A)=2,则R （AB ）=; 3若
A=⎪⎪⎪⎪⎪⎭
⎫
⎝
⎛11
00230
00032001
0，则
=3
A ____________; 4对于n 元齐次线性方程组AX=0,若R(A)=r ，则其基础解系所含向量的个数为__________；
5 若非零向量组m ααα,,,21 两两正交，则m ααα,,,21 的线性关系是___________;
6设s ααα,,,21 是AX=b 0(≠b )的解，则s s c c c ααα+++ 2211也是AX=b 的解的条件是_______；
7若向量），，，（），，，，（53100121=-=βα，则],[βα=_______；
8设A 为正交矩阵，则=-1A _______；
9设5是可逆矩阵A 的一个特征值，则_______一定是*A 的一个特征值；
10设），，（），，，（22211021-=-=αα，且21ααβ+=k ，若使β与2α正
交，则k=_______。

二单项选择题（每小题3分，共18分）
1 如果向量β可由向量组s ααα,,,21 线性表示，则_______
（A ）存在一组不全为零的数
s
k k ,,,k 21 ，使
s s k k k αααβ+++= 2211成立;
（B ）向量组s αααβ,,,,21 线性相关；（C ）β的线性表示式不唯一；（D ）存在一组全为零的数
s
k k ,,,k 21 ，使
s s k k k αααβ+++= 2211成立。

2若n 阶方阵A,B 均可逆，AXB=C ，则X=
（A ）C B A 11-- （B ）11--A CB （C ）11--CB A （D ）11--CA B 3设x 是n 维列向量，则=x λ______. （A ）x λ （B ）x
λ
（C ）x n λ （D ）x
n
λ
4 设-1，5，2是矩阵A 的特征值，则______. （A ）A 不确定（B ）1-A 的特征值分别为1,-5,-2 （C ）A 为实对称矩阵
（D ）A 的这三个特征值对应的特征向量一定线性无关. 5若βα,是非齐次线性方程组AX=b 的两个不同解，则___必是AX=0的一个解。

（A ）βα-2 （B ）βα22- （C ）βα+2 （D ）βα+ 6 n 阶方阵A 可逆的充要条件是A 的秩满足：
（A ）R(A)>n （B ）R(A)<n （C ）R(A)=n （D ）不确定
三求行列式的值a
a a a a x a a a a
x a a a a x （10
分）
四已知
A=⎪⎪⎪
⎭
⎫ ⎝⎛-100110111，且E AB A =-2，求矩阵B(10分)
五求向量组)3,6,2,0(),1,3,0,1(),3,1,1,2(),0,1,4,1(4321-=-=-==αααα的一个最大线性无关组（10分）六讨论k
为何值时，方程组⎪⎪⎩⎪⎪⎨
⎧=+--=+--=+++=+++k
x x x x x x x x x x x x x x x x 432143214
3214321121153533531
有无穷多
解？并求出其通解。

（12分）
七已知实二次型3221232132144),,(x x x x x ax x x x f ---= （1）若该二次型的系数矩阵A ，满足03=+E
A ，求常数
a;
(2) 求矩阵A 的所有特征值和特征向量；
（3）求正交变换X=PY ，将二次型化成标准型。

（14分）八已知A 为3阶可逆方阵，且0223=+-A A A ，证明A 的特征值全等于1（6分）
证明：设矩阵A 的特征值是λ，则矩阵B=A A A +-232的特征值是λλλ+-232
又因为B=O ，所以，B 的特征值0（因为BX=λX=0，但X ≠0，所以B 的特征值为0）所以λλλ+-232=0 所以，01==λλ或
因为A 是可逆矩阵，故0≠λ 所以，A 的特征值全等于1.。