浙江省永嘉县桥下镇瓯渠中学2014届九年级数学总复习《第三十一讲 图形的旋转与中心对称》基础演练
浙江省永嘉县桥下镇瓯渠中学2014届九年级数学总复习《第三十一讲 图形的旋转与中心对称》课件

易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
网 络 构 建 考 点 梳 理
易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读 对 接 中 考
名师助学 要会用辩证统一的观点理解中心对称和中心对称图 形,即将中心对称图形看成是被过对称中心的直线 分成的两个图形,那么,这两个图形就关于这点中 心对称;若把成中心对称的两个图形看成一个图
易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读 对 接 中 考
旋转变换的性质
形状和_____ 大小 ,即旋转变换 1.旋转变换不改变图形的_____
网 络 构 建 考 点 梳 理
前后的图形全等. 相等 ,对应点与旋转中 2.对应点到旋转中心的距离_____
易 错 防 范 课 时 跟 踪 检 测
易 错 防 范 课 时 跟 踪 检 测
上 页
下 页
返 回
中考步步高
课 前 必 读
中心对称和中心对称图形
180° 1.中心对称:把一个图形绕着某一点旋转_____ ,如
另一个图形 重合,那么,就说这两个 果它能够与___________
对 接 中 考
网 络 构 建 考 点 梳 理
图形关于这个点对称或中心对称,这个点叫做
学.科.网
网 络 构 建 考 点 梳 理
第31课 图形的旋转与中心对称-2021届九年级中考数学复习课件

课前热身
考点一 旋转变换 1.图形的旋转三要素是__旋__转___中__心____、___旋__转__方__向____和___旋__转__角__度____. 2.一对对应点与旋转中心连线的夹角等于___旋__转__角___. 3.对应边所在直线的夹角等于__旋__转___角___或___旋__转__角__的__补__角__(当__旋__转__角__小__于__ _等__于__1_8_0_°__时__成___立__) ___. 4.对应点连线的中垂线必过___旋__转__中__心___. 5.旋转变化的两个图形中,一对对应边所在的直线形成的角与旋转角的关 系是___相__等___或__互__补__(当__旋__转__角__小__于__等__于__1_8_0__°__时__成__立__) ___.
(图 31-11)
提示:辅助线如图 D31-4,可证 AG∥EC,设 GF=x,则 AF=2x,AG= 3 x, 故 GE= 3x,EF=( 3-1)x,所以CAFF=GEFF=( 3-x 1)x= 3-1.
◆达标三 旋转的应用 例 5 如图 31-12,在△ABC 中,∠ACB=90°,AC=BC,P 是△ABC 内 的一点,且 PB=1,PC=2,PA=3,求∠BPC 的度数.
(图 31-4)
分类达标
◆达标一 旋转的概念
例 1 (2018 黑龙江)如图 31-5,在正方形网格中,
每个小正方形的边长都是一个单位长度,在平面直
角坐标系内,△ABC 的三个顶点坐标分别为 A(1,4),
B(1,1),C(3,1).
(1)画出△ABC 关于 x 轴对称的△A1B1C1; (2)画出△ABC 绕点 O 逆时针旋转 90°后的△A2B2C2;
浙江省永嘉县桥下镇瓯渠中学2014届九年级数学总复习《第三十讲 图形的轴对称与平移》基础演练
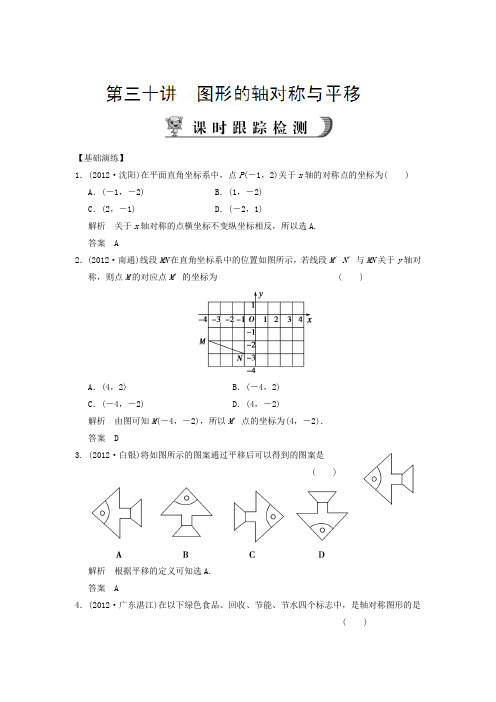
【基础演练】1.(2012·沈阳)在平面直角坐标系中,点P(-1,2)关于x轴的对称点的坐标为( ) A.(-1,-2) B.(1,-2)C.(2,-1) D.(-2,1)解析关于x轴对称的点横坐标不变纵坐标相反,所以选A.答案 A2.(2012·南通)线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )A.(4,2) B.(-4,2)C.(-4,-2) D.(4,-2)解析由图可知M(-4,-2),所以M′点的坐标为(4,-2).答案 D3. (2012·白银)将如图所示的图案通过平移后可以得到的图案是( )解析根据平移的定义可知选A.答案 A4.(2012·广东湛江)在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )解析这是一道较容易的题目,主要考查了轴对称图形的概念:对折后直线两侧的部分完全重合,其中B、D显然不是轴对称图形,易产生错误的是C,正确的答案应选A.本题渗透了保护环境思想,这也是出题人指出的方向.答案 A5.(2012·宜昌)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )A.先把△ABC向左平移5个单位,再向下平移2个单位B.先把△ABC向右平移5个单位,再向下平移2个单位C.先把△ABC向左平移5个单位,再向上平移2个单位D.先把△ABC向右平移5个单位,再向上平移2个单位解析根据平移的定义可知,选A.答案 A6. (2012·江西)如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).解析本题解法很多,不唯一,其中之一的解法为:连结BD、CE,设BD、CE相交于点F,过A、F的直线就是它的一条对称轴.答案7.(2012·兰州)△ABC在平面直角坐标系中的位置如图所示.(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.解(1)A1(0,4),B1(2,2),C1(1,1);(2)A2(6,4),B2(4,2),C2(5,1);(3)△A1B1C1与△A2B2C2关于直线x=3轴对称.8.(2012·广州)如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方,(1)在图中作出⊙P关于y轴对称的⊙P′,根据作图直接写出⊙P′与直线MN的位置关系.(2)若点N在(1)中的⊙P′上,求PN的长.分析在平面直角坐标系中,易知点P′的坐标为(3,2),⊙P′的半径和⊙P的半径相等为3,这样⊙P′就被确定,因为点N在直线MN上,直线MN过(5,0)点且平行于y轴,直线PP′⊥MN,这样利用勾股定理就可求得PN的长度.解(1)如图,⊙P′的圆心为(3,2),半径为3,与直线MN相交.(2)连接PP′,交直线MN于点A,∵点P、P′的纵坐标相同,∴PP′∥x轴,又∵MN∥y轴,∴PP′⊥MN,∴点A的坐标为(5,2).在Rt△P′NA中,P′N=3,P′A=5-3=2.∴AN=P′N2-P′A2=32-22=5,在Rt△PAN中,PA=5-(-3)=8,AN=5,∴PN=PA2+AN2=82+(5)2=69.【能力提升】9.如图,△ABC 与A ′B ′C ′关于直线l 对称,则∠B 的度数为( )A .50°B .30°C .100°D .90°解析 ∵△ABC 与△A ′B ′C ′关于直线l 对称, ∴△ABC ≌△A ′B ′C ′,∴∠C =∠C ′=30°,在△ABC 中,∠B =180°-∠A -∠C =180°-50°-30°=100°.] 答案 C10.如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位得到⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系.(2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A 、B ,求劣弧⌒AB与弦AB 围成的图形的面积.(结果保留π)解 (1)⊙P 1的位置如图所示,它与⊙P 的位置关系为外切.(2)S 扇形OAB =14π×22=π,S △AOB =12×2×2=2.∴劣弧AB 与弦AB 围成的图形的面积为π-2.11.(2012·丽水)如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( )A .①B .②C .⑤D .⑥ 解析 如图,球最后落入①球洞:答案 A12.(2012·徐州)如图,将边长为2的正方形ABCD 沿对角线AC 平移,使点A 移至线段AC 的中点A ′处,得新正方形A ′B ′C ′D ′,新正方形与原正方形重叠部分(图中阴影部分)的面积是 ( )A. 2B.12C .1D.14解析 ∵A ′为AC 的中点,AD ∥A ′D ′ ∴A ′D ′与CD 的交点也为CD 的中点, ∴图中阴影部分正方形的边长为1 ∴阴影部分正方形的面积为1. 答案 C13.(2012·遵义)如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,延长BG 交CD 于F 点,若CF =1,FD =2,则BC 的长为( )A .3 2B .2 6C .2 5D .2 3 解析 连结EF , ∵△ABE ≌△GBE .∴AB =BG =3AE =EG =12AD ,∴EG =ED ∴△EFD ≌△EFG , ∴FG =FD =2. ∴BF =BG +FG =5 在Rt △BCF 中,BC =52-12=2 6. 答案 B14.(2012·宁波)邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作:在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依次类推,若第n 次操作余下的四边形是菱形,则称原平行四边形为n 阶准菱形.如图1,▱ABCD 中,若AB =1,BC =2,则▱ABCD 为1阶准菱形. (1)判断与推理:①邻边长分别为2和3的平行四边形是________阶准菱形;②小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD 沿BE 折叠(点E 在AD 上),使点A 落在BC 边上的点F ,得到四边形ABFE .请证明四边形ABFE 是菱形. (2)操作、探究与计算:①已知▱ABCD 的邻边长分别为1,a (a >1),且是3阶准菱形,请画出▱ABCD 及裁剪线的示意图,并在图形下方写出a 的值;②已知▱ABCD 的邻边长分别为a ,b (a >b ),满足a =6b +r ,b =5r ,请写出▱ABCD 是几阶准菱形.解 (1)①利用邻边长分别为2和3的平行四边形进行两次操作,所剩四边形是边长为1的菱形,故邻边长分别为2和3的平行四边形是2阶准菱形:②由折叠知:∠ABE =∠FBE ,AB =BF , ∵四边形ABCD 是平行四边形, ∴AE ∥BF , ∴∠AEB =∠FBE , ∴∠AEB =∠ABE , ∴AE =AB ,∴AE=BF,∴四边形ABFE是平行四边形,∴四边形ABFE是菱形;(2)①如图所示:②∵a=6b+r,b=5r,∴a=6×5r+r=31r;如图所示:故▱ABCD是10阶准菱形.。
第23章 旋转提纲(2014届)

班级: 座号: 姓名:一、预习内容:课本P56---P58页二、学习目标:了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念及其应用它们解决一些实际问题.重点:旋转及对应点的有关概念及其应用.三、学习过程1.完成教材56页“思考”,以上现象的共同特点是:2.像这样,把一个平面图形绕着平面内某一点O 转动一个角度,就叫做图形的 ,点O 叫做 ,转动的角叫做 .如果图形上的点P 经过旋转变为点P ′,那么这两个点P 和P ′叫做这个旋转的 .3.根据定义填空:如图,ABO ∆绕点O 旋转45°后得到DCO ∆,则点B 的对应点是_____;线段OB 的对应线段是 ;线段AB 的对应线段是 ;∠A 的对应角是 ;∠B 的对应角是_____;旋转中心是_____;旋转的角度是______.△AOB 的边OB 的中点M 的对应点在 .4.完成P56练习2、32. 3.5.细读课本P57的探究,回答:⑴线段OA OA '与、OB OB '与、OC OC '与有什么关系?⑵在旋转的过程中,旋转角有 ,它们有什么关系?⑶ABC A B C '''∆∆与的形状与大小有什么关系?⑷如何确定旋转角?6.归纳:对应点到旋转中心的距离 ;对应点与旋转中心所连线段的夹角等于 ;(任意一对对应点);旋转前后的图形 .7.细读课本P57的例题,完成仿练:如图,△ABC 是等边三角形,D 是BC 边上一点,△ABD 经过旋转后到达△ACE 的位置.(1)旋转中心是哪个点? (2)旋转了多少度?(3)如果M 是AB 的中点,那么经过上述旋转后,点M 转到了什么位置?8.完成P58练习(做在课本上)A B O DC班级: 座号: 姓名:一、预习内容:课本P62---P64页二、学习目标:通过具体实例认识两个图形关于某一点成中心对称的本质;掌握连结对称点的线段经过对称中心并被对称中心平分的基本特征;会熟练地画出已知图形关于某一点成中心对称的图形.三、学习过程1.细读P62的思考,可以发现(1) ;(2) .2.中心对称的概念:指出图23.2-2中的对称点: 思考:全等图形 中心对称,中心对称的两个图形 是全等的.(用“一定”或“不一定”填空)3.细读课本P63的探究,回答:(1)点O 在线段 上,且OA OA '、OB OB '、OC OC ',记点O 是线段 的 .(2)通过证明可得:AB= ,AC= ,BC= ,从而得到:ABC ∆ A B C '''∆.(3)归纳:中心对称的两个图形的性质①②4.细读课本P64的例题,完成课本P64的练习(画在课本上)5.作图:如图,已知AD 是△ABC 的中线,画出以点D 为对称中心,与△ABD •成中心对称的三角形.6.下列说法正确的是( )A .形状大小相同的两个图形成中心对称. B.成中心对称的两个图形必须重合C .成中心对称的两个图形的形状大小完全相同 D.旋转后重合的两个图形是中心对称7.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )A .1组B .2组C .3组D .4组九年数学第二十三章《旋转》自学参考提纲 第3课时 中心对称图形执笔:翁建勇 审核:九年级数学组班级: 座号: 姓名:一、预习内容:课本P65---P66页二、学习目标:了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用;中心对称图形的有关概念及其他应用.三、学习过程1.复习:中心对称的两个图形的性质:2.阅读课本P65的思考并完成思考中的两个作图 :(1) (2)可以发现:①线段AB 绕它的中点旋转180°后________________ ;②平行四边形ABCD 绕它的两条对角线交点旋转180°后_____________________.归纳:线段、平行四边形是___________________,它们的对称中心分别是______________、________________.3.完成课本P66的练习1. 2.4.下面图形中既是轴对称图形又是中心对称图形的是( )A .直角B .等边三角形C .直角梯形D .两条相交直线5.如图,两个图形关于某点中心对称,看谁能用最简单的方法找出对称中心.你的根据是什么?6.归纳:九年数学第二十三章《旋转》自学参考提纲 第4课时 关于原点对称的点的坐标执笔:翁建勇 审核:九年级数学组班级: 座号: 姓名:一、预习内容:课本P66---P67页二、学习目标:理解点P 与P '关于原点对称时,它们的横纵坐标的关系;掌握(),P x y 关于原点的对称点()-,-P x y 三、学习过程1.复习回顾⑴如图,①画出点A 关于x 轴的对称点A ′;②画出点B 关于x 轴的对称点B ′; ③画出点C 关于y 轴的对称点C ′;④画出点A 关于y 轴的对称点D ′。
九年级中考数学《图形的旋转》_知识点 2
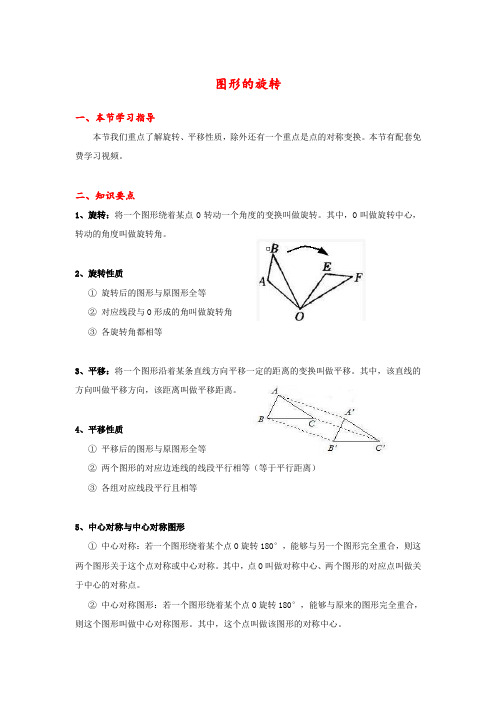
图形的旋转一、本节学习指导本节我们重点了解旋转、平移性质,除外还有一个重点是点的对称变换。
本节有配套免费学习视频。
二、知识要点1、旋转:将一个图形绕着某点O转动一个角度的变换叫做旋转。
其中,O叫做旋转中心,转动的角度叫做旋转角。
2、旋转性质①旋转后的图形与原图形全等②对应线段与O形成的角叫做旋转角③各旋转角都相等3、平移:将一个图形沿着某条直线方向平移一定的距离的变换叫做平移。
其中,该直线的方向叫做平移方向,该距离叫做平移距离。
4、平移性质①平移后的图形与原图形全等②两个图形的对应边连线的线段平行相等(等于平行距离)③各组对应线段平行且相等5、中心对称与中心对称图形①中心对称:若一个图形绕着某个点O旋转180°,能够与另一个图形完全重合,则这两个图形关于这个点对称或中心对称。
其中,点O叫做对称中心、两个图形的对应点叫做关于中心的对称点。
②中心对称图形:若一个图形绕着某个点O旋转180°,能够与原来的图形完全重合,则这个图形叫做中心对称图形。
其中,这个点叫做该图形的对称中心。
6、轴对称与轴对称图形(1)、轴对称:若两个图形沿着某条轴对折,能够完全重合,则这两个图形关于这条轴对称或它们成轴对称。
其中,这条轴叫做对称轴。
注:轴对称的性质:①两个图形全等;②对应点连线被对称轴垂直平分(2)轴对称图形:若一个图形沿着某条轴对折,能够完全重合,则这个图形叫做轴对称图形。
7、点的对称变换(1)、关于原点对称的点的特征两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P'(-x,-y)(2)、关于x轴对称的点的特征两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x 轴的对称点为P'(x,-y)(3)、关于y轴对称的点的特征两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y 轴的对称点为P'(-x,y)(4)、关于直线y=x对称两个点关于直线y=x对称时,横坐标与纵坐标与之前对换,即:P(x,y)关于直线y=x的对称点为P'(y,x)(5)、两个点关于直线y=-x对称时,横坐标与纵坐标与之前完全相反,即:P(x,y)关于直线y=x的对称点为P'(-y,-x)注:y=x的直线是过一三象限的角平分线,y=-x的直线是过二四象限的角平分线。
浙江省永嘉县桥下镇瓯渠中学2014届中考数学总复习《第十九讲 图形的初步知识》基础演练 新人教版

《第十九讲图形的初步知识》基础演练【基础演练】1.(2012·某某)下面四个角中,最有可能与70°互补的是( )解析与70°互补的角为一钝角,只有D项适合.故选D.答案 D2.平面上有三个点,可以确定直线的条数是( )A.1条B.2条C.3条 D.1条或3条解析因为两点确定一条直线,所以当平面内三点在一条直线上时,可以确定一条直线,当平面内三点不在同一直线上时,可以确定三条直线,故选D.答案 D3.如图,点A、O、B在同一直线上,CO⊥AB于点O,若∠1=∠2,则图中互余的角共有( )A.5对 B.4对C.3对 D.2对解析∵CO⊥AB,∴ ∠AOC=∠BOC=90°,∴∠1+∠COD=90°,∠2+∠AOE=90°.又∵∠1=∠2,∴∠2+∠COD=90°,∠2+∠AOE =90°.即图中互余的角有4对.答案 B4.(2011·某某省某某)如图,已知AB ∥CD ,BE 平分∠ABC ,交CD 于点D ,∠CDE =150°,则∠C 的度数是 ( )A .100°B .110°C .120°D .150°解析 ∵∠CDE =150°,∴∠CDB =180°-∠CDE =180°-150°=30°,∵AB ∥CD ,∴∠ABD =∠CDB =30°,又∵BE 平分∠ABC ,∴∠ABC =2∠ABD =2×30°=60°,∵AB ∥CD ,∴∠ABC +∠C =180°,∴∠C =180°-∠ABC =180°-60°=120°.故应选C.答案 C5.(2012·某某)如图,AB ∥CD ,直线EF 交AB 于点 E ,交CD于点F ,EG 平分∠BEF ,交CD 于点G ,∠1=50°,则∠2等于( )A .50°B .60°C .65°D .90°解析 ∵AB ∥CD ,∴∠BEF +∠1=180°∴∠BEF =180°-∠1=180°-50°=130°∵EG 平分∠BEF∴∠BEG =12∠BEF =12×130°=65° ∵AB ∥CD ,∴∠2=∠BEG =65°.故选C.答案 C6.如图,直线l 1∥l 2,∠1=40°,∠2=75°,则∠3= ( )A.55°B.60°C.65°D.70°解析∵l1∥l2,∴∠BCA=∠1=40°,∵∠ABC是∠2的对顶角,∴∠ABC=∠2=75°,在△ABC中,∠3+∠BCA+∠ABC=180°.∴∠3=180°-(∠BCA+∠ABC)=180°-(40°+75°)=65°.故应选C.答案 C7.45°角的余角是( )A.30°B.45°C.60°D.135°解析由余角的定义知45°角的余角为90°-45°=45°.答案 B8.如图,直线a、b相交于点O,若∠1等于40°,则∠2=( )A.50°B.60°C.140°D.160°解析∠2=180°-∠1=180°-40°=140°.答案 C9.(2012·东营)下图能说明∠1>∠2的是( )解析由对顶角相等,得∠1=∠2,A不对.B不对.由外角定理知∠1>∠2,故C对.由同角的余角相等知∠1=∠2,故D不对.答案 C10.(2012·某某)如图,与∠1是内错角的是( )A.∠2B.∠3C.∠4D.∠5解析由内错角定义选B.答案 B11.(2012·崇左)如图,BC∥DE,∠1=108°,∠AED=75°,则∠A的大小是( )A.60°B.33°C.30°D.23°解析∵BC∥DE∴∠ADF=∠1=108°,∵∠A+∠AED=∠ADF,∴∠A=∠ADF-∠AED=108°-75°=33°.答案 B12.(2012·某某)已知∠1=∠2=∠3=59°,则∠4=________.解析∵∠1=∠3=59°,∴a∥b,∴∠4=∠1+∠5,∠1+∠5=180°-∠2=180°-59°=121°,∴∠4=121°.∴填121°.答案121°13.(2012·某某)一个锐角是38度,它的余角是________度.解析这个角的余角为90°-38°=52°,∴填52.答案52【能力提升】14.(2012·义乌)如图,已知a ∥b ,小亮把三角板的直角顶点放在直线b 上,若∠1=40°,则∠2的度数为________.解析 ∵a ∥b ,∴∠2=∠3∵∠3+∠1+90°=180°∴∠3=90°-∠1=90°-40°=50°∴∠2=50°,∴填50°.答案 50°15.(2012·某某)如图,AB ∥CD ∥EF ,那么∠BAC +∠ACE +∠CEF =________度.解析 ∵AB ∥CD∴∠BAC +∠ACD =180°①∵CD ∥EF∴∠CEF +∠ECD =180°②①+②,得∠BAC +∠ACD +∠CEF +∠ECD=180°+180°=360°即∠BAC +∠ACE +∠CEF =360°答案 36016.已知线段AB =8 cm ,在直线AB 上有一点C ,且BC=4 cm ,点M 是线段AC 的中点, 求线段AM 的长.解 (1)当点C 在线段AB 上时,如图(1)AC =AB -BC=8-4=4(cm)∵M 是AC 的中点,∴AM =12AC =12×4=2(cm). (2)当点C 在线段AB 的延长线上时,如图(2)AC =AB +BC =8+4=12(cm)∵M 是AC 的中点,∴AM =12AC =12×12=6(cm),所以线段AM 的长是2 cm 或6 cm. 17.(2012·某某)如图,在△ABC 中,AB =AC ,∠ABC =72°,(1)用直尺和圆规作∠ABC 的平分线BD ,交AC 于点D .(保留作图痕迹,不要求写作法)(2)在(1)中作出∠ABC 的平分线后,求∠BDC 的度数.解 (1)如图,BD 就是所要求作的∠ABC 的平分线.(2)在△ABC 中,∵AB =AC ,∴∠C =∠ABC =72°,∵BD 平分∠ABC ,∴∠CBD =12∠ABC =12×72°=36°, 在△BDC 中,∵∠BDC +∠CBD +∠C =180°.∴∠BDC =180°-(∠CBD +∠C )=180°-(36°+72°)=72°.。
初中数学图形的旋转知识点总复习.doc
初中数学图形的旋转知识点总复习
今天给大家分享有关图形的旋转的知识点,图形的旋转作为几何三大变换之一,图形的旋转在中考出现的频率非常高,包括选择题的中心对称图形的判断、几何压轴大题。
要学好图形的旋转,必须要掌握旋转的基础知识,旋转的定义与性质,中心对称的定义和性质。
如何在条件很少且不知道怎么利用的情况下,如何通过旋转构造把条件利用起来。
常见的构造旋转有三种:构造60°旋转,构造90°旋转,半角旋转。
这些旋转构造前的题目特征是什么,常见的结论又是什么,需要熟悉并理解记住。
可解决大部分学生无法解决的几何难题,让你的优势充分展露出来!。
图形的旋转 初中九年级数学教学课件PPT 人教版
知识回顾 问题探究 课堂小结 探究二:旋转的基本性质
重点、难点知识 ★▲
活动2 集思广益,探索旋转的基本性质
旋转的性质: (1)对应点到旋转中心的距离相等; (2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前、后的图形全等。
知识回顾 问题探究 课堂小结 探究二:旋转的基本性质
重点、难点知识 ★▲
知识回顾 问题探究 课堂小结
探究二:旋转的基本性质
重点、难点知识 ★▲
活动3 旋转性质应用
2.②如图,△COD是△AOB绕点O按顺时针方向旋转40°得到
的图形,点C恰好在AB上,∠AOD=90°,则∠B=__6__0_°_ 。
解 ∵ △COD是由△AOB绕点O按顺时针方向旋转40°得到
∴OA=OC,A ACO 70 ∴OCD A 70 ∴ BCD 40 , ∵AOD 90,AOC BOD 40, ∴ BOC 10, ∴ B 60 。
知识回顾 问题探究 课堂小结
探究二:旋转的基本性质
重点、难点知识 ★▲
活动4 对比探究,平移与旋转的区别与联系
平移与旋转都是图形的变换; 变换前后图形的形状,大小均不变,图形的位置要改变; 平移不改变图形的方向,旋转要改变图形的方向。
知识回顾 问题探究 课堂小结
探究三:拓展应用
重点、难点知识 ★▲
(1)旋转中心是什么?旋转角是什么? 旋转中心是O,∠AOE、∠BOF等都是旋转角。
(2)经过旋转,点A、B分别移动到什么位置? 经过旋转,点A和点B分别移动到点E和点F的位置。
知识回顾 问题探究 课堂小结 探究二:旋转的基本性质
重点、难点知识 ★▲
活动2 集思广益,探索旋转的基本性质
如图:△ABC绕点O按顺时针方向转动一个角度得△DEF。
图形的旋转 初中九年级数学教学课件PPT 人教版
(第二课时)
1这. 旋某节转个课的方定向你义转学:动在一到平定了面的内角什,度么将,一这知个样识图的形图?绕形一运个动定称点为沿旋着转. 你2. 这旋是个转用定的什点性称质么为:方旋转法中获心,得转这动的些角知称为识旋的转角?.
本①节旋课转你不改还变有图形什的么大小地与方形状没,有但可解改决变定吗向?;
2.本图案可以看做是一个菱形通过几次旋转得到的?每 次旋转了多少度?
5次
600, 1200, 1800, 2400, 3000
也可以看做是二个相邻菱形通 过几次旋转得到的?每次旋转 了多少度?
2次 1200 , 2400
还可以看做是几个菱形通过几 次旋转得到的?每次旋转了多 少度?
33个个 1次1次1806000
它们与旋转中心的连线段,你能发现什么规律? 3.量一对下应∠A点O与D旋的转度中数心,连再线任段意的找夹几角对等对于应旋点转,角分.别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
旋转的基本性质 ◆旋转前、后的图形全等. ◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此 相等.
A.旋转改变图形的形状和大小 B.平移改变图形的位置 C. 图形可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到
3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图
形所在的平面上可以作为旋转中心的点共有__3_个___个.
A
D
E
●
B C
F
4、 如图:P是等边ABC内的一点,把ABP按不同的方向通过 旋转得到BQC和ACR,
◆图形的旋转是由旋转中心和旋转的角度决定.
中考数学一轮教材梳理复习课件:第31课图形的平移、对称、旋转
首页
下一页
4.(1)(2020·临沂)下列交通标志中,是中心对称图形的 是( B )
首页
下一页
(2)(2020·盐城)下列图形中,属于中心对称图形的是 ( B)
首页
下一页
(3)(2020·潍坊)下列图形,既是中心对称图形又是轴对 称图形的是( C )
首页
下一页
(4)(2020·黄石)在平面直角坐标系中,点 G 的坐标是(-
这里的 D′与 D 重合.
首页
下一页
7.如图,利用关于原点对称的点的坐标的特点,作 出与△ABC 关于原点对称的图形.
首页
下一页
解:△ABC 的三个顶点 A(-2,2),B(-4,-1),C(1, 1)关于原点的对称点分别为 A′(2,-2),B′(4,1),C′(- 1,-1),依次连接 A′B′,B′C′,A′C′,就可得到与△ABC 关于原点对称的△A′B′C′,如图所示.
首页
下一页
2.(2020·广东)如图,在正方形 ABCD 中,AB=3,点
E,F 分别在边 AB,CD 上,∠EFD=60°.若将四边形
EBCF 沿 EF 折叠,点 B 恰好落在 AD 边上,则 BE 的
长度为( D )
A.1
B. 2
C. 3
D.2
首页
下一页
3.旋转的概念与性质 (1)旋转的定义 把一个图形绕着某一点 O 转动一个角度的图形变换 叫做旋转.点 O 叫做旋转中心,转动的角叫做旋转 角,如果图形上的点 P 经过旋转变为点 P',那么这 两个点叫做这个旋转的对应点.
首页
下一页
11.(2020·赤壁)如图,在 Rt△ABC 中,∠ACB=90°, ∠A=30°,AC=6 3 ,BC 的中点为 D,将△ABC 绕 点 C 顺时针旋转任意一个角度得到△FEC,EF 的中点 为 G,连接 DG 在旋转过程中,DG 的最大值是___9__.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【基础演练】
1.(2011·宁波)平面直角坐标系中,与点(2,-3)关于原点中心对称的点是() A.(-3,2) B.(3,-2)
C.(-2,3) D.(2,3)
解析根据关于坐标原点对称的点的坐标的规律:横纵坐标互为相反数,所以(2,-3)关于原点对称的点为(-2,3).
答案 C
2.(2012·烟台)如图,所给图形中是中心对称图形但不是轴对称图形的是()
解析A.不是轴对称图形,也不是中心对称图形,故本选项错误;B.是轴对称图形,也是中心对称图形,故本选项错误;C.不是轴对称图形,是中心对称图形,故本选项正确;D.是轴对称图形,不是中心对称图形,故本选项错误.
答案 C
3.下列交通标志既是中心对称图形,又是轴对称图形的是()
解析A是轴对称但不是中心对称;B、C既不是轴对称也不是中心对称,D 既是轴对称也是中心对称.
答案 D
4. (2010·永州)如图,这是一个正面为黑,反面为白的未拼完
的拼木盘,给出如下四块正面为黑、反面为白的拼木,现欲
拼满拼木盘并使其颜色一致,请问应选择的拼木是()
解析A、C和D旋转之后都不能与图形拼满,B旋转180°后可得出与图形空白处相同的形状.
答案 B
5.(2012·苏州)如图,将△AOB绕点O按逆时针方向
旋转45°后得到△A′OB′,若∠AOB=15°,则
∠AOB′的度数是()
A.25°B.30°C.35°D.40°
解析∵将△AOB绕点O按逆时针方向旋转45°
后得到△A′OB′,
∴∠A′OA=45°,∠AOB=∠A′OB′=15°,
∴∠AOB′=∠A′OA-∠A′OB′=45°-15°=30°.
答案 B
6. (2012·玉林)如图,两块相同的三角板完全重合
在一起,∠A=30°,AC=10,把上面一块绕直
角顶点B逆时针旋转到△A′BC′的位置,点C′在
AC上,A′C′与AB相交于点D,则C′D=
________.
解析∵∠A=30°,AC=10,∠ABC=90°,
∴∠C=60°,BC=BC′=1
2AC=5,
∴△BCC′是等边三角形,
∴CC′=5,
∵∠A′C′B=∠C′BC=60°,∴C′D∥BC,
∴DC′是△ABC的中位线,
∴DC′=1
2BC=
5
2.
答案5 2
【能力提升】
7.(2012·南通)如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+3;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+3;…按此规律继续旋转,直到点P2012为止,则AP2012等于
()
A.2 011+671 3 B.2 012+671 3
C.2 013+671 3 D.2 014+671 3
解析∵Rt△ABC中,∠ACB=90°,∠B=30°,
AC=1,∴AB=2,BC=3,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+3;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+3+1=3+3;又∵2 012÷3=670…2,
∴AP2 012=670(3+3)+2+3=2 012+671 3.
答案 B
8. (2012·无锡)如图,△ABC 中,∠C =30°,将△ABC 绕点A 顺时针旋转60°得到△ADE ,AE 与BC 交于F ,则∠AFB =________度. 解析 ∵△ADE 是由△ABC 绕点A 顺时针旋转60°得到的, ∴∠CAF =60°; 又∵∠C =30°(已知),
∴在△AFC 中,∠CF A =180°-∠C -∠CAF =90°, ∴∠AFB =90°. 答案 90
9. 如图四边形ABCD 和四边形OEFG 都是正方形,点O
是正方形ABCD 两对角线的交点,已知AB =2,EF =3,正方形OEFG 绕点O 转动,OE 交BC 上一点N ,OG 交CD 上一点M .求四边形OMCN 的面积.
解 ∵四边形ABCD 是正方形,对角线AC 、BD 相交 于点O ,
∴OB =OC ,∠4=∠5=45°,∠BOC =90°, 即∠1+∠2=90°.
又∵四边形OEFG 是正方形, ∴∠EOG =90°, 即∠2+∠3=90°, ∴∠1=∠3.
在△BON 和△COM 中⎩⎨⎧∠1=∠3OB =OC ∠4=∠5
∴△BON ≌△COM (ASA)
∴S 四边形OMCN =S △ONC +S △OCM =S △ONC +S △BON =S △BOC =14S 正方形ABCD =1
4×22=1.
即四边形OMCN 的面积为1.
10.(2012·莱芜)如图①,在△ABC 中,AB =AC ,∠BAC =90°,D 、E 分别是AB 、AC 边的中点,将△ABC 绕点A 顺时针旋转α角(0°<α<180°),得到△AB ′C ′(如图②).
(1)探究DB ′与EC ′的数量关系,并给予证明; (2)当DB ′∥AE 时,试求旋转角α的度数. 解 (1)DB ′=EC ′.理由如下:
∵AB =AC ,∠BAC =90°,D 、E 分别是AB 、AC 边的中点,
∴AD =AE =1
2AB ,∵△ABC 绕点A 顺时针旋转α角(0°<α<180°),得到△AB ′C ′,
∴∠B ′AD =∠C ′AE =a ,AB ′=AB ,AC ′=AC ,∴AB ′=AC ′, 在△B ′AD 和C ′AE 中,
∵⎩⎨⎧AB ′=AC ′
∠B ′AD =∠C ′AE ,∴△B ′AD ≌△C ′AE (SAS ),AD =AE
∴DB ′=EC ′;
(2)∵DB ′∥AE ,∴∠B ′DA =∠DAE =90°, 在Rt △B ′DA 中, ∵AD =12AB =1
2AB ′,
∴∠AB ′D =30°,∴∠B ′AD =90°-30°=60°, 即旋转角α的度数为60°.
11. (2012·宿迁)(1)如图1,在△ABC 中,BA =BC ,D ,E 是AC 边上的两点,且满足∠DBE =1
2∠ABC (0°<
∠CBE <1
2∠ABC ),以点B 为旋转中心,将△BEC 按逆时针旋转,得到△BE ′A (点C 与点A 重合,点E 到 点E ′处)连接DE ′. 求证:DE ′=DE .
(2)如图2,在△ABC 中,BA =BC ,∠ABC =90°,D ,E 是AC 边上的两点,且满足∠DBE =1
2∠ABC (0°<∠CBE <∠45°). 求证:DE 2=AD 2+EC 2. (1)证明 ∵∠DBE =1
2∠ABC , ∴∠ABD +∠CBE =∠DBE =1
2∠ABC , ∵△ABE ′由△CBE 旋转而成, ∴BE =BE ′,∠ABE ′=∠CBE , ∴∠DBE ′=∠DBE , 在△DBE 与△DBE ′中, ∵BE =BE ′,∠DBE =∠DBE ′ BD =BD
∴△DBE ≌△DBE ′(SAS),∴DE ′=DE . (2)如图所示:把△CBE 旋转90°, 连接DE ′,
∵BA =BC ,∠ABC =90°, ∴∠BAC =∠BCE =45°,
∴图形旋转后点C 与点A 重合,CE 与AE ′重合, ∴AE ′=EC ,
∴∠E ′AB =∠BCE =45°, ∴∠DAE ′=90°,
在Rt △ADE ′中,DE ′2=AE ′2+AD 2, ∵AE ′=EC ,
图 2
∴DE′2=EC2+AD2
同(1)可得DE=DE′,∴DE2=AD2+EC2.。
