三角形全等拔高训练
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l 的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.MF E CBA5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCG FEDC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
(完整word版)全等三角形拔高题目附附答案解析

全等三角形提高练习1. 如图所示,△ABC ≌△ADE ,BC 的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF 的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO 的度数为多少?3. 如图所示,在△ABC 中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△C 的度数是多少?4.如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C,A ′B′交AC 于点D ,若∠A ′DC=90°,则∠A=5. 已知,如图所示,AB=AC ,AD ⊥BC 于D ,且AB+AC+BC=50cm ,而,则AD是多少?AB'CA6. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE,垂足分别为D 、E ,若BD=3,CE=2,则DE=7. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、G ,AD 与EF 垂直吗?证明你的结论.8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E,DF ⊥AC 于F,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
9. 已知,如图:AB=AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF=∠DAF ,求证:10. 如图,AD=BD ,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点BCB11. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD ,求证:BE ⊥AC12. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N,求证:(1)AE=BD (2)CM=CN (3)△CMN 为等边三角形 (4)MN ∥BC13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN于点F(1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CDAHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有(A .3个B 。
八年级数学全等三角形证明拔高集训(经典)

八年级数学全等三角形证明拔高集训(经典)1.如图所示,△ABC和△BDE都是等腰直角三角形,其中∠ABC=∠BDE=90,且AB=CB,BD=ED,连接AD并交BE于F,且AF=DF,AD=AB。
证明BE=2CD。
2.在Rt△ABC中,∠BAC=90,且AB=AC。
点D和E 分别位于AC和CA的延长线上,且CD=AE。
连接BD,过点A作AM⊥BD于M交BC于N,连接EN并延长交BD于F。
证明DF=EF。
3.如图所示,△ABC中,∠ACB=90,点D在BC上,且AC=DC。
连接AD,过点C作CE⊥___于E,点F在CE 的延长线上,连接DF。
若∠F=45,证明AE=EF。
4.如图所示,△ABC和△DAF都是等腰直角三角形,其中∠BAC=∠DAF=90,且AB=AC,AD=AF。
DF的延长线交BC于E,且∠AFC=90.证明BE=CE。
5.在Rt△ABC中,∠BAC=90,且AB=AC。
点E为AC 上一点,连接BE,过点A作AE⊥BE于H交BC于D。
点F也为AC上一点,且AE=CF。
连接DF交BE于G,连接AG。
若AG平分∠CAD,证明AH=AC。
6.如图所示,∠ACB=∠CDE=90,且AC=BC,AB=2CD=2ED。
连接BD交CE于G,且GD=GB。
F是AB的中点。
证明___。
7.在Rt△ABC中,∠ACB=90°,且AC=BC。
AD、BE分别垂直于过点C的直线于D、E,延长BE至F。
连接CF,以CF为腰作等腰直角三角形GCF,使∠GCF=90°,连接AG 交过点C的直线于H。
证明BF=2CH。
8.在△ABC中,AD⊥BC于D,点E在BC上,且AB=BE=CD。
点F是AE的中点,连接CF并延长交AB于G。
若AD=BD,证明BG=BD。
9.在Rt△ABC中,∠ABC=90,且AB=CB。
点E、O分别为BC、AC的中点,连接AE。
过点B作BG⊥AE于G交AC于M,过点A作AH⊥GO交其延长线于H。
全等三角形拔高题目附带答案

全等三角形提高练习1. 如下图,△≌△,的延长线过点E ,∠∠105°,∠10°,∠50°,求∠的度数。
2. 如图,△中,∠30°,将△绕点O 顺时针旋转52°,得到△A ′′,边A ′B ′与边交于点C 〔A ′不在上〕,那么∠A3. 如下图,在△中,∠90°,D 、E么∠C 的度数是多少?AB'C4. 如下图,把△绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′假设∠A ′90°,那么∠5. ,如下图,,⊥于D ,且50,而40,那么是多少?6. 如图,△中,∠90°,,分别过点B 、C 作过点A 的垂线、,垂足分别为D 、E ,假设3,2,那么7. 如图,是△的角平分线,⊥,⊥,垂足分别是E 、F 垂直吗?证明你的结论。
A B8.如下图,在△中,为∠的角平分线,⊥于E,⊥于F,△的面积是28220,8,求的长。
9.,如图:,∠∠E,∠∠,∠∠,求证:⊥10.如图,,⊥于D,⊥于E,与相交于点HC B11. 如下图,,为△的高,E 为上一点,交于F ,且有,,求证:⊥12.△、△均是等边三角形,、分别与、交于点M 、N〔3〕△为等边三角形 〔4〕∥ 13.:如图1,点C 为线段上一点,△、△都是等边三角形,交于点E ,交于点F (1) 求证:BAB(2)求证:△为等边三角形14.∠60°;⑤△是等边三角形;⑥∥,其中正确的有〔A.3个 B. 4个 C. 5个 D. 6个15.:、是△的高,点F在上,,点G在的延长线上,16.如图:在△中,、分别是、两边上的高,在上截取,在的延长线上截取,连结、求证:〔1〕〔2〕与的位置关系如何AB B17.如图,E 是正方形的边的中点,点F 在上,且∠∠ 求证:18.如下图,△中,,D 是延长线上一点,∠60°,E 是上一点,且,求证:19.如下图,在△中,∠90°,平分∠,⊥,垂足为F ,,求证:D20.如图:,直线、相交于C ,∠∠180°,∥,交于F21.如图,是∠的平分线,P 是上一点,⊥于D ,⊥于E ,F 是上一点,连接和,求证:22.:如图,⊥于点F ,⊥于点E ,且,求证:〔1〕△≌△ 〔2〕 点D 在∠A 的平分线上B23.如图,∥,O 是∠与∠的平分线的交点,⊥于E距离是多少?24.如图,过线段的两个端点作射线、画∠、∠的平分线交于E 〔1〕∠是什么角?〔2〕过点E 作一直线交于D ,交于C ,观察线段、,你有何发现? 〔3〕无论的两端点在、如何移动,只要经过点E ,①;②谁成立?并说明理由。
(最新最全)全等三角形练习题综合拔高题
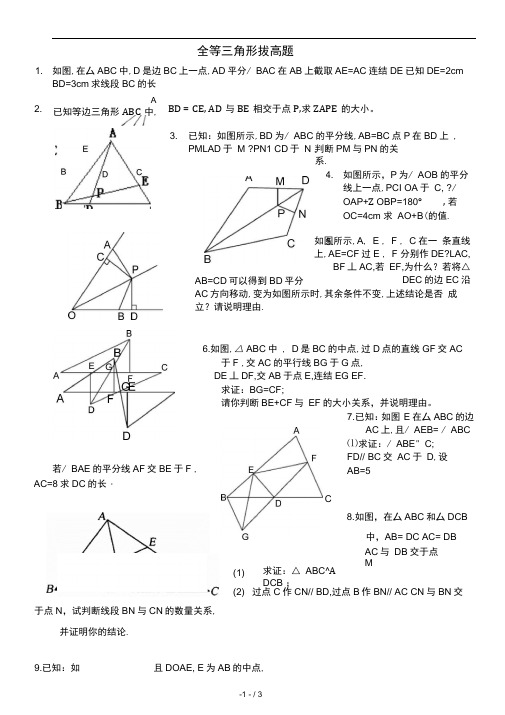
全等三角形拔高题如图,在厶ABC 中,D 是边BC 上一点,AD 平分/ BAC 在AB 上截取AE=AC 连结DE 已知DE=2cmBD=3cm 求线段BC 的长2. BD = CE, AD 与BE 相交于点P,求ZAPE 的大小。
3. A已知等边三角形ABC 中, 若/ BAE 的平分线AF 交BE 于F , AC=8求DC 的长已知:如图所示,BD 为/ ABC 的平分线,AB=BC 点P 在BD 上 ,PMLAD 于 M ?PN1 CD 于 N , 5. 判断PM 与PN 的关系.4. 如图所示,P 为/ AOB 的平分线上一点,PCI OA 于 C, ?/ OAP+Z OBP=180° , 若 OC=4cm 求 AO+B (的值.如图所示,A , E , F , C 在一 条直线上,AE=CF 过E , F 分别作DE?LAC,BF 丄AC,若 EF,为什么?若将△DEC 的边EC 沿 AB=CD 可以得到BD 平分AC 方向移动,变为如图所示时,其余条件不变,上述结论是否 成立?请说明理由.6.如图,△ ABC 中 , D 是BC 的中点,过D 点的直线GF 交AC于F ,交AC 的平行线BG 于G 点, DE 丄DF,交AB 于点E,连结EG EF. 求证:BG=CF;请你判断BE+CF 与 EF 的大小关系,并说明理由。
7.已知:如图 E 在厶ABC 的边AC 上,且/ AEB= / ABC ⑴求证:/ ABE " C; FD// BC 交 AC 于 D ,设AB=5 0(1)(2) 于点N ,试判断线段BN 与CN 的数量关系, 并证明你的结论.9.已知:如C8.如图,在厶ABC 和厶DCB中,AB= DC AC= DB AC 与 DB 交于点M求证:△ ABC^A DCB ;过点C 作CN// BD,过点B 作BN// AC CN 与BN 交 且DOAE, E 为AB 的中点,1.10.14. (1)(2)求证:△ AED^A EBC观看图前,的三角形.A11.E、DE如c A如图①,AF=CE,MBD在不添辅助线的情况下,除厶EBC外,请再写出两个与厶AED的面积相等(直接写出结果,不要求证明):F分别为线段AC上的两个动点,且DEL AC于E, BF L AC于F,若AB=CDBD交AC于点M.(1) 求证:MB=MD ME=MF2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.EF M图,已知在厶ABC中,/BAC为直角,AB=AC D为上一点,CEL BD于E.(1) 若BD平分/1ABC 求证CE=2(2) 若D为AC上一动点,/ AED如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由12.在厶ABC中, ,AB=AC取点E,使CE=BD,在AB边上取点D,在AC延长线上了连接DE交BC于点F,求证DF=EF .“也”表示出BE中线,过C作CF L AE,垂足为F,过(1) 求证:(1)AE=CD;(2)若A、o如图,取一张长方形纸片,用点,将其折叠,使点D与点B重合形,如果有,请先用13.如图△ABC^A A 'E' C , /ACB900, /A=25°,点B 在A'B' 上,求/ ACA'的度数。
最全最新初中数学《全等三角形》精选经典40题强化拔高训练

全等三角形精选经典强化训练40题1. 如图,有一池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C,连结AC 并延长到D,使CD=CA.连结BC 并延长到E,使EC=CB,连结DE,量出DE 的长,就是A 、B 的距离.写出你的证明.i.2. 已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF .3. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .4. 如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D ,BC=DF .求证:AC=EF .5. 如图,在ΔABC 中,AC=AB ,AD 是BC 边上的中线,则AD ⊥BC ,请说明理由。
FGEDCBAAF EDCBA6. 如图,AE 是ΔABC 的角平分线,已知∠B=45°,∠C=60°,求下列角的大小:(1)∠BAE (2)∠AEB7. 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
8. 如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由。
(1)∠DBH=∠DAC ; (2)ΔBDH ≌ΔADC 。
9. 如图,已知ABC ∆为等边三角形,D 、E 、F 分别在边BC 、CA 、AB 上,且DEF ∆也是等边三角形.(1) 除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的; (2) 你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.A B C E A BCDE HA BC D10. 已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
11. 如图,在矩形ABCD 中,F 是BC 边上的一点,AF 的延长线交DC 的延长线于G ,DE ⊥AG 于E ,且DE =DC ,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
河北省八年级数学上册拔高练全等三角形中的动态问题新版新人教版

∵ BP = CQ . 点 P , Q 运动的时间相等,点 P 的运动速度
是3厘米/秒,∴点 Q 的运动速度是3厘米/秒.
1
2
3
②当 CQ = BE , PB = PC 时,△ BPE ≌△ CPQ . 此时3 t
=8-3 t ,∴ t = ,
∵点 E 是 AB 的中点,∴ CQ = BE =5厘米.
∠=∠,
在△ AOB 和△ EOB 中,∵ቐ=,
∠=∠ = °,
∴△ AOB ≌△ EOB (ASA),
∴ AO = EO ,∠ BAO =∠ BEO ,∴∠ AHD =∠ BEO ,
1
2
3
∴∠ BHA =∠ AEC ,
由(1)易得∠ CAE =∠ ABH .
∠=∠,
90°,点 A 、点 B 分别是 x 轴、 y 轴上的两个动点,直角
边 AC 交 x 轴于点 D ,斜边 BC 交 y 轴于点 E .
(2)如图②,在等腰直角三角形 ABC 不断运动的过程中,
若满足 BD 始终是∠ ABC 的平分线,试探究:线段
OA , OD , BD 三者之间是否存在
某一固定的数量关系,并说明理由.
(1)如图①,若 A (0,1), B (2,0),求点 C 的坐标;
1
2
3
解:(1)过点 C 作 CF ⊥ y 轴于点 F ,
∴∠ AFC =90°,∴∠ CAF +∠ ACF =90°.
∵△ ABC 是等腰直角三角形,∠ BAC =90°,
∴ AC = AB ,∠ CAF +∠ BAO =90°,∴∠ ACF =∠ BAO .
∠=∠ = °,
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1 已知:如图,AB 丄AE, AD 丄AC,/ E =Z B, DE = CB . 求证:AD = AC .3.已知:如图,在△ MPN中, H是高MQ和NR的交点,且MQ = NQ . 2. 已知:如图,AD = AE, AB = AC,/ DAE =/ BAC . 求证:BD = CE.求证:HN = PM.i4.如图,在△ ABC中,/ ACB = 90°, AC= BC,直线I经过顶点C,过A、B两点分别作I 的垂线AE、A BBF, E、F为垂足.当直线I不与底边AB相交时,求证:EF = AE+ BF.5.已知:如图,AE丄AB, BC丄AB, AE = AB, ED = AC. 求证:ED丄AC .二、二次全等问题1•已知:如图,线段AC、BD交于O,/ AOB为钝角,AB = CD , BF丄AC于F, DE丄AC 于E, AE = CF .求证:BO = DO .u2. 已知:如图,AC与BD交于0点,AB // DC, AB = DC .若过0点作直线I,分别交AB、DC于E、F两点,求证:OE = OF.3. 如图,E在AB上,/ 1 = Z 2,Z 3=Z 4,那么AC等于AD吗?为什么?4. 已知:如图,DE 丄AC, BF 丄AC, AD = BC, DE = BF. 求证:AB// DC.5、已知:如图,AD平分/ BAC DEL AB于E, DF丄AC于F, DB=DC 求证:EB=FC【练习】1 已知/ B=Z E=90°, CE=CB AB// CD. 求证:△ ADC是等腰三角形。
2、如图:AB=AC M L AB, MF L AC,垂足分别为E、F,ME=MF 求证:MB=MC3、已知,△ ABC^n ^ ECD 都是等边三角形,且点 B , C , D 在 一条直线上求证:BE=AD4、如图:在厶 ABC 中,/ C =90 ° , AD 平分/ BAC , DEI AB 交 AB 于 E , BC=3Q BD: CD=3 2」DE= ___________________________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
C A
F
B
E G
期中复习
1.如图,等边△ABC 中,D 、E 分别为AB 、BC 边上的点,且BD=CE ,AE 与CD 交于点F ,
AG CD 于点G , 求G
AF
F
的值. 首先根据题意推出△CAE ≌△DCB ,
可知∠DCB=∠CAE ,因此∠AFG=∠CAF+∠ACF=∠ACF+∠DCB=60°, 所以∠FAG=30°即可推出结论.
2.如图,△ABC 为等边三角形,直线a//AB ,D 为直线BC 上一点,∠ADE 交直线a 于点E ,且∠
ADE=600。
(1)若D 在BC 上,求证:CD+CE=CA
(2)若D 在CB 延长线上,CD 、CE 、CA 存在怎样数量关系,给出你的结论并证明。
3.已知:等边△A BC 中,点D 为AC 边上的一动点,点E 为BC 延长线上一动点,并且始终满足AD=CE.
(1)当点D 为边AC 的中点时,求证:DB=DE.
(2)当点D 且在边AC 上且不为边AC 的中点时,且其他条件不变,试在下图中补全图形,并猜想第(1)问的结论是否发生变化?判断并证明你的结论.
4.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°.点E 是DC 的中点,过点E 作DC 的垂
线交AB 于点P ,交CB 的延长线于点M .点F 在线段ME 上,且满足CF =AD ,MF =MA . (1)若∠MFC =120°,求证:AM =2MB ;
(2)求证:∠MPB =90°- 1
2 ∠FCM .
5.如图1,BD 是等腰ABC Rt Δ的角平分线, 90=∠BAC .
(1)求证BC=AB+AD ;
(2)如图2,BD AF ⊥于F ,BD CE ⊥交延长线于E ,求证:BD=2CE ; (3)试探究线段EC 、AF 、FD 之间的数量关系,并证明你的结论.
6.如图,C 是线段AB 上一点,△ACD 和△BCE 都是等腰直角三角形,∠ADC=∠CEB=90°(1)连结DE 、M 、N 分别是AC 、BC 上一点,且∠MDC=∠CDE,∠NEC=∠CED,探索DM 、DE 、EN 之间的数量关系,并说明理由。
A B
C D
图1 A B C D F E 图2
A B
C
D E
A C
B
D
(2)延长AD 、BE 交于F 点,连结DE ,CG⊥DE 于G 点,连结CF ,CF 与DE 相交于O 点,OC=OE ,延长GC 到H 点,使得CH=CF ,探索BF 、BH 的关系,并说明理由。
7.已知:如图,平面直角坐标系中,点A(-3,0),点B(0,3),点C 为x 轴正半轴上一动点,过点A 作AD ⊥BC 交y 轴于点E.
(1)若点C 的坐标为(2,0),试求点E 的坐标.
(2)若点C 在x 轴正半轴上运动,且OC<3,其他条件不变,连OD ,求证:∠BDO 的度数不变. (3)若在点A 处有一等腰直角三角形AMN 绕点A 旋转,且AM=MN ,∠AMN=90°,连BN ,点P
为BN 的中点,试猜想OP 与MP
8.如图,等腰Rt△ABC 中,∠BAC=900
,AB =AC ,点
A 、C 分别在y 轴、x 轴上.且点A 、点C 的坐标分别为A (0,2)、(5,0). (1)求点
B 的坐标;(4分)
M C N B
E
D B
(2)如图21,点P是第一、三象限的平分线PQ上的一动点,是否存在点P,使得△PAC的面积是12,若存在,求出P点的坐标,若不存在,说明理由;
过C作CN⊥BF于N点,写出BN-NC与AM之间的数量关系,并证明你的结论.(4分)。
