第一章数的整除
01-第一章-数的整除-六年级(上)-知识点汇总-沪教版

第一章数的整除1.1 整数和整除的意义1、在数物体的时候,用来表示物体个数的数1,2,3,4,5,……,叫做整数2、在正整数1,2,3,4,5,……,的前面添上“—”号,得到的数—1,—2,—3,—4,—5,……,叫做负整数3、零和正整数统称为自然数4、正整数、负整数和零统称为整数5、整数a除以整数b,如果除得的商正好是整数而没有余数,我们就说a能被b整除,或者说b能整除a1.2 因数和倍数1、如果整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数2、倍数和因数是相互依存的3、一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身4、一个数的倍数的个数是无限的,其中最小的倍数是它本身1.3 能被2, 5整除的数1、个位数字是0,2,4,6,8的数都能被2整除2、整数可以分成奇数和偶数,能被2整除的数叫做偶数,不能被2整除的数叫做奇数3、在正整数中(除1外),与奇数相邻的两个数是偶数4、在正整数中,与偶数相邻的两个数是奇数5、个位数字是0,5的数都能被5整除6、0是偶数1.4 素数、合数与分解素因数1、只含有因数1及本身的整数叫做素数或质数2、除了1及本身还有别的因数,这样的数叫做合数3、1既不是素数也不是合数4、奇数和偶数统称为正整数,素数、合数和1统称为正整数5、每个合数都可以写成几个素数相乘的形式,这几个素数都叫做这个合数的素因数6、把一个合数用素因数相乘的形式表示出来,叫做分解素因数7、分解素因数方法:树枝分解法、短除法1.5 公因数与最大公因数1、几个数公有的因数,叫做这几个数的公因数,其最大的一个叫做这几个数的最大公因数2、如果两个整数只有公因数1,那么称这两个数互素数3、把两个数公有的素因数连乘,所得的积就是这两个数的最大公因数4、如果两个数中,较小数是较大数的因数,那么这两个数的最大公因数较小的数5、如果两个数是互素数,那么这两个数的最大公因数是11.6 公倍数与最小公倍数1、几个数公有的倍数,叫做这几个数的公倍数2、几个数中最小的公因数,叫做这几个数的最小公倍数3、求两个数的最小公倍数,只要把它们所有的公有的素因数和他们各自独有的素因数连乘,所得的积就是他们的最小公倍数4、如果两个数中,较大数是较小数的倍数,那么这两个数的最小公倍数是较大的那个数如果两个数是互素数,那么这两个数的最小公倍数是两个数的乘积试试你的身手!一:填空题(每空1分,共22分)1.3.6÷2=1.8,(能,不能)说2整除2.8。
六年级第一学期第一章数的整除概念

2012学年预备级年第一学期期中考试知识点整理第一章数的整除概念1、正整数、负整数、整数、自然数:(1)用来表示物体个数的数1、2、3、4……,叫做正整数。
-1、-2、-3、-4……,叫做负整数。
0、1、2、3、4……,叫做自然数(2)零和正整数统称为自然数,0是最小的自然数,没有最大的自然数。
(3)正整数、零和负整数,统称为整数。
2、整数a除以整数b,如果除得的商正好是整数而没有余数,我们就说a能被b整除,或÷=也叫整除)。
者说b能整除a。
(050整除的条件:(1)除数、被除数都是整数。
(2)被除数除以除数,商是整数而且没有余数。
3、整数a能被整数b整除,a就叫做b的倍数,b就叫做a的因数。
(1)一个数的因数是有限的。
最小的因数是1,最大的因数是它本身。
一个数的因数通常是成对出现的(用两数相乘去检验是否遗漏)。
(2)一个数的倍数的个数是无限的。
最小的倍数是它本身,没有最大的倍数。
(3)因数与倍数是相互依存的。
如果光说谁是倍数,或谁是因数是不完整的。
4、能被特殊的数字整除的特征:(重点掌握前4个)(1)能被2整除的整数,个位上数字为0、2、4、6、8,即:是偶数。
(2)能被5整除的整数,个位上数字为0、5。
(3)能同时被2和5整除的整数(即能被10整除),个位上数字为0。
(4)一个整数的各个位数字之和能被3整除,则这个整数能被3整除。
(5)一个整数能被2和3整除,则这个数能被6整除。
注:一个整数能被n和m整除,则这个数能被m·n整除。
5、整数按能否被2整除可以分为:奇数和偶数。
在正整数中奇数和偶数都是相邻的。
定义:如果一个整数能被2整除,称该整数为偶数。
如果一个整数不能被2整除,称该整数为奇数。
6、(1)只含有因数1和本身的整数叫做素数或质数,如果除了1和它本身还有别的因数,这样的数叫做合数。
(2)几个数共有的因数,叫做这几个数的公因数,最大的一个数叫做这几个数的最大公因数。
数的整除知识讲解

数的整除第一章数的整除知识要点1.整除:整数a除以整数b所得的商是整数,而余数为零,那么我们就说a能被b整除或b能整除a.即只有整数参与的除法。
如:52134,91713,34172÷=÷=÷=都是整除。
判断关键:①被除数与出数都是整数;②商也为除数,且余数为0.2.整数的分类:⑴整数一般分为正整数(1,2,3…)、0、负整数(-1,-2,…,-98,…)⑵按能否被2整除,整数又可以分为奇数与偶数。
能被2整除的整数叫做偶数,不能被2整除的整数叫做奇数。
奇数、偶数有正负之分。
⑶按因数的个数,整数又可以分为素数与合数。
2,3,5,7,11,13,17,19…4,6,8,9,10,15,21,…①特征:素数只有两个因数(1和它本身);合数至少有三个因数。
奇数素数正整数分类:合数偶数 1②判断方法:分解素因数:就是把一个合数分解成几个素数相乘的形式。
所以只有合数可以分解素因数,即能分解的事合数,不能分解的是素数。
熟练掌握短除法分解素因数的。
最好能认识100以内的素数与合数,熟记20以内的素数,理解1-9这九个数字的一切特征。
3.数与数之间的关系:⑴因数与倍数:整数a 能被整数b 整除,那么我们就说a 是b 的倍数,b 是a 的因数。
①如果b 是素数,这时我们又说b 是a 的素因数;②公因数:几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做最大公因数; ③公倍数:几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做最小公倍数; ④因数的个数是有限的,最小的是1,最大的是它本身;倍数的个数是无限的,只有最小的它本身。
⑵互 素:是指两个正整数只有公因数1(或最大公因数是1),那么这两个数称为互素数。
肯定互素的三种情况:①连续的两个正整数;②1与其它正整数;③不相等的素数。
4. 最大公因数和最小公倍数的求法:①列举法;②分解素因数法;③短除法。
求90与72的最大公因数和最小公倍数法一:90=2×3×3×5 法二:72=2×2×2×3×390和72的公有因数分别是2、3、3。
第一章 数的整除性 第四节 最大公因数1

初等数论(4)(第一章数的整除性第四节最大公因数(1))定义1 整数a1,a2, ,a k的公共因数称为a1,a2, ,a k的公因数。
不全为零的整数a1,a2, ,a k的公因数中最大的一个叫做a1,a2, ,a k的最大公因数,记为(a1,a2, ,a k)。
由于每个非零整数的因数的个数是有限的,所以最大公因数是存在的,并且是正整数。
如果(a1,a2, ,a k)=1,则称a1,a2, ,a k是互质的;如果(a i , a j)=1,1 ≤i ≤k,1 ≤ j ≤k,i≠ j,则称a1,a2, ,a k是两两互质的。
显然,由a1,a2, ,a k两两互质可以推出(a1,a2, ,a k)= 1,反之则不然,例如(2,6,15)=1,但(2,6)= 2。
定理1 下面的等式成立:(ⅰ)(a1,a2, ,a k)=(|a1|,|a2|, ,|a k|);(ⅱ)(a,1)=1,(a,0)=|a|,(a,a)=|a|;(ⅲ)(a,b)=(b,a);(ⅳ)若p是质数,a是整数,则(p,a)=1或p∣a;(ⅴ)若a = bq + r,则(a,b)=(b,r)。
证明(ⅰ)我们先证明a1,a2, ,a k与|a1|,|a2|, ,|a k|的公因数相同。
设d是a1,a2, ,a k 任一公因数,由定义d∣ a i,i = 1,2,……,n。
因而d∣| a i | ,i = 1,2,……,n。
故d是|a1|,|a2|, ,|a k|的一个公因数,同样的方法可证|a1|,|a2|, ,|a k|的任一个公因数都是a1,a2, ,a k的一个公因数.即a1,a2, ,a k与|a1|,|a2|, ,|a k|的公因数相同。
由此可直接得(a1,a2, ,a k)=(|a1|,|a2|, ,|a k|);(ⅱ)、(ⅲ)、(ⅳ)显然。
(ⅴ)如果d∣a,d∣b,则有d∣r = a -bq,反之,若d∣b,d∣r,则d∣a = bq + r。
初等数论第一章整除

例1:设 x, y 为整数,且5 | x 9 y 则 5 | 8x 7 y
证:因为 8x 7 y
8( x 9 y) 65y
因为5 | x 9 y
所以有
又
5 | 65y
5 | 8x 7 y
例2:证明若3|n,7|n,则21|n
证:因为3|n,所以n= 3n1 又因为7|n,所以 7 | 3n1 显然有 7 | 7n 1 则有 7 | 7n1 2 3n1 即 7 | n1 有 n1 ห้องสมุดไป่ตู้7n2 即有 n 21n2 所以有21|n
注: (1)连续n个整数中必有一个数被n整除。 可作为一个定理,在证明整除问题时非常 有用。 (2)注意整数的各种表示。 例2: 证明若a不是5的倍数,则
与
中有且仅有一个数被5整除
证明: 这四个数有一个是5的倍数 若 5 | a 1或 又 所以 即 a 1, a 1 有且仅有一个数被5整除
n 是整数,所以 3
n2 2
n3 6
是
注:这里用了连续n个整数的乘积是n!的 倍数的结论.
注:连续n个整数的乘积是n!的倍数。 a、当n个整数都大于零时,由
m( m1)( m n1) n!
C
n m n1
而组合数为整数,可知连续n个整数的乘积是n! 的倍数。 b、当n个整数中有一个为零时,显然成立。
n 注:1、
2、
a b (a b)M1
n
n
a b (a b)M 2 , 2†n
n
3、
(a b) aM3 b ,
n n
例5、试证明任意一个整数与它的各位数 字和的差必能被9整除。
数的整除知识要点

第一章:数的整除基本知识:(1)零和正整数统称为自然数。
最小的自然数为0,最小的正整数为1。
(2)正整数、零和负整数,统称为整数。
(3)整除的条件:1、被除数、除数都是整数。
2、商是整数而且没有余数。
a÷b若整除,则有两种表述方法:a能被b整除, b能整除a(4)一个数的因数的个数是有限的。
最小的因数是1,最大的因数是它本身。
一个数的倍数的个数是无限的。
最小的倍数是它本身,没有最大的倍数。
a÷b若整除,则a是b的倍数,b是a的因数。
相互依存,不能说成a是倍数、b是因数。
(5)能被2整除的整数,个位上数字为0、2、4、6、8。
能被5整除的整数,个位上数字为0、5。
能被3整除的整数,各个数位上数字之和能被3整除。
(6)一个整数能被2整除为偶数,不能被2整除为奇数。
(7)奇+奇=偶偶+偶=偶奇+偶=奇奇⨯奇=奇偶⨯偶=偶奇⨯偶=偶(8)相邻的两个整数相差1。
相邻的两个奇数相差2。
相邻的两个偶数相差2。
(9)只含有因数1和本身的整数叫做素数或质数。
除了1和它本身之外还有别的因数,这样的数叫做合数。
1既不是素数也不是合数。
(10)整数按奇偶可以分为奇数和偶数这两类。
整数按因数个数可以分为素数、1、合数这三类。
(11)100以内的素数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
(12)51=3×17,91=7×13 57=19×3 68=17×4(13)2是唯一的偶素数。
最小的素数是2,最小的合数是4。
(14)几个整数公有的因数,叫做它们的公因数,其中最大的一个叫做它们的最大公因数。
几个整数的公有的倍数叫做他们的公倍数,其中最小的一个叫做它们的最小公倍数。
(15)如果两个整数只有公因数1,那么称这两个数互素。
(16)求两个整数的最大公因数:把所有公有的素因数连乘。
上海六年级数学上册知识点精选
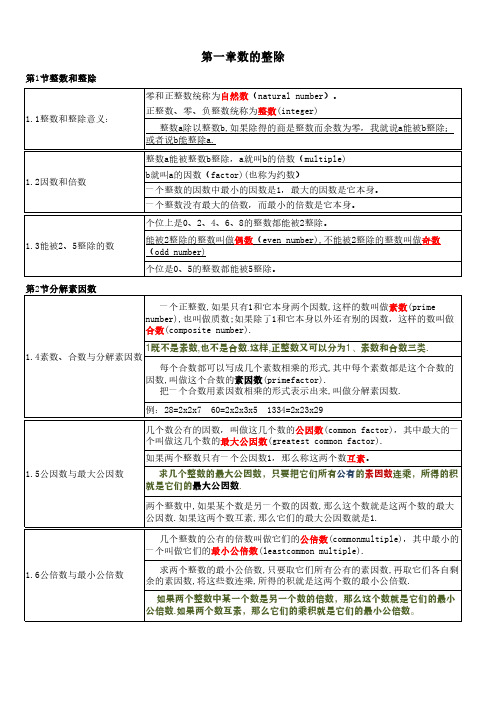
第1节整数和整除第2节分解素因数零和正整数统称为自然数(natural number )。
正整数、零、负整数统称为整数(integer)1.1整数和整除意义:1.2因数和倍数能被2整除的整数叫做偶数(even number),不能被2整除的整数叫做奇数(odd number)1.3能被2、5整除的数个位是0、5的整数都能被5整除。
几个整数的公有的倍数叫做它们的公倍数(commonmultiple),其中最小的一个叫做它们的最小公倍数(leastcommon multiple).求两个整数的最小公倍数,只要取它们所有公有的素因数,再取它们各自剩余的素因数,将这些数连乘,所得的积就是这两个数的最小公倍数.如果两个整数中某一个数是另一个数的倍数,那么这个数就是它们的最小公倍数.如果两个数互素,那么它们的乘积就是它们的最小公倍数。
1.6公倍数与最小公倍数 整数a 除以整数b,如果除得的商是整数而余数为零,我就说a 能被b 整除;或者说b 能整除a.一个正整数,如果只有1和它本身两个因数,这样的数叫做素数(primenumber),也叫做质数;如果除了1和它本身以外还有别的因数,这样的数叫做合数(composite number).整数a 能被整数b 整除,a 就叫b 的倍数(multiple)b 就叫a 的因数(factor)(也称为约数)一个整数的因数中最小的因数是1,最大的因数是它本身。
一个整数没有最大的倍数,而最小的倍数是它本身。
第一章数的整除个位上是0、2、4、6、8的整数都能被2整除。
两个整数中,如果某个数是另一个数的因数,那么这个数就是这两个数的最大公因数.如果这两个数互素,那么它们的最大公因数就是1.1.5公因数与最大公因数 每个合数都可以写成几个素数相乘的形式,其中每个素数都是这个合数的因数,叫做这个合数的素因数(primefactor).把一个合数用素因数相乘的形式表示出来,叫做分解素因数.例:28=2x2x7 60=2x2x3x5 1334=2x23x291.4素数、合数与分解素因数几个数公有的因数,叫做这几个数的公因数(common factor),其中最大的一个叫做这几个数的最大公因数(greatest common factor).如果两个整数只有一个公因数1,那么称这两个数互素。
初等数论第一章第一节

练习题 1证明: 若3 | n且7 | n,则21| n.
2 设a = 2k -1, k 源自 Z ,若a | 2n,则a | n.
4 证明: 若m - p | mn + pq,则m - p | mq + np.
1证明:∵3 | n,∴可设n = 3m, 由7 | n得, 7 | 3m,而7 | 7m,所以7 | (7m - 2× 3m), 即7 | m,∴21| 3m,即21| n.
证明:∵ n = n(ax + by) = nax + nby 又 ab | na, ab | nb ∴ab n.
例3 已知a,b, c, d ∈ Z且a − c | ab + cd. 求证 : a − c | ad + bc.
证明:∵ a − c | (a − c)(b − d ), ∴a − c | ab + cd − (ad + bc) 又a − c ab + cd,∴a − c ad + bc.
2证明:∵ a | 2n,∴a | 2kn, 而2kn = (2k -1)n + n = an + n, ∴a | an + n,又a | an,∴a | n.
4证明:∵ mq + np = (mn + pq) − (m − p)(n − q), 又∵ m − p|mn + pq, ∴m − p|mq + np.
例题
例1 已知a,b, c, d,t ∈ Z,且t |10a − b,t |10c − d. 求证 : t | ad − bc.
证明: ad − bc = c(10a − b) − a(10c − d ) ∵t 10a − b,t 10c − d ∴t ad − bc.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 数的整除1.1整数和整除的意义一.学法指导:1. 知道自然数、整数、整除的定义:⎪⎩⎪⎨⎧⎭⎬⎫负整数自然数正整数整数0 整除——整数a 除以整数b ,除得的商是整数而余数为零。
2.掌握整除的两种表述方法:被除数能被除数整除;除数能整除被除数。
二.友情提示:1.零既不是正整数,也不是负整数;2.零是最小的自然数;3.没有最大的整数;4.整除约定在正整数范围内考虑;5.整除的条件:除数、被除数都是整数;被除数除以除数,商是整数而且余数为零。
三.例题讲解:例1:下列哪一个算式的除数能整除被除数?4÷8; 42÷7; 11÷3; 0.25÷0.05=5解:因为4÷8=0.5(商不是整数)42÷7=611÷3=3……2(余数不为0)0.25÷0.05=5(被除数、除数是小数,不是整数)所以,除数能整除被除数的算式是42÷7。
例2:从下列数中选择适当的数填入相应的圈内:1,-2,0,25%,27,0.3,-100,32 ,56, 自然数 负整数 整数四.本课练习:1.在15,-27,3.8,0,11,-42,67%中,为自然数的是___________正整数的是____________负整数的是_______整数的是_________________。
2.最小的自然数是_______,最小的正整数是________,最大的负整数是________。
3.写出三个比2小的整数________________;比2小的自然数有_______________。
4.能整除12的数有____________________。
5.选择:能整除18的数有( )A.3个B.4个C.5个D.6个6.在下列各组数中,哪个数能整除另一个数?24和8 72和9 16和96 17和51 23和69 100和257.在下列各组数中,28和7 9和6 1.44和1.2 5和125 17和3第一个数能被第二个数整除的是____________________第一个数能被第二个数除尽的是____________________8.在下列数中,哪个数能被另一个数整除?请一一举出:24,8,9,72,16,96,51,17,80,251.2因数和倍数一. 学法指导:1. 知道倍数和因数的定义:整数a 能被整数b 整除,a 就叫做b 的倍数, b 就叫做a 的因数。
2. 会求一个数的倍数和因数。
二.友情提示:1.一个整数的因数个数是有限的,其中最小的因数是1,最大的因数是它本身。
2.一个整数的倍数个数是无限的,其中最小的倍数是它本身。
3.找一个数的因数的方法:(1)能整除这个数的整数就是这个数的因数(2)利用积与因数的关系一对一对找三.例题讲解:例1:分别写出48和17的因数解:48的因数有1、2、3、4、6、8、12、16、24、4817的因数有1、17解答方法:利用积与因数的关系一对一对找48 =1×48 =2×24 =3×16 =4×12 =6×8例2:分别写出3和5的倍数解:3的倍数有3,6,9,12,15,…,5的倍数有5,10,15,20,25,…解答方法:因为能被3、5整除的整数都是3、5的倍数所以3、5与正整数1,2,3,4,5,…的积都能被3、5整除四.本课练习:1.24的因数有__________,91的因数有___________。
2.在4、8、16、32、36、64、80七个数中,80的因数有_________________。
3.一个数的最大的因数是12,这个数是______,它所有的因数有__________。
4.90的因数有____个,这些因数的和是______。
5.能被9整除的数,至少有_______个因数。
6.13的倍数有_________________________。
7.100以内17的倍数有________________,25的倍数有_________________。
8.在下列几道除法算式中,写出哪一个数是哪一个数的因数,哪一个数是哪一个数的倍数?20÷16=1.25 85÷17=5 12÷0.3=409. 如果a=2×3×5,那么a 的所有因数有____________。
10.一个数既是18的倍数,又是18的因数,这个数是_________。
11.一个数的最小倍数是15,这个数的因数有________________。
12.在60的因数中,是4的倍数的数的和是__________13.判断:一个数的最大因数就是它的最小的倍数。
( )14.判断:1是所有自然数的因数。
( )15.甲数的最大因数等于乙数的最小倍数,甲数____乙数(填“〉”或“〈”或“=” )1.3能被2、5整除的数一.学法指导:1.掌握能被2整除的数的特征:个位上是0,2,4,6,8的整数都能被2整除;2.掌握能被5整除的数的特征:个位上是0或者5的整数都能被5整除3.⎩⎨⎧整除的数偶数:能被整除的数奇数:不能被整数22 二.友情提示:1.一个整数不是奇数就是偶数;2.奇数的个位上的数是奇数;3.能同时被2、5整除的数一定能被10整除。
三.例题讲解:例1:由0,1,2,3,4组成一个能被2整除的三位数中,最小的一个数是什么数?由小到大,第十个数是什么数?解:最小的一个数是102,由小到大,第十个数是204。
解答方法:1.根据能被2整除的数的特征,其个位上是0,2,4,6,8;由上述5个数所组成的三位数,最小的百位数是1,最小的十位数是0,而个位数满足能被2整除,所以取2。
2.要找第十个小的三位数,百位数1的有9个,再从百位数是2中去找,且能被2整除的最小三位数是204。
例2:能被2整除的四位数中,最大的数是几?解:能被2整除的四位数中,最大的数是1000。
解答方法:能被2整除的四位数是1000,1002……,其中最大的数是9998。
例3:在下列数中找出既能被2整除又能被5整除的数,填写在适当的圈内,这样的数有什么特点?16,35,60,85,96,125,320,888能被2整除的数能被5整除的数能同时被2、5整除的数解答方法:因为:能同时被2、5整除的数一定能被10整除。
能被2整除的数的个位数字是0,2,4,6,8;能被5整除的数的个位数字是0或5;所以:能同时被2、5整除的数的个位数字是0四.本课练习:1.判断:两个相邻的偶数相差2()2.在110后面连续5个偶数是_____________________________。
3.从17起,连续5个奇数是______________________________。
4.与奇数相邻的两个数是_____数;与偶数相邻的两个数是______数;5.4个连续自然数的和是134,其中最小的一个数是__________;6.5个连续偶数的和是180,这三个数分别是________________;7.下列那些数有因数2、那些数有因数5?13,26,37,48,66,71,94,152,625,900,1002,4050有因数2的数是_______________________。
有因数5的数是_______________________。
8.(1)2143至少加上____才能被2整除;(2)4321至少减少____才能被2整除;(3)1243至少加上___才能被5整除;(4)3142至少减少____才能被5整除;9.写出4个既能被2整除又能被5整除的数_________________;10.在下列数中找出既能被2整除又能被5整除的数,填写在适当的圈内,这样的数有什么特点?18,55,160,825,962,1025,3020,8567能被2整除的数能被5整除的数能同时被2、5整除的数11.不能被2整除的自然数叫____________;12.任何一个奇数加上1以后,一定能被______整除;13.能被2整除的最大两位数是_______;14.能被2整除的三位数中,最大的偶数是________;15.能同时被2和5整除的最小三位数是__________;16.一个两位数,既是5的倍数,又有因数2,这个数最小是____,最大是___;17.一个两位数,它能被3整除,有时5的倍数,而且是偶数,这个数最小是_______;18.(1)在下列每个数的□内填上一个数字,使得这个数有因数2,你还能写出几个?7□□3□(2)在下列每个数的□内填上一个数字,使得这个数有因数5,你还能写出几个?12□□06□19.在12,28,36,75,96,100中能被2整除,又有3这个约数的数是_________;能被5整除,又有2这个约数的数是_________;20.判断:25的倍数中最小的一个是50。
()21.判断:5是5的倍数,5也是5的约数。
( )22.能被5整除的最大三位数是_________;23.能被5整除的两位数中,最小的奇数是______;24.5个连续奇数的和是195,其中最大的一个数是__________;25.写出在120以内能被5整除的奇数(至少写3个)___________________;26.有两个奇数,它们的积是65,差是8,他们的和是_________;27.邻近124前面三个连续奇数的和是________;28.用0,4,5,6四个数字,按要求写出一个没有重复数字的四位数:(1)既能被2整除又能被5整除:(2)不能被2整除,只能被5整除:1.4素数、合数与分解素因数(一)一. 学法指导:1.理解素数、合数的意义:素数——一个正整数,如果只有1和它本身两个因数,这样的数叫做素数。
合数——一个正整数,如果除了1和它本身以外还有别的因素,这样的数叫合数。
2.⎪⎩⎪⎨⎧1合数素数正整数3.会用求因数的方法或用整除的特征来判断一个正整数是否为素数。
4.熟记20以内的全部素数。
二.友情提示:1.“1”既不是素数也不是合数。
2.学会区分奇数和素数、偶数和合数的意义。
三.例题讲解:例1:判断18,29,51和91是素数还是合数。
解法一:18的因数有:1,2,3,6,9,1829的因数有:1,1945的因数有:1,3,5,9,15,4591的因数有:1,7,13,91通过检查每个数的因数的个数,可以知道:18,45,91是合数,29是素数。
解法二:18能被3整除,因此除了1和18以外,18还有因数3,所以18是合数。
同样,45能被5整除,91能被7整除,所以45、91也是合数。
例2:小于30的既是素数,又是偶数的数是哪几个?解:小于30的素数有:2,3,5,7,11,13,17,19,23,29而其中又是偶数的数只有2。
