成像电子光学系统空间和时间像差的均方根半径_RMS_研究
Zemax中的点列图的分析方法

点列图的原理就是显示光学系统在IMA面上的成像。
换句话说,它就就是通过计算,把一系列物方的点通过光学系统以后,成像在IMA面上的情况给实际绘制出来。
为了表现方便,它可以选择一系列预定的模板形式,具体来说,比如一个在轴上的点,从无限远成像到IMA面上,ZEMAX就模拟在无限远有若干个发光点(光束),这些点平行射入入瞳,然后经过光学系统,最后成像在IMA面上。
显然如果光学系统就是完美的光学系统,那么这些点成像点为一个理想的点。
但对于实际的光学系统,就会成像为一个弥散斑。
那么这个弥散斑在IMA面上的像,就就是Spot Diagram。
同理,在非轴上点,也可以参照主光线的角度与位置,形成一系列的发光点,经过入瞳最后成像在IMA面上最后也形成一个弥散斑。
如何通过Spot Diagram观察出光学设计的质量,简单说,这个弥散斑越小越好。
如果您发现弥散斑足够小,满足您对光学系统最小弥散斑的要求(spot diagram的单位就是微米)那么您的光学系统就完全可以进行实际的加工了。
换句话说,就就是您的光学系统已经可以设计完成了。
如何才知道您的光学系统足够的好?这里有个参考,就就是airy 斑的参考。
airy斑就是物理光学的一个概念。
它指出在形成的弥散斑直径在2、44*F*(主波长)以内的时候,该光学系统可以认为就是理想(完美)光学系统。
这样当您在Spot Diagram图中,在setting 菜单中,设置显示airy斑。
然后发现您的点列图完全都在airy斑环之内,您就可以认为您的光学系统设计已经完美。
但实际上,很少有光学系统,可以满足符合airy斑直径的要求。
那么说明您的光学系统有像差。
究竟就是哪种像差在起主要作用?主要的像差有,球差,慧差,像散,场曲,畸变。
这些像差在spot diagram上的表现各不相同。
但由于一个光学系统通常就是各种像差的混合。
因此需要您对spot diagram的形状进行判断。
确认就是主要就是哪种像差,然后通过修改玻璃,或者曲率以及光阑的位置等加以调整。
zemax实验

zemax实验(1)镜头参数输入:在zema某中,对镜头参数输入有如下约定:1)透镜表面个数(面数)2)符号规则:曲率半径r:如曲率中心位于镜片表面右侧,则曲率半径为正;反之为负厚度d:如下一表面位于当前表面的右侧,则两表面之间的厚度为正;否则为负(2)Gen(GeneralLenData通用)这个按钮用于调用系统数据对话框,它用来定义作为整个系统的公共数据,而不是仅仅与单个面有关的数据。
常用的选项有以下几个:1)Aperture(孔径)系统孔径表示在光轴上通过系统的光束大小。
要设置系统孔径,需要定义系统孔径类型和系统孔径值。
ApertureType:EntrancePupilDiameter(入瞳直径)ImageSpaceF/#(像空间F/#)ObjectSpaceNumericalAperture(物空间数值孔径)FloatByStopSize(随光阑浮动)Para某ialWorkingF/#(近轴工作F/#)ObjectConeAngle(物方锥角)2)RayAiming(光线校准)如果光线校准关闭,ZEMA某将会以光线充满入瞳为来确定进入系统的光线方向以及能量大小。
当RayAiming分别为Para某ial和Real时,光线分别按照近轴和实际光线追迹方式。
光线充满光阑Stop面。
某Rayaiming使用前应通过Analyi——Fan——PupilAberration先查看一下入瞳象差某当系统的F/#较小时,使用Para某ialRayAiming会引起较大的误差,应使用RealRayAiming。
(3)Fie(FieldData视场)视场对话框可以确定视场点。
视场可以用Angle(角度)、ObjectHeight(物高)、Para某ialHeight(近轴像高)、RealImageHeight(实际像高)这几种方式描述,具体情况根据系统特点选择。
设计视场的选择一般小视场光学系统(2ω<80°)0、0.707、1.0中等视场光学系统(80°<2ω<140°)0、0.5、0.707、0.866、1.0大视场光学系统(2ω>140°)0、0.3、0.5、0.7、0.85、1.0视场权重:默认为1,最后根据需要不断修改。
变焦结构光成像系统的光学设计

变焦结构光成像系统的光学设计王潇枫;石岩;庄一;汪诗宇【摘要】为了实现快速低成本改变光学系统焦距,设计了基于液体透镜的变焦结构光三维成像镜头和微透镜阵列.系统采用7片球面玻璃镜片和1片液体透镜结构,F#为3.2,全视场大小为10 mm,总长180 mm,焦距变化范围54 mm~61 mm.结果表明:该系统能实现投影距离227 mm~256 mm调节,调焦过程中目标表面清晰,细节分辨率高,系统在整个变焦区域内,在40 lp/mm时,全视场M T F优于0.2,系统场曲小于0.2,畸变小于0.2%.柱面微透镜阵列整体尺寸为10 mm×10 mm,周期宽度为1 mm,厚度为1 mm.随着投影距离的增长,光学系统成像质量先上升后下降,在237 mm处成像质量最优,随着投影距离的增加,光学系统的放大倍率增大,光学系统整体相对照度不均匀性小于0.2.%In order to change the focal length of optical system rapidly and at a low cost,we de-signed the zoom structured light three-dimensional imaging lens and micro-lens array based on liquid lens.The system utilizes the structure of seven spherical glass lenses and one liquid lens, the F# number is 3.2,the full field of view(FOV)is 10 mm,the system total length is 180 mm, and the focal length ranges from 54 mm to 61 mm.The design result shows that,the system can adjust the distance of projection in 227 mm~256 mm;during focusing process the target surface is clear and the resolution ratio has a high quality,while system is within the whole zoom range;at 40 lp/mm,the modulation transfer function(M TF)of full FOV is better than 0.2,the system field curvature is less than0.2,and the distortion is less than 0.2%.The cylindrical micro-lens array has an overall size of 10 mm×10 mm,a period width of 1 mm and a thicknessof 1 mm. With the increase of projection distance,the imaging quality of optical system increases first and then decreases,the imaging quality is optimal at 237 mm;as the projection distance increases,the magnificationof the optical system increases;the overall relative illuminance heterogeneity of op-tical system is less than 0.2.【期刊名称】《应用光学》【年(卷),期】2018(039)001【总页数】6页(P22-27)【关键词】光学设计;结构光;液体透镜;变焦【作者】王潇枫;石岩;庄一;汪诗宇【作者单位】中国计量大学光学与电子科技学院,浙江杭州310018;中国计量大学光学与电子科技学院,浙江杭州310018;中国计量大学光学与电子科技学院,浙江杭州310018;中国计量大学光学与电子科技学院,浙江杭州310018【正文语种】中文【中图分类】TN942.21引言近年来,三维扫描技术在临床医学、文物保护、工业生产等方面得到广泛应用[1-5]。
高分辨率超大幅宽星载成像光谱仪光学系统设计

航天返回与遥感第42卷第1期92SPACECRAFT RECOVERY & REMOTE SENSING2021年2月高分辨率超大幅宽星载成像光谱仪光学系统设计王保华李可唐绍凡张秀茜王媛媛(北京空间机电研究所,北京 100094)摘要针对高空间分辨率、高光谱分辨率和大幅宽成像的遥感应用需求,提出了高分辨率超大幅宽星载成像光谱仪技术方案,分析确定了成像光谱仪光学系统指标,设计了空间成像光学系统和光谱成像光学系统。
空间成像光学系统采用自由曲面离轴三反设计方案,实现了大视场、大相对孔径像方远心设计,系统相对畸变小于0.02%;光谱成像光学系统的狭缝长度超过90mm,采用新型离轴透镜补偿型Offner设计方案,实现了长狭缝高保真光谱成像设计,谱线弯曲和色畸变均小于1/10像元尺寸。
设计结果表明,高分辨率超大幅宽星载成像光谱仪光学系统简单紧凑,成像品质接近系统衍射极限,满足星载高光谱对地成像的数据应用要求。
关键词成像光谱仪光学系统设计自由曲面凸面光栅航天遥感中图分类号: O439文献标志码: A 文章编号: 1009-8518(2021)01-0092-08DOI: 10.3969/j.issn.1009-8518.2021.01.011Optical System Design of a Spaceborne Imaging Spectrometer withHigh Resolution and Super SwatchWANG Baohua LI Ke TANG Shaofan ZHANG Xiuqian WANG Yuanyuan(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)Abstract In order to meet the requirements of remote sensing applications with high spatial resolution, hyperspectral resolution and super swatch, a new scheme of the space imaging spectrometer with high resolution and super swatch is put forward. The spatial resolution and swatch are 50m and 150km respectively, and the hyperspectral resolution can be better than 5nm between 0.4μm and 1.0μm. The comprehensive performance has reached the international advanced level. The index parameters are optimized based on SNR and the modulation transfer function. Then the space imaging optical system and the spectrum imaging optical system are designed according to the optical desigh parameters. The free-form surface is adopted for the off-axis mirror to realize telecentric design of wide field of view and large relative aperture. The relative distortion is lower than 0.02%. The slit length is over 90mm in the spectrum imaging optical system. And the new oftener configuration with off-axis correction lens is put forward to realize high fidelity design. The keystone and smile can be both controlled within 1/10 pixel. The optical system of the space imaging spectrometer with high resolution and super-swatch has so favorable imaging quality and compact volume,收稿日期:2020-03-02基金项目:科技部国家重点研发计划项目(2016YFB0500501)引用格式:王保华, 李可, 唐绍凡, 等. 高分辨率超大幅宽星载成像光谱仪光学系统设计[J]. 航天返回与遥感, 2021, 42(1): 92-99.WANG Baohua, LI Ke, TANG Shaofan, et al. Optical System Design of a Spaceborne Imaging Spectrometer withHigh Resolution and Super Swatch[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(1): 92-99. (in Chinese)第1期王保华等: 高分辨率超大幅宽星载成像光谱仪光学系统设计 93which can satisfy the demand of remote sensing application.Keywords imaging spectrometer; optical system design; free-form surface; convex grating; space remote sensing0 引言成像光谱仪是一种将成像技术与光谱技术相结合的新型光学遥感仪器,可以同时采集目标的空间信息、辐射信息和光谱信息,形成谱像合一的数据立方体,在大气、陆地、海洋、农林、应急减灾、水土和矿产资源调查等领域具有重要应用价值[1-3]。
均方根回转半径

均方根回转半径【实用版】目录1.均方根回转半径的定义2.均方根回转半径的计算方法3.均方根回转半径的应用领域4.均方根回转半径的实际应用案例正文均方根回转半径(Root Mean Square Turning Radius,简称 RMSR)是一种描述旋转对称性的参数,常用于预测和优化旋转对称结构的性能。
它是旋转对称性中的一个重要概念,广泛应用于光学、通信、机械制造等领域。
一、均方根回转半径的定义均方根回转半径是指一个物体在旋转过程中,其形状中心到旋转轴线的距离。
通常用符号 rmsr 表示,单位为米。
在实际应用中,均方根回转半径反映了物体旋转对称性的程度,较小的均方根回转半径意味着更高的旋转对称性。
二、均方根回转半径的计算方法均方根回转半径的计算方法较为复杂,通常需要通过一系列的数学运算和模拟来得到。
一般采用迭代法、近似法或者数值模拟法等方法进行计算。
此外,还有一种基于张正友椭球面的计算方法,可以较为精确地计算出均方根回转半径。
三、均方根回转半径的应用领域均方根回转半径在多个领域都有广泛应用,包括但不限于:1.光学领域:在光学设计中,均方根回转半径是一个重要的性能参数,影响光学系统的成像质量和像差。
2.通信领域:在无线通信中,均方根回转半径可以用来描述天线阵列的旋转对称性,进而影响通信系统的性能。
3.机械制造:在机械制造中,均方根回转半径可以用来预测和优化机械零部件的性能,提高其使用寿命和稳定性。
四、均方根回转半径的实际应用案例以光学领域为例,假设我们要设计一款高性能的望远镜,均方根回转半径的优化是关键。
我们可以通过调整望远镜的镜片形状、材料和排列方式,来降低均方根回转半径,从而提高成像质量和分辨率。
在实际应用中,均方根回转半径的优化往往需要多个领域的知识交叉,才能取得理想的效果。
综上所述,均方根回转半径是一个描述旋转对称性的重要参数,广泛应用于光学、通信、机械制造等领域。
2018-2019-zemax实验报告-实用word文档 (12页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==zemax实验报告篇一:ZEMAX 实验报告基于基本透镜组的照相物镜设计Zemax设计报告徐昕 10272055设计目的通过对设计一个以基本透镜组为基础的照相物镜,学会Zemax软件的基本应用及操作。
设计要求设计一个照相物镜,系统焦距f’=9mm,相对孔径1:4设计过程1.系统建模1.1选取初始结构从《光学设计手册》(李士贤,郑乐年编,北京理工大学出版社,1990)中选取了一个1.2系统特性参数输入在General系统通用数据对话框中设置孔径和玻璃库,如图1-1,图1-2。
打开视场设定对话框设置5个视场,如图1-3。
打开波长设定对话框点击“Select>>F,d,C(visible)”自动加入三个波长,如图1-4。
表1-1图 1- 1图 1- 2图1- 3图1- 41.3初始结构输入对照表1-1,在Lens Data Editor中输入初始结构,如图1-5。
利用Zemax中的“solve”功能,求解透镜组最后一面的厚度。
选取需要设计的单元格,在“Solve”中选取“Thickness”,弹出“Thickness Solve on surface 7”求解对话框。
在对话框“Solve type”中选择“Marginal ray height”,将“Height”值输入为“0”,表示将像面设置在边缘光线聚焦的像方焦平面上,如图1-6,图1-7。
图 1-5图1-6图 1-71.4调整系统焦距打开“System Data”系统数据报告窗口,查看系统现有焦距,为65.65414mm,如图1-8,与设计要求不符,需要通过缩放功能进行调整。
选择“Tools>>Scale Lens”,缩放因子为9/65.65414=0.137082,在Scale By Factor缩放因子后填入0.137082,如图1-9。
zemax中的ray fan和spot diagram的含义

zemax中的ray fan和spot diagram的含义ray fan在zemax中有一个重要的分析手段,就是显示ray fan图。
显示ray fan可以通过多种方式,比如菜单analysis-fans-ray aberration显示;也可以通过直接点击在菜单栏目上的Ray按钮。
ray fan表示是光学系统的综合误差。
它的横坐标是光学系统的入瞳标量,因此总是从-1到+1之间。
显然0的位置对应就是光轴在入瞳中心的焦点。
纵坐标则是针对主光线(发光点直穿光阑中心点的那条光线)在像面上的位置的相对数值。
由于我们在计算光路的时候,通常仅仅考虑两类光线,子午面和弧矢面。
这样对于不同的面,就有两种不同rayfan显示。
要概念上理解ray fan图,我们假设有一个薄透镜的光学系统。
光阑就在这个薄透镜上。
有一个在子午面上的轴外点,发出一束光线射向这个透镜,那么它在子午面的ray fan图将是这样绘制的:首先,这一束光线会射向光学系统的入瞳(同时也是光阑)上,会在子午面上有一个光束的分布。
因此他们每个对应点都将在未来的rayfan图上显示-1到+1的横坐标。
显然主光线的位置是光阑的中点,就是0的位置。
然后这一束光线继续穿过光学系统,最后折射到像面上。
由于由像差的存在;在像面的子午面上将形成由无数光点形成的光线。
(对于理想的光学系统,还是应该形成一个点)这个线上一定会有一个点,是由主光线形成的。
这个点就做为整个像差的参考原点。
其他的各个点到这个点的位置差值就是在ray fan中对应于各个横坐标入瞳位置的纵坐标值!这样,一系列的点就可以在这个下xy的坐标系统中表示出来。
只要有足够的点,就能连接绘制一个完整的ray fan图。
这就是ray fan图的含义,它表示的是这个光学系统参照入瞳位置的像差综合值。
要指出的是:● 由于有子午和弧矢两个面,因此对于每个视场的ray fan都有两个。
一个子午T(对应于PY和EY),和一个弧矢S(对应于PX和EX)● 又由于系统选择的光线不同,在每个视场的ray fan中可能会显示多个光线的不同ray fan。
(完整版)像质评价方法
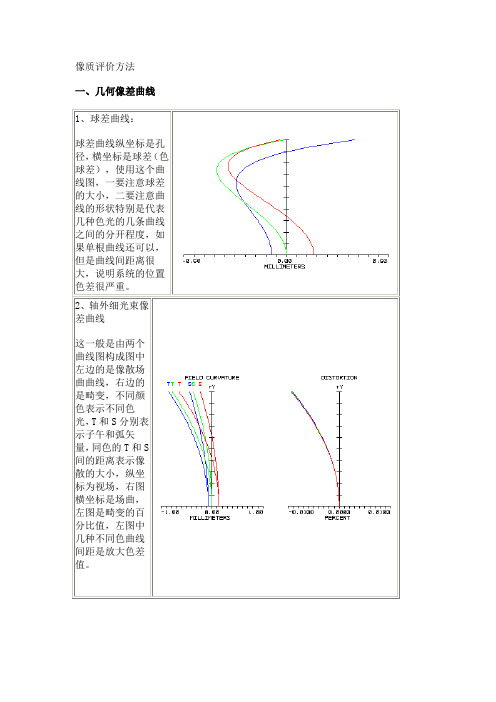
像质评价方法一、几何像差曲线1、球差曲线:球差曲线纵坐标是孔径,横坐标是球差(色球差),使用这个曲线图,一要注意球差的大小,二要注意曲线的形状特别是代表几种色光的几条曲线之间的分开程度,如果单根曲线还可以,但是曲线间距离很大,说明系统的位置色差很严重。
2、轴外细光束像差曲线这一般是由两个曲线图构成图中左边的是像散场曲曲线,右边的是畸变,不同颜色表示不同色光,T和S分别表示子午和弧矢量,同色的T和S间的距离表示像散的大小,纵坐标为视场,右图横坐标是场曲,左图是畸变的百分比值,左图中几种不同色曲线间距是放大色差值。
二、点列图——光束的光亮度由一点发出的许多光线经光学系统后,因像差使其与像面的交点不再集中于同一点,而形成了一个散布在一定范围的弥散图形,称为点列图。
,点列图是在现代光学设计中最常用的评价方法之一。
图中的几个图分别表示给定的几个视场上不同光线与像面交点的分布情况。
使用点列图,一要注意下方表格中的数值,值越小成像质量越好。
二根据分布图形的形状也可了解系统的几何像差的影响,如,是否有明显像散特征,或彗差特征,几种色斑的分开程度如何,有经验的设计者可以根据不同的情况采取相应的措施。
RMS RADIUS:均方根半径值;GEO RADIUS:几何半径(最大半径)三、传递函数调制传递函数MTF:一定空间频率下像的对比度与物的对比度之比。
能反映不同空间频率、不同对比度的传递能力。
一般而言,高频传递函数反映了物体细节传递能力,低频传递函数反映物体轮廓传递能力,中频传递函数反映对物体层次的传递能力。
1、MTF曲线图图中不同色的曲线表示不同视场的复色光(白光)MTF曲线,T和S分别表示子午和弧矢方向,最上方黑色的曲线是衍射极限。
横坐标是空间频率lp/mm(每毫米线对),纵坐标是对比度,最大是1。
曲线越高,表明成像质量越好。
[返回本章要点]2、传函与离焦关系曲线图此图表明对设定空间频率不同视场的子午、弧矢MTF与离焦量的关系,图中横坐标是离焦量,纵坐标是对比度,通过此图可以看出各视场的最佳焦面是否比较一致,MTF是否对离焦比较敏感。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对不同初能分
2
时间像差的均方根半径ΔT
在电子发射的初角度服从朗伯分布和初能量服
布下的空间像差均方根半径给出了更完整和更详细 的研究。 迄今为止, 不同的电子逸出初能分布下的时间 像差均方根半径的表达式尚未给出 。本文旨在研究 成像电子 光 学 系 统 中, 逸出电子的初角度为朗伯 ( Lambert) 分布, 初能量分别为余弦 ( Cosine ) 分布、 贝塔( Beta) 分布和麦克斯韦 ( Maxwell ) 分布下的时 间和空间像差的均方根半径表达式 ΔT 和 Δr, 以及时 间和空间像差的均方根半径的最小值 ΔT min 和 Δr min 及其对应的最佳像面位置, 进一步讨论了时间像差 和空间像差的均方根半径之间的联系 。
[7 ]
2 式中 ε z = ε0 cos α0 为逸出电子的轴向发射初电位;
, 即电子以初角度 α 逸出的概率是 G ( α) = cosα ( 1)
E c 为阴极面的场强, 取负值; ε z1 为理想像面对应的 电子轴向初电位。 公式表明, 一级近轴时间像差与 电极的具体结构和电位分布无关, 而与电子发射的 阴极面上的电场强度有关。 初能、 b ) 中, 将式( 6 ) 代入式( 5a, 经整理后可得 ΔT = 2 m0 槡 ε0 m × e - Ec
业已证明
: 在成像电子光学系统中, 表示空
10 ] ( 2 ) 贝塔分布 [9,
间弥散的均方根半径的大小与系统调制传递函数的 优劣在各个像面上都是一一对应的; 均方根半径最 小的像面, 正好是调制传递函数最佳的像面。 文献 2 [ 2] 给出的以指数形式 exp[- ( πρf) ]表示的调制 传递函数体现了像差均方根半径与调制传递函数之 间的对应关系, 因为式中“聚焦误差系数 ” ρ 正是系 统的均方根半径
第 37 卷 第 4 期 2011 年7 月
光 学 技 术
OPTICAL TECHNIQUE
Vol. 37 No. 4 July 2011
1582 ( 2011 ) 04050706 文章编号: 1002-
成像电子光学系统空间和时间像差的 均方根半径 ( RMS) 研究
*
1 1 1 2 3 公慧 ,周立伟 ,倪国强 ,张智诠 ,艾克聪
Study on the root mean square ( RMS) radius of spatialtemporal aberrations in imaging electronoptical systems
GONG Hui1 ,ZHOU Liwei1 ,NI Guoqiang1 ,ZHANG Zhiquan2 ,AI Kecong3
1 z1 1 z1 0 0m 0 0m
1 /2
= ε0 / ε m , 0 ≤ ξ ≤ 1, 其中 ε m 为电子逸出的最大发射 508
ΔT =
槡
2 m0 槡 ε0 p × e - Ec
第4 期
公慧, 等:
成像电子光学系统空间和时间像差的均方根半径( RMS) 研究
1
1
(1 - + ) ε dξ ] ξ ∫槡 η N( η) dη ξ ∫ ε 槡 = ∫ ξ ( ) ( 1 - ξ) dξ 2. 1 余弦分布 l! ( k - 1 + 1 ) ! l! ( k + 1 ) ! 2 2 , 若当电子逸出初能分布函数为余弦分布时 则 = = 1 将表达式式 ( 2 ) 代入时间像差的均方根半径公式 ! ( k - 2 + l + 2)! ( k + l + 3 2)
4 π 3 3( π - 2) 因为
1 2 0
槡∫
ε z1 ε0 m
1
0
ε z1 ξ dsin π ξ + ε0 m 2
3 /2
( )
] ( 8)
1 /2
槡
2 m0 槡 ε0 m × e - Ec
[
ε z1 4 ( k + l + 1) ! - k! 3 ε0 m
ξ = 0 . 1894305308612978 ∫ ξ dsin ( π 2 ) ξ = 0 . 2552566614716921 ∫ ξ dsin ( π 2 )
11 ] ( 3 ) 麦克斯韦分布 [2,
。 因此, 均方根半径不仅可以
而且可以作为计算传 表示系统的空间分辨率特性, 递函数的一个辅助评价指标。研究逸出电子在不同 便可选取合适的光阴 初能分布下的均方根半径值, , 极及其对应的电子初能分布 使成像质量满足像管 设计的需要。 对 空 间 像 差 均 方 根 半 径 的 研 究,最 早 有 Beurle[5]对麦克斯韦分布下锐聚焦系统均方根半径 的讨论统时间像差的均 方根半径可以表示为 ΔT = ΔT =
2 ΔT = { 槡 — — —
ΔT 槡
— — —2
∫∫ = {∫ ∫
0 ∞ 0
1
π /2
0 π /2
( ΔT) 2 sin2 α0 N( ξ) dα0 dξ} 1 / 2 ( ΔT) 2 sin2 α0 N( η) dα0 dη} 1 / 2 ( 5a, b) , 我们已经证明, 成像系
( 1. School of Optics and Photonics,Beijing Institute of Technology,Beijing 100081 ,China) ( 2. Institute of Armored Force Engineering,Beijing 100072 ,China) an Institute of Applied Optics,Xi’ an 710065 ,Shanxi,China) ( 3. Xi’ Abstract : In imaging electronoptical systems, the root mean square( RMS) radius can not only express the characteristics of spatialtemporal resolutions,but also serve as a supplementary evaluation index of electronoptical modulation transfer function with the advantages of less calculation, more convenience and more visual. The expressions of RMS radius of spatialtemporal aberrations are deduced and discussed with the assumptions that the initial emission angle of photoelectron obeys Lambert distribution and the initial energy obeys Cosine,Beta and Maxwell distributions respectively. The minimum values of RMS radius of spatialtemporal aberrations and their corresponding optimal positions of imaging plane are solved. This research not only has importance in spatialtemporal resolutions’calculation and evaluation of imaging systems,but also provides theoretical guidance for selecting suitable photocathode in the design of image tubes and streak tubes. Key words: spatial aberrations; temporal aberrations; root mean square( RMS) radius; modulation transfer function
0
在前面的研究中 可表示为 ΔT =
[12 ~ 18 ]
统的时间渡越弥散主要取决于一级近轴时间像差 ,
1
逸出光电子的初角度、 初能量分布
槡 {
2 m0 1 ( ε - 槡 ε z1 ) e Ec 槡 z
}
( 6)
在成像系统中, 从阴极面逸出的电子运动的方 向与轴线的夹角 α 被称为逸出角。 一般公认为服 从朗伯分布
0 ≤α≤π /2 。 式中, 在成像系统中, 常用的逸出光电子的初能分布 函数有以下几种形式: ( 1 ) 余弦分布[8] ( 2) ( ) 为电子分布密度函数, ξ ∫ N( ξ) dξ = 1 , π N( ξ) = ξcos π ξ 2( π - 2) 2
1 0 2
式中 N( ξ)
槡 ε ε 4 [1 ] ξN( ξ) dξ - ξ N( ξ) dξ + 槡 ∫ ∫ 2 3 槡 ε ε
∞ 0
[1 2∫
η N( η) dη -
4 3
ε z1 ε0 p
∞
k+ 2
l
1 /2
z1
0
0
1
0p
1 k - 2 +1
l
0
( 7a, b)
( 7a) , 经整理后可得 ΔT =
槡
2 m0 槡 ε0 m π e - Ec 2( π - 2)
[
ξ - ∫ ξ dsin ( π 2 )
1 2 0
将上述积分式代入式( 11 ) , 经整理后可得 ΔT =
( 1. 北京理工大学 光电学院,北京 100081 ) ( 2. 装甲兵工程学院,北京 100072 ) ( 3. 西安应用光学研究所,陕西 西安 710065 ) 摘 要: 在成像电子光学系统中, 均方根半径不仅可以表示系统的时间和空间分辨率特性, 而且可以作为计算调制
