重庆市南开中学2010届高三考前模拟预测(数学文)

合集下载

重庆市2010年高考仿真试卷三数学文(附答案)

2010年普通高等学校招生全国统一考试（重庆卷）数学(文史类)模拟试卷（三）数学试题(文史类)共4页．满分150分．考试时间120分钟．注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上．2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其它答案标号．3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上． 4．所有题目必须在答题卡上作答，在试卷上答题无效． 5．考试结束，将试卷和答题卡一并收回．一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项符合题目要求．1． 4sin ,tan 05θθ=->，则cos θ= A ． 45- B ． 35- C ． 35D ．452．等腰直角∆ABC 中，1AB AC ==，则AB BC ⋅=A ．B ． 1C ．D ． 1-3．计算机是将信息转化为二进制数处理的，二进制即“逢二进一”如2(1101)表示二进制数，将它转化为十进制数为32101212021213⨯+⨯+⨯+⨯=，那么二进制数120102)111(个转化为十进制数为A ． 201121- B ． 201021- C ． 200921- D ． 200821-4．设3,1x R x x x ∈≠≠则“”是“”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．已知正三棱柱111ABC A B C -中，若1AB =，则异面直线1AB 与1C B 所成的角为A ． 60B ． 90C ． 105D ． 756．已知函数()f x 是(,)-∞+∞上的偶函数，若对于0x ≥，都有(2()f x f x +=），且当[0,2)x ∈时，2()log (1f x x =+），则(2010)(2011)f f -+的值为 A ． -2B ． -1C ． 1D ． 27．设双曲线()222200x y a b a b－＝1＞，＞的渐近线与抛物线12+=x y 相切，则该双曲线的离心率等于A ．B ． 2C ．D ．8．将7个人（含甲、乙）分成三个组，一组3人，另两组2人，不同的分组数为a ，甲、乙分到同一组的概率为p ，则,a p 的值分别为A ． 105a =,521p =B ． 105a =,421p =C ． 210a =,521p =D ． 210a =,421p =9．若函数()f x 的导数为'()(1)f x x x =-+，则函数(log )(01)a f x a <<的单调减区间为A ． [1,0]-B ． 1[,),(0,1]a +∞C ． 1[1,]aD ． 11(,],[,)a a-∞+∞10．已知定义域为R 的函数1,1|1|()1,1x x f x x ⎧≠⎪-=⎨⎪=⎩，若关于x 的方程2()()0f x bf x c ++=有3个不同的实根123,,x x x ，则222123x x x ++等于 A ． 5B ． 2222b b+ C ． 13D ． 2232c c+ 二．填空题：本大题共5小题，每小题5分，共25分． 11．若61()x ax+的二项展开式中2x 的系数为52，则a =_____________（用数字作答）． 12．若直线3x +4y +m =0与圆⎩⎨⎧+-=+=θθsin 2cos 1y x `（θ为参数）没有公共点，则实数m 的取值范围是_____________．13．实数,x y 满足不等式组2,24,0,x y x y x y +≥⎧⎪-≤⎨⎪-≥⎩则23x y +的最小值是_____________．14．若关于x 的不等式2||40x a x -+≥恒成立，则a 的取值范围是_____________． 15．给出以下四个命题：① 若cos cos 1αβ=，则sin()0αβ+=； ② 已知直线x m =与函数()sin ,()sin()2f x xg x x π==-的图像分别交于点M ，N ，则||MN③ 若数列2()n a n n n N λ+=+∈为单调递增数列，则λ取值范围是2λ<-； ④ 已知数列{}n a 的通项3211n a n =-，其前n 项和为n S ，则使0n S >的n 的最小值为12．其中正确命题的序号为_____________．三．解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．ABC DEP16．（本题满分13分）小李、小王、小张三人在一起做游戏时，需要确定做游戏的先后顺序，他们约定用“剪刀、布、锤子”的方式确定，在一个回合中．求：（Ⅰ）恰有一人出“布”的概率；（Ⅱ）至少有一人出“布”的概率．17．（本题满分13分）设函数f (x )=2)0(sin sin cos 2cos sin 2πϕϕϕ<<-+x x x 在π=x 处取最小值．（Ⅰ）求ϕ的值；（Ⅱ）在∆ABC 中,c b a ,,分别是角A,B,C 的对边,已知,2,1==b a 23)(=A f ,求角C ．18．（本题满分13分）如图，四棱锥P -ABCD 的底面是平行四边形，PA ⊥平面ABCD ,AC AB ⊥,AB PA =,点E 是PD 上的点，且DE ＝λPE (0<λ≤1)．（Ⅰ）求证：PB ⊥AC ；（Ⅱ）求λ的值，使//PB 平面ACE ；（Ⅲ）当1λ=时，求二面角E -AC -B 的大小．19．（本小题满分12分）已知数列{}n a 满足：11,a =n n n m a a 221⋅+=+n （m 是与无关的常数且0m ≠）．（Ⅰ）设2nn na b =，证明数列{}n b 是等差数列，并求n a ；（Ⅱ）若数列{}n a 是单调递减数列，求m 的取值范围．20．（本题满分12分）设函数329()62f x x x x a =-+-．（Ⅰ）对于任意实数12,[1,0]x x ∈-，求证：12)()(2/1/≤-x f x f ；（Ⅱ）若方程()0f x =有且仅有一个实根，求a 的取值范围．21．（本题满分12分）已知动圆P 过点1(0,)(0)4a a >且与直线14y a=-相切．（Ⅰ）求动圆圆心P 的轨迹E 的方程；（Ⅱ）设直线2y x =+与轨迹E 交于点A 、B ，M 是线段AB 的中点，过M 作x 轴的垂线交轨迹E 于N ．① 证明：轨迹E 点N 处的切线l 与AB 平行；② 是否存在实数a ，使0NA NB ⋅=？若存在，求a 的值；若不存在，说明理由．2010级高三数学（文）模拟试题（三）参考答案一、选择题：本大题共10题，每小题5分，共50分。

南开中学高2010届高三数学文周练

南开中学高2021届高三数学周练(文)一、选择题(此题6个小题，每题10分，共60分)1、{}n a 是等比数列，2512,4a a ==，那么12231n n a a a a a a ++++=…( ) A 、16(14)n --B 、16(12)n --C 、32(14)3n --D 、32(12)3n -- 2、如果1238,,,,a a a a …为各项都大于零的等差数列，公差0,d ≠那么( )A 、1845a a a a >B 、1845a a a a <C 、1845a a a a +>+D 、1845a a a a =3、等差数列{}n a 中，349141510,a a a a a ++++= 那么17S 等于( )A 、34B 、68C 、17D 、514、设数列{}n a 的前n 项和2*32()n S n n n N =-∈，那么当2n ≥时有( )A 、1n n S na na >>B 、1n n S na na <<C 、1n n na S na <<D 、1n n na S na <<5、设有公差不为零的等差数列{}n a 与等比数列{}n b ，两数列有关系；1133,,a b a b ==75a b =，那么( )A 、1113b a =B 、1131b a =C 、1163b a =D 、6311b a = 6、{}n a 是等比数列，且231,a a >=1231231111()()()()0,n n a a a a a a a a -+-+-++->…那么自然数n ( )A 、最大值是4B 、最小值是5C 、最大值是5D 、最小值是6二、填空题(此题4个小题，每题10分，共40分)7、数列{}n a 的前n 项和的公式为2231,n S n n =--那么通项公式为_________。

南开中学高三数学模拟试卷(文科)(参考答案)

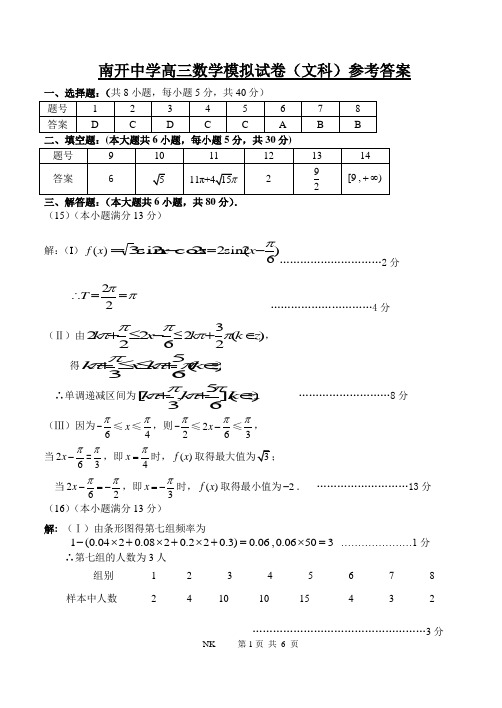
南开中学高三数学模拟试卷（文科）参考答案（15）（本小题满分13分）解：（I ）()f x x x 2cos 2sin 3-=)62sin(2π-=x …………………………2分ππ==∴22T …………………………4分（Ⅱ）由≤-≤+6222πππx k )(232z k k ∈+ππ，得)(653z k k x k ∈+≤≤+ππππ ∴单调递减区间为)](65,3[z k k k ∈++ππππ. ………………………8分（Ⅲ）因为64x ππ-≤≤，则2263x πππ--≤≤，当26x π-=3π，即4x π=时，()f x 当262x ππ-=-，即3x π=-时，()f x 取得最小值为2-． ………………………13分（16）（本小题满分13分）解: （Ⅰ）由条形图得第七组频率为1(0.0420.0820.220.3)0.06,0.06503-⨯+⨯+⨯+=⨯= …………………1分∴第七组的人数为3人组别 1 2 3 4 5 6 7 8 样本中人数 24101015432……………………………………………3分（Ⅱ）由条形图得前五组频率为 (0.008+0.016+0.04+0.04+0.06)×5=0.82，………………………………………4分后三组频率为1－0.82=0.18 …………………………………5分估计这所学校高三年级身高在180cm 以上（含180cm ）的人数800×0.18=144（人） ……………………7分 (Ⅲ)第二组四人记为a 、b 、c 、d ，其中a 为男生，b 、c 、d 为女生，第七组三人记为1、2、3，其中1、2为男生，3为女生，基本事件列表如下：a b c d 1 1a 1b 1c 1d 2 2a 2b 2c 2d 3 3a 3b 3c 3d所以基本事件有12个 …………………………………………………10分恰为一男一女的事件有1b ，1c ，1d ，2b ，2c ，2d ，3a ；共7个 ………12分因此实验小组中，恰为一男一女的概率是712. …………………13分（17）（本小题满分13分）(Ⅰ)证明：因为菱形ABCD ，所以BD AC ⊥, 又因为平面ACEF ⊥平面ABCD ,EC AC ⊥,平面ACEF 平面ABCD AC =故EC ⊥平面ABCD EC BD ⊥所以BD ⊥平面ACEF ---------------5分BD ⊂平面BDE ,所以平面BDE ⊥平面ACEF ；--------------6分 (Ⅱ) 连结EO ,//AM EO ,BEO ∠为异面直线BE 与AM 所成的角或补角，由(Ⅰ)知，90EOB ∠=,在直角三角形EOB 中，EO AM ==BO =所以异面直线BE 与AM ---------------10分 (Ⅲ)由已知易得BF FD =,BE ED =,所以,EO BD FO BD ⊥⊥, EOF ∠为二面角E BD F --的平面角所以二面角E BD F --为90.---------------13分（18）（本小题满分13分）解：（Ⅰ）点A (0,2)代入圆C 方程，得．2(2)9m -=∵2m <，∴1m =-． …… 1分圆C ：22(1)9x y ++=，圆心(0,1)-．设直线PF 1的斜率为1k ，()3,8P当1k 不存在时，1:3PF x =，显然不合题意舍去．当1k 存在时，PF 1：18(3)y k x -=-，即11380k x y k --+=．3=．解得143k =． …………………… 3分直线PF 1：43120x y -+=直线PF 1与x 轴的交点横坐标为－3，∴c ＝3．F 1（－3，0），F 2（3，0）． …………………… 4分 2a ＝|AF 1|＋|AF 2|=，a =a 2＝13，b 2＝4．椭圆E 的方程为：221134x y +=． …………………… 6分（Ⅱ）由||||AM AN =知点A 在线段MN 的垂直平分线上，由2221134y kx x y =-⎧⎪⎨+=⎪⎩消去y 得22(413)520k x kx +-=（*）由0≠k ，得方程（*）的2(52)0k ∆=>，即方程（*）有两个不相等的实数根---8分设),(11y x M 、),(22y x N ，线段MN 的中点),(00y x P ，则12252413k x x k +=+，∴1202262413x x kx k +==+，∴2002226822413413k y kx k k -=-=-=++即22268(,)413413k P k k -++ ……… 10分 0≠k ，∴直线AP 的斜率为200281313y k x k---=，由AP MN ⊥，得2813113k k k--⨯=-，解得：k =， …… 12分 ∴ 存在直线l 满足题意，方程为：0-0+----------------------------13分（19）（本小题满分14分）解：（Ⅰ）方法一：由13n n S S +=得：数列{}n S 是等比数列，公比为3，首项为1…2分11133n n n S --∴=⋅= ……………3分当2n ≥时，12213323n n n n n n a S S ----=-=-=⋅ ……………4分21(1)23(2)n n n a n -=⎧∴=⎨⋅≥⎩……………5分方法二：13n n S S +=，∴ 13(2)n n S S n -=≥以上两式相减得：13(2)n na a n +=≥， ……………2分在13n n S S +=中，取1n =得：1213a a a +=即2122a a ==， ……………3分2123a a ∴=≠ {}n a ∴为第二项起的等比数列，公比为3 ……………4分21(1)23(2)n n n a n -=⎧∴=⎨⋅≥⎩……………5分（Ⅱ）令(1)n nn n b a +=由（Ⅰ）知： {}n a 为第二项起的等比数列，公比为3，22a t =∴当2n ≥时，223n n a t -=⋅，2(1)23n n n n b t -+=⋅ ……………6分1121(1)(2)(1)(1)(1)23233n n n n n n n n n n n b b t t t +---++++--=-=⋅⋅⋅ ……………7分 ① 若0t >，则10n n b b +-<即1(2)n n b b n +<≥∴数列{}n b 是从第二项起的递减数列 ……8分而12b t=，23b t =，21b b >max 23()n b b t∴== ……………9分对任意*n N ∈，都有(1)nn n a λ+>3t λ∴> ……………10分②若0t <，则10n n b b +->即1(2)n n b b n +>≥ ∴数列{}n b 是从第二项起的递增数列 …11分而120b t =<，当2n ≥时，2(1)023n n n n b t -+=<⋅ (,0)n b ∴∈-∞ ……………12分对任意*n N ∈，都有(1)nn n a λ+>，0λ∴≥ ……………13分综合上面：若0t >，则3tλ>；若0t <，则0λ≥。

重庆市重点高中2010届高三模拟试题样卷(数学)_138

重庆市重点高中2010届高三模拟试题样卷（数学）第一部分选择题（共50分）一．选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．请将答案代号填在答题卷的相应位置上． 1．已知点A （－1，0）．B （1，3），向量()21,2k =-a ，若A B ⊥a ，则实数k 的值为A ．－2B ．－1C ．1D ．2 2．设3log2=a ，6log4=b ，9log8=c ，则下列关系中正确的是A ．c b a >>B ．b c a >>C ．a b c >>D ．b a c >>3．已知圆()224x a y -+=被直线1x y +=所截得的弦长为22，则实数a 的值为 A ．0或4B ．1或3C ．－2或6D ．－1或34．已知,,αβγ为平面，命题p ：若,βα⊥βγ⊥，则//αγ；命题q ：若α上不共线的三点到β的距离相等，则βα//．对以上两个命题，下列结论中正确的是 A ．命题“p 且q”为真 B ．命题“p 或q ⌝”为假C ．命题“p 或q”为假D ．命题“p ⌝”且“q ⌝”为假5．设13i22ω=-+，且()443243210x a x a x a x a x a ω+=++++，则2a 等于A ．333i22-+B ．333i22--C ．333i -+D ．333i --6．椭圆)0(12222>>=+b a by ax的四个顶点为A ．B ．C ．D ，若四边形ABCD 的内切圆恰好过椭圆的焦点，则椭圆的离心率是A ．253-B ．853+C ．215- D ．514-7．已知函数()y fx =的大致图像如图所示，则函数()y fx =的解析式应为A ．()2ln x fx x x=-B ．()ln x fx x x=-C ．()ln x fx x x=+D ．()2ln x fx x x=+8．设x ，y 满足约束条件⎪⎩⎪⎨⎧≤+≥≥12340y x x y x 则132+++x y x 的取值范围为A ．[]1,5 B ．[]2,6 C ．[]2,10 D ．[]3,119．如图，P A B ∆所在的平面α和四边形A B C D 所在的平面β互相垂直，且,A D B C αα⊥⊥，4A D =，8B C =，6A B =，若t a n 2t a n10A D PBC P ∠+∠=，则点P在平面α内的轨迹是 A ．圆的一部分 B ．椭圆的一部分 C ．双曲线的一部分 D ．抛物线的一部分 10．已知,,x y z满足方程222(2)(2)2x y z +-++=，则222x y z++的最大值是A ．42B ．23C ．23D ．2第二部分非选择题（共100分）二．填空题：本大题共5小题，每小题5分，满分25分．请将答案填在答题卷的相应位置上．11．等差数列有如下性质：若{}n a 是等差数列，则数列12nn a a a b n+++=也是等差数列．类比上述性质，相应地，若{}n c 是正项等比数列，则数列n d =_______________也是等比数列．12．已知集合{}2340A x x x =--=，{}10B x m x =+=，若B A ⊆，则m 所能取的一切值构成的集合为．13. 若双曲线14422=++ym x的一条准线方程是34-=y ，则m 的值为＿＿＿＿。

南开中学高三数学模拟试卷(文科)(参考答案).doc

南开中学高三数学模拟试卷（文科）参考答案一、选择题:（共8小题,每小题5分,共40分）题号 1 2 3 4 5 67 8答案D C D C C A B B二、填空题：（本大题共6小题，每小题5分，共30分）题号9 10 11 12 13 14答案611兀+471?兀292[9,+ 8)三、解答题：（本大题共6小题，共80分）. （15）（本小题满分13分）解:(I) /(兀)=V^sin2兀一cos2x = 2sin(2x --------------- )67T TT S(II ) ill 2k7T + — < 2x ------- < lk7l + —7l伙W z),2 6 271 5得k/r——< x < k7r + — 7r(k e z)3 6n5/r•••单调递减区间为[尿+ =、k兀七—](k ez). ................................... 8分3 6(III)因为-~^x^~，贝ij-兰W2x —兰 W兰，6 4 2 6 3当2x-- = -,即x =-时，/(兀)取得最大值为馆；6 3 4当2%--=--,即兀―仝时,/⑴取得最小值为_2 •.................................. 13分6 2 3（16）（木小题满分13分）解：（I ）由条形图得第七组频率为1-（0.04x2 + 0.08x2 + 0.2x2 + 0.3） = 0.06,0.06x50 = 3 1 分・••第七组的人数为3人组别 1 2 3 4 5 6 7 8 样本中人数 2 4 10 10 15 4 3 2 (II )由条形图得前五组频率为(0.008+0.016+0.04+0.04+0.06)x5=0.82,.......................................................... 4分=71后三组频率为1一0.82=0.18 ................................................... 5分估计这所学校高三年级身高在180cm以上（含180cm）的人数800x0.18=144 （人）. 7分（皿）第二组四人记为a、b、c、d,其中a为男生,b、c、d为女生,第七组三人记为1、2、3,其屮1、2为男生，3为女生，基木事件列表如下：abed1\a \b \c \d22a 2b 2c 2d3 3 a 3b 3c 3d所以基本事件有12个...................................... 10分恰为一男一女的事件有",lc, Id, 2b, 2c, 2d, 3a；共7个..... 12分7因此实验小组中，恰为一男一女的概率是一................... 13分12（17）（本小题满分13分）（I）证明：因为菱形ABCD,所以3D丄AC,又因为平而ACEF丄平面ABCD ,EC丄AC，平面ACEF Q平面ABCD = AC故EC丄平面ABCDEC 丄BD所以BD丄平面ACEF-------------- 5分BDu平面BDE,所以平面BDE丄平面ACEF ；---------------- 6分（II）连结EO, EO//AM ,ZBEO为界面直线BE与AM所成的角或补角，由（I）知，AEOB = 90°,在直角三角形EOB 中，EO = AM=4i,BO = &所以界而直线BE与4M所成的角的正切值心. -------------- 10分2（III）由已知易得BF = FD,BE = ED，所以EO丄BD, FO丄BD,ZEOF为二面角E-BD-F的平而角13分所以二面角E-BD-F为90°.（18）（本小题满分13分）解：（I ）点A （0,2）代入圆C 方程，得.（2-加尸=9*.* m < 2 ,・*. m = -1 .......... 1 分圆 C ：异+（〉，+ 1）2 =9,圆心（0,-1）・设直线的斜率为心，P （3,8）当K 不存在时，PF I ：x = 3,显然不合题意舍去. 当人存在时，PF“ y -8 = k l （x-3）f 即 k }x- y-3« + 8 = 0 .・••号f .解得k }=- ..................................................... 3分W + 1 3 直线 PF ]: 4x-3.y + 12 = 0总线PF 】与x 轴的交点横他标为一3,・・・c=3. F| (—3, 0), F 2(3, 0)............................... 4 分2« = P4F|| + |AF 2|= VB + V13 =2>/13 , a =屈,«2=13, //=4.椭圆E 的方程为：—+ ^- = 1............................. 6分13 4(II)由|丽冃丽|知点A 在线段MN 的垂直平分线上， y = kx-2由]兀2 2 消去y 得(4 + 13/)兀2 一52也=0 (*) —+ —= 1 〔13 4由Id 得方程（*）的A = （52^）2 >0,即方程（*）有两个不相等的实数根…8分设N （兀2小），线段MN 的中点卩（兀0，儿），26k 4 + 13 衣52k 4 + 13f•宀0,直线仲的斜率为宁=桔由AP 丄MN,得土竺 xk = _l,解得：k = ±—f……12分13R13・・・存在直线/满足题意，方程为：V5x-V13y-2ji3 =0«KV5x + V13y + 2Vi3 =0 -------------------------------- 13 分 (19) (本小题满分14分)解：(I)方法一：由S 曲=3S “得：数列｛S”｝是等比数列，公比为3,首项为1…2分.•.S” =1・3心=3心 ......... 3分当 n>2 时,a n = S n - S n _{ = 3 心一 3W '2 = 2 • 3n '2................... 4 分fl (n = 1)•5=\.................. 5 分[2・3心(n > 2)方法一：•** S“+] = 3S“，「. S n = 3S”](M ' 2) 以上两式相减得：Q “+]=3% (n > 2),.................. 2分在 S n+[ = 3S n 中,取〃 =1 得：a {+a 2= 3a }即 a 2 = 2a } = 2 ,.................. 3 分.・.｛%｝为第二项起的等比数列，公比为3 .................. 4分fl (n = l)/. ci = \.................. 5 分26k 24 + 13p—8 4 + 13/即卩為為)10分2・3宀(n > 2)由(I )知：⑺”｝为第二项起的等比数列，公比为3, s=2t0? + 1)(72 + 2) n(n +1)(/? + 1)(1-/?)① 若r 〉0,则 b n+i -b n <0 HP b n+i < b n (n > 2) .・.数列｛仇｝是从第二项起的递减数列ifij b 、= —, b 2 = — t b 2 >b } 3•••(—b2「 ..................................... 9 分•・•对任意 n e TV * ,都冇 A>/7(Z7 + 1)a“t②若/v0,则b n+} - b n > 0即b n+x > b n (n > 2)・•・数列{仇}是从第二项起的递增数列・・・11 分Ifij/, =-<0,当n >2 时，化=W o't n2r-3w_2b n e (-oo, 0).................. 12 分•• •对任意n e TV * ,都有2>/7(Z7 + 1), > 0 ...................13 分%3综合上面：若/>0,则A>-；若/<0,则A>0o .............................................. 14分t(20) (木小题满分14分)解：(I )当 a = -3ll 寸，/(x) = —x 3 -兀2-3X + 3,所以广(兀)=x 2 -2x-3 = (x-3)(x + l).令/'(兀) = 0,得比=_1,兀2=3.当xv-l 时，广(x)〉0,则/(x)在(-oo,-l) ±单调递增；当一1 v 尢<3时,/'(X )<0 ,则f (x)在(-1,3)上单调递减;・••当心2时,廿2心巴汗畔 “ “ It • 3n_2b n +l ~b n 2r3n-I『•3"10分当x>3时，广(兀)>0 , /(兀)在(3,+00)上单调递增. 所以，当x = -\时，/&)取得极大值为/(-1)=-1-1 + 3 + 3 =—；当*3时,/(x)取得极小值为/*(3)=丄x27-9-9 + 3 =-6.(II )广(兀)=/-2x + d , △ = 4-4° = 4(1-°) •⑴若dhl,则在心上恒有广(兀)》0,于⑴在R 上单调递增，且值域为R.函数/(x)的图象少兀轴有且只有一个交点.(2)若a<l,则△>(), /'(%) = 0有两个不等的实根，不妨设为x l9x 2 (x t <x 2).当x 变化吋，广(x)J(x)的取值情况如下表：X(-°°眄)(西，兀2)厶（兀2，+°°）广(刃+—+极大值极小值由兀]2—2 兀]+a = 0 ,得兀]+兀2=2, x l x 2 = a , JL x ）2= 2x, - <7.f （xj = £ 兀1‘ _ X |2 + ax \ 一 a = * £ （2旺 _ d ） — 壬2 + ax }-同理/(x 2) =|［(n-l)x 2-t/_ •函数子(x)的图象与x 轴有且只有一个交点，等价于/(x 2)< f (x,) <0或0</(X2)</(X l)» 即 /(壬)丁(兀2)>0 •又/(西)丁(兀2)=害［(。

重庆市南开中学2010届高三下学期3月月考数学试题及答案详解(文科)

南开中学高 2010 级高三 3 月月考试卷
数
学 ( 文科 )
本试题分第Ⅰ卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分 . 共 150 分，考试时间 120 分钟 .
第Ⅰ卷 ( 选择题，共 50 分)
注意事项：
1 ．答题前，考生务必将自己的姓名、考号、考试科目填涂在答题卡上
.
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮
0 知 A(
p ,(1
4
2
3 22
2) p), B(
p,(1
2
2) p)
所以 (1 2) p y0 (1 2) p, 则当 y0 p 时， dmax
2 p
2
1
2
则 ( S ABM ) max
4p
p
2 p2
2
2
21． (1) 解： a1 1, a2 3,a3 7 事实上，要将 n 个圆盘全部转移到 C 柱上，只需先将上面 n 1 个圆盘转移到 B 柱上，需
(1) 求函数的单调区间及最值；
D C
B
(2) a 为何值时，方程 f (x) 0 有三个不同的实根 .
20．(12 分 ) 如图，斜率为 1 的直线过抛物线 y 2 M 为抛物线弧 AB 上的动点 .
2 px( p
0) 的焦点，与抛物线交于两点
y
A、 B,
(1) 若 | AB | 8, 求抛物线的方程；
12． -2
13． 2n
14 ． 22 3
三、解答题
16．解： f ( x) a b 2cos x (sin x cos x) 1
15 ． 3 5 , 5
sin 2 x 1 cos2 x 1

南开中学高三数学模拟试卷(文科).doc

南开中学高三数学模拟试卷(文科)说明：1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分，满分150分, 考试时间120分钟.2.请将选择题的答案填涂在答题卡上，填空题、解答题答在答题纸上. 参考公式：・如果事件久〃互斥，那么P(AU〃) = P(4)+P(B) •如果事件右B相互独立,那么関锥侧面积公式S= Tirl其屮厂为底血関半径，/为母线长第I卷(选择题共40分)一.选择题：(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.頊将等家填徐在登題卡上!)-3-1(1)i是虚数单位，复数一「=l + 2i-l-7i 1(A)l-3i (B) (C) -- + i (D) -1 + i5 5(2)已知集合S = [x\x2<2x]t集合T^Lllogj 则S^T =2(A) (0,1) (B) (1,2) (C) (0,1] (D) (0,2](3)已知a,b,c分别是\ABC的三个内角A,B,C所对的边，若a = 2, b = g , B = 60"则c -(A) 5 (B) 77 (C) 2 (D) 1(4)已知直线厶：2x +紗-7 = 0,若过定点(0,2)与已知直线厶垂直的直线厶与x轴、)，轴正半轴所围成的三角形而积为6,则实数k值为3 2(A) -- (B)-2 32 4(C) -- (D)--（5）阅读如图给出的程序框图，运行相应的程序, 输出的结果S为（A） 1008 （B） 1007（C） -1007 （D） -3022（第5颗）（6）通过随机询问110名性别不同的人学牛是否爱好某项运动，得到如下的列联农:男女总计爱好402060不爱好203050总计6050110〃(加一加)2 争 2 - 110X(40X30-20X20)2 〜(a+b)(c+d)(a+c)(b+d)‘心寸'K =6() X 5() X 6() X 5() 〜附表:P（K?汶）0.0500.0100.001k 3.841 6.63510.828参照附表，得到的正确结论是（）（A）有99%以上的把握认为“爱好该项运动与性别有关”（B）有99%以上的把握认为“爱好该项运动与性别无关”（C）在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别育关”（0）在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”（第7顾）(C)-I3(D)--2（8）己知函数/（x）是定义在［-1,1］上的奇函数，且/（1） = 1 ,当以引-1,1］, a+bHO时有/⑷+ /少）>0・若f（x）tn2- a+ b则实数〃7的取值范围是-2am +1 (m e R,/n h 0)对所有XG[-1 ,1] , ae[-\, 1J 恒成立,(A) (-oo,-2]U(2, + oo)(B) (一oc,-2]U[2, + oo)(C) (YO,—2]U(0,+8)(D) (YO,0)U[2,+ OO)第II卷（非选择题共110分）二.填空题：（本大题共6小题，每小题5分，共30分.请将答案填在答题纸上!）y >0（9）设变量兀,），满足约束条件< % +1 > 0 ,则z = 2x+ y的最大值为________x+y-3<Q分别为A"两点，以4B为直径的圆恰好过双曲线右焦点场，则双曲线的离心率为____________（11）将一个圆柱体挖掉一个圆锥后，所得几何体的（12）如图，已知是圆的-条直径，点C是圆上-点满足"=»,43为圆的切线，C为切点，过点B作切线CZ）的垂线BF,交圆于点E-则线段EF的长为___________ ・（10）已知过双曲线与0~9_21 =1（G > 0』> 0）左焦点F\且垂直于A-轴的直线交双曲线两渐近线三视图如图所示, 则该几何体的萄輻积为___________（第11题）（第12题）I m(13)已知不等式(x + 2y)(—+ —)216对任意止实数x,y恒成立，则止实数血的最小值兀 >?为____ .(14)已知: “ 14一入IW 6 ”，g: "I X-IIW Q”(awR,a>0),若非“是非q的必要不充分条件，则实数。

重庆一中2010届高三数学考前模拟文人教版【会员独享】

某某一中高2010级高三下期考前模拟数学试题卷(文科)数学试题共4页。

满分150分。

考试时间120分钟。

注意事项：1.答题前，务必将自己的某某、某某号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

一、选择题：(共10小题，每题5分，共50分．请将唯一正确的选项选出来，并涂在机读卡上的相应位置)1．已知集合{}{}1,(3)0A x x B x x x =<=-<，则AB =( )A ．(0,3)B ．(0,1)C ．(1,3)D ．(1,3)- 2．已知tan 2α=，则sin cos sin cos αααα-=+( )A ．3B ．3-C ．13 D ．13- 3．已知直线20x y a++=与圆225x y +=相切，则实数a =( )A ．5 C ．．5± 4．若等差数列{}n a 的前5项和525S =，且23a =，则7a =( )A ．11B ．12C ．13D ．14 5．已知向量,a b 满足：2,1a b ==且()3a a b ⋅+=，则a 与b 的夹角为( )A ．4π B ．34π C ．3π D ．6π6．设,,l m n 均为直线，其中,m n 在平面α内，则“l α⊥”是“l m ⊥且l n ⊥”的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 7．为了研究某高校大学5000名新生的视力情况，随机地抽查了该校100名进校新生的视力情况，得到其频率分布直方图如右图，若规定视力低于5.0的学生属于近视学生，则估计该校新生中不是近视．．．．的人数约为 ( )A ．300人B ．400人C ．600人D ．1000人8．已知球O 的半径为1，ABC △的顶点都在北纬45 的纬线圈上，且AB BC =，90ABC ∠=，则,A B 两点间的球面距离为( ) A ．6π B ．3π C ．2πD ．π 9．已知函数()y f x =对于x R ∈满足(1)f x +(1)f x =-，且[1,1]x ∈-时,2()f x x =，则()y f x =与5log y x =的图象的交点的个数为( )A ．3B ．4C ．5D ．610．过双曲线22221(0)x y a b a b -=>>的左焦点1(,0)(0)F c c ->作圆22214x y a +=的切线，切点为E ，延长1F E 交双曲线右支于点P ，若11()2OE OF OP =+，O 为坐标原点，则该双曲线的离心率为( )A ．2 B ．12 C ．2 D ．52二、填空题：(共5小题，每题5分，共25分．请将最简答案填在答题卷相应的位置)11．已知曲线2y ax =在点(1,)a 处的切线与直线260x y --=平行，则a =_______．12．我校高三某班照毕业像时，有2位老师和3位学生站成一排合影留恋，则2位教师不相邻的不同排法共有_______种．(用数字作答) 13．若261()x mx +的二项展开式中3x 项的系数为52，则m =______________．(用数字作答)14．设有两个命题p ：关于x 的不等式2240x ax ++>对一切x R ∈恒成立；q ：函数()(52)x f x a =--是减函数．若命题“p 且q ”为假命题，“p 或q ”为真命题，则实数a的取值X 围是____________．15．函数log (2)2(0,1)a y x a a =-+>≠的图象恒过定点A ，且点A 在曲线2y mx n =+上，其中,0m n >，则43m n+的最小值为___________．三、解答题：(共6小题，其中16～18每小题13分，19～21每小题12分，共75分．请将每题的解答过程写在答题卷相应的答题框内)16．(本小题13分)已知向量(cos sin ,3cos ),(cos sin ,2sin )a x x x b x x x =+=-，记(),f x a b x R =⋅∈．⑴求：函数()f x 的最小正周期．⑵在ABC △中，角,,A B C 的对边分别为,,a b c ，若()1f A =，且1,2a b c =+=，求：ABC △的面积．17．(本小题13分)某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是13，遇到红灯时停留的时间都是2分钟． ⑴求这名学生在上学路上到第三个路口时首次遇到红灯的概率． ⑵这名学生在上学路上因遇到红灯停留的总时间至多是4分钟的概率．18．(本小题13分)如图，在直三棱柱111ABC A B C -中，90ACB ∠=，12AC BC CC ===.⑴求证：11AB BC ⊥.⑵求：二面角1C AC B --的大小.19．(本小题12分)已知函数3221()21,()13f x ax bx xg x x x =++-=-++，若函数()f x 与()g x 的图象的一个交点P 的横坐标为1，且两曲线在点P 处的切线互相垂直. ⑴求：函数()()h x f x x =-的单调递增区间.⑵若对任意12,[1,1]x x ∈-，不等式12()()f x k g x +<恒成立，求：实数k 的取值X 围.20．(本小题12分)已知椭圆:C 22221(0)x y a b a b+=>>的离心率为36，短轴一个端点到右焦点的距离为3． ⑴求椭圆C 的方程．⑵设直线l ：y kx m =+与椭圆C 交于A B 、两点，坐标原点O 到直线l 的距离为23，且 AOB △，求：实数k 的值．21．(本小题12分)设1122(,),(,)A x y B x y 是函数21()log 21xf x x=+-图象上的任意两点，点01(,)2M y 为线段AB 的中点． ⑴求：0y 的值． ⑵若*1221()()()(),(2,)n n n S f f f f n n N n nn n--=++++∈≥且，求：n S ． ⑶在⑵的条件下，已知12(1)31(2)(1)(1)n nn n a n S S +⎧=⎪⎪=⎨⎪++⎪⎩≥，记n T 为数列{}n a 的前n 项和，若1(1)n n T S λ+<+对一切*n N ∈都成立，求：λ的取值X 围．某某一中高2010级高三考前模拟数学答案(文科)第一部分(选择题共50分)一、选择题：(每小题5分，共50分)B ．C ．D ．C ．A ． A ．C ．B ．B ．A ．第二部分(非选择题共100分)二、填空题：(每小题5分，共25分)11．1； 12．72； 13．2； 14．(,2]-∞-； 15．274．三．解答题：16．解：22()cos sin 2sin cos 222sin(2)6f x x x x x x x x π=-+⋅=+=+………………… 5分⑴()f x 的最小正周期为22T ππ==．……………………………………… 6分 ⑵∵()1f A =，∴1sin(2)62x π+=，∵A 为ABC △的内角， ∴132666A πππ<+<，∴5266A ππ+=，∴3A π=…………………… 9分由余弦定理有：222b c a bc +-=，∴22()3b c a bc +-=，∴1bc =…11分∴1sin 2ABC S bc A ==△．……………………………………………… 13分 17．解：⑴设这名学生在上学路上到第三个路口时首次遇到红灯为事件A ，因为事件A 等于事件“这名学生在第一和第二个路口没有遇到红灯，在第三个路口遇到红灯”，所以事件A 的概率为()11141133327P A ⎛⎫⎛⎫=-⨯-⨯= ⎪ ⎪⎝⎭⎝⎭.………………… 6分 ⑵设这名学生在上学路上因遇到红灯停留的总时间至多是4min 为事件B ，这名学生在上学路上遇到k 次红灯的事件()0,1,2k B k =.则由题意，得：()40216381P B ⎛⎫==⎪⎝⎭，()()132212142412321224,33813381P B C P B C ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 由于事件B 等价于“这名学生在上学路上至多遇到两次红灯”， ∴事件B 的概率为()()()()01289P B P B P B P B =++=.…………………… 13分18．解：⑴证明：∵直三棱柱111ABC A B C -中，AC BC ⊥，∴AC ⊥平面11BCC B ，连接1B C ，则∵11BCC B 为正方形，∴11BC B C ⊥，∴由三垂线定理知：11AB BC ⊥.…………………… 6分⑵连接A 1C 交AC 1于点O ，连接BO ，则：∵1,BC AC BC CC ⊥⊥，∴BC ⊥平面1ACC ，又1CO AC ⊥， ∴1BO AC ⊥，∴BOC ∠即为二面角1C AC B --的平面角……………… 10分在Rt BCO △中：2,BC CO ==∴tan BCBOC CO∠==∴二面角1C AC B --的大小为： (13)分19．解：⑴由题意：1(1)1(1)13g f a b ===++，∴30a b +=……① 又'()21g x x =-+，∴()g x 的图象在点P 切线的斜率为：'(1)1g =- 又'2()22f x ax bx =++,∴()f x 的图象在点P 切线的斜率为：'(1)221f a b =++=……………②由①②可解得：3,1a b =-=，∴32()21f x x x x =-++-，………………………… 3分∴32()()1h x f x x x x x =-=-++-，∴'2()321(31)(1)h x x x x x =-++=+-+令'()(31)(1)0h x x x =+-+≥，解得：113x -≤≤即函数()h x 的单调递增区间为：1[,1]3-． (6)分⑵对任意12,[1,1]x x ∈-，12()()f x k g x +<恒成立⇔当12,[1,1]x x ∈-时，1max 2min ()()f x k g x +<成立.........(★) (8)分∵'2()322,[1,1]f x x x x =-++∈-，令'()0f x >1x <<∴()f x 区间[-上递减，在区间1]上递增又(1)1,(1)1f f -=-=，∴当[1,1]x ∈-时，max ()(1)1f x f == (10)分而2215()1()24g x x x x =-++=--+，∴当[1,1]x ∈-时，min ()(1)1g x g =-=-∴由(★)式有：11k +<-，∴实数k 的取值X 围为：(,2)-∞-． (12)分20．解：⑴设椭圆的半焦距为c，依题意c a a ⎧=⎪⎨⎪=⎩，∴1b =，∴所求椭圆方程为2213x y +=．……………………………………………… 5分⑵设11()A x y ，，22()B x y ，．由已知2=，得223(1)4m k =+． (7)分又由2213y kx mx y =+⎧⎪⎨+=⎪⎩，消去y 得：222(31)6330k x kmx m +++-=， ∴122631kmx x k -+=+，21223(1)31m x x k -=+．…………………………………… 9分∴22221(1)()AB k x x =+-22222223612(1)(1)(31)31k m m k k k ⎡⎤-=+-⎢⎥++⎣⎦2222212(1)(31)(31)k k m k ++-=+22223(1)(91)(31)k k k ++=+又222222133(1)(91)3(2216(31)4AOBk k SAB k ++=⨯⨯=⨯=+△，化简得：429610k k -+=……………………………………………………… 11分解得：k =………………………………………………………………… 12分21．解：⑴由M 为线段AB 的中点，易得：121x x +=1201212212111()[()()][1log ()]22211x x y y y f x f x x x =+=+=+⋅--12212111(1log )(10)222x x x x =+=+=…………………………… 4分 ⑵由⑴知：121x x +=，1212()()1f x f x y y +=+=1221()()()()n n n S f f f f n n n n--=++++1221()()()()n n n S f f f f n n n n--=++++∴1122112()()()()()()n n n n S f f f f f f nn n n n n ---⎡⎤⎡⎤⎡⎤=++++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦11111n n -=+++=-个∴*1(2,)2n n S n n N -=∈≥………………………………………………… 8分 ⑶当2n ≥时，114114()(1)(1)(1)(2)12n n n a S S n n n n +===-++++++，∴12321124()3322n n nT a a a a n n =++++=+-=++ 由1(1)n n T S λ+<+得：224444(2)444n n n n n n nλ>==+++++ ∵44n n +≥，∴44144424n n=+++≤ ∴12λ>，即λ的取值X 围为1(,)2+∞…………………………………… 12分。

重庆市南开中学高2010级高考考前模拟测试(语文)

重庆南开中学高2010级高考考前模拟测试语文试题语文试题卷考试时间150分钟。

第1至10题为选择题，30分；第11至22题为非选择题，120分。

满分150分。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答第1至10题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答第11至22题时，必须使用0．5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

一、（本大题共4小题，每小题3分，共12分）1．下列词语中加点字的读音，没有错误的一项是（）A．嗔．怒（chēn）纰．漏（pī）一模．一样（mó）奴颜婢．膝（bì）B．择．菜（zhái）谄．媚（cǎn）不容置喙．（huì）浑身解．数（xiè）C．租赁．（lìn）泊．车（bó）博闻强志．（zhì）教．学相长（jiào）D．绚．烂（xuàn）瘦削．（xiāo）力能扛．鼎（káng）审时度．势（duó）2．下列各组词语中，有两个错别字的一组是（）A．题纲敲门砖余勇可贾如愿以偿B．涵养练习薄因噎废食凭白无故C．装潢顷刻间振聋发聩戮力同心D．荒费吊书袋粗制烂造矢志不渝3．下列语句中，加点词语使用恰当的一项是（）A．来到工作现场，唐东平自作主张，结果把事情办砸了。

面对别人的不满和指责，他先是怒目而视，既而．．强词夺理，推卸责任，实在是不可理喻。

B．陕北原生态歌手阿宝与熊汝霖合作的一曲《倾国倾城》，宛转悠扬，天花乱坠．．．．，诉说着一个“流传往同悲欢眷恋”“永远静夜如歌般委婉”的故事。

C．奥巴马政府一会儿会见达赖喇嘛，一会儿出售军火给台湾，其危言危行．．．．极大地伤害了中国人民的感情，严重地影响了中美两国的正常关系。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

重庆2010级考前模拟测试卷文科数学能力测试一、选择题：本大题10小题，每小题5分，共50分.在每小题给出的四个备选项中，只有一项符合题目要求1．已知集合{1,2,3,4,5,6,7},U ={2,4,5,7},A ={3,4,5},B =则()()U U C A C B = ( ) A ．{1,6}B ．{4,5}C ．{2,3,7}D ．{2,3,4,5,7}2．已知向量(2,4),(,1),a b x == 且,a b ⊥则x 的值为( )A ．2-B ．2C ．12-D ．123．已知集合,A B 满足：,A B A = 且,A B ≠ 则“x A ∈”是“x B ∈”的( ) A ．充要条件 B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件4．以点(2,1)为圆心，且与直线21y x =+相切的圆的方程为( )A ．2216(2)(1)5x y +++=B ．2245(2)(1)5x y +++=C ．2216(2)(1)5x y -+-=D ．2245(2)(1)5x y -+-=5．在等差数列{}n a 中，131427,a a a ++= 则其前11项的和11S =( A ．992B ．99C ．198D ．896．三个学校分别有1名、2名、3名学生获奖，这6名学生要排成一排合影，则同校学生相邻排列的概率是( ) A ．130B ．115C ．15D ． 1107．函数()sin()3sin()2f x x x ππ=--+图像的一条对称轴为( )A ．23x π=B ．6x π= C ．6x π=-D ．3x π=8．如题8图，在正三棱柱111ABC A B C -中，已知1,AB = D 在棱1BB 上，且1,BD = 则AD 与平面11AAC C 所成ABCDA 1B 1C 1题8图角的正弦值为( ) A ．22 B ．32 C ．64D ．1049．已知12,F F 是双曲线22221(,0)x y a b a b-=>的左、右焦点，过1F 且垂直于x 轴的直线与双曲线交于,A B 两点，若2ABF ∆为钝角三角形，则该双曲线的离心率e 的取值范围是( ) A ．(1,)+∞B ．(21,)++∞C ．(1,21)+D ．(1,3)10．已知函数3211()(0),32f x ax bx cx a =++> 记()g x 为它的导函数，若()f x 在R 上存在反函数，且(1)0,f ->则'(2)(0)g g 的最小值为( ) A ．4B ．52C ．2D ．32二、填空题：本大题共5小题，共25分.把答案填写在答题卡相应位置上.11．由于甲流暴发，防疫站对学生进行身体健康调查，对男女学生采用分层抽样法抽取. 学校共有学生1600名，抽取一个容量为200的样本.已知女生比男生少抽了20人，则该校的女生人数应是 _______人.12．二项式62()x x+的展开式中的常数项为__________13．已知实数,x y 满足不等式组2,0y x x y y ≤⎧⎪+≤⎨⎪≥⎩则目标函数3z x y =+的最大值为__________.14．已知函数()f x 为R 上的减函数，且值域为,R 点(1,2)A -和点(1,1)B 在()f x 的图像上，1()f x -是它的反函数，则不等式12|(log )|1f x -<的解集为_______________.15．把数列*1{}(N )21n n ∈-的所有项按照从大到小的 113 1517 19 111 113 115 117 119 121 (129)……原则写成如右图所示的数表，其中的第k 行有12k -个数，第k 行的第s 个数(从左数起)记为(,),A k s 则(10,495)A = _____________.三、解答题：本大题共6小题，共75分.各题解答必须写出必要的文字说明、演算步骤和推理过程.16．(本小题满分13分)已知A B C 、、为ABC ∆的三内角，且其对边分别为,a b c 、、若(2cos ,tan ),2Am A =(cos ,cot ),2An A =- 且1.2m n ⋅=(Ⅰ)求角;A(Ⅱ)若4,b c +=ABC ∆的面积为3,求.a17．(本小题满分13分)在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生： (Ⅰ)得50分的概率； (Ⅱ)得40分的概率18．(本小题满分13分 )已知四棱锥P ABCD -的底面是边长为2的正方形，PD ⊥面,ABCD 2,PD =,E F 分别为,BC AD 的中点，ABCD EF P 题18图(Ⅰ)求直线DE 与面PBC 所成角的正弦值； (Ⅱ)求二面角P BF D --的正切值.19．(本小题满分12分) 已知函数32()3f x x ax x =--(Ⅰ)若函数()f x 在[12,)++∞是增函数，导函数'()f x 在(,1]-∞上是减函数，求a 的值； (Ⅱ)令'2()()()3,g x f x f x x =-+ 求()g x 的单调区间.20．(本小题满分12分)已知椭圆2214x y +=的左、右顶点分别为,A B 、曲线E 是以椭圆中心为顶点，B 为焦点的抛物线.(Ⅰ)求曲线E 的方程；(Ⅱ)直线:(1)l y k x =-与曲线E 交于不同的两点,M N 、当17AM AN ⋅≥时，求直线l的倾斜角θ的取值范围.21．(本小题满分12分)设各项为正的数列{}n a 的前n 项和为n S 且满足：1.2n n n S a a += (Ⅰ)求;n a (Ⅱ)求12111;n nT S S S =+++… (Ⅲ)设*,,m n p N ∈且2,m n p += 求证：222112.m n pS S S +≥数学(文史类)参考答案一、选择题：本大题10小题，每小题5分，共50分. 1～5 AABCB 6～10 DCCBA10．'2(),fx ax bx c =++ 即2()(0).g x ax bx c a =++> )(x f 在R 上存在反函数，且0,a > ∴()0g x ≥对x R∈恒成立，即20(0)ax bx c a ++≥>对Rx ∈恒成立. ∴240,b ac ∆=-≤从而0,c >又(1)0,f ->即110,32a b c -+-> ∴110,23b ac >+>从而0,b >于是'2(2)4242222214,(0)g a b c a c acg b b b b++4==++≥+≥+⨯=故选A ．二、填空题：本大题共5小题，共25分题号 1112131415答案72060 4(2,4)1201115．前9行共有981(12)12251112⋅-+++==-…个数，所以(10,495)A 是数列1{}21n -中的第1006项，即1(10,495).2011A =三、解答题：本大题共6小题，共75分． 16．(本小题满分13分解：(Ⅰ)由1,2m n ⋅= 得2112cos1cos ,222A A -+=⇒=- 所以120A = …………6分 (Ⅱ)由11sin sin1203,22ABC S bc A bc ∆===得4,bc =………………9分2222222cos ()12,a b c bc A b c bc b c bc =+-=++=+-=所以23a =.……13分17．(本小题满分13分)解：设“可判断两个选项是错误的”两道题之一选择对为事件,A “有一道可判断一个选项是错误的”选择对为事件,B “有一道因不理解题意”选择对为事件,C 则111(),(),()234P A P B P C ===(Ⅰ)得50分的概率为11111;223448P =⨯⨯⨯=……………………6分 (Ⅱ)得40分的概率为112211231113112117;22342234223448P C C =⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=…13分18．(本小题满分13分)解：(Ⅰ)取PC 的中点,N 连接,,DN EN⊥PD 面,ABCD ,PD BC ⊥∴又由题意，有DC BC⊥BC ⊥∴面,PDC ∴面⊥PBC 面,PDC又DC PD=知,DN PC ⊥DN ⊥∴面,PBC所以DEN ∠为直线DE 与面PBC 所成的角，…………4分由题意2,5,DNDE ==所以210sin .55DEN∠==………………7分(Ⅱ)过D 作,DM BF ⊥交BF 的延长线于,M 连接,PM⊥PD 面,ABCD 所以PM在面ABCD 内的射影为,DM ,PM BF ⊥∴所以PMD ∠为二面角P BFD --的平面角………………10分由Rt DMF ∆与Rt BAF ∆相似，所以25DM DF DM AB BF =⇒= 所以tan 5PDPMDDM∠==……………………13分 19．(本小题满分12分)解：(Ⅰ)'2()323,f x x ax =-- ………………1分)(x f 在),21[+∞+上是增函数，∴'()0f x ≥在),21[+∞+恒成立即x x a 2332-≤在[12,)++∞恒成立2min 33()32x a x-⇒≤=……………3分 ABCDE FPM N又'()f x 在]1,(-∞上是减函数，13,3aa ≥⇒≥∴ ……………………5分3.a =∴ …………………6分(Ⅱ)322232()3(323)3(32)3g x x ax x x ax x x ax a x =-----+=---+'21223()32(23)01,3a g x x ax a x x -=-+-=⇒==………………8分 (ⅰ)当3≥a时，',(),()x g x g x 的变化如下表：x (,1)-∞123(1,)3a - 233a - 23(,)3a -+∞ '()g x+-+()g x∴增区间为：23(,1),(,);3a --∞+∞ 减区间为：)332,1(-a ………………10分 (ⅱ)当3a<时，',(),()x g x g x 的变化如下表x 23(,)3a --∞ 233a - 23(,1)3a - 1(1,)+∞'()g x+-+()g x∴增区间为：23(1,),(,);3a -+∞-∞ 减区间为：23(,1).3a - ……………12分 20．(本小题满分12分)解：(Ⅰ)依题意得：(2,0),(2,0),A B -∴曲线E 的方程为28.y x = ………………4分(Ⅱ)由2(1)8y k x y x⎧=-⎪⎨=⎪⎩得：2(28)0,kxk x k -++=由⎩⎨⎧>>-+=∆004)82(22k k k 0>⇒k …………7分设11(,),M x y 22(,),N x y 则：121228,1,k x x x x k++== ∴11221212(2,)(2,)(2)(2)AM AN x y x y x x y y ⋅=++=+++…………9分121216(1)(2)()4117k x x k x x k k=++-+++=+≥∴01,k <≤ ∴(0,].4πθ∈ ………………12分21．(本小题满分12分)解：(Ⅰ)1,2n n n S a a +=∴22(1)n n n S a a n =+≥……①,21112(2)n n n S a a n ---=+≥……②①-②得：2211112()(1)0nn n n n n n n n a a a a a a a a a ----=-+-⇒+--=0,n a > ∴11,n n a a --= 故}{n a 为等差数列，又在①中令1=n 得11,a =∴1(1)1na n n =+-⋅= ………………4分(Ⅱ)(1),,2nn n n a n S +==∴ ∴121112221223(1)nn T S S S n n =+++=+++⨯⨯+1111122[(1)()()].22311n n n n =-+-++-=++ ………………8分(Ⅲ)2,m n p += ∴2,mn p ≤………………9分∴2111111[()()][()]44m nm n m n m n S S mn a a a a mn a a a a a a =++=+++ 12222112()1(2)[],42p p p p a a p mn mn a a a a S p +≤++=≤ ………………11分 ∴2222211122,m n m n pS S S S S +≥≥ 即222112.m n p S S S +≥ (12)。