人教版初中数学课标版九年级上册第二十三章 23.1图形的旋转(共24张PPT)
合集下载
人教2011课标版初中数学九年级上册第二十三章23.1 图形的旋转(共25张PPT)
(第6题)
(第7题)
(第8题)
课后作业 选做题: 已知:如图,在正方形ABCD中,△CBE是△ABF 绕点B顺时针旋转90°形成的,试用旋转的性质 说明:(1)AF=CE
(2)AF⊥CE
课后作业 思考题:
如图,把一个直角三角尺ACB绕着30°角的顶点
B顺时针旋转,使得点A与CB的延长线上的点E重合.
思考题
已知:如图, △ABE是由△ADC绕点A逆时针旋 转60° 得到,请找出旋转角,并判断△ABD,△AEC 的形状。
D A E
B
C
思考题
已知:如图, △ABD,△AEC都是等边三角形, BE与DC有什么关系?你能用旋转的性质说明上述 关系成立的理由吗?
D A E
B
C
1.知道旋转的相关概念和基本特征
1. 旋转的定义:在平面内,将一个图形绕一个定点沿
着某个方向转动一定的角度,这种图形变换称为旋转. 这个定点称为旋转中心,转动的角称为旋转角 . 这节课你有什么收获?
2.旋转的三要素:旋转中心、旋转方向、旋转角度 3.旋转的性质:
旋转不改变图形的大小与形状;
对应点到旋转中心的距离相等;
旋转前后两图形任意一对对应点与旋转中心的连 线所成的角都是旋转角。
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中: (1)旋转中心是什么? 旋转中心是点O
点D和点E的位置 (2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是哪个角? ∠AOD和∠BOE都是旋转角
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
(1)三角尺旋转了多少度?
人教课标版初中数学九年级上册第二十三章23.1 图形的旋转(共22张PPT)
• 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
•
O
点A的对应点是 A' ;
点B的对应点是 B' ;
A'
B'
若OA=2,则OA'= 2 ;
若OB=1.5,则OB'= 1.5 ;
猜想:对应点到旋转中心的距离相等?
O
B'
点A的对应点是 A' ; 点B的对应点是 B' ;
A'
若∠AOA'=100°,则∠BOB'= 100° ;
猜想:对应点与旋转中心所连线段的夹 角相等?
B
美丽的旋转
风车旋转 重复着历史的记忆 木马旋转 幻想着青春的旋律 钟摆旋转 追赶着时间的极限 地球旋转 带来日夜的交替
……
你可曾 感到 旋转与我们 息息相关 美丽的旋转 让我们的生活 一片灿烂!
这节课中, 有什么收获 ? 还有什么疑惑呢?
在变中寻找不变
人类永恒的追求
1、练习第2题,习题第3题。
猜想:旋转性质 对应点到旋转中心的距离相等? 对应点与旋转中心所连线段的夹角相等?
验证:旋转性质
小试牛刀
A 1、如图,△ABC绕点M旋 转得到△ DEF,则:
B
点C的对应点是___点__F___; 旋转中心是__点__M____;
E
C D
M
九年级上册23.1图形的旋转(共19张PPT)

知识要点
AAA
EEE
FF BB
D
OOO
CCC
旋转的性质
1、对应点到旋转中心的距离相等.
2、对应点与旋转中心所连线段的夹角等于旋转角.
3、旋转前、后的图形全等.
例题讲解
△A′OB′是△AOB绕点O按逆时针方向旋转得
到的.已知∠AOB=20°, ∠ A′OB =24°,
AB=3,OA=5,则A′B′ =
一个具有这种关系的角。相等
由例1归纳:旋转不改变图形的形状 和大小 ,
但图形上的每个点同时都按相同的方式转动相 同的角度。旋转前后两个图形对应点到旋转中 心的距离 相等 ;对应点与旋转中心的连线所 成的角都等于旋转角;对应线段__相__等____, 对应角___相_等_______.
检测反馈
1、判断
A1
线 对应线段之间
C
B
两条对应线段的夹角都是旋转角
图中对应的线段:
___A_C_和__A_1_C_、__B__C_和__B_1_C_、__A__B_和__A_1.B1
面 旋转前后的 到什么结论?
A'
A
B'
C
B
O
C'
角:∠AOA'=∠BOB' =∠COC'
线: AO=A'O ,BO=B'O ,CO=C'O
一个图形经过旋转
①图形上的每一个点到旋转中心的距离相等. ( × )
②图形上可能存在不动点.
(√ )
③图形上任意两点的连线与其对应点的连线相等.
( √)
检测反馈
2、如图是正六边形,这个图案可以看做是由
__△_A__O__B_____“基本图案”通过旋转得到的.
人教版九年级数学上23.1.图形的旋转 (共24张PPT)

. M
E
B D (3)如果M是AB的中点,那么经过上述旋 C
转后,点M转到了什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.
练习2. 如图:P是等边ABC内的一点,把 ABP按不同的方向通过旋转得到BQC和 ACR, (1)指出旋转中心、旋转方向和旋转角度? (2) ACR是否可以直接通过把BQC旋转 得到?
A
R
P B
Q
C
议一议 如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中: (1)旋转中心是什么?
旋转中心是O
(2)经过旋转,点A、B分别移动到什么位置? 点D和点E的位置 (3)旋转角是什么? ∠AOD和∠BOE都是旋转角
(4)AO与DO的长有什么关系?BO与EO呢? AO=DO,BO=EO
(5)∠AOD与∠BOE有什么大小关系?
∠AOD=∠BOE
讨论: (1)图形上的点绕着旋 转中心转过的角度之间 有何关系? (2)你能发现图中线段 之间、角之间有什么关系? (3)ΔABC和ΔA’B’C’的 形状、大小有何变化?
1、图形中每一点都绕着旋转中心旋转了同样大小 的角度(任意一对对应点与旋转中心的连线所 成的角都是旋转角)。
(1)上面情景中的转动现 象,有什么共同的特征?
(2)钟表的指针、秋千在 转动过程中,其形状、大小、 位置是否发生变化呢?
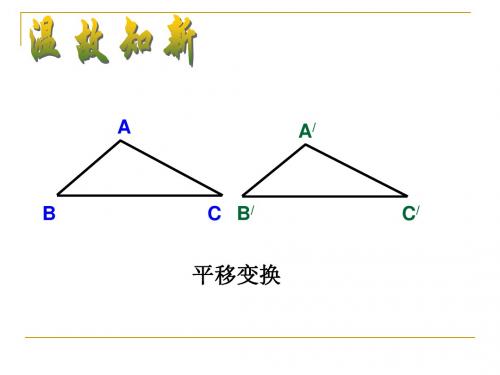
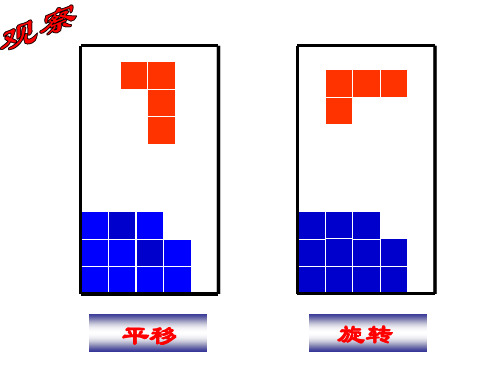
在平面内,将一个图形沿着某个方向移动
一定的距离,这样的图形运动称为平移. 平移不改变图形的大小和形状。 在平面内,将一个图形绕着一个定点沿 某个方向转动一个角度,这样的图形运 动称为旋转 旋转不改变图形的大小和形状。
2.在等腰直角△ABC中,∠C=900, BC=2cm,如果以AC的中点O为旋 转中心,将这个三角形旋转1800, 点B落在点B′处,求BB′的长度.
E
B D (3)如果M是AB的中点,那么经过上述旋 C
转后,点M转到了什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.
练习2. 如图:P是等边ABC内的一点,把 ABP按不同的方向通过旋转得到BQC和 ACR, (1)指出旋转中心、旋转方向和旋转角度? (2) ACR是否可以直接通过把BQC旋转 得到?
A
R
P B
Q
C
议一议 如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得 到四边形DOEF. 在这个旋转过程中: (1)旋转中心是什么?
旋转中心是O
(2)经过旋转,点A、B分别移动到什么位置? 点D和点E的位置 (3)旋转角是什么? ∠AOD和∠BOE都是旋转角
(4)AO与DO的长有什么关系?BO与EO呢? AO=DO,BO=EO
(5)∠AOD与∠BOE有什么大小关系?
∠AOD=∠BOE
讨论: (1)图形上的点绕着旋 转中心转过的角度之间 有何关系? (2)你能发现图中线段 之间、角之间有什么关系? (3)ΔABC和ΔA’B’C’的 形状、大小有何变化?
1、图形中每一点都绕着旋转中心旋转了同样大小 的角度(任意一对对应点与旋转中心的连线所 成的角都是旋转角)。
(1)上面情景中的转动现 象,有什么共同的特征?
(2)钟表的指针、秋千在 转动过程中,其形状、大小、 位置是否发生变化呢?
在平面内,将一个图形沿着某个方向移动
一定的距离,这样的图形运动称为平移. 平移不改变图形的大小和形状。 在平面内,将一个图形绕着一个定点沿 某个方向转动一个角度,这样的图形运 动称为旋转 旋转不改变图形的大小和形状。
2.在等腰直角△ABC中,∠C=900, BC=2cm,如果以AC的中点O为旋 转中心,将这个三角形旋转1800, 点B落在点B′处,求BB′的长度.
人教版初中数学课标版九年级上册第二十三章23.1.1图形的旋转(共17张PPT)

14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年8月24日星期二下午10时39分0秒22:39:0021.8.24
15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年8月下午10时39分21.8.2422:39August 24, 2021
16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021年8月24日星期二10时39分0秒22:39:0024 August 2021
10、阅读一切好书如同和过去最杰出的人谈话。22:39:0022:39:0022:398/24/2021 10:39:00 PM
11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。21.8.2422:39:0022:39Aug-2124-Aug-21
23.1.1图形的旋转
一、创设情境 引出概念
活动一:感受旋转
(1)这些现象有哪些共同 点? (2)钟表的指针、风车的叶片在转动过程中,其形状、 大小、位置是否发生改变?秋千的摆动呢?
活动二 探究旋转定义
O
0
45
B
A
点A绕_O_点,按_顺时针方向,转动了_4_5 度到点B.
活动二 探究旋转定义
B/
B
A
0
/
95
A
O
点A绕_O_点,往_逆_时_针方向,转动了_9_5 度到点
/
A.
活动二 探究旋转定义
B´
A
C0
100
A´
B
O
C´
点A绕_O_点,往_顺_时_针方向,转动了_1_00度到点 A´.
人教版九年级上册23.1图形的旋转 课件

B
A'
A
B'
O
课堂小结
定义
三要素:旋转中心,旋转 方向和旋转角度
旋转 性质
① 对应点到旋转中心的距离 相等;
② 对应点与旋转中心所连线 段的夹角等于旋转角.
③ 旋转前后的图形全等;
课堂小结
旋转的 作图
作旋转 图形
确定旋转 中心
1.明确旋转三要素: 旋转中心、旋转方向 和旋转角度.
作图基本步骤 2.找出关键点; 3.作出关键点的对应点; 4.作出新图形; 5.写出结论.
找两条对应点连 线段的垂直平分 线的交点
第二十三章 旋转
23.1 图形的旋转
学习目标
1.掌握旋转的有关概念及基本性质.(重点) 2.能够根据旋转的基本性质解决实际问题和进行简
单作图.(重点) 3.能够根据旋转的基本性质解决实际问题.
导入新课
情境引入
这些运动有什么共同的特点?
讲授新课
一 旋转的概念
观察与思考
问题 观察下列图形的运动,它有什么特点?
B
A C
O
F
D
E
归纳总结
确定一次图形的旋转时, 旋转中心
必须明确 旋转角
旋转方向 温馨提示: ①旋转的范围是“平面内”, 其中“旋转中心,旋转方向,旋转角度”称之为旋转 的三要素; ②旋转变换同样属于全等变换.
例2 如图,点A、B、C、D都在方格纸的格点上,若 △AOB绕点O按逆时针方向旋转到△COD的位置,则 旋转的角度为( C )
A.30° B.45° C.90° D.135°
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图 可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角 为90°.故选C.
23.1 图形的旋转课件 2024-2025学年人教版数学九上
A.格点M
B.格点N
C.格点P
D.格点Q
知识讲解
知识点2 旋转的性质
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等;
3.旋转中心是唯一不动的点;
4.旋转不改变图形的形状和大小.
知识讲解
知识点2 旋转的性质
【例 3】如图,四边形ABCD是边长为4的正方形且DE=1,△ABF是
又∵DF=DF,DE=DM,∴△DEF≌△DMF,
∴EF=MF.
随堂练习
5. 如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,
且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(2)当AE=1时,求EF的长.
(2)解:设EF=MF=x,∵AE=CM=1,AB=BC=3,
旋转作图
利用旋转设计图案
作图步骤
平面直角坐标系中的图形旋
转
飞行中的飞机的螺旋桨、高速运转中的电风扇等均属于旋转现
象.你还能举出类似现象吗?
知识讲解
知识点1 旋转的定义
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样
的图形运动称为旋转.这个定点称为旋转中心.转动的角称为旋转角.如果
图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.转动
∴DE=AD-AE=8-5=3.
随堂练习
3. 如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、
C、D对应的点的位置,以及旋转后的四边形.
随堂练习
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF,∠COG,
∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
B.格点N
C.格点P
D.格点Q
知识讲解
知识点2 旋转的性质
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等;
3.旋转中心是唯一不动的点;
4.旋转不改变图形的形状和大小.
知识讲解
知识点2 旋转的性质
【例 3】如图,四边形ABCD是边长为4的正方形且DE=1,△ABF是
又∵DF=DF,DE=DM,∴△DEF≌△DMF,
∴EF=MF.
随堂练习
5. 如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,
且∠EDF=45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(2)当AE=1时,求EF的长.
(2)解:设EF=MF=x,∵AE=CM=1,AB=BC=3,
旋转作图
利用旋转设计图案
作图步骤
平面直角坐标系中的图形旋
转
飞行中的飞机的螺旋桨、高速运转中的电风扇等均属于旋转现
象.你还能举出类似现象吗?
知识讲解
知识点1 旋转的定义
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样
的图形运动称为旋转.这个定点称为旋转中心.转动的角称为旋转角.如果
图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.转动
∴DE=AD-AE=8-5=3.
随堂练习
3. 如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、
C、D对应的点的位置,以及旋转后的四边形.
随堂练习
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF,∠COG,
∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
人教版数学九年级上册:23.1《图形的旋转》 PPT课件(共24页)
转动硬纸板,再描出这个挖掉的三角形洞
(△A′B′C′),移开硬纸板.
请大家运用刻度尺和量角器度量线段和有关角,并
探索旋转的性质.
O
A'
C'
B'
归纳总结
旋转的性质
对应点到旋转中心的距离相等. 对应点与旋转中心所连线段的夹角等于旋转角. 旋转前后的图形全等.
三、掌握新知
例 如图,E是正方形ABCD中CD边上任意一点,以点A为
中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的 A
D
对应点,即它们旋转后的位置.
E
B
C
解: 因为点A是旋转中心,所以它
A
D
的对应点是它本身.
在正方形ABCD中,
E
AD=AB,∠DAB=90°,所以旋
E' B
C
转后点D与点B重合.
设点E的对应点为点E′,因为旋转后的图形与旋转
(1)选择不同的旋转中心、不同的旋转角,看看旋转 效果; (2)改变三角形的形状,看看旋转效果.
五、运用新知
请以下列图形为基纳小结
第二十三章 旋 转
23.1 图形的旋转
第1课时 旋转的概念及性质
一、复习导入
问题 我们以前学过图形的平移、对称等变换,它们 有哪些特征? 生活中是否还有其他运动变化呢?回答是肯定的,下 面我们就来研究.
二、探索新知
探索1
归纳总结
把一个图形绕着某一定点O 转动一定角度的图 形变换叫做_旋__转_____.这个定点O 叫旋__转__中__心___,转
动的角叫做_旋__转__角_. 如果图形上的点P经过旋转变为点P′,那么点P
23.1 图形的旋转(共19张PPT)人教版初中数学九年级上册
A.30° B.45° C.90° D.135°
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知, OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
合作探究
A
. A′
△ABC是如何运动 到△A′B′C的位置?
.
绕点C逆时针旋转45°.
B′
... ห้องสมุดไป่ตู้5°
CM
B
根据上图填空.
第二十三章 旋 转
23.1 图形的旋转
情境引入
这些运动有什么共同的特点?
观察与思考
问题 观察下列图形的运动,它有什么特点?
O
0
45
B
A
思考:怎样来定
义这种图形变换?
把时针当成一个图形,那么它可以绕着中心 固定点转动一定角度.
钟表的指针在不停地转动,从12时到6时,时 针转动了__1_8_0__度.
证明:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
由旋转的性质,可得
A1B=AB=BC,∠A=∠A1=∠C,∠A1BD= ∠CBC1, 在△BCF与△BA1D中,
A1 C,
A1B
BC,
A1BD CBF,
△BCF≌△BA1D;
例4 如图,点E是正方形ABCD内一点,连接AE、BE、CE,将 △ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2, CE=3则∠BE′C=___1_3_5___度.
怎样来定义 这种图形变换?
把叶片当成一个平面图形,那么它可以绕着 平面内中心固定点转动一定角度. 风车风轮的每个叶片在风的吹动下转动到新的位置.
知识要点
旋转的定义
在平面内,将一个图形绕一 个定点按某个方向转动一个角 度,这样的图形运动称为旋转.
解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知, OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.
合作探究
A
. A′
△ABC是如何运动 到△A′B′C的位置?
.
绕点C逆时针旋转45°.
B′
... ห้องสมุดไป่ตู้5°
CM
B
根据上图填空.
第二十三章 旋 转
23.1 图形的旋转
情境引入
这些运动有什么共同的特点?
观察与思考
问题 观察下列图形的运动,它有什么特点?
O
0
45
B
A
思考:怎样来定
义这种图形变换?
把时针当成一个图形,那么它可以绕着中心 固定点转动一定角度.
钟表的指针在不停地转动,从12时到6时,时 针转动了__1_8_0__度.
证明:∵△ABC是等腰三角形,
∴AB=BC,∠A=∠C,
由旋转的性质,可得
A1B=AB=BC,∠A=∠A1=∠C,∠A1BD= ∠CBC1, 在△BCF与△BA1D中,
A1 C,
A1B
BC,
A1BD CBF,
△BCF≌△BA1D;
例4 如图,点E是正方形ABCD内一点,连接AE、BE、CE,将 △ABE绕点B顺时针旋转90°到△CBE′的位置,若AE=1,BE=2, CE=3则∠BE′C=___1_3_5___度.
怎样来定义 这种图形变换?
把叶片当成一个平面图形,那么它可以绕着 平面内中心固定点转动一定角度. 风车风轮的每个叶片在风的吹动下转动到新的位置.
知识要点
旋转的定义
在平面内,将一个图形绕一 个定点按某个方向转动一个角 度,这样的图形运动称为旋转.
23.1图形的旋转(课件)2024-2025学年九年级数学上册(人教版)
P
对应点
O
120°
P′
合作探究
探究 如图,在硬纸板上,挖一个三角形洞,再挖一个小洞O作为
旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图
案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形
(△A′B′C′),移开硬纸板.
△A′B′C′是由△ABC绕点O按顺时针方向旋转得到的.
小试牛刀
3.如图,△ABC是等边三角形,D是BC边上的中点,
△ABD经过旋转后到达△ACE的位置,那么
A
(1)旋转中心是______;
点A
(2)点B、D的对应点分别是点_________;
点C和点E
(3)线段AB、BD、DA的对应线段
分别是___________;
AC、CE、AE
(4)∠B的对应角是_______;
人教版数学九年级上册
第23.1 图形的旋转
学习目标
1.认识旋转,理解图形旋转的三要素.
2.理解旋转的性质.
3.利用旋转的性质设计图形.
情境引入
情境引入
【问题】观察这些图形,你发现了什么?
它们都是沿某个方向绕定点转动.
互动新授
思考 如图(1),钟表的指针在不停地转动,从3时到5时,
时针转动了多少度?
问:线段OA与OA′有什么关系?_______;
OA=OA′
∠AOA′与∠BOB′有什么关系?______________;
∠AOA′=∠BOB′
△ABC与△A′B′C′形状和大小有什么关系?
__________________.
△ABC≌△A′B′C′
总结归纳
旋转的性质:
对应点到旋转中心的距离相等.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)旋转中心是哪一点? (2)旋转了多少度? (3)如果M是AB的中点,那么经过上述旋 A 转后,点M转到了什么位置? 解:(1)旋转中心是A; . M E C
(2)旋转了60度; B D (3)现象中属于旋转的有( C )个 ①地下水位逐年下降;②传送带的移动;③方向盘 的转动;④水龙头开关的转动;⑤钟摆的运动;⑥
B'
B
A' E
C
A
这节课中, 有什么收获 ? 还有什么疑惑呢?
小结
1、旋转的概念:
在平面内,将一个图形绕着一个定点沿某个方 向转动一个角度,这样的图形运动称为旋转
2、旋转的性质:
1、对应点到旋转中心的距离相等. 2、每一对对应点与旋转中心所连线段的夹 角等于旋转角. 3、旋转前、后的图形全等.
在生活中,遇到问题不妨换个角度去思考,也许 会峰回路转,柳暗花明,也许会变得更明智。不同的 角度,不同的视野,你就会发现不一样的精彩,你会 拥有一片更广阔的天空。
活动三: 探究发现
(1)△A' B' C '可以 看作 △ABC 经过怎样的运 动得到的? (2)线段 OA 和 OA' 有什么关系?∠AOA'和 ∠BOB'有什么关系? (3)你还能发现哪些 有类似关系的线段和角? (4)△ABC和△A ' B' C' 的形状和大小有什么关系?
活动三: 探究发现
P 旋转的决定因素:
120°
O
旋转中心和旋转角度(旋转方向).
P′
练习1
1.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
练习2
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转 中心在哪里?旋转角是哪个角?
活动三: 探究发现
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出 这个挖掉的三角形图案(△ABC),然后围绕旋转中心 转动硬纸板,再描出这个挖掉的三角形(△A ' B' C' ), 移开硬纸板.请同学们思考以下问题:
(5)这一发现对于任意三 角形的任意旋转都成立吗? (6)你能把以上发现,用 自己的语言归纳概括一下吗?
活动四:归纳性质
旋转的性质
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹
角等于旋转角.
◆ 旋转前、后的图形全等.
你能用符号语言表示这三条性质吗?
活动五:知识应用
例 :如图,ABC是等边三角形,D是BC上一点, ABD 经过 旋转后到达ACE的位置。
荡秋千运动.
A.2 B.3 C.4 D.5
活动五:知识应用
2.如图E是正方形ABCD内一点,将△ABE绕点B顺时针 方向旋转到△CBF,其中EB=3cm,则BF=_____cm , ∠EBF=______
A D
E
B F
C
活动五:知识应用
3.如图将△ABC绕C点逆时针旋转30°后,点B落在B′, 点A落在A ′点位置,若A ′ C⊥AB,求∠B’A’C的度 数。
世界如此美丽 请你留心观察
自转与公转
学习目标
1、经历对生活中旋转现象的观察分析过程,学会 用数学的眼光看待生活中的有关问题。 2、认识旋转,理解旋转的三要素。 3、探索旋转的性质,运用性质进行计算和证明。
重点:图形旋转的概念和性质。 难点:探索图形旋转的性质和运用性质计算和证明。
活动一: 感受旋转
问题一:你能举出一些生活的类似例子吗? 问题二:它们转动有什么共同特点吗? 问题三:你能用自己的语言准确描述这个旋转吗?
活动二: 定义旋转
把一个平面图形绕着平面内某一点 O 转动一个角度 的图形变换叫做图形的旋转.这个点 O 叫 旋转中心 , 转动的角叫做 旋转角 . 如果图形上的点 P 经过旋转变为点 P′,那么这两个 点叫做这个旋转的 对应点 .
(2)旋转了60度; B D (3)现象中属于旋转的有( C )个 ①地下水位逐年下降;②传送带的移动;③方向盘 的转动;④水龙头开关的转动;⑤钟摆的运动;⑥
B'
B
A' E
C
A
这节课中, 有什么收获 ? 还有什么疑惑呢?
小结
1、旋转的概念:
在平面内,将一个图形绕着一个定点沿某个方 向转动一个角度,这样的图形运动称为旋转
2、旋转的性质:
1、对应点到旋转中心的距离相等. 2、每一对对应点与旋转中心所连线段的夹 角等于旋转角. 3、旋转前、后的图形全等.
在生活中,遇到问题不妨换个角度去思考,也许 会峰回路转,柳暗花明,也许会变得更明智。不同的 角度,不同的视野,你就会发现不一样的精彩,你会 拥有一片更广阔的天空。
活动三: 探究发现
(1)△A' B' C '可以 看作 △ABC 经过怎样的运 动得到的? (2)线段 OA 和 OA' 有什么关系?∠AOA'和 ∠BOB'有什么关系? (3)你还能发现哪些 有类似关系的线段和角? (4)△ABC和△A ' B' C' 的形状和大小有什么关系?
活动三: 探究发现
P 旋转的决定因素:
120°
O
旋转中心和旋转角度(旋转方向).
P′
练习1
1.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
练习2
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转 中心在哪里?旋转角是哪个角?
活动三: 探究发现
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出 这个挖掉的三角形图案(△ABC),然后围绕旋转中心 转动硬纸板,再描出这个挖掉的三角形(△A ' B' C' ), 移开硬纸板.请同学们思考以下问题:
(5)这一发现对于任意三 角形的任意旋转都成立吗? (6)你能把以上发现,用 自己的语言归纳概括一下吗?
活动四:归纳性质
旋转的性质
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹
角等于旋转角.
◆ 旋转前、后的图形全等.
你能用符号语言表示这三条性质吗?
活动五:知识应用
例 :如图,ABC是等边三角形,D是BC上一点, ABD 经过 旋转后到达ACE的位置。
荡秋千运动.
A.2 B.3 C.4 D.5
活动五:知识应用
2.如图E是正方形ABCD内一点,将△ABE绕点B顺时针 方向旋转到△CBF,其中EB=3cm,则BF=_____cm , ∠EBF=______
A D
E
B F
C
活动五:知识应用
3.如图将△ABC绕C点逆时针旋转30°后,点B落在B′, 点A落在A ′点位置,若A ′ C⊥AB,求∠B’A’C的度 数。
世界如此美丽 请你留心观察
自转与公转
学习目标
1、经历对生活中旋转现象的观察分析过程,学会 用数学的眼光看待生活中的有关问题。 2、认识旋转,理解旋转的三要素。 3、探索旋转的性质,运用性质进行计算和证明。
重点:图形旋转的概念和性质。 难点:探索图形旋转的性质和运用性质计算和证明。
活动一: 感受旋转
问题一:你能举出一些生活的类似例子吗? 问题二:它们转动有什么共同特点吗? 问题三:你能用自己的语言准确描述这个旋转吗?
活动二: 定义旋转
把一个平面图形绕着平面内某一点 O 转动一个角度 的图形变换叫做图形的旋转.这个点 O 叫 旋转中心 , 转动的角叫做 旋转角 . 如果图形上的点 P 经过旋转变为点 P′,那么这两个 点叫做这个旋转的 对应点 .
