全国高考试题分类解析(简易逻辑)
2023届全国高考数学真题分类专项(集合与常用逻辑用语)汇编解析(附答案)

2023届全国高考数学真题分类专项(集合与常用逻辑用语)汇编解析第一节 集合1.(2023全国甲卷理科1)设集合 31,A x x k k Z ,32,B x x k k Z ,U 为整数集,则 U A B ð( )A. 3,x x k k ZB. 31,x x k k ZC. 32,x x k k ZD.【要点分析】根据整数集的分类,以及补集的运算即可解出.【过程解析】因为整数集 3,3+1,3+2,x x k k x x k k x x k k Z Z Z Z ,=U Z ,所以 3,U A B x x k k Z ð. 故选A .2.(2023全国甲卷文科1)设全集 1,2,3,4,5U ,集合 1,4M , 2,5N ,则U N M ð( )A. 2,3,5B. 1,3,4C. 1,2,4,5D. 2,3,4,5 【要点分析】利用集合的交并补运算即可得解.【过程解析】因为全集{1,2,3,4,5}U ,集合{1,4}M ,所以 2,3,5U M ð, 又{2,5}N ,所以{2,3,5}U N M ð.故选A.3.(2023全国乙卷理科2)设集合U R ,集合 1M x x , 12N x x ,则 2x x …( )A. U M N ðB.U N M ðC. U M N ðD.U M N ð 【要点分析】由题意逐一考查所给的选项运算结果是否为 2x x …即可.【过程解析】由题意可得 2M N x x ,则 2U M N x x ð…,选项A 正确; 1U M x x ð…,则 1U N M x x ð ,选项B 错误;11M N x x ,则 11U M N x x x 或ð剠,选项C 错误;12U N x x x 或ð剠,则 12U M N x x x 或ð…,选项D 错误;故选A.4.(2023全国乙卷文科2)设全集 0,1,2,4,6,8U ,集合 0,4,6M , 0,1,6N ,则U M N ð( )A. 0,2,4,6,8B. 0,1,4,6,8C. 1,2,4,6,8D.U 【要点分析】由题意可得U N ð的值,然后计算U M N ð即可. 【过程解析】由题意可得 2,4,8U N ð,则 0,2,4,6,8U M N ð. 故选A.5.(2023新高考I 卷1)已知集合 2,1,0,1,2M ,260N x x x ,则M N( ) A. 2,1,0,1B. 0,1,2C. 2D. 2【过程解析】260,23,N x x x ,所以 2M N ,故选C.6.(2023新高考II 卷2)2.设集合 0,,1,2,22A a B a a ,若A B ,则a ( ) A. 2 B. 1 C.23D.1 【过程解析】因为A B ,所以必有20a 或220a ,解得2a 或1a . 当2a 时, 0,2,1,0,2A B ,不满足A B ; 当1a 时, 0,1,1,1,0A B ,符合题意.所以1a . 故选B.7.(2023北京卷1)已知集合 20M x x …, 10N x x ,则M N ( ) A. 21x x … B. 21x x … C. 2x x … D. 1x x【要点分析】先化简集合,M N ,然后根据交集的定义计算.【过程解析】由题意,{20}{|2}M xx x x ∣,{10}{|1}N x x x x ∣, 根据交集的运算可知,{|21}M N x x .故选A.8.(2023天津卷1)已知集合 1,2,3,4,5,1,3,1,2,4U A B ,则U B A ð( ) A . 1,3,5B . 1,3C . 1,2,4D . 1,2,4,5【要点分析】对集合B 求补集,应用集合的并运算求结果;【过程解析】由{3,5}U B ð,而{1,3}A ,所以{1,3,5}U B A ð. 故选A.第二节 充分条件与必要条件、全称量词与存在量词1.(2023全国甲卷理科7)“22sin sin 1 ”是“sin cos 0 ”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件【要点分析】根据充分条件、必要条件概念及同角三角函数的基本关系得解. 【过程解析】当2,0 时,有22sin sin 1 ,但sin cos 0 , 即22sin sin 1 推不出sin cos 0 ;当sin cos 0 时, 2222sin sin cos sin 1 ,即sin cos 0 能推出22sin sin 1 .综上可知,22sin sin 1 是sin cos 0 成立的必要不充分条件. 故选B.2.(2023新高考I 卷7)已记n S 为数列 n a 的前n 项和,设甲: n a 为等差数列;乙:n S n为等差数列,则( )A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件【过程解析】 n a 为等差数列,设首项为1a 公差为d ,则112n n n S na d,111222n S n d d a d n a n ,所以n S n为等差数列,所以甲是乙的充分条件. n S n为等差数列,即 1111111n n n n n n nS n S S S na S n n n n n n 为常数, 设为t ,即11n nna S t n n ,故 11n n S na tn n , 1112n n S n a t n n n ,两式相减得 1112n n n n n a S S na n a tn ,12n n a a t 为常数,对1n 也成立,所以 n a 为等差数列,所以甲是乙的必要条件. 所以,甲是乙的充要条件,故选C.3.(2023北京卷8)若0xy ,则“0x y ”是“2x yy x”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件【要点分析】解法一:证明充分性可由0x y 得到x y ,代入x yy x化简即可,证明必要性可由2x y y x 去分母,再用完全平方公式即可;解法二:由x y y x通分后用配凑法得到完全平方公式,证明充分性可把0x y 代入即可;证明必要性把2x yy x代入,解方程即可.【过程解析】解法一:充分性:因为0xy ,且0x y ,所以x y , 所以112x y y y y x y y,所以充分性成立; 必要性:因为0xy ,且2x yy x, 所以222x y xy ,即2220x y xy ,即 20x y ,所以0x y .所以必要性成立.所以“0x y ”是“2x yy x”的充要条件.故选C. 解法二:充分性:因为0xy ,且0x y ,所以 2222222222x y xy x y x y x y xy xy xy y x xy xy xy xy,所以充分性成立; 必要性:因为0xy ,且2x yy x, 所以 22222222222x y xy x y x y x y x y xy xy y x xy xy xy xy, 所以20x y xy,所以 20x y ,所以0x y ,所以必要性成立.所以“0x y ”是“2x yy x”的充要条件. 故选C.4.(2023天津卷2)“22a b ”是“222a b ab ”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分又不必要条件【要点分析】根据充分、必要性定义判断条件的推出关系,即可得答案.【过程解析】由22a b ,则a b ,当0a b 时222a b ab 不成立,充分性不成立; 由222a b ab ,则2()0a b ,即a b ,显然22a b 成立,必要性成立; 所以22a b 是222a b ab 的必要不充分条件. 故选B.。
五年(2018-22)全国高考数学真题分类汇编(全国卷新高考卷卷等)专题11 简易逻辑(解析版)

这四个命题中,所有真命题的编号是( )
A.①③B.①②C.②③D.③④
【答案】【答案】A
【解析】作出等式组 的平面区域为 .在图形可行域范围内可知:命题 , ;是真命题,则 假命题;
命题 , .是假命题,则 真命题;
所以:由或且非逻辑连词连接的命题判断真假有:
1 真;② 假;③ 真;④ 假;
A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件
【答案】A
解析:若函数 在 上单调递增,则 在 上的最大值为 ,
若 在 上的最大值为 ,比如 ,
但 在 为减函数,在 为增函数,
故 在 上的最大值为 推不出 在 上单调递增,
故“函数 在 上单调递增”是“ 在 上的最大值为 ”的充分不必要条件,
【题目来源】2020天津高考·第2题
7.(2020北京高考·第9题)已知 ,则“存在 使得 ”是“ ”的().
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
【答案】C
【解析】(1)当存在 使得 时,
若 为偶数,则 ;
若 为奇数,则 ;
(2)当 时, 或 , ,即 或 ,亦即存在 使得 .
故答案①③真,正确.故选:A.
【答案】【答案】A
【解析】解法一:当 时,若 ,则 ,即 ,故充分性成立;当 时,满足 ,但 ,必要性不成立.综上所述,“ ”是“ ”的充分不必要条件.故选A.
解法二:如图所示,在平面直角坐标系中,满足条件“ , , ”的点 是 的内部及边界线段 (不含端点 , );而满足条件“ , , ”的点 是位于第一象限且在曲线 的下方(或该曲线上).因为直线 与曲线 相切,切点为 .故由区域的包含关系可解.故选A.
高考数学试题解析分项 专题2 简易逻辑 理 试题

2021年高考试题解析数学〔理科〕分项版02 简易逻辑创 作人:荧多莘 日 期: 二O 二二 年1月17日一、选择题:1.(2021年高考卷理科7)假设,a b 为实数,那么“01ab <<〞是11a b b a<>或的 〔A 〕充分而不必要条件〔B 〕必要而不充分条件〔C 〕充分必要条件〔D 〕既不充分也不必要条件2. (2021年高考卷理科2)设,,x y R ∈那么“2x ≥且2y ≥〞是“224x y +≥〞的 A. 充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .即不充分也不必要条件 【答案】A【解析】由2x ≥且2y ≥可得224x y +≥,但反之不成立,应选A. 3.(2021年高考卷理科7)命题“所有能被2整除的数都是偶数〞的否认..是〔A 〕所有不能被2整除的数都是偶数 〔B 〕所有能被2整除的数都不是偶数 〔C 〕存在一个不能被2整除的数是偶数 〔D 〕存在一个能被2整除的数不是偶数 【答案】D【命题意图】此题考察全称命题的否认.属容易题.【解析】把全称量词改为存在量词,并把结果否认. 【解题指导】:要注意命题否认与否命题之间的区别与联络。
4. (2021年高考全国新课标卷理科10)a 与b 均为单位向量,其夹角为θ,有以下四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是〔A 〕14,P P 〔B 〕13,P P 〔C 〕23,P P 〔D 〕24,P P 答案:A1>可得,21cos 21.cos ,0cos 21,1222<->∴>±∴>±+θθθ或b a b a⎪⎭⎫⎝⎛∈⎪⎭⎫⎢⎣⎡∈∴ππθπθ,,,3,3,0应选D点评:该题考察平面向量的的概念、数量积运算以及三角函数值与角的取值范围,要纯熟把握概念及运算。
简易逻辑全国高考试题精选(含答案)

简易逻辑全国卷试题精选一、选择题1. “21=m ”是“直线03)2()2(013)2(=-++-=+++y m x m my x m 与直线相互垂直”的( )A .充分必要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件 2. 设集合A ={x |11+-x x <0},B ={x || x -1|<a },若“a =1”是“A ∩B ≠”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分又不必要条件3. 命题p :“有些三角形是等腰三角形”,则┐p 是( )A .有些三角形不是等腰三角形B .所有三角形是等腰三角形C .所有三角形不是等腰三角形D .所有三角形是等腰三角形4. 设命题p :方程2310x x +-=的两根符号不同;命题q :方程2310x x +-=的两根之和为3,判断命题“p ⌝”、“q ⌝”、“p q ∧”、“p q ∨”为假命题的个数为( )A .0B .1C .2D .35.“a >b >0”是“ab <222b a +”的 ( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件6. 若不等式|x -1| <a 成立的充分条件是0<x <4,则实数a 的取值范围是 ( )A .a ≤1B .a ≤3C .a ≥1D .a ≥37. 下列命题中,其“非”是真命题的是( )A .∀x ∈R ,x ²-22x + 2 ≥ 0B .∃x ∈R ,3x-5 = 0C .一切分数都是有理数D .对于任意的实数a,b,方程ax=b 都有唯一解8. 0a <是方程2210ax x ++=至少有一个负数根的( ) A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件二、填空题9. (1)命题:,R x ∈∃ x 2+x +1<0的否定是 ,(2) 命题“∀x ∈R ,x 2-x +3>0”的否定是 , (3) 命题 “对任意的x ∈{x|-2<x<4},|x-2|<3”的否定形式 (4)命题 “∀x ,y ∈R ,有x ²+ y ² ≥ 0”的否定是 (5) 命题 “不等式x 2+x -6>0的解是x <-3或x >2”的逆否命题是(6)命题“∀a ,b ∈R ,如果ab >0,则a >0”的否命题是(7)命题 “△ABC 中,若∠C=90°,则∠A 、∠B 都是锐角”的否命题为:,否定形式: 。
十年高考分类解析:第1章 集合与简易逻辑

十年高考分类解析 第一章 集合与简易逻辑一、选择题1.(2003京春理,11)若不等式|ax +2|<6的解集为(-1,2),则实数a 等于( ) A.8 B.2 C.-4 D.-82.(2002京皖春,1)不等式组⎩⎨⎧<-<-030122x x x 的解集是( )A.{x |-1<x <1}B.{x |0<x <3}C.{x |0<x <1}D.{x |-1<x <3}3.(2002北京,1)满足条件M ∪{1}={1,2,3}的集合M 的个数是( ) A.4 B.3 C.2 D.14.(2002全国文6,理5)设集合M ={x |x =412+k ,k ∈Z },N ={x |x =214+k ,k ∈Z },则( )A.M =NB.M NC.M ND.M ∩N =∅ 5.(2002河南、广西、广东7)函数f (x )=x |x +a |+b 是奇函数的充要条件是( ) A.ab =0 B.a +b =0 C.a =b D.a 2+b 2=06.(2001上海,3)a =3是直线ax +2y +3a =0和直线3x +(a -1)y =a -7平行且不重合的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件7.(2000北京春,2)设全集I ={a ,b ,c ,d ,e },集合M ={a ,b ,c },N ={b ,d ,e },那么I M ∩I N是( )A.∅B.{d }C.{a ,c }D.{b ,e } 8.(2000全国文,1)设集合A ={x |x ∈Z 且-10≤x ≤-1},B ={x |x ∈B 且|x |≤5},则A ∪B 中元素的个数是( )A.11B.10C.16D.15 9.(2000上海春,15)“a =1”是“函数y =cos 2ax -sin 2ax 的最小正周期为π”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分条件也非必要条件10.(2000广东,1)已知集合A ={1,2,3,4},那么A 的真子集的个数是( ) A.15 B.16 C.3 D.4 11.(1999全国,1)如图1—1,I 是全集,M 、P 、S 是I 的3个子集,则阴影部分所表示的集合是( )A.(M ∩P )∩SB.(M ∩P )∪SC.(M ∩P )∩I SD.(M ∩P )∪I S12.(1998上海,15)设全集为R,A={x|x2-5x-6>0},B={x||x-5|<a}(a 为常数),且11∈B,则()A.R A∪B=RB.A∪R B=RC.R A∪R B=RD.A∪B=R13.(1997全国,1)设集合M={x|0≤x<2},集合N={x|x2-2x-3<0},集合M ∩N等于()A.{x|0≤x<1}B.{x|0≤x<2}C.{x|0≤x≤1}D.{x|0≤x≤2}14.(1997上海,1)设全集是实数集R,M={x|x≤1+2,x∈R},N={1,2,3,4},则R M∩N等于()A.{4}B.{3,4}C.{2,3,4}D.{1,2,3,4}15.(1996上海,1)已知集合M={(x,y)|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为()A.x=3,y=-1B.(3,-1)C.{3,-1}D.{(3,-1)}16.(1996全国文,1)设全集I={1,2,3,4,5,6,7},集合A={1,3,5,7},B={3,5},则()A.I=A∪BB.I=I A∪BC.I=A∪I BD.I=I A∪I B17.(1996全国理,1)已知全集I=N*,集合A={x|x=2n,n∈N*},B={x|x=4n,n∈N},则()A.I=A∪BB.I=I A∪BC.I=A∪I BD.I=I A∪I B18.(1996上海文,6)若y=f(x)是定义在R上的函数,则y=f(x)为奇函数的一个充要条件为()A.f(x)=0B.对任意x∈R,f(x)=0都成立C.存在某x0∈R,使得f(x0)+f(-x0)=0D.对任意的x∈R,f(x)+f(-x)=0都成立19.(1995上海,2)如果P={x|(x-1)(2x-5)<0},Q={x|0<x<10},那么()A.P∩Q=B.P QC.P QD.P∪Q=R20.(1995全国文,1)已知全集I ={0,-1,-2,-3,-4},集合M ={0,-1,-2},N ={0,-3,-4},则I M ∩N等于( )A.{0}B.{-3,-4}C.{-1,-2}D.∅21.(1995全国理,1)已知I 为全集,集合M 、N I ,若M ∩N =N ,则( ) A.I M⊇I N B.M I NC.IM I ND.M⊇I N22.(1995上海,9)“ab <0”是“方程ax 2+by 2=c 表示双曲线”的( ) A.必要条件但不是充分条件 B.充分条件但不是必要条件 C.充分必要条件 D.既不是充分条件又不是必要条件 23.(1994全国,1)设全集I ={0,1,2,3,4},集合A ={0,1,2,3},集合B ={2,3,4},则I A ∪I B等于( )A.{0}B.{0,1}C.{0,1,4}D.{0,1,2,3,4} 24.(1994上海,15)设I 是全集,集合P 、Q 满足P Q ,则下面的结论中错误的是( ) A.P ∪I Q =∅ B.I P ∪Q =IC.P ∩I Q =∅D.I P ∩I Q =I P二、填空题25.(2003上海春,5)已知集合A ={x ||x |≤2,x ∈R },B ={x |x ≥a },且A B ,则实数a 的取值范围是_____.26.(2002上海春,3)若全集I =R ,f (x )、g (x )均为x 的二次函数,P ={x |f (x )<0},Q ={x |g (x )≥0},则不等式组⎩⎨⎧<<0)(0)(x g x f 的解集可用P 、Q 表示为_____.27.(2001天津理,15)在空间中①若四点不共面,则这四点中任何三点都不共线; ②若两条直线没有公共点,则这两条直线是异面直线. 以上两个命题中,逆命题为真命题的是_____. 28.(2000上海春,12)设I 是全集,非空集合P 、Q 满足P Q I .若含P 、Q 的一个集合运算表达式,使运算结果为空集∅,则这个运算表达式可以是 (只要写出一个表达式).29.(1999全国,18)α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线,给出四个论断:①m ⊥n ②α⊥β ③n ⊥β ④m ⊥α 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个..命题:_____. 三、解答题30.(2003上海春,17)解不等式组⎪⎩⎪⎨⎧>-+>+-2130862x x x x .31.(2000上海春,17)已知R 为全集,A ={x |lo g 21(3-x )≥-2},B ={x |25+x ≥1},求R A ∩B .32.(1999上海,17)设集合A ={x ||x -a |<2},B ={x |212+-x x <1},若A ⊆B ,求实数a 的取值范围.●答案详析 1.答案:C解析:∵|ax +2|<6,∴-6<ax +2<6,-8<ax <4当a >0时,有ax a 48<<-,而已知原不等式的解集为(-1,2),所以有: ⎪⎪⎩⎪⎪⎨⎧-=-=1824aa.此方程无解(舍去). 当a <0时,有a x a 48<<-,所以有⎪⎪⎩⎪⎪⎨⎧-==-1428aa解得a =-4,当a =0时,原不等式的解集为R ,与题设不符(舍去),故a =-4.评述:本题主要考查绝对值不等式的解法,方程的根与不等式解集的关系,考查了分类讨论的数学思想方法及逻辑思维能力,此题也可以利用选项的值代入原不等式,去寻找满足题设条件的a 的值.2.答案:C解析:依题意可得⎩⎨⎧<<<<-3011x x ,可得0<x <1.3.答案:C解析:M ={2,3}或M ={1,2,3}评述:因为M ⊆{1,2,3},因此M 必为集合{1,2,3}的子集,同时含元素2,3. 4.答案:B解析:方法一:可利用特殊值法,令k =-2,-1,0,1,2可得}1,43,21,41,0{},45,43,41,41,43{=--=N M∴M N方法二:集合M 的元素为:412412+=+=k k x(k ∈Z ),集合N 的元素为:x =42214+=+k k (k ∈Z ),而2k +1为奇数,k +2为整数,因此M N .∴M N 5.答案:D解析:若a 2+b 2=0,即a =b =0时,f (-x )=(-x )|x +0|+0=-x |x |=-f (x ) ∴a 2+b 2=0是f (x )为奇函数的充分条件.又若f (x )为奇函数即f (-x )=-x |(-x )+a |+b =-(x |x +a |+b ),则 必有a =b =0,即a 2+b 2=0,∴a 2+b 2=0是f (x )为奇函数的必要条件. 6.答案:C解析:当a =3时,直线l 1:3x +2y +9=0,直线l 2:3x +2y +4=0 显然a =3⇔l 1∥l 2. 7.答案:A 解析:∵I M ={b ,e },I N ={a ,c },∴I M ∩I N =∅.8.答案:C解析:∵A ={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1} B ={-5,-4,-3,-2,-1,0,1,2,3,4,5}∴A ∪B ={-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5}共有16个元素.9.答案:A解析:若a =1,则y =cos 2x -sin 2x =cos2x ,此时y 的最小正周期为π,故a =1是充分条件.而由y =cos 2ax -sin 2ax =cos2ax ,此时y 的周期为|2|2a π=π, ∴a =±1,故a =1不是必要条件.评述:本题考查充要条件的基本知识,难点在于周期概念的准确把握. 10.答案:A解析:根据子集的计算应有24-1=15(个).评述:求真子集时千万不要忘记空集∅是任何非空集合的真子集.同时,A 不是A 的真子集.11.答案:C解析:由图知阴影部分表示的集合是M ∩P 的子集且是I S的子集,故答案为C.评述:本题源于课本,属送分题,是前几年高考题的回归. 12.答案:D解析:由已知A ={x |x >6或x <-1},B ={x |5-a <x <5+a },而11∈B ,∴⇒⎩⎨⎧>+<-115115a a a >6. 此时:5-a <-1,5+a >6,∴A ∪B =R .评述:本题考查集合基本知识,一元二次不等式、绝对值不等式的解法及分析问题解决问题的能力.13.答案:B解析:方法一:N ={x |x 2-2x -3<0}={x |-1<x <3},所以M ∩N ={x |0≤x <2},故选B.方法二:由(23)2-2²(23)-3<0,知1.5∈N ,又1.5∈M ,因此1.5∈M ∩N ,从而排除A 、C;由交集定义与M 的表达式,可排除D ,得B.评述:本题考查对交集的理解和掌握,所设定的集合实质是不等式的解集,兼考处理不等式解集的基本技能.14.答案:B解析:R M ={x |x >1+2,x ∈R },又1+2<3.故R M ∩N ={3,4}.故选B.15.答案:D 解析:方法一:解方程组⎩⎨⎧=-=+,4,2y x y x 得⎩⎨⎧-==.1,3y x 故M ∩N ={(3,-1)},所以选D.方法二:因所求M ∩N 为两个点集的交集,故结果仍为点集,显然只有D 正确. 评述:要特别理解集合中代表元素的意义,此题迎刃而解.16.答案:C 解析:方法一:显然I B ={1,2,4,6,7}, 于是A ∪I B =I ,故选C.方法二:利用文氏图1—3知I =A ∪I B ,应选C.17.答案:C解析:方法一:I A 中元素是非2的倍数的自然数,I B 中元素是非4的倍数的自然数,显然,只有C选项正确.方法二:因A ={2,4,6,8…},B ={4,8,12,16,…},所以I B ={1,2,3,5,6,7,9…},所以I =A ∪I B ,故答案为C.方法三:因B A ,所以I AI B ,I A ∩I B =I A ,故I =A ∪I A =A ∪IB .方法四:根据题意,我们画出文氏图1—4来解,易知B A ,如图:可以清楚看到I = A ∪I B是成立的.评述:本题考查对集合概念和关系的理解和掌握,注意数形结合的思想方法,用无限集考查,提高了对逻辑思维能力的要求.18.答案:D解析:由奇函数定义可知:若f (x )为奇函数,则对定义域内任意一个x ,都有f (-x )=-f (x ),即f (-x )+f (x )=0,反之,若有f (x )+f (-x )=0,即f (-x )=-f (x ),由奇函数的定义可知f (x )为奇函数.评述:对于判断奇偶性问题应注意:x 为定义域内任意值,因此定义域本身应关于原点对称,这是奇偶性问题的必要条件.19.答案:B解析:由集合P 得1<x <25,由集合Q 有0<x <10.利用数轴上的覆盖关系,易得P Q . 20.答案:B 解析:由已知I M ={-3,-4},∴I M ∩N ={-3,-4}.21.答案:C解析一:∵M ∩N =N ,∴N ⊆M ,∴I N⊇I M解析二:画出韦恩图1—5,显然:I M⊆I N .故选C.评述:本题主要考查集合的概念和集合的关系,题目中不给出具体集合,对分析问题解决问题能力提高了要求.22.答案:A解析:如果方程ax 2+by 2=c 表示双曲线,即122=+bc ya c x 表示双曲线,因此有0<⋅b c a c ,即ab <0.这就是说“ab <0”是必要条件;若ab <0,c 可以为0,此时,方程不表示双曲线,即ab <0不是充分条件.评述:本题考查充要条件的推理判断和双曲线的概念. 23.答案:C解析:∵I A ={4},I B ={0,1},∴I A ∪I B ={0,1,4}.24.答案:D解析:依题意画出文氏图:如图1—6,显然A 、B 、C 均正确,故应选D.25.答案:a ≤-2解析:∵A ={x |-2≤x ≤2},B ={x |x ≥a },又A ⊆B ,利用数轴上覆盖关系:如图1—7因此有a ≤-2.评述:本题主要考查集合的概念和集合的关系. 26.答案:P ∩I Q解析:∵g (x )≥0的解集为Q ,所以g (x )<0的解集为I Q ,因此⎩⎨⎧<<0)(0)(x g x f 的解集为P ∩I Q .评述:本题以不等式为载体,重点考查集合的补集、交集的概念及其运算,活而不难. 27.答案:②解析:①中的逆命题是:若四点中任何三点都不共线,则这四点不共面.我们用正方体AC 1做模型来观察:上底面A 1B 1C 1D 1中任何三点都不共线,但A 1B 1C 1D 1四点共面,所以①中逆命题不真.②中的逆命题是:若两条直线是异面直线,则两条直线没有公共点. 由异面直线的定义可知,成异面直线的两条直线不会有公共点. 所以②中逆命题是真命题.评述:本题考查点共线、点共面和异面直线的基本知识,考查命题的有关概念.28.答案:P ∩I Q解析:阴影部分为I Q (如图1—8)显然,所求表达式为I Q ∩P =∅,或I Q ∩(Q ∩P )或I Q ∩(Q ∪P )=∅.评述:本题考查集合的关系及运算.29.答案:m ⊥α,n ⊥β,α⊥β⇒m ⊥n ,或m ⊥n ,m ⊥α, n ⊥β⇒α⊥β.(二者任选一个即可)解析:假设①、③、④为条件,即m ⊥n ,n ⊥β,m ⊥α成立, 如图1—9,过m 上一点P 作PB ∥n ,则PB ⊥m ,PB ⊥β,设垂足为B .又设m ⊥α的垂足为A ,过P A 、PB 的平面与α、β的交线l 交于点C ,因为l ⊥P A ,l ⊥PB ,所以l ⊥平面P AB ,得l ⊥AC ,l ⊥BC ,∠ACB 是二面角α-l -β的平面角.显然∠APB +∠ACB =180°,因为P A ⊥PB ,所以∠ACB =90°,得α⊥β.由①、③、④推得②成立.反过来,如果②、③、④成立,与上面证法类似可得①成立.评述:本题主要考查线线、线面、面面之间关系的判定与性质,但题型较新颖,主要表现在:题目以立体几何知识为背景,给出了若干材料,要求学生能将其组装成具有一定逻辑关系的整体,解题的关键是将符号语言转化为图形语言.考查知识立足课本,对空间想象能力、分析问题的能力、操作能力和思维的灵活性等方面要求较高,体现了加强能力考查的方向.30.解:由x 2-6x +8>0,得(x -2)(x -4)>0,∴x <2或x >4. 由13-+x x >2,得15-+-x x >0,∴1<x <5.∴原不等式组的解是x ∈(1,2)∪(4,5)评述:本题主要考查二次不等式、分式不等式的解法.31.解:由已知lo g 21(3-x )≥lo g 214,因为y =lo g 21x 为减函数,所以3-x ≤4.由⎩⎨⎧>-≤-0343x x ,解得-1≤x <3.所以A ={x |-1≤x <3}.由25+x ≥1可化为22302)2(5≥+-⇒≥++-x xx x ⎩⎨⎧≠+≤+-020)2)(3(x x x 解得-2<x ≤3,所以B ={x |-2<x ≤3}. 于是R A ={x |x <-1或x ≥3}.故R A ∩B ={x |-2<x <1或x =3}评述:本题主要考查集合、对数性质、不等式等知识,以及综合运用知识能力和运算能力.32.解:由|x -a |<2,得a -2<x <a +2,所以A ={x |a -2<x <a +2}. 由212+-x x <1,得23+-x x <0,即-2<x <3,所以B ={x |-2<x <3}. 因为A ⊆B ,所以⎩⎨⎧≤+-≥-3222a a ,于是0≤a ≤1.评述:这是一道研究集合的包含关系与解不等式相结合的综合性题目.主要考查集合的概念及运算,解绝对值不等式、分式不等式和不等式组的基本方法.在解题过程中要注意利用不等式的解集在数轴上的表示方法.体现了数形结合的思想方法.。
高考试卷分类汇编01----集合与简易逻辑

高考试卷分类汇编集合与简易逻辑一、选择题•(安徽理)集合A -R|y=lgx,x 1, B =「-2, -1,1,2?则下列结论正确的是()•AnB-「-2,—1? •G R A)U B=(」:,0)•A[JB =(0, =)•(e R A)n B・._2,-1解:A m y R y0 ?, 6 A) = { y | y 岂0},又B—-2,-1,1,2}••• (e R A)PlB J—2,-1 ?,选。
.(安徽理文)a :0是方程ax2 2x ^0至少有一个负数根的()•必要不充分条件•充分不必要条件•充分必要条件•既不充分也不必要条件2 1解:当,=2…4a_0,得a_1时方程有根。
<时,X1X2 0,方程有负根,又时,方程根为ax = -1,所以选•(安徽文)若A为位全体正实数的集合,B_-2,-1,1,2?则下列结论正确的是()APl B = :-2,-1 f •G R A) U B =(-〜0)•AUB =(0,二)•(e R A)n^f.-2^1 /解:e R A是全体非正数的集合即负数和,所以(€R A)p]B =「-2,-1•(北京理)已知全集U = R,集合A,x| -2 < x< 3 , B=「x|x :::-1或x - 4,那么集合A「| $B 等于()•'x| -2 < x 4• x | x < 3或x > 4』•「x| -2 < x :-1 • 1x|—1W x < 3?解: U [, ], AR e u B = 'x| -1 < x < 3?•(北京理)“函数f(x)(x・R)存在反函数”是“函数f(x)在R上为增函数”的()•充分而不必要条件•必要而不充分条件•充分必要条件•既不充分也不必要条件解:函数f(x)(x・R)存在反函数,至少还有可能函数f(x)在R上为减函数,充分条件不成立;而必有条件显然成立。
最新高中数学简单逻辑专题解析(精编版)

全国高考数学试题分类解析——简单逻辑1.(安徽理科第7题)命题“所有能被2整除的数都是偶数”的否定..是( ) (A )所有不能被2整除的数都是偶数(B )所有能被2整除的数都不是偶数(C )存在一个不能被2整除的数是偶数(D )存在一个不能被2整除的数不是偶数解析:全称命题的否定是特称命题,选D2.(北京文科第4题)若p 是真命题,q 是假命题,则( )(A )p q ∧是真命题 (B)p q ∨是假命题(C)p ⌝是真命题 (D)q ⌝是真命题答案: D3.(福建理科第2题)若R a ∈,则2=a 是0)2)(1(=--a a 的( )A.充分而不必要条件 B 必要而不充分条件C.充要条件D.既不充分又不必要条件答案:A4.(福建文科3)若a ∈R ,则“a=1”是“|a|=1”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分又不必要条件答案:A5.(湖北理科9、文科10)若实数b a ,满足0,0≥≥b a ,且0=ab ,则称a 与b 互补,记()b a b a b a --+=22,ϕ,那么()0,=b a ϕ是a 与b 互补( )A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要的条件 答案:C解析:若实数b a ,满足0,0≥≥b a ,且0=ab ,则a 与b 至少有一个为0,不妨设0=b ,则()0,2=-=-=a a a a b a ϕ,反之,若()0,22=--+=b a b a b a ϕ 则022≥+=+b a b a ,两边平方得ab b a b a 22222++=+0=⇔ab ,则a 与b 互补,故选C.6.(湖南理科2)设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”。
(完整版)高考数学简易逻辑知识点+例题+练习(学生),推荐文档
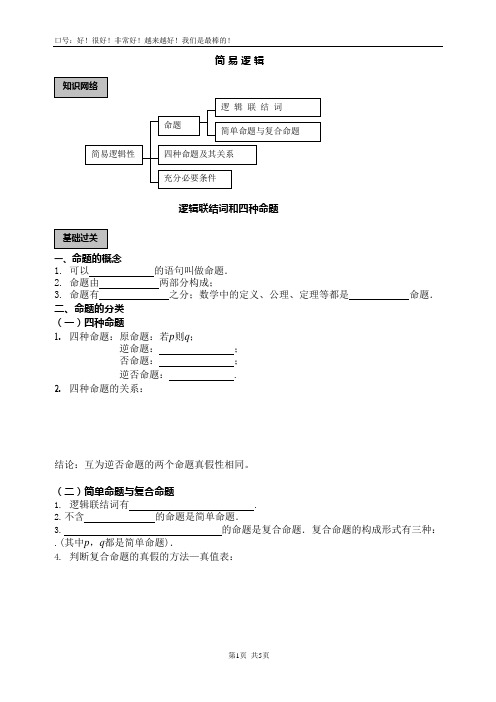
简 易 逻 辑逻辑联结词和四种命题一、命题的概念1. 可以 的语句叫做命题.2. 命题由 两部分构成;3. 命题有 之分;数学中的定义、公理、定理等都是 命题.二、命题的分类 (一)四种命题1. 四种命题:原命题:若p 则q ;逆命题: ; 否命题: ; 逆否命题: .2. 四种命题的关系:结论:互为逆否命题的两个命题真假性相同。
(二)简单命题与复合命题 1. 逻辑联结词有 . 2. 不含 的命题是简单命题. 3. 的命题是复合命题.复合命题的构成形式有三种: .(其中p ,q 都是简单命题).4. 判断复合命题的真假的方法—真值表:(三)全称命题与存在命题1.全称量词:,用表示;2.存在量词:,用表示。
3.全称命题:,;4. 存在命题:,。
三、区分“命题的否定”和“否命题”1.命题的否定只否定结论:;2.否命题条件、结论都否定:。
例1. 分别写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假:(1) 若q<1,则方程x2+2x+q=0有实根;(2) 若ab=0,则a=0或b=0;(3) 若x2+y2=0,则x、y全为零.变式训练:写出下列命题的否命题,并判断原命题及否命题的真假:(1)如果一个三角形的三条边都相等,那么这个三角形的三个角都相等;(2)矩形的对角线互相平分且相等;(3)相似三角形一定是全等三角形.例2:如果命题“p或q”是真命题,“p且q”是假命题.那么()A.命题p和命题q都是假命题B.命题p和命题q都是真命题C.命题p和命题“非q”真值不同D.命题q和命题p的真值不同变式训练:下列结论中正确的是()(A)命题p是真命题时,命题“P且q”一定是真命题。
(B)命题“P且q”是真命题时,命题P一定是真命题(C)命题“P且q”是假命题时,命题P一定是假命题(D)命题P是假命题时,命题“P且q”不一定是假命题例3.已知p:x2 +mx + 1 = 0 有两个不等的负根,q:4x2 + 4(m - 2)x + 1 = 0 无实根.若p或q为真,p且q 为假,求m的取值范围.分析:由p或q为真,知p、q必有其一为真,由p且q为假,知p、q必有一个为假,所以,“p假且q真”或“p真且q假”.可先求出命题p及命题q为真的条件,再分类讨论.变式训练:已知下列三个方程:①x2+4ax-4a+3=0,②x2+(a-1)x+a2=0,③x2+2 ax-2a=0中至少有一个方程有实根,求实数a的取值范围.充要条件p ⇒q 则p 叫做q 的 条件,q 叫做p 的条件. 2. 必要条件:如果q ⇒ p 则p 叫做q 的 条件,q 叫做p 的条件.p ⇒q 且q ⇒ p 则p 叫做q 的条件.例1:下列“若p ,则q ”形式的命题中,哪些命题中的 p 是q 的充分条件?(1)若x = 1,则x 2 - 4x + 3 = 0;(2) 若f (x ) = x ,则 f ( x )为增函数; (3) 若x 为无理数,则x 2为无理数.例2:下列“若p ,则q ”形式的命题中,哪些命题中的q 是p 的必要条件?(1) 若x = y ,则x 2 = y 2 ;(2) 若两个三角形全等,则这两个三角形的面积相等;(3) 若a > b ,则ac > bc .例3.在下列各题中,判断A 是B 的什么条件,并说明理由. 1. A : p ≥ 2, p ∈ R ,B :方程 x 2 + px + p + 3 = 0 有实根; 2.A : 2x - 3 > 1 ;B :1x 2+ x - 6> 0 ;变式训练:指出下列命题中,p 是q 的什么条件(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要条件”中选出一种作答). (1) 对于实数x 、y ,p :x+y≠8,q:x≠2或y≠6; (2) 非空集合A 、B 中,p :x∈A∪B,q :x∈B; 例4.已知p :-2<m <0,0<n <1;q :关于x 的方程x 2+mx +n =0有两个小于1的正根,试分析p 是q 的什么条件.变式训练:证明一元二次方程ax 2+bx+c=0有一正根和一负根的充要条件是ac<0.简易逻辑章节测试题一、选择题1. 下列语句中是命题的是( ) (A )语文和数学 (B )sin45°=1 (C)x 2+2x-1 (D )集合与元素2. 已知下列三个命题 1 方程x 2-x+2=0的判别式小于或等于零;②矩形的对角线互相垂直且平分;③2是质数,其中真命题是()(A)①和②(B)①和③(C)②和③(D)只有①3.下列结论中正确的是()(A)命题p是真命题时,命题“P且q”一定是真命题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简易逻辑一、选择题1.(全国卷Ⅰ)设I 为全集,321S S S 、、是I 的三个非空子集,且I S S S =⋃⋃321,则下面论断正确的是(C)(A )Φ=⋃⋂)(321S S S C I(B )123I I S C S C S ⊆⋂() (C )Φ=⋂⋂)321S C S C S C I I I(D )123I I S C S C S ⊆⋃()2.(北京卷)设全集U =R ,集合M ={x | x >1,P ={x | x 2>1},则下列关系中正确的是(C) (A )M =P (B )P ÜM (C )M ÜP ( D )U M P =∅ð3.(北京卷)“m =21”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的 (B)(A )充分必要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件 4、(上海卷)已知集合{}R x x x M ∈≤-=,2|1||,⎭⎬⎫⎩⎨⎧∈≥+=Z x x x P ,115|,则P M 等于 (B )A .{}Z x x x ∈≤<,30|B .{}Z x x x ∈≤≤,30|C .{}Z x x x ∈≤≤-,01|D .{}Z x x x ∈<≤-,01| 5.(天津卷)设集合{}R x x x A ∈≥-=,914, ⎭⎬⎫⎩⎨⎧∈≥+=R x x x xB ,03, 则A ∩B= (D )A .]2,3(--B .]25,0[]2,3(⋃--C .),25[]3,(+∞⋃--∞ D .),25[)3,(+∞⋃--∞6.(天津卷)给出下列三个命题①若1->≥b a ,则bb aa +≥+11②若正整数m 和n 满足n m ≤,则2)(n m n m ≤-③设),(11y x P 为圆9:221=+y x O 上任一点,圆O 2以),(b a Q 为圆心且半径为 1.当1)()(2121=-+-y b x a 时,圆O 1与圆O 2相切其中假命题的个数为 ( B ) A .0 B .1 C .2 D .3 7.(天津卷)设γβα、、、为平面,l n m 、、为直线,则β⊥m 的一个充分条件是(D )A . l m l ⊥=⋂⊥,,βαβαB . γβγαγα⊥⊥=⋂,,mC . αγβγα⊥⊥⊥m ,,D . αβα⊥⊥⊥m n n ,,(D) αβα⊥⊥⊥m n n ,,8. (福建卷)已知集合∈≤-=x x x P ,1|1|||R|,Q P N x x Q 则},|{∈=等于(D )A .PB .QC .{1,2}D .{0,1,2}9.(福建卷)已知直线m 、n 与平面βα,,给出下列三个命题: ①若;//,//,//n m n m 则αα ②若;,,//m n n m ⊥⊥则αα ③若.,//,βαβα⊥⊥则m m 其中真命题的个数是 ( C ) A .0 B .1C .2D .310.(福建卷)已知p :,0)3(:,1|32|<-<-x x q x 则p 是q 的( A ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件11.(广东卷)若集合{}2M x x =≤,{}230N x x x =-=,则M N =(B)(A){}3(B){}0(C){}0,2(D){}0,312.(广东卷)给出下列关于互不相同的直线m 、l 、n 和平面α、β的四个命题: ①若m α⊂,lA α=,点A m ∉,则l 与m 不共面;②若m 、l 是异面直线,l α,m α,且n l ⊥,n m ⊥,则n α⊥; ③若l α,m β,αβ,则l m ; ④若l α⊂,m α⊂,lm =点A ,l β,m β,则αβ.其中为假命题的是(C)(A)①(B)②(C)③(D)④13.(湖北卷)设P 、Q 为两个非空实数集合,定义集合P+Q=},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ,则P+Q 中元素的个数是( B )A .9B .8C .7D .614.(湖北卷)对任意实数a ,b ,c ,给出下列命题:①“b a =”是“bc ac =”充要条件; ②“5+a 是无理数”是“a 是无理数”的充要条件③“a >b ”是“a 2>b 2”的充分条件;④“a <5”是“a <3”的必要条件. 其中真命题的个数是 ( B ) A .1 B .2 C .3 D .415.(江苏卷)设集合A={1,2},B={1,2,3},C={2,3,4}则=⋃⋂C B A )((D ) ( A ) {1,2,3} ( B ) {1,2,4} ( C ) {2,3,4} ( D ) {1,2,3,4} 16(江苏卷)设γβα,,为两两不重合的平面,l,m,n 为两两不重合的直线,给出下列四个命题:① 若;,则,βαγβγα//⊥⊥②若;则βαββαα//,//,//,,n m n m ⊂⊂③;则若βαβα//,,//l l ⊂④.//,//,,,n m l n m l 则若γαγγββα=⋂=⋂=⋂其中真命题的个数是(B )( A ) 1 ( B ) 2 ( C ) 3 ( D )417.(江西卷)设集合⋃--==∈<=A B A Z x x x I 则},2,1,2{},2,1{},,3|||{(I C B )=(D )A .{1}B .{1,2}C .{2}D .{0,1,2}18.(江西卷) “a =b ”是“直线222()()2y x x a y b =+-++=与圆相切”的 (A )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 19(辽宁卷)极限)(lim 0x f x x →存在是函数)(x f 在点0x x =处连续的(B )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分也不必要的条件20.(辽宁卷)已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:①若βαβα//,,则⊥⊥m m ; ②若βααβγα//,,则⊥⊥; ③若βαβα//,//,,则n m n m ⊂⊂; ④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂⊂其中真命题是(D )A .①和②B .①和③C .③和④D .①和④21.(浙江卷)设全集U ={1,2,3,4,5,6,7},P ={1,2,3,4,5},Q ={3,4,5,6,7},则P ∩ðU q =( A )(A) {1,2} (B) (3,4,5) (C) {1,2,6,7} (D) {1,2,3,4,5} 22.(浙江卷)设α、β 为两个不同的平面,l 、m 为两条不同的直线,且l ⊂α,m ⊂β,有如下的两个命题:①若α∥β,则l ∥m ;②若l ⊥m ,则α⊥β.那么 ( D )(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题 (C) ①②都是真命题 (D) ①②都是假命题23.(浙江卷)设f (n )=2n +1(n ∈N ),P ={1,2,3,4,5},Q ={3,4,5,6,7},记P ∧={n ∈N |f (n )∈P },Q ∧={n ∈N |f (n )∈Q },则(P ∧∩N ðQ ∧)∪(Q ∧∩N ðP ∧)=( A )(A) {0,3} (B){1,2} (C) (3,4,5) (D){1,2,6,7} 24.(湖南卷)设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则( U A )∩B= (C ) A .{0} B .{-2,-1} C .{1,2} D .{0,1,2} 25.(湖南卷)设集合A ={x |11+-x x <0},B ={x || x -1|<a },若“a =1”是“A ∩B ≠ ”的( A )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件26.(湖南卷)集合A ={x |11+-x x <0=,B ={x || x -b|<a },若“a =1”是“A ∩B ≠φ”的充分条件, 则b 的取值范围是(D )A .-2≤b <0B .0<b ≤2C .-3<b <-1D .-1≤b <2填空题:1.(福建卷)把下面不完整的命题补充完整,并使之成为真命题:若函数x x f 2log 3)(+=的图象与)(x g 的图象关于 对称,则函数)(x g = 。
(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形)..如 ①x 轴,-3-log 2x ②y 轴,3+log 2(-x )③原点,-3-log 2(x ) ④直线y=x , 2x -3 2.(江西卷)以下同个关于圆锥曲线的命题中:①设A 、B 为两个定点,k 为非零常数,||||PA PB k -=,则动点P 的轨迹为双曲线;②设定圆C 上一定点A 作圆的动点弦AB ,O 为坐标原点,若1(),2OP OA OB =+则动点P 的轨迹为椭圆;③方程22520x x -+=的两根可分别作为椭圆和双曲线的离心率;④双曲线221259x y -=与椭圆22135x y +=有相同的焦点. 其中真命题的序号为 ③④ (写出所有真命题的序号)。
