同济大学材料力学习题解答(练习册PP)
同济大学材料力学期末复习
A 1
C 2
刚杆 D
[F1]=2[FN1] =2×30＝60kN
2）CD杆的强度计算 CD杆的许用应力
B
200 [ 2 ] 100MPa n n 2 CD杆的许用轴力
0
s
F
( MPa)
500 400 300 200 100
0.02
a)
AB杆材料
[FN2 ] [ 2 ]A2 100106 400106 40kN
FN l1 Tl1 EA FN 1 3.46 6 12 10 30 3.46 200 109 1000 106 l1
B
图a
1
l 2
FN 2 l 2 EA
FN 2 3 20010 100010
9 6
A
A2 l2
300 2
代入变形方程得补充方程
能量法
2 2 2 F ( x ) dx M ( x ) dx M ( x)dx N n 应变能 U 2EA 2GI p 2EI l l l U 卡氏第二定理及应用 i Fi
i
F ( x) FN ( x) U N dx Fi EA Fi l
应力状态和强度理论
斜截面上的应力
x y
2 x y
x y
2
2 sin 2 xy cos 2
(
cos 2 xy sin 2
主应力的大小和方位
max
min
x y
2
x y
2
) 2 xy
2
tg 2 0
l 3m
A
材料力学课后习题答案
材料⼒学课后习题答案8-1 试求图⽰各杆的轴⼒，并指出轴⼒的最⼤值。
(1) ⽤截⾯法求内⼒，取1-1、2-2截⾯；(2) 取1-1(3) 取2-2(4) 轴⼒最⼤值： (b)(1) 求固定端的约束反⼒；(2) 取1-1(3)取2-2截⾯的右段；(4) 轴⼒最⼤值： (c)(1) ⽤截⾯法求内⼒，取1-1、2-2、3-3截⾯；(2) 取1-1(3) 取2-2截⾯的左段；(4) 取3-3截⾯的右段；(c)(d)N 1F RF N 1F RF N 2F N 1N 2(5) 轴⼒最⼤值： (d)(1) ⽤截⾯法求内⼒，取1-1、2-2截⾯；(2) 取1-1(2) 取2-2(5) 轴⼒最⼤值：8-2 试画出8-1所⽰各杆的轴⼒图。
解：(a) (b)(c) (d)8-5段的直径分别为d 1=20 mm 和d 2=30 mm F 2之值。
解：(1) (2) 求1-1、2-2截⾯的正应⼒，利⽤正应⼒相同；8-6 题8-5图所⽰圆截⾯杆，已知载荷F 1=200 kN ，F 2=100 kN ，AB 段的直径d 1=40 mm ，如欲使AB 与BC 段横截⾯上的正应⼒相同，试求BC 段的直径。
解：(1) ⽤截⾯法求出1-1、2-2截⾯的轴⼒；(2) 求1-1、2-2截⾯的正应⼒，利⽤正应⼒相同；8-7 图⽰⽊杆，承受轴向载荷F =10 kN 作⽤，杆的横截⾯⾯积A =1000 mm 2，粘接⾯的⽅位⾓θ= 450，试计算该截⾯上的正应⼒与切应⼒，并画出应⼒的⽅向。
F N 3F N 1F N 2解：(1)(2)8-14 图⽰桁架，杆1d 1=30 mm 与d 2=20 mm ，两杆材料相同，许⽤应⼒[σ]=160 MPa 。
该桁架在节点A 处承受铅直⽅向的载荷F =80 kN 作⽤，试校核桁架的强度。
解：(1) 对节点A(2) 列平衡⽅程解得：(2) 所以桁架的强度⾜够。
8-15 图⽰桁架，杆1为圆截⾯钢杆，杆2为⽅截⾯⽊杆，在节点A 处承受铅直⽅向的载荷F 作⽤，试确定钢杆的直径d 与⽊杆截⾯的边宽b 。
最新同济大学 材料力学 习题解答2(练习册P65-P70)
满足强度条件
WP
FC1 FC1 ∵ FC = 2FC1
t ＜ 2t1
d
3
3 挤压
∴剪切校核主板
t1 t
2 1
b
2
1
FC
FC =
F 4
AC = dt
FS =
FC 2
=
F 8
AS =
pd2 4
F
F
FsC =
FC AC
≤
[sC
]
t = FS ≤ [t ]
AS
主板： 拉压
F ≤ 100 kN
F ≤ 62.83 kN
1-1截面：FN1 2-2截面：FN2
= =
F
3 4
A1 F
=( b–d )t
A2=( b–2d F ≤ 224 kN
s1
)t
=
FN1 A1
s2 =
则
≤[s ] F≤180kN FN2 ≤[s ]
A2 [ F ]= 62.83 kN
P69 38-1
T4
T3
A
B
T2
T1
C
D
1.0kN·m
0.2kN·m 基线
0.2kN·m
0.4kN·m
Mn图
A pd2
a
C
FCx
a
FCy
B
D
a
F
(2) 令 s = sb
F=
pd2 8
sb
= 62.8 kN
(1) 令 s = sS
F=
pd2 8
sS
=
37.7
kN
若 s = sP ( ≈ se )
F=
pd2 8
材料力学习题集(含答案)
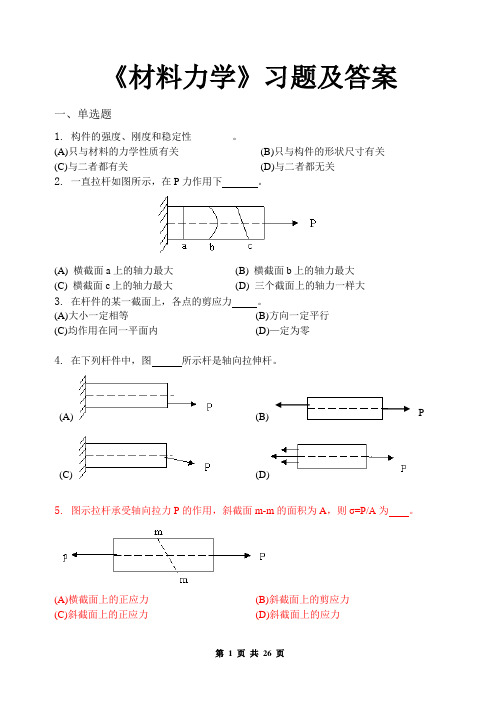
《材料力学》习题及答案一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示，在P 力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上，各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中，图所示杆是轴向拉伸杆。
P (A) (B)(C) (D)5.图示拉杆承受轴向拉力P的作用，斜截面m-m的面积为A，则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后，消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍，则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示，已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面，则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(C)绝对值不等，正负号相同(D)绝对值不等，正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内；(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上，各个截面上的。
(A)剪力相同，弯矩不同(B)剪力不同，弯矩相同(C)剪力和弯矩均相同(D)剪力和弯矩均不同13.当横向力作用于杆件的纵向对称面内时，关于杆件横截面上的内力与应力有以下四个结论。
材料力学习题解答
解： (3) 梁可简化， 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
（逆时针）
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4．如图所示各梁旳抗弯刚度为EI，试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解： (4) 梁可简化，为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7．试用叠加法计算图示各梁C点旳挠度。
解： (1) 梁可简化， 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
（逆时针）
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI （向下）
4．如图所示各梁旳抗弯刚度为EI，试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
大学材料力学习题及答案(题库)精选全文
可编辑修改精选全文完整版一．是非题：（正确的在括号中打“√”、错误的打“×”） （60小题） 1．材料力学研究的主要问题是微小弹性变形问题，因此在研究构件的平衡与运动时，可不计构件的变形。
( √ )2．构件的强度、刚度、稳定性与其所用材料的力学性质有关，而材料的力学性质又是通过试验测定的。
( √ ) 3．在载荷作用下，构件截面上某点处分布内力的集度，称为该点的应力。
(√ ) 4．在载荷作用下，构件所发生的形状和尺寸改变，均称为变形。
( √ ) 5．截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ，它们的单位相同。
( √ )6．线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量，它们都是无量纲的量。
( √ )7．材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( ) 8．在强度计算中，塑性材料的极限应力是指比例极限p σ，而脆性材料的极限应力是指强度极限b σ。
( )9．低碳钢在常温静载下拉伸，若应力不超过屈服极限s σ，则正应力σ与线应变ε成正比，称这一关系为拉伸（或压缩）的虎克定律。
( )10．当应力不超过比例极限时，直杆的轴向变形与其轴力、杆的原长成正比，而与横截面面积成反比。
( √ )11．铸铁试件压缩时破坏断面与轴线大致成450，这是由压应力引起的缘故。
( )12．低碳钢拉伸时，当进入屈服阶段时，试件表面上出现与轴线成45o 的滑移线，这是由最大剪应力max τ引起的，但拉断时截面仍为横截面，这是由最大拉应力max σ引起的。
( √ )13．杆件在拉伸或压缩时，任意截面上的剪应力均为零。
( ) 14．EA 称为材料的截面抗拉（或抗压）刚度。
( √ ) 15．解决超静定问题的关键是建立补充方程，而要建立的补充方程就必须研究构件的变形几何关系，称这种关系为变形协调关系。
( √ ) 16．因截面的骤然改变而使最小横截面上的应力有局部陡增的现象，称为应力集中。
材料力学习题及答案
材料力学习题一一、计算题1．（12分）图示水平放置圆截面直角钢杆（2ABC π=∠），直径mm 100d =，m l 2=，m N k 1q =，[]MPa 160=σ，试校核该杆的强度。
2．（12分）悬臂梁受力如图，试作出其剪力图与弯矩图。
3．（10分）图示三角架受力P 作用，杆的截面积为A ，弹性模量为E ，试求杆的内力和A 点的铅垂位移Ay δ。
4．（15分）图示结构中CD 为刚性杆，C ，D 处为铰接，AB 与DE 梁的EI 相同，试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为：在水平平面内P 1=800N ，在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2，试确定其尺寸。
三．填空题 （23分）1．（4分）设单元体的主应力为321σσσ、、，则单元体只有体积改变而无形状改变的条件是＿＿＿＿＿＿＿＿＿＿；单元体只有形状改变而无体积改变的条件是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
2．（6分）杆件的基本变形一般有＿＿＿＿＿＿、＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿四种；而应变只有＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿两种。
3．（6分）影响实际构件持久极限的因素通常有＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿，它们分别用＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿、＿＿＿＿＿＿＿＿＿＿＿＿＿＿来加以修正。
4.（5分）平面弯曲的定义为＿＿＿＿＿＿＿＿＿＿＿＿_＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿_。
5.（2分）低碳钢圆截面试件受扭时，沿 ＿＿＿＿＿＿＿＿＿＿＿＿ 截面破坏；铸铁圆截面试件受扭时，沿 ＿＿＿＿＿＿＿＿＿＿＿＿ 面破坏。
四、选择题（共2题，9分）2．（5分）图示四根压杆的材料与横截面均相同，试判断哪一根最容易失稳。
答案：（ ）材料力学习题二二、选择题：（每小题3分，共24分）1、危险截面是______所在的截面。
同济大学 材料力学练习册答案
第二章 轴向拉伸与压缩
1．略 2．º， 75MPa ， 43.3MPa
º， 50 MPa ， 50 MPa º， 25MPa ， 43.3MPa
3． l
b Pl ln 2 Et (b2 b1 ) b1
3
0xa，M=0； x=2a， M= -qa2/2； x=3a， M=0 （b）x=0, Q= -P；x=a+, Q= -2P； x=2a, Q= -2P x=0, M=0；x=a, M=Pa；x=2a, M=3Pa 2． （a）x=0, Q=3qa /2； x=a+, Q=qa/2； x=3a，Q=-3qa /2；x=4a, Q=-3qa /2 x=0, M=0； x=a, M=1.5qa2； x=1.5a, Mmax=1.625qa2；x=3a-, M=0.5qa2； x=3a+, M=1.5qa2；x=4a, M=0 （b）x=0, Q=0；x=a-, Q=qa； x=a+, Q= -qa/2； x=2a, Q= -3qa / 2 x=0, M=0；x=a, M=qa2/2； x=2a, M=-qa2/2 （c）x=0, Q=0；x=a, Q= -qa； x=2a-, Q= -qa； x=2a+, Q=qa； x=3a, Q=qa x=0, M=0；x=a, M=-qa2/2；x=2a-, M=-3/2qa2；x=2a+, M=qa2；x=3a, M=0 （d）x=0, Q=16；x=2, Q= -4；x=4-, Q= -4；x=4+,Q= -24；x=5, Q= -24 (单位：kN) x=0, M=0；x=1.6, M=12.8； x=2, M=12； x=3-, M=8；x=3+, M=28；x=4, M=24；x=5, M=0 (单位：kN-m) 3． （a） x=0, Q=P； x=l/3(左), Q=P； x=l/3 （右） , Q=0； x=2/3（ l 左） , Q=0； x=2/3l （右）, Q=P； x=l, Q=P x=0, P(上)；x=l/3, P（下） ； x=2l/3, P（上）, M=2 Pl /3（逆时针） ； x=l, P （下） （b）x=0, Q= -3； x=1-, Q= -3； x=1+, Q=4.2； x=5, Q= -3.8； x=6, Q= -3.8 x=0, P= -3（下） ； x=1, P=7.2（上） ； 1<x<5, q= -2（下） ； x=5, M=6（顺 时针） ； x=6, P=3.8（上）(单位：kN/m，kN，kN-m) 4． （a）x=0, Q=0； x=a, Q= -qa； x=2a-, Q= -qa； x=2a+, Q=qa； x=3a, Q=qa x=0, M=qa2/2； x=0, M=0；x=2a, M=qa2； x=3a, M=0 （b）x=0, Q=P/2； x=l/2, Q=P/2； x=l-, Q=P/2； x=l+, Q= -P/2； x=3/2l, Q= -P/2 x=0, M= -5/4Pl； x=l-/2, M= -Pl；x=l+/2, M=0；x=l, M=Pl/4；x=3/2l, M=0 5． （a）x=0, M= -qa2/8； x=a/2, M=0； x=a, M= -qa2/8 （b）x=0, M=0； x=a, M= -qa2； x=3/2a, M=0
同济大学材料力学考研题解_第十二章
12-8 ................................................................................................................................................................5
12-33 ............................................................................................................................................................23
12-34 ............................................................................................................................................................24
(也可通过左侧的题号书签直接查找题目与解)
12-2 图示变宽度平板，承受轴向载荷 F 作用。试计算板件的总伸长。板件的厚度为 δ ，
长度为 l，左、右端的截面宽度分别为 b1 与 b2，材料的弹性模量为 E。
解：由题图可知，
题 12-2 图
1
A(x)
=δBiblioteka b1+b2
− l
b1
x
σ (x) =
F
12-26 ............................................................................................................................................................17
材料力学练习题与答案-全
材料力学练习题与答案-全1.当T三Tp时，剪切虎克定律及剪应力互等定理。
A、虎克定律成立，互等定理不成立B、虎克定律不成立，互等定理成立（正确答案）C、均不成立D、二者均成立2.木榫接头，当受F力作用时,接头的剪切面积和挤压面积分别是A、ab,lcB、cb,lbC、lb,cb（正确答案）D、lc,ab3.在下列四种材料中，（）不可以应用各向同性假设。
A、铸钢B、玻璃C、松木（正确答案）D、铸铁4.一细长压杆当轴向压力P达到临界压力Pcr时受到微小干扰后发生失稳而处于微弯平衡状态，此时若解除压力P，则压杆的微弯变形。
A、有所缓和B、完全消失（正确答案）C、保持不变D、继续增大；5.矩形截面偏心受压杆件发生变形。
A、轴向压缩、平面弯曲B、轴向压缩、平面弯曲、扭转C、轴向压缩、斜弯曲（正确答案）D、轴向压缩、斜弯曲、扭转6.当杆件处于弯扭组合变形时，对于横截面的中性轴有这样的结论，正确的是：A、一定存在（正确答案）B、不一定存在C、一定不存在7.梁在某一段内作用有向下的分布载荷时，在该段内它的弯矩图为。
A、上凸曲线；（正确答案）B、下凸曲线；C、带有拐点的曲线；D、斜直线8.图示结构中，AB为钢材，BC为铝，在P力作用下（）A、AB段轴力大B、BC段轴力大C、轴力一样大（正确答案）D、无法判断9.圆截面的悬臂梁在自由端受集中力的作用，若梁的长度增大一倍，其他条件不变，最大挠度是原来的倍。
图片2.pngA、2B、16C、8（正确答案）D、410.托架由横梁与杆组成。
若将杆由位于梁的下方改为位于梁的上方，其他条件不变，则此托架的承载力。
A、提高（正确答案）B、降低C、不变D、不确定11.单位长度的扭转角e与（）无关A、杆的长度（正确答案）B、扭矩C、材料性质D、截面几何性质12.矩形截面拉弯组合变形时，对于横截面的中性轴有以下的结论。
正确的是：。
A、过形心B、过形心且与ZC轴有一夹角；C、不过形心，与ZC轴平行；（正确答案）D、不过形心，与ZC轴有一夹角。
【精品】同济大学材料力学练习册答案
【精品】同济大学材料力学练习册答
案
同济大学材料力学练习册答案
1. 弹性力学
题目：一根悬臂梁，长度为L，截面为矩形，宽度为b，高度为h，杨氏模量为E，悬臂梁一端固定，另一端受到一个集中力F，求悬臂梁在受力端的最大弯矩。
解答：根据悬臂梁的受力情况，可以得到受力端的最大弯矩为M = F * L。
2. 塑性力学
题目：一根钢材的屈服强度为400MPa，抗拉强度为600MPa，断后伸长率为20%，求该钢材的应变硬化指数。
解答：应变硬化指数n = ln(σt/σy) / ln(εt/εy)，其中σt为抗拉强度，σy为屈服强度，εt为断后伸长率。
3. 破裂力学
题目：一根圆柱形试样在拉伸过程中发生断裂，断口的直径为10mm，断口的延伸长度为4mm，试样的断裂韧性为40J/m²，求试样的断裂强度。
解答：断裂强度σf = 2 * Gc / (π * df * lf)，其中Gc为断裂韧性，df 为断口直径，lf为断口延伸长度。
4. 疲劳力学
题目：一根钢材的疲劳极限为200MPa，应力幅为100MPa，寿命为10^5次，求该钢材的疲劳强度系数。
解答：疲劳强度系数Sf = σf/ σa，其中σf为疲劳极限，σa为应力幅。
5. 断裂力学
题目：一根圆柱形试样在拉伸过程中发生断裂，载荷为1000N，试样的直径为10mm，试样的断裂韧性为40J/m²，求试样的断裂应力。
解答：断裂应力σf = 2 * Gc / (π * df²)，其中Gc为断裂韧性，df为试样直径。
同济大学 材料力学 习题解答4(练习册P75-P82)ppt课件
ME =
1 2
qa2
h 4 h
P80 43-1 反力
指定截面 F
C FC
1
1l
1.5l
1.5l
形心主轴
D
A
z
FD
yB b
mD = 0 Fy = 0
FC = 10 kN FD = 20 kN
M1 = FC×1.5 = 15 kN·m
Iz =
bh3 = 8×103 cm4 12
yA = - 5 cm yB = 10 cm
P81 43-3
A FA l
F CD
F
ll
B FB
y
z
mA = 0 Fy = 0
FB =
1 3
F
FA = 13F
I 20 a
1 Fl 3
查表 ：导学篇 附录B-3 P380中 I 20a
M图
Wz = 236.9 cm3
1 Fl
3
M│max
=
1 3
Fl
smax =
M│max Wz
≤ [s ]
F ≤ 56.9 kN
习题解答(四)
P78 42-2-1 叠加法 (过程)
F M0(Fa)
F
A
BCA
aa
M0(Fa)
BCA
BC
F
FS 图 3Fa
2Fa Fa
M图
F
FS 图(F)
2Fa
FS 图(M0)
Fa
M 图(F)
M 图(M0)
(单个荷载)
P78 42-2-2
(抛物线 - 中点 或 极值点)
q M0(ql2/4)
q
M0(ql2/4)
材料力学1-(答案)
资料力学请在以下五组题目中任选一组作答，满分100 分。
第一组：计算题（每题25 分，共 100 分）1.梁的受力状况以以下图，资料的 a。
若截面为圆柱形，试设计此圆截面直径。
q10kN / m4m2.求图示单元体的：（1）图示斜截面上的应力；（ 2）主方向和主应力，画出主单元体；（ 3）主切应力作用平面的地点及该平面上的正应力，并画出该单元体。
y100MPa60MPa50MPaO 300 50MPa xn60MPa 100 MPa解：（ 1）、斜截面上的正应力和切应力：30o MPa , 300M Pa （ 2）、主方向及主应力：最大主应力在第一象限中，对应的角度为00，则主应力为：1 121.0(MPa ), 3（ 3）、主切应力作用面的法线方向：/ 0,/ 02主切应力为：/ /1 225.0( MPa ) ，主单元体如图3-2所示。
此两截面上的正应力为：/ /1 2y1xO03图 3-125.67 0O图 3-23.图中所示传动轴的转速 n=400rpm，主动轮 2 输入功率 P2=60kW,从动轮 1，3，4和 5 的输出功率分别为 P1=18kW,P3=12kW,P4=22kW,P5=8kW。
试绘制该轴的扭矩图。
4.用积分法求图所示梁的挠曲线方程和转角方程，并求最大挠度和转角。
各梁EI 均为常数。
第二组：计算题（每题25 分，共 100 分）1. 简支梁受力以下图。
采纳一般热轧工字型钢，且已知 = 160MPa。
试确立工字型钢型号，并按最大切应力准则对梁的强度作全面校核。
（已知选工字钢： W = 692.2 cm3， Iz = 11075.5 cm4）解：1．F RA = F RB = 180kN （↑）kN·mkN·mkN3m由题设条件知：W = 692.2 cm 2， Iz = 11075.5 cm 4cmE截面：MPaMPa2． A ＋、 B－截面：MPaMPa3．C－、 D＋截面：MPaMPa∴选 No.32a 工字钢安全。
(完整版)材料力学习题册答案..
练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。
（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（ 是 ） （4）应力是内力分布集度。
（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。
（是 ） （6）若物体产生位移，则必定同时产生变形。
（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。
（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。
（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。
（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。
（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。
（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。
（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。
根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。
（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。
变形。
（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。
（8）根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
同济大学材料力学习题解答(练习册PP等)
FS1 = FA = 40 kN
M1 = 0
特殊位置截面
FS2 = FA = 40 kN
M2 = FA×2 = 80 kN·m FS3 = FA - 3q×2 = - 20 kN M3 = FA×4 - 3q×2×1
= 100 kN·m
P73 40-1(c)
A FA
12 3 F BC
1 2FB 3
相邻截面
M2 = F×2 = 20 kN·m
C F
FS3 = FS2 = - 10 kN
M3 = M2 = 20 kN·m
P73 40-1(b)
12
33 q
A
B
C
1FFAS1 2
3
FC
A M1
FA
FS2
A FA
M2
3q FS3
A
B
M3
FA
3q
M3
C
FS3
FC
mA = 0 FC = 80 kN
Fy = 0 FA = 40 kN
G·IP p
d ≥ 4 180 × 32 Mnl = 19.8 mm
Gp2 [j]
≤ [q ]
=
1° 2m
取 d = 20 mm
P72 39-3 T0
圆轴：
T0
FC FC
FC FC
FC
FC
FC T0 FC
WP =
pd3 16
FC FC
= 196.3 cm3 tmax =
Mn
令 = 70
MPa
WP
T0 = Mn = WPtmax = 13.74 kN·m
R
zC
O R
z1
z2
Iz = IzC+Ab2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
20 MPa 30 MPa
sx = 30 MPa
sy = 50 MPa
30º
18.66
tx = - 20 MPa
2
a = 30º
cos2a – tx sin2a
= 52.32 MPa
sa =
ta =
sx + sy sx - sy
2
+
sx - sy
2
sin6 MPa
h
P91 48-3
A FA l 3 ql 8
q
C FC l B FB
静定基
多余约束力： FC
+0yCF = 0 变形协调条件： yCq 变形几何方程 C= FC(2l)3 yCF = 48EI
5 ql 8
5 q ( 2 l) 4 查表： yCq = 384EI
5 ql 8 1 ql2 8 9 ql2 128
a
s1 = s2 = 0 s3 = - 100 MPa s1 = 30 MPa = - s3 s2 = 0 t = 22.5 MPa s = 100 MPa d s = 50 MPa c s1 = 100 MPa s2 = s3 = 0 s1 = 58.6 MPa s2 = 0 sx - sy 2 sx + sy ± ( ) + tx 2 s max = s3 = - 8.6 MPa 2 2 min
P90 48-1
q
A
l B b ≤ [s ]
1 ql2 2
smax =
M│max
Wz
1 2 M│max = ql 2 = 45 kN· m bh2 h3 Wz = = 6 12 3 12 M│max h≥ = 16.5 cm [s ]
ql4 bh3 h4 M 图 查表： ymax = 8EI 其中： I = 12 = 24 4 ymax f ql3 3ql3 = h≥ = 17.8 cm ≤[ ] f l l 8EI E[ ] l 取 h = 17.8 cm b = 8.9 cm
2qa3 M(2a) =qCM = EI EI
P224 表19-1 序号3
qCF = qBF
P224 表19-1 序号5
Fa2 qa3 = = 2EI 2EI
qa3 = 6EI
qCq = qBq
P88 47-2(a)
A
0.5l
F M(Fl) F
C
B
0.5l
Ml Fl2 == qBM yCM = 0 P225 表19-1 序号8 qAM = 24EI 24EI Fl2 Fl3 P225 表19-1 序号9 qAF = = - qBF yCF = 16EI 48EI Fl2 qA = qAM + qAF = Fl3 48EI y = y + y C CM CF = 2 48EI 5Fl qB = qBM + qBF = 48EI
P87 46-4 q
9 3 mA = 0 FB = qa Fy = 0 FA = qa 4 4 C 弯矩方程 AB BC A xD B q 1 3 FB M (x)= qax - qx2 M (x)= - (3a - x)2 FA 2 a a a 1 2 2 4 d2y1 1 2 3 d2y2 q EI 2 = 挠曲线近似微分方程 qx - qax EI 2 = (3a - x)2 4 2 dx dy2 dx q 2 3 dy1 1 EI = qx3 - qax 2 + C1 EI dx = - 6 (3a - x)3 + C2 dx 1 6 3 8 q EIy1= qx4 - qax3 + C1x +D1 EIy2= (3a - x)4 + C2x + D2 24 24 24 1 3 C = qa = 0 ： x =2a, q = q = q D = 0 2 2 1 B 连续 边界 x = 0, y1= 0： 1 6 qa 3 3 条件 x =2a, y2= yB = 0： C1= 条件 x =2a, y1= 0： D2 = - qa4 6 8 q q q1(x)= (4x3 -9ax2+ 4a3) q2(x)= [a3 - (3a - x)3] 6EI q 24EI q y1(x)= (x4-3ax3+4a 3x) y2(x)= [(3a-x)4+4a3x-9a4] 24EI 3 24EI 4 qa qa qa4 qA = qB = 0 yD = yC = 6EI 12EI 8EI
P88 47-1(b) M(qa2) q F(qa)
A a B a C
P224 表19-1 序号1
4qa3 qC = qCM + qCF + qCq = 3EI 7qa4 yC = yCM + yCF + yCq = 8EI
2qa4 M(2a)2 =yCM = EI 2EI yCF = yBF + qBF· a Fa3 5qa4 = + qBF· a= 3EI 6EI yCq = yBq + qBq· a qa4 7qa4 = + qBq· a= 8EI 24EI
- 2t x tan2a0 = sx - sy 57.02 MPa sx - sy 2 sx + sy ± ( ) + tx 2 = s max = - 7.02 MPa 2 2 min s1 = 57.02 MPa s2 = 0 s3 = - 7.02 MPa 57.02 MPa 32.02 MPa sx - sy 2 ) + tx 2 = t max = ± ( 19.33º - 32.02 MPa 2 min 7.02 MPa sx - sy tan2a1 = = 1.25 a1 = 64.33º 2t x a1' = - 25.67º 64.33º sx + sy s a1 = = 25 MPa 25 MPa 32.02 MPa 2
3T0
T0 T0
t
F
B
F
A
Mn Mn = 2T0 tmax = 3 p d WP W = P 16
横截面位置 应力方向
t
C
s
FN s= FN = F A
F s= A Mn tmax = WP
s
Mn = T0 pd3 WP = 16
P92 49-2(a) 应力表示(方向 数值)
50 MPa 52.32
P92 49-2(b)
20 MPa 27.32 40 MPa 27.32
sx = - 40 MPa tx = 20 MPa
2
+
sy = 0 a = 60º
30º
sa = ta =
sx + sy sx - sy
2
sx - sy
2
cos2a – tx sin2a = - 27.32 MPa
sin2a + tx cos2a
= - 27.32 MPa
P93 49-3(a) 解析法 sx = 50 MPa
20 MPa
11.65 54.82
50 MPa
sy = 0 tx = - 20 MPa a = 30º sx + sy sx - sy sa = + cos2a – tx sin2a
2 2 = 54.82 MPa sx - sy ta = sin2a + tx cos2a = 11.65 MPa 2 = 0.8 a0 = 19.33º a0' = 109.33º
2 bh P93 49-4 M = 10 kN· m Wz = = 100 cm3 6 h/ 2 a M M smax = = 100 MPa = sd = - sa = 2sc Wz FS 3 bh b h/4 FS = 120 kN Iz = = 500 cm4 c 12 d Sz*max = 75 cm3 Sz*3 = 56.25 cm3 * * F · S FS· Sz max z S = 22.5 MPa = 30 MPa = tb tc = 3 tmax = Iz· b Iz· b s = 100 MPa t = 30 MPa b
1 ql2 16
3 4 F ( 2 l ) 5 q ( 2 l ) C FS 图 补充方程： =0 48EI 384EI 3 ql 5 8 FC = ql （简便方法） 4 3 平衡： FA = FB = ql 8 M图
P92 49-1 危险截面(内力分布) 危险点(应力分布)
A
B C
F
T0
2T0
30º
P93 49-3(e)sx = - 20 MPa sy = 30 MPa tx = 20 MPa a = - 30º 30 MPa sx + sy sx - sy + cos2a – tx sin2a 20 MPa sa = 2 2 30º 20 MPa = 9.82 MPa s s x y 9.82 ta = sin2a + tx cos2a = 31.65 MPa 31.65 2 - 2t x tan2a0 = = 0.8 a0 = 19.33º a0' = 109.33º sx - sy 37.02 MPa sx - sy 2 sx + sy 2 ± ( ) + tx = s max = - 27.02 MPa 2 2 min s1 = 37.02 MPa s2 = 0 s3 = - 27.02 MPa 27.02 MPa 32.02 MPa smax + smin )= 19.33ºt max = ±( - 32.02 MPa 2 min 37.02 MPa 5 MPa a1 = a0 + 45º= 64.33º a1' = - 25.61º sx + sy 64.33º s a1 = = 5 MPa 2 32.02 MPa