电磁场与电磁波典型习题及答案恒定磁场
恒定磁场部分例题及思考题

ω
3.长直圆柱形铜导线半径为 R1 , 外面一层相 对磁导率为 µr的圆桶形磁介质外半径R2 , 设导线内有均匀分布电流I 通过,铜的相对 磁导率 = 1 ,求导线和磁介质内外的磁场 强度和磁感应强度的分布
r oR
R2
1
µ 0 = 4π ×10 N ⋅ A
−7
−2
例:R,I的半圆形闭合线圈,绕直径为轴旋转, 均匀磁场,求线圈受的磁力矩。 a. Ⅰ法 均匀场 M = m × B
M = I(
πR 2
2
)B
y
方向:沿oy轴正方向
b. Ⅱ法 一般方法 (对非均匀场也适用)
en
x
Idl → dF → dM → M = ∫ dM
µ 0 I1 B1 = 2πr
d F2 µ 0 I1 I 2 d F1 = = d l2 2πr d l1
I1 d l1
B2
B1
d F1 d F2
I 2 d l2
国际单位制中电流单位安培的定义
I1
I2
r
在真空中两平行长直导线相距 1 m ,通有大小 相等、方向相同的电流,当两导线每单位长度上的 吸引力为 2 × 10 −7 N ⋅ m −1 时,规定这时的电流为 1 A 可得
I 2πr
r = 0.4 mm
I m = 2πrH c = 0.4A
思考题: 1. 宽度为b的长金属薄板,电流为I,求 (1)在薄板平面上,距板的一边为r的P点 的磁感强度; (2)板的中心线正上方Q点的磁感强度
I p
b
r
2. 有一长为 b,电荷线密度为 λ 的带电线 段 AB ,绕垂直轴 OO′ 在水平面内匀角速 转动,设 A 点距轴为a ,角速度 ω , 求带电 线段在O点产生的磁感强度和磁矩
电磁场与电磁波试题及答案(2021版)

电磁场与电磁波试题及答案(2021版)1. 恒定磁场是( A )A. 无散场B. 旋涡场C.无旋场D. 既是有散场又是旋涡场 2. 已知(25)(2)(23)x y z D x y e x y e y x e =-+-+-,如已知电介质的介电常数为0ε,则自由电荷密度ρ为( C )A. 03εB. 03/εC. 1D. 0 3. 磁场的矢量磁位的单位是( D )A. V/mB. TC. A/mD. T m 4. 导体在静电平衡下,其内部电场强度( A )A.为零B.为常数C.不为零D.不确定 5. 对于载有时变电流的长直螺线管中的坡印廷矢量S ,下列陈述中,正确的是( C )A. 无论电流增大或减小,S 都向内B. 无论电流增大或减小,S 都向外C. 当电流增大,S 向内;当电流减小时,S 向外D. 无法判断S 的方向6. 根据恒定磁场中磁感应强度B 、磁场强度H 与磁化强度M 的定义可知,在各向同性媒质中( A )A. B 与H 的方向一定一致,M 的方向可能与H 一致,也可能与H 相反B. B 、M 的方向可能与H 一致,也可能与H 相反C. 磁场强度的方向总是使外磁场加强。
D. 三者之间没有联系。
7. 以位函数ϕ为带求量的边值问题中,设()()12,f s f s 都为边界点S 的点函数,则所谓的纽曼问题是指给定( B )A. ()1s f s ϕ=B. ()2sf s nϕ∂=∂C. ()()12112212s s f s f s nϕϕ∂==+=∂和,s s s D.以上皆不对8. 若要增大两线圈直接的互感,可以采用以下措施( A )A.增加两线圈的匝数B.增加两线圈的电流C.增加其中一个线圈的电流D.无法实现 9. 磁场能量密度等于( D )A. E DB. B HC.21E D D. 21B H 10. 以下四个矢量函数中,能表示磁感应强度的矢量函数是( A )A. x y B e y e x =+B. x y B e x e y =+C. 22x y B e xy e x =+D. 2x y B e x e xy =+1. 在恒定磁场中,若令磁矢位A 的散度等于零,则可以得到A 所满足的微分方程__2A J μ∇=-_____。
恒定磁场答案-清华版-终稿(1)

恒定磁场(一)参考解答一、选择题1、D2、B3、C 二、填空题 1、大小:00(1122II R R μμπ+方向:⊗2、2cos B r πα- 3、0ln 22Iaμπ三、计算题1.(1)解:金属薄片单位弧长上的电流为I Rπ IdI Rd Rθπ=θπμπμd RIR dI dB 20022==j dB i dB j dB i dB B d y x )cos (sin θθ-+=+=00220020sin 2cos 02x x y y I IB dB d R RIB dB d Rππμμθθππμθθπ=====-=⎰⎰⎰⎰∴02I B i Rμπ=r r1.(2)解:金属薄片单位弧长上的电流为2I Rπ 2IdI Rd Rθπ=0022sin (cos )x y dI I dB d R R dB dB i dB j dB i dB j μμθππθθ===+=+-r r r r r 002220002220sin cos x x y y I IB dB d R RI IB dB d R Rππμμθθππμμθθππ=====-=-⎰⎰⎰⎰∴0022x y I I B B i B j i j R Rμμππ=+=-r r r r r2.解:(1)010212()112222I I B I I dd d μμμπππ=+=+ 方向:⊙(2)010222()I I B r d r μμππ=+- 121010*******121322()ln ln 22r r m m S S S r I I d B dS BdS ldx r d r I l I l r r r r r r μμππμμππ+⎡⎤Φ=Φ===+⋅⎢⎥-⎣⎦++=+⎰⎰⎰⎰r r g四.讨论题32003200321000000440044O I IO R RI IO R Rμμππμμππ=======⊗=====101010、(1)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B (2)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B (3)圆环电流的B ;两直导线的B 、B ;点总磁感应强度B e ee323232000001100O O O ======⊗=⊗=+=-⊗====101012102、(1)三角形电流的B ;两直导线的B 、B ;点总磁感应强度B (2)三角形电流的B ;两直导线的B 、 B ; 点总磁感应强度B B B (3)三角形电流的B ;两直导线的B 、B ; 点总磁感应强度B 04Ilπ⊗;恒定磁场(二)参考解答一、选择题1、C二、填空题1、环路内包围的电流代数和;环路上积分点的磁场;所有电流产生的。
《第5章 电磁场与电磁波》试卷及答案_高中物理必修 第三册_沪教版_2024-2025学年

《第5章电磁场与电磁波》试卷(答案在后面)一、单项选择题(本大题有7小题,每小题4分,共28分)1、关于电磁场理论,以下哪个陈述是正确的?A. 变化的电场周围一定产生变化的磁场。
B. 恒定电流周围可以产生稳定的磁场,但不会产生电场。
C. 静止电荷产生的电场会随时间变化而改变。
D. 光速在任何惯性参考系中都是不同的。
2、对于电磁波传播特性,下列说法中哪一项是错误的?A. 电磁波可以在真空中传播。
B. 电磁波传播不需要介质。
C. 所有电磁波在真空中的传播速度相同。
D. 不同频率的电磁波在同一介质中的折射率总是相同。
3、关于电磁波的传播特性,以下说法正确的是:A. 电磁波只能在真空中传播B. 电磁波的传播速度在任何介质中都相同C. 电磁波传播不需要介质D. 电磁波不能被反射或折射4、对于麦克斯韦方程组,下列叙述哪一项是准确的?A. 麦克斯韦方程组只适用于静态电场和磁场B. 麦克斯韦方程组预言了电磁波的存在C. 麦克斯韦方程组无法解释光的偏振现象D. 麦克斯韦方程组表明变化的电场不会产生磁场5、在真空中,一个均匀带电的无限长直导线周围产生的磁场强度(H)与距离导线的距离(r)成反比。
如果导线单位长度上的电流为(I),那么在距离导线(r)处的磁场强度(H)可以用下列哪个公式表示?(真空中的磁导率(μ0=4π×10−7 T⋅m/A)))A.(H=μ0I2πr)B.(H=μ0Iπr)C.(H=2μ0Iπr)D.(H=μ0I4πr6、当电磁波在真空中传播时,下面哪一个描述是不正确的?A. 电磁波的速度等于光速(c)。
B. 电磁波的电场和磁场相互垂直。
C. 电磁波的能量密度由其频率决定。
D. 电磁波的传播不需要介质。
7、一个电子在电场中沿着电场线方向从A点移动到B点,下列说法中正确的是:A. 电子在A点的电势能大于在B点的电势能。
B. 电子在A点的电势能小于在B点的电势能。
C. 电子在A点的电势能等于在B点的电势能。
电磁场与电磁波习题及答案

11 麦克斯韦I 方程组.的微分形式 是:J . H =J JD,\ E = _。
「|_B =0,七出=:2静电场的基本方程积分形式为:性£虏=03理想导体(设为媒质 2)与空气(设为媒质 1)分界 面上,电磁场的边界条件为:4线性且各向同性媒质的 本构关系方程是:5电流连续性方程的微分形式为:。
6电位满足的泊松方程为;在两种完纯介质分界面上 电位满足的边界 。
7应用镜像法和其它间接方法解静 态场边值问题的理论依据是。
8.电场强度E Aj 单位是,电位移D t 勺单位是。
9.静电场的两个基本方程的微分 形式为“黑E =0 Q D = P ; 10.—个直流电流回路除 受到另一个直流电流回路的库仑力作用外还将受到安 培力作用1 .在分析恒定磁场时,引入矢量磁位A,并令冒=%,的依据是(c.V 值=0)2 . “某处的电位 中=0,则该处的电场强度 E=0的说法是(错误的)。
3 .自由空间中的平行双线传输线,导线半径为a ,线间距为D ,则传输线单位长度的电容为4 .点电荷产生的电场强度随距离变化的规律为( 1/r2)。
5 . N 个导体组成的系统的能量 W =1£ q * ,其中e i 2 t i i 是(除i 个导体外的其他导体)产生的电位。
6 .为了描述电荷分布在空间流动的状态, 定义体积电流密度J,其国际单位为(a/m2 )7 .应用高斯定理求解静电场要求电场具有(对称性)分布。
8 .如果某一点的电场强度为零,则该点电位的(不一 定为零 )。
9 .真空中一个电流元在某点产生的磁感应强度dB 随该点到电流元距离变化的规律为( 1/r2 )。
10.半径为a 的球形电荷分布产生的电场的能量储存于(整个空间)。
三、海水的电导率为 4S/m,相对介电常数为 81,求频 率为1MHz 时,位幅与导幅比值?三、解:设电场随时间作正弦变化,表示为:E = e x E m cos t则位移电流密度为:J d =— = -ex :-. ■ 0 r E m Sin t;t其振幅彳1为:J dm = 网 5E m = 4.5X10- E m 传导电 流的振幅值为: J cm -二- E m = 4E m 因此:Jm =1.125/0J -cm四、自由空间中,有一半径为a 、带电荷量q 的导体球。
(完整版)电磁场与电磁波试题及答案.

1. 写出非限定情况下麦克斯韦方程组的微分形式,并简要说明其物理意义。
2.答非限定情况下麦克斯韦方程组的微分形式为,,0,D B H J E B D t tρ∂∂∇⨯=+∇⨯=-∇⋅=∇⋅=∂∂,(3分)(表明了电磁场和它们的源之间的全部关系除了真实电流外,变化的电场(位移电流)也是磁场的源;除电荷外,变化的磁场也是电场的源。
1. 写出时变电磁场在1为理想导体与2为理想介质分界面时的边界条件。
2. 时变场的一般边界条件 2n D σ=、20t E =、2t s H J =、20n B =。
(或矢量式2n D σ=、20n E ⨯=、2s n H J ⨯=、20n B =)1. 写出矢量位、动态矢量位与动态标量位的表达式,并简要说明库仑规范与洛仑兹规范的意义。
2. 答矢量位,0B A A =∇⨯∇⋅=;动态矢量位A E t ϕ∂=-∇-∂或AE tϕ∂+=-∇∂。
库仑规范与洛仑兹规范的作用都是限制A 的散度,从而使A 的取值具有唯一性;库仑规范用在静态场,洛仑兹规范用在时变场。
1. 简述穿过闭合曲面的通量及其物理定义 2.sA ds φ=⋅⎰⎰ 是矢量A 穿过闭合曲面S 的通量或发散量。
若Ф> 0,流出S 面的通量大于流入的通量,即通量由S 面内向外扩散,说明S 面内有正源若Ф< 0,则流入S 面的通量大于流出的通量,即通量向S 面内汇集,说明S 面内有负源。
若Ф=0,则流入S 面的通量等于流出的通量,说明S 面内无源。
1. 证明位置矢量x y z r e x e y e z =++ 的散度,并由此说明矢量场的散度与坐标的选择无关。
2. 证明在直角坐标系里计算 ,则有()()xy z x y z r r e e e e x e y e z x y z ⎛⎫∂∂∂∇⋅=++⋅++ ⎪∂∂∂⎝⎭3x y z x y z∂∂∂=++=∂∂∂ 若在球坐标系里计算,则 232211()()()3r r r r r r r r r∂∂∇⋅===∂∂由此说明了矢量场的散度与坐标的选择无关。
电磁场与电磁波典型习题及答案(恒定磁场)
E
=
ez
π
a12γ 1
+π
I (a22
−
a12 )γ 2
J1
=
γ1E
=
ez
5 ×10 7 12π
A/m2
,
J2
=
γ2E
=
ez
5 ×10 7 3π
A/m2
(2) 当 r < a1 时,有 2π rB = π r 2 µ0 J1 ⇒ B = 0.833r
当 a1
<
r
<
a2
时,有
2π rB
=
µ0[π a12 J1
解:(1) 由安培环路定律,可得
H
= eφ
I 2π r
所以得到
B1
= µ0H
= eφ
µ0I 2π r
B2
= µH
= eφ
µI 2π r
(2) 磁介质的磁化强度为
则磁化电流体密度为
M
=
1 µ0
B2
−
H
= eφ
(µ − µ0 )I 2πµ0 r
JM
=∇× M
= eZ
1 r
d dr
(rM
φ
)
=
eZ
(µ − µ0 )I 2πµ0
习题四
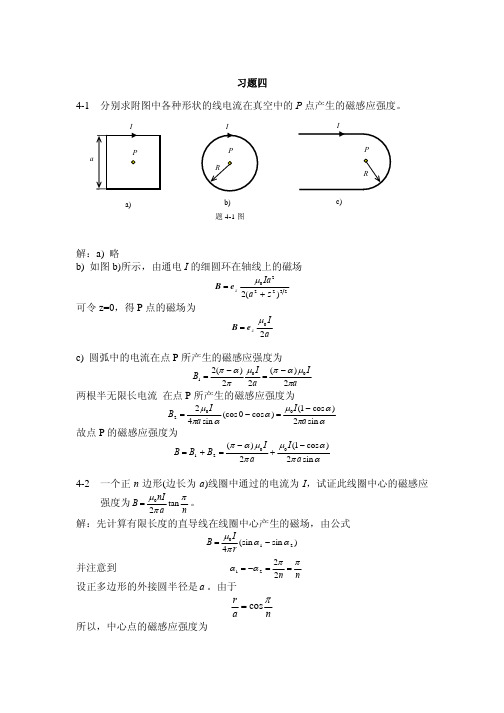
4-1 分别求附图中各种形状的线电流在真空中的 P 点产生的磁感应强度。
I
I
I
P
P
P
a
R R
a)
b)
c)
题 4-1 图
解:a) 略
b) 如图 b)所示,由通电 I 的细圆环在轴线上的磁场
B = ez
µ0 Ia 2 2(a 2 + z 2 )3 2
(完整版)电磁场与电磁波试题整理

2I 1I 1l l⨯•《电磁场与电磁波》自测试题1.介电常数为ε的均匀线性介质中,电荷的分布为()r ρv,则空间任一点E ∇=v g ____________, D ∇=v g_____________。
2. /ρε;ρ1. 线电流1I 与2I 垂直穿过纸面,如图所示。
已知11I A =,试问1.l H dl =⎰v Ñ__ _______;若.0lH dl =⎰v Ñ, 则2I =_____ ____。
2. 1-; 1A1. 镜像法是用等效的 代替原来场问题的边界,该方法的理论依据是___。
2. 镜像电荷; 唯一性定理1. 在导电媒质中, 电磁波的相速随频率改变的现象称为_____________, 这样的媒质又称为_________ 。
2. 色散; 色散媒质1. 已知自由空间一均匀平面波, 其磁场强度为0cos()y H e H t x ωβ=+vv, 则电场强度的方向为__________, 能流密度的方向为__________。
2. z e v ; x e -v1. 传输线的工作状态有________ ____、_______ _____、____________三种,其中________ ____状态不传递电磁能量。
2. 行波; 驻波; 混合波;驻波1. 真空中有一边长为的正六角 形,六个顶点都放有点电荷。
则在图示两种情形 下,在六角形中心点处的场强大小为图中____________________;图中____________________。
2. ;1. 平行板空气电容器中,电位(其中 a 、b 、c 与 d 为常数), 则电场强度__________________,电荷体密度_____________________。
2.;1. 在静电场中,位于原点处的电荷场中的电场强度线是一族以原点为中心的__________________ 线, 等位线为一族_________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:用安培环路定律,
当计算的点位于柱内(r<a),
B
=
µ0 J 0 3a
r 2eφ
r>a
时, B
=
µ0 J 0 3r
a 2eφ
4-9 有一圆截面的环形螺线管,其圆形截面积为 S,平均半径为 l,铁环的相对 磁导率为 µr,环上绕的线圈匝数为 N,通过恒定电流 I。假设铁心内部的磁 场均匀分布且空气中没有漏磁,求:(1)铁心内磁场强度 H 和磁感应强度 B; (2)环内的总磁通;(3)计算该螺线管的电感。(4)磁场能量。
b) F = Areφ
c) F = 12(xex − yey )
d) F = 4er + 3reθ
e) F = − Aex + Aey
f) F = 3rer + 2e z
解:由恒定磁场的基本方程 ∇ ⋅ B = 0 ,满足该式的矢量可能表示磁感应强度 B,
否则不表示磁感应强度。由 ∇ × H = J 求的电流密度 J。
=
8 r
+ 3cotθ
≠
0 ,F
不表示磁感应强度
B。
e) ∇ ⋅ F = − ∂A + ∂A = 0 (A 为常数), J = ∇ ⋅ B = ∇ ⋅ F = 0
∂x ∂y
µ0
µ0
f) ∇ ⋅ F = 1 ∂ (r3r) + ∂2 = 6 ≠ 0 ,F 不表示磁感应强度 B。
r ∂r
∂z
4-4 无限长直线电流垂直于磁导率分别为 µ1 和 µ2 的两种介质的分界面,试求: (1) 两种介质中的磁感应强度 B1 和 B2;(2) 磁化电流分布。
B0
M
=
B µ0
−H
=
1 µ0
⎜⎜⎝⎛
µ µ0
− 1⎟⎟⎠⎞B0
=
4999 µ0
M
=
4999 µ0
ez
对于很薄的圆铁盘样品,根据边界条件有
B = B0 H = B / µ = B0 / µ
M
=
B µ0
−H
=
⎜⎜⎝⎛
1 µ0
−
1 µLeabharlann ⎟⎟⎠⎞B0=4999 5000µ 0
M
=
4999 5000µ0
ez
4-6 证明磁介质内部的磁化电流是传导电流的( µr − 1 )倍。
B ≈ µ0M
4-11 已知一个平面电流回路在真空中产生的磁场强度为 H0,若此平面电流回路 位于磁导率分别为 µ1 和 µ2 的两种均匀磁介质的分界平面上,试求两种磁介
质中的磁场强度 H1 和 H2。 解:由于是平面电流回路,当其位于两种均匀磁介质的分界平面上时,分界面上
的磁场只有法向分量,根据边界条件,有 B1 = B2 = B 。在分界面两侧做一个小矩
c) 圆弧中的电流在点 P 所产生的磁感应强度为
B1
=
2(π − α ) 2π
µ0I 2a
=
(π
− α)µ0I 2πa
两根半无限长电流 在点 P 所产生的磁感应强度为
B2
=
2µ0 I 4πa sin α
(cos 0
−
cosα )
=
µ0 I (1 − cosα ) 2πa sin α
故点 P 的磁感应强度为
Jm = ∇×M = 0
铁盘上、下底面的磁化电流线密度
K m1 = M × en = MeZ × (±eZ ) = 0
铁盘侧面周边边缘上的磁化电流线密度
K m = M × en = MeZ × er = Meφ
这样可将圆盘视为相当于 I = Kmb 的圆形磁化电流,求此电流在各处产生的磁场。 又由于 b >> a ,可视为圆环电流产生的磁场。在铁盘轴线上产生的磁场为
解:设磁介质中的磁感应强度为 B = Bxex + Bye y + Bzez 根据边界条件 B1n = B2n , H1t = H 2t 有
By = By0 = −10
Bx = B0x = 0.5 µ0µr µ0 µ0
所以
Bz = B0z = 0 µ0µr µ0
Bx = 2500 , By = −10 , Bz = 0
形回路,分别就真空和存在介质两种情况,应用安培环路定理即可导出 H1、H2 和 H0 的关系。
在分界面两侧,做一个尺寸为 2∆h × ∆l 的小矩形回路 c。根据安培回路定律有
∫H c
⋅ dl
=
H1 (P1 )∆h
+
H2
(P1 )∆h
−
H1 (P2
)∆h
−
H 2 (P2 )∆h
=
I
因 H 垂直于分界面,所以积分式中 H ⋅ ∆l = 0 。这里 I 为与小矩形回路交链的电流。
即
B = ex 2500 − e y10
设空气中的磁感应强度为 B0 = ex B0x + e y B0 y + ez B0z
根据边界条件 B1n = B2n , H1t = H 2t 有 B0 y = By = 0.5
B0x = Bx = 10 µ0 µ0µr 5000µ0
所以
B0z = Bz = 0 µ0 µ0µr
a) 由 ∇ ⋅ F = ∂40x + ∂(−30 y) = 0 ,F 可能表示磁感应强度 B。
∂y
∂x
J
=∇⋅ B µ0
=∇⋅ F µ0
=
∂40x µ0∂x
− ∂(−30 y) µ0∂y
=
70 µ0 ez
b) 按圆柱坐标系求解, ∇ ⋅ F = 1 ∂(Ar) = 0 ,F 可能表示磁感应强度 B。 r ∂φ
解:(1)安培环定理
∫ H ⋅ dl = NI
l
有 2πHr = NI
H
=
NI 2πr
eφ
,
B
=
µ0µr H
=
µ0µr NI 2πr
eφ
(2)ψ = NΦ = NBS = µ0µr N 2 IS 2πr
(3) L = ψ = µ0µr N 2S Ι 2πr
(4) W = 1 LI 2 = µ0µr N 2SI 2
B=
µ0 Ia2 2(z 2 + a 2 )3/ 2
=
µ 0 Mba 2 2(z 2 + a 2 )3/ 2
H
=
B µ0
=
Mba 2 2(z 2 + a 2 )3/ 2
B 、 H 的方向沿 z 方向。铁盘内由于 µ >> µ0 ,可得
⎜⎜⎝⎛1 −
µ0 µ
⎟⎟⎠⎞B
=
µ0
M
在铁盘内是均匀分布的磁场。
+ π (r 2
− a12 )J 2 ] ⇒
B
=
eφ
⎜⎜⎝⎛
10 3
r
− 10−5 r
⎟⎟⎠⎞
当r
>
a2 时,有 B
= eφ
µ0I 2π r
=
eφ
2 ×10−5 r
4-8 已知在半径为 a 的圆柱区域内有沿轴向方向的电流,其电流密度为
J
= ex
J0r a
,其中 J0 为常数,求圆柱内外的磁感应强度。
习题四
4-1 分别求附图中各种形状的线电流在真空中的 P 点产生的磁感应强度。
I
I
I
P
P
P
a
R R
a)
b)
c)
题 4-1 图
解:a) 略
b) 如图 b)所示,由通电 I 的细圆环在轴线上的磁场
B = ez
µ0 Ia 2 2(a 2 + z 2 )3 2
可令 z=0,得 P 点的磁场为
B = ez
µ0 I 2a
解:(1) 由安培环路定律,可得
H
= eφ
I 2π r
所以得到
B1
= µ0H
= eφ
µ0I 2π r
B2
= µH
= eφ
µI 2π r
(2) 磁介质的磁化强度为
则磁化电流体密度为
M
=
1 µ0
B2
−
H
= eφ
(µ − µ0 )I 2πµ0 r
JM
=∇× M
= eZ
1 r
d dr
(rM
φ
)
=
eZ
(µ − µ0 )I 2πµ0
B0x = 0.002 , B0 y = 0.5 , B0z = 0
即
B0 = ex 0.002 + e y 0.5
4-13 真空中有一厚度为 d 的无限大载流块,电流密度为 ez J0 ,在其中心位置有 一半径为 a 的圆柱形空腔。求腔内的磁感应强度。
解:设空腔中同时存在有密度为 ±ez J0 的电流,则可利用安培环路定律和迭加原 理求出空腔内的 B 。
电流密度为 ez J0 的均匀载流块产生的磁场为:
B1 = e y µ0 J 0 x
⎜⎛ x ≤ d ⎟⎞ ⎝ 2⎠
电流密度为 −ez J0 的均匀载流圆柱产生的磁场为
B2
=
µ0 J 0 2
(ex
y
−
ey x)
(x2 + y2 < a2)
由此得到空腔中的磁场
B
=
B1
+
B2
=
µ0 J 0 2
(ex
y
+
率 γ 2 = 4 ×107 S/m 。导体圆柱中沿轴线方向流过的电流为 I = 100A ,求:(1)
两层导体中的电流密度 J1 和 J2;(2)求导体圆柱内、外的磁感应强度。
