《材料力学 第2版》_顾晓勤第09章第3节 三向应力状态分析
合集下载
材料力学三向应力状态PPT课件
第243页/共72页
90 45 0
直角应变花: x 0 , y 90
由 45
x
y
2
xy
2
可求得:
xy 0 90 2 45
第254页/共72页
CL10TU28
§9-6 复杂应力状态下的变形比能
一、微元体应变能
1.单向拉伸变形比能:
v
1
2
2
2、微元体变形功
dy
3 dx
CL10TU50
3.最大剪应力理论(第三强度理论)
假设:无论材 料 内 各 点的 应 力 状 态 如何 , 只 要 有 一点 的 最 大 剪 应力 τ max达到 单 向 拉 伸屈服剪应力τS时,材料就在该处出现明显塑性变形或屈服。
屈服破坏条件是:
max s
max
1
2
3
,
s
s 2
用应力表示的屈服破坏条件:
应变的实测:
用应变仪直接测出三个选定方向 1、 2、 3的线应变 1 、 2 、 3 ,由下式
1
2
3
x x x
y
2
y
2
y
2
x x x
y
2
y
2
y
2
cos2 1 cos2 2 cos2 3
xy
2
xy
2
xy
2
sin 2 1 sin 2 2 sin 2 3
求出 x 、 y 、 xy
3
2
1
第21页/共72页
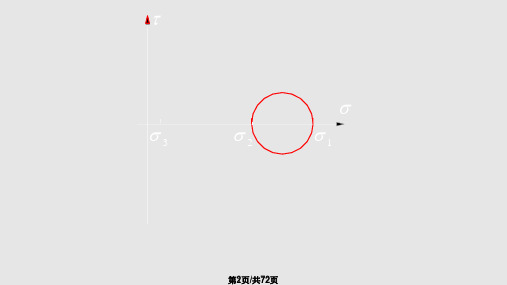
同理,在平行于 σ2 的各个斜截面上,其应力对应于由主应力 σ1 和 σ3 所画的 应力圆圆周上各点的坐标。
主单元体:六个平面都是主平面
精品课件-材料力学(张功学)-第9章

9-3)。图9- 4(a)所示狭长矩形截面梁,当载荷F达到或超过一定数值时, 梁将突然发生翘曲;图9-4(b)所示承受径向外压的圆柱形薄 壳,当外压p达到或超过一定数值时,圆环形截面将突然变为 椭圆形。
第9章 压杆稳定 图9-3
第9章 压杆稳定 图9-4
第9章 压杆稳定
9.2 细长压杆的临界载荷
第9章 压杆稳定 表9-1 几种常见细长压杆的长度因数及临界载荷
第9章 压杆稳定 例9-1 图9-10所示细长圆截面连杆,长度l=800 mm,
直径d=20mm,材料为Q235钢,其弹性模量E=200 GPa。试计 算该连杆的临界载荷。
图9-10
第9章 压杆稳定
解 该连杆为两端铰支细长压杆,μ=1。根据欧拉公式, 其临界载荷为
第9章 压杆稳定 图9-1
第9章 压杆稳定
对于轴向受压的细长弹性直杆也存在类似情况。图9-2所示两 端铰支的细长理想直杆,受力后处于直线平衡构形。在任意微 小侧向干扰下,压杆将产生微小弯曲(见图9-2 (a))。外 界微小干扰去除后将出现两种不同情况:当轴向压力较小时, 压杆最终将恢复其直线平衡构形(见图9-2 (b));当轴向 压力较大时,压杆不仅不能恢复其直线平衡构形,而且将继续 弯曲,产生显著的弯曲变形(见图9-2(c)),甚至破坏。上 述情况表明:当轴向压力小于临界载荷Fcr时,压杆直线平衡 构形是稳定的;当轴向压力大于临界载荷Fcr时,压杆直线平 衡构形是不稳定的,在任意微小的外界扰动下,压杆的直线平 衡构形会突然转变为弯曲的平衡构形,这种过程称为屈曲或失 稳。在临界载荷Fcr作用下,压杆既可在直线构形下保持平衡, 也可在微弯构形下保持平衡。所以,当轴向压力达到或超过临 界载荷时,压杆直线平衡构形将会失稳。
界应力,并用σcr表示。根据式(9-6),细长压杆临界应力
第9章 压杆稳定 图9-3
第9章 压杆稳定 图9-4
第9章 压杆稳定
9.2 细长压杆的临界载荷
第9章 压杆稳定 表9-1 几种常见细长压杆的长度因数及临界载荷
第9章 压杆稳定 例9-1 图9-10所示细长圆截面连杆,长度l=800 mm,
直径d=20mm,材料为Q235钢,其弹性模量E=200 GPa。试计 算该连杆的临界载荷。
图9-10
第9章 压杆稳定
解 该连杆为两端铰支细长压杆,μ=1。根据欧拉公式, 其临界载荷为
第9章 压杆稳定 图9-1
第9章 压杆稳定
对于轴向受压的细长弹性直杆也存在类似情况。图9-2所示两 端铰支的细长理想直杆,受力后处于直线平衡构形。在任意微 小侧向干扰下,压杆将产生微小弯曲(见图9-2 (a))。外 界微小干扰去除后将出现两种不同情况:当轴向压力较小时, 压杆最终将恢复其直线平衡构形(见图9-2 (b));当轴向 压力较大时,压杆不仅不能恢复其直线平衡构形,而且将继续 弯曲,产生显著的弯曲变形(见图9-2(c)),甚至破坏。上 述情况表明:当轴向压力小于临界载荷Fcr时,压杆直线平衡 构形是稳定的;当轴向压力大于临界载荷Fcr时,压杆直线平 衡构形是不稳定的,在任意微小的外界扰动下,压杆的直线平 衡构形会突然转变为弯曲的平衡构形,这种过程称为屈曲或失 稳。在临界载荷Fcr作用下,压杆既可在直线构形下保持平衡, 也可在微弯构形下保持平衡。所以,当轴向压力达到或超过临 界载荷时,压杆直线平衡构形将会失稳。
界应力,并用σcr表示。根据式(9-6),细长压杆临界应力
《材料力学 第2版》_顾晓勤第06章第4节 弯曲时的正应力
第 4 节 弯曲时的正应力
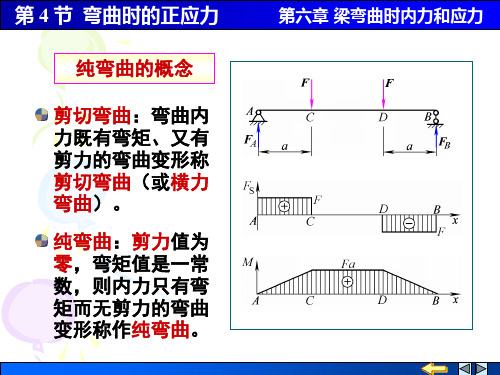
纯弯曲的概念
剪切弯曲:弯曲内 力既有弯矩、又有 剪力的弯曲变形称 剪切弯曲(或横力 弯曲)。
纯弯曲:剪力值为 零,弯矩值是一常 数,则内力只有弯 矩而无剪力的弯曲 变形称作纯弯曲。
第六章 梁弯曲时内力和应力
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
一、实验现象及假设
梁表面 mm 、nn 等一组横向直线变形后仍为直 线,并与已变成弧线的 ab 、cd 等一组横向直线 正交,只是相对地转了一个角度。
纵向线变成圆弧线,位于中间位置的纵向线长度 不变,上部的纵向线缩短,下部的纵向线伸长。
变形后横截面的高度不变,而宽度在纵向线伸长 区减小,在纵向线缩短区增大,如图所示 b)。
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
假设
平面假设:梁变形后横截面依然保持平面,且与梁 变形后的轴线垂直,横截面绕自身某轴作了转动。
纵向纤维单向受力假设:梁内各纵向纤维只产生轴 向拉伸或压缩变形。
中性层:梁在弯曲变形 时,一部分纤维伸长, 一部分纤维缩短,必然 有一部分纤维既不伸长 也不缩短的层。
中性轴:中性层与横截面的交线。
第 4 节 弯曲时的正应力
二、变形几何关系
bb oo
oo
(
y) d d
d
y
三、物理关系
根据纵向纤维假设,各
纵向“纤维”处于单向受 力状态。当应力不超过材 料的比例极限时,应用胡 克定律可得横截面上距中 性轴为 y 处的正应力
第六章 梁弯曲时内力和应力
E
E
第六章 梁弯曲时内力和应力
截面所有微面积上的力对 z 轴的合力矩即为作用在该截 面上的弯矩:
纯弯曲的概念
剪切弯曲:弯曲内 力既有弯矩、又有 剪力的弯曲变形称 剪切弯曲(或横力 弯曲)。
纯弯曲:剪力值为 零,弯矩值是一常 数,则内力只有弯 矩而无剪力的弯曲 变形称作纯弯曲。
第六章 梁弯曲时内力和应力
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
一、实验现象及假设
梁表面 mm 、nn 等一组横向直线变形后仍为直 线,并与已变成弧线的 ab 、cd 等一组横向直线 正交,只是相对地转了一个角度。
纵向线变成圆弧线,位于中间位置的纵向线长度 不变,上部的纵向线缩短,下部的纵向线伸长。
变形后横截面的高度不变,而宽度在纵向线伸长 区减小,在纵向线缩短区增大,如图所示 b)。
第 4 节 弯曲时的正应力
第六章 梁弯曲时内力和应力
假设
平面假设:梁变形后横截面依然保持平面,且与梁 变形后的轴线垂直,横截面绕自身某轴作了转动。
纵向纤维单向受力假设:梁内各纵向纤维只产生轴 向拉伸或压缩变形。
中性层:梁在弯曲变形 时,一部分纤维伸长, 一部分纤维缩短,必然 有一部分纤维既不伸长 也不缩短的层。
中性轴:中性层与横截面的交线。
第 4 节 弯曲时的正应力
二、变形几何关系
bb oo
oo
(
y) d d
d
y
三、物理关系
根据纵向纤维假设,各
纵向“纤维”处于单向受 力状态。当应力不超过材 料的比例极限时,应用胡 克定律可得横截面上距中 性轴为 y 处的正应力
第六章 梁弯曲时内力和应力
E
E
第六章 梁弯曲时内力和应力
截面所有微面积上的力对 z 轴的合力矩即为作用在该截 面上的弯矩:
材料力学应力分析(共143张PPT)

Mz Wz
17
y
1
4
z
2
x
3
S平面
18
y
1
FQy
1
4
4 Mz
x
z
2
Mx
3
3
19
应力状态的概念
主平面:单元体中剪应力等于零的平面。
主单元体:在单元体各侧面只有正应力而
无剪应力
3
2
主应力:主平面上的正应力。
主方向:主平面的法线方向。
约定:
1
12 320
应力状态的分类
3
2
1
1
2
3
单向应力状态:三个主应力中,只有一个主应力不等于零的情况。
3
一、什么是应力状态?
〔一〕、应力的点的概念:
最大正应力所在的面上切应力一定是零; 它与塑性较好材料的试验结果比第三强度理论符合得更好; 7-2 二向应力状态分析--解析法 面将单元体截为两局部, 并注意到 化简得 三、如何描述一点的应力状态 应力圆上一点( , ) 7-8 广义胡克定律 该单元体的三个主应力按其代数值的大小顺序排列为 解: 该单元体有一个主应力 例2:纯剪切状态的主应力 它与塑性较好材料的试验结果比第三强度理论符合得更好;
5
F
F
A
F
co2s
2
sin2
过同一点不同方向面上的应力各不相同, 即应力的面的概念
6
应力的点的概念与面的概念
应力
指明
哪一个面上? 哪一点?
哪一点? 哪个方向面?
应力状态: ——过同一点不同方向面上应力的集合,称为
这一点的应力状态;
7
二、为什么要研究应力状态?
《材料力学 第2版》_顾晓勤第02章 轴向拉伸和压缩第6节 应力集中的概念

第二章 轴向拉伸和压缩
总结
在静载荷作用下,塑性材料对应力集中不敏感,实 际工程计算中可按应力均匀分布计算。
脆性材料因无屈服阶段,当应力集中处的最大应力
max 达到强度极限b时,该处首先产生裂纹。因此
对应力集中十分敏感,必须考虑应力集中的影响。
对于灰铸铁,其内部的不均匀性和缺陷往往是产生 应力集中的主要因素,而构件外形改变所引起的应 力集中是次要因素,可以不考虑应力集中的影响。
第 6 节 应力集中的概念
应力集中的程度用理论 应力集中系数表示:
max
式中max 为最大拉应力, 为假设应力均匀分布时
该截面上的名义应力。
第二章 轴向拉伸和压缩
第 6 节 应力集中的概念
第二章 轴向拉伸和压缩
注意
应力集中系数 值取决于截面的几何形状与尺寸,
截面尺寸改变越急剧,应力集中的程度就越严重。 因此,在杆件上应尽量避免带尖角、槽或小孔,在 阶梯轴肩处,过渡圆弧的半径以尽可能大些为好。
第 6 节 应力集中的概念
第二章 轴向拉伸和压缩
应力集中:工程中常在一些构件上钻孔、开槽(如 退刀槽、键槽等)及车削螺纹等,有些则需要制成 阶梯状的,这就引起杆件横截面尺寸的突变。研究 表明,杆在轴向拉伸时,在杆件截面突变处附近的 小范围内,应力的数值急剧增大;而离开这个区域 稍远处,应力就大为降低。并趋于均匀分布,这种 现象称为应力集中。
继续增大,则该处相邻
的材料将进入屈服阶段
而停止增长。增大的载
荷由截面上尚未屈服的
材料来承担,使截面1-1 上材料的屈服区域将随 载荷的不断增大而扩大(图b),直至截面 1-1 上各点处 的应力都达到屈服极限(图c)。因此,塑性材料可使截 面上的应力逐渐趋于平均,降低应力不均匀程度。
六、 材料力学应力状态分析(2)

(MPa)
τ σ
(0,-100)
tmax
(300,100)
τmax = 180MPa;
Hale Waihona Puke σOσσ三向应力状态 特例分析
作为三向应力状态的特例,平面应力状态特点:
σ =0 σ、σ 、σ σ1 、σ 2、σ3
广义胡克定律
1、胡克定律、横向变形与泊松比
y
sx x = ; E sx y = x = ; E — 泊松比
tmax
(-300,50)
300
(MPa)
τ
σ
σ
(-200,-50)
σ
O
σ
三向应力状态 特例分析
例3、如图平面应力状态,求: 主应力s1、s2 、 s3和最大切 应力tmax。
300 100
解:如图作应力圆 R=180MPa; s1 = 330MPa; s2 = 0; s3 = -30MPa;
A
2、平衡方法是分析一点处应 力状态最重要、最基本的方法
A
论证A-A截面上 必然存在切应力,而 且是非均匀分布的; 怎样证明A-A截 面上各点的应力状态 不会完全相同。
结论与讨论
A
ζ
ζ η
A
关于A点的应力状态有多种答 案、请用平衡的概念分析哪 一种是正确的。
η
η
ζ
结论与讨论
3、怎样将应力圆作为一 种分析问题的重要 手段,求解较为复杂的 应力状态问题
P
x =
由变形方程: x =
1 [s x (s y s z )] = 0; E s x = s z = 0.3( 60) = 18 MPa
P σx σy
所以铅块主应力为: ζ1 = 0;ζ2 = -18MPa; ζ3 = -60MPa;
《材料力学 第2版》_顾晓勤第09章第2节 二向应力状态分析
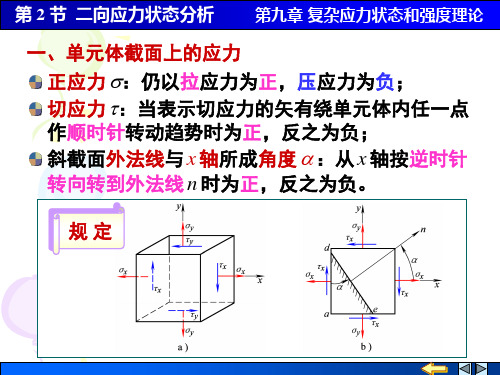
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
最大主应力和最小主应力的计算式
max m in
x
y
2
x
2
y
2
2 x
确定 max 和 min 所在平面的方法
1)若x>y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定max 所在的平面;
2)若x <y,则所求的两个角度0 和 90º+0 中, 绝对值较小的一个确定min 所在的平面;
2
及
2sin cos sin 2 对以上二式进行整理得到:
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
x
y
2
x
y
2
cos2
x
sin 2
x
y
2
sin 2
x
cos2
利用上述两式可以求得 de 斜截面上的正应力和切
设 de 斜截面面积为 dA,则 ae 面的面积为 dAsin , ad面的面积为 dAcos 。取 t 和 n 为参考轴,建立棱
柱体 ade 的受力平衡方程如下:
dA ( xdAcos ) sin ( xdAcos ) cos ( ydAsin ) cos ( ydAsin ) sin 0
y
2
2 x
105 MPa
第 2 节 二向应力状态分析 第九章 复杂应力状态和强度理论
0
1 2
arctan(
2 x x
材料力学——应力分析【可修改】.ppt

(2)主平面的位置
tg
2α 0
σ
2τ xy
x σ
y
α1 α 2 α1 900
} σ max
σ min
σx σy 2
(σ
x σ 2
y
2
)
τ
2 xy
以1代表max作用面的方位角, 2代表min作用面的方位角。
精选
σ x σ y ,则 α1 450 (α1在 900 范围内取值)
若 σ x σ y ,则 α1 450
x
在坐标系内画出点A( x,
xy)和B(y,yx)
2a C
A(
x
,
a
xy)
AB与a 轴的交点C便是
圆心。
O
以C为圆心,以AC为
B( y ,yx)
半径画圆——应力圆;
精选
y
n 三、单元体与应力圆的对应关系
面上的应力( , )
a xy x 应力圆上一点( , )
y
面的法线 应力圆的半径
Oa n D(xa , a)
所在的平面)垂直的
1
斜截面上的应力。
3
精选
2
3
1
2
用截面法,沿求应力的截 面将单元体截为两部分, 取左下部分为研究对象。
2
3
3
1
1
1
3
2
3
2
精选
主应力 3 所在的两平面上是一对
自相平衡的力, 因而该斜面上的
3
应力, 与 3无关, 只由主应力
1
1 , 2 决定。
3 2
与3所在的面垂直的斜截面上的应力可由
精选
应力的点的概念与面的概念
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、一点处的最大切应力
取平行于一个主应力3 的任一斜截面 m-m,用
截面法研究其左边部分,根据平衡条件可得:
x 1, y 2, x 0122sin 2
第 3 节 三向应力状态分析 第九章 复杂应力状态和强度理论
当
1
2
2
sin 2
450 时,切应力为最大,记作
12
1
2
2
同理,可得到平行于1和2 的两组截面上的正
第 3 节 三向应力状态分析 第九章 复杂应力状态和强度理论
复杂应力状态下一点处的最大应力 1、一点处的最大正应力
设一点处的主应力单元体如图 a 所示,研究证
明,当主应力按 1 2 3 排列时,则有
max 1
min 3
第 3 节 三向应力状态分析 第九章 复杂应力状态和强度理论
号极值切应力分别为:
23
2
3
2
31
1
3
2
因 1 2 3,显然 12、23、31 三个极值切
应力中,31为最大,即
max
1
2
3
