材料力学(金忠谋)第六版答案第06章
材料力学(金忠谋)第六版答案第06章(整理).pptxPPT共24页

71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
材料力学(金忠谋)第六版答案第06章 (整理).pptx
21、静念园林好,人间良可辞。 22、步步寻往迹,有处特依依。 23、望云惭高鸟,临木愧游鱼。 24、结庐在人境,而无车马喧;问君 何能尔 ?心远 地自偏 。 25、人生归有道,衣食固其端。
谢谢你的阅读
Байду номын сангаас
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第06章.doc

弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
材料力学习题第六章应力状态分析答案详解

第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ=; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的; (C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版答案第08章
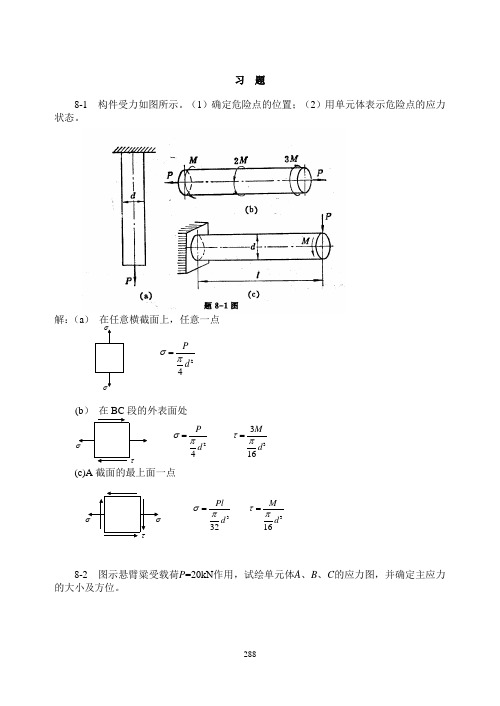
288习 题8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a ) 在任意横截面上,任意一点σσ24Pdσπ=(b ) 在BC 段的外表面处24Pdσπ=3316Mdτπ=τσ(c)A 截面的最上面一点στσ332Pldσπ=316Mdτπ=8-2 图示悬臂粱受载荷P =20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
289解:σσ2620100060520106A M MPa W σ--⨯===-⨯⨯BσB σBτ2386282200005103052010620000557.5102250 2.25520105106B B B M y MPaJKPa MPa στ-----⨯⨯===-⨯⨯⨯⨯⨯⨯===⨯⨯⨯⨯Cτ4020000 1.51.5320510C C Q MPa A στ-=⨯===⨯⨯3σ1σστA <>点1306090σσα=== 1σ3σστB <>点130.16830.16885.7σσα==-=στ1σ3σC<>点133345σσα==-=-8—3 主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa)。
解:(a)()()1212205205cos2cos6013.752222MPa ασσσσσα+---+-=+=+=290291()12205sin 2sin 6010.82522MPa ασστα---=== ()max 20512.52MPa τ--==45α= (与120σ=方向夹角)(b)()()()121220102010cos 2cos 135 5.6062222MPa ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=-()max 2010152MPa τ--== 45α= (与1σ方向夹角)或135(与水平方向交角)(c )()121240104010cos 2cos 12017.52222MPaασσσσσα+-+-=+=+-= ()124010sin 2sin 12013.022MPa ασστα--==-=- max 4010152MPa τ-== 45α= (与140σ=方向夹角)(d) ()121220202020cos 2cos 45202222MPa ασσσσσα+-+-=+=+= 0ατ=max 0τ=8—4 单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
材料力学课后标准答案

解:取轴向长为 的管分析:微元 上,作用力为
向分量 ,积分得
则: ,而
则:
题6-12图题6-13图
6-13长输水管受内压 ,管的内径为 , , ,用第四强度理论计算壁厚。(提示:可设管的轴向应变为零。)
解: ,数据代入,得:
,
所以
现已知
,
得
题6-5图
题6-6图题6-7图
6-6图示简支梁为 工字梁, , 。 点所在截面在集中力 的左侧,且无限接近 力作用的截面。试求: 点在指定斜截面上的应力; 点的主应力及主平面位置(用单元体表示)。
解: 所处截面上弯矩、剪力:
,
查型钢表后, 点以下表面对中性轴静矩:
,
同理,积分得
所以, 处转角为 ,为顺时针方向; 处挠度为 ,为竖直向下。
8-6试求图示各刚架 点的竖直位移,已知刚架各杆的 相等。
解: 段: ; 段上
由卡氏定理, 处的竖直位移
分段带入后面积分:
为正值,则与 同向,竖直向下
分析可知, 处已经作用有竖直方向的力,为了能利用卡氏定理解题, 处和竖杆中间处的 分别为
(压), (拉)
进而求得 (拉),由
求得:
8-3计算图示各杆件结构的变形能。
题8-3图
解: 首先求解 处的约束反力为
弯矩方程为:
则
分段积分:
解: 以逆时针方向为正,
,积分得
8-4试求图示各梁的 点的挠度的转角。
题8-4图
解: 以 点为 轴起点,结构的弯矩方程为:
则:
得
撤去 和 ,在 处作用逆时针向
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力6-1求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题 6-1图解:( a)M m m 2.5KN m Mmax 3.75 KN mJ x d 410 410 8490.8 108 m4 6464A 2.510 3410220 .37 MPa(压)490.81083.751035102max490 .810838.2MPa ( b)M m m60 KN m M max 67.5KN mJ x bh 31218310 85832 10 8 m 4 1212A 6010 3610 261.73 MPa(压)583210867 .510 39102max583210 8104.2MPa ( c)M m m1KN m M max1KN m J x25.610 8 m4W x7.810 6 m3y A 1.520.530.99cmA 110 30.9910238 .67 MPa(压)25.6108max110 3128 .2 MPa 25.61086-2 图示为直径 D = 6 cm的圆轴,其外伸段为空心,内径d= 4cm,求轴内最大正应力。
解: W x1D 3 (1 4 )32631061 (4)432617.02 10 6 m 3Wx2D 3 63 10 6 21.21 10 4 m 3323210 .9 10 352 .88 MPa17 .02 10 611.172 10 355.26 MPa21 .21 106max55 .26 M P a6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
4解: A 截面:max 140 10 3 8 9.65 10 2 37.95 M p a (拉)10170 10min 140103815 .35 10 250 .37 M p a(压)1017010 E截面max 220103815.351021017010min 22010 39.651021017010830 .19 M p a (拉)18.98 M p a (压)6-4 一根直径为 d的钢丝绕于直径为D的圆轴上。
( 1)求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)( 2)若 d=lmm ,材料的屈服极限s =700MPa ,弹性模量 E=210GPa,求不使钢丝产生残余变形的轴径 D 。
解:1MEJEJ E d 4M32Dm a x M32M E dW d 3DE d21010 9110 3D70010 60.3m 30cms6-5 矩形悬臂梁如图示.已知l= 4m,b2, q=10kN/m ,许用应力 [σ ]=10Mpa 。
h3试确定此梁横截面尺寸。
解: M max 1 ql21104280KN m226 h 22h h2h 3W3669M M8010 3h 2W1010 69Wh0. 416 m41 .6 cmb27 .7 cm6-6 20a工字钢梁的支承和受力情况如图所示。
若[σ ]= 160MPa,试求许用载荷P。
解:W237 cm 32P2P KN 3M max m3M W160 10 6237 10 62 P33P237 56 .880 KN1602(M 图)2P36-7压板的尺寸和载荷情况如图所示。
材料为45钢,s =380 MPa,取安全系数n 1.5 。
试校核压板强度。
1 30 20 33012 3 1568 mm 2解: W(12)1012M 18 10320 10 3360 N mM 360229 .6 M P aW1568 1096-8 由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ ] = 150 MPa ,试选择槽钢号码。
解: M max60 KN mW xMm ax60 10 30.4 10 3 m 3400 cm 3150 10 6查表:( 22a , W x217 . 6cm 3200 cm 3 )60KN m20KN m(M 图)6-9 割刀在切割工件时,受到 P= 1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解: M p 81038 N mM p3010 330 N mW 2 .513 270 .42 mm36W415 2150 mm 36m ax m ax M8W70.410M30W1501099114MPa200MPa6-10图示圆木,直径为 D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高, h、 b分别为何值?( 2)如要使所切矩形截面的抗弯刚度最高, h、 b又分别为何值?bh 2 b ( D 2 b 2 )解: W66dWdbD 23b 26b 2 D 23h2D2D2 2 D233从强度讲: b0.57735Dh 0.8165DJ bh 2b( D 2 b 2 ) 3 1212dJ0 db331( D 2b2) 2b( D 2b2) 2( 2b) 02从刚度讲 b0.50Dh0.866 D6- 11T字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知 h= 12cm, t=3cm ,试确定其翼板宽度 b之值。
压y上max=3解:拉y下maxy上=3y下y上+y下=h 12y 下=12=3cm 4S ( b 3)( 33) (9 3) 4.5 0934. 5227 cmb1.536-12图示简支梁,由No.18 工字钢制成,在外载荷作用下,测得横截面A处梁底面的纵向正应变 3.0 10 4,试计算梁的最大弯曲正应力σ max。
已知钢的弹性模量E=200GPa, a=1m。
解:A E20010 9 3.0 10 460 MPamax Mmax 3 / 42 M A 3 / 8Amax 2 A260120 M P a3 qa2 3 qa2481 qa24(M 图)6-13试计算图示矩形截面简支梁的1-1面上 a点和 b点的正应力和剪应力。
解: 1-1 截面Q 3.6364 KNM 3.6364 KN mJ bh 37.515 32109 . 375 cm 41212M 3.63641033.5102a y2109.37510 8J6 .03 MPa3.6364 1037.5 10 2b2109.375 10 812 .93 M P aQS 3.6364 103(47.5) 5.5 10 6a2109.3751087.510 2Jb0.379 M P a6-14 计算在均布载荷q=10 kN /m作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解: M max 1 ql211010312881.25 103 N mQ max 1ql1101031 225 103NM 1.2510 3m a x W5310632101 .86 MPa在跨中点上、下边缘Q4510 34max A3243451025 .46 MPa在梁端,中性轴上6-15 试计算6-12 题工字钢简支梁在图示载荷下梁内的最大剪应力。
3 qa21解:860MPaW qa4 W 1 8 5cm 36010 6185106829 .6KN / m 3q312qa 4Qmax 3qa329 .6122.2 KN(Q 图)44max QS22.210 322 .12 M P a Jt15.4102 6.51036-16矩形截面木梁所受载荷如图示,材料的许用应力[σ ]=10Mpa 。
试选择该梁的截面尺寸,设 h : b 2 : 119KN141KN m8KN9KN1KN8KN m21KN(Q 图)(M图)解: R A19 KN R B29 KNW 1 bh2h 3612m ax M1410 3 W h 312h31410 3120 .256 m25 . 6 cm10 610b 12 . 8cmQ1. 521 1030.961 M P amax 1 .525 .6104A12 .86-17 试为图示外伸梁选择一工字形截面,材料的许用应力[ σ ]= 160MPa , [ τ ] =80Mpa 。
解:W M201000125 cm 316010 6取 I16, W 1 4 cm1 3J : S 13.8(cm)QS151030 .181 M P aJt13.8610 3故取 No16 工字钢Q( x)15KN M (x)20KN m5KN10KN m 10KN(Q 图)(M 图)6-18图示起重机安装在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采用工字型钢的号码。
已知l = 10 m , a= 4 m , d=2 m 。
起重机的重量W= 50 kN ,起重机的吊重 P=10 kN ,钢梁材料的许用应力[σ] =160 MPa, [τ ]= 100Mpa 。
解:轻压: 10KN, 50KN150 (10x ) 10 ( 8x )58 6 xR10M ( x)Rx(58 6 x )xdM5812x0dxx 4 .833 mMmax( 586 4.833 ) 4 .833140 .17 KN mM m a x140 .17 10 3W1601060.87610 3 m 3876 cm 3取两个 I 28a W z508 .15 cm 3W 4 3 8cm3210KN50KNd10m6-19等腰梯形截面梁,其截面高度为h。
用应变仪测得其上边的纵向线应变142 10 6,下边的纵向线应变21410 6。
试求此截面形心的位置。
= M y1 E 1解:上J b下=M y 2 E 2J b1 =y14232y 214y 1 y 2 h3 y 2 y 2hy 21 y 1 3 h h446-20 简支梁承受均布载荷 q ,截面为矩形 bh ,材料弹性模量 E ,试求梁最底层纤维的总伸长。
解: M ( x )ql xqx 22 2M ( x)(x)E bh 26l ( x) dx6qll x 2ql 3lEbh 2() dx222 Ebh 26-21 矩形截面悬臂梁受力如图(a )所示,若假想沿中性层把梁分开为上下两部分:( 1)试求中性层截面上剪应力沿 x 轴向的变化规律,参见图( b );( 2)试说明梁被截下的部分是怎样平衡的?解:( 1) x3Q 3 qx 2 A2 bh( 2)由产生的合力为 TTlx bdxl3 qx 3ql 22 bhbdx4 h由弯曲产生的轴间力为Nql2h / 2M maxyNh / 2 b dyh / 2 2bdy (自证)b dyJbh 312j ql 24 hT6-22 正方形截面边长为 a ,设水平对角线为中性轴。
试求(1)证明切去边长为a的上下两棱角后,截面的抗弯模量最大;9(2)若截面上的弯矩不变,新截面的最大正应力是原截面的几倍?(提示:计算I z 时可按图中虚线分三块来处理)。
