新冀教版九年级上《25.4相似三角形的判定》练习题

合集下载

相似三角形的判定冀教版九年级数学上册同步测试(含答案)

25.4 相似三角形的判定班级：姓名：成绩：一、单选题1．如图，在△ABC 与△ADE 中，B D ∠=∠，添加下列条件，不能得到．．．．△ABC 与△ADE 相似的是（）A ．E C ∠=∠B ．BAD CAE ∠=∠C ．AB ADBC DE= D ．AE DEAC BC=2．下列所给四对三角形中，根据条件不能判断△ABC 与△DEF 相似的是（）A ．AB ．BC ．CD ．D3．如图，E 为线段AB 上一点，EC ∥AD ，DE ∥BC ，若1BEC S ∆=，3ADE S ∆=，则：ADEC=（）A ．3:1B ．9:1C ．3:1D ．1.5:14．如图，△ABC 中，D 为BC 中点，E 为AD 的中点，BE 的延长线交AC 于F ，则AFFC为（）A ．1:5B ．1:4C ．1:3D ．1:25．如图，下列条件不能判定△ABC 与△ADE 相似的是（）A ．AE ADAC AB= B ．∠B=∠ADE C ．∠C=∠AED D ．AE DEAC BC=6．如图，在ABC △中，60A ∠=︒，BE 、CF 分别是AC 、AB 边上的高，连接EF ，AEF 和ABC △的周长比为（）A ．3:2B ．1:2C ．3:4D ．1:47．如图，已知AD ∥BC ，AC 与BD 相交于点O ，点G 是BD 的中点，过G 作GE ∥BC 交AC 于点E ，如果AD=1，BC=3，GE ：BC 等于（）A ．1：2B ．1：3C ．1：4D ．2：38．如图，在中，，分别为，边上的中线，，若，则的面积为（）A ．4B ．8C ．12D ．169．如图，已知△ABC 与△BDE 都是等边三角形，点D 在边AC 上（不与A 、C 重合），DE 与AB 相交于点F ，则图中相似三角形有（）A ．2对B ．3对C ．4对D ．5对10．下面四组图形中，必是相似三角形的为（） A ．有一个角为40°的两个等腰三角形 B ．两个直角三角形C ．两条边对应成比例，一个对应角相等的两个三角形D ．有一个角为100°的两个等腰三角形11．在图1、图2所示的ABC △中，4AB =，6AC =.将ABC △沿图示中的虚线剪开（裁剪方法已在图上标注），对于各图中剪下的两个阴影三角形，下列说法正确的是（）A ．只有图1中的阴影三角形与ABC △相似B ．只有图2中的阴影三角形与ABC △相似 C ．两图中的阴影三角形都与ABC △相似D ．两图中的阴影三角形都与ABC △不相似12．ABC ∆和A B C '''∆符合下列条件，其中使ABC ∆与A B C '''∆不相似的是（） A ．45,26,109A A B B ∠=∠=︒∠='︒∠='︒B ．1, 1.5,2,12,8,16AB AC BC A B A C B C ''''''====== C ．153, 1.5,,, 2.1142A B AB AC A B B C ∠=∠===''=''' D ．,,,,,BC a AC b AB c B C a A C b A B c ''====''''==13．如图，正方形ABCD 中，E 为AB 中点，BF ⊥CE 于F ，那么S △BFC =（）S 正方形ABCD ．A ．12B ．13C ．14D ．1514．如图所示，四边形ABCD 是正方形，E 是CD 的中点，P 是BC 边上的一点，下列条件：①∠APB ＝∠EPC ；②∠APE ＝∠APB ；③P 是BC 的中点；④BP ∶BC ＝2∶3.其中能推出△ABP ∽△ECP 的有（）A ．1个B ．2个C ．3个D ．4个二、填空题15．如图，∠B=∠C ，AC 与BD 交于点O ，如果2AO =，32DO =，4AB =，那么CD 的长是_________.16．如图，在△ABC 中，∠ACB=90°，CD 是斜边AB 上的高，已知BC=5，BD=4，则AD 的长度=______．17．如图，若OAOB=______，则OAC OBD ∆∆∽.18．如图，在△ABC 中，AB AC =，BE 、AD 分别是边AC 、BC 上的高，1CD =，4AC =，那么EC =___________.19．如图，D 是ABC ∆的边AB 上一点，若1____∠=，则ADC ∆∽ACB ∆，若2____∠=，则ADC ∆∽ACB ∆．20．在△ABC中，AB＝8，AC＝6，在△DEF中，DE＝4，DF＝3，要使△ABC与△DEF相似，则需要添加一个条件是____．(写出一种情况即可)∥，若OA∶OC＝4∶3，ABO的面积是2，则CDO 21．如图，线段AC与BD相交于点O，AB CD的面积等于________．22．已知：如图，矩形ABCD中，BC边上有一动点M,∠AMN=90°,AB=3，BC=4，CN=1，当BM=_______________,△ABM相似于△MCN。

九年级数学上册《254相似三角形的判定(二)》同步测试卷(新版)冀教版.docx

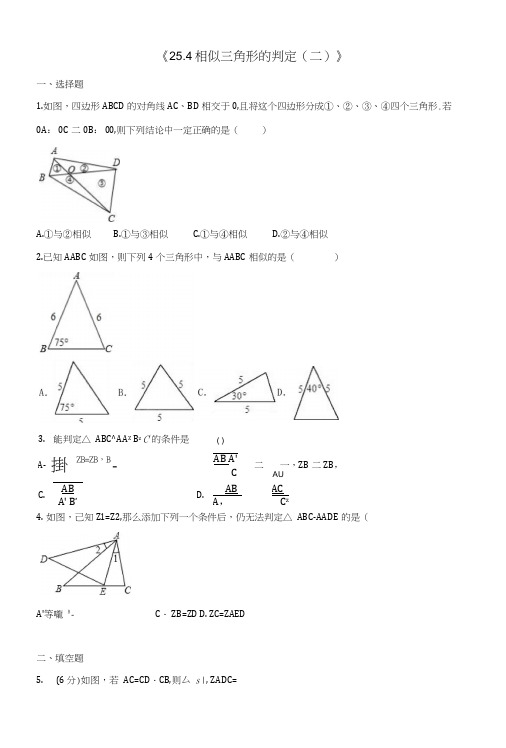
《25.4相似三角形的判定（二）》一、选择题1.如图，四边形ABCD 的对角线AC 、BD 相交于0,且将这个四边形分成①、②、③、④四个三角形.若 0A ： 0C 二0B ： 00,则下列结论中一定正确的是（）A.①与②相似B.①与③相似C.①与④相似D.②与④相似2.已知AABC 如图，则下列4个三角形中，与AABC 相似的是（）4. 如图，己知Z1=Z2,那么添加下列一个条件后，仍无法判定△ ABC-AADE 的是（A'等嚨 B - C ・ ZB=ZD D. ZC=ZAED二、填空题5. (6 分)如图，若 AC=CD ・CB,则厶 s\ , ZADC=能判定△ ABC^AA Z B z C f 的条件是 A- 掛 ZB=ZB ，B - AB A' C 二一，ZB 二ZB ，AUC. ABA' B‘ D. AB A ， ACz 3. ( )B D C6. 在AABC 中，AB 二5, AC 二 10, ZA 二40。

,在ADEF 中，DE 二6，DF 二 12,填上一个合适的条件能使△ ABC^ADEF.7. _______________________________________________________ 如图所示MB, CD 交于点 0,且 0C=45, 0D=30, 0B 二36,当 02 _________________________________________________ 时，△AOCs/^BOD ；当 0/\二8. 如图，B, C 分别在Z\ADE 的边 AD, AE 上，且 AC 二6, AB 二5, EC 二4, DB 二7,贝ij BC ： DE 二9.如图，BD 平分ZABC, A ABM, BC 二6,则当 BD 二时，AABD<^ADBC.10. __________________________________________________ 如图，AABC 中，CD 丄AB 于 D, AD 二8, CD 二6,则当 BD 二 _______________________________ 时，AADC^ACDB, ZACB=APB二——或等——P 是AC 上一点，连接BP •要使△ ABP^AACB,则必须有ZABP=13. 在方格纸屮，每个小格的顶点称为格点，以格点为顶点的三角形叫做格点三角形.在如图5X5 的方格纸中，以A 、B 为顶点作格点三角形与AOAB 相似（相似比不能为1）,则另一个顶点C 的坐三、解答题14. 如图，判断两个三角形是否相似，并求出x 和y.15. 如图，在AABC 中,ZC=90° , D 、E 分别为AB 、AC 边上的两点,且AD ・AB 二16. 已知：如图,在正方形ABCD 中，P 是BC 上的点,且BP=3PC, Q 是CD 的中点.AC=18, D 是 AC 上一点 AD=12,在 AB 上取一点 E,使 A 、D 、E三点组成的三角形与ABC 相似，则AE二标为 ______AEMC.求证：DE 丄AB.四、综合运用题17.如图，在AABC中,AB=8cm, BC=16cm,点P从点A开始沿AB向B以2cm/s的速度移动，点Q 从点B开始沿BC向C点以4cni/s的速度移动.如果P, Q分别从A, B同时出发，经过几秒钟APBQ 与△ABC相似？《25.4相似三角形的判定（二）》答案B ； .ZD 二40二；7. 54； 37.5； 8.寺;9. zW 10. 90； 11. ZC ； ZABC ；（5, 2）或（4, 4）；一、选择题1. B ；2. C ；3. C ；4.二、填空题5. AO ）； BCA ； ZBAC ；（戛；12. 16 或 9； 13.。

2020年冀教版数学九年级上册 25.4 相似三角形的判定(含答案)

拓展训练 2020年冀教版数学九年级上册 25.4 相似三角形的判定基础闯关全练1．如图，在△ABC 中，D 为AC 边上一点，∠DBC= ∠A ，，AC=3，则CD 的长为 ( )A.1B.C.2D.2．如图所示，∠C=∠E=90°，AC=3，BC=4，AE=2，则AD=_______.3．如图，△ACD 和△ABC 相似需具备的条件是( )A.BC AB CD AC =B.AC BC AD CD =C.AC ²=AD ·ABD.CD ²=AD ·BD 4．如图，在△ABC 与△ADE 中，∠BAC= ∠D ，要使△ABC 与△ADE 相似，还需满足下列条件中的 ( )A. B. C. D.5．如果△ABC 中,AB=AC ，BC =AB ，那么∠A 的度数是 ( ) A ．30° B ．36° C ．45° D ．60° 6．(1)在△ABC 的AB 边上取一点D ，使AD=AB ，在AC 边上取一点E ，使AE= AC ，那么△ADE 与△ABC 是否相似？为什么？(2)在△ABC 的AB 边上取一点D ，使AD=1，在AC 边上取一点E ，使AE=1，那么△ADE 与△ABC 是否相似？如果不相似，那么当△ABC 是什么三角形时，这两个三角形一定相似？7．如图，小正方形的边长均为1，则下列各三角形（阴影部分）与△ABC 相似的是 ( )A. B. C. D.能力提升全练如图，△ABC 中，P 为AB 上一点，在下列四个条件中：①；②∠APC= ∠ACB;③AC ²=AP ·AB;④AB ·CP= AP ·CB ，能满足△APC 和△ACB 相似的条件是 ( )A.①②④B.①③④C.②③④D.①②③三年模拟全练一、选择题1．（2019河北唐山滦州期中，5．★☆☆）如图，在△ABC中，如果DE与BC不平行，那么下列条件中，不能判断△ADE与△ABC相似的是( )A.∠ADE= ∠CB.∠AED= ∠BC. D.2．（2019河北唐山乐亭期中，8，★★☆）在三角形纸片ABC中，AB=8，BC=4，AC=6，按下列方法沿虚线剪下，能使阴影部分的三角形与△ABC相似的是( )A. B. C. D.二、填空题3.（2017江苏镇江丹阳三中月考，12，★☆☆）如图，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在格点上（小正方形的顶点）.P₁，P₂，P₃，P₄，P₅是△DEF边上的5个格点，请在这5个格点中选取2个作为三角形的顶点，使它们和点D构成的三角形与△ABC相似，写出所有符合条件的三角形：____．三、解答题4.（2018四川宜宾期中，21，★☆☆）已知，如图所示，AF⊥BC，CE⊥AB，垂足分别是F，E，试证明：（1）△BAF∽△BCE；（2）△BEF∽△BCA.五年中考全练选择题（2016河北中考，15，★☆☆）如图，△ABC中，∠A= 78°，AB=4，AC=6，将△ABC沿下列选项中的虚线剪下，剪下的阴影三角形与原三角形不相似的是（）A. B. C. D.核心素养全练1．如图，△ABC 中，∠ACB= 90°，AC=3，BC=4，点D 是AB 的中点，点E 在DC 的延长线上，且CE=CD ，过点B 作BF ∥DE 交AE 的延长线于点F ，交AC 的延长线于点G ．(1)求证：AB =BG ；(2)若点P 是射线BG 上的一点，试确定点P 的位置，使△BCP 与△BCD 相似．2．如图，在△ABC 中，已知AB=AC=5，BC=6，且△ABC ≌△DEF ，将△DEF 与△ABC 重合在一起，△ABC 不动，△DEF 运动，并满足：点E 在边BC 上沿B 到C 的方向运动，且DE 始终经过点A ，EF 与AC 交于M 点．(1)求证：△ABE ∽△ECM ；(2)探究：在△DEF 运动过程中，重叠部分能否构成等腰三角形？若能，求出此时BE 的长；若不能，请说明理由.25.4相似三角形的判定基础闯关全练1．C 由题意知：在△BCD 和△ACB 中，∠C= ∠C （公共角），∠DBC= ∠A （已知），根据两角对应相等的两个三角形相似，可得△BCD ∽△ACB ，可得，可由BC=，AC=3，求得CD=2．故选C ．2．答案解析在Rt △ABC 中，∵∠C= 90°， ∴．∵∠C=∠E=90°，∠BAC=∠DAE.∴△ABC ∽△ADE ．∴即，∴AD=．3．C ∵在△ACD 和△ABC 中，∠A= ∠A ， ∴根据两边对应成比例，且夹角相等的两个三角形相似，得出添加的条件是ACAD AB AC ，即AC ²=AD ·AB ．故选C ．4.C ∵∠BAC= ∠D ，，∴△ABC ∽△DEA ，选项A 、B 、D 中的条件均不满足题意，故选C ．5.B 如图，在AC上截取AD=BC，连接BD.∵，AD=BC,AB=AC,∴，∴点D是线段AC的黄金分割点，∴AD²=CD·CA,∴BC²=CD·CA,∴．∵∠C=∠C.∴△BCD∽△ACB,∴∠BDC= ∠ABC，∠DBC= ∠A.∵AB=AC．∴∠ABC= ∠C= ∠BDC.∴AD= BD,∴∠A= ∠ABD,设∠A=x，则∠C= ∠ABC=2∠A=2x．∴x+2x+2x= 180°，x=36°，故选B．6．解析(1)△ADE∽△ABC．因为，并且∠A=∠A，故根据两边对应成比例，且夹角相等的两个三角形相似，可知△ADE∽△ABC．(2)△ADE与△ABC不一定相似，当△ABC是等腰三角形，并且AB=AC时，有，又∠A是公共角，则△ADE∽△ABC．7.B ∵小正方形的边长均为1，∴△ABC三边长分别为2，，．A中三角形各边的长分别为，3，；B中三角形各边的长分别为，1，；C中三角形各边的长分别为1，，；D中三角形各边的长分别为2，，．只有B项中的三角形的三边长与△ABC的三边长对应成比例，故两个三角形相似，故选B．能力提升全练D当时，△APC∽△ACB；当∠APC=∠ACB时，因为∠A= ∠A，所以△APC∽△ACB;当AC²=AP·AB，即AC：AB=AP：AC时，因为∠A= ∠A，所以△APC∽△ACB；当AB·CP=AP·CB，即时，它们的夹角不相等，所以不能判断△APC和△ACB相似，故选D．三年模拟全练一、选择题1．C A项，∠ADE= ∠C，∠A= ∠A，则△ADE∽△ACB，故本选项不符合题意；B项，∠B= ∠AED，∠A=∠A，则△ADE∽△ACB，故本选项不符合题意；C项，，此时不能确定∠ADE与∠ABC是否相等，故不能确定△ADE与△ABC相似，故本选项符合题意；D项，，∠A=∠A，则△ADE∽△ACB，故本选项不符合题意．故选C2.D三角形纸片ABC中，AB=8，BC=4，AC=6．A项，，∠A= ∠A，，则沿虚线剪下的阴影部分的三角形与△ABC不相似，故A项错误；B项，，∠A= ∠A，，则沿虚线剪下的阴影部分的三角形与△ABC不相似，故B项错误；C项，，∠A= ∠A，，则沿虚线剪下的阴影部分的三角形与△ABC不相似，故C项错误；D项，，∠B=∠B，，则沿虚线剪下的阴影部分的三角形与△ABC相似，故D项正确，故选D．二、填空题3．答案△DP₂P₅，△DP₂P₄，△DP₄P₅解析AC=5，AB=20，BC=25，DP₅=，DP₂=，P₂P₅=，∵，∴△ACB∽△DP₅P₂．同理可找到△DP₂P₄，△DP₄P₅和△ACB相似。

冀教版九年级数学上册25.4 相似三角形的判定定理3同步练习题(无答案)

25.4相似三角形的判定定理31．在△ABC与△A′B′C′中，AB＝9 cm，BC＝8 cm，CA＝5 cm，A′B′＝4.5 cm，B′C′＝2.5 cm，C′A′＝4 cm，则下列说法错误的是()A．△ABC和△A′B′C′相似B．AB和A′B′是对应边C．∠C和∠C′是对应角D．BC和B′C′是对应边2．如图，在4×4的正方形网格中，点上，则与图25－4－15中△ABC相似的三角形所在的网格图形是()3．有甲、乙两个三角形木框，甲三角形木框的三边长分别为1，2，5，乙三角形木框的三边长分别为5，5，10，则甲、乙两个三角形木框()A．一定相似B．一定不相似C．不一定相似D．无法判断是否相似4．下列各选项不能判断△ABC与△DEF相似的是()A．∠C＝∠D＝90°，∠B＝32°，∠E＝58°B．∠C＝∠D＝90°，AB＝15，BC＝9，FE＝5，DF＝4C．∠C＝∠D＝90°，AC＝15，BC＝9，ED＝5，FD＝3D．∠C＝∠D＝90°，AC＝15，BC＝9，EF＝5，DF＝35．在△ABC与△A′B′C′中，有下列条件：①ABA′B′＝BCB′C′；②BCB′C′＝ACA′C′；③∠A＝∠A′；④∠C＝∠C′.如果从中任取两个条件组成一组，那么能判定△ABC∽△A′B′C′的共有() A．1组B．2组C．3组D．4组6．如图所示，要使△ABC∽△DEF，则x＝________．7．要判定△ABC∽△A′B′C′，已知ABA′B′＝BCB′C′，还要添加条件：______________(填角的关系)或________________(填边的关系)．8在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，当AC＝3，AB＝5，DE＝10，EF＝8时，Rt△ABC和Rt△DEF________(填“相似”或“不相似”)．9．如图，AB⊥BC于点B，AC⊥CD于点C，AB＝4，AC＝6，当AD＝________时，△ABC∽△ACD.10．如图，点B ，A ，E 在同一条直线上，AD ⊥BD ，CE ⊥AE ，垂足分别为D ，E ，AB ＝3CA ，BD ＝3AE .求证：△ABD ∽△CAE .11．如图，O 是△ABC 外的一点，分别在射线OA ，OB ，OC 上取一点A ′，B ′，C ′，使得OA ′OA ＝OB ′OB ＝OC ′OC ＝3，连接A ′B ′，B ′C ′，A ′C ′，所得△A ′B ′C ′与△ABC 是否相似？请证明你的结论．12．在方格纸中，每个小方格的顶点称为格点，以格点为顶点的三角形叫做格点三角形．在如图25－4－21所示的5×5的方格纸中，以A ，B 为顶点作格点三角形与△OAB 相似(相似比不能为1)，则另一个顶点C 的坐标为________________________________．图25－4－2113．如图，网格图中每个小方格都是边长为1的正方形．若A，B，C，D，E，F都是格点，求证：△ABC∽△DEF.14．如图所示，已知AB∶AD＝BC∶DE＝AC∶AE，请猜想∠ABD与∠ACE的关系，并说明理由．15．如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，P1，P2，P3，P4，P5是△DEF边上的5个格点，请按要求完成下列各题：(1)求证：△ABC是直角三角形；(2)判断△ABC和△DEF是否相似，并说明理由；(3)画一个三角形，使它的3个顶点为P1，P2，P3，P4，P5中的3个格点，并且与△ABC 相似(要求：不写作法与证明)．。

初中数学冀教版九年级上册第二十五章图形的相似25.4 相似三角形的判定-章节测试习题(5)

章节测试题1.【题文】如图，在△ABC中，AC＝8cm，BC＝16cm，点P从点A出发，沿着AC边向点C以1cm/s的速度运动，点Q从点C出发，沿着CB边向点B以2cm/s的速度运动，如果P与Q同时出发，经过几秒△PQC和△ABC相似？【答案】4秒或秒.【分析】本题考查了利用相似三角形的性质对应边成比例求解，但发现对应边不明确，需要分两种情况解决是本题的关键．本题可设经过x秒△PQC和△ABC相似，先求出CP=8-x，CQ=2x，再利用相似三角形性质对应边成比例列式求解即可得到答案，∵对应边不明确，答案要分两种情况①当CP与CA是对应边时，②当CP与BC 是对应边时．【解答】设经过x秒，两三角形相似，则CP=AC-AP=8-x，CQ=2x，①当CP与CA是对应边时，，即，解得x=4秒；②当CP与BC是对应边时，，即，解得x=秒；故经过4或秒，两个三角形相似．2.【题文】如图，AD是Rt△ABC斜边上的高，若AB=4cm，BC=10cm，求BD的长．【答案】1.6．【分析】本题考查的是相似的判定以及相似的性质，发现本题中得相似并利用性质列出比例式是解决本题的关键.先判断Rt△ABC∽Rt△DBA，再根据相似的性质对应边成比例，得到=，进而代入数据求出BD【解答】∵在Rt△ABC与Rt△DBA中∠ADB=∠BAC，∠B=∠B，∴Rt△ABC∽Rt△DBA，∴=，∴AB2=BD•BC，则==1.6．3.【题文】定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB 的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．【答案】（1）见解答；（2）AD=.【分析】（1）判断△ABC∽△BDC，根据对应边成比例可得出答案；（2）根据（1）列出方程即可求出AD的长度．【解答】（1）∵∠A=36°，AB=AC，∴∠ABC=∠ACB=72°．∵BD平分∠ABC，∴∠CBD=∠ABD=36°，∠BDC=72°．∴AD=BD，BC=BD．∴△ABC∽△BDC．∴，即．∴AD2=AC•CD．∴点D是线段AC的黄金分割点．（2）由（1）AD2=AC•CD，即AD2=AC•（AC﹣AD），AD2=1﹣AD，AD2+AD﹣1=0．解得AD=（舍去负值）．∴AD=．4.【题文】如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t 秒．（1）当t为何值时，AD＝AB，并求出此时DE的长度；（2）当△DEG与△ACB相似时，求t的值．【答案】（1）当t=1时，AD=AB，AE=1；（2）当t=或或或时，△DEG与△ACB 相似．【分析】本题第一问比较简单，第二问的讨论较多，关键是要理清头绪，相似三角形的讨论，和线段的大小的选择，做题时要分清，分细．（1）根据勾股定理得出AB=5，要使AD=AB=5，∵动点D每秒5个单位的速度运动，∴t=1；（2）当△DEG与△ACB相似时，要分两种情况讨论，根据相似三角形的性质，列出比例式，求出DE的表达式时，要分AD＜AE和AD＞AE两种情况讨论．【解答】（1）∵∠ACB=90°，AC=3，BC=4，∴AB==5．∵AD=5t，CE=3t，∴当AD=AB时，5t=5，即t=1；∴AE=AC+CE=3+3t=6，DE=6﹣5=1．（2）∵EF=BC=4，G是EF的中点，∴GE=2．当AD＜AE（即t＜）时，DE=AE﹣AD=3+3t﹣5t=3﹣2t，若△DEG与△ACB相似，则或，∴或，∴t=或t=；当AD＞AE（即t＞）时，DE=AD﹣AE=5t﹣（3+3t）=2t﹣3，若△DEG与△ACB相似，则或，∴或，解得t=或t=；综上所述，当t=或或或时，△DEG与△ACB相似．5.【答题】如图，能推得DE∥BC的条件是（）A. AD∶AB=DE∶BCB. AD∶DB=DE∶BCC. AE∶AC=AD∶DBD. AD∶DB=AE∶EC【答案】D【分析】本题考查三角形相似的判定以及平行线的判定．【解答】A选项不一定能推出∠ADE=∠B，故不一定能推得DE∥BC，∴不符合题意．根据平行线分线段成比例定理B，C选项也不能推得DE∥BC，故不符合题意．D选项能推出AD：AB=AE：AC，∠A是公共角，△ADE∽△ABC，对应角∠ADE=∠B，能推得DE∥BC，选D．6.【答题】如图，已知点D、E分别在△ABC的边AC、AB上，下列条件中，不能推出△ABC∽△ADE的是（）A. B. ∠B=∠ADE C. D. ∠C=∠AED【答案】C【分析】本题考查相似三角形的判定.【解答】∵∠DAE=∠BAC，∴当∠AED=∠C或∠ADE=∠B时，△ABC∽△AED；当时，△ABC∽△AED．选C．7.【答题】如图，△ABC中，∠BAC＝90°，AD⊥BC于D，若AB＝2，BC＝4，则CD的长是（）A. 1B. 4C. 3D. 2【答案】C【分析】本题考查相似三角形的判定和性质.先由∠BAC＝90°，AD⊥BC，∠B＝∠B证得△ABD∽△CBA，再根据相似三角形的性质求得BD的长，即可求得结果．【解答】∵∠BAC＝90°，AD⊥BC，∠B＝∠B，∴，∵AB＝2，BC＝4，∴，解得，∴CD＝BC-BD＝3，选C．8.【答题】如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列比例式中错误的是（）A. B. C. D.【答案】C【分析】本题考查相似三角形的判定和性质.【解答】∵四边形ABCD是平行四边形，∴CD∥AB，AD∥BC，CD=AB，AD=BC，∴，故A正确，选项不符合题意；∴故B正确，B选项不符合题意；∴，错误，C选项符合题意；∴，故D正确，D选项不符合题意．选C．9.【答题】如图，已知，那么添加下列一个条件后，仍然无法判定的是（）A. B. C. D.【答案】A【分析】本题考查了相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．先根据∠DAB=∠CAE得出∠DAE=∠BAC，再由相似三角形的判定定理对各选项进行逐一判定即可．【解答】∵∠DAB=∠CAE，∴∠DAE=∠BAC．A．∵，∠B与∠D的大小无法判定，∴无法判定△ABC∽△ADE，故本选项正确；B．∵，∴△ABC∽△ADE，故本选项错误；C．∵∠B=∠D，∴△ABC∽△ADE，故本选项错误；D．∵∠C=∠AED，∴△ABC∽△ADE，故本选项错误．选A．10.【答题】如图，△ABC中，D是AC的中点，E是BC延长线上一点，过A作AH∥BE，连结ED并延长交AB于F，交AH于H，如果AB=4AF，EH＝8，则DF的长为______．【答案】2【分析】本题考查相似三角形的判定与性质．【解答】∵AB=4AF，AH∥BE，∴△AFH∽△BFE.∴AF：AB=HF：HE=1：4.∴HF=2．∵AH∥BE，D是AC的中点，∴点D也是EH的中点．∴HD=EH=4．∴DF=HD-HF=2．11.【答题】如图，点D、E分别在AB、AC上，且∠ABC＝∠AED．若DE＝4，AE＝5，BC＝8，则AB的长为______.【答案】10【分析】本题考查相似三角形的判定和性质.【解答】在△ABC和△AED中，∵∠ABC=∠AED，∠BAC=∠EAD，∴△AED∽△ABC，又∵DE=4，AE=5，BC=8，∴AB=10．故答案为10．12.【答题】如图，将两块直角三角形的一条直角边重合叠放，已知AC=BC=+1，∠D=60°，则两条斜边的交点E到直角边BC的距离是______．【答案】1【分析】本题考查相似三角形的判定与性质，角平分线的性质，勾股定理．过点E作EH⊥BC，垂足为H，根据AC=BC=+1，∠D=60°，得∠BCD=30°，求得BD，可证明△BDE∽△ACE，得，从而得出BE和AE，再由∠ACB=90°，得△BHE∽△BCA，，从而得出EH即可．【解答】∵∠CBD=90°，∠D=60°，∴∠BCD=30°，∴∠ACE=60°，∵AC=BC=+1，∴BD=，AB=，∵∠AEC=∠BED，∴△BDE∽△ACE，∴，∴，∴BE=，AE=，∵∠ACB=90°，∴△BHE∽△BCA，∴，∴，∴EH=1，故答案为1．13.【答题】如图，正方形ABCD的边长为3，延长CB至点M，使S△ABM=，过点B 作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为______．【答案】【分析】本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．先根据三角形的面积公式求出BM的长，由条件可证得△ABN∽△BNM∽△ABM，且可求得AM=，利用对应线段的比相等可求得AN和MN，进一步可得到=，且∠CAM=∠NAO，可证得△AON∽△AMC，利用相似三角形的性质可求得ON．【解答】∵正方形ABCD的边长为3，S△ABM=，∴BM=，∵AB=3，BM=1，∴AM=，∵∠ABM=90°，BN⊥AM，∴△ABN∽△BNM∽△AMB，∴AB2=AN×AM，BM2=MN×AM，∴AN=，MN=，∵AB=3，CD=3，∴AC=3，∴AO=，∵=，=，∴=，且∠CAM=∠NAO，∴△AON∽△AMC，∴==，∴ON=．故答案为．14.【题文】已知：如图，Rt△ABC中，CD是斜边AB上的高．求证：AC2=AD·AB【答案】见解答．【分析】本题考查相似三角形的判定与性质.根据相似三角形的判定定理得出△ACD∽△ABC，再根据相似三角形的对应边成比例即可得出结论．【解答】∵△ABC是直角三角形，CD⊥AB，∴∠A+∠B=90°，∠A+∠ACD=90°，∴∠B=∠ACD，∴△ACD∽△ABC，∴，∴AC2=AD•AB．15.【答题】下列说法中，不正确的是（）A. 直角边长分别是6、4和4.5、3的两个直角三角形相似B. 底角为40°的两个等腰三角形相似C. 一个锐角为30°的两个直角三角形相似D. 有个角为30°的两个等腰三角形相似【答案】D【分析】本题考查了相似三角形的判定，熟悉相似三角形的判定是解题关键．根据相似三角形的判定即可解题．【解答】A.直角边长分别是6、4和4.5、3的两个直角三角形相似，∵对应边比=，∴正确；B.底角为40°的两个等腰三角形相似，∵有两个角对应相等的三角形是相似三角形，∴正确；C.一个锐角为30°的两个直角三角形相似，∵有两个角对应相等的三角形是相似三角形，∴正确；D.有个角为30°的两个等腰三角形不一定相似，∵30°可能是顶角（此时三角形是锐角三角形）也可能是底角（此时三角形是钝角三角形），∴三角形不一定相似．选D．16.【答题】如图，△ABC中，∠BCD＝∠A，DE∥BC，与△ABC相似的三角形（△ABC 自身除外）的个数是（）A. 1个B. 2个C. 3个D. 4个【答案】B【分析】本题考查相似三角形的判定，有两组角相等的两个三角形相似．【解答】∵DE∥BC，∴△ADE∽△ABC，∠BCD=∠A，∠B=∠B，∴△BCD∽△ABC，∴有两个与△ABC相似的三角形，选B．17.【答题】如图，若D、E分别为△ABC中AB、AC边上的点，且∠AED=∠B，AD=3，AC=6，DB=5，则AE的长度为（）A. B. C. D. 4【答案】D【分析】本题考查了相似三角形的判定及性质．有两角对应相等的两个三角形相似．相似三角形的三边对应成比例．根据相似三角形的判定首先证出△ADE∽△ACB，然后根据相似三角形的性质得出=，从而求出AE的长度．【解答】∵∠A=∠A，∠AED=∠B，∴△ADE∽△ACB，∴=，又∵AD=3，AC=6，DB=5，∴AB=AD+DB=8，∴AE=8×3÷6=4．选D．18.【答题】如图，锐角△ABC的高CD和BE相交于点O，图中与△ODB相似的三角形有（）A. 1个B. 2个C. 3个D. 4个【答案】C【分析】本题考查相似三角形的判定.【解答】∵∠BDO=∠BEA=90°，∠DBO=∠EBA，∴△BDO∽△BEA，∵∠BOD=∠COE，∠BDO=∠CEO=90°，∴△BDO∽△CEO，∵∠CEO=∠CDA=90°，∠ECO=∠DCA，∴△CEO∽△CDA，∴△BDO∽△BEA∽△CEO∽△CDA．选C．19.【答题】如图，正方形ABCD的对角线AC，BD相交于点O，AB=，E为OC上一点，OE=1，连接BE，过点A作AF⊥BE于点F，与BD交于点G，则BF的长是（）A. B. C. D. 【答案】A【分析】本题考查相似三角形的判定和性质.【解答】∵四边形ABCD是正方形，AB=，∴∠AOB=90°，AO=BO=CO=3．∵AF⊥BE，∴∠EBO=∠GAO．在△GAO和△EBO中，∵∠GAO=∠EBO，AO=BO，∠AOG=∠BOE，∴△GAO≌△EBO，∴OG=OE=1，∴BG=2．在Rt△BOE中，BE==，∵∠BFG=∠BOE=90°，∠GBF=∠EBO，∴△BFG∽△BOE，∴，即，解得BF=．选A．20.【题文】如图，在△ABC中，点D，E分别在边AB，AC上，若DE∥BC，DE=2，BC=3，求的值．【答案】.【分析】本题考查相似三角形的判定和性质.【解答】∵DE∥BC，∴△ADE∽△ABC．∵DE＝2，BC＝3，∴.。

冀教版数学九年级上册《25.4 相似三角形的判定(二)》.docx

《25.4 相似三角形的判定（二）》一、选择题1．如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA：OC=OB：OD，则下列结论中一定正确的是（）A．①与②相似B．①与③相似C．①与④相似D．②与④相似2．已知△ABC如图，则下列4个三角形中，与△ABC相似的是（）A．B．C．D．3．能判定△ABC∽△A′B′C′的条件是（）A．=，∠B=∠B′B．=，∠B=∠B′C．=，∠A=∠A′D．=，∠A=∠A′4．如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（）A．B．C．∠B=∠D D．∠C=∠AED二、填空题5．（6分）如图，若AC2=CD•CB，则△______∽△______，∠ADC=______．6．在△ABC中，AB=5，AC=10，∠A=40°，在△DEF中，DE=6，DF=12，填上一个合适的条件______，能使△ABC∽△DEF．7．如图所示，AB，CD交于点O，且OC=45，OD=30，OB=36，当OA=______时，△AOC∽△BOD；当OA=______时，△AOC∽△DOB．8．如图，B，C分别在△ADE的边AD，AE上，且AC=6，AB=5，EC=4，DB=7，则BC：DE=______．9．如图，BD平分∠ABC，且AB=4，BC=6，则当BD=______时，△ABD∽△DBC．10．如图，△ABC中，CD⊥AB于D，AD=8，CD=6，则当BD=______时，△ADC∽△CDB，∠ACB=______°．11．如图，在△ABC中，P是AC上一点，连接BP．要使△ABP∽△ACB，则必须有∠ABP=______或∠APB=______或=______．12．如图，在三角形ABC中，AB=24，AC=18，D是AC上一点AD=12，在AB上取一点E，使A、D、E三点组成的三角形与ABC相似，则AE=______．13．在方格纸中，每个小格的顶点称为格点，以格点为顶点的三角形叫做格点三角形．在如图5×5的方格纸中，以A、B为顶点作格点三角形与△OAB相似（相似比不能为1），则另一个顶点C的坐标为______．三、解答题14．如图，判断两个三角形是否相似，并求出x和y．15．如图，在△ABC中，∠C=90°，D、E分别为AB、AC边上的两点，且AD•AB=AE•AC．求证：DE⊥AB．16．已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点．求证：△ADQ∽△QCP．四、综合运用题17．如图，在△ABC中，AB=8cm，BC=16cm，点P从点A开始沿AB向B以2cm/s的速度移动，点Q 从点B开始沿BC向C点以4cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒钟△PBQ与△ABC相似？《25.4 相似三角形的判定（二）》答案一、选择题1．B；2．C；3．C；4．B；二、填空题5．ACD；BCA；∠BAC；6．∠D=40°；7．54；37.5；8．；9．2；10．；90；11．∠C；∠ABC；；12．16或9；13．（5，2）或（4，4）；初中数学试卷桑水出品。

初中数学冀教版九年级上册第二十五章图形的相似25.4 相似三角形的判定-章节测试习题(7)

章节测试题1.【题文】如图，在平行四边形ABCD中，点E在边BC上，连结AE并延长，交对角线BD于点F、DC的延长线于点G．如果，求的值．【答案】【分析】本题考查了相似三角形的判定与性质以及平行四边形的性质，利用相似三角形的性质，找出AE EF及GE AE是解题的关键．由平行四边形的性质可得出AD∥BC，AD＝BC，由AD∥BE可得出△BEF∽△DAF，利用相似三角形的性质结合可得出AE EF，由CE∥AD可得出△CEG∽DAG，利用相似三角形的性质可得出GE GA AE，代入AE EF即可得出．【解答】∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC．∵AD∥BE，∴△BEF∽△DAF，∴．又∵BC＝BE+CE，，∴BE BC DA，∴EF AF，∴AE EF EF．∵CE∥AD，△CEG∽DAG，∴，∴GE GA，∴GE AE EF EF，∴．2.【题文】已知，如图，在平行四边形ABCD中，M是BC边的中点，E是边BA延长线上的一点，连接EM，分别交线段AD于点F、AC于点G．（1）求证：△AFG∽△CMG；（2）求证：．【答案】见解答.【分析】本题考查平行四边形的性质，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识．（1）可得出∠FAG＝∠MCG，又∠AGF＝∠CGM，则结论得证；（2）由（1）可得出，证明△AEF∽△BEM，可得出，由BM＝CM，则结论得出．【解答】（1）证明：∵AD∥BC，∴∠FAG＝∠MCG，∵∠AGF＝∠CGM，∴△AFG∽△CMG；（2）证明：∵△AFG∽△CMG，∴.∵AD∥BC，∴△AEF∽△BEM，∴.又∵CM＝BM，∴，∴．3.【答题】如图，D、E分别是△ABC的边BC、AB上的点，AD、CE相交于点F，AE EB，BD BC，则CF：EF＝______．【答案】12【分析】本题考查的是相似三角形的判定和性质，掌握作辅助线构造相似三角形的一般方法是解题的关键．作EH∥BC，根据△AEH∽△ABD，得到，证明△CFD∽△EFH，根据相似三角形的性质列出比例式，计算即可．【解答】作EH∥BC交AD于H，则△AEH∽△ABD，∴，∵BD BC，∴CD＝2BD，∴，∵EH∥BC，∴△CFD∽△EFH，∴12，即CF：EF＝12，故答案为12．4.【答题】如图，AD是△ABC的中线，点E是线段AD上的一点，且AE AD，CE交AB于点F．若AF＝2cm，则AB＝______cm．【答案】10【分析】本题考查了相似三角形的判定与性质的运用，过A作AG∥BC，构造相似三角形是解决此题的关键．过A作AG∥BC，交CF的延长线于G，依据相似三角形的对应边成比例，即可得到，进而得出BF＝4AF＝8cm，可得AB的长度．【解答】如图所示，过A作AG∥BC，交CF的延长线于G，∵AE AD，AG∥BC，∴△AEG∽△DEC，∴，又∵AD是△ABC的中线，∴BC＝2CD，∴，∵AG∥BC，∴△AFG∽△BFC，∴，∴BF＝4AF＝8cm，∴AB＝AF+BF＝10cm，故答案为10．5.【答题】如图，等边三角形ABC中，AB＝3，点D是CB延长线上一点，且BD＝1，点E在直线AC上，当∠BAD＝∠CDE时，AE的长为______．【答案】2或【分析】本题考查了等边三角形的性质、相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造相似三角形解决问题．分两种情形分别画出图形，利用相似三角形的性质解决问题即可．【解答】∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，AC＝BC＝AB＝3，∴∠ABD＝120°，分两种情况：①当点E在边AC上时．作EF∥AB交BC于F，如图1所示：则△EFC是等边三角形．∴∠CFE＝60°，EF＝CF＝CE，∴∠BFE＝120°＝∠ABD，∵∠BAD＝∠CDE，∴△ABD∽△DFE，∴，即，∴DF＝3EF，∴DF＝3CF，∴CD＝4CF，∵BC＝3，BD＝1，∴CD＝BC+BD＝4，∴CF＝1，∴CE＝1，∴AE＝AC﹣CE＝2；②点E在AC的延长线上时．如图2所示：∵∠ABD＝∠DCE＝120°，∠BAD＝CDE，∴△ABD∽△DCE，∴，即，解得CE，∴AE＝AC+CE＝3；综上所述，当∠BAD＝∠CDE时，AE的长为2或；故答案为2或．6.【答题】如图，在△ABC中，∠ACB＝90°，CD是AB边上的高．如果BD＝4，CD＝6，那么BC：AC是（）A. 3：2B. 2：3C.D. ．【答案】B【分析】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题．只要证明△ACD∽△CBD，可得，由此即可解决问题．【解答】∵∠ACB＝90°，CD是AB边上的高，∴∠ADC＝∠CDB＝∠ACB＝90°，∵∠A+∠B＝90°，∠A+∠ACD＝90°，∴∠ACD＝∠B，∴△ACD∽△CBD，∴，∴，选B．7.【答题】边长为1的正方形ABCD，在BC边上取一动点E，连接AE，作EF⊥AE，交CD边于点F，若CF的长为，则CE的长为______．【答案】或【分析】本题考查了相似三角形的判定与性质、正方形的性质以及三角形内角和定理，利用“两角对应相等的三角形相似”找出△ABE∽△ECF是解题的关键．由正方形的性质结合三角形内角和定理可得出∠BAE+∠AEB＝90°，结合∠AEB+∠CEF＝90°可得出∠BAE＝∠CEF，由∠B＝∠C，∠BAE＝∠CEF可证出△ABE∽△ECF，再利用相似三角形的性质可求出CE的长．【解答】∵四边形ABCD为正方形，∴∠B＝∠C＝90°，∴∠BAE+∠AEB＝90°．∵EF⊥AE，∴∠AEF＝90°，∴∠AEB+∠CEF＝90°，∴∠BAE＝∠CEF，∴△ABE∽△ECF，∴，即，∴CE或CE．故答案为：或．8.【答题】如图，AC是矩形ABCD的对角线，过点B作BE⊥AC于点E，BE的延长线交AD于点F，若DF＝EF，BC＝2，则AF的长为______．【答案】【分析】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定．设AF＝x，∴FD＝2﹣x，由题意可知：EF＝FD＝2﹣x，易证△AFE∽△CBE，∴BE，再证明△AFE∽△BFA，根据相似三角形的性质即可列出方程求出x的值．【解答】设AF＝x，∴FD＝2﹣x，∴EF＝FD＝2﹣x，∵AD∥BC，∴△AFE∽△CBE，∴，∴，∴BE，∴BF＝BE+EF，∵∠AFE＝AFB，∠AEF＝∠BAF＝90°，∴△AFE∽△BFA，∴AF2＝EF•BF，∴x2•（2﹣x），解得x1，故答案为1．9.【答题】如图，在△ABC与△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE，连接BD、CE，若AC：BC＝3：4，则BD：CE为（）A. 5：3B. 4：3C. ：2D. 2：【答案】A【分析】本题考查相似三角形的判定和性质，关键是根据相似三角形的判定得出△ABC与△ADE相似．根据相似三角形的判定得出△ABC与△ADE相似，利用相似三角形的性质得出∠BAC＝∠DAE，进而证明△AEC与△ABD相似，利用相似三角形的性质解答即可．【解答】∵∠ACB＝∠AED＝90°，∠ABC＝∠ADE，∴△ABC∽△ADE，∴∠BAC＝∠DAE，，∵∠BAC+∠BAE＝∠DAE+∠BAE，即∠CAE＝∠BAD，∵，∴△ACE∽△ABD，∴，∵AC：BC＝3：4，∠ACB＝∠AED＝90°，∴AC：BC：AB＝3：4：5，∴BD：CE＝5：3，选A．10.【答题】如图，AB＝3，AC＝2，BC＝4，AE＝3，AD＝4.5，DE＝6，∠BAD＝20°，则∠CAE的度数为（）A. 10°B. 20°C. 40°D. 无法确定【答案】B【分析】本题考查的是相似三角形的判定和性质，掌握三边对应成比例的两个三角形相似是解题的关键．证明△ABC∽△ADE，根据相似三角形的性质得到∠BAC＝∠DAE，结合图形解答即可．【解答】∵AB＝3，AC＝2，BC＝4，AE＝3，AD＝4.5，DE＝6，∴，∴△ABC∽△ADE，∴∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠CAE＝∠BAD＝20°，选B．11.【答题】如图，△ABC∽△ADE，∠BAC＝∠DAE＝90°，AB与DE交于点O，AB＝4，AC＝3，F是DE的中点，连接BD，BF，若点E是射线CB上的动点，下列结论：①△AOD∽△FOB，②△BOD∽△EOA，③∠FDB+∠FBE＝90°，④BF AE，其中正确的是（）A. ①②B. ③④C. ②③D. ②③④【答案】D【分析】本题考查相似三角形的判定和性质，直角三角形斜边中线的性质，勾股定理等知识，解题的关键是熟练掌握基本知识．首先证明△AOD∽△EOB，推出△BOD∽△EOA，再证明∠DBE＝90°，可得②③正确，利用直角三角形斜边中线的性质即可判断④正确．【解答】∵△ABC∽△ADE，∴∠ADO＝∠OBE，∵∠AOD＝∠BOE，∴△AOD∽△EOB，∴，∴，∵∠BOD＝∠AOE，∴△BOD∽△EOA，故②正确，∵△AOD∽△EOB，△BOD∽△EOA，∴∠ADO＝∠EBO，∠AEO＝∠DBO，∵∠ADO+∠AEO＝90°，∴∠DBE＝∠DBO+∠EBO＝90°，∵DF＝EF，∴FD＝FB＝FE，∴∠FDB＝∠FBD，∴∠FDB+∠FBE＝∠FBD+∠FBE＝90°，故③正确，在Rt△ABC中，∵AB＝4，AC＝3，∴BC5，∵△ABC∽△ADE，∴，∵BF DE，∴，∴BF AE，故④正确，∵∠ADO＝∠OBE，∴无法判断△AOD∽△FOB，故①错误．选D．12.【题文】已知：如图，在△ABC中，点D、E分别在边BC、AC上，点F在DE的延长线上，AD＝AF，AE•CE＝DE•EF．（1）求证：△ADE∽△ACD；（2）如果AE•BD＝EF•AF，求证：AB＝AC．【答案】见解答.【分析】本题考查等腰三角形的判定和性质，相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题．（1）由AE•CE＝DE•EF，推出△AEF∽△DEC，可得∠F＝∠C，再证明∠ADF＝∠C，即可解决问题；（2）欲证明AB＝AC，利用相似三角形的性质证明∠B＝∠C即可；【解答】证明：（1）∵AD＝AF，∵AE•CE＝DE•EF，∴，又∵∠AEF＝∠DEC，∴△AEF∽△DEC，∴∠F＝∠C，∴∠ADF＝∠C，又∵∠DAE＝∠CAD，∴△ADE∽△ACD．（2）∵AE•BD＝EF•AF，∴，∵AD＝AF，∴，∵∠AEF＝∠EAD+∠ADE，∠ADB＝∠EAD+∠C，∴∠AEF＝∠ADB，∴△AEF∽△ADB，∴∠F＝∠B，∴∠C＝∠B，∴AB＝AC．13.【答题】如图，在△ABC中，AB＝AC＝6，D是AC中点，E是BC上一点，BE，∠AED＝∠B，则CE的长为（）A. B. C. D.【答案】C【分析】本题考查相似三角形的判定和性质，等腰三角形的性质等知识，解题的关键是正确寻找相似三角形解决问题．证明△BAE∽△CED，推出可得结论．【解答】∵AB＝AC，∴∠B＝∠C，∵∠AEC＝∠AED+∠DEC＝∠B+∠BAE，∠AED＝∠B，∴∠DEC＝∠BAE，∴△BAE∽△CED，∴，∵AB＝AC＝6，AD＝DC＝3，BE，∴，∴CE，选C．14.【答题】如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°，BP＝2，CD＝1，则△ABC的边长为（）A. 3B. 4C. 5D. 6【答案】B【分析】本题考查了相似三角形的性质和判定，等边三角形的性质，三角形的内角和定理的应用，关键是推出△ABP∽△PCD，主要考查了学生的推理能力和计算能力．根据等边三角形性质求出AB＝BC＝AC，∠B＝∠C＝60°，推出∠BAP＝∠DPC，即可证得△ABP∽△PCD，据此解答即可．【解答】∵△ABC是等边三角形，∴AB＝BC＝AC，∠B＝∠C＝60°，∴∠BAP+∠APB＝180°﹣60°＝120°，∵∠APD＝60°，∴∠APB+∠DPC＝180°﹣60°＝120°，∴∠BAP＝∠DPC，即∠B＝∠C，∠BAP＝∠DPC，∴△ABP∽△PCD；，∵BP＝2，CD＝1，∴，∴AB＝4，∴△ABC的边长为4．选B．15.【题文】如图，已知在△ABC中，AB＝AC＝6，BC＝5，D是AB上一点，BD＝2，E 是BC上一动点，联结DE，并作∠DEF＝∠B，射线EF交线段AC于F．（1）求证：△DBE∽△ECF；（2）当F是线段AC中点时，求线段BE的长；（3）联结DF，如果△DEF与△DBE相似，求FC的长．【答案】（1）见解答；（2）2或3；（3）2或．【分析】本题考查了相似三角形的判定和性质，等腰三角形的性质，平行线的判定和性质，角平分线的性质，正确的作出辅助线是解题的关键．（1）根据等腰三角形的性质得到∠B＝∠C，由三角形的内角和和平角的定义得到∠DEF＝∠B，根据相似三角形的判定定理即可得到结论；（2）根据相似三角形的性质得到结论；（3）当∠BED＝∠EDF，得到DF∥BC，根据平行线的性质得到∠ADF＝∠B，∠AFD ＝∠C，根据等腰三角形的性质得到CF＝2；当∠DFE＝∠BED，推出点E在∠BDF 与∠DFC的角平分线上，过E作EM⊥AB于M，EN⊥AC于N，EG⊥DF于G，连接AE，得到AE是∠BAC的角平分线，根据相似三角形的性质即可得到结论．【解答】（1）∵AB＝AC＝6，∴∠B＝∠C，∵∠BDE＝180°﹣∠B﹣∠BED，∠CEF＝180°﹣∠DEF﹣∠BED，∵∠DEF＝∠B，∴∠BDE＝∠CEF，∴△DBE∽△ECF；（2）∵△DBE∽△ECF，∴，∵F是线段AC中点，∴CF AC＝3，∴，∴BE＝2或3；（3）∵△DEF与△DBE相似，∴∠BED＝∠EDF，或∠DFE＝∠BED，当∠BED＝∠EDF，∴DF∥BC，∴∠ADF＝∠B，∠AFD＝∠C，∴∠ADF＝∠AFD，∴AD＝AF＝4，∵AC＝6，∴CF＝2；当∠DFE＝∠BED，∵△DBE∽△ECF，∴∠BED＝∠CFE，∴∠DFE＝∠CFE，∠BDE＝∠FDE，∴点E在∠BDF与∠DFC的角平分线上，过E作EM⊥AB于M，EN⊥AC于N，EG⊥DF于G，连接AE，∴EM＝EG＝EN，∴AE是∠BAC的角平分线，∴BE＝CE，∵△DBE∽△ECF，∴，即，∴CF．综上所述，FC的长为2或．16.【题文】已知：△ABC，AB＝AC，∠BAC＝90°，点D是边BC的中点，点E在边AB 上（点E不与点A、B重合），点F在边AC上，联结DE、DF．（1）如图1，当∠EDF＝90°时，求证：BE＝AF；（2）如图2，当∠EDF＝45°时，求证：．【答案】见解答.【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质等知识；熟练掌握等腰直角三角形的性质，证明三角形全等和三角形相似是解题的关键．（1）连接AD，证△BDE≌△ADF（ASA），即可得出结论；（2）证明△BDE∽△CFD．得出，得出，由BD＝CD，即可得出结论．【解答】证明：（1）连接AD，如图1所示：在Rt△ABC中，∵AB＝AC，∠BAC＝90°，∴∠B＝∠C＝45°，∵点D是边BC的中点，∴AD BC＝BD，AD⊥BC，∠BAD＝∠CAD＝45°，∴∠B＝∠CAD，∵∠EDF＝90°，∴∠ADF+∠ADE＝90°，∵∠BDE+∠ADE＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（ASA），∴BE＝AF；（2）∵∠BDF＝∠BDE+∠EDF，∠BDF＝∠C+∠CFD，∴∠BDE+∠EDF＝∠C+∠CFD．又∵∠C＝∠EDF＝45°，∴∠BDE＝∠CFD，∴△BDE∽△CFD．∴，∴，又∵BD＝CD，∴．17.【题文】如图，Rt△ABC，∠C＝90°，AC＝10cm，BC＝8cm．点P从点C出发，以2cm/s的速度沿CA向点A匀速运动，同时点Q从点B出发，以1cm/s的速度沿BC 向点C匀速运动，当一个点到达终点时，另一个点随之停止．（1）求经过几秒后，△PCQ的面积等于△ABC面积的？（2）经过几秒，△PCQ与△ABC相似？【答案】（1）4秒；（2）秒或秒.【分析】本题考查了三角形的面积，直角三角形，相似三角形的判定等知识点，能得出关于x的方程是解（1）的关键，能求出符合的所有情况是解（2）的关键．（1）设经过x秒，△PCQ的面积等于△ABC面积的，根据三角形的面积和已知列出方程，求出方程的解即可；（2）根据相似三角形的判定得出两种情况，再求出t即可．【解答】（1）设经过x秒，△PCQ的面积等于△ABC面积的，，解得x1＝x2＝4，答：经过4秒后，△PCQ的面积等于△ABC面积的；（2）设经过t秒，△PCQ与△ABC相似，∵∠C＝∠C，∴分为两种情况：①，，解得t；②，，解得t；答：经过秒或秒时，△PCQ与△ABC相似．18.【题文】如图所示，在等腰△ABC中，AB＝AC＝10cm，BC＝16cm．点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s．连接DE，设运动时间为t（s）（0＜t＜10），解答下列问题：（1）当t为何值时，△BDE的面积为7.5cm2；（2）在点D，E的运动中，是否存在时间t，使得△BDE与△ABC相似？若存在，请求出对应的时间t；若不存在，请说明理由．【答案】（1）5秒；（2）秒或秒.【分析】本题考查了相似三角形的判定和性质、等腰三角形的性质，解决本题的关键是动点变化过程中形成不同的等腰三角形．（1）根据等腰三角形的性质和相似三角形的判定和性质求三角形BDE边BE的高即可求解；（2）根据等腰三角形和相似三角形的判定和性质分两种情况说明即可．【解答】（1）如图，分别过点D、A作DF⊥BC、AG⊥BC，垂足为F、G.∴DF∥AG，∵AB＝AC＝10，BC＝16，∴BG＝8，∴AG＝6．∵AD＝BE＝t，∴BD＝10﹣t，∴，解得DF（10﹣t）.∵S△BDE BE•DF＝7.5，∴（10﹣t）•t＝15，解得t＝5．答：t为5秒时，△BDE的面积为7.5cm2．（2）存在．理由如下：①当BE＝DE时，△BDE∽△BCA，∴，即，解得t，②当BD＝DE时，△BDE∽△BAC，，即，解得t．答：存在时间t为或秒时，使得△BDE与△ABC相似．19.【题文】如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠B＝∠ADE＝∠C．（1）证明：△BDA∽△CED；（2）若∠B＝45°，BC＝2，当点D在BC上运动时（点D不与B、C重合），且△ADE是等腰三角形，求此时BD的长．【答案】（1）见解答；（2）1或．【分析】本题考查了相似三角形的判定和性质，运用相似比进行线段的计算；熟练掌握等腰直角三角形的性质；学会运用分类讨论的思想解决数学问题．（1）根据相似三角形的判定定理即可得到结论；（2）当AD＝AE时，则∠1＝∠AED＝45°，得到∠DAE＝90°，则点D与B重合，不合题意舍去；当EA＝ED时，如图1，则∠EAD＝∠1＝45°，∴有AD平分∠BAC，得到AD垂直平分BC，则BD＝1；当DA＝DE时，如图2，由△ADE∽△ACD，易得△CAD 为等腰三角形，则DC＝CA，于是有BD＝BC﹣DC＝2．【解答】（1）证明：∵∠B＝∠ADE＝∠C，∴∠BAD＝180°﹣∠ADB﹣∠ADE，∵∠CDE＝180°﹣∠ADB﹣∠ADE，∴∠BAD＝∠CDE，∴△BDA∽△CED；（2）当AD＝AE时，∴∠1＝∠AED，∵∠1＝45°，∴∠1＝∠ADE＝45°，∴∠DAE＝90°，∴点D与B重合，不合题意舍去；当EA＝ED时，如图1，∴∠EAD＝∠1＝45°，∵∠BAC＝90°，∴∠BAD＝∠EAD＝45°，∴AD平分∠BAC，∴AD垂直平分BC，∴BD＝1；当DA＝DE时，如图2，∵∠1＝∠C，∠DAE＝∠CAD，∴△ADE∽△ACD，∴DA：AC＝DE：DC，∴DC＝CA，∴BD＝BC﹣DC＝2，∴综上所述，当△ADE是等腰三角形时，BD的长为1或2．20.【题文】如图，已知矩形ABCD中，AB＝4，动点P从点A出发，沿AD方向以每秒1个单位的速度运动，连接BP，作点A关于直线BP的对称点E，设点P的运动时间为t（s）．（1）若AD＝6，P仅在边AD运动，求当P，E，C三点在同一直线上时对应的t的值．（2）在动点P在射线AD上运动的过程中，求使点E到直线BC的距离等于3时对应的t的值．【答案】（1）；（2）或4．【分析】本题考查了相似三角形的判定与性质、矩形的性质、平行线的性质、轴对称的性质、勾股定理等知识，通过作辅助线构建相似三角形是解题的关键．（1）设AP＝t，则PD＝6﹣t，由点A、E关于直线BP对称，得出∠APB＝∠BPE，由平行线的性质得出∠APB＝∠PBC，得出∠BPC＝∠PBC，在Rt△CDP中，由勾股定理得出方程，解方程即可得出结果；（2）①当点E在BC的上方，点E到BC的距离为3，作EM⊥BC于M，延长ME交AD于N，连接PE、BE，则EM＝3，EN＝1，BE＝AB＝4，四边形ABMN是矩形，AN＝BM，证出△BME∽△ENP，得出，求出NP，即可得出结果；②当点E在BC的下方，点E到BC的距离为3，作EH⊥AB的延长线于H，则BH＝3，BE＝AB＝4，AH＝AB+BH＝7，HE，证得△AHE∽△PAB，得出，即可得出结果．【解答】（1）设AP＝t，则PD＝6﹣t，如图1所示：∵点A、E关于直线BP对称，∴∠APB＝∠BPE，∵AD∥BC，∴∠APB＝∠PBC，∵P、E、C共线，∴∠BPC＝∠PBC，∴CP＝BC＝AD＝6，在Rt△CDP中，CD2+DP2＝PC2，即42+（6﹣t）2＝62，解得t＝6﹣2或6+2（不合题意舍去），∴t＝（6﹣2）s时，P、E、C共线；（2）①当点E在BC的上方，点E到BC的距离为3，作EM⊥BC于M，延长ME交AD于N，连接PE、BE，如图2所示：则EM＝3，EN＝1，BE＝AB＝4，四边形ABMN是矩形，在Rt△EBM中，AN＝BM，∵点A、E关于直线BP对称，∴∠PEB＝∠PAB＝90°，∵∠ENP＝∠EMB＝∠PEB＝90°，∴∠PEN＝∠EBM，∴△BME∽△ENP，∴，即，∴NP，∴t＝AP＝AN﹣NP；②当点E在BC的下方，点E到BC的距离为3，作EH⊥AB的延长线于H，如图3所示：则BH＝3，BE＝AB＝4，AH＝AB+BH＝7，在Rt△BHE中，HE，∵∠PAB＝∠BHE＝90°，AE⊥BP，∴∠APB+∠EAP＝∠HAE+∠EAP＝90°，∴∠HAE＝∠APB，∴△AHE∽△PAB，∴，即，解得t＝AP＝4，综上所述，t或4．。

冀教版-数学-九年级上册-25.4 相似三角形的判定第2课时作业

25.4 相似三角形的判定第2课时1.下列判断正确的是（）A.两个直角三角形相似B.两个相似三角形一定全等C.凡等边三角形都相似D.所有等腰三角形都相似2.下列各对三角形中一定不相似的是（）A.△ABC中，∠A=54°，∠B=78°；△A′B′C′中，∠C′=48°，∠B′=78°B.△ABC中，∠C=90°，AC=4cm，BC=3cm；△A′B′C′中，∠C′=90°，A′C′=12cm，B′C′=15cmC.△ABC中，∠B=90°，AB=5，AC=13 ；△A′B′C′中，∠B′=90°，A′B′=2.5a，B′C′=6aD.△ABC中，∠C=90°，∠A=45°，AB=5；△A′B′C′中，∠A′=45°，A′B′=53.在△ABC中，MN∥BC，MC.NB交于O，则图中共有（）对相似三角形.A.1B.2C.3D.44.下列说法正确的个数是( )①有一个角相等的两个等腰三角形相似；②有一个底角相等的两个等腰三角形相似；③所有的等腰三角形相似；④顶角相等的两个等腰三角形相似.A.1B.2C.3D.45.下列三角形中相似的是：相似，相似，相似．6.如图1，D 为△AB C 的边AB 上一点,且∠ABC =∠ACD ，AD =3 cm ，AB =4 cm ，则AC 的长为_______________.7.如图，已知△ABC 中D 为AC 中点，AB =5，AC =7，∠AED =∠C ，则AE =.8.将两块完全相同的等腰直角三角形板摆放成如图4所示的样子，假设图中的所有点，线都在同一平面内.请问图中(1)共有多少个三角形？把它们一一写出来.(2)有相似(不包括全等)三角形吗？若有，请把它们一一写出来.图4参考答案1.C2.D3.B4.B5.（1）与（6）（2）与（4）（3）与（5）与（7）；2 cm6.37. 4.9【解析】8.(1)7个，△ABD.△ABE.△ABC.△ADC.△ADE.△AEC.△AFG；(2)有，△ADE∽△CDA，△BAE∽△ADE，△ABE∽△DCA.。

2022-2023学年冀教版九年级数学上册《25-4相似三角形的判定》同步达标测试题(附答案)

2022-2023学年冀教版九年级数学上册《25.4相似三角形的判定》同步达标测试题（附答案）一．选择题（共5小题，满分20分）1．如图，在△ABC中，高BD、CE相交于点F．图中与△AEC一定相似的三角形有（）A．1个B．2个C．3个D．4个2．如图，在△ABC中，AB＝AC，∠C的平分线交AB于点D，增添下列条件仍然不能判断△ABC∽△CBD的是（）A．∠A＝36°B．BC＝DC C．BC2＝BD⋅AB D．∠B＝∠ACB 3．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（）A．B．C．D．4．如图，在△ABC中，∠C＝45°，将△ABC绕着点B逆时针方向旋转，使点C的对应点C'落在CA的延长线上，得到△A'BC'，连接AA'，交BC'于点O．下列结论：①∠AC'A'＝90°；②AA'＝BC'；③∠A'BC'＝∠A'AC'；④△A'OC'∽△BOA．其中正确结论的个数是（）A．1B．2C．3D．45．如图，在正方形网格中有5个格点三角形，分别是：①△ABC，②△ACD，③△ADE，④△AEF，⑤△AGH，其中与⑤相似的三角形是（）A．①③B．①④C．②④D．①③④二．填空题（共9小题，满分36分）6．如图，在△ABC中，∠ACB＝90°，CD⊥AB，DE⊥BC，垂足分别为点D，E，则图中与△ABC相似的三角形个数有个．7．如图△ABC中，AB＝8，AC＝6，点D在AC上，AD＝2，要在AB上找一E，使△ADE 与△ABC相似，AE＝．8．如图，线段AB＝9，AC⊥AB于点A，BD⊥AB于点B，AC＝2，BD＝4，点P为线段AB 上一动点，且以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似，则AP的长为．9．如图，正方形ABCD的边长为4，AE＝EB，MN＝2，线段MN的两端在CB、CD上滑动，当CM＝时，△ADE与△CMN相似．10．如图，一次函数y＝﹣x+6的图象与x轴交于点B，与y轴交于点A，过线段AB的中点P（4，3）作一条直线与△AOB交于点Q，使得所截新三角形与△AOB相似，则点Q 坐标是．11．如图，点E在线段AB上，CA⊥AB于点A，DB⊥AB于点B，AC＝1，AB＝5，EB＝2，点P是射线BD上的一个动点，则当BP＝时，△CEA与△EPB相似．12．如图，在矩形ABCD中，AB＝10，AD＝4，P是CD边上的一个动点，则当△ADP与△BCP相似时，DP＝．13．如图，AB、CD交于点O，且OC＝45，OD＝30，OB＝36，当OA＝时，△AOC 与△BOD相似．14．如图，在矩形ABCD中，E，F分别是CD，BC上的点，∠AEF＝90°，有以下结论：①△ADE∽△AEF；②△ECF∽△AEF；③△ADE∽△ECF；④△AEF∽△ABF；⑤△ADE∽△ABF，其中正确的是（把你认为正确的序号都填上）．三．解答题（共8小题，满分64分）15．如图，点D为△ABC边AB上一点，AD＝2，BD＝6，AC＝4．求证：△ACD∽△ABC．16．如图，AD为△ABC的角平分线，AD的垂直平分线交BC的延长线于E，交AB于F，连接AE．求证：△BAE∽△ACE．17．如图，在边长为4的正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，求证：△ADQ∽△QCP．18．如图，在△ABC中，∠C＝90°，AC＝3，CB＝5，D是BC边上一点，且DB＝1，点E 是AC边上的一个点，且AE＝，过点E作EF∥CB交AD于点F．（1）求EF的长．（2）求证：△DEF∽△ABD．19．如图，△ABC与△DEF在5×7的长方形网格中，它们的顶点都在边长为1的小正方形的顶点位置，试判断△ABC与△DEF是否相似，并说明理由．20．如图，在四边形ABCD中，点E、F分别是AB、CD的中点，过点E作AB的垂线，过点F作CD的垂线，两垂线交于点G，联结AG、BG、CG、DG，且∠AGD＝∠BGC．（1）求证：AD＝BC；（2）求证：△AGD∽△EGF．21．在△ABC中，AB＝AC，∠BAC＝120°，P为BC的中点，小明拿着含有30°角的透明直角三角板，使30°角的顶点落在点P上，三角板绕P点旋转．（1）如图1，当三角板的一直角边和斜边分别与AB、BC交于点E、F时，连接EF，请说明△BPE∽△CFP；（2）操作：将三角板绕点P旋转到图2情形时，三角板的两边分别交BA的延长线、边AC于点E、F，连接EF．①探究1：△BPE与△CFP相似吗？请说明理由；②探究2：△BPE与△PFE相似吗？请说明理由．22．如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．（1）求证：PE•PF＝PC2．（2）如图2，连接AC交BD于O，连接OE，若CE⊥BC，求证：△POC∽△AEC．参考答案一．选择题（共5小题，满分20分）1．解：∵∠A＝∠A，∠AEC＝∠ADB＝90°，∴△AEC∽△ADB，∴∠ACE＝∠ABD，又∵∠AEC＝∠BEC＝90°，∴△AEC∽△FEB，∵∠ACE＝∠ACE，∠AEC＝∠ADB＝90°，∴△AEC∽△FDC，故选：C．2．解：∵AB＝AC，∴∠ABC＝∠ACB，∵CD平分∠ACB，∴∠ACD＝∠BCD，当∠A＝36°时，∴∠ABC＝∠ACB＝72°，∴∠DCB＝36°，∴∠A＝∠DCB，又∵∠DBC＝∠ABC，∴△ABC∽△CBD，故选项A不符合题意；当BC＝DC时，∴∠CDB＝∠CBD，∴∠ABC＝∠ACB＝∠CBD＝∠CDB，∴△ABC∽△CBD，故选项B不符合题意；当BC2＝BD•AB时，∴，又∵∠CBD＝∠ABC，∴△ABC∽△CBD，故选项C不符合题意；故选：D．3．解：在△ABC中，∠ACB＝135°，AC＝，BC＝2，在B、C、D选项中的三角形都没有135°，而在A选项中，三角形的钝角为135°，它的两边分别为1和，因为＝，所以A选项中的三角形与△ABC相似．故选：A．4．解：∵将△ABC绕着点B逆时针方向旋转，∴∠C＝∠BC'A'＝45°，∠CBC'＝∠ABA'，BC＝BC'，AB＝BA'，∴∠C＝∠BC'C＝45°，∴∠A'C'A＝90°＝∠CBC'＝∠ABC'，故①正确；∴点A，点B，点A'，点C'四点共圆，∴AA'是直径，∠A'BC'＝∠A'AC'，故②错误，③正确，∵点A，点B，点A'，点C'四点共圆，∴∠BC'A'＝∠BAA'，又∵∠AOB＝∠A'OC'，∴△AOB∽△A'OC'，故④正确，故选C．5．解：由图形知，⑤中∠AHG＝135°，而①②③④中，只有①∠BAC＝135°和③∠ADE＝135°，再根据两边成比例可判断，与⑤相似的三角形是①③，故选：A．二．填空题（共9小题，满分36分）6．解：∵CD⊥AB，DE⊥BC，∴∠CDA＝∠CDB＝∠DEB＝∠DEC＝90°＝∠ACB，∴∠A+∠B＝90°＝∠A+∠ACD＝∠B+∠DCB＝∠B+∠BDE＝∠DCB+∠CDE，∴∠A＝∠BDE＝∠BCD，∠B＝∠ACD＝∠CDE，∴△ACB∽△ADC∽△DEB∽△CDB∽△CED，故答案为：4．7．解：∵∠A是公共角，∴当，即时，△AED∽△ABC，解得：AE＝；当，即时，△ADE∽△ABC，解得：AE＝，故答案为：或8．解：设AP＝x．∵以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似，①当时，，解得x＝3．②当时，，解得x＝1或8，∴当以A、C、P为顶点的三角形与以B、D、P为顶点的三角形相似时，AP的长为1或3或8，故答案为1或3或8．9．解：∵AE＝EB，∴AD＝2AE，又∵△AED与以M、N、C为顶点的三角形相似，∴分两种情况：①CM与AD是对应边时，CM＝2CN，∴CM2+CN2＝MN2＝4，即CM2+CM2＝4，解得：CM＝；②CM与AE是对应边时，CM＝CN，∴CM2+CN2＝MN2＝4，即CM2+4CM2＝4，解得：CM＝．综上所述：当CM为或时，△AED与△CMN相似．故答案是：或．10．解：∵一次函数y＝﹣x+6的图象与x轴交于点B，与y轴交于点A，∴A（0，6），B（8，0），∴OA＝6，OB＝8，AB＝＝＝10，如图有两种情形：①当PQ∥OB时，满足条件．∵AP＝PB，∴AQ＝OQ，∴Q（0，3）．②当PQ′⊥AB时，满足条件．连接AQ′．∵P A＝PB，PQ′⊥AB，∴Q′A＝Q′B，设Q′A＝Q′B＝m，在Rt△AOQ′中，则有m2＝62+（8﹣m）2，解得m＝，∴OQ′＝8﹣＝，∴Q′（，0）．③当PQ∥y轴时，同法可得P（4，0）．综上所述，满足条件的点Q的坐标为（0，3）或（，0）或（4，0）．11．解：∵CA⊥AB，DB⊥AB，∴∠A＝∠B＝90°，又∵AB＝5，EB＝2，∴AE＝AB﹣EB＝3，①当△CAE∽△PBE时，＝，即＝，解得：PB＝；②当△CAE∽△EBP时，＝，即＝，解得：BP＝6；综上，当BP＝或6时，△CEA与△EPB相似．故答案为：或6．12．解：①当△APD∽△PBC时，＝，即＝，解得：PD＝2或PD＝8；②当△P AD∽△PBC时，＝，即＝，解得：DP＝5．综上所述，DP的长度是2或8或5．故答案是：2或8或5．13．解：∵OC＝45，OD＝30，OB＝36，△AOC∽△BOD，∴，即，解得OA＝54；若△AOC∽△DOB，∴，即，解得OA＝，综上所述OA的长为54或．故答案为：54或．14．解：在矩形ABCD中，∵∠D＝∠C＝90°，∠AEF＝90°，∴∠DEA+∠CEF＝90°，∠DEA+∠DAE＝90°，∴∠DAE＝∠CEF，∴△ADE∽△ECF，其余都不符合相似的条件．故答案为：③．三．解答题（共8小题，满分64分）15．解：∵AD＝2，BD＝6，∴AB＝8，∴，，∴，又∵∠A＝∠A，∴△ACD∽△ABC．16．证明：∵AD是∠BAC的平分线，∴∠BAD＝∠CAD，∵EF是AD的垂直平分线，∴AE＝DE，∴∠EAD＝∠EDA，∵∠EAC＝∠EAD﹣∠CAD，∠B＝∠ADE﹣∠BAD，∴∠CAE＝∠B，∴△BAE∽△ACE．17．证明：∵四边形ABCD是正方形，BP＝3PC，Q是CD的中点，∴QC＝QD＝AD，CP＝AD，∴，又∵∠ADQ＝∠QCP＝90°，∴△ADQ∽△QCP．18．解：（1）∵AC＝3，CB＝5，DB＝1，AE＝，∴CD＝CB﹣DB＝5﹣1＝4，∵EF∥CB，∴△AEF∽△ACD，∴，∴EF＝＝＝．（2）∵CE＝AC﹣AE＝3﹣＝，∴＝＝，∵＝，∴＝，∵∠C＝∠C，∴△CED∽△CAB，∴∠EDC＝∠B，∵∠EDC＝∠DEF，∴∠DEF＝∠B，∵∠DFE＝∠ADB，∴△DEF∽△ABD．19．解：相似．理由如下：∵AB＝＝，BC＝5，AC＝＝，DE＝1，EF＝＝，DF＝，∴＝，＝＝，＝＝，∴＝＝，∴△ABC∽△DEF．20．证明：（1）∵GE是AB的垂直平分线，∴GA＝GB，同理：GD＝GC，在△AGD和△BGC中，，∴△AGD≌△BGC（SAS），∴AD＝BC；（2）∵GA＝GB，GD＝GC，∴，∵∠AGD＝∠BGC，∴∠AGD+∠DGB＝∠BGC+∠DGB，即∠AGB＝∠DGC，∴△AGB∽△DGC，∴∠GAB＝∠GDC，又∵GE、GF是对应高，∴，∠AGE＝∠DGF，∴，∠AGD＝∠EGF，∴△AGD∽△EGF．21．（1）证明：∵在△ABC中，∠BAC＝120°，AB＝AC，∴∠B＝∠C＝30°．∵∠B+∠BPE+∠BEP＝180°，∴∠BPE+∠BEP＝150°，又∵∠BPE+∠EPF+∠CPF＝180°，∠EPF＝30°，∴∠BPE+∠CPF＝150°，∴∠BEP＝∠CPF，∴△BPE∽△CFP（两角对应相等的两个三角形相似）．（2）解：①△BPE∽△CFP；②△BPE与△PFE相似．下面证明结论：同（1），可证△BPE∽△CFP，∴CP：BE＝PF：PE，∵CP＝BP，∴BE：BP＝PE：PF．又∵∠EBP＝∠EPF，∴△BPE∽△PFE（两边对应成比例且夹角相等的两个三角形相似）．22．证明：（1）∵四边形ABCD菱形，∴AD＝CD，∠CDP＝∠ADP，CD∥AB，在△CDP和△ADP中，，∴△CDP≌△ADP（SAS），∴PC＝P A，∠DCP＝∠DAP，∵CD∥AB，∴∠DCP＝∠F，∴∠DAP＝∠F，∵∠APE＝∠FP A，∴△P AE∽△PF A，∴，∴P A2＝PE•PF，∴PE•PF＝PC2；（2）∵CE⊥BC，∴∠ECB＝90°，∵AD∥BC，∴∠CEA＝∠BCE＝90°，∵四边形ABCD是菱形，∴AC⊥BD，∴∠COP＝90°，∴∠COP＝∠CEA，∵∠OCP＝∠ECA，∴△POC∽△AEC．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

25.4 相似三角形的判定练习题
一、填空题。

1．______三角形一边的______和其他两边______，所构成的三角形与原三角形相似．2．如果两个三角形的______对应边的______，那么这两个三角形相似．
3．如果两个三角形的______对应边的比相等，并且______相等，那么这两个三角形相似．4．如果一个三角形的______角与另一个三角形的______，那么这两个三角形相似．
5．在△ABC和△A′B′C′中，如果∠A＝56°，∠B＝28°，∠A′＝56°，∠C′＝28°，那么这两个三角形能否相似的结论是______．理由是________________．
6．在△ABC和△A'B′C′中，如果∠A＝48°，∠C＝102°，∠A′＝48°，∠B′＝30°，那么这两个三角形能否相似的结论是______．理由是________________．
7．在△ABC和△A'B′C′中，如果∠A＝34°，AC＝5cm，AB＝4cm，∠A′＝34°，A'C′＝2cm，A′B′＝1.6cm，那么这两个三角形能否相似的结论是______，理由是____________________．
8．在△ABC和△DEF中，如果AB＝4，BC＝3，AC＝6；DE＝2.4，EF＝1.2，FD＝1.6，那么这两个三角形能否相似的结论是____________，理由是__________________．。

新冀教版九年级上《25.4相似三角形的判定》练习题

相似三角形的判定 冀教版九年级数学上册同步测试(含答案)

九年级数学上册《254相似三角形的判定(二)》同步测试卷(新版)冀教版.docx

2020年冀教版数学九年级上册 25.4 相似三角形的判定(含答案)

冀教版九年级数学上册25.4 相似三角形的判定定理3同步练习题(无答案)

最新冀教版初中数学九年级上册专题练习25.4 相似三角形的判定

初中数学冀教版九年级上册第二十五章 图形的相似25.4 相似三角形的判定-章节测试习题(5)