六年级下册数学试题-奥数专练:计算汇总(含答案)全国通用
六年级下册数学试题-奥数专练:一半模型(含答案)全国通用
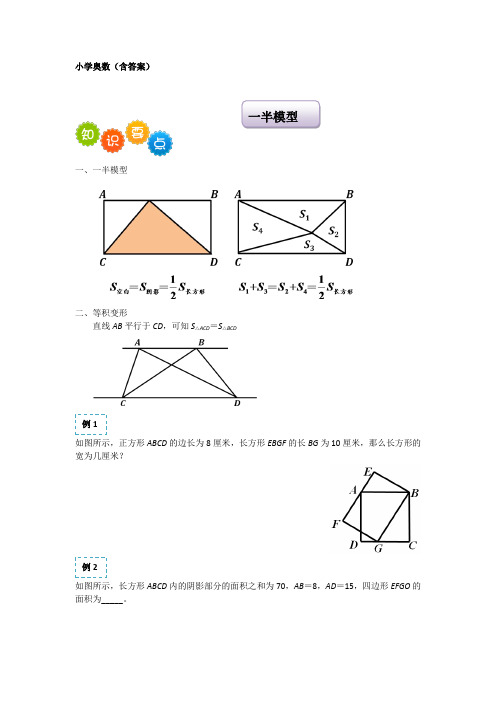
小学奥数(含答案)一、一半模型二、等积变形直线AB平行于CD,可知S△ACD=S△BCD如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为_____。
例2例1一半模型如图,正方形的边长为10,四边形EFGH的面积为5,那么阴影部分的面积是______。
如图,p为长方形ABCD内的一点,三角形PAB的面积为5,三角形PBC的面积为13,求△PBD 的面积是多少?如图,长方形ABCD的面积是2平方厘米,EC=2DE,F是DG的中点。
四边形EFGC的面积是多少平方厘米?如图,在平行四边形ABCD中,BE=EC,CF=2FD。
求阴影面积与空白面积的比。
例6例5例4例3测试题1.如图,1,5,4,,ABC S BC BD AC EC DG GS SE AF FG ======V ,求FGS S V 。
SGF E DC BA2.如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?GF ED CBA3.如右图,正方形ABCD 的边长为l ,E 、F 分别是BC 、DC 的中点,求四边形MECN 的面积为多少?4.如图,长方形ABCD 中,E 为AD 中点,AF 与BE 、BD 分别交于G 、H ,已知AH =5cm ,HF =3cm ,求AG 。
HGF E DCBA5.如图,ABCD 是长方形,ED 与宽平行,GH 与长平行,AB 的长是8厘米,BC 的长是6厘米,那么图中阴影的面积是__________平方厘米。
HGFDCBA6.(2005全国华罗庚金杯数学邀请赛)如图1,长方形的长为8,宽为4,将长方形沿一条对角线折起压平,如图2所示,求重叠部分(阴影部分)的面积。
答案1.答案:本题是我喜欢的一道题目,题目本身很简单,但它把本节课的两个重要知识点融合到一起,既可以看作是“当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况,好题!最后求得FGS S V 的面积为4321115432210⨯⨯⨯⨯=。
六年级下册数学试题-奥数专题:行程问题(1)变速问题(含答案)全国通用

变速问题【例题1】小红上学,每分钟行60米,需要30分钟,如果速度提高,可以提前几分钟?【思路一】可以从如下方面进行来分析:1.先算出路程。
60×30=1800米。
2.再算后来的速度。
60×+60=72米/分。
3.接着算后来需要的时间。
1800÷72=25分。
4.最后算提前的时间。
30-25=5分钟。
【思路二】利用工程问题思想分析:设原来每分钟行1份的路程,后来每分钟行1+=1.2份的路程,原来30分钟就行30份,提高速度后只需要30÷(1+)=25分。
则提前30-25=5分钟。
【练习1】小明乘车去公园,每小时行45千米,需要3.6小时,如果速度提高,可以提前多少小时到达?【解答】3.6-3.6÷(1+)=0.9小时【例题2】甲从A地去B地,每小时行15千米。
返回时速度提高,结果少用3小时。
请问A、B两地的距离是多少千米?【思路一】盈亏问题思想返回每小时多行15×=3千米,返回每小时行15+3=18千米,如果继续行3小时,可以多行3×18=54千米,说明去的时间是54÷3=18小时。
因此两地之间的距离是15×18=270千米。
【思路二】工程问题思想去的时间看作单位1,返回的时间是1÷(1+)=,3小时就相当于1-=,则去用的时间是3÷=18小时。
两地之间的距离是15×18=270千米。
返回每小时行15×(1+)=18千米,往返1千米少用-=小时,现在少用3小时,需要往返3÷=270千米。
【练习2】小芳放学回家,每分钟行75米。
原路去上学,每分钟比原来慢,结果多用2分钟。
小芳家到学校有多少米?【解答】上学的速度75×(1-)=60米/分,小芳家到学校有2÷(-)=600米。
【例题3】王师傅用3.2小时在家和工厂之间往返了一次,去时每小时25千米,返回时减速,求他家到工厂相距多少千米?【解答】返回的速度是25×(1-)=15千米/时,往返1千米需要+=小时,现在用3.2小时可以往返3.2÷=30千米。
六年级下册数学专项练习奥数思维练习100题及详解全国版

六年级下册数学专项练习奥数思维练习100题及详解全国版解:原式=765÷27×(213+327)= 765÷27×540=765×20=15300(9999+9997+...+9001)-(1+3+ (999)解:原式=(9999-999)+(9997-997)+(9995-995)+……+(9001-1) =9000+9000+…….+9000 (500个9000)=45000003.20212021×20212021-20212021×20212021解:(20212021+1)×20212021-20212021×20212021=20212021×20212021-20212021×20212021+20212021=20212021-20212021=100004.(873×477-198)÷(476×874+199)解:873×477-198=476×874+199因此原式=15.2021×2021-2021×2021+2021×2021-2021×2021+…+2×1解:原式=2021×(2021-2021)+2021×(2021-2021)+…+3×(4-2)+2×1=(2021+2021+…+3+1)×2=2021000。
6.297+293+289+…+209解:(209+297)*23/2=58197.运算:解:原式=(3/2)*(4/3)*(5/4)*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(9 8/99)=50*(1/99)=50/998.解:原式=(1*2*3)/(2*3*4)=1/49. 有7个数,它们的平均数是18。
六年级下册数学试题-奥数思维训练题库---计算(解析版)全国通用

奥数思维训练题库---计算【分组】【2】计算:1-2+3-4+5-……-1994+1995=【答案】998【分组】【2】计算:1-2+3-4+5-……-2014+2015=【答案】1008【分组】【2】计算:(2+4+6+…+1996)-(1+3+5+…+1995)=【答案】998【分组】【2】计算:(2+4+6+…+2014)-(1+3+5+…+2013)=【答案】1007【分组】【2】3-5+7-9+11-13+…+2011-2013+2015=【答案】1009【提取公因数】【2】计算:222+333+444+555+666=【答案】2220444×5=2220【提取公因数】【2】计算:111+222+333+444+555+666=【答案】2331【位值原理】【2】(123456+234561+345612+456123+561234+612345)÷111111= 【答案】21【提取公因数】【2】计算:1÷2015+2÷2015+3÷2015+…+2014 ÷2015+2015÷2015= 【答案】1008【提取公因数】【乘法凑整】【2】计算:3.6×31.4+(31.4+12.5)×6.4=【答案】394【提取公因数】【乘法凑整】【2】计算:3.6×30.4+(30.4+12.5)×6.4=【答案】384【提取公因数】【分拆】【3】计算:161.8×6.18+2618×0.382=【答案】2000【提取公因数】【3】计算:(4.16×84-2.08×54-0.15×832)÷0.32【答案】1248【分拆】【凑整】【2】计算:0.75+9.75+99.75+999.75+1=【答案】1111【分拆】【提取公因数】【3】7210810846(118142118134)⨯+⨯-⨯-⨯【答案】11800【提取公因数】【2】计算:0.9999×0.7+0.1111×2.7=【答案】0.9999【提取公因数】【2】1994.5×81+0.24×800+2.4+8.1×31=【答案】162000【凑整】【1】计算:98+998+9998+99998=【答案】111092【凑整】【1】计算:8+998+9998+99998=【答案】111002【提取公因数】【凑整】【2】计算:(8.88+8.88+8.88+8.88)×1.25= 【答案】44.4【提取公因数】【2】20.14×37-201.4×1.9+2.014×820=【答案】2014【提取公因数】【2】计算:17.48×37-174.8×1.9+1.748×820=【答案】1748【提取公因数】【2】计算:2098-5.5×7.5-0.25×55-45=【答案】19982098-5.5×7.5-0.25×55-45=2098-55×(0.75+0.25)-45=2098-(55+45)=1998【提取公因数】【2】8.1×1.3-8÷1.3+1.9×1.3+11.9÷1.3=【答案】10【提取公因数】【2】999.99×222.22+333.33×333.34 =【答案】333330【提取公因数】【2】51.2×32.5+512×6.74+5.12=【答案】5120【分拆】【2】325.24+425.24+625.24+925.24+525.24=【答案】2826.2【分拆】【提取公因数】【3】计算:333×332332333-332×333333332【答案】665【分拆】【重码数】【3】19501950×2010-20112011×1949=【答案】61061【提取公因数】【2】计算:9.99×0.13-0.111×2.7【答案】0.999【定义新运算】【3】对于任意两个自然数A 和B 、规定一种新运算“※”:A ※B=A (A +1)(A +2)……(A +B -1)。
六年级下册数学试题-奥数专题讲练:钟表上的行程(含答案)全国通用

六年级下册数学试题-奥数专题讲练:钟表上的行程(含答案)全国通用钟表上的行程时钟问题可以看做是一个特殊的圆形轨道上2人追及或相遇问题,不过这里的两个“人”分别是时钟对于正常的时钟,具体为:整个钟面为360度,上面有12个大格,每个大格为30度;60个小格,每个小格为6度。
分针速度:每分钟走1小格,每分钟走6度1时针速度:每分钟走1 【例1】⑴现在是4点,至少再经过多少分钟,时针与分针重合?2小格,每分钟走0.5度【例1】⑵2点钟以后,什么时刻分针与时针第一次成直角?【例2】小红在9点与10点之间开始解一道数学题,当时时针和分针正好成一条直线,当小红解完这道题时,时针和分针刚好第一次重合,小红解这道题用了多少时间?【例3】一部动画片放映的时间不足1时,小明发现结束时手表上时针、分针的位置正好与开始时时针、分针的位置交换了一下。
这部动画片放映了多长时间?【例4】(北京市第11届迎春杯小学数学竞赛决赛试题)有一座时钟现在显示10时整,那么,经过多少分钟,分针与时针第一次重合?再经过多少分钟,分针与时针第二次重合?经典例题妙解【例5】钟面上3点几分钟时,时针与分针到3 的距离相等?测试题1.2点几分时,分针与时针的夹角是150 ?2.小明在两点到三点之间解一道题目,开始时时针与分针正好重合,解完题时时针与分针正好在一条直线上。
求小明解题用了多少时间?3.钟面上5点到6点之间,分针与时针夹角是直角的是什么时候?4.星期天,豆豆和爸爸、妈妈去动物园。
上午8点多从家里出发,临出门,豆豆看了墙上的挂钟,钟面上的时针和分针恰好重合。
下午3点多,豆豆回家后,又看了看挂钟,这时,时针和分针恰好反向成一条直线。
问:他们是几点从家出发,几点回家的?共出去了多长时间?5.吴老师看一集电视剧,他在刚播出时看了一下手表,结束时又看了一下手表,他发现时针与分针刚好交换了一下位置。
已知电视剧时间不足一个小时,求电视剧播出了多长时间?答案1.答案:从两点开始计算,此时夹角是60 ,那么分针需要比时针多走150 + 60 = 210度或者是360 - (150 - 60) = 270度,2 1 2 1分针与时针的夹角是150 。
六年级下册奥数专题练习-立体图形的计算(含答案) 全国通用

立体图形的计算【表面积的计算】例1 一个正方体木块,棱长1米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大小不等的长方体60块(如图5.69)。
那么,这60块长方体的表面积的和是平方米。
(1988年北京小学数学奥林匹克邀请赛试题)讲析:不管每次锯的长方体大小如何,横着锯2次一共增加了4个正方形面;前后竖直方向锯3次共增加了6个正方形面;左右竖直方向锯4次共增加了8个正方形面。
原来大正方体有6个正方形面,所以一共有24个正方形面。
所以,60块长方体的表面积之和是(1×1)×24=24(平方米)。
例2 图5.70是由19个边长都是2厘米的正方体重叠而成的。
求这个立体图形的外表面积。
(北京市第一届“迎春杯”小学数学竞赛试题)讲析:如果按每一层有多少个正方体,然后再数出每层共有多少个外表面正方形,则很麻烦。
于是,我们可采用按不同的方向来观察的方法去计算。
俯视,看到9个小正方形面;正视,看到10个小正方形面;侧视,看到8个小正方形面。
所以,这个立体图形的表面积是(2×2)×[(9+10+8)×2]=216(平方厘米)。
【体积的计算】例1 一个正方体的纸盒中恰好能放入一个体积为628立方厘米的圆柱体,如图5.71,纸盒的容积有多大?(π取3.14)(全国第四届“华杯赛”复赛试题)讲析:因圆柱体的高、底面直径以及正方体的棱长都相等。
故可设正方即:正方体纸盒的容积是800立方厘米。
例2 在一个棱长4厘米的正方体的上面、右面、前面这三个面的中心分别挖一个边长1厘米的正方形小孔(如图5. 72所示),并通过对面,求打孔后剩下部分的体积。
(北京市第二届“迎春杯”小学数学竞赛试题)。
讲析:打完孔之后,在大正方体正中央就有一个1×1×1的空心小正方体。
三个孔的体积是(1×1×4)×3-(1×1×1)×2=10(立方厘米)。
(完整版)小学六年级下册最新经典奥数题及答案(最全)汇总

小学六年级下册的奥数题及答案一.工程问题:1.甲乙两个水管单独开,注满一池水,分别需要20小时,16小时.丙水管单独开,排一池水要10小时,若水池没水,同时打开甲乙两水管,5小时后,再打开排水管丙,问水池注满还是要多少小时?2.修一条水渠,单独修,甲队需要20天完成,乙队需要30天完成。
如果两队合作,由于彼此施工有影响,他们的工作效率就要降低,甲队的工作效率是原来的五分之四,乙队工作效率只有原来的十分之九。
现在计划16天修完这条水渠,且要求两队合作的天数尽可能少,那么两队要合作几天?3.一件工作,甲、乙合做需4小时完成,乙、丙合做需5小时完成。
现在先请甲、丙合做2小时后,余下的乙还需做6小时完成。
乙单独做完这件工作要多少小时?4.一项工程,第一天甲做,第二天乙做,第三天甲做,第四天乙做,这样交替轮流做,那么恰好用整数天完工;如果第一天乙做,第二天甲做,第三天乙做,第四天甲做,这样交替轮流做,那么完工时间要比前一种多半天。
已知乙单独做这项工程需17天完成,甲单独做这项工程要多少天完成?5.师徒俩人加工同样多的零件。
当师傅完成了1/2时,徒弟完成了120个。
当师傅完成了任务时,徒弟完成了4/5这批零件共有多少个?6.一批树苗,如果分给男女生栽,平均每人栽6棵;如果单份给女生栽,平均每人栽10棵。
单份给男生栽,平均每人栽几棵?7.一个池上装有3根水管。
甲管为进水管,乙管为出水管,20分钟可将满池水放完,丙管也是出水管,30分钟可将满池水放完。
现在先打开甲管,当水池水刚溢出时,打开乙,丙两管用了18分钟放完,当打开甲管注满水是,再打开乙管,而不开丙管,多少分钟将水放完?8.某工程队需要在规定日期内完成,若由甲队去做,恰好如期完成,若乙队去做,要超过规定日期三天完成,若先由甲乙合作二天,再由乙队单独做,恰好如期完成,问规定日期为几天?9.两根同样长的蜡烛,点完一根粗蜡烛要2小时,而点完一根细蜡烛要1小时,一天晚上停电,小芳同时点燃了这两根蜡烛看书,若干分钟后来点了,小芳将两支蜡烛同时熄灭,发现粗蜡烛的长是细蜡烛的2倍,问:停电多少分钟?二.鸡兔同笼问题1.鸡与兔共100只,鸡的腿数比兔的腿数少28条,问鸡与兔各有几只?三.数字数位问题1.把1至2005这2005个自然数依次写下来得到一个多位数123456789.....2005,这个多位数除以9余数是多少?2.A和B是小于100的两个非零的不同自然数。
六年级下册数学试题-奥数专练:质数与合数(含答案)全国通用

小学奥数(含答案)质数与合数一般地,如a、b、c为整数,b≠0,且a÷b=c,即整数a除以整数b(b不等于0),除得的商c正好是整数而没有余数(或者说余数是0),我们就说,a能被b整除否则,称为a不能被b整除,(或b不能整除a)。
如果整数a能被整数b整除,a就叫做b的倍数,b就叫做a的约数。
一、自然数除0和1外,按约数的个数分为质数和合数两类。
质数:一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数)。
合数:一个数除了1和它本身,还有别的约数,这个数叫做合数。
二、质数与合数重要知识点⑴要特别记住:0和1不是质数,也不是合数。
⑵任何一个合数都可以写成几个质数相乘的形式。
⑶最小的质数是2 ,2是唯一的偶质数,其他质数都为奇数;最小的合数是4。
⑷质数是一个数,是含有两个约数的自然数。
互质数是指两个数,是公约数只有1的两个数,组成互质数的两个数:可能是两个质数(3和5),可能是一个质数和一个合数(3和4),可能是两个合数(4和9)或1与另一个自然数。
⑸如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
例1请找出100以内的所有质数。
例2若将17拆成若干个不同的质数之和,使得这些质数的乘积尽可能大,那么这个最大的乘积是多少?例3将八个不同的合数填入下面的括号中,如果要求相加的两个合数互质,那么A最小是几?A=( )+( )=( )+( )=( )+( )=( )+( )今有17、23、31、41、53、67、79、83、101、103共10个质数。
如果把它们分成两组,使每一组5个数,并且每组的5个数之和相等,那么把含有101的这组数从小到大排列,第2个数是多少?从小到大写出5个质数,使后面的数都比前面的数大12。
这样的数有几组?如果某整数同时具备如下三条性质:①这个数与1的差是质数,②这个数除以2所得的商也是质数,③这个数除以9所得的余数是5,那么我们称这个整数为幸运数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.凑整法
将算式中的数分成若干组,是每组的运算结果都是整十、整百、整千……,如果算式中的数是小数,那么就凑成整数,再将各组的结果求和(差)。
2.提取公因式法
如果一个多项式的各项含有公因式,那么可以把这个公因式提取出来,再将剩余的项求和(差)。
3.定义新运算
定义新运算通常是用某些特定的符号表示特定的运算含义,这些符号只在指定题目中有意义,离开指定题目这种运算法则没有任何意义。
(5.6×2.7×0.48×7.4)÷(0.12×37×0.28×9)=( )
(“中环杯”小学生思维能力训练活动五年级初赛填空题第2题)
计算:666666.6666×333.3333333=( )
计算:
2009200920091999999999⋅⋅⋅+⋅⋅⋅⨯⋅⋅⋅个个个123123123
例3
例2 例1 计算汇总
已知:a △b =3a +2b ,32a b a b ∇=-又知,7993x ∆∇=,求x 的值
(“中环杯”小学生思维能力训练活动五年级初赛填空题第1题)
已知A *B =AB +A +B ,则101*9*9**9*9_____=共次运算L 144424443
测试题
1.(“中环杯”小学思维能力训练活动五年级初赛填空题第3题),
计算:()()0.720.750.0760.190.14437.5⨯⨯÷⨯⨯的值。
2.(“中环杯”小学生思维能力训练活动五年级复赛填空题第2题)
计算(532)(533)(534)(5352)+⨯++⨯++⨯+++⨯L 的值。
3.(“中环杯”小学生思维能力训练活动五年级决赛填空题第2题)
计算:2.5 2.7 3.45 5.4 6.87.58.110.21010.813.6⨯⨯+⨯⨯+⨯⨯+⨯⨯。
4.如果2*3234=++,3*43456=+++,4*545678=++++,求1*2*3*4*5的值。
5.(“中环杯”小学生思维能力训练活动五年级初赛填空题第4题)已知,a b 为自然数,
2a b a b ∆=+,234567893039a a a a a a a a a ∆∆∆∆∆∆∆∆=,则求a 。
答案
1.()()0.720.750.0760.190.14437.5⨯⨯÷⨯⨯
0.720.750.0760.14437.50.19
=
⨯⨯ 50.020.4=⨯⨯
0.04=
2.(532)(533)(534)(5352)+⨯++⨯++⨯+++⨯L
515553=++++⨯
L L 1442443个(2+3+4+52)
25531377=+⨯
2554131=+
4386=
3.2.5 2.7 3.45 5.4 6.87.58.110.21010.813.612.513.517⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯
2.5 2.7
3.4 2.5 2.7 3.4222 2.5 2.7 3.4333 2.5 2.7 3.4444=⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯ 2.5 2.7 3.4(182764)=⨯⨯⨯+++
5163.75=
4.观察容易发现*的运算方法是,从*前面一个数开始,连续的n 数之和(n 等于*后面的数字),所以:1*2*3*4*5
(12)*3*4*5
(345)*4*5
(12131415)*5
5455565758280=+=++=+++=++++=
5.23456789a a a a a a a a a ∆∆∆∆∆∆∆∆
43456789a a a a a a a a =∆∆∆∆∆∆∆
11456789a a a a a a a =∆∆∆∆∆∆
2656789a a a a a a =∆∆∆∆∆
576789a a a a a =∆∆∆∆
120789a a a a =∆∆∆
24789a a a =∆∆
50291013a a a =∆=
10133039a =,所以3a =。
