2021-2022学年河南省郑州市上街区上街实验高一年级上册学期期末数学试题【含答案】
河南省郑州市2024小学数学一年级上学期人教版期末阶段质量检测(自测卷)完整试卷

河南省郑州市2024小学数学一年级上学期人教版期末阶段质量检测(自测卷)完整试卷一、填一填(共10小题,28分) (共10题)第(1)题1个十和3个一组成的数是( )。
第(2)题比3大2的数是( ),比6小3的数是( )。
第(3)题4后面的一个数是( );2前面的一个数是( )。
第(4)题涂一涂,填一填。
●●●●○○○○○○ 4+()=10○○○○○○○○○○ 7+()=10○○○○○○○○○○ 5+()=10第(5)题数一数,填一填。
( )个,( )个,( )个,( )个,一共有( )个物体。
第(6)题如果要让每个鱼缸里的鱼都有7条,每个鱼缸还要再放进去几条呢?写在对应的括号里。
( )( )( )( )( )( )第(7)题小华从下面几盒蛋糕种,买了不同的两盒,共6块,从左边数,他买的不可能是第( )盒。
第(8)题比6少3的数是( );比4多6的数是( )。
第(9)题填一填。
5-( )=0 5-( )=2( )-2=2 2+3=( )( )+3=4 ( )+5=50-( )=0 1+( )=5第(10)题接着算。
(1)(2)二、轻松选择(共4题,12分) (共4题)第(1)题()A.2只B.3只C.4只第(2)题如图,数一数,()图形最多。
A.B.C.第(3)题如果一次只能端两盘,那么一次最多能端几个梨?()A.12个B.13个C.14个第(4)题小华的姐姐今年10岁,小华6岁,5年后,姐姐比小华大多少岁?()A.4B.5C.9三、算一算(共4题,32分) (共4题)第(1)题直接写出得数。
4+4= 10+8= 6-3= 17-5-2=5+7= 7-1= 8+4= 4+9+2=第(2)题看图列式。
第(3)题用2、8、6组成一道加法算式或两道减法算式。
第(4)题口算。
8-5= 7-3= 9-2= 6-5= 7-4=四、解答题(共4题,28分) (共4题)第(1)题小红拿了10元钱,买了一个笔记本4元,又买了一支铅笔2元,还剩下多少钱?(元)第(2)题哥哥有4支,弟弟有1支,哥哥和弟弟一共有几支?(支)第(3)题阳阳今年多少岁?果果:我今年10岁了。
河南省郑州市2021版一年级上册数学期末测试C卷D卷

河南省郑州市2021版一年级上册数学期末测试C卷D卷姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、用心思考,我会填 (共4题;共12分)1. (2分) (2020一上·景县期末) 个位上和十位上都是1的两位数是________,这个数读作________。
2. (6分) (2020一上·大冶期末) 在横线上填上“>”、“<”或“=”。
5+8________13 16________7+9 8+6________1515-9________4 17________17-0 7+8________123. (2分)庆祝“六·一”文娱表演。
________唱歌和跳舞共用了________时间。
4. (2分)阳光下的人影与人的左右是相同的。
二、反复比较我会选:选择正确答案的序号填在括号里。
(共5题;共10分)5. (2分)图中有三角形的个数是()A . 4B . 5C . 6D . 76. (2分)求一共有多少个西瓜,列式为()。
A . 3+4=7B . 3+3+3=12C . 4+4+4=12D . 4+4=87. (2分) (2019三下·路桥期末) 解答下图中的问题,需要用到的信息是()。
A . 8元,4支,6元,2支B . 8元,6元,2支C . 8元,6元D . 6元8. (2分) 1个十和5个一组成的数是()。
A . 10B . 5C . 15D . 519. (2分)判断下图中哪个是长方体()A .B .C .三、按要求填: (共3题;共9分)10. (6分) (2019一上·江干期末) 请你在横线上填上“>”“<”或“=”。
8+7________15 10+5________19-6 16-8________16-7 12+5________12-5 6+8________13 17-4________7+911. (1分) (2018一上·永宁期中) 数一数,下面由几个正方体摆成的?________12. (2分)在横线上填上合适的数。
河南省郑州市2024小学数学一年级上学期人教版期末考试(强化卷)完整试卷

河南省郑州市2024小学数学一年级上学期人教版期末考试(强化卷)完整试卷一、填一填(共10小题,28分) (共10题)第(1)题在12、9、7、20、10中,最大的数是( ),最小的数是( )。
第(2)题画△,比★多4个。
★★★★★★( )第(3)题下面能搭稳的画“√”。
()()()()第(4)题从小到大数一数,14前面一个数是( ),后面一个数是( );17里面有( )个一和( )个十,它在( )和( )的中间。
第(5)题数墙。
(1)(2)第(6)题在下面的括号里填上合适的数。
4+( )=7 9-( )=1 ( )+10=15( )-2=8 ( )+5=9 ( )-2=10第(7)题在长方体下面画“√”,正方体下面画“×”,圆柱下面画“△”。
( )( )( )( )第(8)题看图写数。
( ) ( ) ( )第(9)题圈一圈,填一填。
猫的数量和鱼的数量(不相等同样多)。
3()3第(10)题○+○=10,△+9=□,○+□=18,△=( ),□=( ),○=( )。
二、轻松选择(共4题,12分) (共4题)第(1)题下面第()个算式的计算结果等于8。
A.9+9B.10-2C.6+3第(2)题18-5的计算结果与下面第()个算式的计算结果相等。
A.9+2B.8+5C.16-4第(3)题()-6<12,括号里最大能填()。
A.17B.18C.16第(4)题比15大比19小的数是()。
A.16B.14C.19三、算一算(共4题,32分) (共4题)第(1)题看图写算式。
第(2)题看图列式计算。
(只)第(3)题我能直接写出答案。
2+5= 6-1= 3+3= 7-6= 6-4=1+3= 5+0= 5-1= 4+1= 4-4=第(4)题别粗心,要全对!5+3-7= 5-2+4= 0+0= 3+6=8-3= 4+6-3= 7-2-5=四、解答题(共4题,28分) (共4题)第(1)题妈妈买了8瓶酸奶,小巧喝掉了6瓶,还剩几瓶?第(2)题今天,小猫钓了9条鱼,猫妈妈和它钓得一样多,它们一共钓了多少条鱼?(条)第(3)题用自己的方式表示出下面算式的意思。
河南省2021年高一上学期期末数学试卷A卷

河南省2021年高一上学期期末数学试卷A卷姓名:________ 班级:________ 成绩:________一、选择题(共10小题,每小题4分,满分40分) (共10题;共20分)1. (2分)已知集合P={x|x2=1},Q={x|mx=1},若Q⊆P ,则实数m的数值为()A . 1B . -1C . 1或-1D . 0,1或-12. (2分)直线l过点P(1,3),且与x、y轴正半轴所围成的三角形的面积等于6,则l的方程是()A . 3x+y-6=0B . x+3y-10=0C . 3x-y=0D . x-3y+8=03. (2分) (2017高一上·汪清月考) 下列函数中,是同一函数的是()A .B .C .D .4. (2分) (2016高一上·翔安期中) 已知a= ,b=20.5 , c=0.50.2 ,则a,b,c三者的大小关系是()A . b>c>aB . b>a>cC . a>b>cD . c>b>a5. (2分) (2017高二上·定州期末) 已知a>0,b>0,且ab=1,则函数f(x)=ax与函数g(x)=﹣logbx 的图象可能是()A .B .C .D .6. (2分) (2020高二上·古县期中) 已知直线和互相平行,则间的距离是()A .B .C .D .7. (2分)如果直线l:y=kx﹣5与圆x2+y2﹣2x+my﹣4=0交于M、N两点,且M、N关于直线2x+y=0对称,则直线l被圆截得的弦长为()A . 2B . 3C . 4D . 28. (2分)(2017·潮南模拟) 某几何体的三视图如图所示,则该几何体的体积是()A .B .C .D . π9. (2分) (2020高一上·吉安期中) 已知是定义在上的偶函数,且在上为增函数,则的解集为()A .B .C .D .10. (2分) (2018高二上·汕头期中) 已知方程有两个不同的实数解,则实数的取值范围是()A .B .C .D .二、填空题 (共4题;共4分)11. (1分) (2020高一上·辽宁期中) 函数的定义域为,则的定义域为________.12. (1分) (2019高一上·漯河月考) 若,则实数a的取值范围是________。
河南省郑州市2021版一年级上学期数学期末试卷D卷

河南省郑州市2021版一年级上学期数学期末试卷D卷姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、算一算 (共4题;共8分)1. (5分) (2019一下·香洲期末) 直接写出得数17-9= 45+6= 54-6= 14+6+54=50+50= 32-9= 8+66= 26-4+20=39-9= 55+20= 22+9= 60-(14+6)=7角+5角=()元()角 8元5角-2角=()元()角2. (1分)接力赛________________________3. (1分)填>、<或=.7+9________179+4________134. (1分)在横线上填上“>”、“<”或“=”。
(2) 6+9________9二、填一填。
(共7题;共13分)5. (1分)在横线上填上>、<或=.(1) 37+20________60(2) 65-40________256. (3分) (2020一下·陇县期末) 按规律填数。
(填在括号和图形里)(1) 80,75,70,65,________,________,________。
(2)7. (1分)运用给出的数字,组成最大数和最小数。
8. (1分)在横线上填上>、<或=.(1) 20________10(3) 9+1________2+79. (1分) (2018一上·罗湖期末) 下面几个数中,最接近10的是________ ,最接近20的是________,大于14又小于16的数是________。
10. (1分)正方体是长、宽、高都相等的________.11. (5分) (2019一上·龙华) 比一比,圈一圈。
(1)比 (小,大)比 (小,大)(2)女孩比男孩(多,少)男孩比女孩(多,少)三、选一选。
(共6题;共12分)12. (2分)小明左手边是东北方,他的右手边是()A . 东北B . 西北C . 西南13. (2分) (2020一上·都匀期末) 和16相邻的两个数是()。
【三套试卷】郑州市小学一年级数学上册期末试卷(含答案)

班级姓名得分7+6= 11+5= 20-10= 3+9= 10-4=16-5= 6+7= 11+4= 3+4= 8+6=8+5=18-7= 4+12=4+10= 5+6= 9-6=5+10= 19-9=15+2=15+3=6+7=16-3= 2+3= 8-2= 2+9=10-7=11+6= 9+6=10+4=17-6=18-10=5+14= 15-5= 9+8= 19-10=19-6= 9-9= 12+5=2+10=5+10=8+1= 5+6= 14+5= 7+7=16-6= 6-6= 4+8=7+9= 3+6= 6+8=6+6= 3+7= 12-2= 11+2= 14-10=9+7=14-4=8+6=10+9= 9+5=17-7= 8+8= 5+5= 7+6= 12-10=19-2= 4+7= 16-4= 3+8= 6+7=7+8=10-5= 7-5=14+3= 7+0=13-3=15+4= 2+7= 2+12= 10+6=17-5= 6+4= 10+9= 8+5= 7+4=16+4=10-9= 17+2=10+7= 13-10=3+6=13-1=3+3=14-2= 11-1=2+4= 6+6= 2+10= 9+2= 13+4= 7-2= 3+8= 13-0= 4+8= 4+8=9+5=18-5= 9+7= 7+7= 3+9=10-8= 9+6= 6+8= 11+2= 3+16=3+12= 12+7= 16-5= 8+5= 9+4=一、小巧的爸爸喜欢喝浓茶,下面三杯放入同样多的茶叶,应该端哪一杯给爸爸?()A.B.C.二、比少(_____)个,比多(_____)个三、在里填上合适的数。
四、最小的两位数是________,它比9多________。
五、20里面有2个十。
(____)六、画,使比多2_____________________和同样多______________七、按规律画一画。
______________________________。
2021-2022学年人教版一年级上期末考试数学试卷及答案解析

2021-2022学年一年级上学期期末考试数学试卷一、口算下面各题。
(10分)1.口算下面各题。
7+4=2+5=5+3=5+4=8﹣3=1+8=8﹣6=9﹣3=2+7=0+8=10﹣8=10+4=5+5=3+7=9+6=9+2=9﹣7=10﹣6=4+6=13+2=二、填空题。
(12分)2.(2分)1个十和2个一合起来是。
3.(2分)19里面有个十和个一.4.(2分)15前面一个数是,后面一个数是.5.(2分)一个数,十位上是1,个位上是6,这个数是。
6.(2分)时针指着9,分针指着12,这时的时间是.7.(2分)星期一的前一天是星期。
三、在横线里填上合适的数。
(12分)8.(12分)在横线里填上合适的数。
6+=157+=165+=13 9+=125+=113+=12 8+=127+=107+=11 10+=1211+=136+=14四、解答题(共1小题,满分4分)9.(4分)连一连。
五、比一比、画一画、填一填。
(8分)10.(4分)按要求画一画,填一填。
(1)画〇,比☆多两个。
☆☆☆☆(2)画△,比少3个。
11.(2分)看图写数。
12.(2分)按规律填数。
14、、、17、、.12、10、、、、.六、填一填。
(4分)13.(4分)填一填。
(1)小狗跑在最面,小象跑在最面。
(2)小象跑在小牛的面。
(3)小兔跑第,它的后面还有只小动物。
七、在横线里填上“>”“<”、“=”。
(12分)14.(12分)在横线里填上“>”“<”、“=”。
8+4135+9145+715 6+5127+6123+91410﹣877+8169+615 8+3118+8177+812八、(12分)15.(12分)3+6+4=8+5+2=19﹣3﹣5=17﹣7+3=3+8+2=9﹣5﹣4=6+4+2=9+1+8=5+8﹣3=8+5+6=11﹣1+5=6+4+9=九、想一想,填一填。
(4分)16.(4分)个个个个十、看图列式计算。
(8分)17.(8分)看图列式计算。
郑州市一年级上学期数学期末试卷
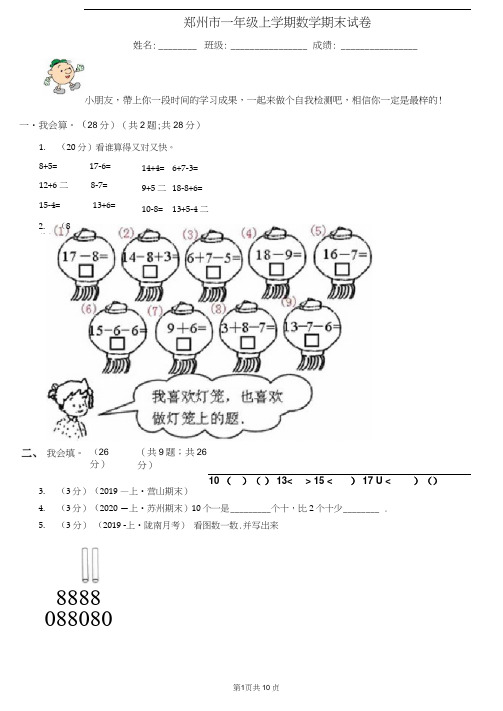
郑州市一年级上学期数学期末试卷姓名: ________ 班级: ________________ 成绩: ________________小朋友,帶上你一段时间的学习成果,一起来做个自我检测吧,相信你一定是最梓的! 一・我会算。
(28分)(共2题;共28分)1. (20分)看谁算得又对又快。
14+4= 6+7-3=9+5二18-8+6=10-8= 13+5-4二10 ()() 13< > 15 < ) 17 U < )()3.(3分)(2019 —上•营山期末)4.(3分)(2020 —上•苏州期末)10个一是_________ 个十,比2个十少________ .8888088080我会填。
(26分)(共9题;共26分)8+5=17-6=12+6 二8-7=15-4=13+6=5. (3 分)(2019 -上•陇南月考)看图数一数.并写岀来2. (8分)6.(3分)(2018 —上•福田期末)6个一和1个十是_________ •它比157.(2分)在横线上填上“〉”、“<”或“二”.66 _______ 56+969+5 _______ 758.(2分)填表.(先从左到右填写表格中的总数,在填需次)9.(3分)看谁算得快。
(1)8托二 _____ 3+9 二______ 11-10= _________ 12-9= _________(2)15-7=13-5=8+7 二14-9=(3)9+9 二18-9=17-8=13-6=(4)16-8=7+9=16-6 二3+8 二10.(4分)计算:99 + 19+-7 + 2 =■8+31 = X(1) + s = 0+55 =X(2)+==7+77 =(3)X——我是小小审判官。
(5分)(共5题;共5分)12.(1分) 西瓜属于蔬菜类。
()13.(1分) ♦• ■ ***:**•,第五个点阵中点的个数是1+4X5=21.14.(1分) 17里而有7个十和1个一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021-2022学年河南省郑州市上街区上街实验高级中学高一上学期期末数学试题一、单选题1.设x ∈R ,则2-0x ≥“”是111x -≤-≤“” 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】B【分析】根据充分条件、必要条件的定义结合集合的包含关系可解. 【详解】设p :若2-0x ≥,则2x ≤, q :若111x -≤-≤,则02x ≤≤; 则q 表示的集合是p 表示的集合真子集, 即2-0x ≥“”是111x -≤-≤“”必要不充分条件, 故选:B .2.若正数a ,b 满足1a b +=,则91a b+的最小值为( )A .16B .13C .20D .15【答案】A【分析】根据()9191a b a b a b ⎛⎫+=++ ⎪⎝⎭,再结合基本不等式求解即可.【详解】因为正数a ,b 满足1a b +=,则()91919101016b a a b a b a b a b ⎛⎫+=++=++≥+= ⎪⎝⎭, 当且仅当9b a a b =且1a b +=,即34a =,14b =时取等号,此时91a b +取得最小值16.故选:A .3.若对于一切实数x 不等式240x ax -+>恒成立,则实数a 的取值范围为( ) A .()4,4- B .[]4,4-C .(],4∞-D .()4,+∞【答案】A【分析】x ∀∈R ,不等式240x ax -+>恒成立240x ax ⇔-+=无实数根,利用判别式小于零可得答案.【详解】∵对于一切实数x 不等式240x ax -+>恒成立,∴二次函数24=-+y x ax 的图象在x 轴上方, ∴240x ax -+=无实数根,∴()2244160a a --⨯=-<,解得44a -<<, 故选:A .4.一个半径为4的扇形,其弧长为1,则该扇形的圆心角的弧度数为( ) A .12B .13C .14D .2【答案】C【分析】利用扇形的弧长公式,列出方程,即可求解. 【详解】设该扇形的圆心角的弧度数为α,因为扇形所在半径为4的扇形,其弧长为1,可得41α⨯=,解得14α=. 故选:C.5.函数2()ln(28)f x x x =--的单调递增区间是 A .(,2)-∞- B .(,1)-∞ C .(1,)+∞ D .(4,)+∞【答案】D【详解】由228x x -->0得:x ∈(−∞,−2)∪(4,+∞), 令t =228x x --,则y =ln t ,∵x ∈(−∞,−2)时,t =228x x --为减函数; x ∈(4,+∞)时,t =228x x --为增函数; y =ln t 为增函数,故函数f (x )=ln(228x x --)的单调递增区间是(4,+∞), 故选D.点睛:形如()()y f g x =的函数为()y g x =,()y f x =的复合函数,() y g x =为内层函数,() y f x =为外层函数.当内层函数()y g x =单增,外层函数()y f x =单增时,函数()()y f g x =也单增; 当内层函数()y g x =单增,外层函数()y f x =单减时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单增时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单减时,函数()()y f g x =也单增.简称为“同增异减”.6.函数log (3)1a y x =-+(0a >且1a ≠)的图像恒过定点P ,则点P 的坐标是( ) A .(4,1) B .(3,1) C .(4,0) D .(3,0)【答案】A【分析】令对数的真数等于1,求得x y 、 的值,可得它的图像恒过定点P 的坐标,即可求得答案. 【详解】 函数log (3)1a y x =-+,(0a >且1a ≠). ∴令31x -=,解得4x =当4x =,1y =∴ 函数log (3)1a y x =-+(0a >且1a ≠)的图像恒过定点(4,1)P .故选:A .【点睛】本题考查了对数函数的图像经过定点问题,解题关键是掌握对数函数定义和函数过定点的解法,考查了分析能力和计算能力,属于基础题. 7.命题“R sin 10x x ∀∈+≥,”的否定是( ) A .R sin 10x x ∃∈+<, B .R sin 10x x ∀∈+,< C .R sin 10x x ∃∈+≥, D .R sin 10x x ∀∈+≥,【答案】A【分析】根据全称量词命题的否定为存在量词命题即得. 【详解】因为全称量词命题的否定为存在量词命题可得,所以命题“R sin 10x x ∀∈+≥,”的否定是R sin 10x x ∃∈+<,. 故选:A .8.若角θ的始边与x轴的非负半轴重合,终边过点(p ,则2sin cos θθ+=( )A.12B.1CD1【答案】A【解析】根据任意角的三角函数的定义求出sin θ,cos θ,从而代入计算可得; 【详解】解:因为角θ的始边与x轴的非负半轴重合,终边过点(p ,所以sin θ==1cos 2θ==,所以112sin cos 222θθ+=+= 故选:A9.下列函数定义域为()0,∞+且在定义域内单调递增的是( )A .x y e =B .1πy log x =-C .y =D .12y log x =【答案】B【分析】根据题意,依次分析选项中函数的定义域以及单调性,即可得答案. 【详解】解:根据题意,依次分析选项:对于A ,x y e =,为指数函数,其定义域为R ,不符合题意; 对于B ,1ππy log x log x=-=,为对数函数,定义域为()0,∞+且在定义域内单调递增,符合题意;对于C ,y =[)0,∞+,不符合题意; 对于D ,12y log x=,为对数函数,定义域为()0,∞+且在定义域内单调递减,不符合题意;故选B .【点睛】本题考查函数的定义域以及单调性的判定,涉及对数函数的性质,属于基础题. 10.已知定义在R 上的函数()f x 的图象是连续不断的,且有如下对应值表:那么函数()f x 一定存在零点的区间是( )A .(1,2) B .(2,3) C .(3,4)D .(4,+)∞【答案】A【解析】利用函数零点的存在定理进行函数零点所在区间的判断,关键要判断函数在相应区间端点函数值的符号,如果端点函数值异号,则函数在该区间有零点.【详解】解:因为函数()f x 是定义在R 上的连续函数,且()10f >,()20f <, 根据函数零点的存在定理可知故函数()f x 在区间()1,2内存在零点. 故选:A .【点睛】本题考查函数零点的判断方法,关键要弄准函数零点的存在定理,把握好函数在哪个区间的端点函数值异号,属于基础题.11.已知函数(2),2()1,2x a x x f x a x +≥⎧=⎨+<⎩是R 上的单调递增函数,则实数a 的取值范围是( )A .(,0)-∞B .(0,1)C .(0,3)D .(1,3)【答案】D【分析】利用分段函数的单调性进行求解即可.【详解】解:若()f x 在R 上为增函数,则满足220112(2)a a a a +>⎧⎪>⎨⎪+≤+⎩,即221230a a a a >-⎧⎪>⎨⎪--≤⎩,得2113a a a >-⎧⎪>⎨⎪-<<⎩,得13a <<,即实数a 的取值范围是(1,3). 故选:D .12.函数()()1ln 23f x x x =++-的定义域为( ) A .()2,-+∞ B .[)2,-+∞C .()()2,33,⋃-+∞D .[)()2,33,-⋃+∞【答案】C【分析】根据对数函数的概念和分式的意义计算即可.【详解】由题意知,2030x x +>⎧⎨-≠⎩,解得2x >-且3x ≠,所以函数的定义域为(23)(3)-+∞,,,故选:C13.与y x =为同一函数的是( ) A .y x =B.y C .()(),0,0x x y x x ⎧>⎪=⎨-<⎪⎩D .log ax y a =【答案】B【分析】根据定义域和对应法则,逐项判断即可得解.【详解】对于A ,函数y x =与y x =的对应法则不同,所以两函数不是同一函数,故A 错误; 对于B,函数y x ==,与函数y x =的对应法则相同,且定义域均为R , 所以两函数为同一函数,故B 正确;对于C ,函数()(),0,0x x y x x ⎧>⎪=⎨-<⎪⎩的定义域为{}0x x ≠,y x =的定义域为R , 两函数定义域不同,不是同一函数,故C 错误;对于D ,函数log ax y a =的定义域为{}0x x >,y x =的定义域为R ,两函数定义域不同,不是同一函数,故D 错误. 故选:B.14.已知20.6a =,0.62b =,2log 0.6c =,则a ,b ,c 的大小关系为( ) A .a b c >> B .b a c >> C .b c a >> D .c b a >>【答案】B【分析】由指数函数、对数函数的单调性可得10b a c >>>>,即可得解. 【详解】由题意,2000.60.61a <=<=,0.60221b =>=,22log 0.6log 10=<=c , 所以10b a c >>>>. 故选:B.15.02341lg8lg125161)7-⎛⎫+-++ ⎪⎝⎭=( ) A .﹣38 B .﹣37 C .﹣39 D .﹣40【答案】B【分析】由已知结合指数幂的运算性质及对数的运算性质进行化简即可求解.【详解】()233024441lg8lg125161)lg 812572134981377-⎛⎫+-++⨯=++++ ⎪⎝⎭()-=-=﹣.故选:B . 16.若1tan()2αβ-=,1tan()3αβ+=,则tan 2β等于 A .17B .43C .17-D .43-【答案】C【详解】11tan()tan()132tan2tan[()()]11tan()tan()716αβαββαβαβαβαβ-+--=+--===-++⋅-+,故选C. 点睛:在三角化简求值类题目中,常常考“给值求值”的问题,遇见这类题目一般的方法为——配凑角:即将要求的式子通过配凑,得到与已知角的关系,进而用两角和差的公式展开求值即可.二、解答题17.已知不等式2(21)(1)0x a x a a -+++≤的解集为集合A ,集合(2,2)B =-.(1)若2a =,求A B ⋃;(2)若A B ⋂=∅,求实数a 的取值范围. 【答案】(1)(]2,3A B = (2){|3a a ≤-或}2a ≥【分析】(1)可得出[],1,2A a a a =+=时,可得出集合A ,然后进行并集的运算即可;(2)根据[],1,(2,2)A a a B =+=-,并且A B ⋂=∅即可得出12a +≤-或2a ≥,从而可得出a 的取值范围.【详解】(1)2a =时,2(21)(1)0x a x a a -+++≤解得23x ≤≤,[]2,3A =,且(2,2)B =-,∴(]2,3A B =-;(2)由2(21)(1)0x a x a a -+++≤解得1a x a ≤≤+, [],1A a a =+,(2,2)B =-,且A B ⋂=∅,12a ∴+≤-或2a ≥,3a ∴≤-或2a ≥,∴实数a 的取值范围为{|3a a ≤-或}2a ≥. 18.已知函数()331x x m f x +=+是奇函数.(1)求实数m 的值;(2)用函数单调性定义证明()f x 是R 上的增函数. 【答案】(1)1-; (2)证明见解析.【分析】(1)f (x )是R 上奇函数,则f (0)=0,或根据()()f x f x -=-求解m ; (2)分离常数化简f (x )解析式,用定义法研究其单调性即可. 【详解】(1)∵函数()331x x mf x +=+是奇函数,∴()()f x f x -=-,333131x x x xm m--++=-++,133x x m m +⋅=--,即()()1310xm ++=,1m =-.(2)()31213131x x x f x -==-++, 设12x x <,则1233x x <,∴1203131x x <+<+.12113131x x >++,∴12223131x x -<-++,∴1222113131x x -<-++. ∴()()12f x f x <,函数()f x 在R 上单调递增.19.已知函数()()()log 3log 3a a f x x x =-++(0a >且1a ≠). (1)求函数()f x 的定义域;(2)判断函数()f x 的奇偶性,并说明理由; (3)当3a =时,求函数()f x 的最大值. 【答案】(1)()3,3-; (2)偶函数,理由见解析; (3)2.【分析】(1)根据对数的真数大于零可得出关于x 的不等式组,由此可解得函数()f x 的定义域; (2)判断出函数()f x 为偶函数,再利用偶函数的定义可说明结论成立; (3)利用二次函数的基本性质结合对数函数的单调性可求得函数()f x 的最大值.【详解】(1)解:对于函数()f x ,有3030x x ->⎧⎨+>⎩,解得33x -<<,故函数()f x 的定义域为()3,3-.(2)解:函数()f x 为偶函数,理由如下:函数()f x 的定义域为()3,3-,且()()()()log 3log 3a a f x x x f x -=++-=, 因此,函数()f x 为偶函数.(3)解:当3a =时,()()()()2333log 3log 3log 9f x x x x =-++=-,因为33x -<<,则2099x <-≤,且函数3log y u =为增函数,故()()(]23log 9,2f x x =-∈-∞,即函数()f x 的最大值为2.20.已知函数2()2cos cos (0,R)f x x x x a a ωωωω=++∈>的最大值为1,且()f x 图象的两条相邻对称轴之间的距离为π2,求:(1)ω和a 的值;(2)当,22ππx ⎡⎤∈-⎢⎥⎣⎦,求函数()f x 的单调递增区间.【答案】(1)1,2ω==-a (2)ππ,36⎡⎤-⎢⎥⎣⎦【分析】(1)由题意,利用三角恒等变换化简函数的解析式,再根据正弦函数的图象和性质,求出ω和a 的值;(2)由题意可知,利用整体代入即可得出正弦函数的单调性,进而求出函数的单调递增区间.【详解】(1)由2()2cos cos (0,R)f x x x x a a ωωωω=++∈>得 π()1cos 2212sin 26f x x x a a x ωωω⎛⎫=++=+++ ⎪⎝⎭所以,函数()f x 的最大值为121a ++=,得2a =-; 即函数π()2sin 216f x x ω⎛⎫=+- ⎪⎝⎭;又因为()f x 图象的两条相邻对称轴之间的距离为12ππ222ω⨯=, 所以,1ω=,即π()2sin 216f x x ⎛⎫=+- ⎪⎝⎭.(2)对于函数π()2sin 216f x x ⎛⎫=+- ⎪⎝⎭,令πππ2π22π+,Z 262k x k k -≤+≤∈,得ππππ+,Z 36k x k k -≤≤∈, 可得函数()f x 的增区间为πππ,π+,Z 36k k k ⎡⎤-∈⎢⎥⎣⎦ ;故当,22ππx ⎡⎤∈-⎢⎥⎣⎦时,函数的增区间为ππ,36⎡⎤-⎢⎥⎣⎦.21.已知函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图.(1)求函数()f x 的解析式;(2)将函数()f x 的图象上所有点的横坐标变为原来的2倍,纵坐标不变,再将所得图象向左平移6π个单位,得到函数()g x 的图象,当,6x ππ⎡⎤∈-⎢⎥⎣⎦时,求()g x 值域.【答案】(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭;(2)[3,2]-.【分析】(1)根据图象由函数最值求得A ,由函数周期求得ω,由特殊点求得ϕ,即可求得解析式; (2)根据三角函数图象的变换求得()g x 的解析式,再利用整体法求函数值域即可.【详解】(1)由图象可知,()f x 的最大值为2,最小值为2-,又0A >,故2A =,周期453123T πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦,2||ππω∴=,0ω>,则2ω=, 从而()2sin(2)f x x ϕ=+,代入点5,212π⎛⎫⎪⎝⎭,得5sin 16⎛⎫+=⎪⎝⎭πϕ, 则5262k ππϕπ+=+,Z k ∈,即23k πϕπ=-+,Z k ∈, 又||2ϕπ<,则3πϕ=-.()2sin 23f x x π⎛⎫∴=- ⎪⎝⎭.(2)将函数()f x 的图象上所有点的横坐标变为原来的2倍,纵坐标不变,故可得2sin 3y x π⎛⎫=- ⎪⎝⎭;再将所得图象向左平移6π个单位,得到函数()g x 的图象 故可得()2sin()6g x x π=-;[,]6x ππ∈-5[,]636x πππ∴-∈-,3sin ,162x π⎡⎤⎛⎫-∈-⎢⎥ ⎪⎝⎭⎣⎦, 2sin 3,26x π⎛⎫⎡⎤-∈- ⎪⎣⎦⎝⎭,()[3,2]g x ∴-的值域为. 22.已知函数()443sin 2cos sin 1f x x x x ωωω=+-+(其中01ω<<),若点,16π⎛⎫- ⎪⎝⎭是函数()f x 图象的一个对称中心.(1)求()f x 的解析式,并求距y 轴最近的一条对称轴的方程;(2)先列表,再作出函数()f x 在区间[],ππ-上的图象.【答案】(1)()2sin 16f x x π⎛⎫=++ ⎪⎝⎭,函数()f x 的图象距y 轴最近的一条对称轴的方程为3x π=; (2)答案见解析.【分析】(1)化简函数()f x 的解析式,由16f π⎛⎫-= ⎪⎝⎭结合ω的取值范围求出ω的值,利用函数()f x 的对称性可求得该函数图象距y 轴最近的一条对称轴的方程; (2)由[],x ππ∈-可得57666x πππ-≤+≤,然后利用五点法,通过列表、描点、连线可作出函数()f x 在区间[],ππ-上的图象.【详解】(1)解:()()()22223sin 2cos sin cos sin 1f x x x x x x ωωωωω=++-+ 32cos 212sin 216x x x πωωω⎛⎫=++=++ ⎪⎝⎭, 点,16π⎛⎫- ⎪⎝⎭是函数()f x 图象的一个对称中心, 则36k ωπππ-+=,Z k ∈,132k ω∴=-+,Z k ∈, 01ω<<,则0k =,12ω=,故()2sin 16f x x π⎛⎫=++ ⎪⎝⎭, 由()62x n n Z πππ+=+∈得()3x n n Z ππ=+∈,令0k =,得函数()f x 图象距y 轴最近的一条对称轴方程为3x π=.(2)解:由(1)知,()2sin 16f x x π⎛⎫=++ ⎪,当[],x ππ∈-时,57666x πππ-≤+≤,列表如下:则函数()f x 在区间[],ππ-上的图象如图所示.。
