最新层次分析法和灰色聚类分析法在绩效评估中的应用
层次分析法在业绩评价上的运用

层次分析法在业绩评价上的运用近期,我公司准备对今年聘用的技术质量科长进行业绩和能力评优,由于指标较多,不易直接进行评比,同时,四个技术质量科长分属四个不同的分厂,各分厂人员、技术状况、产品品种、工作复杂程度、基础条件等方面存在事实上的一些差异,导致如果仅仅凭业绩绝对结果来进行评比,则不能完全反映其各自的工作能力情况,基础条件好的具有先天的优势,但如果将各分厂业绩指标参照基础条件进行适当修正后,再利用数据、模型和决策中的层次分析法,构建层次分析模型,完全可以进行相对公平的定量评比。
一、层次分析法(Analytic Hierarchy Process简称AHP)原理层次分析法是20世纪70年代,美国著名运筹学专家,匹兹堡大学教授 T.L.Satty提出来的,通过建立层次结构模型,将决策有关的元素分解成目标、准则、方案等层次,构造判断矩阵求得对象层元素的合成权重排序,在此基础之上进行定性和定量分析的决策方法。
其构建的层次结构模型分为三个层次:最高层,只包括一个元素是决策分析的总目标,也叫总目标层;其次是中间层,包括许多个元素,是实现总目标的各个子目标,包括各种准则,约束,策略,也叫目标层;最后是最底层,是实现各决策目标的可行方案,措施等,称为方案层或对象层。
二、构建层次结构模型进行定量计算根据人力资源部提供的业绩记录资料,建立如下层次结构模型目标层:为能力和业绩最优决策(D),新品开发(A1),废品指标(A2),顾客投诉指标(A3),制程质量改进(A4),考核通报(A5),员工培训(A6),这六个因素组成了层次结构模型中的准则层A k。
一分厂技术质量科长(B1)、二分厂技术质量科长(B2)、三分厂技术质量科长(B3)、四分厂分厂技术质量科长(B4)则构成了的层次结构模型中的方案层。
根据以上信息,建立如下的层次结构模型:按照上述层次模型,六个指标A K相对于能力和业绩最优决策(D)的得分,经考评组评议,得出以下判断矩阵经计算可得,A1至A6得分分别为2.040,1.020,0.680,2.040,0.510,0.778。
层次分析和模糊熟悉在高校教师绩效评价中的应用

层次分析和模糊熟悉在高校教师绩效评价中的应用绩效评价是高校教师日常工作中非常重要的一环。
对教师的绩效评价不仅可以帮助教师及时检视自身的工作表现,有针对性地改进自己的工作方法,还可以为高校合理配置优秀教师资源、提高教育质量提供参考依据。
而层次分析和模糊熟悉等多种方法在高校教师绩效评价中应用广泛,本文将从两种方法的特点和运用角度进行阐述。
首先,层次分析法是一种用于帮助人们做出决策的定量技术。
在教师绩效评价中,层次分析法可通过逐级分解、对比各项指标的重要性,确定不同指标的权重,进而综合评价教师的工作表现。
具体而言,教师绩效评价存在许多指标因素,如教学水平、科研能力、师生互动等,而这些指标因素之间的重要程度却往往不同。
层次分析法可通过构建由上到下的层级结构,逐层对参数之间的比较和分析,最终确定各项指标的权重和分值体系。
该方法在高校教师绩效评价中的运用,不仅能够准确测量教师的工作效率、质量及卓越表现,也能为个性化因材施教的培养模式提供指导建议,提高教育质量,更好地满足学生和社会的需求。
其次,模糊熟悉的方法则是一种用于处理不确定性、模糊性问题的数学方法。
在教师绩效评价中,模糊熟悉方法可以利用集合论中的模糊综合评价法,把检查的每项指标运用三角模糊数表现出来,然后利用其重要程度或排序关系,采用模糊等级法对教师工作进行评价。
模糊熟悉的方法不仅能够依据数学模型,得出相对准确的教师工作能力评价结果,而且可以在评价过程中,在保证评价结果相对准确的前提下,体现“人文”的因素,如对评价结果的理解、谅解、接受程度等。
总体而言,高校教师绩效评价需要对教师的能力、成果、效应进行研究和评价。
层次分析法和模糊熟悉方法作为现代决策科学方法之一,在教师绩效评价中的运用取得了良好的效果。
其中,层次分析法在逐级分解且细致的过程中,精度相对较高;模糊熟悉方法则能够体现人文和因材施教的特点,更加全面。
因此,在实际运用中需要综合考虑多种或结合原理互补的方法,在专业性、科学性和全面性上进行协调,以全面、准确、公正地评价教师的工作表现。
2021层次分析法与灰色聚类法在保险公司投资风险评价中的应用分析范文2

2021层次分析法与灰色聚类法在保险公司投资风险评价中的应用分析范文 随着社会和经济的迅速发展,人口急剧膨胀和高度集中,灾害对人类的威胁也在不断增长,造成的破坏和损失与日俱增.保险公司是经营灾害风险的专业金融机构,本文以保险公司投资风险为研究对象,对保险公司投资风险进行风险分析. 本文主要采用层次分析法和灰色聚类法,对保险公司投资所涉及的风险因素进行分析.构建保险公司投资风险评价指标体系,选用主客观相融合的层次分析法计算指标权重,再结合灰色聚类的方法进行灰色聚类分析,得出各指标因素的风险值,并最后定量分析保险投资项目在运行中的风险等级.本文计算结果为保险公司降低或规避风险提供了理论依据,提高偿付能力,从而维护保险公司和被保险人的利益. 一、风险评价方法研究 本文研究主要采用层次分析法和灰色聚类法,对其主体所涉及的风险因素进行分析,构建保险投资风险评价指标体系.选用主客观相融合的层次分析法(AHP)计算指标权重,量化聚类指标权重,再通过灰色聚类的方法进行聚类分析,得出风险值,最后定量分析保险投资项目在运行中的风险等级. (一)层次分析法 层次分析法的基本思路是,首先将问题分成不同的层次,相应的层次包括若干的影响因素,根据相应的评价标度对不同的影响因素进行比较从而得到判断矩阵,计算获得不同影响因素的权重,为决策者提供依据。
第一步,构建评价体系。
评价体系主要包括目标层和准则层。
构建问题的评价体系,首先要明确该问题的评价目标,再明确影响问题评价的准则,可以分为若干层次,每一层都有相关的相应因素。
第二步,依据评价标度构造判断矩阵。
判断矩阵A中的元素 aij表示,根据某一判断准则以及表 1层次分析法评价标度,要素i 对要素 j 相对重要性的数量表示,且有aij>0,aij=1/aji,aii=1. 第三步,确定要素的相对权重。
设判断矩阵为A=(aij)n×n,计算该判断矩阵特征矩阵和最大特征根. 第四步,对判断矩阵进行一致性检验. 第五步,计算综合权重.为获得层次目标中的每一指标或评价方案的相对权重,必须进行各层次的综合计算,然后对相关权重进行总排序. (二)灰色聚类法.灰色聚类系统的概念是我国的邓聚龙教授根据"灰箱"的概念进而演变而来的. 灰色聚类系统是指部分信息不是完全模糊的,但是对于这些信息的关系也可进行灰色系统的提前掌控和控制. 第一步,确定灰类白化权函数.λkj为第j个聚类指标第k类白化函数的阀值. 白化函数根据闽值阀值情况有3种形式, 二、AHP-灰色聚类在保险公司投资风险评价中的应用 对保险公司投资风险评价是一项复杂的系统工程,要求建立一个保险公司投资风险评价指标体系,应用AHP-灰色聚类对保险公司投资进行风险评价,其步骤如下: (一)建立保险公司投资风险评价指标体系. 为了对保险公司投资风险作出正确的评价,应从政策层面风险因素、市场层面风险因素和管理层面风险因素三个角度建立保险公司投资风险评价体系.而政策层面风险因素、市场层面风险因素和管理层面风险因素的评价又分别有一些与其相关的要素构成. (二)基于AHP 法的评价指标权重的确定. 运用层次分析法,计算出准则层因素权重向量和指标层因素权重向量.为获得层次目标中的每一指标的相对权重,必须进行各层次的综合计算,然后对相关权重进行总排序. (三)灰色聚类风险评价。
基于灰色关联分析的市政工程项目绩效评价研究

基于灰色关联分析的市政工程项目绩效评价研究市政工程项目的绩效评价对于提高项目管理水平、优化资源配置、推动城市发展具有重要意义。
随着数据分析技术的发展,灰色关联分析作为一种有效的评价方法,被广泛应用于市政工程项目绩效评价领域。
本文将探讨基于灰色关联分析的市政工程项目绩效评价研究。
一、绩效评价的背景和意义市政工程项目绩效评价是对项目实施过程中的成本、进度、质量、安全等方面进行评估和分析的过程。
通过绩效评价,可以全面了解项目的运行情况,发现问题并及时采取措施进行改进。
绩效评价的结果可以为项目的决策提供依据,为项目的管理和控制提供参考。
二、灰色关联分析的原理和方法灰色关联分析是一种基于灰色系统理论的数据分析方法,它可以用于评价指标之间的关联程度。
灰色关联分析的基本原理是通过建立灰色关联度模型,计算各指标之间的关联度,并根据关联度的大小进行排序。
在进行灰色关联分析时,首先需要确定评价指标。
市政工程项目的绩效评价指标可以包括项目成本、工期进度、质量合格率、安全事故率等。
然后,将每个指标的数据进行标准化处理,以消除量纲和单位的影响。
接下来,计算各指标之间的关联度。
最后,根据关联度的大小,对指标进行排序,以确定各指标对绩效评价的影响程度。
三、基于灰色关联分析的市政工程项目绩效评价实例为了更好地说明基于灰色关联分析的市政工程项目绩效评价方法的应用,我们以某市政工程项目为例进行分析。
该市政工程项目的绩效评价指标包括项目成本、工期进度、质量合格率、安全事故率。
通过对各指标数据进行标准化处理,我们可以得到标准化后的数据。
然后,根据灰色关联度模型,计算各指标之间的关联度。
在计算关联度时,我们发现项目成本与工期进度之间的关联度较高,说明项目成本对工期进度有较大的影响。
而质量合格率与安全事故率之间的关联度较低,说明两者之间的关联性较弱。
通过对各指标的关联度进行排序,我们可以得到各指标对绩效评价的影响程度。
四、灰色关联分析在市政工程项目绩效评价中的应用前景基于灰色关联分析的市政工程项目绩效评价方法具有较高的应用价值和广阔的应用前景。
层次分析法在绩效评估中的应用研究

层次分析法在绩效评估中的应用研究绩效评估是人力资源管理的问题之一。
本文针对目前绩效评估指标权重确定方法中存在的问题,把层次分析法应用于绩效评估的研究中,解决了绩效评估权重确定方法主观性强,精度不够的问题。
标签:层次分析法绩效评估权重绩效评估又称员工绩效考核,即对员工在一定时期内的工作情况进行评价的过程,是人力资源开发与管理中的重要内容。
常用的绩效考评的方法主要有360度评价法、目标管理法、排列法、强制分布法、关键事件法、等级考评法、行为观察量表法、行为锚定法等,这些考评方法都偏重于定性分析,主观性、随意性较大。
如果将层次分析法应用于绩效评估中,就可以实现定量和定性相结合的方法,提高绩效评估的可靠性,进行有效的绩效评估。
1 层次分析法在确定绩效评估指标中应用的步骤美国运筹学家T.L.Saty教授于70年代初期提出了层次分析法(Analytic Hierarchy Process,简称AHP),层次分析法是针对一些较为复杂、较为模糊的问题作出决策的方法,适合解决那些难于进行完全定量分析的问题。
运用层次分析法建模的四个步骤为:建立递阶层次结构模型;构造出各层次中的所有判断矩阵;层次单排序及一致性检验;层次总排序及一致性检验。
下面阐述一下应用层次分析法对评测指标进行重要度判断的具体步骤:首先,确立评价指标体系。
通过提取公司人员包含的各类人员的绩效评估指标,在明确绩效指标体系之间的相互关系的基础上,建立一个目标层(被评估的岗位)、准则层(绩效评估一级指标)、指标层(绩效评估二级指标)组成的递阶层次模型。
其次,确定各判断矩阵。
通过两两比较下层元素对于上層元素的相对重要性,并把比较的结果用一个数值表示出来,建立判断矩阵。
本文按照1- 9 标度评判准则(表1)填写如下判断矩阵P=(Xij)n×m,其中Xij为i指标相对于j 指标的重要程度。
然后,确定每一个层次各评测指标的重要度值,并进行一致性检验。
计算权重向量W=(w1,…,wn)T。
灰关联度层次分析法在煤炭企业班组绩效考核中的应用

灰关联度层次分析法在煤炭企业班组绩效考核中的应用在煤炭企业班组人员绩效考核中,影响绩效的指标众多且具有不同属性。
为了使考核结果尽可能多地体现这些属性,且避免多指标权重难以确切分配这一弊端,文章根据灰色系统关联度原理,首先按指标集的不同属性分类得到低层次子集,然后,对每一子集求权重并进行关联度分析,最后,按灰色关联度最大原则,确定绩效考核结果。
实例分析表明,该方法层次分明,简便实用,对煤炭企业班组的绩效考核有较好的适用性。
标签:灰关联度层次分析煤炭企业班组绩效考核一、前言影响煤炭企业绩效考核的因素很多,人们在对煤炭企业进行绩效考核评价时,只能选取有限的主要指标来进行分析;所选取的评价指标,有些是定性的,有些是定量的;而有些定性指标数据,可以从现有的统计资料中获得,有些却是无法从统计资料中获得。
因此,绩效考核体系具有信息不完全的“灰色”特征。
鉴于此, 运用灰色系统理论对绩效考核指标体系进行评价优选非常适宜,而且完全可行。
建立一套科学、完善、合理的绩效考核综合评价指标体系并采用科学技术手段对其进行客观、科学、动态的定量评价,为煤炭行业绩效考核部门制定薪酬及培训策略,提供准确、及时的科学依据。
对此,本文将灰色关联度层次分析法应用于煤炭企业的绩效考核中,大大提高了绩效考核的准确性。
二、AHP 确定权重本文以神华神东煤炭集团一分公司班组的考核指标为例。
各考核指标的选取及其相对权重是通过调查问卷的统计和访谈方式, 对神华煤炭企业相关专家和人力资源部门的领导进行咨询,利用AHP来确定的。
1.建立层次结构模型班组绩效考核综合评价指标体系除了应该考虑安全、生产效益等一般性原则外,还必须遵循动态性、可测性、可比性。
其目的是节约能源和资源,减少安全隐患,使员工在安全的环境下高效率的工作。
在对指标体系进行系统分析的基础上, 将指标分组按照最高层(目标层)、指标层(准则层)、子指标层(子准则层)的形式分层排列起来,如图所示。
基于灰色层次分析法与灰聚类相结合的供应商风险评价研究

制造 中心 、 后勤 保障 中心 和质量 、 成本控 制 中心 , 同时对 供应
链 中企 业 的新产 品 开 发 有着 相 当 重要 的 作 用 。在 企 业 所 面 临
的风险空前巨大的今天 , 供应 商风 险管理对 企业生 存与发 展
具有十分重要 的现实意义 。供应商风险评估是 供应商风 险管 理的重要 基础。本文综合了灰色层次分析法 与灰聚类 的评价
g e l se n n d f al p l st emo e n e i c t d f h u p irr k e a u t n o et i n ep s r y cu t r g,a n l a p i d l n a mpr a su y o e s p l s v l ai fa c ran e tr r e,v ia i i y e h i i l t e i o i l a d- t g t e fa i i t n f cie e so e mo e . i e sb l y a d e e t n s ft d 1 n h i v h
益 的探 讨 。
供应商产品合格率 l 供应 商优 等产 品率 u2 3
供应商信息系统的先进性 u . / t 供应商信息系统与企业
沟 通 性 U2 7
2 确定供应商风 险指标体 系
供应商风险指在与供应商合作 中 , 通过合作关 系, 供应 从
S p l r Rik E a u t n Ba e n Co i e u p i s v l a i s d o mb n d GAHP a d Gr y Cl s e i g e o n e u trn
L ANG Z I e—bn,JANG i I Yu—h n ,XI h o—mo og ASa
灰色关联度分析法在综合绩效评价中的应用
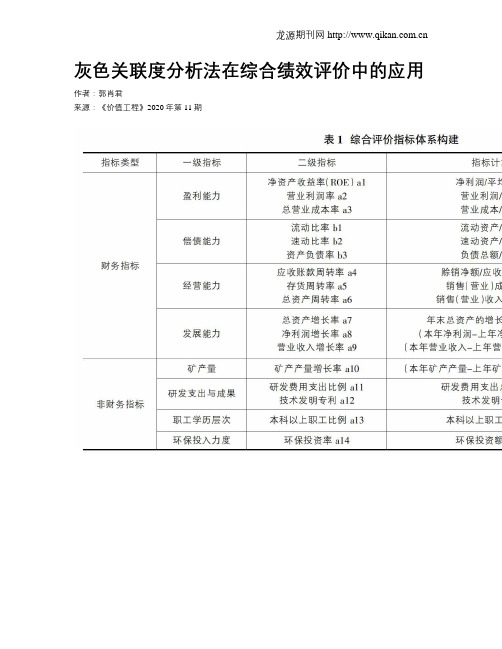
灰色关联度分析法在综合绩效评价中的应用作者:郭肖君来源:《价值工程》2020年第11期摘要:在复杂变化且信息不对称的市场经济环境中,企业的财务状况、综合绩效是一个典型的灰色系统。
因此,本文以有色金属类上市公司H企业并购V项目为例,从与企业财务绩效相关的盈利能力、偿债能力、经营能力、发展能力四个指标入手,同时,根据有色金属行业特点和H企业的战略发展目标,又融入了研发支出与成果、职工学历层次、环保投入等非财务指标,构建了评价H企业综合绩效的灰色关联分析模型,进而分析样本组指标与对照组指标的接近程度。
旨在通过实证分析的方法,研究在不确定的经济环境因素下评价企业综合绩效的可行性。
Abstract: In the market economy environment with complex changes and asymmetric information, the financial situation and comprehensive performance of an enterprise is a typical grey system. Therefore, Therefore, this article takes the non-ferrous metal listed company H enterprisemerger and acquisition V project as an example, starting with four indicators related to corporate financial performance: profitability, solvency, operating capacity, and development capacity,at the same time, according to the characteristics of non-ferrous metal industry and the strategic development goals of H enterprise, and integrating non-financial indicators such as R & D expenditure and achievements, staff education level, environmental protection investment,constructes a grey correlation analysis model to evaluate the comprehensive performance of H enterprise, and then analyzes the proximity of sample group indicators and control group indicators. The purpose is to study the feasibility of evaluating the comprehensive performance of an enterprise under the uncertain economic environment by empirical analysis.关键词:综合绩效评价;灰色关联度分析法Key words: comprehensive performance evaluation;grey correlation analysis中图分类号:F275; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 文献标识码:A; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 文章编号:1006-4311(2020)11-0104-040; 引言财务状况不仅是企业经营状态的晴雨表,对于上市企业而言,更是投资者了解企业发展的重要渠道。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
层次分析法和灰色聚类分析法在绩效评估中的应用层次分析法和灰色聚类分析法在绩效评估中的应用施狄峰摘要 绩效考核的评估是帮助企业维持和提高生产力、实现企业经营目标的手段之一,它一个复杂的大系统,一般企业的绩效评估是建立在关键考核指标得分乘以权系数的线性关系的基础上,但如果有两个下属分公司考核得分分别是97分和94分,究竟它们都属于优,还是一个是优、一个是良,原先的方法显然无法判断。
笔者运用运筹学决策分析法的层次分析法和灰色系统理论的灰聚类法两种方法对绩效加以评估,能将被考核企业的经营情况很清楚地区分开来,分类排序出来。
关键词 绩效评估 层次分析法 灰色聚类分析法设以某公司下属11个分公司绩效考核情况数据为例,记为K C B A i ,, ;并选取经营效绩考核中三个指标记为***3,2,1。
一、用层次分析法:1、权重设置:根据三个指标的权重系数A 1,A 2,A 3两两比较,得到数值a ij ,其定义和解释见表1,得出表2所示系数。
表1考核指标比值考核指标*1*2*3*1 1 1.13 3*20.89 1 2.67*30.33 0.38 1表2得到矩阵A=(a ij)3×3矩阵A为经营效绩的判断矩阵。
A=相应的特征向量为:B3=( 0.45 0.40 0.15 )T得出3个考核指标权重分别为0.45、0.40、0.152、类似地根据表3可用特征向量法求下属11个分公司相对于上述3个指标中每一个的权系数。
成对比较的结果如表4、表5、表6所示:下属分公司代号*1*2*3A 1.02 0.97 1.05B 1.16 1.10 1.07C 0.90 0.79 1.01D 1.00 0.98 1.13E 1.05 1.06 1.26F 0.79 0.64 1.10G 0.96 1.00 1.06H 0.95 1.11 1.07I 1.00 1.14 0.92J 0.82 0.71 0.98K 0.89 1.00 1.11表3指标*1:A B C D E F G H I J KA 1.00 0.88 1.13 1.02 0.97 1.29 1.06 1.07 1.02 1.24 1.15B 1.14 1.00 1.29 1.16 1.10 1.47 1.21 1.22 1.16 1.41 1.30C 0.88 0.78 1.00 0.90 0.86 1.14 0.94 0.95 0.90 1.10 1.01表4指标*2:表5指标*3:表6。
3、由此可求出3个指标的相应特征向量,按列组成矩阵B3B3=若记B k为第k层次上所有因素相对于上一层上有关因素的权向量按列组成的矩阵,则第k层次的组合权系数向量W k满足:W k=Bk ·Bk-1··········B2·B1由W3=B3B2=(0.0938 0.1050 0.0815 0.0944 0.1013 0.0721 0.0926 0.0965 0.0979 0.0745 0.0903 )T可以得出以下11个分公司经营绩效排名:排名分公司考核结果向量1 B 0.10502 E 0.10133 I 0.09794 H 0.09655 D 0.09446 A 0.09387 G 0.09268 K 0.09039 C 0.081510 J 0.074511 F 0.0721表7以上矩阵特征向量的计算是根据方根法近似计算。
二、用灰色聚类分析法:上例经营效绩考核中三个指标为聚类指标,记为***3,2,1;以好、中、差为三个考核结果等级,记为k =1,2,3;以下按11个分公司3个考核指标(表3数据)进行聚类。
第一步、给出聚类白化值ij d (如果灰类的白化值相差很大,应先作无量纲处理)⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=11.100.189.098.071.082.092.014.100.107.111.195.006.100.196.010.164.079.026.106.105.113.198.000.101.179.090.007.110.116.105.197.002.1ij d 第二步、确定灰类的白化函数设jk f 为j 项考核指标第k 个灰类的白化函数。
*1 考核指标好的灰数为),1.1[11∞∈⊗,表示*1考核指标在1.1以上就算好; *2 考核指标好的灰数为),1.1[21∞∈⊗,表示*2考核指标在1.1以上就算好; *3 考核指标好的灰数为),2.1[31∞∈⊗,表示*1考核指标在1.2以上就算好;*1 考核指标在0.9左右为中,]9.0[12ξ±∈⊗;*2 考核指标在0.9左右为中,]9.0[22ξ±∈⊗;*3 考核指标在1.0左右为中,]0.1[32ξ±∈⊗;*1 考核指标在0.8以下为差,]8.0,0[13∈⊗;*2 考核指标在0.8以下为差,]8.0,0[23∈⊗;*3 考核指标在0.9以下为差,]9.0,0[33∈⊗;第3步、求标定聚类权jk r ,利用公式m k r nj jkjkjk ,3,2,1,**1 ==∑=λλ可求得*1考核指标属于好的权11r 为324.02.11.11.11.1312111113111111**=++=++==∑=λλλλλλj j r同理,*2考核指标属于好的权21r 为0.324; *3考核指标属于好的权31r 为0.353; *1考核指标属于中的权12r 为321.019.09.09.0322212123121212**=++=++==∑=λλλλλλj j r同理,*2考核指标属于中的权22r 为0.321; *3考核指标属于中的权32r 为0.357;*1考核指标属于差的权13r 为 32.09.08.08.08.0332313133131313**=++=++==∑=λλλλλλj j r同理,*2考核指标属于差的权23r 为0.32; *3考核指标属于差的权33r 为0.36;第四步、求聚类系数ik σ,利用公式∑==**1)(n j jk ij jk ik r d f σ可得第1个分公司属于好的聚类系数11σ∑==**3111111)(j j j j r d f σ=311331211221111111)()()(r d f r d f r d f ++=353.0)05.1(324.0)97.0(324.0)02.1(312111⨯+⨯+⨯f f f图1 查图1(1),(4),(7),有927.0)02.1(11=f ,882.0)97.0(21=f ,875.0)05.1(31=f8950.0353.0875.0324.0882.0324.0927.011=⨯+⨯+⨯=σ 第1个分公司属于中的聚类系数12σ∑==**3121212)(j j j j r d f σ=321332221222121112)()()(r d f r d f r d f ++=357.0)05.1(321.0)97.0(321.0)02.1(322212⨯+⨯+⨯f f f 查图1(2),(5),(8),有867.0)02.1(12=f ,922.0)97.0(22=f ,95.0)05.1(32=f9134.0357.095.0321.0922.0321.0867.012=⨯+⨯+⨯=σ 第1个分公司属于差的聚类系数13σ∑==**3131313)(j j j j r d f σ=331333231223131113)()()(r d f r d f r d f ++=36.0)05.1(32.0)97.0(32.0)02.1(322313⨯+⨯+⨯f f f 查图1(3),(6),(9),有8.0)02.1(13=f ,845.0)97.0(23=f ,875.0)05.1(33=f8414.036.0875.032.0845.032.08.013=⨯+⨯+⨯=σ第五步、构造聚类行向量对于第1个分公司的聚类行向量记为1σ [][]8414.09134.08950.01312111==σσσσ第六步:聚类由于第1个分公司聚类向量中,以12σ为最大,所以第1个分公司属于第2类,即考核结果为中,同理可求:[][]7569.08100.09629.02322212==σσσσ [][]9378.09563.07949.03332313==σσσσ [][]8202.08884.09157.04342414==σσσσ [][]7438.07954.09748.05352515==σσσσ [][]9399.08314.07449.06362616==σσσσ[][]8475.09204.08891.07372717==σσσσ [][]8151.08812.09188.08382818==σσσσ [][]8368.08491.08893.09392919==σσσσ[][]9701.08956.07388.010*********==σσσσ [][]8525.09206.08832.011311211111==σσσσ聚类的总结果是:好的分公司有:B 、D 、E 、H 、I 中的分公司有:A 、C 、G 、K 差的分公司有:F 、J 。
三、按照传统的关键考核指标得分乘以权系数的线性关系的基础上得分排名情况:四、 结论:层次分析法和灰色聚类分析法所得的结果完全一致。
层次分析法用矩阵法来计算,从理论上讲较为合理,而且有数学推导证明。
其次如果要调整考核指标权重,只需调整相关的系数矩阵即可,而且相关矩阵还可作为效绩评价定量分析的依据;同时能将矩阵转换成曲线或图表格式,使考核结果一目了然。
层次分析法可以得到绩效评估的排序,但无法做到分类,灰色聚类分析法恰好弥补其不足。
