杨浦区暑假补习班新王牌高中数学王WI老师椭圆标准方程附性质
第14讲 椭圆(教师版)-2023年新高二暑期数学衔接(新人教版)
第14讲椭圆【学习目标】1.了解圆锥曲线的实际背景，感受圆锥曲线在刻画现实世界和解决实际问题中的作用2.经历从具体情境中抽象出椭圆的过程，掌握椭圆的定义，标准方程及简单几何性质3.通过椭圆与方程的学习，进一步体会数形结合的思想．4.了解椭圆的简单应用【基础知识】一、椭圆的概念平面内与两个定点F 1，F 2的距离之和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．集合P ＝{M ||MF 1|＋|MF 2|＝2a }，|F 1F 2|＝2c ，其中a >0，c >0，且a ，c 为常数：(1)若a >c ，则集合P 为椭圆；(2)若a ＝c ，则集合P 为线段；(3)若a <c ，则集合P 为空集．二、椭圆的标准方程和几何性质标准方程x 2a 2＋y 2b 2＝1(a >b >0)y 2a 2＋x 2b 2＝1(a >b >0)图形性质范围－a ≤x ≤a －b ≤y ≤b－b ≤x ≤b －a ≤y ≤a对称性对称轴：坐标轴对称中心：原点顶点A 1(－a,0)，A 2(a,0)B 1(0，－b )，B 2(0，b )A 1(0，－a )，A 2(0，a )B 1(－b,0)，B 2(b,0)轴长轴A 1A 2的长为2a ；短轴B 1B 2的长为2b焦距|F 1F 2|＝2c 离心率e ＝ca ∈(0,1)a ，b ，ca 2＝b 2＋c 2的关系【解读】1.利用椭圆的定义定形状时，一定要注意常数2a >|F 1F 2|这一条件．2.注意长轴长、短轴长、焦距不是a,b,c,而应是a,b,c 的两倍.3.求椭圆标准方程的基本方法是待定系数法，具体过程是先定形，再定量，即首先确定焦点所在位置，然后再根据条件建立关于a ，b 的方程组．如果焦点位置不确定，要考虑是否有两解，有时为了解题方便，也可把椭圆方程设为mx 2＋ny 2＝1(m >0，n >0，m ≠n )的形式．4.用标准方程研究几何性质的步骤(1)将椭圆方程化为标准形式.(2)确定焦点位置.(3)求出a,b,c.(4)写出椭圆的几何性质.5.利用椭圆几何性质的注意点及技巧①注意椭圆几何性质中的不等关系在求与椭圆有关的一些量的范围，或者最大值、最小值时，经常用到椭圆标准方程中x ，y 的范围，离心率的范围等不等关系．②利用椭圆几何性质的技巧求解与椭圆几何性质有关的问题时，要结合图形进行分析，当涉及顶点、焦点、长轴、短轴等椭圆的基本量时，要理清它们之间的内在联系．三、焦点三角形椭圆上的点P (x 0，y 0)与两焦点构成的△PF 1F 2叫做焦点三角形．r 1＝|PF 1|，r 2＝|PF 2|，∠F 1PF 2＝θ，△PF 1F 2的面积为S ，则在椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)中：①当r 1＝r 2时，即点P 的位置为短轴端点时，θ最大；②S ＝b 2tan θ2＝c |y 0|，当|y 0|＝b 时，即点P 的位置为短轴端点时，S 取最大值，最大值为bc.四、焦点弦(过焦点的弦)焦点弦中以通径(垂直于长轴的焦点弦)最短，弦长l min ＝2b 2a .五、弦长公式AB 为椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的弦(斜率为k )，A (x 1，y 1)，B (x 2，y 2)，弦中点M (x 0，y 0)，则弦长l ＝1＋k 2|x 1－x 2|＝1＋1k2|y 1－y 2|六、求椭圆的离心率问题的一般思路求椭圆的离心率或其范围时，一般是依据题设得出一个关于a ，b ，c 的等式或不等式，利用a 2＝b 2＋c 2消去b ，构造关于a ，c 的齐次式，再转化为关于e 的方程或不等式，求椭圆离心率或取值范围七、椭圆中的最值问题1.椭圆中距离的最值问题的解法①利用椭圆的定义结合平面几何知识求解(适用于所求的表达式中隐含有长轴或者离心率e )或利用均值不等式；②根据椭圆标准方程的特点，把距离问题转化为二次函数求最值的问题(适用于定点在椭圆的对称轴上)；③用椭圆的参数方程设动点的坐标，转化为三角问题求解．2.椭圆中常见的最值问题(1)椭圆上的点P 到二焦点的距离之积||||21PF PF 取得最大值的点是椭圆短轴的端点，取得最小值的点在椭圆长轴的端点。
杨浦区补习班 高中辅导班 新王牌数学龚Y老师 函数的性质
杨浦新王牌小班3.4 函数的基本性质（3）基本问题及方法理解并能求解函数的最值和值域，综合运用函数的性质练习一、填空题1． 函数()2f x x =________2． 函数2()4,[1,5]f x x x x =-∈的最小值为__________；最大值为___________3． 函数221()1x f x x -=+的值域为_____________二、选择题4． 下列函数中，值域是(0,)+∞的是（ ）（A ）y =B ）21(0)y x x =+>（C ）21y x x =++（D ）21y x =5． 函数222(03)()6(20)x x x f x x x x ⎧-≤≤=⎨+-≤<⎩的最大值，最小值分别是（ ）（A ）0和－3 （B ）1和－9 （C ）1和－8 （D ）0和－8 6． 函数2()f x =（ ）（A ）有最小值2，无最大值 （B ）有最小值2.5，无最大值 （C ）有最大值2.5，最小值2 （D ）既无最大值，也无最小值三、解答题7． 求函数()2f x x =8． 设2()21f x x x =--在[,1]t t +上的最小值为()g t ，求()g t四、拓展题9．对,a b R ∈，记,max{,},a a b a b b a b≥⎧=⎨<⎩，求函数2()max{43,|3|}f x x x x =-+-的最小值。
第三章单元测试一、填空题1． 函数0(4)y x =--的定义域为________ 2． 函数2()21f x x =-，则(1)f x -＝___________ 3． 函数32()2f x x x =+，1()2g x x =+，则()()f x g x ＝_____________4． 函数y =的递减区间是__________5． 偶函数()f x ，当x >0时，2()22f x x x =-+，则x <0时，()f x ＝____________ 6． 两个同心圆，已知小圆半径为a 米，设大圆半径为x 米，则两个同心圆间的圆环面积y与x 之间的函数关系为_____________ 7． 已知53()8f x x ax bx =++-，且(2)10f -=，则(2)f ＝__________8． 函数y =R ，则k 的取值范围是___________9． 已知函数()||2f x x b =-+在(0,)+∞上为增函数，则实数b 满足的条件是___________ 10． 函数()y f x =同时满足条件：①定义域[1,1]-；②偶函数；③值域[1,0]-。
高二数学暑假讲义 第五节 椭圆的定义与标准方程
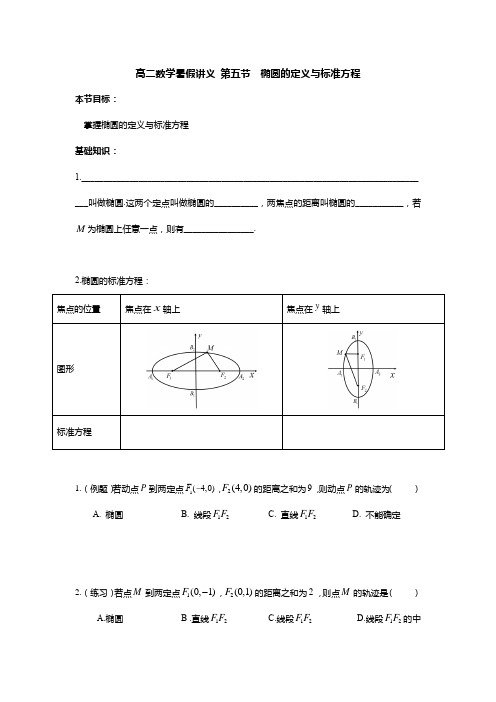
高二数学暑假讲义 第五节 椭圆的定义与标准方程本节目标：掌握椭圆的定义与标准方程 基础知识：1.________________________________________________________________________________叫做椭圆.这两个定点叫做椭圆的__________，两焦点的距离叫椭圆的___________，若为椭圆上任意一点，则有________________.2.椭圆的标准方程：1.（例题）若动点到两定点，的距离之和为，则动点的轨迹为（ ）A. 椭圆B. 线段C. 直线D. 不能确定2.（练习）若点到两定点，的距离之和为，则点的轨迹是（ ） A.椭圆B .直线C.线段D.线段的中M P F 1(-4,0)2(4,0)F 9P 12F F 12F F M 1(0,1)F 2(0,1)F 2M 12F F 12F F 12F F垂线3.（练习）若点到两定点,的距离之和为，则点的轨迹是（ ）A.椭圆B . 线段 C. 线段的中垂线D. 不存在4.（例题）椭圆上的点到点的距离与它到点的距离的和的等于，求此椭圆的标准方程.5.（练习）椭圆上的点到点的距离与它到点的距离的和的等于，求此椭圆的标准方程.6.（练习）在平面直角坐标系中，(5,0)B ，(5,0)C -， P 为一个动点，且26PB PC +=，求动点P 的轨迹方程．7.（练习）表示的曲线方程是__________________M(0,3)A (0,3)B -5M 12F F 12F F P F 1(-4,0)2(4,0)F 10P 1(0,6)F 2(0,6)F -206=8.（例题）已知椭圆22116x y m +=上的一点P 到椭圆一个焦点的距离为3,到另一焦点距离为7,则m 等于（ ）A ．10B ．5C ．15D ．259.（练习）已知椭圆221644x y +=上一点P 到一个焦点的距离为3，则点P 到另一个焦点的距离为( ) A ．2B ．5C ．6D ．710.（练习）已知椭圆221259x y +=上一点M 到焦点1F 的距离为2，N 是1MF 的中点，O 为坐标原点，则ON =（ ） A ．2 B ．4C ．8D ．3211.（例题）已知椭圆的两个焦点坐标分别为，并且经过点，求它的标准方程.(2,0),(2,0)-53,22⎛⎫-⎪⎝⎭12.（练习）过点 且与椭圆 有相同的焦点的椭圆方程为_____________．13.（练习）过点且与椭圆 22162x y += 有相同焦点的椭圆的标准方程为_____________14.（例题）中心在原点，且经过点的椭圆的标准方程是_________________ .15.（练习）若椭圆中心在原点，且经过(1,2)A,B ，求椭圆的标准方程.16.（练习）已知椭圆中心在原点，且过点，，则该椭圆的标准方程为________________．⎝⎭22134x y+=2),(M N --12⎫⎪⎭1,2⎛ ⎝⎭17.（例题）一动圆与已知圆外切，与圆内切，求动圆圆心的轨迹方程。
杨浦补习班 杨浦新王牌 周末同步提高拓展 高一数学王WI老师
杨浦新王牌学员日校： 年 级：高一 课时数：2学员姓名： 辅导科目： 数学 学科教师：王老师课 题 幂函数和指数函数授课日期及时段教学目的1、掌握一些常见幂函数的图像和性质2、掌握指数函数的图像和性质3、能利用幂函数和指数函数解决一些常见问题教学内容一．【知识精要】<1>幂函数： 形如:)(Q k x y k∈=常用幂函数性质及其图像性质如下：（1）0>k 时，幂函数的图象形如抛物线且恒通过原点）0,0(和）1,1(；0<k 时，幂函数的图象形如双曲线 且恒通过）1,1(（2）0>k 时，幂函数的图象在区间),0[+∞上是增函数．特别地，当1>k 时，幂函数的图象上扬；当10<<k 时，幂函数的图象下杨；0<k 时，幂函数的图象在区间),0(+∞上是减函数（3）幂函数在第一象限必有图像，在第四象限必没有图像，其它象限图像根据函数奇偶性四．【巩固训练】 （1）函数y =1－11-x 的图象是（ ）（2）如图为指数函数xxxxd y c y b y a y ====)4(,)3(,)2(,)1(，则d c b a ,,,与1的大小关系为 （ ）.A d c b a <<<<1 .B c d a b <<<<1 .C d c b a <<<<1 .D c d b a <<<<1（3）已知集合{}11M =-，，11242x N xx +⎧⎫=<<∈⎨⎬⎩⎭Z ，，则M N =I （ ）.A {}11-， .B {}1- .C {}0.D {}10-，（4）若函数m y x +=+-12的图象不经过第一象限，则m 的取值范围是 （ ）.A 2-≤m .B 2-≥m .C 1-≤m .D 1-≥m（5）已知222)(xx x f --=，则下列正确的是（ ）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数（6）方程1349+⋅-x x＋27＝0的解的平方和是（7）幂函数mx m m y )33(2--=在区间()+∞,0上是减函数，则m 的取值范围 （8）若函数|1|()2x f x m --=-的图象与x 轴有交点，则实数m 的范围是Oxya dc b（9）①函数xx x f 22)51()(-=的单调递增区间 ，值域②函数2323x y -=的单调递减区间 ，值域 ③函数)13()31(1822≤≤-=+--x y x x 的单调递增区间 ，值域（10）已知幂函数97222)199(--+-=m mx m m y 的图像不过原点，则m 的值为（11）一批设备价值a 万元，由于使用磨损，每年比上一年价值降低%b ，则n 年后这批设备的价值为 （12）若关于x 的指数方程043)4(9=+⋅++xxa 有实数解，则a 的取值范围 （13）设1,0≠>a a ，如果函数122-⋅+=x xa a y 在[]1,1-上的最大值为14，求a 的值（14）已知[]2,3-∈x ，求12141)(+-=x x x f 的最小值与最大值 五．【课后作业】（1）二次函数2y ax bx =+与指数函数()xby a=的图象只可为（ ）（2）设函数)(x f 定义在实数集上，它的图像关于直线1=x 对称，且当1≥x 时，13)(-=xx f ，则有（ ）)32()23()31(.f f f A << )31()23()32(.f f f B <<)23()31()32(.f f f C << )31()32()23(.f f f D <<（3）若幂函数dcbax y x y x y x y ====,,,在同一坐标系中的图象如下，则d c b a ,,,的大小关系是（ ） A 、d ＞c ＞b ＞aB 、a ＞b ＞c ＞dC 、d ＞c ＞a ＞bD 、a ＞b ＞d ＞c。
上海市-高二学科教师辅导教案12.3椭圆
2.掌握椭圆的简单凡何性质;掌握“力,等参数的儿何意义及关系.教学内容1.椭圆的两种定义：(1) 平面内与两定点A 扬的距离的和等于定长24>|氏川)的点的轨迹，即点集 |PF||+|PF 2|=2a, 2a>|F|F 2|}： (& = |站|时为线段 , 2a<\F l F 2\ 无轨迹)。
其中两定 点Fi ，凡叫焦点，定点间的距离叫焦距。
(2) 平面内一动点到一个定点和一定直线的距离的比是小于1的正常数的点的轨迹，即点 3 = 1为抛物线：为双曲线)2.标准方程:学员编号: 学员姓名: 课程主题：椭圆的方程及性质 学习目标教师辅导教案年 级：高二 辅导科目：数学授课时间:1.掌握椭圆的定义、标准方程，了解椭圆的参数方程学科教师:集M={H 胜=e ，0<e<l 的常数 d(1)焦点在】轴上，中心在原点: 4+4=i(。
》＞0):4 .点与椭圆的位置关系设为），椭圆（?:』+ £ = 1，焦点为f；,则：a' h"⑴点P在椭圆外十吝 _I =|必;| + |吒| _曷a b⑵点P在椭圆上=号+丢 _I D尸鸟I + IPKI _&；（I U⑶点P在椭圆内。
导唔—1勺斯I +1吒IM_ M -5.有关圆锥曲线弦的中点和斜率问题可利用“点差法”及结论：设椭圆：4 + 4 = 1上弦A8的中点为的如痫,则斜率k商-乌五, r扩cC月2 2 2对椭圆：£+打=|.则如=—£&・『b‘"肉【例题精讲】例1、求适合下列条件的椭圆的标准方程:（1）焦点在.' 轴上，焦距为8,椭圆上一点到两个焦点的距离的和为10;（2）两个焦点坐标为（0,2）和（0,-2）,且过点(3)焦点在坐标轴上，且关于原点对称，焦距为2化，且经过点«,旧。
2 2解：(1)设椭圆的标准方程为二+号=1 (a>/>>0),由题意知M = 10,.・.〃 =5, 5 b-今 ♦又2C = 8,..C = 4, 3—2=9,.・.所求椭圆标准方程为(2)设椭圆的标准方程为4 + ^ = 1 («>/>>0),由题意知：c=2即b 2=a 2-4又椭圆过点勺，・.•吝+料7 = 1」* +必二=4,化简此方程可得：\ 2 2) 4/ 4b- cr /-42</3 4-25^+50 = 0解得：疽=10 (a 2=|舍去)，.•方=6,.••所求椭圆标准方程为弟+P;说明：此题也可通过求定点到两个焦点的距离和2“来求标准方程，即当椭圆的焦点在.'轴上时，设椭圆的标准方程为4 + ^ = 1（a>b>0）,a' h"由已知c = *可得：胪=W-6,又过点（右，很），・・・号+3)2 j⑶ 当焦点在X 轴上时，设椭圆的标准方程为W +我=1 E>b>0),a tr由已知c = x/6可得：甘=疽-6,又过点(73,72),化简方程可得：疽-1成+ 18 = 0,.・・解得：a 2 =9 (疽=2舍去)， 所求椭圆标准方程为『5=1;32芬+罗-6* =而，又c ・ = 2, W =10-4 = 6,.・.所求椭圆标准方程为三+ = = 1； 10 6日^ = 1，化简方程可得：疽・11疽+ 12 = 0,.・.解得：疽=土买带=LL*舍去）， 2 2二所求棉圆标准方程为二^= +底_ = 1 ；ll + x/73 V73-1综上所述，所求椭圆的标准方程为《+兰=1和2〉二_^_ ="9 3 11 +妨V73-1例2、已知8、C为两个定点，且|8。
杨浦区暑假新高一补习班新王牌新高一数理化高L老师磁场知识点
杨浦新王牌磁场一、电流的磁场1．如图所示，两根平行放置的长直导线a和b载有大小相同方向相反的电流，a受到的磁场力大小为F1，当加入一与导线所在平面垂直的匀强磁场后，a受到的磁场力大小变为F2，则此时b受到的磁场力大小变为（）（A）F2（B）F1－F2（C）F1＋F2（D）2F1－F22．关于磁感线，下列说法中正确的是（）（A）磁感线从N极出发，终止于S极，是不连续的曲线（B）磁感线是实际存在的描绘磁场性质的曲线（C）磁感线能反映磁场中各点磁场的方向（D）磁体内部也有磁感线3．如图，在光滑水平桌面上有两根弯成直角的相同金属棒，它们的一端可绕固定转动轴O自由转动，另一端b相互接触，组成一个正方形线框。
正方形每边长度均为L，匀强磁场的方向垂直桌面向下，磁感应强度为B，当线框中通以图示方向的电流时，两金属棒在b点的相互作用力为f，求此时线框中的电流的大小。
4．取两根完全相同的长导线，用其中一根绕成如图（a）所示的螺线管，当在该螺线管中通以电流强度为I的电流时，测得螺线管内中部的磁感应强度大小为B，若将另一根长导线对折后绕成如图（b）所示的螺线管，并通以电流强度也为I的电流，则在该螺线管内中部的磁感应强度大小为（）（A）0 （B）0.5B （C）B （D）2B5．有两条长直导线垂直水平纸面放置，交纸面于a、b两点，通有大小相等的恒定电流，方向如图，a、b的连线水平。
c是ab的中点，d点与c点关于b点对称。
已知c点的磁感应强度为B1，d点的磁感应强度为B2，则关于a处导线在d点的磁感应强度的大小及方向，下列说法中正确的是（）（A）B1/2 ＋B2，方向竖直向上（B）B1/2 －B2，方向竖直向下（C）B1＋B2，方向竖直向下（D）B1－B2，方向竖直向上6．在真空的直角坐标系中，有两条互相绝缘且垂直的长直导线分别与x、y轴重合，电流方向如图所示. 已知真空中距无限长通电直导线距离为r处的磁感应强度B＝kI/r ，k＝2×10－7T?m/A，若I1＝4.0A，I2＝3.0A。
椭圆标准方程及其性质知识点大全
【专题七】椭圆标准方程及其性质知识点大全(一)椭圆的定义及椭圆的标准方程：●椭圆定义：平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ , 这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距. 注意：①若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ； ②若)(2121F F PF PF <+，则动点P 的轨迹无图形(二)椭圆的简单几何性：●标准方程是指中心在原点，坐标轴为对称轴的标准位置的椭圆方程。
标准方程12222=+b y a x )0(>>b a 12222=+b x a y )0(>>b a 图形性质焦点 )0,(1c F -，)0,(2c F ),0(1c F -，),0(2c F焦距 c F F 221= c F F 221= 范围a x ≤，b y ≤b x ≤，a y ≤对称性 关于x 轴、y 轴和原点对称顶点 )0,(a ±，),0(b ± ),0(a ±，)0,(b ±轴长长轴长12A A ,12A A =a 2，短轴长12B B ,12B B =b 2离心率①(01)c e e a =<< ，②21()b e a=-③222b a c -=（离心率越大，椭圆越扁）【说明】：1.方程中的两个参数a 与b ，确定椭圆的形状和大小，是椭圆的定型条件，焦点F 1，F 2的位置，是椭圆的定位条件，它决定椭圆标准方程的类型，常数a ，b ，c 都大于零，其中a 最大且a 2=b 2+c 2.2. 方程22Ax By C +=表示椭圆的充要条件是：ABC ≠0，且A ，B ，C 同号，A≠B 。
A ＞B 时，焦点在y 轴上，A ＜B 时，焦点在x 轴上。
(三)焦点三角形的面积公式：122tan2PF F S b θ∆=如图：●椭圆标准方程为:12222=+by a x )0(>>b a ，椭圆焦点三角形：设P 为椭圆上任意一点，12,F F 为焦点且∠12F PF θ=，则△12F PF 为焦点三角形，其面积为122tan2PF F S b θ∆=。
浦东暑假新高一数学补习班椭圆典型例题
椭圆典型例题一、已知椭圆焦点的位置，求椭圆的标准方程。
例1 :已知椭圆的焦点是F i（O, —1）、F2（0,1）, P是椭圆上一点，并且PF i+ PF2 = 2卩汩2, 求椭圆的标准方程。
解：由PF i+ PF2= 2F i F2 = 2X 2 = 4,得2a = 4.又c= 1,所以b2= 3.2 2所以椭圆的标准方程是y4 +号=1.2•已知椭圆的两个焦点为F1（—1,0）, F2（1,0），且2a = 10,求椭圆的标准方程.2 2解：由椭圆定义知c = 1,.・.b= 52— 1 = 24. •••椭圆的标准方程为25 + 24= 1.二、未知椭圆焦点的位置，求椭圆的标准方程。
例：1.椭圆的一个顶点为A 2,0，其长轴长是短轴长的2倍，求椭圆的标准方程.分析：题目没有指出焦点的位置，要考虑两种位置.解：（1 ）当A 2,0为长轴端点时，a =2 , b=1,2 2椭圆的标准方程为：—y 1;4 1（2）当A 2,0为短轴端点时，b = 2 , a = 4,2 2椭圆的标准方程为：—=1;4 16_ y M_1-1M2X M a 4五、求椭圆的离心率问题。
例一个椭圆的焦点将其准线间的距离三等分，求椭圆的离心率.2 2■ 1、、3…3c a ，…e =三、椭圆的焦点位置由其它方程间接给出，求椭圆的标准方程。
2 2例•求过点（-3,2）且与椭圆符+着=1有相同焦点的椭圆的标准方程.2解：因为C = 9-4= 5,所以设所求椭圆的标准方程为 9 上知g+2a 2— 5 = 1.由点（ 3,2）在椭圆4a 2— 5=1,所以a 2= 15.所以所求椭圆的标准方程为 yio=i. 四、与直线相结合的问题，求椭圆的标准方程。
例： 已知中心在原点，焦点在x 轴上的椭圆与直线 x • y -1 = 0交于A 、 为AB中点，0M 的斜率为0.25，椭圆的短轴长为 2,求椭圆的方程.2解：由题意，设椭圆方程为 笃• y 2 =1，aB 两点，M得 1 a 2x 2 -2a 2x =0，x-i x 221 a2 2~， a yM = 1 - X M2 /••• a =4，2解：幕2^ —cV3 31=1的离心率e，求k 的值.22 2 21 解：当椭圆的焦点在 x 轴上时，a = k 8 ,b =9，得c 二k-1.由e ，得k=4 .2当椭圆的焦点在 y 轴上时，a 2 =9 , b 2=k ・8，得c 2=1-k . 出 1 1 —k 1 加 5 由e ，得，即k =29445•••满足条件的k=4或k =-5 .4六、由椭圆内的三角形周长、面积有关的问题例：1•若△ ABC 的两个顶点坐标 A （ — 4,0）, B （4,0） , △ ABC 的周长为18,求顶点C 的 轨迹方程。
杨浦暑假补习班五角场新王牌高中数学春季新课开班
5.1 任意角及其度量（2）1.2018是第__________象限角.2.与π495-角的终边相同的最小正角是____________. 3.将集合},22,5|{Z k k ∈<<--=παπππαα用列举法表示为________________________. 4.半径为5cm ，圆心角为π54的扇形面积为_______________2cm . 5.若圆的一段弧长等于该圆的内接正三角形的边长，则这弧所对的圆心角的弧度数是________________.6.直径是20cm 的轮子，每秒旋转45弧度，轮周上一点经过3秒所转过的弧长是___________cm.7.与335π-角的终边相同的角可以表示为：①ππ352-k ，k ∈Z ；②ππ352+-k ，k ∈Z ； ③ππ312+-k ，k ∈Z ；④ππ312-k ，k ∈Z 其中正确的序号是_________________（请填写所有正确答案的序号）8.终边在x 轴的正半轴和y 轴的负半轴的夹角平分线上的角α的集合是（）A.{α|α=ππ432+k ，k ∈Z}B.{α|α=ππ43+k ，k ∈Z} C.{α|α=ππ412-k ，k ∈Z} D.{α|α=ππ41-k ，k ∈Z} 9.若集合},122|{Z k k A ∈+==ππαα，},1211|{Z k k B ∈-==ππαα，则（） A. A B B. A B C. A B =∅ D. A B=∅10.已知一个扇形OAB 的面积为1cm 2，周长是4cm ，求它的圆心角和弧AB 的长.11.（1）已知集合}032|{2≤-+=x x x A ，4|{πππ+<<=k x k x B ，k ∈Z}，求A∩B. （2）已知集合4242|{ππππ+<<-=k x k x A ，k ∈Z}，B ={y |0<y <π4}，求A∩B.12.根据下列条件，写出角α与角β的一个关系式：（1）角α与角β的终边关于x 轴对称；（2）角α与角β的终边关于y 轴对称；（3）角α与角β的终边关于原点对称；（4）角α与角β的终边关于直线y =x 对称.。
金桥高中补习班新王牌数学讲义椭圆的标准方程及其性质
【例7】设椭圆C：＋＝1(a>b>0)的右焦点为F，过F的直线l与椭圆C相交于A，B两点，直线l的倾斜角为60°，椭圆的半焦距为c，且 .如果|AB|＝，求椭圆C的方程.
【例8】（1）已知F是椭圆＋＝1的左焦点，P是此椭圆上的动点，A(1，1)是一定点，求|PA|＋|PF|的最大值和最小值.
【例4】(2014·高考安徽卷)设F1，F2分别是椭圆E：x2＋＝1(0<b<1)的左、右焦点，过点F1的直线交椭圆E于A，B两点．若|AF1|＝3|F1B|，AF2⊥x轴，则椭圆E的方程为________．
【例5】设F1，F2为椭圆＋＝1的两个焦点，P为椭圆上的一点，已知P，F1，F2是一个直角三角形的三个顶点，且＞，求的值.
（2）求A(0，2)到椭圆＋y2＝1上的动点的距离的最大值和最小值.
（3）在椭圆＋＝1上求一点，使它到直线2x－3y＋15＝0的距离最短.
【例9】()设P，Q分别为圆x2＋(y－6)2＝2和椭圆＋y2＝1上的点，则P，Q两点间的最大距离是()
A.5B.＋C.7＋D.6
【例10】（1）已知椭圆＋y2＝1的左、右焦点分别为F1、F2，点M在该椭圆上，且 · ＝0，则点M到y轴的距离为()
椭圆的标准方程及几何性质焦点在x轴上焦点在y轴上定义??212122ffaamfmf???图形标准方程y2a2x2b21ab0范围axabybayabxb对称中心原点o00顶点a1a0a2a0b10bb20b对称轴x轴y轴焦点f10cf20c焦距2c2a2b23
§4椭圆的标准方程及其性质（学案）
一、基础知识点
A．(－3，0) B．(－4，0) C．(－10，0) D．(－5，0)
沪教版(上海)数学高二下册-12.3椭圆的标准方程_(课件)PPT
上式两边再平方，得
a4 2a2cx c2 x2 a2 x2 2a2cx a2c2 a2 y2
整理得 (a2 c2 )x2 a2 y2 a2 (a2 c2 )
a2 c2 x2 a2 y2 a2 a2 c2
a2 c2 0
的点到两焦点的距离和为10。
解： 由题意可知 2a 10，∴ a 5
2c 6，c 3
b2 a2 c2 16
所以所求椭圆的标准方程为:
x2 y2 1
或 y2 x2 1
25 16
25 16
2．焦点在x轴上，焦距为2 6 ，且过
点 3, 2。
解:设所求的标准方程为
x2 a2
y2 b2
M( x, y)为椭圆上
y
M
的任意一点，又设
M与 F1、F2 的距离
F1
O F2
x
的和等于2a (2a 2c)
椭圆上点 M 的集合为 P M MF1 MF2 2a
( x c)2 y2 ( x c)2 y2 2a
移项平方，得
( x c)2 y2 4a2 4a ( x c)2 y2 ( x c)2 y2
x2 a2
y2 b2
1a
b
0
y2 a2
x2 b2
1a
b
0
（1）椭圆标准方程是关于 不含有一次项；
的二元二次方程，
（2）方程的左边是平方和的情势，右边是常数1；
（3）方程中 的系数不相等；
两种情势的标准方程的比较：
x2 a2
y2 b2
1a
b
0
与
y2 a2
x2 b2
1a b 0
奉贤最好的补习班,新王牌老师解析椭圆的性质
12．4 椭圆的性质二、教学目标设计掌握椭圆的对称性，顶点，范围等几何性质.能根据椭圆的几何性质对椭圆方程进行讨论，在此基础上会画椭圆的图形．学会判断直线与椭圆的位置，能够解决直线与椭圆相交时的弦长问题，中点问题等.在对椭圆几何性质的讨论中，注意数与形的结合与转化，学会分类讨论、数形结合等数学思想和探究能力的培养；培养探究新事物的欲望，获得成功的体验，树立学好数学的信心.三、教学重点及难点重点：椭圆的几何性质及初步运用难点：直线与椭圆相交时的弦长问题和中点问题五、教学过程设计一、引入课题“曲线与方程”是解析几何中最重要最基本的内容其中有两类基本问题：一是由曲线求方程，二是由方程画曲线．前面由椭圆定义推导出椭圆的标准方程属于第一类问题，本节课将研究第二类问题，由椭圆方程画椭圆图形，为使列表描点更准确，避免盲目性，有必要先对椭圆的范围、对称性、顶点进行讨论.二、讲授新课（一）对称性问题1：观察椭圆标准方程的特点，利用方程研究椭圆曲线的对称性？-代x后方程不变，说明椭圆关于y轴对称；x-代y后方程不变，说明椭圆曲线关于x轴对称；y-、yx-代x，y后方程不变，说明椭圆曲线关于原点对称；问题2：从对称性的本质上入手，如何探究曲线的对称性？以把x换成－x为例，如图在曲线的方程中，把x换成－x方程不变，相当于点P（x，y）在曲线上，点P点关于y轴的对称点Q（－x，y）也在曲线上，所以曲线关于y轴对称．其它同理.相关概念：在标准方程下，坐标轴是对称轴，原点是对称中心，椭圆的对称中心叫做椭圆的中心.（二） 顶点问题1：观察椭圆标准方程的特点，利用方程求出椭圆曲线与对称轴的交点坐标？在椭圆的标准方程中，令0=x ，得b y ±=，0=y ，得a x ±= 顶点概念：椭圆与对称轴的交点叫做椭圆的顶点.顶点坐标；)0,(),0,(21a A a A -，),0(),,0(21b B b B -.相关概念：线段2121,B B A A 分别叫做椭圆的长轴和短轴，它们的长分别等于b a 2,2，a 和b 分别叫做椭圆的长半轴长和短半轴长.在椭圆的定义中，c 2表示焦距，这样，椭圆方程中的c b a ，,就有了明显的几何意义.问题2：在椭圆标准方程的推导过程中令222b c a =-能使方程简单整齐，其几何意义是什么？c 表示半焦距，b 表示短半轴长，因此，联结顶点2B 和焦点2F ，可以构造一个直角三角形，在直角三角形内，2222222OB F B OF -=，即222b c a =-.（三） 范围问题1：结合椭圆标准方程的特点，利用方程研究椭圆曲线的范围？即确定两个变量的允许值范围．12222=+b y a x 变形为：a x a a x a x ax b y ≤≤-⇒≤⇒≤≥-=22222201， 这就得到了椭圆在标准方程下x 的范围：a x a ≤≤-同理，我们也可以得到y 的范围：b y b ≤≤- 问题2：思考是否还有其他方法？ 方法一：可以把12222=+b y a x 看成1cos sin 22=+αα，利用三角函数的有界性来考虑bya x ,的范围；方法二：椭圆的标准方程表示两个非负数的和为1，那么这两个数都不大于1，所以122≤ax ，同理可以得到y 的范围，由椭圆方程中y x ,的范围得到椭圆位于直线a x ±=和b y ±=所围成的矩形里. 三、例题解析例1 已知椭圆的方程为364922=+y x .（1） 求它的长轴长、短轴长、焦点坐标和顶点坐标;（2） 写出与椭圆364922=+y x 有相同焦点的至少两个不同的椭圆方程.解：[说明] 这是本节课重点安排的基础性例题，是椭圆几何性质的简单应用. 例2（1）求以原点为中心，一个焦点为),1,0(-且长轴长是短轴长的2倍的椭圆方程;（2）过点（2，0），且长轴长是短轴长的2倍的椭圆方程.解：（1） （2）[说明] 此题利用椭圆标准方程中c b a ,,的关系来解题，要注意焦点在x 轴上或y 轴上的椭圆标准方程.例3已知直线03=+-y kx 与椭圆141622=+y x ，当k 在何范围取值时， （1） 直线与椭圆有两个公共点； （2） 直线与椭圆有一个公共点； （3） 直线与椭圆无公共点.解：由⎪⎩⎪⎨⎧=++=1416322y x kx y 可得02024)14(22=+++kx x k )516(162-=∆∴k ；（1）当45450)516(162-<>>-=∆k k k 或即时，直线03=+-y kx 与椭圆141622=+y x 有两个公共点；（2）当45450)516(162-===-=∆k k k 或即时，直线03=+-y kx 与椭圆141622=+y x 有一个公共点；（3）当45450)516(162<<-<-=∆k k 即时，直线03=+-y kx 与椭圆141622=+y x 无公共点. [说明] 由直线方程与椭圆方程联立的方程组解的情况直接说明两曲线的交点状况，而方程解的情况由判别式来决定，直线与椭圆有相交、相切、相离三种关系，直线方程与椭圆方程联立，消去y 或x 得到关于x 或y 的一元二次方程，则（1）直线与椭圆相交0>∆⇔（2）直线与椭圆相切0=∆⇔（3）直线与椭圆相离0<∆⇔，所以判定直线与椭圆的位置关系，运用方程及其判别式是最基本的方法.例4若直线)(1R k kx y ∈+=与椭圆1522=+my x 恒有公共点，求实数m 的取值范围.解法一：由⎪⎩⎪⎨⎧=++=15122m y x kx y 可得05510)5(22=-+++m kx x m k ，0152≥--=∆∴k m 即1152≥+≥k m 51≠≥∴m m 且.解法二：直线恒过一定点)1,0(当5<m 时，椭圆焦点在x 轴上，短半轴长m b =，要使直线与椭圆恒有交点则1≥m 即51<≤m当5>m 时，椭圆焦点在y 轴上，长半轴长5=a 可保证直线与椭圆恒有交点即5>m 综述：51≠≥m m 且解法三：直线恒过一定点)1,0(要使直线与椭圆恒有交点，即要保证定点)1,0(在椭圆内部115022≤+m 即1≥m51≠≥∴m m 且[说明]法一转化为k 的恒成立问题；法二是根据两曲线的特征观察所至；法三则紧抓定点在椭圆内部这一特征：点),(o o y x M 在椭圆内部或在椭圆上则12222≤+bya x o o .例5 椭圆中心在原点，长轴长为103，一个焦点1F 的坐标)5,0(，求经过此椭圆内的一点)21,21(-M ，且被点M 平分的弦所在的直线方程.解：由已知，5,35==c a ，且焦点在y 轴上，50222=-=c a b ，椭圆方程为1507522=+x y .设过点M 的直线交椭圆于点),(21y x A 、),(22y x B . M是弦AB 的中点，则1,12121-=+=+y y x x ，将B A ,两点的坐标代入椭圆方程，⎪⎪⎩⎪⎪⎨⎧=+=+150751507522222121x y x y ，两式相减整理得：232321212121=++⋅-=--y y x x x x y y ，即23=k . 所求的直线方程为)21(2321-=+x y ，即0546=--y x . [说明]此题因为涉及椭圆的弦中点问题，除通法外，可以优先考虑“点差法”.但需注意两点：1）斜率是否存在？2）应检验直线和椭圆是否相交？即联立直线和椭圆方程，得到关于x 或y 的一元二次方程，检验其根的判别式是否大于0？例6求椭圆1422=+y x 中斜率为1的平行弦的中点的轨迹. 解：见书本P50[说明] 此题因为涉及椭圆的弦中点问题，本题也可使用“点差法”.例7 已知椭圆11222=+y x 的左右焦点分别为F 1,F 2，若过点P （0，-2）及F 1的直线交椭圆于A,B 两点，求⊿ABF 2的面积 解法一：由题可知：直线AB l 方程为022=++y x由⎪⎩⎪⎨⎧=+--=1122222y x x y ,可得04492=-+y y ，91044)(2122121=-+=-y y y y y y ,1212129S F F y y ∆∴=-= 解法二：2F 到直线AB 的距离554=h , 由⎪⎩⎪⎨⎧=+--=1122222y x x y 可得061692=++x x ，又92101212=-+=x x k AB ,910421==∴∆h AB S . [说明] 在利用弦长公式212212111y y k x x k AB -+=-+=（k 为直线斜率）应结合韦达定理解决问题.例8 已知直线1+=x y 交椭圆12222=+b y a x 于Q P ,两点，210=PQ ，OQ OP ⊥，求椭圆方程.解：为简便运算，设椭圆为122=+ny mx ，),0,0(n m n m ≠>>⎩⎨⎧+==+1122x y ny mx ，1)12(22=+++∴x x n mx ，整理得： 012)(2=-+++n nx x n m （1）n m nx x +-=+221，nm n x x +-=⋅121，设),(11y x P 、),(22y x Q ， OQ OP ⊥ ，02121=+∴y y x x ，即0)1)(1(2121=+++x x x x ，有2=+n m .方程（1）变形为：01222=-++n nx x .21,2121-=⋅-=+n x x n x x .210=PQ ，2521=-∴x x ，有03842=+-n n ，得：⎪⎪⎩⎪⎪⎨⎧==2123m n ，⎪⎪⎩⎪⎪⎨⎧==2321m n ∴椭圆的方程为123222=+y x 或123222=+x y . [说明] 应注意Q P ,两点设而不求，善于使用韦达定理. 四、巩固练习练习12.4（1）;练习12.4（2） 五、课堂小结3．弦长问题和弦中点问题 4．有关弦中点问题，“点差法”的应用 六、课后作业 补充作业：1．椭圆221ax by +=与直线1y x =-交于A 、B 两点，过原点与线段AB 中点的直线的斜率为2，求 a b 值.2.椭圆B A O F F y x 、作直线交椭圆于，过、的焦点为212212045=+两点，若2ABF ∆的面积为20，求直线AB 方程.3.已知椭圆()012222>>=+b a by a x 上一点()8,6P ，21F F 、为椭圆的焦点，且21PF PF ⊥，求椭圆的方程.4．中心在原点，焦点坐标为(0, ±52)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为21，求椭圆方程.5.已知椭圆1222=+y x .（1） 过椭圆的左焦点F 引椭圆的割线，求截得的弦的中点P 的轨迹方程；（2） 求斜率为2的平行弦中点Q 的轨迹方程.6．P 为直线09=+-y x 上的点，过P 且以椭圆131222=+y x 的焦点为焦点作椭圆，问P 在何处时所作椭圆的长轴最短？并求出相应椭圆的方程.7．已知椭圆C ：)0(235222>=+m m y x ，经过其右焦点F 且以()1,1=为方向向量的直线l 交椭圆C 于A 、B 两点，M 为线段AB 的中心，射线OM 交椭圆C 于N 点．（1）证明：=+（2）求⋅的值．8．已知A （－2，0）、B （2，0），点C 、点D 满足).(21,2||+== （1）求点D 的轨迹方程；（2）过点A 作直线l 交以A 、B 为焦点的椭圆于M 、N 两点，线段MN 的中点到y 轴的距离为54，且直线l 与点D 的轨迹相切，求该椭圆的方程.9.设A，B分别是直线5y x=和5y x=-上的两个动点，并且20=，动点P满足+=．记动点P的轨迹为C．（1）求轨迹C的方程；（2）若点D的坐标为（0，16），M、N是曲线C上的两个动点，且DNDMλ=，求实数λ的取值范围．10.如图所示，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个端点，BC过椭圆中心O，且0=⋅=（1）建立适当的坐标系，求椭圆方程；（2）如果椭圆上有两点P、Q，使∠PCQ的平分线垂直于AO，证明：存在实数λ，使λ=．。
2024-2025上海沪教版同步精品培优课堂-高二-19-椭圆
1、定义和标准方程：（1）我们把平面上到两个定点12,F F 的距离之和等于常数2a （122a F F >）的点的轨迹称为椭圆. 用集合的记号表示，椭圆就是下述点集：{}12122,2P M MF MF a a F F =+=>.定点12,F F 叫做椭圆的焦点，12F F 称为椭圆的焦距．注：若设动点为P ，则①当1212||||||PF PF F F +>时，动点P 的轨迹是椭圆． ②当1212||||||PF PF F F +=时，动点P 的轨迹是线段． ③当1212||||||PF PF F F +<时，动点P 的轨迹不存在． （2）标准方程： ① 焦点在x 轴上的椭圆：设椭圆上一点(),P x y ，()()12,0,,0F c F c −，设距离和122PF PF a +=，则椭圆的标准方程为：22221x y a b+=，其中()2220,a b b a c >>=−②焦点在y 轴上的椭圆：设椭圆上一点(),P x y ，()()120,,0,F c F c −，设距离和122PF PF a +=，则椭圆的标准方程为：22221y x a b+=，其中()2220,a b b a c >>=−（3）椭圆的参数方程①椭圆22221x y a b +=的参数方程是cos ,(02)sin x a y b ϕϕπϕ=⎧≤<⎨=⎩．②椭圆22221y x a b +=的参数方程是()cos ,02sin ,x b y a φφπφ=⎧≤≤⎨=⎩.第19讲 椭圆知识梳理模块一：椭圆的概念与方程~~~~~~~~~~~~~~~~~~~~~~~~~题型一、椭圆的定义【例1】椭圆22149100x y +=上一点到两个焦点的距离之和为 ． 【难度】★【例2】已知椭圆2212516x y +=上的点P 到一个焦点的距离为3，则P 到另一个焦点的距离为 ． 【难度】★【例3】已知椭圆2214x y +=的左、右焦点分别为1F ，2F ，过1F 作直线交椭圆于A ，B 两点，则2ABF ∆的周长为 ． 【难度】★【例4】在平面直角坐标系xOy 中，已知ABC ∆顶点(4,0)A −和(4,0)C ，顶点B 在椭圆221259x y +=上，则sin sin sin A C B += ． 【难度】★★【例5】若方程22153x y m m +=−−表示焦点在x 轴上的椭圆，则实数m 的取值范围为 ． 【难度】★★【例6】若方程22(2)(4)(2)(4)m x m y m m −+−=−−表示焦点在y 轴上的椭圆，则实数m 的取值范围是 . 【难度】★★例题分析题型二、椭圆的标准方程【例1】椭圆的焦点坐标为(3,0)−和(3,0)，椭圆上任一点到两个焦点的距离之和为10的椭圆的标准方程为 . 【难度】★【例2】过点(3,0)与椭圆229436x y +=有共同焦点的椭圆的标准方程是 ． 【难度】★【难度】★★题型三、椭圆的结构特征【例2】已知1F ，2F 是椭圆22:194x y C +=的两个焦点，点M 在C 上，则12||||MF MF ⋅的最大值为 ． 【难度】★★【例3】点P 是椭圆221169x y +=上一点，1F ，2F 分别是椭圆的左、右焦点，若12||||12PF PF ⋅=，则12F PF ∠的大小 ． 【难度】★★【例4】若点O 和点F 分别为椭圆2212x y +=的中心和左焦点，点P 为椭圆上的任意一点，则22||||OP PF +的取值范围为 ． 【难度】★★【例5】已知椭圆22:143x y C +=的右焦点为F ，直线l 经过椭圆右焦点F ，交椭圆C 于P 、Q 两点（点P 在第二象限），若点Q 关于x 轴对称点为Q '，且满足PQ FQ ⊥'，求直线l 的方程是 ． 【难度】★★题型三、椭圆轨迹【例1】已知P 为椭圆2211612x y +=上一动点，记原点为O ，若2OP OQ =，则点Q 的轨迹方程为 ． 【难度】★★【例3】设(),P x y ，若()()2222228x y x y ++++−=，则点P 的轨迹方程为 .【难度】★★以焦点在x 轴的椭圆为例：()222210x y a b a b+=>>1. a ：与长轴的顶点有关：()()12,0,,0A a A a −，122A A a =称为长轴长.2. b ：与短轴的顶点有关：()()120,,0,B b B b −，122B B b =称为短轴长.3. c ：与焦点有关：()()12,0,,0F c F c −，122F F c =称为焦距. 注：椭圆中的a 、b 、c 重要平方关系：222a b c =+.4. 对称性：椭圆关于x 轴，y 轴对称，且关于原点中心对称.5. 椭圆上点的坐标范围：设()00,P x y ，则00,a x a b y b −≤≤−≤≤，221x a ≤，221y b≤.6. 椭圆的离心率（1）离心率：椭圆的焦距与长轴长的比ce a=叫做椭圆的离心率．()01e <<. （2）离心率的意义：e 越大越接近1，椭圆越扁平，相反，e 越小越接近0，椭圆越圆．当且仅当a ＝b 时，c ＝0，椭圆变为圆，方程为x 2+y 2＝a 2． 7. 通径：焦点弦长度的最小值. （1）焦点弦：椭圆中过焦点的弦.（2）过焦点且与长轴垂直的弦22b PQ a=（称为通经，为最短的过交点的弦）8. 焦半径：椭圆上的点P 到焦点的距离为椭圆的焦半径，焦半径的最大值为a c +，最小值为a c −9. 焦点三角形面积：122tan2PF F S b θ=（其中12F PF θ=∠）因为1200122PF F Sc y c y =⋅⋅=⋅，所以2120tan 2F PF b c y ∠=⋅. 10. 点与椭圆的位置关系模块二：椭圆的性质~~~~~~~~~~~~~~~~~~~~~~~~~知识梳理已知点00(,)P x y与椭圆22221(0)x y a b a b+=>>（1F ，2F 为椭圆的焦点），则（1）点P 在椭圆上220012221||||2x y PF PF a a b ⇔+=⇔+=；（2）点P 在椭圆外220012221||||2x y PF PF a a b ⇔+>⇔+>；（3）点P 在椭圆内220012221||||2x y PF PF a a b⇔+<⇔+<．题型一、椭圆中的基本量【例1】椭圆221169y x +=的长轴长为 ． 【难度】★【例2】点()1,1与椭圆221259x y+=的位置关系为（ ）A ．点在椭圆上B ．点在椭圆内C ．点在椭圆外D ．不确定【难度】★【例3】若焦点在x 轴上的椭圆221102x y m m +=−−的焦距为22，则实数m 的值为 ． 【难度】★【例4】椭圆221124x y +=和221168x y +=满足（ ）A ．长轴长相等B ．短轴长相等C ．焦距相等D ．顶点相同【难度】★【例5】设P 是椭圆222:1(6)6x y C a a +=>上任意一点，F 为C 的右焦点，||PF 的最小值为2，则椭圆C 的长轴长为 ．【难度】★★例题分析【例6】设AB 是椭圆Γ的长轴，点C 在Γ上，且4CBA π∠=，若4AB =，BC =，则Γ的两个焦点之间的距离为 ． 【难度】★★题型二、椭圆离心率【例1】椭圆22195x y +=的离心率为 ． 【难度】★【例2】著名的天文学家、数学家开普勒发现了行星运动三大定律，其中开普勒第一定律又称为轨道定律，即所有行星绕太阳运动的轨道都是椭圆，且太阳中心处在椭圆的一个焦点上．记地球绕太阳运动的轨道为椭圆C ，在地球绕太阳运动的过程中，若地球轨道与太阳中心的最远距离与最近距离之比为2，则C 的离心率为 ． 【难度】★★【例3】已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为2F ，左顶点为1A ，若E 上的点P 满足2PF x ⊥轴，123sin 5PA F ∠=，则E 的离心率为（ ）A ．12B ．25C ．14 D ．15【难度】★★【例4】已知1F ，2F 是椭圆2222:1(0,0)x y C a b a b+=>>的左，右焦点，A 是C 的左顶点，点P 在过A 且斜率为6的直线上，△12PF F 为等腰三角形，12120F F P ∠=︒，则椭圆C 的离心率为 ．【难度】★★【例5】已知椭圆22221(0)x y a b a b +=>>的左右焦点分别为1F ，2F ，椭圆存在点P 满足12120F PF ∠=︒，则椭圆的离心率取值范围为（ ）A ．⎣⎦B ．1,12⎡⎫⎪⎢⎣⎭C ．⎫⎪⎪⎣⎭D ．12⎡⎢⎣⎦【难度】★★题型三、焦点三角形【例2】已知△12AF F 是等边三角形，M 、N 分别是边1AF 和2AF 的中点．若椭圆以1F 、2F 为焦点，且经过M 、N ，则椭圆的离心率等于 ．【例3】已知椭圆22221(0)x y a b a b+=>>的离心率为35，左，右焦点分别为1F ，2F ，过左焦点1F 作直线与椭圆在第一象限交点为P ，若△12PF F 为等腰三角形，则直线1PF 的斜率为（ ）A ．7B ．8C ．D ．7【难度】★★【例4】1F 、2F分别为椭圆2214x y +=的左、右焦点，P 为该椭圆上一点，且1260F PF ∠=︒，则△12F PF 的面积等于 ． 【难度】★★题型一、与椭圆的位置关系【例1】已知椭圆22:1259x y C +=，直线:(2)(4)20()l m x m y m m R +−++−=∈，则直线l 与椭圆C 的位置关系为（ ） A ．相交 B ．相切C ．相离D ．不确定【难度】★★【例2】点(,)P m n 是椭圆2241x y +=上的动点且点P 不在坐标轴上，称动点11,Q m n ⎛⎫⎪⎝⎭构成的轨迹为曲线Γ．若圆222(0)x y r r +=>与曲线Γ无公共点，则实数r 的取值范围为 ． 【难度】★★题型二、最值问题【例1】已知椭圆22:143x y Γ+=的右焦点为F ，过原点O 的直线与椭圆Γ交于A 、B 两点，则11||||AF BF +的最小值为 ． 【难度】★★模块三：椭圆综合问题~~~~~~~~~~~~~~~~~~~~~~~~~例题分析MA MB ⋅的最大值是【难度】★★【例3】已题型三、椭圆综合问题【例1】已知椭圆22221(0)x y a b a b +=>>的离心率3e =，焦距是（1）求椭圆的方程；（2）若直线2(0)y kx k =+≠与椭圆交于C 、D 两点，||CD =，求k 的值． 【难度】★★【难度】★★【例3】已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点分别为1F ，2F ，离心率为12，且经过点31,2⎛⎫ ⎪⎝⎭（1）求椭圆C 的方程；（2）动直线:l y x m =+与椭圆C 相切，点M ，N 是直线l 上的两点，且1F M l ⊥，2F N l ⊥，求四边形12F MNF 的面积；（3）过椭圆C 内一点(,0)T t 作两条直线分别交椭圆C 于点A ，C ，和B ，D ，设直线AC 与BD 的斜率分别是1k ，2k ，若||||||||AT TC BT TD ⋅=⋅试问12k k +是否为定值，若是，求出定值，若不是，说明理由． 【难度】★★★1. 椭圆22194x y +=的短轴长为 ． 【难度】★ 2. 过点()5,3且与椭圆221259x y +=有相同焦点的椭圆的长轴长为 .【难度】★3. 已知1F ，2F 是椭圆22198x y +=的左、右焦点，P 是椭圆上的一点，若1||2PF =，则2||PF = ．【难度】★4. 已知椭圆的两个焦点坐标分别是()()0,5,0,5−，椭圆上一点P 到两个焦点的距离之和为26，则该椭圆方程为 . 【难度】★5. 已知焦点在x 轴上的椭圆2218x ym +=的焦距是2，则该椭圆的长轴长为 .【难度】★6. 曲线221259x y +=与221(09)925x y k k k +=<<−−的关系是（ ） A ．有相等的焦距，相同的焦点 B ．有不等的焦距，相同的焦点 C ．有不等的焦距，不同的焦点 D ．有相等的焦距，不同的焦点【难度】★师生总结巩固练习7. 设1F 和2F 为椭圆22421x y +=的两个焦点，点P 在椭圆上，且满足1||2OP =，则△12F PF 的面积是 ． 【难度】★8. 椭圆2221x my −=的一个焦点坐标为(0,，则实数m =（ ） A ．23B ．25 C ．23−D ．25−【难度】★★【难度】★★10. 已知:13P m <<，22:113x y Q m m+=−−表示椭圆，则P 是Q 的 条件．【难度】★★11. 画法几何创始人蒙日发现：椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆上，且圆半径的平方等于长半轴、短半轴的平方和，此圆被命名为该椭圆的蒙日圆．若椭圆22216x y b+=的蒙日圆为2210x y +=，则该椭圆的离心率为（ ）A ．23B ．13C D 【难度】★★满足OP mOA nOB =+，其中【难度】★★11 OP=【难度】★★14. 已知P为椭圆221259x y+=上一点，1F，2F是椭圆的两个焦点，1260F PF∠=︒，则△12F PF的面积S=．【难度】★★，若12PF F的面积为【难度】★★【难度】★★【难度】★★）若11F P QF λ=且λ∈，求OP OQ ⋅的最大值【难度】★★1. 古希腊数学家阿波罗尼奥斯在研究圆锥曲线时发现了椭圆的光学性质：从椭圆的一个焦点射出的光线，经椭圆反射，其反射光线必经过椭圆的另一焦点．设椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1F ，2F ，若从椭圆右焦点2F 发出的光线经过椭圆上的点A 和点B 反射后，满足AB AD ⊥，且3cos 5ABC ∠=，则该椭圆的离心率为（ ）【难度】★★★2. 椭圆22:14x C y +=中，点A 为左顶点，点B 为上顶点，直线l 过原点且与椭圆交于M ，N两点（M 在第一象限），则四边形ABMN 的面积最大值为 . 【难度】★★★能力提升。
杨浦区补习班 新王牌高中数学王WI老师周末同步提高拓展-推荐下载
| k 360 பைடு நூலகம் 90, k Z
| k 360 180, k Z
| k 360 270, k Z
| k 180, k Z
| k 180 90, k Z
| k 90, k Z
16 （2） cos
5
60 90 120 135 150 180 270 360
（3） cos(80 )
（2）在 0 ~ 360 范围内，找出与 650 角终边相同的角，并写出所有与 650 终边相同的角的集合。
（3）已知、 角的终边关于 y 轴对称，则 与 的关系为
y
a的终边
P(x,y
O
x
| OM || x || cos | 。
我们知道，指标坐标系内点的坐标与坐标轴的方向有关.当角 的终 边不在坐标轴时,以 O 为始点、 M 为终点，规定：
当线段 OM 与 x 轴同向时， OM 的方向为正向，且有正值 x ；当线段 OM 与 x 轴反向时， OM 的方向为负向，且有正值 x ；其中 x 为 P 点的
6
，5 6
180
课时数：2 学科教师：王老师
扇形面积公式： S 1 l r 1 | | r 2 22
补充：几种终边在特殊位置时对应角的集合为：
角的终边所在位置
X 轴正半轴
Y 轴正半轴
X 轴负半轴
Y 轴负半轴
X轴
Y轴
坐标轴
<4>三角函数定义
角的集合
| k 360, k Z
弧长公式： l | | r （ 是圆心角的弧度数），
杨浦区暑假最好的新高一数理化补习班 新王牌补习 二次函数及最值
杨浦新王牌高中数学预备知识强化训练二次函数与最值【要点回顾】1． 二次函数2y ax bx c =++()0a ≠的图像和性质问题[1] 函数2y ax =与2y x =的图象之间存在怎样的关系？问题[2] 函数()2y a x h k =++与2y ax =的图象之间存在怎样的关系？由上面的结论，我们可以得到研究二次函数2y ax bx c =++()0a ≠的图象的方法：由于22222244b b b b y ax bx c a x x c a x x c a a a a ⎛⎫⎛⎫=++=++=+++- ⎪ ⎪⎝⎭⎝⎭ 224()24b b ac a x a a-=++， 所以2y ax bx c =++()0a ≠的图象可以看作是将函数2y ax =的图象作左右平移、上下平移得到的，二次函数2y ax bx c =++()0a ≠具有下列性质：[1]当a ＞0时，函数2y ax bx c =++图象开口方向 ；顶点坐标为 ，对称轴为直线 ；当 时，y 随着x 的增大而 ；当 时，y 随着x 的增大而 ；当 时，函数取最小值 ．[2]当a ＜0时，函数2y ax bx c =++图象开口方向 ；顶点坐标为 ，对称轴为直线 ；当 时，y 随着x 的增大而 ；当 时，y 随着x 的增大而 ；当 时，函数取最大值 ．上述二次函数的性质可以分别通过上图直观地表示出来．因此，在今后解决二次函数问题时，可以借助于函数图像、利用数形结合的思想方法来解决问题．2．二次函数的三种表示方式[1]一般式： ；[2]顶点式： ； [3]交点式： ．说明：确定二此函数的关系式的一般方法是待定系数法，在选择把二次函数的关系式设成什么形式时，可根据题目中的条件灵活选择，以简单为原则．二次函数的关系式可设如下三种形式：（1）给出三点坐标可利用一般式来求；（2）给出两点，且其中一点为顶点时可利用顶点式来求．（3）给出三点，其中两点为与x 轴的两个交点)0,(1x .)0,(2x 时可利用交点式来求． 3.二次函数2 (0)y ax bx c a =++≠的最值．二次函数在自变量x 取任意实数时的最值情况:当0a >时，函数在2b x a=-处取得最小值244ac b a -，无最大值；当0a <时，函数在x =______处取得最___值__________，无最____值．4．二次函数最大值或最小值的求法．第一步确定a 的符号，0a >有最___值，0a <有最___值； 第二步配方求顶点，顶点的纵坐标即为对应的最大值或最小值．5．求二次函数在某一范围内的最值．如：2y ax bx c =++在m x n ≤≤（其中m n <）的最值． 第一步：先通过配方，求出函数图象的对称轴：0x x =； 第二步：讨论：[1]若0a >时求最小值或0a <时求最大值，需分三种情况讨论： ①对称轴小于m 即0x m <，即对称轴在m x n ≤≤的左侧； ②对称轴0m x n ≤≤，即对称轴在m x n ≤≤的内部； ③对称轴大于n 即0x n >，即对称轴在m x n ≤≤的右侧。
高一升高二暑期数学衔接学习与指导：椭圆的定义及标准方程
椭圆的定义及标准方程一.知识要点1.椭圆的定义平面内与两个定点1F 、2F 的距离的和等于常数（大于21||F F ）的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点的距离叫椭圆的焦距.注:(1).在椭圆的定义中,若这个距离之和小于|1F 2F |，则这样的点不存在；若距离之和等于|1F 2F |，则动点的轨迹是线段1F 2F .(2).椭圆的的内外部①点00(,)P x y 在椭圆22221(0)x y a b a b+=>>的内部2200221x y a b ⇔+<. ②点00(,)P x y 在椭圆22221(0)x y a b a b+=>>的外部2200221x y a b ⇔+>. 2. 椭圆的标准方程3. 椭圆的参数方程4. 椭圆的标准方程与性质二.题型、方法2. 已知F 1、F 2是椭圆162x +92y =1的两个焦点，过F 1的直线与椭圆交于M 、N 两点，则△MNF 2的周长为( ) A.8 B.16 C.25 D.323.若点O 和点F 分别为椭圆x 22＋y 2＝1的中心和左焦点，点P 为椭圆上的任意一点，则|OP |2＋|PF |2的最小值为________．题组二1.求经过点35(,)22-，且229545x y +=与椭圆有共同焦点的椭圆方程.2.已知椭圆以坐标轴为对称轴，且长轴长是短轴长的3倍，点P （3,0）在该椭圆上，求椭圆的方程.3.在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x 轴上，离心率为2.过1F 的直线L 交C 于,A B 两点，且2ABF 的周长为16，那么C 的方程为 .4. 若椭圆12222=+by a x 的焦点在x 轴上，过点)21,1(作圆122=+y x 的切线，切点分别为A ，B ，直线AB 恰好经过椭圆的右焦点和上顶点，则椭圆方程是 .题组三1. 已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于( )A.12B.22C. 2D.322.已知F 1、F 2是椭圆的两个焦点，P 为椭圆上一点，∠F 1PF 2＝60°.(1)求椭圆离心率的范围；(2)求证：△F 1PF 2的面积只与椭圆的短轴长有关．【评析】椭圆中△F 1PF 2往往称为焦点三角形，求解有关问题时，要注意正、余弦定理，面积公式的使用；求范围时，要特别注意椭圆定义(或性质)与不等式的联合使用.从本题的解题过程,也能得出如下两个结论:(1)()12122max FPF FB F ∠=∠这一结论.(2)设点P 是椭圆22a x +22by =1（a ＞b ＞0）上任意一点, 12F F 与为椭圆的焦点∠F 1PF 2=2θ,则△PF 1F 2的面积S =b 2tan θ.3.(1)设12,F F 分别为椭圆2213x y +=的左、右焦点，点,A B 在椭圆上，若125F A F B =;则点A 的坐标是 ．（2）已知F 1、F 2是椭圆的两个焦点，满足120MF MF ⋅=的点M 总在椭圆内部，则椭圆离心率的取值范围是 .4.设椭圆C : ()222210x y a b a b+=>>过点（0，4），离心率为35． （1）求C 的方程；（2）求过点（3，0）且斜率为45的直线被C 所截线段的长度及的中点坐标．练习一、选择题（共5个小题，每小题只有一个正确答案）1.椭圆221168x y +=的离心率为（ ）（A ）13 （B ）12 （C ）3 （D ）22. 椭圆x 24＋y 23＝1的右焦点到直线y ＝3x 的距离是( ) A.12 B.32 C ．1 D. 33. 设0≤α<2π，若方程x 2sin α－y 2cos α＝1表示焦点在y 轴上的椭圆，则α的取值范围是( )A.⎝⎛⎭⎫0，3π4∪⎝⎛⎭⎫7π4，2πB.⎣⎡⎭⎫π2，3π4C.⎝⎛⎭⎫π2，3π4D.⎝⎛⎭⎫3π4，3π24. 椭圆x 2100＋y 264＝1的焦点为F 1、F 2，椭圆上的点P 满足∠F 1PF 2＝60°，则△F 1PF 2的面积是( ) A.6433 B.9133 C.1633 D.6435.已知椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P .若AP →＝2PB →，则椭圆的离心率是( )A.32B.22C.13D.12二、填空题（共3个小题）6. 若椭圆x 22＋y 2m ＝1的离心率为12，则m ＝ 7. 若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1，则椭圆长轴长的最小值为8.已知椭圆x 24＋y 22＝1的左右焦点分别为F 1、F 2，过F 2且倾角为45°的直线l 交椭圆于A 、B 两点，以下结论中：①△ABF 1的周长为8；②原点到l 的距离为1；③|AB |＝83；其中所有正确命题的序号是 (请写出所有正确命题的序号)三、解答题9.设1F ，2F 分别为椭圆2222:1x y C a b+=(0)a b >>的左、右焦点，过2F 的直线l 与椭圆C 相交于A ,B 两点，直线l 的倾斜角为60，1F 到直线l 的距离为23.（1）求椭圆C 的焦距；（2）如果222AF F B =,求椭圆C 的方程.10.已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的长轴长为4. (1)若以原点为圆心、椭圆短半轴为半径的圆与直线y ＝x ＋2相切，求椭圆C 的焦点坐标；(2)若点P 是椭圆C 上的任意一点，过原点的直线l 与椭圆相交于M ，N 两点，记直线PM ，PN 的斜率分别为k PM 、k PN ，当k PM ·k PN ＝－14时，求椭圆的方程．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
杨浦新王牌
x
y
A B
C
D
O y x (7)设椭圆的方程为
122
2
2=+b
y a x )0(>>b a ，椭圆与y 轴正半轴的一个交点B 与两焦点21,F F 组成的三角形的 周长为324+，且3
221π
=
∠BF F ，则此椭圆的方程为 (8)椭圆14
162
2=+y x 上的点到直线022=-+y x 的最大距离是
(9)椭圆1492
2=+y x 的焦点1F 、2F ，点P 为其上的动点，当∠1F P 2F 为钝角时,点P 横坐标的取值范围是 (10)若点P 是椭圆2
219
x y +=上的动点，定点A 的坐标为(2,0)，则||PA 的取值范围是 (11)过点)0,2(-M 的直线m 与椭圆12
22
=+y x 交于21,P P ，线段21P P 的中点为P ，设直线m 的斜率为1k （01≠k ）， 直线OP 的斜率为2k ，则21k k 的值为
(12)如图，在平面直角坐标系xOy 中，椭圆122
22=+b
y a x
（0>>b a ）被围于由4条直线a x ±=，b y ±=所围成的
矩形ABCD 内，任取椭圆上一点P ，若OB n OA m OP ⋅+⋅= （m 、R n ∈），则m 、n 满足的一个等式是______________
(11)如图，在直角坐
标系xOy 中，设椭圆)0(1:22
22>>=+b a b
y a x C 的左右两个焦点分别为21F F 、.
过右焦点2F 且与x 轴垂直的直线l 与椭圆C 相交，其中一个交点为()
1,2M . (1) 求椭圆C 的方程；
(2) 设椭圆C 的一个顶点为),0(b B -，直线2BF 交椭圆C 于另一点N ，求△BN F 1的面积.
（12）椭圆)0(1:22
22>>=+b a b
y a x C 的左、右焦点分别是)0,(1c F -，)0,(2c F ，过1F 斜率为1的直线l 与椭圆C 相
交于A ，B 两点，且2AF ，AB ，2BF 成等差数列．
（1）求证：c b =；
（2）设点)1,0(-P 在线段AB 的垂直平分线上，求椭圆C 的方程．。