全国大学生数学建模竞赛C题国家奖一等奖优秀论文
全国大学生数学建模国 家奖优秀论文

全国大学生数学建模国家奖优秀论文在当今高度数字化和信息化的时代,数学建模已经成为解决各种实际问题的重要工具。
全国大学生数学建模竞赛作为一项具有高度影响力的赛事,每年都吸引着众多优秀学子参与,而能够获得国家奖的优秀论文更是代表着学生在数学建模领域的卓越成就。
数学建模的本质是将实际问题转化为数学问题,并通过建立数学模型来求解,从而为实际问题提供有效的解决方案。
这些获奖论文通常具有一些显著的特点。
首先,它们能够准确地把握问题的关键。
在面对复杂的实际问题时,参赛学生需要迅速理清问题的核心,明确问题的约束条件和目标。
例如,在研究城市交通拥堵问题时,关键可能在于分析车流量、道路容量、信号灯设置等因素之间的关系,并确定如何优化交通流量以减少拥堵。
其次,优秀论文中的模型建立具有创新性和合理性。
学生们不会拘泥于传统的模型和方法,而是敢于尝试新的思路和技术。
他们可能会结合多种数学方法,如概率论、线性规划、微分方程等,构建一个综合性的模型,以更精确地描述问题。
再者,数据处理和分析能力也是至关重要的。
为了验证模型的有效性,需要收集大量的数据,并进行有效的清洗、整理和分析。
在这个过程中,学生们需要运用统计学知识,判断数据的可靠性和代表性,运用合适的方法对数据进行拟合和预测。
以一篇关于电商平台商品推荐系统的数学建模论文为例。
在这篇论文中,学生们深入研究了用户的购买历史、浏览行为、评价等数据,通过构建协同过滤模型和基于内容的推荐模型,为用户提供个性化的商品推荐。
他们不仅考虑了用户的兴趣偏好,还考虑了商品的热门程度、时效性等因素,使得推荐结果更加准确和实用。
在模型求解方面,他们采用了高效的算法和计算工具,如 Python 中的相关库和机器学习框架,快速得到模型的解。
并且,通过大量的实验和对比分析,验证了模型的性能和优越性。
此外,优秀的论文还注重结果的解释和应用。
模型求解得到的结果不是孤立的数字,而是需要结合实际情况进行合理的解释和分析。
数学建模答辩 (国家奖)

0.01965
1.00742
0.99372
0.013599
基于感官分析和理化指标对葡萄酒的评价
中央民族大学
红酒
白酒
真实值
计算值
误差
真实值
计算值
误差
15
0.931719
0.97886
-0.0506
1.024406
0.96779
0.055267
16
0.991281
1.02102
-0.03
0.879369
-0.011208
1.0649121
1.04548
0.0182476
6
0.940228
0.99707
-0.060456
0.9865136
1.01114
-0.024963
7
0.9260466
0.93762
-0.012498
0.9695273
0.98163
-0.012483
8
0.9359736
0.95033
模型的结果 由下图显然可见,无论是红葡萄酒还是白葡萄酒,二组的各
项指标评分标准差都小于一组的评分标准差,说明第二组评酒 员的评分更集中,波动性比较小。由此可见,第二组的评酒结 果更可信。
基于感官分析和理化指标对葡萄酒的评价
模型一的结果
中央民族大学
红葡萄酒评分标准差
70 60 50 40 30 20 10
模型三建立:
1、葡萄与葡萄酒的理化指标之间的联系—相关分析、多元回归分析法
根据相关系数矩阵。剔除影响程度低的指标后,列出对葡萄酒有显著 影响的葡萄指标。
建立多元线性回归模型,线性回归模型的一般形式为:
国家奖学金获奖学生的优秀事迹材料

国家奖学金获奖学生的优秀事迹材料关于国家奖学金获奖学生的优秀事迹材料一、个人简介钱XX,女,汉族,1994年6月出生,中共党员。
现就读于中央财经大学金融学院金融工程专业,20XX年入学。
曾获国家奖学金,学校全面发展一等奖学金,学校学业优秀奖学金,全美数学建模比赛二等奖,全国数学竞赛二等奖,学校数学竞赛一等奖,校数学信息检索比赛三等奖,全国数学建模比赛(报送全国阅卷),校级三好学生,校园委会优秀层长。
二、事迹正文恰同学少年恰同学少年,风华正茂;书生意气,挥斥方遒。
——毛泽东1925年,已经32岁的毛泽东,途经长沙,望湘江滚滚东去,想起自己的学生时代,写下这首《沁园春长沙》。
我尤其喜欢这四句,也许是因为我正好处于毛主席怀念的时代——我的大学时代。
即使对他的功过争论不一,我还是比较喜欢毛泽东这个人,尤其是年轻时候的他。
尤其羡慕他的大学,羡慕他有志在“欲栽大木拄长天”的良师和可以“指点江山,激扬文字,粪土当年万户侯”的益友,羡慕他有深爱着的文学和历史,当然,还有他“为万世开太平”的理想。
庆幸的是,在我的大学里,我也有良师益友和一个显得不那么伟大的梦想。
虽然我没有像毛泽东一样如痴如醉地爱上文学和历史,但我热爱数学;文学历史之于毛主席,正如数学之于我。
(一)主教,偌大的教室里稀稀拉拉坐着几个人。
“同学,该锁门了!”保洁阿姨出现在门口。
放下手中解了一半的高等代数题,抬起头,看看表,晚上十点半,伸个懒腰,又一天结束了。
校园里,昏黄的路灯下,除了几对还在聊天的情侣外,只有三三两两出去玩了一天结伴回来的同学。
自从从信息学院转专业到金融学院金工专业之后,我已经记不清这是第多少次我以这样的方式结束我的一天了。
转专业之后,首先面临的便是补修学分的问题,高等代数就这样出现在我的补修科目的名单。
面对这样一门与高等数学和概率论一起高居央财挂科率榜首的学科,困难可想而知;为补修的同学开的课因为和专业课冲突没法去上,更是雪上加霜。
2016年全国大学生数学建模竞赛题
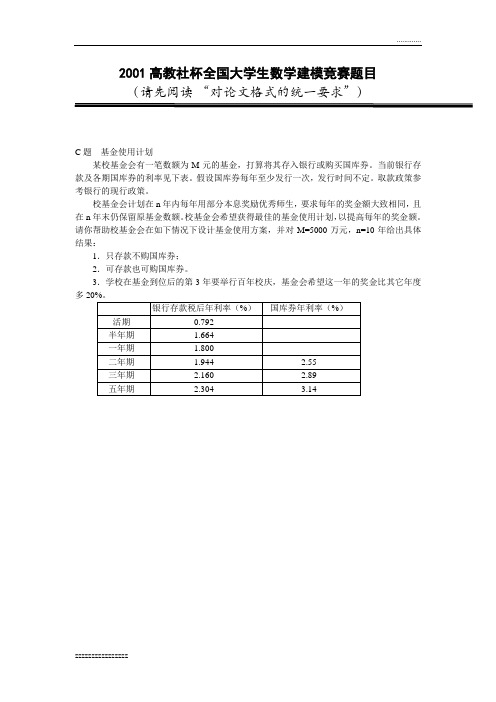
2001高教社杯全国大学生数学建模竞赛题目(请先阅读“对论文格式的统一要求”)C题基金使用计划某校基金会有一笔数额为M元的基金,打算将其存入银行或购买国库券。
当前银行存款及各期国库券的利率见下表。
假设国库券每年至少发行一次,发行时间不定。
取款政策参考银行的现行政策。
校基金会计划在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额。
校基金会希望获得最佳的基金使用计划,以提高每年的奖金额。
请你帮助校基金会在如下情况下设计基金使用方案,并对M=5000万元,n=10年给出具体结果:1.只存款不购国库券;2.可存款也可购国库券。
3.学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多摘要:运用基金M分成n份(M1,M2,…,Mn),M1存一年,M2存2年,…,Mn存n 年.这样,对前面的(n-1)年,第i年终时M1到期,将Mi及其利息均取出来作为当年的奖金发放;而第n年,则用除去M元所剩下的钱作为第n年的奖金发放的基本思想,解决了基金的最佳使用方案问题.关键词:超限归纳法;排除定理;仓恩定理1问题重述某校基金会有一笔数额为M元的基金,欲将其存入银行或购买国库券.当前银行存款及各期国库券的利率见表1.假设国库券每年至少发行一次,发行时间不定.取款政策参考银行的现行政策.表1 存款年利率表校基金会计在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额.校基金会希望获得最佳的基金使用计划,以提高每年的奖金额.需帮助校基金会在如下情况下设计基金使用方案,并对M=5 000万元,n=10年给出具体结果:①只存款不购国库券;②可存款也可购国库券.③学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多20%.2模型的分析、假设与建立2.1模型假设①每年发放的奖金额相同;②取款按现行银行政策;③不考虑通货膨胀及国家政策对利息结算的影响;④基金在年初到位,学校当年奖金在下一年年初发放;⑤国库券若提前支取,则按满年限的同期银行利率结算,且需交纳一定数额的手续费;⑥到期国库券回收资金不能用于购买当年发行的国库券.2.2符号约定K——发放的奖金数;ri——存i年的年利率,(i=1/2,1,2,3,5);Mi——支付第i年奖金,第1年开始所存的数额(i=1,2,…,10);U——半年活期的年利率;2.3模型的建立和求解2.3.1情况一:只存款不购国库券(1)分析令:支付各年奖金和本金存款方案———Mij (i =1,…,10,i ;j 属于N ). 将各方案ij M 看成元素,构成集合A则ij M 属于A1,210;I =所以A 按I 取值分10行根据仓恩定理:分行集中,任何一单行有上界,则必包含一个极大元素。
大学生数学建模

第2章大学生数学建模竞赛简介大学生数学建模竞赛在20世纪八十年代产生于美国。
我国应用数学家在国际交流中,深感美国的高科技水平及先进的大学教育理念对国家发展进步所起的推动作用,便积极呼吁、发起、组织中国的大学生数学建模竞赛,1996年,由教育部高教司和中国工业与应用数学学会共同主办了首届全国大学生数学建模竞赛,为我国一年一度的大学生数学建模竞赛拉开了序幕。
§2.1 数学建模竞赛的兴起1.Putnam(普特南)数学竞赛Putnam(普特南)家族几代人都擅长数学,关心数学教育,竞赛的首创者是William Lowell Putnam,他曾在美国著名的哈佛大学数学系任职(后来当过校长),1921年撰文论述仿照奥林匹克运动会举办大学生数学竞赛的好处,得到他的妻兄、哈佛大学校长A.L.洛厄尔的支持,在20世纪20年代末举办过几次校际竞赛作为实验。
1935年逝世,他的遗孀秉承其遗志,设立了一笔12.5万美元的普特南基金会,并命他的两个儿子执行,这件事得到他们全家的挚友、著名美国数学家G.D.伯克霍夫的支持,伯克霍夫认为,再没有一门学科比数学更易于通过考试来测定能力的了。
G.D.伯克霍夫起草了竞赛的四项规定:①遵照普特南的遗愿,各校应派代表队参加,以集体成绩为自己的学校争取荣誉,代表队由三人组成,另外还可派个别选手参加,这对于派不出三个高水平学生组成代表队的一些较小的学校尤为相宜。
②由美国数学会管理,该协会是美国大学数学教师的专业组织,不但名正言顺,而且便于动员和组织各校参加竞赛。
③给优胜队及个人颁发奖金和予以荣誉鼓励。
④给个人第一名提供在哈佛大学攻读“普特南研究学位”和奖学金。
首届普特南数学竞赛于1938年4月16日在哈佛大学举行, 1943年~1945年因第2次世界大战暂停了3届,到1946年第6届又恢复了,这时已由G.D.伯克霍夫之子B伯克霍夫经管此事,竞赛的组织也越来越完善,迄今已举行了70届,每年有数百所大学,数千名大学生参加,许多这一活动造优胜者,后来成为著名的科学家、数学家和企业家。
2013年全国大学生数学建模竞赛国家奖获奖名单

天津
天津职业技术师范大学
苏静
刘梦楠
宋垚
曲克杰
22
天津
天津商业大学
王彦清
常丹丹
张剑
李景焕
23
天津
军事交通学院
王学全
王作夫
刘金鹏
李梅英
24
天津
军事交通学院
邹梦
张龙
丁帅毅
郭彦
25
天津
南开大学
郑皓珺
周玉
马磊
王奎
26
天津
南开大学
李栩
李紫珅
刘炜男
27
河北
华北电力大学
汤潘
邓睿
臧晓玲
孔倩
28
2013高教社杯全国大学生数学建模竞赛获奖名单(本科组)
全国大学生数学建模竞赛组委会
2013年11月23日
本科组高教社杯获得者:刘世尧、王钰聪、李文然(厦门大学)
本科组MATLAB创新奖获得者:向航、王帆、郭树璇(国防科技大学)
本科组IBM SPSS创新奖获得者:周晨阳、周登岳、孔垂烨(北京理工大学)
冯艳
万建
贺衎
36
山西
中北大学
薛志强
王立超
廖金明
肖亚峰
37
山西
运城学院
郑路通
杨雯雯
陶佳琪
买阿丽
38
内蒙古
内蒙古大学
李美玲
张楠
李小平
何斯日古楞
39
内蒙古
河套学院
关美玲
李伟
王泽奇
成乐
40
辽宁
大连海事大学
黄春龙
贾晓岩
王义
教师组
41
辽宁
全国大学生数学建模国家奖优秀论文

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国评阅编号(由全国组委会评阅前进行编号):城市表层土壤重金属污染分析摘要随着工业的迅猛发展、城市污染的加剧和农用化学物质种类、数量的不断增加,含重金属污染物通过各种途径进入土壤,造成土壤重金属污染程度日益严重。
研究土壤重金属的空间分布和污染状况对农业发展规划和城市土地利用具有重要的意义。
土壤重金属含量属于空间连续的变量,具有区域化变量特征,将GIS和地统计学相结合应用到土壤重金属空间分布和污染评价研究近年来已越来越普遍。
本文以城市为研究区域,运用GIS和地统计学相结合的方法,对中等尺度下的土壤重金属含量进行空间变异结构分析、空间分布特征和污染状况的研究,主要内容如下:(1)土壤重金属空间分布理论方法的研究,即地统计学理论方法研究。
(2)运用地统计学方法,对研究区域的土壤重金属含量样品数据进行分析,研究土壤重金属含量的空间变异结构特征,并指出对土壤样点布设的指导意义。
(3)研究八种土壤重金属在内的空间区域化变量的相关关系;运用GIS强大的空间数据管理能力和空间分析能力与地统计学的理论方法,利用GIS开发技术,采用以“点”代“面”的方式生成土壤重金属含量的空间分布图,相比常用的基于采样点进行常规统计分析在空间表达上更加直观。
数学建模竞赛获奖论文范文

数学建模竞赛获奖论文范文数学的运用越来越广泛了,利用建立数学模型解决实际问题的数学建模活动也应运而生了。
下面是店铺为大家推荐的数学建模论文,供大家参考。
数学建模论文范文篇一:《高中开设数学建模课程的意义与定位》1、高中开设数学建模课程的背景在高中设置的课程中,数学是一门必修课程,也是高考比重最大的一门课程,其最终目标是将数学知识融入现实问题中去,从而解决问题,这也是教育教学的最终目的。
要达到教育教学的最终目的,必须改革高中的数学课程教学,建设高中数学建模课程。
高中数学建模课程可以根据简单的现实问题设置,针对实际生活中的一些简单问题进行适当的假设,建立高中数学知识能解决该问题的数学模型,进而解决该实际问题。
因此,可以说高中数学建模课程是利用所学高中数学知识解决实际问题的课程,是将高中数学知识应用的一门课程,是培养出高技能人才的基础课程。
国家教育部制定的高中数学课程标准,重点强调:"要重视高中学生从自己的生活经验和所学知识中去理解数学、学习数学和应用数学,通过自己的感知和实际操作,掌握基本的高中数学知识和数学逻辑思维能力,让高中生体会到数学的乐趣,对数学产生兴趣,让其感觉到数学就在身边。
"但是现实中高中数学的教学情况堪忧,基本上都是满堂灌的教学,学生不会应用,对数学毫无兴趣可言,主要体现在三个方面。
第一,虽然有很多学生以高分成绩进入高中学习,但是其数学应用的基础非常差,基本上是会生搬硬套,不会解决实际问题,更不会将数学知识联系到生活中来;也有少数学生数学基础差,没有养成好的数学学习习惯,导致产生厌恶数学的情绪,数学基础知识都没学好,更不用说是用数学解决实际问题。
这少数学生就是上课睡觉混日子,根本不去学习,这与高中数学课程的开设目标截然不符。
第二,高中数学课程的教学内容与实际问题严重脱节,高中的数学教材中涉及的数学知识基本上都是计算内容,而不是用来处理和解决生活问题的,更是缺少数学与其他学科(比如化学、物理、生物、地理等)的相互渗透,即便高中数学课程中有一些数学应用的例子,也属于选学内容,教师根本不去讲、不涉及,这样导致高中数学课的教学达不到其教学目的,发挥不出功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国大学生数学建模竞赛C题国家奖一等奖优秀论文TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-脑卒中发病环境因素分析及干预摘要本文主要讨论脑卒中发病环境因素分析及干预问题。
根据题中所给出的数据,利用SPSS20 软件进行相关性统计分析,分别对各气象因素进行单因素分析,进而建立后退法线性回归分析模型,得到脑卒中与气压、气温、相对湿度之间的关系。
同时在广泛收集各种资料并综合考虑环境因素,对脑卒中高危人群提出预警和干预的建议方案。
首先,利用SPSS20软件,从患病人群的性别、年龄、职业进行统计分析,得到2007-2010年男性患病人数高于女性,且男性所占比例有逐年下降趋势,女性则有上升趋势,因此,性别比例呈减小趋势。
分析不同年龄段患病人数,得到患病高峰期为75-77岁之间,且青少年比例逐年呈增长趋势,可见患病比例趋于年轻化。
同时在不同的职业中,农民发病人数最多,教师,渔民,医务人员,职工,离退人员的发病人数较少。
其次,由题中所给数据先进行单因素分析,剔除对脑卒中影响不显着的因素,得出气温、气压、相对湿度对脑卒中的影响程度大小,进而采用后退法线性回归分析建立模型,利用SPSS20对数据进行分析,求得脑卒中发病率与气温、气压、相对湿度之间的关系。
即发病率与平均温度成正相关,与最高温度成负相关,发病率与平均气压成正相关,与最低气压成负相关,与平均相对湿度成负相关,与最小相对湿度成正相关。
最后,通过查找资料发现,影响脑卒中的因素有两类,一类是不可干预因素,如年龄、性别、家族史,另一类是可干预因素,如高血压、高血脂、糖尿病、肥胖、抽烟、酗酒等因素。
分析这些因素,建立双变量因素分析模型,并结合问题1和问题2,对高危人群提出预警和干预的建议方案。
关键词脑卒中单因素分析后退法线性回归分析双变量因素分析一问题的重述脑卒中(俗称脑中风)是目前威胁人类生命的严重疾病之一,它的发生是一个漫长的过程,一旦得病就很难逆转。
这种疾病的诱发已经被证实与环境因素,包括气温、湿度之间存在密切的关系。
对脑卒中的发病环境因素进行分析,其目的是为了进行疾病的风险评估,对脑卒中高危人群能够及时采取干预措施,也让尚未得病的健康人,或者亚健康人了解自己得脑卒中风险程度,进行自我保护。
同时,通过数据模型的建立,掌握疾病发病率的规律,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际的指导意义。
数据(见Appendix-C1)来源于中国某城市各家医院2007年1月至2010年12月的脑卒中发病病例信息以及相应期间当地的逐日气象资料(Appendix-C2)。
请你们根据题目提供的数据,回答以下问题:1.根据病人基本信息,对发病人群进行统计描述。
2.建立数学模型研究脑卒中发病率与气温、气压、相对湿度间的关系。
3.查阅和搜集文献中有关脑卒中高危人群的重要特征和关键指标,结合1、2中所得结论,对高危人群提出预警和干预的建议方案。
二问题分析问题的背景随着城市进程的加快、人口密度的加大、生活习性的改变、全球气候的变暖,一些严重威胁人们健康的疾病,如脑卒中的发病率呈现上升趋势。
全球每年有460万人死于脑卒中,中国每年死于脑卒中的病人有160多万。
脑卒中以其发病率高、死亡率高、致残率高的特点严重影响了人们的正常生活,成为仅次于癌症的“第二号杀手”。
脑卒中一旦发生,多数患者治疗效果不能满意,完全恢复正常者只占少数,大多数患者会遗留严重的后遗症,给患者和家庭带来沉重的心理和经济负担。
其成因包括环境、情绪、生活习惯、生理状况等多种因素,气象条件是脑卒中诱发的主要因素之一,根据气象条件变化对脑卒中发生的可能性进行预测,可以指导人们在不同天气条件下对脑卒中采取不同的预防措施,从而预防、减少脑卒中的发生。
如果能对脑卒中高危人群高位程度、患脑卒中的类型、患病风险、以及患病时间进行准确的评估,从而提出有针对性的防范措施,可以帮助医护人员对脑卒中的诊断,对于卫生行政部门和医疗机构合理调配医务力量、改善就诊治疗环境、配置床位和医疗药物等都具有实际的指导意义。
对发病人群的统计描述根据题中所给出的数据,利用SPSS20 软件,分别从性别、年龄、职业这几个因素出发,对数据进行统计性分析。
男女之间不同的生理结构,抵御环境的能力的不同,对脑卒中的影响也不同,分析男女在2007-2010年间患病的比例,进而可以更好的预防脑卒中。
随着的年龄的增长,患病人数在逐渐增长,分析不同年龄段患病人数的比例,得到脑卒中达到高峰时的年龄段。
不同的职业工作的环境不同,受教育程度不同,个人习惯也不同,进而影响到其得病的概率。
其次,不同的职业对脑卒中的预防与重视度不同。
农民可能由于经济状况的原因,不及时治疗,使得患病人数所占比例较大,而其他职业则相对较小。
脑卒中发病率与气温、气压、相对湿度间的关系由于平均温度、最高温度、最低温度、平均气压、最低气压、最高气压、平均相对湿度、最小相对湿度对脑卒中的影响并不都非常显着,所以本文先通过单因素分析得出最低气温、最高气压对脑卒中的影响不显着。
然后建立后退法线性回归分析模型,利用SPSS20软件得出脑卒中发病率与气温、气压、相对湿度之间的关系。
即发病率与平均温度成相关,与最高温度成负相关,发病率与平均气压成正相关,与最低气压成负相关,与平均相对湿度成负相关,与最小相对湿度成正相关高危人群提出预警和干预的建议方案广泛收集各种资料并综合考虑环境因素,发现影响脑卒中的因素有两类,一类是不可干预因素,如年龄、性别;另一类是可干预因素,如高血压、糖尿病、血脂异常、肥胖、饮酒等因素。
分别分析这些因素对脑卒中的影响,建立双变量分析模型,进而提出高危人群预警和干预的建议方案。
三问题的假设1.假设不考虑该地区人数的变化。
2.假设不考虑脑卒中的患病类型。
3.假设影响脑卒中发病率的各因素之间互不相关。
4.假设不考虑影响遗传因素、个体差异对脑卒中的影响。
四符号说明五模型的建立与求解模型一的建立与求解随着社会的发展,统计学在医疗气象研究中的作用越来越重要,成为一种普遍应用的方法,并为人们所认可,发挥着极其重要的指导性作用。
本文运用SPSS 20 软件分别从性别、年龄、职业对发病人群进行统计分析。
从上表可以看出,2007年-2010年脑卒中发病人群中,男性高于女性。
分析可能男性普遍有吸烟饮酒的不良生活习惯,还与当前男性可能比女性面临更多的生活压力,导致高血压、糖尿病、高血脂等脑卒中危险因素的增加。
同时从上图可以看出,男性所占比例有下降趋势,女性有上升趋势,因此,性别比例呈减小趋势。
(1)农民的发病人数最多,其原因可能与农民高血压病例规则用药治疗所占的比率低,抽烟饮酒在人群中比例大,以及膳食结构不合理、摄入膳食结构不合理、摄入动物性优质蛋白少等因素有关。
也可能由于经济状况,对脑卒中的不重视,不能及时治疗脑卒中。
(2)退休人员发病人数较多,其原因可能是退休人员年龄较大,脑供血,脑供氧不足等原因引发脑卒中。
(3)教师,渔民,医务人员,职工,离退人员的发病人数较少。
其原因可能与受教育程度,工作环境等因素有关。
(1)18岁以下的青少年患病比例逐年基本呈增长趋势,可见患病年龄比例趋于年轻化。
(2)。
患病人数主要集中在41-80岁,其原因可能是年龄逐渐增长,血液循环所需能量减少,代谢减慢。
(3)80岁以上的患病人群中,女性高于男性图二2007年脑卒中不同年龄段发病人数趋势图 图三2008年脑卒中不同年龄段发病人数趋势图 图四2009年脑卒中不同年龄段发病人数趋势图 图五2010年脑卒中不同年龄段发病人数趋势图从上图中可以看出,脑卒中发病高峰年龄段2007年为75-77岁之间,2008年为74-76岁之间,2009年76-78岁之间,2010年为75-78岁之间。
由此可知,脑卒中发病率高峰年龄段为75-77岁之间。
模型二的建立与求解通过题中所给数据,首先通过单因素分析得出气温、气压、相对湿度对脑卒中发病情况的影响关系大小,其次建立多元线性回归分析模型,最后利用SPSS20软件对数据进行分析,得到气温、气压、相对湿度与发病情况的关系。
5.2.1 单因素模型的建立假设a 为给定的显着性水平,则列出:气温、气压、相对湿度分别对脑卒中的影响程度分析,即单因素分析,公式如下:若a F F ≥,表明均值之间的差异显着,该因素对观测值有显着影响。
若a F F ≤,表明均值之间的差异不显着,该因素对观测值没有显着影响。
5.2.2 模型的求解利用SPSS20 得出平均温度、最高温度、平均气压、最低气压、平均相对湿度、最小相对湿度对脑卒中的影响显着,而最低气温、最高气压对脑卒中的影响不显着。
5.2.3 多元化线性回归模型的建立在大多数的实际问题中,影响因变量的因素不止一个而是多个,因此对这类的问题本文采用多元化的线性回归分析。
根据脑卒中发病率与气温、气压、相对湿度之间的关系建立多元化线性回归模型,如下: 5.2.4 多元线性回归模型的基本假定假设1,解释变量是非随机的或固定的,且各x 之间互不相关(无多重共线性) 假设2,随机误差项具有零均值、同方差及不序列相关性,即:假设3,解释变量与随机项不相关,即:假设4,随机项满足正态分布,即:在医学病学研究中经常会遇到某一疾病的发生与变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况,而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用,这时采用一元回归分析预测法是难以奏效的,需要采用多元回归分析预测法。
列出多元线性回归模型的一般表现形式为:将n个统计数据代入上述模型,则问题转化为:5.2.5 模型的求解利用SPSS20 软件对数据进行分析,得到气温、气压、相对湿度之间的关系如下:分析以上结果得到最优化的回归方程:图七 2007-2010年月平均气压与患病比例的双轴变化图图八 2007-2010年月平均相对湿度与患病比例的双轴变化图图九 2007-2010年月平均温度与患病比例的双轴变化图由回归方程结合折线图可得出各因素与脑卒中发病率的影响如下:(1)脑卒中发病率与平均温度成正相关,即平均温度越高,发病率越高。
与最高温度成负相关,即最高温度越低,发病率越高。
(2)脑卒中发病率与平均气压成正相关,即平均气压越高,发病率越高。
与最低气压成负相关,即最低气压越低,发病率越高。
(3)脑卒中发病率与平均相对湿度成负相关,即平均相对湿度越低,发病率越高。
与最小相对湿度成正相关,即最小相对湿度越高,发病率越高。
模型三的建立与求解5.3.1脑卒中的危险因素研究中发现脑卒中的发病因素可以分为以下几类,第一类是生来具有的难以改变的先天性因素,如性别、年龄;第二类是环境因素,如感染或气候的影响;第三类是个体生活方式和饮食习惯因素,包括吸烟、饮酒、不合理膳食等,是可以控制的因素;第四类是家庭因素与环境因素相结所致的疾病,如高血压、心脏病、糖尿病等,是可以调节和治疗的病证。
