秋九年级数学上册正切习题新湘教
九年级数学上册第4章锐角三角函数4.2正切练习(新版)湘教版【含解析】

!!" !"²(^º´ !"-.TI. t1 I¦ Q | í+º» "¸`s S K # t6t8G^t()T²t1M^O^ H t 1M^ :t T6I¦Q$ t 1^ & S K (*D # S K &$D # H äät1I¦QSsU$ ÜH & #&$ !H S K 5$D ( % ! " E '3 4 5( +5# 8$D > L F3 # U * H S K 4H "" $ & & ( ( - ""1 - "". $ / - ""0 & ( * * , ! I
$ ! J!
!$ %$!* D e 6 " % f H K (* D -5 " $ C "0
N
4 5(+5 # 8$ D + 4 3 5 # &$ D v > 5 3ÿ E ; ¼ 89E'3 #5 $ ;# 3 4 VS 4 ; U H S K ;# "%' 槡& "$ # 3 ! 6 $ + # !) H S K (! D %& < *7 M 2 # % B # ! $ * Å + 2 B % ì£ÿ槡 # B / 0 ! 1 . % 槡 % % 3 +3 2 "$ # Ö/Â$C"B S K (* D # !$ 56H $$ 77 # !$ 77 À B 3 +3 2 $ # 56+.!) ! ïq #7 $ %$ H 4 5(+5 # 8$D F J K3 # U H S K3 "$ 89E G '3 -5)". % %H S K 5$ D ) ! ' # ! %$!* wxÔÓDe !6 " 5 f ' % & 槡 槡 0 / # 槡 &' 槡% )槡!% % % # % > & (* D ) H ' F J K &$ D ) H S K (* D ' > L F 5$ D $ L F S K &$ D & 槡 ( 1 . & # 槡 & # - ! ZA #!' !) %槡 %$ %槡 &) &# &$ %$!* ajDe!$ " & f JI ( ' %' ! E = Ö( £ # ! ! & ! ! % )& ; 槡 & '! ) 4 5bEÖ E Y U +3 4 5-_ 槡 _OQ-P > uC ! E 3 % ZA # ! ' # ) ; ' ) ( ( ( & ) % % % ( & % # % ) " $ G5) ". # !'! #& $ % * % ( / % 0 -槡 # * 8 $ %$!( 4 5 <=>?De%& "5 f 89 Ù :.: Q 3 # ! * 槡 5- v >$ Y VS 3 ; K +; 3 4# 8$ D +3 5 4# . 1 # E ;E 4 * % & # % +; 3 ;#% 3 5# ° ± ¡ ã " v ¡ I < H S K +; 5 À 3 5 # 3 4# 4 # %槡 5 #槡 5) % 4 !$ , 3 56@% 3 槡% 3 % # 3 5 % ! -5$ - # 4 5 , + 5 3 4 # 8$ D ,H S K+ 3 4 5 # #槡 # $ gh . 3 4 %槡 % % # -_PãIJI$ # # # # Ý 8 I """" # ++3 5 4 # ) 3 ; + 3 5 4 # % +; %' ! %' % +; +5 I (' I (' # ,+5 3 ;# , 5 3 # 5 ; $ +; %U ($ 4 5-.PFG C + 2 B Ç + ? 2? B # ! ? & ? 89'3 槡 # ++4 3 ; # 8$ D , 4 ) ; # 8$ D $ + + F J K3 ) H S K 3H "/ " $ # ++4 3 5 ) 3 ;# 8$ D +5 &) % & !) % & # , 4# 4 / - 槡 0 - 槡 5 $ + + 3 5 % # ,5 4 # 5 3 , 4 ;# %3 5 $ &) ! & 槡 # 1 - 槡 . & & % % 5 # , 4 ;# &$ # +3 % 4 5D + + ?2?B #! ? ? % , 5 #8$ D & 56|'3 + 槡 # EG H 3 ;(+3 ;# % '4 & + + ! ! &) %槡 # $ $ ,F J K3 ) H S K3 # ) # ) # gh / 3 4 槡 * B 2 % 槡 5 & 4 # $ ,H S K ;# # 槡* $ # ,3 3 ; % *$ %' % E G H 4 5 ( + #6 2#%( U H S K 3## JI ( ' '3 6 %( # " " H S K4 # " "$ %( 6 #
2020年秋九年级数学上册4.2正切作业新版湘教版_3100

2020年精品试题芳草香出品4.2 正切一、选择题1.如图K-33-1,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于( )图K-33-1A.513B.1213C.512D.1252.若tan(α+10°)=3,则锐角α的度数是( )A .20° B.30° C.35° D.50°3.2017·宜昌△ABC 在网格中的位置如图K -33-2所示(每个小正方形的边长均为1),AD ⊥BC 于点D ,则下列四个选项中错误的是( )图K -33-2A .sin α=cos αB .tanC =2C .sin β=cos βD .tan α=14.在△ABC 中,若锐角A ,B 满足⎪⎪⎪⎪⎪⎪cos A -32+(1-tan B )2=0,则∠C 的大小是( ) A .45° B.60° C.75° D.105°5.在Rt △ABC 中,∠C =90°,sin A =23,那么tan B 的值是( ) A.52 B.53 C.2 55 D.23 6.如图K -33-3,厂房屋顶人字形(等腰三角形)钢架的跨度BC =10米,∠B =36°,则中柱AD (D 为底边的中点)的长是( )图K -33-3A .5sin36°米B .5cos36°米C .5tan36°米D .10tan36°米7如何求tan75°的值,按下列方法作图可解决问题.如图K -33-4,在Rt △ABC 中,AC =k ,∠ACB =90°,∠ABC =30°,延长CB 至点M ,在射线BM 上截取线段BD ,使BD =AB ,连接AD ,依据此图可求得tan75°的值为( )。
2020年秋九年级数学上册 第4章 锐角三角函数 4.2 正切同步练习 (新版)湘教版
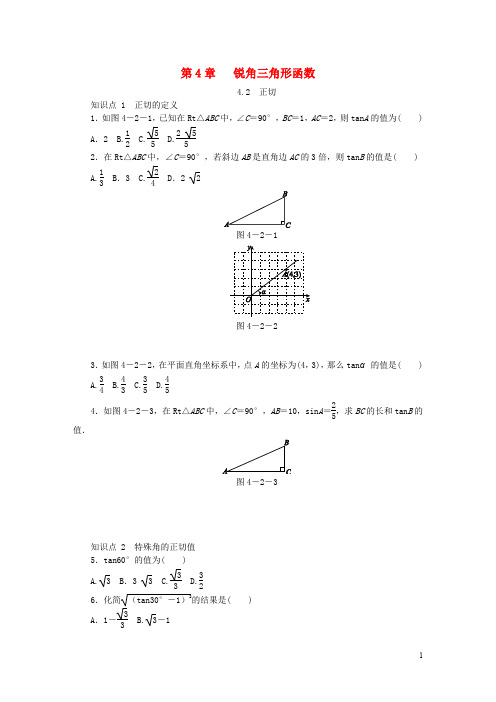
第4章 锐角三角形函数4.2 正切知识点 1 正切的定义 1.如图4-2-1,已知在Rt△ABC 中,∠C =90°,BC =1,AC =2,则tan A 的值为( ) A .2 B.12 C.55 D.2 552.在Rt△ABC 中,∠C =90°,若斜边AB 是直角边AC 的3倍,则tan B 的值是( ) A.13 B .3 C.24D .2 2图4-2-1图4-2-23.如图4-2-2,在平面直角坐标系中,点A 的坐标为(4,3),那么tan α的值是( ) A.34 B.43 C.35 D.454.如图4-2-3,在Rt△ABC 中,∠C =90°,AB =10,sin A =25,求BC 的长和tan B 的值.图4-2-3知识点 2 特殊角的正切值 5.tan60°的值为( ) A. 3 B .3 3 C.33 D.326.化简(tan30°-1)2的结果是( ) A .1-33B.3-1C.33-1 D.3+1 7.计算:(1)tan 230°-2tan60°sin60°+3tan45°;(2)3sin60°-2cos30°-tan60°·tan45°.知识点 3 用计算器求正切值或角度8.用计算器计算tan44°的结果是(精确到0.01)( ) A .0.95 B .0.96 C .0.97 D .0.989.已知tan A =5.2137,那么锐角A ≈________.(精确到1°) 知识点 4 锐角三角函数10.如图4-2-4,在Rt△ABC 中,∠C =90°,AB =13,BC =12,则下列三角函数表示正确的是( )图4-2-4A .sin A =1312B .cos A =1213C .tan A =512D .tan B =51211.已知α为锐角,且cos α=35,求sin α,tan α的值.12.李红同学遇到了这样一道题:3tan(α+20°)=1,则锐角α的度数应是( ) A .40° B.30° C.20° D.10° 13.在△ABC 中,若锐角∠A ,∠B 满足|cos A -32|+(1-tan B )2=0,则∠C 的度数为( ) A .45° B.60° C.75° D.105°14.2017·怀化模拟已知在Rt△ABC 中,∠C =90°,tan B =43,则cos A =________.15.如图4-2-5,在△ABC 中,AB =AC =5,BC =8.若∠BPC =12∠BAC ,则tan∠BPC =________.图4-2-5图4-2-616.如图4-2-6,在菱形ABCD 中,DE ⊥AB 于点E ,cos A =35,则tan∠DBE 的值是________.17.计算:(1)sin 245°+tan60°·cos30°2cos45°+tan45°;(2)sin60°-1tan60°-2tan45°-3cos30°+2sin45°.18.如图4-2-7,△ABC的顶点都是正方形网格中的格点,求tan∠BAC的值.图4-2-719.在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,∠C=90°.若定义cot A=∠A的邻边∠A的对边=ba,则称它为锐角A的余切.根据这个定义解答下列问题:(1)求cot30°的值;(2)已知∠A为锐角,tan A=34,试求cot A的值;(3)求证:tan A=cot(90°-∠A).1.B 2.C3.A [解析] 过点A 作AB 垂直x 轴于点B ,则AB =3,OB =4,所以tan α=AB OB =34.故选A.4.解:∵sin A =BC AB =25,AB =10,∴BC =4.又∵AC =AB 2-BC 2=221, ∴tan B =ACBC =212. 5.A 6.A 7.解:(1)原式=(33)2-2 3×32+3=13-3+3=13. (2)原式=3×32-2×32-3×1=3 32-3-3=-32. 8.C [解析] tan44°≈0.97. 9.79°10. D [解析] ∵∠C =90°,AB =13,BC =12, ∴AC =AB 2-BC 2=5.选项A 中,sin A =BC AB =1213,错误;选项B 中,cos A =AC AB =513,错误;选项C 中,tan A =BCAC=125,错误;选项D 中,tan B =AC BC =512,正确.故选D. 11.解:如图所示,∵cos α=AC AB =35,∴设AC =3a ,AB =5a (a >0),则BC =AB 2-AC 2=(5a )2-(3a )2=4a ,∴sin α=BC AB =4a 5a =45,tan α=BC AC =4a 3a =43.12.D [解析] ∵3tan(α+20°)=1,∴tan(α+20°)=33.∵α为锐角,∴α+20°=30°,α=10°.故选D.13.D [解析] ∵锐角∠A ,∠B 满足|cos A -32|+(1-tan B )2=0,∴∠A =30°,∠B =45°,∴∠C =105°.故选D.14.45 [解析] 如图,由tan B =43,可设AC =4k ,BC =3k (k >0),由勾股定理,得AB =5k ,∴cos A =AC AB =4k 5k =45.故答案为45.15.4316.2 17.解:(1)原式=(22)2+3×322×22+1=1.(2)原式=32-13-2×1-3×32+2×22=12-32+1=0. 18.解:设小正方形的边长为1,延长AC 与网格交于点E ,连接BE , 由勾股定理,得BE =2,AE =3 2,AB =2 5,则BE 2+AE 2=AB 2,所以△ABE 为直角三角形,且∠AEB =90°,所以tan∠BAC =BE AE =23 2=13.19. (1)在Rt△ABC 中,∠C =90°,设∠A =30°,则AB =2BC ,AC =3BC , ∴cot30°=AC BC=3BCBC= 3.(2)在Rt△ABC 中,∠C =90°,∵tan A =BC AC =34,∴可设BC =3k (k >0),则AC =4k ,∴cot A =AC BC =4k 3k =43.(3)证明:在Rt△ABC 中,∠C =90°,则∠A +∠B =90°,即∠B =90°-∠A . ∵tan A =BC AC ,cot B =BC AC,∴tan A =cot B ,即tan A =cot(90°-∠A ).。
湘教版数学九年级上4.2《正切》课时练习含答案

4.2 正切知识点一 正切的意义1.如图,在Rt △ABC 中,∠ACB=90°,CD 是AB 边上的高, ①tanA= = ; ②tanB= = ; ③tan ∠ACD= ; ④tan ∠BCD= .2.在Rt △ABC 中,90C ∠=,若三角形的各边都扩大3倍,则tan A 的数值( ).A .没有变化B .扩大了3倍C .缩小到13D .不能确定 3.在Rt △ABC 中,90C ∠=,65cm AB =,12tan 5B =,则AC 边的长为( ).A .25cmB .60cmC .20cmD .48cm4.如图,正方形ABCD 的边长为4,点M 在边DC 上,M 、N 两点关于对角线AC 对称,若DM =1,则tan ∠ADN = .5.如图,在ABC △中,90ACB ∠=,CD AB ⊥于D ,若AC =AB =tan BCD ∠的值.知识点一 坡度与坡角6.正切常用来描述坡面的坡度,如图,坡面的铅直高度h 和水平宽度l 的比叫做坡面的 (或 ),记作i ,即i = .7.已知一个斜坡的长为10米,高度为8米,则坡度为 .8.小敏沿着直坡度i=1山坡向上走了50m ,这时他离地面______m .9.有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为米,那么此拦水坝斜坡的坡度为 . 技能点一 求实际问题中的正切值A第4题图B DMNC ·· AD第1题图第6题图第10题图10.为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是A.14B.4 C D技能点二坡度在生活中的应角11.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1,坡面AB的水平距离为,上底宽AD为4m,求坝高AE和坝底BC的长.第11题图参考答案1.CDADBCACCDBDACBCADCDBDCD2.A 3.B4.4 35.26.坡度坡比h l7.4 38.259 110.A11.坝高AE和坝底BC的长分别为3m、4)m。
初中数学湘教版九年级上册第四章4.2正切练习题

初中数学湘教版九年级上册第四章4.2正切练习题一、选择题1.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是()A. sinα=cosαB. tanC=2C. sinβ=cosβD. tanα=12.cos30°的值是()A. 1B. √32C. 12D. √223.在Rt△ABC中,∠C=90°,tanA=512,则cos A等于()A. 512B. 125C. 513D. 12134.在△ABC中,若∠C=90°,cosA=12,则∠A等于()A. 30°B. 45°C. 60°D. 90°5.在Rt△ABC中,∠C=90°,若AB=5,BC=3,则sin A的值为()A. 43B. 35C. 34D. 456.计算tan60°的值等于()A. √33B. √32C. 1D. √37.已知在Rt△ABC中,∠C=90°,sinA=35,则∠A的正切值为()A. 43B. 45C. 54D. 348.已知sinA=12,则锐角A的度数是()A. 30°B. 45°C. 60°D. 75°9.已知cosα=34,则锐角α的取值范围是()A. 0°<α<30°B. 30°<α<45°C. 45°<α<60°D. 60°<α<90°10.在Rt△ABC中,∠C=90°,AC=3,BC=4,tanB=()A. 34B. 35C. 43D. 45二、填空题11.若√3tan(α+10°)=1,则锐角α=______.12.在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2√3,则AB=______.13.在△ABC中∠C=90°,tanA=√33,则cosB=______.14.已知如图:CD是Rt△ABC斜边上的高线,且AB=10,若BC=8,则cos∠ACD=______ .三、解答题15.计算:(−1)3+√9−(π−112)0−2√3tan60°16. 先化简,再求值:(a −1+3a−3a−2)÷a 2−2a+1a−2,其中a =2sin60°+1.17. 如图1,在△ABC 中,D 是AB 上一点,已知AC =10,AC 2=AD ⋅AB .(1)当tanA =34,∠ADC =90°时,求BC 的长.(2)如图2,过点C 作CE//AB ,且CE =6,连结DE 交BC 于点F ; ①若四边形ADEC 是平行四边形,求CFCB 的值; ②设AD =x ,CDCF =y ,求y 关于x 的函数表达式.答案和解析1.【答案】C【解析】解:观察图象可知,△ADB是等腰直角三角形,BD= AD=2,AB=2√2,AD=2,CD=1,AC=√5,∴sinα=cosα=√22,故A正确,tanC=ADCD=2,故B正确,tanα=1,故D正确,∵sinβ=CDAC =√55,cosβ=2√55,∴sinβ≠cosβ,故C错误.故选:C.观察图形可知,△ADB是等腰直角三角形,BD=AD=2,AB=2√2,AD=2,CD=1,AC=√5,利用锐角三角函数一一计算即可判断.本题考查锐角三角函数的应用.等腰直角三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.2.【答案】B【解析】解:cos30°=√32.故选:B.根据我们熟练记忆的特殊角的三角函数值即可得出答案.本题考查了特殊角的三角函数值,一些特殊角的三角函数值是需要我们熟练记忆的内容.3.【答案】D【解析】解:如图:设BC=5x,∵tanA=512,∴AC=12x,AB=√AC2+BC2=13x,∴cosA=ACAB =12x13x=1213.故选:D.根据tanA=512求出第三边长的表达式,求出cos A即可.本题利用了勾股定理和锐角三角函数的定义.解题的关键是掌握勾股定理和锐角三角函数的定义.4.【答案】C【解析】解:∵△ABC中,∠C=90°,cosA=12,∴∠A=60°.故选:C.根据∠A为△ABC的内角,且∠C=90°可知∠A为锐角,再根据cosA=12即可求出∠A的度数.本题比较简单,考查的是直角三角形的性质及特殊角的三角函数值.5.【答案】B【解析】【分析】本题主要考查锐角三角函数的意义,熟练掌握是解决问题的关键.找出∠A的对边与斜边,求出比值即可.【解答】解:∵在Rt△ABC中,∠C=90°,AB=5,BC=3,∴sinA=BCAB =35.故选B.6.【答案】D【解析】解:原式=√3,故选:D.根据特殊角的三角函数值进行计算即可.本题考查了特殊角的三角函数值,掌握特殊角的三角函数值是解题的关键.7.【答案】D 【解析】解:∵在Rt△ABC中,∠C=90°,sinA=35=BCAB,∴设BC=3x,AB=5x,由勾股定理得:AC=√AB2−BC2=4x,∴tanA=BCAC =3x4x=34,即∠A的正切值为34,故选:D.设BC=3x,AB=5x,根据勾股定理求出AC=4x,再根据锐角三角函数的定义求出即可.本题考查了锐角三角函数的定义和勾股定理,能熟记锐角三角函数的定义的内容是解此题的关键.8.【答案】A【解析】解:∵sinA=12,∴A=30°.故选:A.根据30°角的正弦值等于12解答.本题考查了特殊角的三角函数值,需熟记.9.【答案】B【解析】解:∵cos30°=√32,cos45°=√22,∵√22<34<√32,∴30°<α<45°,故选:B.根据余弦值随着角度的增大(或减小)而减小(或增大);考查了锐角三角函数的增减性,关键是熟练掌握当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).10.【答案】A【解析】解:如图所示:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,∴tanB=ACBC =34.故选:A.根据题意画出图形,进而利用锐角三角函数定义求出即可.此题主要考查了锐角三角函数定义,正确把握其定义是解题关键.11.【答案】20°【解析】解:由题意得,tan(α+10°)=√33,又∵tan30°=√33,∴α+10°=30°,解得:α=20°.故答案为:20°.根据tan30°=√33,结合α为锐角,即可得出α的度数.此题考查了特殊角的三角函数值,属于基础题,解答本题的关键是熟练记忆一些特殊角的三角函数值,难度一般.12.【答案】4【解析】解:∵CE所在直线垂直平分线段AD,∴CE平分∠ACD,∴∠ACE=∠DCE.∵CD平分∠BCE,∴∠DCE=∠DCB.∵∠ACB=90°,∴∠ACE=13∠ACB=30°,∴∠A=60°,∴AB=BCsin60∘=√3√32=4.故答案为:4.由CE所在直线垂直平分线段AD可得出CE平分∠ACD,进而可得出∠ACE=∠DCE,由CD平分∠BCE利用角平分线的性质可得出∠DCE=∠DCB,结合∠ACB=90°可求出∠ACE、∠A的度数,再利用余弦的定义结合特殊角的三角函数值,即可求出AB的长度.本题考查了线段垂直平分线的性质、角平分线的性质以及特殊角的三角函数值,通过角的计算找出∠A=60°是解题的关键.13.【答案】12【解析】解:利用三角函数的定义及勾股定理求解.∵在Rt△ABC中,∠C=90°,tanA=√33,设a=√3x,b=3x,则c=2√3x,∴cosB=ac =12.故答案为:12.本题可以利用锐角三角函数的定义求解,也可以利用互为余角的三角函数关系式求解.此题考查的知识点是特殊角的三角函数值,关键明确求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.14.【答案】45【解析】【分析】本题考查了锐角三角函数的定义,熟练掌握锐角三角函数是关键,在直角三角形中常运用同角或等角的三角函数来计算三角函数值.根据同角的余角相等得:∠ACD=∠B,利用同角的余弦得结论.【解答】解:∵CD是Rt△ABC斜边上的高线,∴CD⊥AB,∴∠A+∠ACD=90°,∵∠ACB=90°,∴∠B+∠A=90°,∴∠ACD=∠B,∴cos∠ACD=cos∠B=BCAB =810=45,故答案为:45.15.【答案】解:原式=−1+3−1−2√3×√3=1−2×3=−5;【解析】根据实数的运算法则,特殊角的三角函数值,算术平方根的运算分别进行化简即可;本题考查实数的运算,零指数幂,特殊角的三角函数值;牢记特殊角的三角函数值,掌握实数的运算性质是解题的关键.16.【答案】解:原式=(a2−3a+2a−2+3a−3a−2)÷(a−1)2a−2=a2−1a−2÷(a−1)2a−2=(a+1)(a−1)a−2⋅a−2(a−1)2=a+1a−1,当a=2sin60°+1=2×√32+1=√3+1时,原式=√3+1+1√3+1−1=√3+2√3=3+2√33.【解析】先根据分式的混合运算顺序和运算法则化简原式,再代入三角函数值求出a的值,代入计算可得.本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则及特殊锐角的三角函数值.17.【答案】解:(1)∵tanA=34,∠ADC=90°,∴CDAD =34,∴设CD=3a,CD=4a,∴AC=√AD2+CD2=√9a2+16a2=5a=10,∴a=2,∴CD=6,AD=8,∵AC2=AD⋅AB,∴ACAD =ABAC,且∠A=∠A,∴△ACD∽△ABC,∴∠ADC=∠ACB=90°,∵AC2=AD⋅AB,∴100=8⋅AB,∴AB=252,∴BD=9 2∴BC=√BD2+CD2=√814+36=152;(2)①∵四边形ADEC是平行四边形,∴AD=CE=6,DE//AC,∵AC=10,AC2=AD⋅AB,∴AB=503,∵DE//AC,∴△BDF∽△BAC,∴CFCB =ADAB=6503=925;②∵AC=10,AD=x,AC2=AD⋅AB,∴AB=100x,∵AC2=AD⋅AB,∴ACAD =ABAC,且∠A=∠A,∴△ACD∽△ABC,∴CDBC =ACAB=10100x=x10,∴BC=10⋅CDx,∵CE//AB,∴BDCE =BFCF,∴BD+66=BF+CFCF∴BD+66=BCCF,∴BD+66=10⋅CDx⋅CF∴y=x60[(100x−x)+6]=−160x2+110x+53.【解析】(1)由锐角三角形函数和勾股定理可求CD,AD的长,通过证明△ACD∽△ABC,可得∠ADC=∠ACB=90°,由勾股定理可求BC的长;(2)①由平行四边形的性质可得AD=CE=6,DE//AC,可证△BDF∽△BAC,可求解;②通过证明△ACD∽△ABC,可得BC=10⋅CDx ,由平行线分线段成比例可得BDCE=BFCF,代入可求解.本题是相似形综合题,考查了相似三角形的判定和性质,平行四边形的性质,勾股定理,锐角三角函数等知识,由相似三角形的性质求线段的长度是本题的关键.第11页,共11页。
湘教版九年级上册数学第4章 锐角三角函数 正 切

11.如图,在△ABC中,AB=AC=5,BC=6, 求tanB的值.
错解:在△ABC 中,tan B=AABC=55=1.
诊断:造成错解的原因是忽略了锐角三角 函数是在直角三角形中定义的.
15.要求 tan 45°的值,可构造直角三角形进行计算,如 图,作 Rt△ABC,使∠C=90°,直角边 AC=BC=1, 斜边 AB= 2,∠ABC=45°,则 tan 45°=ABCC=1.
(1)在此图的基础上,通过添加适当的辅助线,可 求出tan22.5°的值,请简要写出你添加的辅助 线,并求出tan22.5°的值;
7.【 中考·包头】如图,点 O 在△ABC 内,且到三边的
距离相等.若∠BOC=120°,则 tan A 的值为( A )
3
3
2
A. 3 B. 3 C. 2 D. 2
8.如图,一个人从山脚下的 A 点出发,沿山坡小路 AB 走到山顶 B 点,已知倾斜角为 20°,山高 BC =2 千米,用科学计算器计算小路 AB 的长度, 下列按键顺序正确的是( A ) A. 2 ÷sin 2 0 = B. 2 ×sin 2 0 = C. 2 ÷cos 2 0 = D. 2 ×tan 2 0 =
解:如图①,延长CA到D,使AD=AB,连接BD,构造 Rt△BCD,则∠D=22.5°.
在 Rt△BCD 中,BC=AC=1,AB= 2,AB=AD, ∴AD= 2,CD= 2+1, ∴tan 22.5°=CBDC= 21+1= 2-1.
(2)仿照(1)求出tan15°的值.
解:可先构造一个含 30°角的 Rt△ABC,再构造一 个含 15°角的 Rt△BCD. 如图②,∠C=90°,∠BAC=30°,BC=1,AD= AB=2,AC= 3,∠D=15°. 在 Rt△BCD 中,tan 15°=DBCC=2+1 3=2- 3.
湘教版九年级上册数学4.2《正切》【同步练习】(含答案)
《正切》同步练习1、在直角三角形中,各边都扩大2倍,则锐角A 的正弦值与余弦值都( )A 、缩小2倍B 、扩大2倍C 、不变D 、不能确定2、如图1,已知点P 的坐标是(a ,b ),则tan α等于( )A .B .C .3、如图2,在△ABC 中,AC =3,BC =4,AB =5,则tanB 的值是( )A .B .C .D . 4、在Rt △ABC 中,∠C =900,则下列式子成立的是( )A 、sinA =sinB B 、cosA =sinBC 、tanA =tanBD 、sinA =tanB5、若∠A 是锐角,且tanA =32,则( ) A 、00<∠A <300 B 、300<∠A <450 C 、450<∠A <600 D 、600<∠A <9006、已知α为锐角,且tan (α+120)=3,则α= ;7、如图,△ABC 的顶点都是正方形网格中的格点,则tan ∠ABC = 。
◆ 选择题◆ 解答题8、等腰三角形中,腰长为5,底边长8,则底角的正切值是 。
9、在Rt △ABC 中,∠C =900,a =8,b =6,则最小角的正切值是 ;10、若cosA =31,则AA A A tan 2sin 4tan sin 3+-= 。
11、计算:cos 2300-tan 600·cos 450+sin 230012、已知在Rt △ABC 中,∠C =900,AC =5,AB =7,求sin ∠A 、cosA 、tanA 这三个三角函数值。
13、如图,在Rt △ABC 中,∠ACB =900,CD ⊥AB 于D ,若BD :AD =1:3,求tan ∠BCD 。
参考答案1、C2、B3.A4、B5、B6、α= 48°7、an ∠ABC =128、34◆ 解答题C A B D9、34 ; 10、AA A A tan 2sin 4tan sin 3+-=0 11、计算:cos 2300-tan 600·cos 450+sin 2300=1-232⨯=1-62 12、解:BC =227526-= ,所以267sin A ∠=,57cosA = ,tanA =265 13、解:设BD =x ,则AD =3x ,所以23,3CD x x CD x =⨯= tan ∠BCD =333x x=。
秋九年级数学上册湘教版习题课件:4.2 正 切(共17张PPT)
15.如图,在△ABC 中,∠C=150°,AC=4,tanB=18. (1)求 BC 的长; (2)利用此图形求 tan15°的值.(精确到 0.1,参考数据: 2=1.4, 3=1.7, 5 =2.2)
解:(1)如图,过 A 作 AD⊥BC,交 BC 的延长线于点 D,在 Rt△ADC 中, AC=4,∠ACD=30°, ∴AD=21AC=2,CD=AC·cos30°=4× 23=2 3.在 Rt△ABD 中,tanB=ABDD= B2D=81,∴BD=16.BC=BD-CD=16-2 3.
53 A. 6
33 B. 2
C.12+ 3
D.12+
3 3
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 7:02:09 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
【规范解答】 B
能熟记特殊角的三角函数值. 【例 2】若 tan2x-( 3+1)tanx+ 3=0,求锐角 x. 【思路分析】 先求解关于 tanx 的一元二次方程,再求锐角 x 的值. 【规范解答】 解:∵tan2x-( 3+1)tanx+ 3=0 (tanx- 3)(tanx-1)=0 tanx- 3=0 或 tanx-1=0 tanx= 3或 tanx=1 ∴x=60°或 45°
新湘教版九上数学同步练习:4.2正切练习
4.2 正切知|识|目|标1 •通过对教材“探究”的学习,理解锐角的正切的定义,并能在直角三角形中求锐角的正切值.2•利用含30°, 45° , 60°角的直角三角形探索这些特殊角的正切值,并能进行有关计算.3•通过回顾用计算器计算锐角的正弦值,掌握用计算器求锐角的正切值及已知锐角的正切值求它的对应锐角.4.通过对锐角的正弦、余弦、正切的比较,归纳提炼出锐角三角函数的概念.、目标突破\_______________________ 有的菠矢目标一会求锐角的正切值例1教材补充例题如图4—2 —1所示,在Rt△ ABC中,/ C= 90°, AC= 10, AB= 26. 求tan A, tan B 的值.【归纳总结】锐角的正切的含义a b1. 在Rt△ ABC中, Z C= 90°, a, b 分别是/ A,Z B 的对边,则tan A=~, tan B= —.b a2. 在直角三角形中,求一个锐角的正切值只需要确定两条直角边的长,与斜边无关.3. 直角三角形中,两个锐角的正切值互为倒数.B ------------------ BBC 如图 4 — 2— 2,在 Rt △ ABC 中,/ O 90°, tan A = AC2例2教材补充例题已知在 Rt △ ABC 中,/ C= 90°, tan B = - , BC= 9.求AB 的长.3【归纳总结】 利用锐角的正切求三角形边长的条件(1)在直角三角形中;(2)已知其中一锐角的度数和两直角边中一边的长度. 目标二用特殊角的正切值进行计算例3教材例题针对训练计算:tan30 ° — 1 — 2tan60 ° + tan 260°+ tan45 ° • cos45 ° .1.tan B = AC 所以 tan A ・ tan B =【归纳总结】特殊角的正切值1. tan30 °=亏,tan45 ° = 1, tan60 °= 3.2. 锐角a的正切值tan a的变化规律:锐角a 的正切值tan a随着角度a的增大而增大.3. 若a 是锐角,则tan a • tan(90 ° —a ) = 1.目标三用计算器求锐角的正切值例4教材练习第2题变式利用计算器计算(精确到0.01):⑴tan81 ° ; (2)tan43.27 ° ; (3)tan22 ° 18'.【归纳总结】用计算器求值时要注意按键顺序,结果要按要求取近似值.目标四 会进行锐角三角函数的化简与求值1COS a 例5教材补充例题 已知a 为锐角,且COS a=7,求tan a +的值.31 十 Sin a【归纳总结】 锐角三角函数的化简计算中常用到的公式2 2COS a = 1(用于正、余弦之间的互化 );(1) Sin a + (2) tan a =Sina(用于正弦、余弦与正切之间的互化).例6 教材补充例题如图 4 — 2 — 3,在Rt △ ABC 中,/ C - 90°, BC= AC D 为AC 的中 点,求tan / ABD 的值.COS a【归纳总结】求锐角三角函数值的方法(1)采用转移法,通过作辅助线或利用三角形全等(相似)将锐角转移到直角三角形中;(2)在直角三角形中应用勾股定理分别求出各边的长;(3)利用锐角三角函数的定义求解即可.§总结反思* ______________ 小结感悟厂小结•学知识点一正切的定义在直角三角形中,锐角a的_________ 与______ 的比叫作角a的正切,记作tan a ,即tan a = __________ .如图4一2—4,在Rt△ ABC中,锐角a的对边是BC,邻边是AC,贝U tan a =知识点二特殊角的正切值tan30 ° =______ , tan45 ° =_____ , tan60 ° = ______ .知识点三用计算器由正切值求角度与用计算器由锐角的正、余弦值求角度相同,仅按的键不同.由正切值求角度时按键顺序应为“ 2ndF, tan,数值,=”或“ SHIFT, tan,数值,=”.知识点四锐角三角函数的概念定义:我们把锐角a的正弦、余弦和正切统称为角a的锐角三角函数.取值范围:当a为锐角时,正弦:O v sin a v 1,余弦:0 v cos a v 1,正切:tan a> 0.厂反思' --------- ---------- k1 如图4—2- 5,在Rt△ ABC中,/ 0= 90°, AB= 10, tan A=彳求BC的长.1 解:T tan A= •设B0= 2x,则A0= x.根据勾股定理,得(2X)2+ x2= 102,解得X= 2八;5(负值已舍去),.•• B0= 4 "J5.上述解题过程有错误吗?若有,请指出来,并写出正确的解题过程.详解详析【目标突破】例 1 解:•••/ C = 90°, AC= 10, AB= 26,BC= ./A B — A C = 24,2例 2 解:•••在 Rt A ABC 中,/ C =90°, tan B = 3,3••• tanB = AC = 3,即AC = 3,解得 AO 6. ••• AB= AC + BC = 62+ 92= 3 13. 例 3 解:原式=ta n 30°—(1 — tan 60°) 2+ tan 45°・ cos 45=tan 30°— |1 — tan 60° | + tan 45°・ cos 45°例6 解:如图,过点D 作DE I AB 于点E.设AC = BC = 2a,根据勾股定理得 AB= 2 ,2a. TD 为 AC 的中点,• AD = a. T 在 Rt △ ABC 中, BC= AC, ABC 是等腰直角三角形,A =Z ABC=45 ° .又•/ DE I ABADE 是 等腰直角三角形, • DE = AEn^a , • BE = AB- AE = ^^^a ,DE 1•tan "BA BE = 3.ta n A = BC 24Ac =io12T,tan B= AC 10BC = 24子―(3— 1) +芒一 2 ~2 =— 一例4解:(1) tan 81〜6.31.tan 43.27~ 0.94.tan 22° 180.41.5 解:原式sin a+ cos asin a (1 + sin cos a1 + sin a cos a (1 + sin a ) a )cos a 2cos a(1 + sin a )2COS a cos a ( 1 + sin a )2Sin a + sin a + sin a13 (1 + sin a )亠=3.【总结反思】知识点二 彳 13[反思]解:有错误.锐角的正切值应是锐角的对边与邻边的比.•••设 BC= x ,贝V AC = 2x.根据勾股定理,得 x 2+ (2x) 2= 102,解得x = 2 5,A BC= 25[小结]知识点一― 加、斗角a 的对边 对边邻边角a 的邻边 正确的解题过程如下:tan A = BC 1A C =2,。
