湖南省耒阳市九年级数学下册27圆27.2与圆有关的位置关系27.2.1点与圆的位关系导学案无答案新版
新华师版初中数学九年级下册精品课件27.2.1 点与圆的位置关系

27.2 与圆有关的位置关系
第1课时 点与圆的位置 关系
1 课堂讲解 点和圆的位置关系
确定圆的条件
2 课时流程 三角形的外接圆
逐点 导讲练
课堂 小结
作业 提升
我国射击运动员在里约奥运会上获得金牌,为我国赢得 荣誉,如图是射击靶的示意图,它是由许多同心圆(圆 心相同,半径不相同)构成的,你知道击中靶上不同位 置的成绩是如何计算的吗? 提示:解决这个问题要研究点和圆的位置关系.
作这两条弦的垂直平分线即可确定圆轮所在圆的圆心.
解:如图②所示:
(1)在圆轮所在的圆弧上任取三点A,
B,C,并连结AB,BC;
(2)分别作AB,BC的垂直平分线DE,
FG,DE,FG相交于点O;
(3)以O为圆心,OA为半径作⊙O,
⊙O就是圆轮所在的圆.
(来自《 》)
总结
知2-讲
经过不在同一条直线上的三点A,B,C作圆,圆心O 是线段AB,BC的垂直平分线的交点,再以OA(或OB, OC)为半径作圆即可,这样的圆只能作一个.
导引:要判断点和圆的位置关系,实质上是要比较点到圆心的 距离与半径的大小,而半径为已知量,即需求出相关点 到圆心的距离.
(来自《 》)
知2-讲
解:如图,连结OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,
∴OP= PD2 OD2 42 32 =5 (cm)=r,
∴点P在⊙O上;
知识点 1 点和圆的位置关系
知1-导
问题1:观察图中点A,点B,点C与圆的位置关系? 答:点A在圆内,点B在圆上,点C在圆外
(来自《 》)
知1-导
问题2:设⊙O半径为r,说出来点A,点B,点C与圆心O的距 离与半径的关系。 答:OA < r,OB = r,OC > r 问题3:反过来,已知点到圆心的距离和圆的半径,能否判断 点和圆的位置关系? 答:设⊙O的半径为r,点P到圆心的距离OP = d,则有:
九年级数学下册第27章圆27.2与圆有关的位置关系1点和圆的位置关系教学初中九年级下册数学

图所示,为配到与原来大小一样的圆形玻璃,小明带到商店
去的一块玻璃碎片应该是( )
D
A.第①块
B.第④块
C.第③块
D.第②块
第三十一页,共三十七页。
9.画出由所有到已知点的距离大于或等于2cm并且 (bìngqiě)小于或等于3cm的点组成的图形.
1
2cm O·
第三十二页,共三十七页。
10.如图,已知 Rt△ABC 中 ,C90
解析:由外心的定义可知外接圆的半径等于OB,过
点O作OD⊥BC,易得BD=12cm.由此可求它的外接
圆的半径.
解:连接(liánjiē)OB,过点O作OD⊥BC.
则OD=5cm, BD1BC12cm.
D
2
在Rt△OBD中
O BO D 2BD 213cm .
即△ABC的外接圆的半径(bànjìng)为13cm.
针对(zhēnduì) 训练
某一个城市在一块空地新建了三个居民小区,它们分 别为A、B、C,且三个小区不在同一直线上,要想规划
一所中学(zhōngxué),使这所中学(zhōngxué)到三个小区的距离相 等。请问同学们这所中学(zhōngxué)建在哪个位置?你怎么 确定这个位置呢?
●A
B●
第十七页,共三十七页。
能力拓展:一个8×12米的长方形草地,现要安装自动喷
水装置,这种装置喷水的半径为5米,你准备(zhǔnbèi)安装几个?
怎样安装? 请说明理由.
第三十四页,共三十七页。
课堂小结
点与圆的位 置(wèi zhi)关
系
作圆
位置(wèi zhi)关系数量化
点在圆外 点在圆上
d>r d=r
九年级数学下册 第27章 圆 27.2 与圆有关的位置关系教学课件

12/10/2021
第二十二页,共四十一页。
解:过C作CD⊥AB,垂足(chuízú)为D
在△ABC中,
AB= AC2 BC2 32 42 5
根据三角形的面积(miàn jī)公式有
D
1
1
CD AB ACBC
2
2
所以C D A C BC 342.4(c)m
AB 5
即圆心C到AB的距离d=2.4cm
O
E
B DC
12/10/2021
第二十六页,共四十一页。
3.切线(qiēxiàn)
12/10/2021
第二十七页,共四十一页。
回忆
直线和圆的位置(wèi zhi)关系有几种?
⑴ 相 离:
.O
dr ┐
用数量关系(guān xì)如何来判 断?
d>r
l
⑵ 相 切:
.O
d ┐r
l
d=r
⑶ 相 交:
12/10/2021
动手做一做
画一个圆O及半径OA,画一条直线l经过(jīngguò)⊙O 的半 径OA的外端点A,且垂直于这条半径OA,这条直线与圆
有几个交点?
●O
思考:
┐
l
A
直线l一定(yīdìng)是圆O的切线吗?由此,你知道如何画圆的
切线吗? 12/10/2021
第三十页,共四十一页。
一、圆的切线:
探索新知
同学们看过奥运会的射击比赛吗?射击的
靶子是由许多圆组成的,射击的成绩是由
击中靶子不同位置所决定的;右图是一位 运动员射击10发子弹在靶上留下(liú xià)的痕迹. 你知道这个运动员的成绩吗?请同学们算一算.
(击中最里面的圆的成绩为10环,依次为9、8、…、1环)
湖南省耒阳市九年级数学下册 27 圆 27.2 与圆有关的位置关系 27.2.2 直线与圆的位置关系
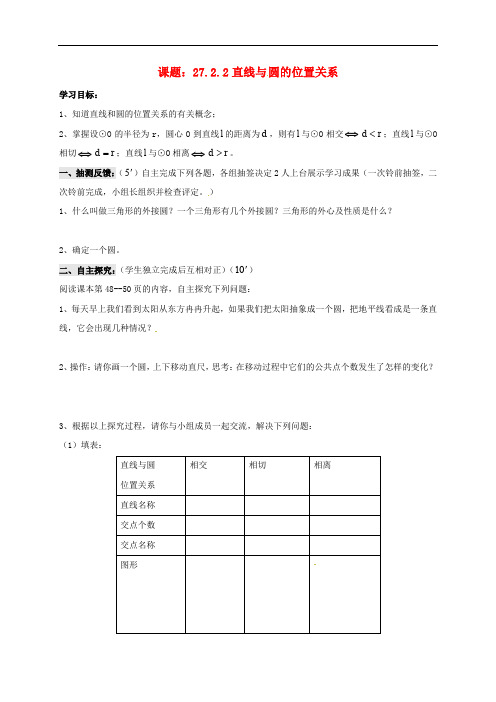
课题:27.2.2直线与圆的位置关系学习目标:1、知道直线和圆的位置关系的有关概念;2、掌握设⊙O 的半径为r ,圆心O 到直线l 的距离为d ,则有l 与⊙O 相交⇔d r <;直线l 与⊙O 相切⇔d r =;直线l 与⊙O 相离⇔d r >。
一、抽测反馈:(5')自主完成下列各题,各组抽签决定2人上台展示学习成果(一次铃前抽签,二次铃前完成,小组长组织并检查评定。
)1、什么叫做三角形的外接圆?一个三角形有几个外接圆?三角形的外心及性质是什么?2、确定一个圆。
二、自主探究:(学生独立完成后互相对正)(10') 阅读课本第48--50页的内容,自主探究下列问题:1、每天早上我们看到太阳从东方冉冉升起,如果我们把太阳抽象成一个圆,把地平线看成是一条直线,它会出现几种情况?2、操作:请你画一个圆,上下移动直尺,思考:在移动过程中它们的公共点个数发生了怎样的变化?3、根据以上探究过程,请你与小组成员一起交流,解决下列问题: (1)填表:(2)下图是直线与圆的三种位置关系,若⊙O半径为r圆心O到直线l的距离为d,则d与r的数理关系和直线与圆的位置关系:①直线l与圆相交⇔d r;②直线l与圆相切⇔d r;③直线l与圆相离⇔d r;4、⊙O的直径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是()A、相离B、相切C、相交D、相切或相交5、直线l上的一点到圆心O的距离等于⊙O的半径,则直线l与⊙O的位置关系是()A、相切B、相交C、相离D、相切或相交三、合作交流与展示提升(30')∆的斜边AB=8cm,AC=4cm.1、如图,已知Rt ABC(1)以点A为圆心,r为半径作圆,当r为多长时,直线BC与⊙A:①相交;②相切;③相离?(2)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?为什么?(3)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?2、如图,A 城气象台测得台风中心在A 城正西方向300km 的B 处,并以/h 的速度向北偏东60︒的BF 方向移动,距台风中心200km 的范围是受台风影响的区域。
2020学年数学九年级下册第27章圆27.2与圆有关的位置关系教案

27.2.1 点与圆的位置关系教学目标1、探索并掌握点与圆的三种位置关系,知道这三种位置关系中点与圆心的距离与半径的大小关系;2、知道经过不在同一直线上的三点确定一个圆,了解三角形与圆的关系;3、理解数形结合的方法。
教学重点、难点重点:探索并掌握点与圆的三种位置关系,知道这三种位置关系中点与圆心的距离与半径的大小关系;难点:知道经过不在同一直线上的三点确定一个圆,了解三角形与圆的关系。
教学准备:课件教学方法:操作体验法教学过程一、引入以课本的图片引入。
你玩边飞镖吗?它的靶子是由一些圆组成的,你知道击中靶子上不同的位置的成绩是计算的吗?这其中体现了平面内点与圆的位置关系。
二、操作1、画⊙O,在圆的外部、圆上、圆的内部分别画点A、B、C,测量OA、OB、OC的长度,测量圆的半径R;2、比较OA、OB、OC与半径R的大小关系;3、思考点与圆的位置关系;4、班级展示。
5、教师总结(1)点与圆有三种位置关系:点在圆内,点在圆上,点在圆外;(2)点与圆的位置关系与点到圆心的距离与半径的大小关系。
6、提出问题:圆上的点有无数个,那么多少个点可以确定一个圆呢?三、学习试一试1、画出过点A的圆。
2、画出过点A和B的圆,这些圆的圆心在哪里?3、班级展示。
4、老师总结。
过一个点A可以画无数个圆;过两个点A和B可以画无数个圆,圆心在线段AB的垂直平分线上。
5、提出问题:经过三点一定能画出一个圆吗?如果能,那么如何找出这个圆的圆心呢?四、学习思考1、分组操作:(4人一组)画过三个点的圆。
2、班级展示;3、老师总结:(1)如果三个点在同一直线上,不能画圆;(2)如果三个点不在同一直线上,可以画一个圆,圆心就是连接三个点的线段的中垂线的交点。
五、学习三点共圆1、不在同一直线上的三个点确定一个圆。
2、这时三个点形成的三角形就是圆的内接三角形;圆就是三角形的外接圆,圆心叫做外心。
外心在三角形三条边的垂直平分线上。
3、提了问题:课本练习第2题。
九年级数学下册第27章圆27.2与圆有关的位置关系27.2.2

27.2.2 直线与圆的位置关系
【归纳总结】判断直线和圆的位置关系的“三个步骤”:
图 27-2-3
27.2.2 直线与圆的位置关系
目标三 由直线与圆的位置关系求半径的值或取值范围
例 3 [教材补充例题] 如图 27-2-4,在 Rt△ABC 中,∠C= 90°,AC=3,AB=5,若以点 C 为圆心,r 为半径作圆,则:
(1)当直线 AB 与⊙C 相切时, 求 r 的值;
(2)当直线 AB 与⊙C 相离时, 求 r 的取值范围.
图 27-2-4
27.2.2 直线与圆的位置关系
解:(1)过点 C 作 CD⊥AB 于点 D.
∵在 Rt△ABC 中,AC=3,AB=5,
∴BC= AB2-AC2=4. ∵12AC·BC=21AB·CD,∴CD=d=2.4. ∵当直线 AB 与⊙C 相切时,d=r, ∴r=2.4. (2)由(1)知,圆心 C 到直线 AB 的距离 d=2.4. ∵当直线 AB 与⊙C 相离时,d>r, ∴0<r<2.4.
解:∵OP=2 cm,⊙O的半径r=2 cm,① ∴OP=r,② ∴圆心O到直线l的距离OP等于圆的半径,③ ∴直线l与⊙O相切.④ 以上推理在第________步开始出现错误.请你写出正确的推 理过程.
27.2.2 直线与圆的位置关系
解:③ 正确的推理过程如下:
∵OP=2 cm,⊙O的半径r=2 cm,
27.2.2 直线与圆的位置关系
【归纳总结】根据直线和圆的位置关系求圆的半径的值或取值 范围的步骤:
(1)过圆心作已知直线的垂线; (2)求出圆心到直线的距离; (3)根据直线与圆的位置关系求出半径的值或取值范围.
27.2.2 直线与圆的位置关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:27.2.1点与圆的位置关系
学习目标:
1、知道平面内点与圆的三种位置关系;
2、知道确定一个圆的条件,掌握三角形外接圆及三角形的外心的概念。
一、抽测反馈:(5')自主完成下列各题,各组抽签决定2人上台展示学习成果(一次铃前抽签,二次铃前完成,小组长组织并检查评定。
)
1、在平面内,⊙O的半径为5cm,点P到⊙O的距离为3cm,则点P与⊙O的位置关系是。
点与圆的位置关系
2、如图是一个圆形靶的示意图,O为圆心,小明向上面投了A、B、C、D、E 5枚飞镖,则①__________在⊙O内,__________在⊙O外,点B在__________
②试比较每个点到O点的距离与⊙O 半径r的大小
__________ >r; __________ = r ; __________ <r.
点与圆的位置关系可以按以下方法判断
点在圆上⇔点到圆心的距离d等于圆的半径r,即:d = r
点在圆内⇔点到圆心的距离d________圆的半径r,即:d ____ r
点在圆外⇔点到圆心的距离d________圆的半径r,即:d ____ r
二、自主探究:(学生独立完成后互相对正)(10')
阅读课本第46---48页的内容,自主探究下列问题:
(1)作经过已知点A的圆,这样的圆能作出多少个?
(2)经过A、B两点作圆,这样的圆能作出多少个?它们的圆心分布有什么特点?
(3)经过A 、B 、C 三点作圆,有哪些情况?三点应符合什么条件才能作圆?
(4)什么叫做三角形的外接圆?一个三角形有几个外接圆?三角形的外心及性质是什么?
(5)经过同一条直线上的三个点能作出一个圆吗?
三、合作交流与展示提升(30')
1、等腰直角三角形的腰长为4,则它的外接圆半径为。
2、直角三角形的两直角边分别为6和8,求它的外接圆半径。
3、用尺规作图分别画出经过下列三角形的外接圆。
4、如图,在Rt ABC ∆中,90ACB ∠=︒,AC=6,AB=10,CD 是斜边AB 上的中线,以AC 为直径作⊙O,设线段CD 的中点为P ,则点P 与⊙O的位置关系是怎样?
四、梳理巩固(2')整理导学案,梳理本节所学知识,检查导学案完成导学案以上所有内容,小组长检查!
五、达标测试:
1、已知⊙O的半径为4,OP=3.4,则P 在⊙O。
2、下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三
角形;④三角形的外心是各边垂直平分线的交点⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内。
其中正确的个数有( )
A 、1个
B 、2个
C 、3个
D 、4个
3、如图,ABC ∆中,AB=AC=10,BC=12,求ABC ∆的外接圆半径。
六、课后反思:
1、这节课我的表现:( )A 、很满意 B 、满 C 、一般 D 、有待改进
批阅情况
评定等级:⎽⎽⎽⎽⎽⎽⎽小组长签名:⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽年⎽⎽⎽⎽⎽月⎽⎽⎽⎽⎽日。
