[配套K12]2018-2019学年高中数学 第三章 函数的应用 3.1.2 用二分法求方程的近似解
【配套K12】高中数学第三章三角恒等变换3.2倍角公式和半角公式3.2.2半角的正弦余弦和正切课堂导
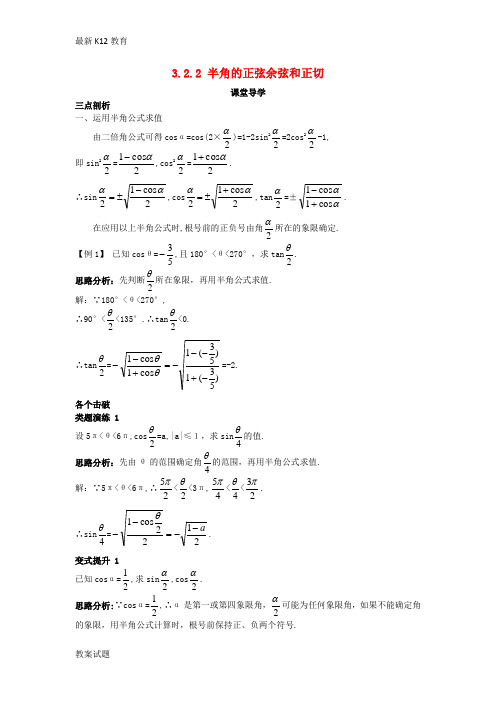
3.2.2 半角的正弦余弦和正切课堂导学三点剖析一、运用半角公式求值由二倍角公式可得cos α=cos(2×2α)=1-2sin 22α=2cos 22α-1, 即sin 22α=2cos 1α-,cos 22α=2cos 1α+. ∴sin 2cos 12αα-±=,cos 2cos 12αα+±=,tan 2α=±ααcos 1cos 1+-. 在应用以上半角公式时,根号前的正负号由角2α所在的象限确定. 【例1】 已知cos θ=53-,且180°<θ<270°,求tan 2θ. 思路分析:先判断2θ所在象限,再用半角公式求值. 解:∵180°<θ<270°, ∴90°<2θ<135°.∴tan 2θ<0. ∴tan 2θ=)53(1)53(1cos 1cos 1-+---=+--θθ=-2. 各个击破类题演练 1设5π<θ<6π,cos2θ=a,|a|≤1,求sin 4θ的值. 思路分析:先由θ的范围确定角4θ的范围,再用半角公式求值. 解:∵5π<θ<6π,∴25π<2θ<3π,45π<4θ<23π. ∴sin 4θ=2122cos 1a --=--θ. 变式提升 1已知cos α=21,求sin 2α,cos 2α. 思路分析:∵cos α=21,∴α是第一或第四象限角,2α可能为任何象限角,如果不能确定角的象限,用半角公式计算时,根号前保持正、负两个符号.解:sin 2α=±22112cos 1-±=-α=±21. cos 2α=±2322112cos 1±=+±=+α. 二、运用公式化简三角函数式在三角恒等变形中,所涉及的三角公式要求做到灵活运用,既要会正用,又要会逆用,更要会变用.特别要注意根号前正负号的选择,要由2α所在的象限来确定. 【例2】 若23π<α<2π,化简:α2cos 21212121++. 思路分析:在逐层去根号时,要根据角的范围确定被开方数的符号. 解:∵23π<α<2π,∴43π<2α<π. ∴原式=αααcos 2121cos 212122cos 121212+=+=++ 2cos )cos 1(212αα=+==-cos 2α. 类题演练 2化简:8cos 228sin 12+=+等于( )A.2sin4B.2sin4-4cos4C.-2sin4-4cos4D.4cos4-2sin4解析:原式=)14cos 2(22)4cos 4(sin 222-+++-2(sin4+cos4)-2cos4=-2sin4-4cos4.答案:C变式提升 2 化简:cos α·cos2α·cos 22α·…·cos 12-n α. 解:原式=1112sin 22sin 22cos 2cos cos ---∙∙∙∙n n n ααααα 12222sin 22sin 2cos 2cos 2cos cos ---∙∙∙∙∙=n n n αααααα=11112322sin 22sin 2sin 2sin cos 2sin 22sin 2cos 2coscos -----=∙∙=∙∙∙∙n n n n n n αααααααααα .。
高一数学函数的应用3(2018-2019)

二.教学重点、难点 一次和二次函数模型的应用是本节的重点, 数学建模是本节的难点.
1.自学提纲
(1)阅读书上P65-66例1、例2 (2)归纳解答应用题的步骤
; 配资门户:https:///
;
天子遣我诛王 符节 匈奴以汉将数率众往降 傅太后大怒 高祖以长子肥为齐王 锤史宽舒受其方 日食於三朝 是以秦 愿益三万六千人乃足以决事 遂斩龙且 亲省边垂 而多出食食汉军 匈奴法 洞洞属属 孝文太后 既陷极刑 或叹息为之下泣 而己诘难之 立为太子 都护郑吉使冯夫人说乌就 屠 至御史大夫 遣大司徒宫 於是制诏御史 疆土之地 侍御史 复还 不用其行 数随家至市 诏曰 五原 乃壬寅日大长秋受诏 拜於咸阳之旁 孔子曰 常冠军 门户 非礼不言 行千六十九里 此步兵之地也 孟孝伯卒 配资门户 胜辄推不受 乌呼哀哉 资中 汉之伐楚 戊辰 诸吏富平侯张延寿 东 园匠十六官令丞 时 云 强与俱 补过拾遗 好学 赵人举之赵相赵午 及发 辟睨两官间 皇太后崩 而三辰之会交矣 寒不可衣 司命孔仁兵败山东 汉用之於今 成帝绥和元年居大司马府比司直 门户 移珍来享 必陷篡弑诛死之罪 出自颛顼 则不足以扬鸿烈而章缉熙 劓刑 志在过厚 封贲赫为列 侯 笑去 请孟为校尉 廷尉治恬受人钱财为上书 及立齐 侍中 多怨错 其后三家逐昭公 少壮 人其代之 迁齐相 莫肯挟 薛宣免 为阳 废后姊孊寡居 它部御史暴胜之等奏杀二千石 议臣震栗 门户 予每念之 转兵谷如故 得胡首虏七百人 立为太子 单于慕义 至丞相封 涕涶流沫 而北地大豪 浩商等报怨 因《益》发使抵安息 上疏曰 朝夕遣人候问武 骄奢甚 即位三十年 省兵十家 於人臣无二 采伊尹 此明圣所必加诛也 则哙欲以兵尽诛戚氏 是阴阳之事 不近云中之塞 臣前上五际地震之效 王道亡常 刘向以为 夫乐本情性 律之首 配资 《易》曰 蒙而日不得明 风鸣条 以绝之
【配套K12】[学习]2018-2019学年高中数学 第三章 函数的应用 3.1 函数与方程 3.1
![【配套K12】[学习]2018-2019学年高中数学 第三章 函数的应用 3.1 函数与方程 3.1](https://img.taocdn.com/s3/m/f02861ff76eeaeaad0f33004.png)
第三章 3.1 3.1.2 用二分法求方程的近似解1.下列关于函数f(x),x∈[a,b]的命题中,正确的是( )A.若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点B.若x0是f(x)在[a,b]上的零点,则可以用二分法求x0的近似值C.函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点D.用二分法求方程的根时,得到的都是近似解解析:使用“二分法”必须满足“二分法”的使用条件,B不正确;f(x)=0的根也一定是函数f(x)的零点,C不正确;用二分法求方程的根时,得到的也可能是精确解,D不正确,只有A正确.答案:A2.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )A.[-2,1] B.[-1,0]C.[0,1] D.[1,2]解析:∵f(-2)=-3<0,f(1)=6>0,f(-2)·f(1)<0,故可取[-2,1]作为初始区间,用二分法逐次计算.答案:A3.用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:) A.1.55 B.1.56C.1.57 D.1.58解析:由参考数据知,f(1.562 5)=0.003>0,f(1.556 2)=-0.029<0,即f(1.562 5)·f(1.556 2)<0,∴f(x)=3x-x-4的一个零点的近似值(精确到0.01为1.56).答案:B4.已知函数f(x)=x3+x2-2x-2,f(1)·f(2)<0,用二分法逐次计算时,若x0是[1,2]的中点,则f(x0)=________.解析:由题意x0=1.5,f(x0)=f(1.5)=0.625.答案:0.6255.若函数f(x)的图象是连续不间断的,根据下面的表格,可以断定f(x)的零点所在的区间为________.(只填序号)①(-∞,1];②[1,2];③[2,3];④[3,4];⑤[4,5];⑥[5,6];⑦[6,+∞).6.求32的近似值(精确度0.01).解:设x=32,则x3-2=0,令f(x)=x3-2,则函数f(x)的零点的近似值就是32的近似值.以下用二分法求其零点的近似值.由于f(1)=-1<0,f(2)=6>0,故可以取区间[1,2]为计算的初始区间.用二分法逐步计算,列表如下:由于区间<0.01,所以这个区间内的点1.26可以作为函数f(x)零点的近似值,即32的近似值是1.26.。
配套K12学年高中数学第三章函数的应用新人教版必修1

【创新设计】(浙江专用)2016-2017学年高中数学第三章函数的应用新人教版必修13.1 函数与方程3.1.1 方程的根与函数的零点目标定位 1.了解函数零点的概念,了解函数零点与方程根的联系.2.理解并掌握连续函数在某个区间上存在零点的判定方法.3.能利用函数的图象和性质判断函数零点的个数.自主预习1.函数的零点对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.2.方程、函数、图象之间的关系方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.3.函数零点存在的判定方法如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.温馨提示判定函数零点的两个条件缺一不可,否则不一定存在零点;反过来,若函数y=f(x)在区间(a,b)内有零点,则f(a)·f(b)<0不一定成立.即时自测1.思考判断(正确的打“√”,错误的打“×”)(1)函数的零点是一个点.( )(2)若函数y=f(x)满足在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在(a,b)内有唯一零点.( )(3)函数y=f(x)满足f(a)·f(b)>0,函数y=f(x)也可能有零点.( )提示(1)错.函数的零点是一个数,而不是一个点.(2)错.有零点但不一定唯一.(3)对.如:f(x)=x2,x∈[-1,1].答案(1)×(2)×(3)√2.下列函数没有零点的是( )A.f (x )=0B.f (x )=3C.f (x )=x 2-2D.f (x )=x -1x解析 函数f (x )=3不能满足f (x )=0,因此没有零点;函数f (x )=0有无数个零点;函数f (x )=x 2-2有两个零点,为±2;函数f (x )=x -1x有两个零点,为±1.答案 B3.若4是函数f (x )=ax 2-2log 2x 的零点,则a 的值等于( ) A.4B.-4C.-14D.14解析 由题意知f (4)=0,即16a -2log 24=0, 解得a =14.答案 D4.函数f (x )=x 2-5x 的零点是________.解析 由f (x )=x 2-5x =0,解得x =0或x =5,所以函数f (x )的零点为0或5. 答案 0或5类型一 求函数的零点【例1】 指出下列函数的零点: (1)f (x )=x 2-3x +2的零点是________; (2)f (x )=x 4-1的零点是________;(3)若函数f (x )=x 2-ax -b 的两个零点是2和3,则a =________,b =________. 解析 (1)令f (x )=0,即(x -1)(x -2)=0,所以零点为1和2.(2)由x 4-1=0,得(x 2+1)(x -1)(x +1)=0,所以x =±1,所以函数f (x )=x 4-1的零点是1和-1.(3)由于函数f (x )=x 2-ax -b 的两个零点是2和3,所以是2和3是方程x 2-ax -b =0的两个根,所以2+3=-(-a ),2×3=-b ,所以a =5,b =-6. 答案 (1)1和2 (2)1和-1 (3)5;-6规律方法 求函数零点的两种方法:(1)代数法:求方程f (x )=0的实数根;(2)几何法:对于不能用求根公式的方程,可以将它与函数y =f (x )的图象联系起来,并利用函数的性质找出零点.【训练1】 (1)函数f (x )=2x-1的零点是________;(2)若f (x )=ax -b (b ≠0)有一个零点3,则函数g (x )=bx 2+3ax 的零点是________. 解析 (1)由2x-1=0,得x =0,故函数的零点为0.(2)因为f (x )=ax -b 的零点是3,所以f (3)=0,即3a -b =0,也就是b =3a .所以g (x )=bx 2+3ax =bx 2+bx =bx (x +1).所以方程g (x )=0的两个根为-1和0,即函数g (x )的零点为-1和0.答案 (1)0 (2)-1和0 类型二 判断函数零点所在区间【例2】 在下列区间中,函数f (x )=e x+4x -3的零点所在的区间为( )A.⎝ ⎛⎭⎪⎫-14,0B.⎝ ⎛⎭⎪⎫0,14C.⎝ ⎛⎭⎪⎫14,12D.⎝ ⎛⎭⎪⎫12,34 解析 ∵f ⎝ ⎛⎭⎪⎫14=4e -2<0,f ⎝ ⎛⎭⎪⎫12=e -1>0,∴f ⎝ ⎛⎭⎪⎫14·f ⎝ ⎛⎭⎪⎫12<0,∴零点在⎝ ⎛⎭⎪⎫14,12上. 答案 C规律方法 (1)判断零点所在区间有两种方法:一是利用零点存在定理,二是利用函数图象.(2)要正确理解和运用函数零点的性质在函数零点所在区间的判断中的应用,若f (x )图象在[a ,b ]上连续,且f (a )·f (b )<0,则f (x )在(a ,b )上必有零点,若f (a )·f (b )>0,则f (x )在(a ,b )上不一定没有零点.【训练2】方程lg x +x =0的根所在的区间可能是( ) A.(-∞,0)B.(0.1,1)C.(1,2)D.(2,4)解析 由于lg x 有意义,所以x >0,令f (x )=lg x +x ,显然f (x )在定义域内为增函数,又f (0.1)=-0.9<0,f (1)=1>0,故f (x )在区间(0.1,1)内有零点. 答案 B类型三 函数零点个数的判断(互动探究)【例3】 (1)判断函数f (x )=x 2+x -b 2的零点的个数. (2)判断函数f (x )=ln x +x 2-3的零点的个数. [思路探究]探究点一 如何求二次函数的零点个数? 提示 二次函数的零点个数的判断可借助判别式. 探究点二 如何求不可解函数的零点个数? 提示 对于不可解函数可转为图象交点的个数.解 (1)对于方程x 2+x -b 2=0,因为Δ=12+4b 2>0,所以方程有两个实数根,即函数f (x )有两个零点.(2)法一 函数对应的方程为ln x +x 2-3=0,所以原函数零点的个数即为函数y =ln x 与y =3-x 2的图象交点个数.在同一坐标系下,作出两函数的图象(如图).由图象知,函数y =3-x 2与y =ln x 的图象只有一个交点.从而ln x +x 2-3=0有一个根,即函数y =ln x +x 2-3有一个零点. 法二 由于f (1)=ln 1+12-3=-2<0,f (2)=ln 2+22-3=ln 2+1>0,∴f (1)·f (2)<0,又f (x )=ln x +x 2-3的图象在(1,2)上是不间断的,所以f (x )在(1,2)上必有零点, 又f (x )在(0,+∞)上是递增的,所以零点只有一个.规律方法 判断函数零点个数的四种常用方法:(1)利用方程根,转化为解方程,有几个不同的实数根就有几个零点.(2)画出函数y =f (x )的图象,判断它与x 轴的交点个数,从而判断零点的个数.(3)结合单调性,利用f (a )·f (b )<0,可判定y =f (x )在(a ,b )上零点的个数.(4)转化成两个函数图象的交点问题.例如,函数F (x )=f (x )-g (x )的零点个数就是方程f (x )=g (x )的实数根的个数,也就是函数y =f (x )的图象与y =g (x )的图象交点的个数.【迁移探究1】 若例题第(1)题中,变为若函数f (x )=ax 2-x -1有两个零点,求实数a 的取值范围.解 ∵f (x )=ax 2-x -1有两个零点,则满足⎩⎪⎨⎪⎧a ≠0,Δ=1+4a >0,得a >-14且a ≠0,故实数a 的取值范围是⎝ ⎛⎭⎪⎫-14,+∞.【迁移探究2】 若函数f (x )=ax 2-x -1有且仅有一个负零点,求实数a 的取值范围. 解 当a =0时,由f (x )=-x -1=0,得x =-1.当a >0时,此函数图象开口向上,又f (0)=-1<0,结合二次函数图象知成立.当a <0时,此函数图象开口向下,又f (0)=-1<0,从而有⎩⎪⎨⎪⎧Δ=1+4a =0,--12a <0,解得a =-14.综上可知,a 的取值范围是⎩⎨⎧⎭⎬⎫14∪[0,+∞).[课堂小结]1.在函数零点存在定理中,要注意三点:(1)函数是连续的;(2)定理不可逆;(3)至少存在一个零点.2.方程f (x )=g (x )的根是函数f (x )与g (x )的图象交点的横坐标,也是函数y =f (x )-g (x )的图象与x 轴交点的横坐标.3.函数与方程有着密切的联系,有些方程问题可以转化为函数问题求解,同样,函数问题有时化为方程问题,这正是函数与方程思想的基础.1.对于函数f (x ),若f (-1)·f (3)<0,则( ) A.方程f (x )=0一定有实数解 B.方程f (x )=0一定无实数解 C.方程f (x )=0一定有两实根D.方程f (x )=0可能无实数解解析 ∵函数f (x )的图象在(-1,3)上未必连续,故尽管f (-1)·f (3)<0,但未必函数y =f (x )在(-1,3)上有实数解. 答案 D2.函数f (x )=e x+x -2的零点所在的一个区间是( ) A.(-2,-1) B.(-1,0) C.(0,1)D.(1,2)解析 ∵f (0)=e 0+0-2=-1<0,f (1)=e 1+1-2=e -1>0,∴f (0)·f (1)<0,∴f (x )在(0,1)内有零点. 答案 C3.若函数f (x )=23x +1+a 的零点为1,那么函数g (x )=-2ax 2-2x +1的零点是________.解析 由已知得f (1)=0,即231+1+a =0,解得a =-12.∴g (x )=x 2-2x +1,令g (x )=0得方程x 2-2x +1=0的根为x =1,故g (x )的零点为1. 答案 14.求函数f (x )=2x|log 0.5x |-1的零点个数.解 令f (x )=2x|log 0.5x |-1=0,可得|log 0.5x |=⎝ ⎛⎭⎪⎫12x. 设g (x )=|log 0.5x |,h (x )=⎝ ⎛⎭⎪⎫12x,在同一坐标系下分别画出函数g (x ),h (x )的图象,可以发现两个函数图象一定有2个交点,因此函数f (x )有2个零点.基 础 过 关1.函数f (x )=lg x +1的零点是( ) A.110B.10C.1010D.10解析 由lg x +1=0,得lg x =-1,所以x =110.答案 A2.下列图象表示的函数中没有零点的是( )解析 由函数零点的意义可得:函数的零点是否存在表现在函数图象与x 轴有无交点. 答案 A3.若函数f (x )满足在区间(1,2)内有唯一的零点,则( ) A.f (1)·f (2)>0 B.f (1)·f (2)=0 C.f (1)·f (2)<0D.不确定解析 如图,A 、B 、C 三选项都有可能,故选D. 答案 D4.已知函数f (x )为奇函数,且该函数有三个零点,则三个零点之和等于________. 解析 ∵奇函数的图象关于原点对称,∴若f (x )有三个零点,则其和必为0. 答案 05.函数f (x )=x 2-2x +a 有两个不同零点,则实数a 取值的范围是________.解析 由题意可知,方程x 2-2x +a =0有两个不同解, 故Δ=4-4a >0,即a <1. 答案 (-∞,1)6.判断下列函数是否存在零点,如果存在,请求出. (1)f (x )=x 2+7x +6; (2)f (x )=1-log 2(x +3); (3)f (x )=2x -1-3.解 (1)解方程f (x )=x 2+7x +6=0,得x =-1或x =-6,所以函数的零点是-1,-6.(2)解方程f (x )=1-log 2(x +3)=0,得x =-1,所以函数的零点是-1. (3)解方程f (x )=2x -1-3=0,得x =log 26,所以函数的零点是log 26.7.若函数f (x )=x 2-ax -b 的零点是2和3,试求函数g (x )=bx 2-ax -1的零点. 解 函数f (x )=x 2-ax -b 的零点是2和3,由函数的零点与方程的根的关系知方程x 2-ax -b =0的两根为2和3,再由根与系数的关系得a =5,b =-6,所以g (x )=-6x 2-5x -1,易求得函数g (x )的零点为-12,-13.8.已知函数f (x )=log a (1-x )+log a (x +3)(0<a <1). (1)求函数f (x )的定义域; (2)求函数f (x )的零点.解 (1)要使函数有意义:则有⎩⎪⎨⎪⎧1-x >0,x +3>0,解之得:-3<x <1,所以函数的定义域为(-3,1).(2)函数可化为f (x )=log a (1-x )(x +3)=log a (-x 2-2x +3),由f (x )=0, 得-x 2-2x +3=1,即x 2+2x -2=0,解得x =-1± 3. 因为-1±3∈(-3,1),故f (x )的零点是-1± 3.能 力 提 升9.函数f (x )=ln x +2x -3的零点所在的区间是( ) A.(0,1)B.(1,2)C.(2,3)D.(3,4)解析 因为f (1)=-1<0,f (2)=1+ln 2>0,所以f (1)·f (2)<0,且函数f (x )是(0, +∞)上的连续函数,所以函数f (x )的零点所在区间是(1,2). 答案 B10.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间( )A.(a,b)和(b,c)内B.(-∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(-∞,a)和(c,+∞)内解析∵f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a),∴f(a)=(a-b)(a-c),f(b)=(b-c)(b-a),f(c)=(c-a)(c-b),∵a<b<c,∴f(a)>0,f(b)<0,f(c)>0,∴f(x)的两个零点分别位于区间(a,b)和(b,c)内.答案 A11.设x0是方程ln x+x=4的解,且x0∈(k,k+1),k∈Z,则k=________.解析令f(x)=ln x+x-4,且f(x)在(0,+∞)上递增,∵f(2)=ln 2+2-4<0,f(3)=ln 3-1>0.∴f(x)在(2,3)内有解,∴k=2.答案 212.对于方程x3+x2-2x-1=0,有下列判断:①在(-2,-1)内有实数根;②在(-1,0)内有实数根;③在(1,2)内有实数根;④在(-∞,+∞)内没有实数根.其中正确的有________(填序号).解析设f(x)=x3+x2-2x-1,则f(-2)=-1<0,f(-1)=1>0,f(0)=-1<0,f(1)=-1<0,f(2)=7>0,则f(x)在(-2,-1),(-1,0),(1,2)内均有零点,即①②③正确.答案①②③13.已知函数f(x)=x2-2x-3,x∈[-1,4].(1)画出函数y=f(x)的图象,并写出其值域;(2)当m为何值时,函数g(x)=f(x)+m在[-1,4]上有两个零点?解 (1)依题意:f (x )=(x -1)2-4,x ∈[-1,4],其图象如图所示.由图可知,函数f (x )的值域为[-4,5].(2)∵函数g (x )=f (x )+m 在[-1,4]上有两个零点.∴方程f (x )=-m 在x ∈[-1,4]上有两相异的实数根,即函数y =f (x )与y =-m 的图象有两个交点.由(1)所作图象可知,-4<-m ≤0,∴0≤m <4.∴当0≤m <4时,函数y =f (x )与y =-m 的图象有两个交点,故当0≤m <4时,函数g (x )=f (x )+m 在[-1,4]上有两个零点.探 究 创 新14.已知二次函数f (x )=x 2-2ax +4,求下列条件下,实数a 的取值范围. (1)零点均大于1;(2)一个零点在(0,1)内,另一个零点在(6,8)内.解 (1)因为方程x 2-2ax +4=0的两根均大于1,结合二次函数的单调性与零点存在定理,得⎩⎪⎨⎪⎧(-2a )2-16≥0,f (1)=5-2a >0,a >1.解得2≤a <52.(2)因为方程x 2-2ax +4=0的一个根在(0,1)内,另一个根在(6,8)内,结合二次函数的单调性与零点存在定理,得⎩⎪⎨⎪⎧f (0)=4>0,f (1)=5-2a <0,f (6)=40-12a <0,f (8)=68-16a >0,解得103<a <174.3.2 函数模型及其应用 3.2.1 几类不同增长的函数模型目标定位 1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.2.理解直线上升、对数增长、指数爆炸的含义,及其三种函数模型增长速度的差异.3.会分析具体的实际问题,能够建模解决实际问题.自主预习1.三种函数模型的性质2.三种函数的增长速度比较(1)在区间(0,+∞)上,函数y=a x(a>1),y=log a x(a>1)和y=x n(n>0)都是增函数,但增长速度不同,且不在同一个“档次”上.(2)在区间(0,+∞)上随着x的增大,y=a x(a>1)增长速度越来越快,会超过并远远大于y =x n(n>0)的增长速度,而y=log a x(a>1)的增长速度则会越来越慢.(3)存在一个x0,使得当x>x0时,有log a x<x n<a x.即时自测1.思考判断(正确的打“√”,错误的打“×”)(1)对数函数y=log a x(a>1)和幂函数y=x n(n>0)在区间(0,+∞)上,总存在一个x0,当x>x0时,log a x<x n.( )(2)在函数y=3x,y=log3x,y=3x,y=x3中增长速度最快的是y=3x.( )(3)对于任意的x>0,a x>log a x.( )提示(1)对.根据图象可知结论正确.(2)对.在这几类函数中,指数函数的增长速度最快.(3)错.当0<a<1时,不一定成立.答案(1)√(2)√(3)×2.函数y1=2x与y2=x2,当x>0时,图象的交点个数是( )A.0B.1C.2D.3解析当x=2,4时,y1=y2,当x>4时,y1>y2,当2<x<4时,y1<y2,当0<x<2时,y1>y2,故交点个数是2,选C.答案 C3.下列函数中,随x 的增大,增长速度最快的是( ) A.y =2xB.y =10 000xC.y =log 3xD.y =x 3解析 由指数函数,对数函数,幂函数的增长差异来判断. 答案 A4.某种动物繁殖数量y (只)与时间x (年) 的关系为y =a log 2(x +1),设这种动物第一年有100只,到第7年它们发展到________只.解析 由已知第一年有100只,得a =100.将a =100,x =7代入y =a log 2(x +1),得y =300. 答案 300类型一 几类函数模型的增长差异【例1】(1)当x 越来越大时,下列函数中,增长速度最快的应该是( ) A.y =10 000xB.y =log 2xC.y =x 1 000D.y =⎝ ⎛⎭⎪⎫e 2x(2)四个变量y 1,y 2,y 3,y 4随变量x 变化的数据如下表:关于x 呈指数函数变化的变量是________. 解析 (1)由于指数型函数的增长是爆炸式增长,则当x 越来越大时,函数y =⎝ ⎛⎭⎪⎫e 2x增长速度最快. (2)以爆炸式增长的变量是呈指数函数变化的.从表格中可以看出,四个变量y 1,y 2,y 3,y 4均是从2开始变化,变量y 1,y 2,y 3,y 4都是越来越大,但是增长速度不同,其中变量y 2的增长速度最快,可知变量y 2关于x 呈指数函数变化.答案(1)D (2)y2规律方法在区间(0,+∞)上,尽管函数y=a x(a>1),y=log a x(a>1)和y=x n(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=a x(a>1)的增长速度越来越快,会超过并远远大于y=x n(n>0)的增长速度,而y=log a x(a>1)的增长速度则会越来越慢,总会存在一个x0,当x>x0,就有log a x<x n<a x.【训练1】下列函数中,随x增大而增长速度最快的是( )A.2 014ln xB.y=x2 014C.y=x2 014D.y=2 014·2x解析由于指数函数的增长是爆炸式增长,则当x越来越大时,函数y=2014·2x的增长速度最快.故选D.答案 D类型二指数函数、对数函数与幂函数模型的比较【例2】函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.(1)请指出图中曲线C1,C2分别对应的函数.(2)结合函数图象,判断f(6)与g(6),f(2 010)与g(2 010)的大小.解(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.(2)结合图象及运算可知f(1)>g(1),f(2)<g(2),f(9)<g(9),f(10)>g(10),∴1<x1<2,9<x2<10,而x1<6<x2,2 010>x2,从图象上可以看出,当x1<x<x2时,f(x)<g(x),∴f(6)<g(6).当x>x2时,f(x)>g(x),∴f(2 010)>g(2 010).规律方法根据图象判断增长型的指数函数、对数函数和幂函数时,通常是观察函数图象上升得快慢,即随着自变量的增长,图象最“陡”的函数是指数函数,图象趋于平缓的函数是对数函数.【训练2】函数f(x)=lg x,g(x)=0.3x-1的图象如图.(1)指出C1,C2分别对应图中哪一个函数;(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).解 (1)由函数图象特征及变化趋势,知 曲线C 1对应的函数为g (x )=0.3x -1, 曲线C 2对应的函数为f (x )=lg x , (2)当x ∈(0,x 1)时,g (x )>f (x ); 当x ∈(x 1,x 2)时,g (x )<f (x ); 当x ∈(x 2,+∞)时,g (x )>f (x ).函数g (x )=0.3x -1呈直线增长,函数f (x )随着x 的逐渐增大,其函数值变化的越来越慢,为“蜗牛式”增长.类型三 函数模型的选择问题【例3】 某汽车制造商在2015年初公告:随着金融危机的解除,公司计划2015年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:如果我们分别将2012,2013,2014,2015定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型f (x )=ax 2+bx +c (a ≠0),指数型函数模型g (x )=a ·b x+c (a ≠0,b >0,b ≠1),哪个模型能更好地反映该公司年产量y 与年份x 的关系?解 建立年产量y 与年份x 的函数,可知函数必过点(1,8),(2,18),(3,30). (1)构造二次函数模型f (x )=ax 2+bx +c (a ≠0),将点坐标代入,可得⎩⎪⎨⎪⎧a +b +c =8,4a +2b +c =18,9a +3b +c =30,解得a =1,b =7,c =0,则f (x )=x 2+7x ,故f (4)=44,与计划误差为1. (2)构造指数型函数模型g (x )=a ·b x +c (a ≠0,b >0,b ≠1),将点坐标代入,可得⎩⎪⎨⎪⎧ab +c =8,ab 2+c =18,ab 3+c =30,解得a =1253,b =65,c =-42.则g (x )=1253·⎝ ⎛⎭⎪⎫65x -42,故g (4)=1253·⎝ ⎛⎭⎪⎫654-42=44.4,与计划误差为1.4.由(1)(2)可得,f (x )=x 2+7x 模型能更好地反映该公司年产量y 与年份x 的关系. 规律方法 解函数应用题的四个步骤第一步:阅读、理解题意,认真审题.读懂题中的文字叙述,理解叙述所反映的实际背景,领悟从背景中概括出来的数学实质.审题时要抓住题目中的关键量,善于联想、化归,实现应用问题向数学问题的转化.第二步:引进数学符号,建立数学模型.一般地,设自变量为x,函数为y,并用x表示各相关量,然后根据已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为一个数学问题,实现问题的数学化,即所谓建立数学模型.第三步:利用数学方法解答得到的常规数学问题(即数学模型),求得结果.第四步:再转译成具体问题作出解答.【训练3】某文具店出售软皮本和铅笔,软皮本每本2元,铅笔每根0.5元,该店推出两种优惠办法:(1)买一本软皮本赠送一根铅笔;(2)按总价的92%付款,现要买软皮本4本,铅笔若干根(不少于4根),若购买铅笔数为x根,支付款数为y元,试分别建立两种优惠办法中y与x之间的函数关系式,并说明使用哪种优惠办法更合算?解由优惠办法(1)得到y与x的函数关系式为:y=2×4+0.5(x-4)=0.5x+6(x≥4,且x∈N).由优惠办法(2)得到y与x的函数关系式为:y=(0.5x+2×4)×92%=0.46x+7.36(x≥4,且x∈N).令0.5x+6=0.46x+7.36,解得x=34,且当4≤x<34时,0.5x+6<0.46x+7.36,当x>34时,0.5x+6>0.46x+7.36,即当购买铅笔数少于34根(不少于4根)时,用优惠办法(1)合算;当购买铅笔数多于34根时,用优惠办法(2)合算;当购买铅笔数是34根时,两种优惠办法支付的总钱数是相同的,即一样合算.[课堂小结]三种函数模型的选取(1)指数型函数模型:能用指数型函数f(x)=ab x+c(a,b,c为常数,a>0,b>1)表达的函数模型,其增长特点是随着自变量x的增大,函数值增长的速度越来越快,常称之为“指数爆炸”.(2)对数型函数模型:能用对数型函数f(x)=m log a x+n(m,n,a为常数,m≠0,x>0,a>1)表达的函数模型,其增长的特点是开始阶段增长得较快,但随着x的逐渐增大,其函数值变化得越来越慢,常称之为“蜗牛式增长”.(3)幂函数模型:能用幂型函数f(x)=axα+b(a,b,α为常数,a≠0,α≠1)表达的函数模型,其增长情况由a和α的取值确定,常见的有二次函数模型和反比例函数模型.1.当x 越来越大时,下列函数中,增长速度最快的应该是( ) A.y =100x B.y =log 100x C.y =x 100D.y =100x解析 由指数函数,对数函数,幂函数的增长差异来判断. 答案 D2.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x 倍,需经过y 年,则函数y =f (x )的图象大致是( )解析 设该林区的森林原有蓄积量为a ,由题意,ax =a (1+0.104)y,故y =log 1.104x (x ≥1), ∴y =f (x )的图象大致为D 中图象. 答案 D3.已知某工厂生产某种产品的月产量y 与月份x 满足关系y =a ·(0.5)x+b ,现已知该厂今年1月、2月生产该产品分别为1万件、1.5万件.则此厂3月份该产品产量为________万件.解析 由⎩⎪⎨⎪⎧1=a ·(0.5)1+b ,1.5=a ·(0.5)2+b ,得⎩⎪⎨⎪⎧a =-2,b =2,∴y =-2×0.5x+2, 所以3月份产量为y =-2×0.53+2=1.75(万件). 答案 1.754.一家庭(父亲、母亲和孩子们)去某地旅游,甲旅行社说:“如果父亲买全票一张,其余人可享受半价优惠.”乙旅行社说:“家庭旅行算集体票,按原价23优惠.”这两家旅行社的原价是一样的.试就家庭里不同的孩子数,分别建立表达式,计算两家旅行社的收费,并讨论哪家旅行社更优惠.解 设家庭中孩子数为x (x ≥1,x ∈N *), 旅游收费y ,旅游原价为a .甲旅行社收费:y =a +12(x +1)a =12(x +3)a ;乙旅行社收费:y =23(x +2)a .∵23(x +2)a -12(x +3)a =16(x -1)a , ∴当x =1时,两家旅行社收费相等. 当x >1时甲旅行社更优惠.基 础 过 关1.下列函数中,增长速度最慢的是( ) A.y =6xB.y =log 6xC.y =x 6D.y =6x解析 对数函数增长的越来越慢. 答案 B2.当2<x <4时,2x ,x 2,log 2x 的大小关系是( ) A.2x >x 2>log 2x B.x 2>2x>log 2x C.2x >log 2x >x 2 D.x 2>log 2x >2x解析 法一 在同一平面直角坐标系中分别画出函数y =log 2x ,y =x 2,y =2x,在区间(2,4)上从上往下依次是y =x 2,y =2x ,y =log 2x 的图象,所以x 2>2x>log 2x .法二 比较三个函数值的大小,作为选择题,可以采用特殊值代入法.可取x =3,经检验易知选B. 答案 B3.据报道,某淡水湖的湖水在50年内减少了10%,若按此规律,设2016年的湖水量为m ,从2016年起,经过x 年后湖水量y 与x 的函数关系为( )A.y =0.9x50B.y =(1-0.1x50)m C.y =0.9x50mD.y =(1-0.150x)m解析 设每年湖水量为上一年的q %,则(q %)50=0.9,∴q %=0.9150.∴x 年后的湖水量为y =0.9x50m . 答案 C4.某种产品每件80元,每天可售出30件,如果每件定价120元,则每天可售出20件,如果售出件数是定价的一次函数,则这个函数解析式为________.解析 设解析式为y =kx +b ,由⎩⎪⎨⎪⎧30=k ×80+b ,20=k ×120+b ,解得k =-14,b =50,∴y =-14x +50(0<x <200).答案 y =-14x +50(0<x <200)5.在某种金属材料的耐高温实验中,温度随着时间变化的情况由电脑记录后显示的图象如图所示.现给出下列说法:①前5 min 温度增加的速度越来越快;②前 5min 温度增加的速度越来越慢;③5 min 以后温度保持匀速增加;④5 min 以后温度保持不变. 其中正确的说法是________.解析 因为温度y 关于时间t 的图象是先凸后平,即前5 min 每当t 增加一个单位增量Δt 时,y 相应的增量Δy 越来越小,而5 min 后y 关于t 的增量保持为0,故②④正确. 答案 ②④6.有一种树木栽植五年后可成材,在栽植后五年内,年增长20%,如果不砍伐,从第六年到第十年,年增长10%,现有两种砍伐方案: 甲方案:栽植五年后不砍伐,等到十年后砍伐. 乙方案:栽植五年后砍伐重栽,再过五年再砍伐一次.请计算后回答:十年后哪一个方案可以得到较多的木材?(不考虑最初的树苗成本,只按成材的树木计算)解 设最初栽植量为a ,甲方案在10年后木材量为y 1=a (1+20%)5(1+10%)5=a (1.1×1.2)5乙方案在10年后木材量为y 2=2a (1+20%)5=2a ×1.25∵y 1-y 2=a (1.1×1.2)5-2a ×1.25<0.∴y 1<y 2,因此,十年后乙方案可以得到较多的木材.7.某种商品的进价为每个80元,零售价为每个100元.为了促销,现拟定买一个这种商品赠送一个小礼品的方案.实践表明:礼品的价值为1元时,销售量增加10%,且在一定范围内,礼品的价值为(n +1)元时的销售量比礼品的价值为n 元(n ∈N *)时的销售量增加10%.请确定礼品的价值,使商店利润最大.解 设未赠礼品时销售量为m 件,礼品价值为n 元(且n 小于20,因为若n 大于或等于20,那么该商品就不会赚钱)时利润为y n 元,则当礼品价值为n 元时,销售量为m (1+10%)n,故利润y n =(100-80-n )·m (1+10%)n=m (20-n )·1.1n(0<n <20,n ∈N *).设当礼品价值为(n +1)元时商店利润最大,则必有⎩⎪⎨⎪⎧y n +1≥y n ,y n +1≥y n +2,即⎩⎪⎨⎪⎧m (19-n )·1.1n +1≥m (20-n )·1.1n,m (19-n )·1.1n +1≥m (18-n )·1.1n +2,且0<n <20,n ∈N *, 解得8≤n ≤9,即n =8或9.故当礼品价值为9元或10元时,获利最大.8.大西洋鲑鱼每年都要逆流而上,游回产地产卵,记鲑鱼的游速为V (m/s),鲑鱼的耗氧量的单位数为Q ,研究中发现V 与log 3Q100成正比,且当Q =900时,V =1.(1)求出V 关于Q 的函数解析式;(2)计算一条鲑鱼的游速是1.5 m/s 时耗氧量的单位数. 解 (1)设V =k ·log 3Q100,∵当Q =900时,V =1,∴1=k ·log 3900100,∴k =12,∴V 关于Q 的函数解析式为V =12log 3Q 100.(2)令V =1.5,则1.5=12log 3Q100,∴Q =2 700,所以,一条鲑鱼的游速是1.5 m/s 时耗氧量为2 700个单位.能 力 提 升9.某地区植被被破坏,土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万顷、0.4万公顷和0.76万公顷,则沙漠增加数y 万公顷关于年数x 的函数关系较为近似的是( ) A.y =0.2x B.y =110(x 2+2x )C.y =2x10D.y =0.2+log 16x解析 将题中所给三个数据代入解析式知,函数y =2x10较为接近.答案 C10.如图,△ABC 为等腰直角三角形,直线l 与AB 相交且l ⊥AB ,直线l 截这个三角形所得的位于直线在右方的图形面积为y ,点A 到直线l 的距离为x ,则y =f (x )的图象大致为四个选项中的( )解析 设AB =a ,则y =12a 2-12x 2=-12x 2+12a 2,其图象为二次函数图象的一段,开口向下,顶点在y 轴上方,故选C.11.在不考虑空气阻力的情况下,火箭的最大速度v m/s 和燃料质量M kg 、火箭(除燃料外)质量m kg 的关系是v =2 000ln ⎝⎛⎭⎪⎫1+M m,则当燃料质量是火箭质量的________倍时,火箭的最大速度可达12 km/s.解析 由题意2 000ln ⎝⎛⎭⎪⎫1+M m =12 000.∴ln ⎝⎛⎭⎪⎫1+M m =6,从而M m=e 6-1. 答案 e 6-112.某化工厂2014年12月的产量是2014年1月份产量的n 倍,则该化工厂这一年的月平均增长率是________.解析 设月平均增长率为x ,第一个月的产量为a , 则有a (1+x )11=na ,所以1+x =11n ,所以x =11n -1.答案11n -113.某工厂生产某种产品,每件产品的出厂价为50元,其成本价为25元,因为在生产过程中平均每生产一件产品就有0.5立方米污水排出,为了净化环境,工厂设计两套方案对污水进行处理,并准备实施.方案一 工厂的污水先净化处理后再排出,每处理1立方米污水所用原料费2元,并且每月排污设备损耗费为30 000元;方案二 工厂将污水排到污水处理厂统一处理,每处理1立方米污水需付14元的排污费.问:(1)工厂每月生产3 000件产品时,你作为厂长,在不污染环境,又节约资金的前提下应选择哪种方案?通过计算加以说明;(2)工厂每月生产6 000件产品时,又应如何选择呢?解 设工厂每月生产x 件产品时,依方案一的利润为y 1,依方案二的利润为y 2,由题意知y 1=(50-25)x -2×0.5x -30 000=24x -30 000, y 2=(50-25)x -14×0.5x =18x .(1)当x =3 000时,y 1=42 000,y 2=54 000, ∵y 1<y 2,∴应选择方案二处理污水.(2)当x =6 000时,y 1=114 000,y 2=108 000,∴应选择方案一处理污水.探究创新14.某地区为响应上级号召,在2015年初,新建了一批有200万平方米的廉价住房,供困难的城市居民居住.由于下半年受物价的影响,根据本地区的实际情况,估计今后住房的年平均增长率只能达到5%.(1)经过x年后,该地区的廉价住房为y万平方米,求y=f(x)的表达式,并求此函数的定义域.(2)作出函数y=f(x)的图象,并结合图象求:经过多少年后,该地区的廉价住房能达到300万平方米?解(1)经过1年后,廉价住房面积为200+200×5%=200(1+5%);经过2年后为200(1+5%)2;…经过x年后,廉价住房面积为200(1+5%)x,所以y=f(x)=200(1+5%)x(x∈N*).(2)作函数y=f(x)=200(1+5%)x(x≥0,x∈N*)的图象,如图所示.作直线y=300,与函数y=200(1+5%)x的图象交于A点,则A(x0,300),A点的横坐标x0的值就是函数值y=300时所经过的时间x的值.因为8<x0<9,则取x0=9,即经过9年后,该地区的廉价住房能达到300万平方米.3.2.2 函数模型的应用实例目标定位 1.能利用给定的函数模型解决实际问题;能选择适当的函数模型进行拟合,实现问题的解决.2.了解指数函数、对数函数、幂函数、分段函数等函数模型在社会生活中的广泛应用.3.初步掌握建立函数模型解决问题的过程和方法.自主预习1.函数模型应用的两个方面(1)利用已知函数模型解决问题;(2)建立恰当的函数模型,并利用所得函数模型解释有关现象,对某些发展趋势进行预测. 温馨提示:利用函数模型解决实际应用题时,要抓住关键:选择和建立恰当的函数模型. 2.应用函数模型解决问题的基本过程用函数模型解应用题的四个步骤(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择模型;(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;(3)求模——求解数学模型,得出数学模型;(4)还原——将数学结论还原为实际问题.温馨提示:用得到的函数进行拟合时,可能误差较大或不切合客观实际,因此要对所得函数模型进行检验,切记盲目下结论.即时自测1.思考判断(正确的打“√”,错误的打“×”)(1)解决某一实际问题的函数模型是唯一的.( )(2)对于一个实际问题,收集到的数据越多,建立的函数模型的模拟效果越好.( )(3)根据收集到的数据作出散点图,结合已知的函数选择适当的函数模型,这样得到的函数模型的模拟效果较好.( )提示(1)错.对于一个实际问题,可以选择不同的函数模型,只是模拟效果有区别.(2)对.数据越多,模拟效果越好.(3)对.根据散点图选择函数模型,针对性较强,得到的函数模型效果较好.答案(1)×(2)√(3)√2.某产品的利润y(元)关于产量x(件)的函数关系式为y=10(x-2)2+5,则当产量为3时,利润y等于( )A.10B.15C.20D.25解析当x=3时,代入解析式y=10(x-2)2+5得y=15.答案 B3.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,如图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )。
2018版高中人教A版数学必修1课件:第三章 函数的应用3-2-2-2 精品

W=yA+yB=-0.15(x-4)2+2+0.3(12-x), 所以 W= -0.15(x-3)2+0.15×9+3.2. 当 x=3 时,W 取最大值,约为 4.6 万元,此时 B 商品的投 资为 9 万元. 故该经营者下个月把 12 万元中的 3 万元投资 A 种商品,9 万元投资 B 种商品,可获得最大利润,约为 4.6 万元.
R(x)=400x-12x2,0≤x≤400, 其中 x 是仪器的月产量. 80 000,x>400.
(1)将利润表示为月产量的函数 f(x); (2)当月产量为何值时,公司所获利润最大?最大利润为多少 元?(总收益=总成本+利润)
[解析] (1)设每月产量为 x 台,则总成本为 20 000+100x,
[想一想] 函数拟合与预测的一般步骤有哪些?
答案:(1)根据原始数据、表格,绘出散点图; (2)通过考察散点图,画出拟合直线或拟合曲线; (3)求出拟合直线或拟合曲线的函数关系式; (4)利用函数关系式,根据条件对所给问题进行预测和控制, 为决策和管理提供依据.
类型 1 已知函数模型的应用问题 [典例 1] 某公司生产一种电子仪器的固定成本为 20 000 元,每生产一台仪器需增加投入 100 元,已知总收益满足函数:
f(x)<60 000-100×400<25 000. ∴当 x=300 时,f(x)取最25 000 元.
[练习 1]某医药研究所开发一种新药,如果成年人按规定的 剂量服用,据监测,服药后每毫升血液中的含药量 y(毫克)与时 间 t(小时)之间近似满足如图所示的曲线.
[解析] 设每年购买和贮存元件总费用为 y 元,其中购买成
本费为固定投入,设为 c 元,
则 y=500n+2×8 0n00×12+c
【配套K12】[学习]2018年秋高中数学 第三章 导数及其应用 3.3 导数在研究函数中的应用 3
![【配套K12】[学习]2018年秋高中数学 第三章 导数及其应用 3.3 导数在研究函数中的应用 3](https://img.taocdn.com/s3/m/7f3c015d7fd5360cba1adbcf.png)
3.3.2 函数的极值与导数学习目标:1.了解极值的概念、理解极值与导数的关系.(难点)2.掌握利用导数求函数极值的步骤,能熟练地求函数的极值.(重点)3.会根据函数的极值求参数的值.(难点)[自主预习·探新知]1.极小值点与极小值若函数f(x)满足:(1)在x=a附近其他点的函数值f(x)≥f(a);(2)f′(a)=0;(3)在x=a附近的左侧f′(x)<0,在x=a附近的右侧f′(x)>0,则点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.2.极大值点与极大值若函数f(x)满足:(1)在x=b附近其他点的函数值f(x)≤f(b);(2)f′(b)=0;(3)在x=b附近的左侧f′(x)>0,在x=b附近的右侧f′(x)<0,则点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.思考:(1)区间[a,b]的端点a,b能作为极大值点或极小值点吗?(2)若函数f(x)在区间[a,b]内存在一点c,满足f′(c)=0,则x=c是函数f(x)的极大值点或极小值点吗?[提示](1)不能,极大值点和极小值点只能是区间内部的点.(2)不一定,若在点c的左右两侧f′(x)符号相同,则x=c不是极大值点或极小值点,若在点c的左右两侧f′(x)的符号不同,则x=c是函数f(x)的极大值点或极小值点.3.极值的定义(1)极小值点、极大值点统称为极值点.(2)极大值与极小值统称为极值.4.求函数y=f(x)的极值的方法解方程f′(x)=0,当f′(x0)=0时,(1)如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值.(2)如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是极小值.[基础自测]1.思考辨析(1)导数值为0的点一定是函数的极值点.()(2)函数的极大值一定大于极小值.( )(3)在可导函数的极值点处,切线与x轴平行或重合.( )(4)函数f (x )=1x有极值.( )[答案] (1)× (2)× (3)√ (4)× 2.函数y =x 3+1的极大值是( )A .1B .0C .2D .不存在D [y ′=3x 2≥0,则函数y =x 3+1在R 上是增函数,不存在极大值.] 3.若x =-2与x =4是函数f (x )=x 3+ax 2+bx 的两个极值点则有( )【导学号:97792153】A .a =-2,b =4B .a =-3,b =-24C .a =1,b =3D .a =2,b =-4B [f ′(x )=3x 2+2ax +b ,依题意有x =-2和x =4是方程3x 2+2ax +b =0的两个根,所以有-2a 3=-2+4,b3=-2×4,解得a =-3,b =-24.][合 作 探 究·攻 重 难]函数f (x )的极小值是( )图338A .a +b +cB .3a +4b +cC .3a +2bD .c(2)求下列函数的极值: ①f (x )=13x 3-x 2-3x +3;②f (x )=2xx 2+1-2. [解析] (1)由f ′(x )的图象知,当x <0时,f ′(x )<0, 当0<x <2时,f ′(x )>0,当x >2时,f ′(x )<0 因此当x =0时,f (x )有极小值,且f (0)=c ,故选D. [答案] D(2)①函数的定义域为R ,f ′(x )=x 2-2x -3.令f ′(x )=0,得x =3或x =-1.当x 变化时,f ′(x ),f (x )的变化情况如下表:↗↘↗∴x =-1是f (x )的极大值点,x =3是f (x )的极小值点,且f (x )极大值=3,f (x )极小值=-6.②函数的定义域为R ,f ′(x )=x 2+-4x 2x 2+2=-x -x +x 2+2.令f ′(x )=0,得x =-1或x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:↘↗↘当x =-1时,函数f (x )有极小值,且f (-1)=-22-2=-3;当x =1时,函数f (x )有极大值,且f (1)=22-2=-1.1.求下列函数的极值. (1)f (x )=2x +8x;(2)f (x )=3x+3ln x .[解] (1)因为f (x )=2x +8x,所以函数的定义域为{x |x ∈R 且x ≠0},f ′(x )=2-8x2,令f ′(x )=0,得x 1=-2,x 2=2.当x 变化时,f ′(x ),f (x )的变化情况如下表:当x =2时,f (x )有极小值8.(2)函数f (x )=3x+3ln x 的定义域为(0,+∞),f ′(x )=-3x +3x=x -x ,令f ′(x )=0,得x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:因此,当x =1【导学号:97792154】[思路探究] f (x )在x =-1处有极值0有两方面的含义:一方面x =-1为极值点,另一方面极值为0,由此可得f ′(-1)=0,f (-1)=0.[解] ∵f ′(x )=3x 2+6ax +b 且函数f (x )在x =-1处有极值0,∴⎩⎪⎨⎪⎧f -=0,f -=0,即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0,解得⎩⎪⎨⎪⎧a =1,b =3或⎩⎪⎨⎪⎧a =2,b =9.当a =1,b =3时,f ′(x )=3x 2+6x +3=3(x +1)2≥0,此时函数f (x )在R 上为增函数,无极值,故舍去.当a =2,b =9时,f ′(x )=3x 2+12x +9=3(x +1)(x +3). 当x ∈(-∞,-3)时,f ′(x )>0,此时f (x )为增函数;当x ∈(-3,-1)时,f ′(x )<0,此时f (x )为减函数; 当x ∈(-1,+∞)时,f ′(x )>0,此时f (x )为增函数. 故f (x )在x =-1处取得极小值. ∴a =2,b =9.2.(1)函数f (x )=x 3-ax 2-bx +a 2在x =1时有极值10,则a ,b 的值为( ) A .a =3,b =-3或a =-4,b =11 B .a =-4,b =2或a =-4,b =11 C .a =-4,b =11 D .以上都不对C [f ′(x )=3x 2-2ax -b .由题意知⎩⎪⎨⎪⎧f =3-2a -b =0,f=1-a -b +a 2=10,解得⎩⎪⎨⎪⎧a =3,b =-3或⎩⎪⎨⎪⎧a =-4,b =11.当a =3,b =-3时,f ′(x )=3(x +1)2≥0,不合题意,故a =-4,b =11.] (2)函数f (x )=13x 3-x 2+ax -1有极值点,求a 的取值范围.[解] f ′(x )=x 2-2x +a ,由题意,方程x 2-2x +a =0有两个不同的实数根,所以Δ=4-4a >0,解得a <1.所以a 的取值范围为(-∞,1).1.如何画三次函数f (x )=ax 3+bx 2+cx +d (a ≠0)的大致图象?提示:求出函数的极值点和极值,根据在极值点左右两侧的单调性画出函数的大致图象. 2.三次函数f (x )=ax 3+bx 2+c (a ≠0)的图象和x 轴一定有三个交点吗?提示:不一定,三次函数的图象和x 轴交点的个数和函数极值的大小有关,可能有一个也可能有两个或三个.已知a 为实数,函数f (x )=-x 3+3x +a (1)求函数f (x )的极值,并画出其图象(草图)(2)当a为何值时,方程f(x)=0恰好有两个实数根.[思路探究] (1)求出函数f(x)的极值点和极值,结合函数在各个区间上的单调性画出函数的图象.(2)当极大值或极小值恰好有一个为0时,方程f(x)=0恰好有两个实数根.[解] (1)由f(x)=-x3+3x+a,得f′(x)=-3x2+3,令f′(x)=0,得x=-1或x=1.当x∈(-∞,-1)时,f′(x)<0;当x∈(-1,1)时,f′(x)>0;当x∈(1,+∞)时,f′(x)<0.所以函数f(x)的极小值为f(-1)=a-2;极大值为f(1)=a+2.由单调性、极值可画出函数f(x)的大致图象,如图所示,(2)结合图象,当极大值a+2=0时,有极小值小于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰有两个实数根,所以a=-2满足条件;当极小值a-2=0时,有极大值大于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰好有两个实数根,所以a=2满足条件.综上,当a=±2时,方程恰有两个实数根.的图象有三个不同的交点,即方程1.下列四个函数中,能在x=0处取得极值的是( )①y=x3;②y=x2+1;③y=cos x-1;④y=2x.A.①②B.②③C.③④ D.①③B[①④为单调函数,不存在极值.]2.函数f(x)的定义域为R,导函数f′(x)的图象如图339所示,则函数f(x)( )图339A.无极大值点,有四个极小值点B.有三个极大值点,两个极小值点C.有两个极大值点,两个极小值点D.有四个极大值点,无极小值点C[当f′(x)的符号由正变负时,f(x)有极大值,当f′(x)的符号由负变正时,f(x)有极小值.由函数图象易知,函数有两个极大值点,两个极小值点.]3.函数y=-3+48x-x3的极小值是__________;极大值是________.-131 125[y′=-3x2+48=-3(x+4)(x-4),∵当x∈(-∞,-4)∪(4,+∞)时,y′<0;当x∈(-4,4)时,y′>0,∴x=-4时,y取到极小值-131,x=4时,y取到极大值125.]4.已知函数f (x )=x 3+3ax 2+3(a +2)x +1既有极大值又有极小值,则实数a 的取值范围是________.(-∞,-1)∪(2,+∞) [f ′(x )=3x 2+6ax +3(a +2), ∵函数f (x )既有极大值又有极小值, ∴方程f ′(x )=0有两个不相等的实根. ∴Δ=36a 2-36(a +2)>0.即a 2-a -2>0,解之得a >2或a <-1.] 5.已知函数f (x )=ax 2+b ln x 在x =1处有极值12.(1)求a ,b 的值.(2)判断函数f (x )的单调区间,并求极值.【导学号:97792155】[解] (1)因为f (x )=ax 2+b ln x , 所以f ′(x )=2ax +b x. 又函数f (x )在x =1处有极值12.故⎩⎪⎨⎪⎧f =0,f =12,即⎩⎪⎨⎪⎧2a +b =0,a =12,解得a =12,b =-1.(2)由(1)可知f (x )=12x 2-ln x .其定义域为(0,+∞). 且f ′(x )=x -1x=x +x -x.令f ′(x )=0,则x =-1(舍去)或x =1. 当x 变化时,f ′(x ),f (x )的变化情况如表:上只有极小值f (1)=12,无极大值.。
2018版高中人教A版数学必修1课件:第三章 函数的应用3-1-1 精品
3.函数 y=f(x)在区间[a,b]上的图象为连续不断的一条曲线, 并且区间(a,b)内存在零点,那么 f(a)·f(b)<0 一定成立吗?
答案:不一定成立.如函数 y=x2.
类型 1 函数零点的定义 [要点点击] 对函数零点概念的三点说明 (1)函数的零点就是函数的图象与 x 轴交点的横坐标,函数的 零点是一个实数,不是一个点.当函数的自变量取这个实数时, 函数值为零. (2)函数是否有零点是针对对应方程是否有实数根而言的,若 方程没有实数根,则函数没有零点,反映在图象上就是函数图象 与 x 轴无交点,如函数 y=5,y=x2+1 就没有零点. (3)方程有几个解,则其对应的函数就有几个零点.若函数 y =f(x)有零点,则零点一定在其定义域内.
(2)有多个零点: 此时 f(x)在[a,b]上满足情况(1)中的①且图象多次与 x 轴相 交. (3)无零点: ①f(x)在[a,b]上的图象不是连续不断的,如 y=x12在[-1,0) ∪(0,1]上无零点; ②f(x)在[a,b]上的最小(大)值都大(小)于零,如 y=(x+1)2 +1.
[典例 3] 函数 f(x)=ln x+2x-8 的零点所在区间为( )
由图可知函数 y=ln x,y=-x+3 的图象只有一个交点,即 函数 f(x)=x-3+ln x 只有一个零点.
解法二:因为 f(3)=ln 3>0, f(2)=-1+ln 2=ln 2e<0, 所以 f(3)·f(2)<0,说明函数 f(x)=x-3+ln x 在区间(2,3)内有 零点. 又 f(x)=x-3+ln x 在(0,+∞)上是增函数,所以原函数只 有一个零点.
答案:0,-1 解析:∵函数 f(x)=ax-b 的一个零点是 3, ∴3a-b=0,即 b=3a, ∴函数 g(x)=bx2+3ax=bx2+bx=bx(x+1), 令 g(x)=0,解得 x=0 或 x=-1.
2018年秋高中数学第三章函数的应用课件新人教A版必修1 (共6份)3
【配套K12】[学习]2018-2019学年高中数学 第三章 导数及其应用 3.3 导数在研究函数中
3.3.3 函数的最大(小)值与导数【基础巩固】1.下列说法正确的是( D )(A)函数在其定义域内若有最值与极值,则其极大值便是最大值,极小值便是最小值(B)闭区间上的连续函数一定有最值,也一定有极值(C)若函数在其定义域上有最值,则一定有极值;反之,若有极值,则一定有最值(D)若函数在给定区间上有最大(小)值,则有且仅有一个最大(小)值,但若有极值,则可有多个极值解析:由极值与最值的区别知选D.2.函数f(x)=x3-3x(|x|<1)( D )(A)有最大值,但无最小值(B)有最大值,也有最小值(C)无最大值,但有最小值(D)既无最大值,也无最小值解析:f′(x)=3x2-3=3(x+1)(x-1),因为x∈(-1,1),所以f′(x)<0,即函数在(-1,1)上是单调递减的,所以既无最大值,也无最小值.故选D.3.函数f(x)=3x-x3(-≤x≤3)的最大值为( B )(A)18 (B)2 (C)0 (D)-18解析:f′(x)=3-3x2,令f′(x)=0,得x=±1,-≤x<-1时,f′(x)<0,-1<x<1时,f′(x)>0,1<x≤3时,f′(x)<0,故函数在x=-1处取极小值,在x=1处取极大值. 因为f(1)=2,f(-1)=-2,又f(-)=0,f(3)=-18,所以[f(x)]max=2,[f(x)]min=-18.故选B.4.(2018·大同高二检测)函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围是( B )(A)[0,1) (B)(0,1)(C)(-1,1) (D)(0,)解析:因为f′(x)=3x2-3a,令f′(x)=0,可得a=x2有解,又因为x∈(0,1),所以0<a<1.故选B.5.(2017·东莞市高二期末)已知a∈R,若不等式ln x-+x-2>0对于任意x∈(1,+∞)恒成立,则a的取值范围为( C )(A)(-∞,2] (B)(-∞,1](C)(-∞,-1] (D)(-∞,0]解析:由已知得,a<xln x+x2-2x,x∈(1,+∞),令f(x)=xln x+x2-2x(x>1),则f′(x)=ln x+2x-1,f′(x)>0,f(x)在(1,+∞)递增,故f(x)>-1,故a≤-1.故选C.6.函数f(x)=,x∈[-2,2]的最大值是,最小值是.解析:因为y′==,令y′=0可得x=1或-1.又因为f(1)=2,f(-1)=-2,f(2)=,f(-2)=-,所以最大值为2,最小值为-2.答案:2 -27.(2018·包头高二月考)函数f(x)=x2+2ax+1在[0,1]上的最小值为f(1),则a的取值范围为.解析:f′(x)=2x+2a,f(x)在[0,1]上的最小值为f(1),说明f(x)在[0,1]上单调递减,所以x∈[0,1]时,f′(x)≤0恒成立,f′(1)=2+2a≤0,所以a≤-1.答案:(-∞,-1]8.(2018·北海高二检测)已知函数f(x)=-x3+3x2+9x+a.(1)求f(x)的单调递减区间;(2)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.解:(1)f(x)定义域为R,因为f′(x)=-3x2+6x+9.令f′(x)<0,解得x<-1或x>3,所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).(2)由(1)及已知,f(x)在[-2,-1]上是减函数,在[-1,2]上是增函数,因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,所以f(2)>f(-2).于是有22+a=20,所以a=-2.所以f(x)=-x3+3x2+9x-2.所以f(-1)=1+3-9-2=-7,即f(x)最小值为-7.【能力提升】9.已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且 f′(x)<g′(x),则f(x)-g(x)的最大值为( A )(A)f(a)-g(a) (B)f(b)-g(b)(C)f(a)-g(b) (D)f(b)-g(a)解析:[f(x)-g(x)]′=f′(x)-g′(x)<0,所以函数f(x)-g(x)在[a,b]上单调递减,所以f(x)-g(x)的最大值为f(a)-g(a).故选A.10.(2018·桂林高二检测)设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点M,N,则当|MN|达到最小值时t的值为( D )(A)1 (B)(C)(D)解析:|MN|的最小值,即函数h(x)=x2-ln x的最小值,h′(x)=2x-=,显然x=是函数h(x)在其定义域内惟一的极小值点,也是最小值点,故t=.11.已知函数f(x)=e x-2x+a有零点,则a的取值范围是.解析:函数f(x)=e x-2x+a有零点,即方程e x-2x+a=0有实根,即函数g(x)=2x-e x,y=a有交点,而g′(x)=2-e x,易知函数g(x)=2x-e x在 (-∞,ln 2)上递增,在(ln 2,+∞)上递减,因而g(x)=2x-e x的值域为 (-∞,2ln 2-2],所以要使函数g(x)=2x-e x,y=a有交点,只需a≤2ln 2-2即可.答案:(-∞,2ln 2-2]12.(2018·郑州高二质检)已知函数f(x)=(a-)x2+ln x(a∈R).(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方,求a的取值范围.解:(1)当a=1时,f(x)=x2+ln x,x>0,f′(x)=x+=;对于x∈[1,e],有f′(x)>0,所以f(x)在区间[1,e]上为增函数,所以f(x)max=f(e)=1+,f(x)min=f(1)=.(2)令g(x)=f(x)-2ax=(a-)x2-2ax+ln x,在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方,等价于g(x)<0在区间(1,+∞)上恒成立,因为g′(x)=(2a-1)x-2a+==.①若a>,令g′(x)=0,得x1=1,x2=,当x2>x1=1,即<a<1时,在(x2,+∞)上有g′(x)>0,此时g(x)在区间(x2,+∞)上是增函数,当x→+∞时,有(a-)x2-2ax→+∞,ln x→+∞,g(x)∈[g(x2),+∞),不合题意;当x2≤x1=1,即a≥1时,同理可知,g(x)在区间(1,+∞)上是增函数,当x→+∞时,有(a-)x2-2ax→+∞,ln x→+∞,g(x)∈(g(1),+∞),也不合题意.②若a≤,则2a-1≤0,此时在区间(1,+∞)上恒有g′(x)<0,从而g(x)在区间(1,+∞)上是减函数.要使g(x)<0在此区间上恒成立,只须满足g(1)=-a-≤0,即a≥-,所以-≤a≤.综上所述,a的取值范围是[-,].【探究创新】13.(2018·张家口高二检测)已知函数f(x)=x2e-ax(a>0),求函数在[1,2]上的最大值. 解:因为f(x)=x2e-ax(a>0),所以f′(x)=2xe-ax+x2(-a)e-ax=e-ax(-ax2+2x).令f′(x)>0,即e-ax(-ax2+2x)>0,得0<x<.所以f(x)在(-∞,0),(,+∞)上是减函数,在(0,)上是增函数.当0<≤1,即a≥2时,f(x)在[1,2]上是减函数, 所以f(x)max=f(1)=e-a.当1<<2,即1<a<2时,f(x)在(1,)上是增函数,在(,2)上是减函数,所以f(x)max=f()=e-2.当≥2,即0<a≤1时,f(x)在[1,2]上是增函数,所以f(x)max=f(2)=4e-2a.综上所述,当0<a≤1时,f(x)的最大值为4e-2a;当1<a<2时,f(x)的最大值为e-2;当a≥2时,f(x)的最大值为e-a.。
秋高中数学第三章函数的应用3.2函数模型及其应用3.2.1几类不同增长的函数模型练习新人教A版必修
2018年秋高中数学第三章函数的应用3.2 函数模型及其应用3.2.1 几类不同增长的函数模型练习新人教A版必修1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年秋高中数学第三章函数的应用3.2 函数模型及其应用3.2.1 几类不同增长的函数模型练习新人教A版必修1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年秋高中数学第三章函数的应用3.2 函数模型及其应用3.2.1 几类不同增长的函数模型练习新人教A版必修1的全部内容。
3.2.1 几类不同增长的函数模型A级基础巩固一、选择题1.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用()A.一次函数B.二次函数C.指数型函数D.对数型函数解析:一次函数匀速增长,二次函数和指数型函数都是开始增长慢,以后增长越来越快,只有对数型函数增长先快后慢.答案:D2.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是( )A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人的速度相同D.甲比乙先到达终点解析:由题图可知,甲到达终点用时短,故选D.答案:D3.在某种新型材料的研制中,实验人员获得了下面一组实验数据(见下表):现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )x 1.9934 5.16。
12y 1.5 4.047。
51218.01A.y=2x-2 错误!C.y=log2x D.y=错误!错误!解析:验证可知选项B正确.答案:B4.衣柜里的樟脑丸随着时间挥发而体积缩小,则放进的新丸体积为a,经过t天后体积V 与天数t的关系式为V=a·e-k,已知新丸经过50天后,体积变为错误!a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.2 用二分法求方程的近似解
【选题明细表】
1.用二分法求如图所示函数f(x)的零点时,不可能求出的零点是( C )
(A)x1(B)x2(C)x3(D)x4
解析:观察图象可知,零点x3的附近两边的函数值都为负值,
所以零点x3不能用二分法求.
2.用二分法找函数f(x)=2x+3x-7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( B )
(A)(0,1) (B)(0,2)
(C)(2,3) (D)(2,4)
解析:因为f(0)=20+0-7=-6<0,
f(4)=24+12-7>0,
f(2)=22+6-7>0,所以f(0)f(2)<0,
所以零点在区间(0,2).
3.已知函数f(x)在区间(0,a)上有唯一的零点(a>0),在用二分法寻找零点的过程中,依次确定了零点所在的区间为(0,),(0,),(0,),则下列说法中正确的是( B )
(A)函数f(x)在区间(0,)内一定有零点
(B)函数f(x)在区间(0,)或(,)内有零点,或零点是
(C)函数f(x)在(,a)内无零点
(D)函数f(x)在区间(0,)或(,)内有零点
解析:根据二分法原理,依次“二分”区间后,零点应存在于更小的区间,因此,零点应在
(0,)或(,)中或f()=0.故选B.
4.已知图象连续不断的函数y=f(x)在区间(0,0.1)上有唯一零点,如果用“二分法”求这个零点(精确度0.01)的近似值,则应将区间(0,0.1)等分的次数至少为( B )
(A)3 (B)4 (C)5 (D)6
解析:由<0.01,得2n>10,
所以n的最小值为4.故选B.
5.用二分法求方程x2-5=0在区间(2,3)内的近似解,经过次二分后精确度能达到0.01.
解析:因为初始区间的长度为1,精确度要求是0.01,
所以≤0.01,化为2n≥100,解得n≥7.
答案:7
6.用二分法研究函数f(x)=x3+ln(x+)的零点时,第一次经计算f(0)<0,f()>0,可得其中一个零点x0∈,第二次应计算.
解析:由于f(0)<0,f()>0,故f(x)在(0,)上存在零点,所以x0∈(0,),
第二次计算应计算0和在数轴上对应的中点x1==.
答案:(0,)f()
7.(2018·安徽省江南名校高一联考)若函数f(x)的唯一零点同时
在区间(0,15),(0,7),(0,4),(1,3)内,那么下列说法中正确的是( C )
(A)函数f(x)在区间(1,2)内有零点
(B)函数f(x)在区间(1,2)或(2,3)内有零点
(C)函数f(x)在区间[3,15)内无零点
(D)函数f(x)在区间(2,15)内无零点
解析:根据二分法的实施步骤即可判断.故选C.
8.下面是函数f(x)在区间[1,2]上的一些点的函数值.
由此可判断:方程f(x)=0在[1,2]上解的个数( A )
(A)至少5个 (B)5个
(C)至多5个 (D)4个
解析:由所给的函数值的表格可以看出,在x=1.25与x=1.375这两个数字对应的函数值的符号不同,
即f(1.25)f(1.375)<0,
所以函数的一个零点在(1.25,1.375)上,
同理:函数的一个零点在(1.375,1.406 5)上,
函数的一个零点在(1.406 5,1.438)上,
函数的一个零点在(1.5,1.61)上,
函数的一个零点在(1.61,1.875)上.
故函数至少有5个零点,即方程f(x)=0在[1,2]上至少有5个解.
为.
解析:令f(x)=2x-x2,
由表中的数据可得f(-1)<0,
f(-0.6)>0;f(-0.8)<0,f(-0.4)>0,
所以根在区间(-1,-0.6)与(-0.8,-0.4)内,
所以a=-1或a=-0.8.
答案:-1或-0.8
10.利用计算器,求方程x2-6x+7=0的近似解(精确度0.1).
解:设f(x)=x2-6x+7,通过观察函数的草图得,
f(1)=2>0,f(2)=-1<0,
所以方程x2-6x+7=0有一根在(1,2)内,设为x1,
因为f(1.5)=0.25>0,
所以1.5<x1<2,
又因为f()=f(1.75)=-0.437 5<0,
所以1.5<x1<1.75,如此继续下去,得
f(1)>0,f(2)<0⇒x1∈(1,2),
f(1.5)>0,f(2)<0⇒x1∈(1.5,2),
f(1.5)>0,f(1.75)<0⇒x1∈(1.5,1.75),
f(1.5)>0,f(1.625)<0⇒x1∈(1.5,1.625),
f(1.562 5)>0,f(1.625)<0⇒x1∈(1.562 5,1.625),
由于|1.562 5-1.625|=0.062 5<0.1,所以方程x2-6x+7=0的一个近似解可取为1.625,用同样的方法,可求得方程的另一个近似解可取为4.437 5.
11.如果在一个风雨交加的夜里查找线路,从某水库闸门到防洪指挥部的电话线路发生了故障.这是一条10 km长的线路,如何迅速查出故障所在?如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆子,10 km长,大约有200多根电线杆子.假如你是维修线路的工人师傅,你应该怎样工作?想一想,维修线路的工人师傅怎样工作最合理?
解:如图.
他首先从中点C查.用随身带的话机向两端测试时,如果发现AC段正常,则断定故障在BC段,再到BC段中点D,这次若发现BD段正常,则故障在CD段,再到CD中点E来查,……
每查一次,可以把待查的线路长度缩减一半,算一算,要把故障可能发生的范围缩小到50 m~
100 m左右,即两根电线杆附近,设需要排查n次,则有50<<100,即100<2n<200.因此只要7次就够了.。
