第三章 正弦波振荡器3.2 LC正弦波振荡器 高频电子线路教学课件
合集下载
《正弦波振荡器》PPT课件

可见,这种振荡器不满足振幅起 振条件,必须加大的电冲击,产生大 于ViB 的起始扰动电压,才能进入平衡 点 A,产生持续等幅振荡。
.
图 3-1-3
19
硬激励:靠外加冲击而产生振荡。 软激励:接通电源后自动进入稳定平衡状态。
3.振幅稳定条件
要使平衡点稳定,T(osc) 必须在 ViA 附近具有随 Vi 增
则:① 振幅平衡条件:环路增益的模 T(osc) = 1
② 相位平衡条件:环路增益的相角
T(osc) = 2n
(n 0,1,2,···)
3.讨论
反馈振荡器需同时满足起振条件与平衡条件:
① 起振时,T(osc) > 1,Vi 迅速增长;
② 随后,T(osc)下降,Vi 的增长速度变慢;
.
14
③ 到 T(osc) = 1 时,Vi 停止
选频网络:LC振荡器,晶体. 振荡器,RC振荡器
4
四、振荡的基本原理
j
R2 1 4L2 LC
202
LCR 回路的自由振荡
.
5
R=0 时,有:
0 osc
1 LC
振荡器的振荡频率等于选频回路的中心频率。
获得等幅持续振荡的条件: 1、引入一个负电阻,以抵消LC 回路中固有的正电阻; 2、引入正反馈;
.
6
LC 正反馈振荡器必须具备的三个条件: 1、一套振荡回路,包含两个(或两个以上的)异性质
储能元件。能量在储能元件间交换,每秒钟能量交换的 次数即为振荡器的振荡频率。该频率值取决于LC的值, 即该回路决定 f0 ;
2、一个能量来源,即直流电源;
3、一个控制元件(设备),由有源器件和正反馈电路 组成。
2.掌握的基本理论和方法:
正弦波振荡器-PPT

2
2001年9月--12月
6
导致振荡频率不稳定得原因(续2)
2、 影响环路 Q 值得因素
o
Q1 Q2
2
Q2
Q1
f01 f02
f0
f
▪ 器件输入、输出阻抗中得有功 部分。
▪ 负载电阻得变化。
▪ 回路损耗电阻尤其就是电抗元 件 得高频损耗,环路元器件得高频 响应等。
2
2001年9月--12月
7
导致振荡频率不稳定得原因(续3)
• 泛音晶体振荡器:利用石英谐振器得泛音振动特性对频率 实行控制得振荡器称为泛音晶体振荡器。这种振荡器可以将 振荡频率扩展到甚高频以至超高频频段。
2001年9月--12月
19
1、 并联型晶体振荡电路
(1)皮尔斯(C-B)电路
RFC
Rb1
C
B
VCC
Rb 2
E
C1
Cb Re C2
JT
C
C1
E
C2
B
Lq
• 温度隔离法:将关键电抗元件置于特制得恒温槽内,使槽内得 温度基本上不随外界环境温度得变化。
▪ 利用石英谐振器等固体谐振系统代替由电感、电容构成得电 磁谐振系统,她就是高稳频率源得一个重要形式。 由于这种谐振系统构成得振荡器,不但频率稳定性、频率准确 度高,而且体积、耗电均很小,因此,在许多领域已被广泛地 采用。
0
2 L C
▪ 等号右边得负号表示频率变化得方向与电抗变化得方向刚好 相反。如电感量加大,振荡频率将降低。
2001年9月--12月
9
主要稳频措施(续1)
▪ 温度补偿法和温度隔离法:引起电抗元件电感量和电容量 变化最明显得环境因素就是温度得变化。
高频电子线路正弦波振荡器概述.ppt

合 肥 工 业 大 学
平衡条件:
T AF 1
振幅平衡条件
.
.
.
T AF 1 T A F 2nπ n=0,1,2…
相位平衡条件
等幅振荡
EXIT
通信电子线路
4.2
反馈型正弦波振荡器的工作原理
ui 晶体管 ic1 LC 选 频 网络 Z uc1 uf 反馈网络
平衡条件的另一种表示形式:
非正弦波: 产生三角波、锯齿波、矩形波等 EXIT
通信电子线路
4.1 概述
四、正弦波振荡器的用途
通信系统: 发射机(载波频率fC) 接收机(本地振荡频率fL) 测量仪器:信号源 数字系统:时钟信号 高频能源: 高频加热设备、主要技术指标
振荡频率、振荡波形、振荡幅度、频率稳定度 EXIT
U i Y fe
Y
Ic1
z p1
z
F U c1 F
U f
Y
F
振幅平衡条件:
Yfe Z p1F 1
合 肥 相位平衡条件: Y Z F 2n 工 业 大 其中: : 为集电极基波电流 i c 1 与基极输入电压 u i的相角 学
Z : 为 LC 谐振回路基波谐振阻抗 的相角
通信电子线路
4.2
反馈型正弦波振荡器的工作原理
4.2 反馈型正弦波振荡器的工作原理
主要要求:
掌握反馈振荡器的组成和基本工作原理
合 肥 工 业 大 学
理解反馈振荡器的起振条件和平衡条件,
了解其稳定条件。 掌握反馈振荡器能否振荡的判断方法。
EXIT
通信电子线路
4.2
反馈型正弦波振荡器的工作原理
一、 反馈型正弦波振荡器的组成 定义:从放大器的输出信号中取出一部分反馈到输入端 作为输入信号,无需外部提供激励信号,能产生等幅正 弦波输出称为反馈型振荡器。 放大器 Vo Vi
《LC正弦波振荡电路》课件

LC正弦波振荡电路的构成
原理和特点
LC振荡电路利用电感和电容器构成共振电 路,产生稳定且纯净的正弦波信号。
重要组件
振荡电路由电感、电容器和电阻组成,这 些元件起到不同的作用。
LC正弦波振荡电路的运行原理
1
共振条件
当电感和电容的参数满足一定条件
频率调节方法
2
时,振荡电路会产生共振现象。
通过调节电容和电感的数值,我们
《LC正弦波振荡电路》 PPT课件
本课件将介绍LC正弦波振荡电路的原理和应用。首先,我们会了解振荡电路 的定义和作用,以及为什么学习正弦波振荡电路。让我们一起探索这个令人 着迷的主题!
振荡电路的基本原理
1 基本组成部分
振荡电路由放大器、反馈网络和能量源组成。
2 工作原理
通过正反馈,振荡电路能够产生连续不断的信号输出。
可以改变振荡电路的输出频率。
3
幅度调节方法
可以通过改变电阻的数值来调节振 荡电路的输出幅度。
例题分析
电路ห้องสมุดไป่ตู้形图
我们将分析一个具体的LC正 弦波振荡电路的波形图并解 读其特点。
电路元件
了解电路中各个元件的作用 和参数对波形的影响。
频谱分析
通过频谱分析仪观察电路输 出的频谱特性。
高频电子线路正弦波振荡器.ppt
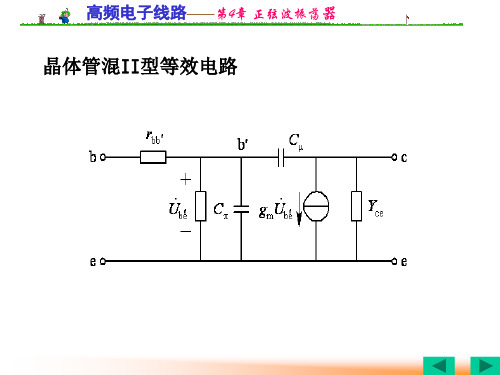
单调谐放大器
高频电子线路——第4章 正弦波振荡器
3.相位(频率)稳定条件
相位稳定条件和频率稳定条件实质上是一回事
正弦信号相位φ和频率ω的关系:
d
dt
dt
振荡器的角频率 增大导致相位不断超前 相位 的不断超前表明角频率 增大
高频电子线路——第4章 正弦波振荡器
(1)相位(频率)稳定过程
原平衡态: L (0 ) f F 0
4.1.2 起振条件
1.起振过程分析
单调谐放大器
刚通电:电路中存在很宽的频谱的电的扰动,幅值很小
通电后:
1)谐振回路的选频功能,从扰动中选出 osc 分量(osc 0)
2)放大器工作在线性放大区, |T (josc)|>1 ,形成增幅振荡
3)忽略晶体管内部相移: f =0
回路谐振: L=0
T (josc) =0,相移为零
起振 过程
平衡 状态
起振 过程
平衡 状态
输出波形:
高频电子线路——第4章 正弦波振荡器
4.1.4 稳定条件
1.平衡状态稳定分析:
(1)振荡电路中存在干扰
单调谐放大器
① 外部:电源电压、温度、湿度的变化,引起管子和回 路参数的变化。
② 内部:存在固有噪声(起振时的原始输入电压,进入平 衡后与输入电压叠加引起波动)。
单调谐放大器
外界干扰后: L (0 ) f F 0
Ub 相位超前 Ub 相位
升高
振荡回路相频特性 L 下降
L () f F 下降
L () f F 0
达到新的平衡 > 0
外界干扰消失后: L () f F 0
Ub 相位滞后 Ub 相位
降低
正弦波振荡电路ppt课件

所以 Q 1 Lq 非常高, rq Cq
具有很好的选择性和频稳度。
2. 石英晶体谐振器的符号、等效电路和电抗特性
Co — 静态电容,较大
Lq — 晶体振动时的动态电感 ,很大
Cq —晶体振动时的动态电容,很小
rq — 等效摩擦损耗电阻,很小
串联谐振频率 并联谐振频率
1 fs 2 LqCq
1
fP 2
起振时,热敏电阻处于冷态,RF 阻值较大, A•u 1 RF / R1 大,
.
起振容易。U o
.
If
T RF A•u
最后达到 A•u =3,
进入平衡状态。由于运放始终线性工作,因此波形好。
例8.1.1
图示为一实用RC桥式振荡电路。(1)求f0 ;(2) 说明二极管的作用;(3)说明 RP 如何调节。
.1
因为振荡频率处,Fu 3
为满足起振振幅条件
A•uF• u
1,应使
.
Au
3
.
即 Au 1 (RF / R1 ) 3
2. 常用的RC 桥式振荡电路
参数选择:
1 f0 2RC
RF 2R1
RF 不能太大, 否则正弦波将
失真,甚至变
成方波。
稳幅措施:采用负温度系数热 敏电阻实现外稳幅。
1. 石英谐振器结构
石英是一种各向异性的结晶体,其化 学成分是SiO2 。从一块晶体上按一定的方 位角切割成的薄片称为晶片。在晶片的两 面涂上银层作为电极,电极上焊出两根引 线固定在管脚上,封装后就构成了石英晶 体谐振器。
2. 石英晶体的压电效应与谐振特性
压电效应: 电极间加电场
电极间加机械力
晶体机械变形 晶体产生电场
起振时,二极管未导通,
具有很好的选择性和频稳度。
2. 石英晶体谐振器的符号、等效电路和电抗特性
Co — 静态电容,较大
Lq — 晶体振动时的动态电感 ,很大
Cq —晶体振动时的动态电容,很小
rq — 等效摩擦损耗电阻,很小
串联谐振频率 并联谐振频率
1 fs 2 LqCq
1
fP 2
起振时,热敏电阻处于冷态,RF 阻值较大, A•u 1 RF / R1 大,
.
起振容易。U o
.
If
T RF A•u
最后达到 A•u =3,
进入平衡状态。由于运放始终线性工作,因此波形好。
例8.1.1
图示为一实用RC桥式振荡电路。(1)求f0 ;(2) 说明二极管的作用;(3)说明 RP 如何调节。
.1
因为振荡频率处,Fu 3
为满足起振振幅条件
A•uF• u
1,应使
.
Au
3
.
即 Au 1 (RF / R1 ) 3
2. 常用的RC 桥式振荡电路
参数选择:
1 f0 2RC
RF 2R1
RF 不能太大, 否则正弦波将
失真,甚至变
成方波。
稳幅措施:采用负温度系数热 敏电阻实现外稳幅。
1. 石英谐振器结构
石英是一种各向异性的结晶体,其化 学成分是SiO2 。从一块晶体上按一定的方 位角切割成的薄片称为晶片。在晶片的两 面涂上银层作为电极,电极上焊出两根引 线固定在管脚上,封装后就构成了石英晶 体谐振器。
2. 石英晶体的压电效应与谐振特性
压电效应: 电极间加电场
电极间加机械力
晶体机械变形 晶体产生电场
起振时,二极管未导通,
第3章 正弦波振荡器

)
AF = 1 = n = 0,1,2, L ϕ A + ϕ F = 2 nπ
分别称为振幅平衡条件和相位平衡条件。
1. 振幅平衡条件
Uo
U0 U f U f AF = . = =1 Ui U0 Ui U f = Ui
Uf
0
Uo
θ>90° θ<90°
放大特性
A B
Ui
① ②
F 0 Uo
0
C Ui=Uf
ω02 < ω g < ω01
图3.9 多回路三点式振荡器组成
ωg < M min (ω01 , ω02 )
实际上电抗元件总有电阻损耗;管子各极间存在极间 阻抗,这些都影响振荡器的工作状态。工程中,振荡器工 作频率ωg近似等于回路谐振角频率ω0。
例3.1 在右图所示振 荡器交流等效电路中, 三 个LC并联回路的谐振频 率分别是f01, f02, f03, 试问 f01、 f02、f03满足什么 条件时该振荡器能正常工 作? 解: 只要满足三点式组成 法则, 该振荡器就能正常 工作。
(6)利用自偏置保证振荡器能自行起振,并使放大器由甲 类工作状态转换成丙类工作状态。 根据振荡条件,振荡器应包括放大器、选频网络、反馈 网络。 放大器采用有源器件,如晶体三极管、场效应管、差分 放大器、运算放大器等。 选频网络可用LC并联谐振回路、RC选频网络、晶体滤波 LC RC 器等。 反馈网络可以是RC移相网络、电容分压网络、电感分压 网络、变压器耦合反馈网络或电阻分压网络等。
V X1 C2 X3 L (a) X2 C1 L2 X1 X3
V L1 X2 C (b)
反馈网络是由电容元件完成的, 称为电容反馈振荡器, 也称 为考必兹(Colpitts)振荡器。图(b)称为电感反馈振荡器,也 称哈特莱(Hartley)振荡器。
第三章正弦波振荡器ppt课件
2、 相位平衡的稳定条件
相位平衡的稳定条件为:
Байду номын сангаас
T (osc )
T ()
0SC
0
' osc
osc
()arctanQ0 2 0
——当相位平衡条件遭到破坏时,线路本身 重新建立起相位平衡点的条件。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
A
1
V iA
Vi
图3-1-2 满足起振和平衡条件时的环路增益
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3.1.2 稳定条件
平衡状态有稳定平衡和不稳定平衡,振荡器工作 时要处于稳定平衡状态。
如果振荡器在各种不稳定因素作用下,能在原平 衡点附近达到新的平衡,而一旦排除了不稳定因素 ,振荡器又能自动回到原平衡状态,则称这种平衡 状态是稳定的。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
互感耦合振荡器
根据振荡回路(相移网络)与三极管不同电极的连 接点分为集电极调谐型、发射极调谐型和基极调谐型。
+(+) - -
三种互感耦合振荡器
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
X3异性
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
相位平衡的稳定条件为:
Байду номын сангаас
T (osc )
T ()
0SC
0
' osc
osc
()arctanQ0 2 0
——当相位平衡条件遭到破坏时,线路本身 重新建立起相位平衡点的条件。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
A
1
V iA
Vi
图3-1-2 满足起振和平衡条件时的环路增益
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3.1.2 稳定条件
平衡状态有稳定平衡和不稳定平衡,振荡器工作 时要处于稳定平衡状态。
如果振荡器在各种不稳定因素作用下,能在原平 衡点附近达到新的平衡,而一旦排除了不稳定因素 ,振荡器又能自动回到原平衡状态,则称这种平衡 状态是稳定的。
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
互感耦合振荡器
根据振荡回路(相移网络)与三极管不同电极的连 接点分为集电极调谐型、发射极调谐型和基极调谐型。
+(+) - -
三种互感耦合振荡器
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
X3异性
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在实际电路中,一般满足
o2C1C2 gigL
因此,工程估算时可近似认为:
osc o
1 LC
主讲 杨霓清
3.2.2
高频电子线路
作业三 P.92 3.9 3.10 3.11
主讲 杨霓清
高频电子线路
三、电感三点式电路(哈特莱电路,Hartley)
X X
be ce
0 成立。即 X c e
X b e 必须是同
性质电抗,因而
X
cb
必须是异性质的电抗。 主讲 杨霓清
3.2.2
高频电子线路
例 3.2.2 在例图3.2.4所示振荡器交流等效电路中,三个LC并
联回路的谐振频率分别是:f1
1
(2
L1C1)
f2
1
(2
L2C2 )
f3
1
(2
L3C3 )
主讲 杨霓清
3.2.2
高频电子线路
(4)振幅起振条件
令T() 1 即可求ngm gL ge
1
起振条件又可以表示为
gm1 n(gL ge )1 ngLnge
其中 gL RL1Re0 , ge1r ber1e
(5)电路的反馈系数
kf
n C1 C1 C2
3.2.2
高频电子线路
由(a)到(b):
C2 C2Cbe
V f
1 nVf
接入系数 n C 1
C 1 C 2
(通常re Re )
ren12 (re//Re)n12 re
由(b) 到(c):
GgL
ge
1 RL
1 re
BC
1
(L)
C C1C 2 C1 C 2
图3.2.6
主讲 杨霓清
推导T ( j ) 的等效电路
Vf
gmVi
Z2
1 1 Z1 Z2
Z1 Z2 Z3
所以
T(j)V f gm Z2
gm
V i 1 1 Z1Z2 11Z1
Z1Z2 Z3
Z2 Z3 Z2Z3
将 Z 1 、Z 2 、Z 3 代入上式整理后得
T(j) gm T( )ejT()
AjB
主讲 杨霓清
高频电子线路
式中 T() gm
令:RL Re0 RL
且忽略晶体管输 出电容的影响。 可以得到微变等 效电路:
Re0 Q0oscL
主讲 杨霓清
微变等效电路
3.2.2
高频电子线路
2、考毕兹电路起振条件的近似分析 (1)电路的简化
电容三点式电路高频等效电路
在×处断开,并 考虑到负载作用, 得到:
图3.2.6 小信号 等效电路
主讲 杨霓清
一、电路组成法则(相位条件)
在三点式电路中,LC回 路中与发射极相连接的两个电 抗元件必须为同性质,另外一 个电抗元件必须为异性质。同 时满足 XceXbeXbc0
图3.2. 3 三点式振荡器的原理图
主讲 杨霓清
3.2.2
高频电子线路
证明:假定LC回路由纯电抗元件组成,分别为
X c e X b e X c b 同时忽略晶体管的电抗效应,则当回路谐振
主讲 杨霓清
3.2.2
高频电子线路
二、 电容三点式电路(又称考毕兹电路,Coplitts)
1、电路分析
L回路电感
Cb 高
频旁 路电 容
电耦容合回C 路1 电C 容2
图3.2.5 电容三点式电路 (a)原理电路 (b)高频交流等效电路
主讲 杨霓清
3.2.2
高频电子线路
(b) 电容三点式高频交流等效电路
试问 f1 、f 2 、f 3 满足什么条件时该振荡
器能正常工作?
图3.2.4 例3.2.2图
解:若组成电容三点式, 则在振荡频 f o s c 1 处,
所以应满足 f1f2fosc1f3 或 f2f1fosc1f3
若组成电感三点式,则在振荡频率 f o s c 2处,所以应满足
f1f2fosc2f3 或 f2f1fosc2f3
( 0)时,回路呈纯阻性,有
XceXbe Xbc0
即
XceXbeXbc
由于V f 是 V c 在 X b e X b c 支路分配在 X b e 上的电压,即
Vf j(XjX bebeVX cbc)X XbceeVc
因为这是一个由反相放大器组成的正反馈电路,V i 与 V f 同相,
V
c与V
i 反相,所以必有
解:这是一个共基— 共集反馈电路,容易满足
振幅条件。
相位条件判断:
图3.2.2 例3.2.1图
e 1 c 1 b 2 e 2 (e 1 )
可见电路是负反馈,不能产生振荡。
怎样修改才能能产生振荡?
主讲 杨霓清
3.2.1
高频电子线路
3.2.2 三点式振荡电路
三点式振荡器的工作频率可达到几百兆赫。
3.2.2
高频电子线路
(2)环路增益计算:
因为
Vf
gmVi G jB
1 nVf
所以 T(j)V Vif G n gm jBgL ge n 图jg(3 m .2C .61推L)导T ( j ) 的等效电路
(3)振荡频率的计算:
令T ( j ) 分母的虚部为零,即可得到振荡器的振荡角频率为
osc
1 LC
A2 B2
B
T () arctan A
且
AgL gigL C C 1 2 gi(2LC 1)
BC 2 1 C 1gigL C 2 (L C 1)1L
根据起振条件,令B=0可以求得振荡器的振荡角频率为
o s cL 1 C C g 1 iC g L 2 L 1 C1 g o 2 C ig 1 C L 2 o1 g o 2 C ig 1 C L 2
高频电子线路
3.2 LC正弦波振荡器
采用LC谐振回路作为选频网络的振荡器。 LC正弦波振荡器有三种实现电路:
互感耦合振荡器 三点式振荡器 集成电路LC振荡器
LC振荡器可用来产生几十千赫到几百兆赫的 正弦波信号。
主讲 杨霓清
3.2
高频电子线路
主讲 杨霓清
高频电子线路
主讲 杨霓清
高频电子线路
例3.2.1 判断图例3.2.2所示两极互感耦合振荡电路 能否起振。
一般要求T ( osc ) 为3~5。
k
f
的取值一般为
1 8
~
1 2
。
主讲 杨霓清
3.2.2
高频电子线路
3、实际考虑
在图3.2.6(a)中,令
Z1
1 j C1
Z3
g L
1 1
j L
Z2
gi
1
jC2
gi
1 re
1 Re
C2 C2Cbe
得到(b)图。 主讲 杨霓清
3.2.2
高频电子线路
由(b)图求得反馈电压
振幅起振条件为
gmAgL (1C C 1 2 )gi(1o 2 sc 1 LC 1)
主讲 杨霓清
3.2.2
高频电子线路
上述分析表明,电容三点式振荡器的振荡角频率 o s c
不仅与 o 有关,还与 g i 、g L 即回路固有谐振电阻 R e o 、外 接电阻 R L 和三极管输入电阻 r e 有关,且osc o
o2C1C2 gigL
因此,工程估算时可近似认为:
osc o
1 LC
主讲 杨霓清
3.2.2
高频电子线路
作业三 P.92 3.9 3.10 3.11
主讲 杨霓清
高频电子线路
三、电感三点式电路(哈特莱电路,Hartley)
X X
be ce
0 成立。即 X c e
X b e 必须是同
性质电抗,因而
X
cb
必须是异性质的电抗。 主讲 杨霓清
3.2.2
高频电子线路
例 3.2.2 在例图3.2.4所示振荡器交流等效电路中,三个LC并
联回路的谐振频率分别是:f1
1
(2
L1C1)
f2
1
(2
L2C2 )
f3
1
(2
L3C3 )
主讲 杨霓清
3.2.2
高频电子线路
(4)振幅起振条件
令T() 1 即可求ngm gL ge
1
起振条件又可以表示为
gm1 n(gL ge )1 ngLnge
其中 gL RL1Re0 , ge1r ber1e
(5)电路的反馈系数
kf
n C1 C1 C2
3.2.2
高频电子线路
由(a)到(b):
C2 C2Cbe
V f
1 nVf
接入系数 n C 1
C 1 C 2
(通常re Re )
ren12 (re//Re)n12 re
由(b) 到(c):
GgL
ge
1 RL
1 re
BC
1
(L)
C C1C 2 C1 C 2
图3.2.6
主讲 杨霓清
推导T ( j ) 的等效电路
Vf
gmVi
Z2
1 1 Z1 Z2
Z1 Z2 Z3
所以
T(j)V f gm Z2
gm
V i 1 1 Z1Z2 11Z1
Z1Z2 Z3
Z2 Z3 Z2Z3
将 Z 1 、Z 2 、Z 3 代入上式整理后得
T(j) gm T( )ejT()
AjB
主讲 杨霓清
高频电子线路
式中 T() gm
令:RL Re0 RL
且忽略晶体管输 出电容的影响。 可以得到微变等 效电路:
Re0 Q0oscL
主讲 杨霓清
微变等效电路
3.2.2
高频电子线路
2、考毕兹电路起振条件的近似分析 (1)电路的简化
电容三点式电路高频等效电路
在×处断开,并 考虑到负载作用, 得到:
图3.2.6 小信号 等效电路
主讲 杨霓清
一、电路组成法则(相位条件)
在三点式电路中,LC回 路中与发射极相连接的两个电 抗元件必须为同性质,另外一 个电抗元件必须为异性质。同 时满足 XceXbeXbc0
图3.2. 3 三点式振荡器的原理图
主讲 杨霓清
3.2.2
高频电子线路
证明:假定LC回路由纯电抗元件组成,分别为
X c e X b e X c b 同时忽略晶体管的电抗效应,则当回路谐振
主讲 杨霓清
3.2.2
高频电子线路
二、 电容三点式电路(又称考毕兹电路,Coplitts)
1、电路分析
L回路电感
Cb 高
频旁 路电 容
电耦容合回C 路1 电C 容2
图3.2.5 电容三点式电路 (a)原理电路 (b)高频交流等效电路
主讲 杨霓清
3.2.2
高频电子线路
(b) 电容三点式高频交流等效电路
试问 f1 、f 2 、f 3 满足什么条件时该振荡
器能正常工作?
图3.2.4 例3.2.2图
解:若组成电容三点式, 则在振荡频 f o s c 1 处,
所以应满足 f1f2fosc1f3 或 f2f1fosc1f3
若组成电感三点式,则在振荡频率 f o s c 2处,所以应满足
f1f2fosc2f3 或 f2f1fosc2f3
( 0)时,回路呈纯阻性,有
XceXbe Xbc0
即
XceXbeXbc
由于V f 是 V c 在 X b e X b c 支路分配在 X b e 上的电压,即
Vf j(XjX bebeVX cbc)X XbceeVc
因为这是一个由反相放大器组成的正反馈电路,V i 与 V f 同相,
V
c与V
i 反相,所以必有
解:这是一个共基— 共集反馈电路,容易满足
振幅条件。
相位条件判断:
图3.2.2 例3.2.1图
e 1 c 1 b 2 e 2 (e 1 )
可见电路是负反馈,不能产生振荡。
怎样修改才能能产生振荡?
主讲 杨霓清
3.2.1
高频电子线路
3.2.2 三点式振荡电路
三点式振荡器的工作频率可达到几百兆赫。
3.2.2
高频电子线路
(2)环路增益计算:
因为
Vf
gmVi G jB
1 nVf
所以 T(j)V Vif G n gm jBgL ge n 图jg(3 m .2C .61推L)导T ( j ) 的等效电路
(3)振荡频率的计算:
令T ( j ) 分母的虚部为零,即可得到振荡器的振荡角频率为
osc
1 LC
A2 B2
B
T () arctan A
且
AgL gigL C C 1 2 gi(2LC 1)
BC 2 1 C 1gigL C 2 (L C 1)1L
根据起振条件,令B=0可以求得振荡器的振荡角频率为
o s cL 1 C C g 1 iC g L 2 L 1 C1 g o 2 C ig 1 C L 2 o1 g o 2 C ig 1 C L 2
高频电子线路
3.2 LC正弦波振荡器
采用LC谐振回路作为选频网络的振荡器。 LC正弦波振荡器有三种实现电路:
互感耦合振荡器 三点式振荡器 集成电路LC振荡器
LC振荡器可用来产生几十千赫到几百兆赫的 正弦波信号。
主讲 杨霓清
3.2
高频电子线路
主讲 杨霓清
高频电子线路
主讲 杨霓清
高频电子线路
例3.2.1 判断图例3.2.2所示两极互感耦合振荡电路 能否起振。
一般要求T ( osc ) 为3~5。
k
f
的取值一般为
1 8
~
1 2
。
主讲 杨霓清
3.2.2
高频电子线路
3、实际考虑
在图3.2.6(a)中,令
Z1
1 j C1
Z3
g L
1 1
j L
Z2
gi
1
jC2
gi
1 re
1 Re
C2 C2Cbe
得到(b)图。 主讲 杨霓清
3.2.2
高频电子线路
由(b)图求得反馈电压
振幅起振条件为
gmAgL (1C C 1 2 )gi(1o 2 sc 1 LC 1)
主讲 杨霓清
3.2.2
高频电子线路
上述分析表明,电容三点式振荡器的振荡角频率 o s c
不仅与 o 有关,还与 g i 、g L 即回路固有谐振电阻 R e o 、外 接电阻 R L 和三极管输入电阻 r e 有关,且osc o
