湖南省祁阳县2014年下学期期末教学质量检测九年级数学试卷及答案湘教版
湖南省祁阳县2014-2015学年九年级(上)期末数学试题(含答案)

湖南省祁阳县2014年下学期期末教学质量检测九年级数学(试题卷)(时量120分钟,满分120分)温馨提示:1.本试卷包括试题卷和答题卡。
考生作答时,选择题和非选择题均须作答在答题卡上,在本试题卷上作答无效。
考生在答题卡上按答题卡中注意事项的要求答题。
2.考试结束后,将本试题卷和答题卡一并交回。
一、选择题(本大题共8小题,每小题3分,共计24分.)1.下列各点中,在函数xy 3-=的图象上的点是( )A. )621(-,B. )6,21(-- C. )62(-,D. )62(,- 2.一元二次方程042=-y 的实数根是( )A. 2B. 2C.2±D.2±3.已知⊙O 的半径r=5,圆心O 到直线l 的距离为( )时,圆与直线l 相交A. 7B. 6C. 5D. 4 4.若点)(3,1-,)(3,3是二次函数c bx ax y ++=2图象上的两点,则此二次函数的对称轴是( )A. 直线x=-1B. 直线0=xC. 直线x=1D. 直线2=x5.点M 、N 、P 是ABC ∆三边的中点,下列说法正确的是( )A. MNP ABC ∆∆与的面积之比为2:1B. MNP ABC ∆∆与的周长之比是2:1C. MNP ABC ∆∆与的高之比是1:1D. MNP ABC ∆∆与的中线之比是4:16.在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m.如果在坡度为0.75的山坡上种树,也要求株距为4 m ,那么相邻两树间的坡面距离为( )A. 4B. 5C. 7D. 87.下列命题中:①所有的等腰三角形都相似;②在三角形内不存在到三条边的距离相等的点;③圆的内接正多边形是轴对称图形;④三角形的外心不会在该三角形的边上. 其中正确命题的个数为( )A. 1个B. 2个C. 3个D. 4个 8.已知二次函数c bx ax y ++=2的图象如图所示,其对称轴为1-=x ,给出下列结论: ①0>abc ②02=+b a ③0>++c b a ④0<+-c b a ,其中正确的结论是( )A. ①②B. ①④C. ②③D. ③④二、填空题(本大题共8小题,每小题3分,共计24分.)9.某工厂生产了一批零件,从中随机抽取了100件来检查,发现有20件次品.试估计这批产品的次品率是 . 10.已知5:2:=b a ,且14=+b a ,则b= .11.点A ),(m 1,B ),(n 2-在反比例函数x y 3-=的图象上,则m n (填“>”“<”或“=”)12.已知圆的半径为4,圆心为O ,︒=∠60AOB ,则扇形OAB 的面积是 . 13.函数342++-=x x y 有 值(填“最大”或“最小”),所求最值是 .14.在ABC Rt ∆中,︒=∠90C ,AB AC 21=,则=∠ABC tan .第8题图15.当m= 时,关于x 的方程5)3(72=---x x m m是一元二次方程.16.将二次函数342+-=x x y 的图象向左平移2个单位,再向上平移3个单位,则两次平移后的图象的表达式是 . 三、解答题(本大题共9小题,共计72分,请你写出必要的解题步骤.) 17.(本题6分)解下列方程(1)022=+-x x (2)05322=--x x18.(本题6分)已知反比例函数xy 2-=.(1)画出该函数的大致图象。
湘教版九年级下册数学试题 期末质量评估试卷(一)(含答案)
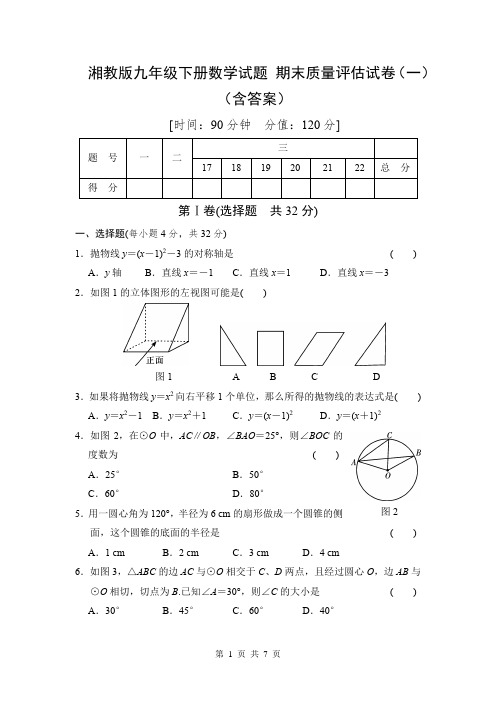
湘教版九年级下册数学试题期末质量评估试卷(一)(含答案)[时间:90分钟分值:120分]题号一二三171819202122总分得分第Ⅰ卷(选择题共32分)一、选择题(每小题4分,共32分)1.抛物线y=(x-1)2-3的对称轴是() A.y轴B.直线x=-1 C.直线x=1 D.直线x=-32.如图1的立体图形的左视图可能是()图1A B C D3.如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是() A.y=x2-1 B.y=x2+1 C.y=(x-1)2D.y=(x+1)24.如图2,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为()A.25°B.50°C.60°D.80°5.用一圆心角为120°,半径为6 cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是() A.1 cm B.2 cm C.3 cm D.4 cm6.如图3,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是() A.30°B.45°C.60°D.40°图2图3图47.如图4所示,在平面直角坐标系中,二次函数y =ax 2+bx +c 的图象顶点为A (-2,-2),且过点B (0,2),则y 与x 的函数关系式为( )A .y =x 2+2B .y =(x -2)2+2C .y =(x -2)2-2D .y =(x +2)2-28.从1、2、3、4中任取两个不同的数,其乘积大于4的概率是( )A.16B.13C.12D.23第Ⅱ卷(非选择题 共88分)二、填空题(每小题4分,共32分)9.下列事件:①打雷后会下雨;②明天是晴天;③1小时等于60分钟;④从装有2个红球,2个白球的袋子中摸出一个蓝球.其中是确定性事件的是________.(填序号)10.如图5,对称轴平行于y 轴的抛物线与x 轴交于(1,0)、(3,0)两点,则它的对称轴为____________.图5图611.二次函数y =x 2-2x -3的图象如图6所示.当y <0时,自变量x 的取值范围是____________.12.如图7,在⊙O中,弦AB垂直平分半径OC,垂足为D,若☉O的半径为2,则弦AB的长为______.图7图813.某涵洞是抛物线形,如图8所示,现测得水面宽AB=8 m,涵洞顶点O到水面的距离为12 m,在图中的平面直角坐标系内,涵洞所在抛物线的函数解析式是____________.14.如图9,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于________.图9图1015.在一个不透明的口袋中,有3个完全相同的小球,他们的标号分别是2、3、4,从袋中随机地摸取一个小球然后放回,再随机的摸取一个小球,则两次摸取的小球标号之和为5的概率是__________.16.如图10,有一直径是 2 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:(1)AB的长为________m;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为________m.三、解答题(共6小题,满分56分)17.(8分)如图11,AC ︵=CB ︵,D 、E 分别是半径OA 和OB 的中点,CD 与CE 的大小有什么关系?为什么?图1118.(8分)已知抛物线y =-x 2+bx +c 经过点A (3,0)、B (-1,0). (1)求抛物线的解析式; (2)求抛物线的顶点坐标.19.(8分)一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.(1)从袋中摸出一个球是黄球的概率;(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是13,求从袋中取出黑球的个数.20.(10分)已知二次函数y=x2-4x+3.(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;(2)求函数图象与x轴的交点A、B的坐标,及△ABC的面积.图1221.(10分)如图13,矩形ABCD的两边长AB=18 cm,AD=4 cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以2 cm/s的速度匀速运动,Q 在边BC上沿BC方向以1 cm/s的速度匀速运动,设运动时间为x s,△PBQ 的面积为y cm2.(1)求y关于x的函数关系式,并写出x的取值范围;(2)求△PBQ的面积的最大值.图1322.(12分)如图14,AB 是⊙O 的直径,点F 、C 是⊙O 上两点,且AF ︵=FC ︵=CB ︵,连接AC 、AF ,过点C 作CD ⊥AF 交AF 延长线于点D ,垂足为D . (1)求证:CD 是⊙O 的切线; (2)若CD =23,求⊙O 的半径.图14参考答案1.C 2.A 3.C 4.B 5.B 6.A7.D8.C 9.③④10.直线x=211.-1<x<312.2313.y=-34x214.36°15.2916.(1)1(2)1417.CD=CE,理由略.18.(1)y=-x2+2x+3;(2)抛物线的顶点坐标为(1,4).19.(1)从袋中摸出一个球是黄球的概率为1 4;(2)从袋中取出黑球的个数为2个.20.(1)顶点C的坐标是(2,-1),当x≤2时,y随x的增大而减少;当x>2时,y随x的增大而增大;(2)A点的坐标是(1,0),B点的坐标是(3,0),S△ABC=1. 21.(1)y=-x2+9x(0<x≤4);(2)△PBQ的最大面积是20 cm2.22.(1)证明略(2)⊙O的半径为4.。
湘教版九年级下册数学期末测试卷及含答案

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、如图仔细观察其中的两个尺规作图痕迹,两直线相交于点O,则下列说法中不正确的是()A.EF是△ABC的中位线B.∠BAC+∠EOF=180°C.O是△ABC的内心D.△AEF的面积等于△ABC的面积的2、如图,PA,PB分别切⊙O于点A,曰,PA=12,CD切⊙O于点E,交削,PB 于点C,D两点,则△PCD的周长是()A.12B.18C.24D.303、如图,扇形AOB中,∠AOB=150°,AC=AO=6,D为AC的中点,当弦AC沿扇形运动时,点D所经过的路程为()A.3 πB.C.D.4 π4、已知如图抛物线y=ax2+bx+c,下列式子正确的是()A.a+b+c<0B.b 2﹣4ac<0C.c<2bD.abc>05、对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )A.y =-2x 2 + 8x +3B.y =-2x 2–8x +3C.y = -2x 2 + 8x –5 D.y =-2x 2–8x +26、某学校在进行防溺水安全教育活动中,将以下几种在游泳时的注意事项写在纸条上并折好,内容分别是:①互相关心;②互相提醒;③不要相互嬉水;④相互比潜水深度;⑤选择水流湍急的水域;⑥选择有人看护的游泳池.小颖从这6张纸条中随机抽出一张,抽到内容描述正确的纸条的概率是()A. B. C. D.7、已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个,随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为()A.2B.3C.4D.58、已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是()A.k>-B.k>- 且k≠0C.k≥-D.k≥- 且k≠09、如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是()A.CE=DEB.AE=OEC.D.△OCE≌△ODE10、将抛物线y =(x-4)2+2向右平移1个单位,再向下平移3个单位,则平移后抛物线的表达式为()A.y =(x-3) 2+5B.y =(x-3) 2-1C.y =(x-5) 2+5D.y =(x-5) 2-111、下列事件中,必然事件是( )、A.打开电视,它正在播广告B.掷两枚质地均匀的正方体骰子,点数之和一定大于6C.早晨的太阳从东方升起D.没有水分,种子发芽12、抛物线y=ax2﹣2ax+4(a>0),下列判断正确的是( )A.当x>2时,y随x的增大而增大B.当x<2时,y随x的增大而增大 C.当x>1时,y随x的增大而增大 D.当x<1时,y随x的增大而增大13、下列说法中,正确的是()A.将一组数据中的每一个数据都加同一个正数,方差变大B.为了解全市同学对书法课的喜欢情况,调查了某校所有女生C.“任意画出一个矩形,它是轴对称图形”是必然事件D.为了审核书稿中的错别字,选择抽样调查14、如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是()A.△ACD的外心B.△ABC的外心C.△ACD的内心D.△ABC的内心15、如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为()A.25°B.30°C.40°D.50°二、填空题(共10题,共计30分)16、如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC= ________度.17、如图,在⊙O中,圆心角∠AOB=120°,弦AB=2 cm,则⊙O的半径是________.18、把抛物线先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式为________19、如图,中,为的中点,以为圆心,长为半径画一弧交于点,若,,,则扇形的面积为________.20、在一个不透明的布袋中有除颜色外其它都相同的红、黄、蓝球共200个,某位同学经过多次摸球试验后发现,其中摸到红色球和蓝色球的频率稳定在35%和55%,则口袋中可能有黄球________个.21、如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为________ cm2.22、小李和小王在拼图游戏中,从如图三张纸片中任取两张,如拼成房子,则小李赢;否则,小王赢.你认为这个游戏公平吗?________(填“公平”或“不公平”)23、△ABC中,∠A=40°,若点O是△ABC的外心,则∠BOC=________°;若点I是△ABC的内心,则∠BIC=________°.24、对某批乒乓球的质量进行随机抽查,结果如下表所示:随机抽取的乒乓球数优等品数优等品率当越大时,优等品率趋近于概率________.(精确到)25、一个圆的半径为2,那么它的弦长d的取值范围________.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
(全优)湘教版九年级下册数学期末测试卷及含答案(适用考试)

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.正确说法是().A.从甲箱摸到黑球的概率较大B.从乙箱摸到黑球的概率较大C.从甲、乙两箱摸到黑球的概率相等D.无法比较从甲、乙两箱摸到黑球的概率2、在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣1(m>0)与x轴的交点为A,B.若横、纵坐标都是整数的点叫做整点,当抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,可得m的取值范围为()A. <m≤B. ≤m<C.0<m<D.0<m≤3、一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是A.3B.4C.5D.64、抛物线y=-2(x-3)2-4的顶点坐标是()A.(3,4)B.(-3,4)C.(3,-4)D.(2,4)5、将抛物线向左平移个单位,再向下平移个单位后所得抛物线的解析式为()A. B. C. D.6、抛掷一个质地均匀的正方体玩具(它的每个面上分别标有数字1,2,3,4,5,6),它落地时向上的数是3的概率是()A. B.1 C. D.7、抛物线经过点与,若,则b的最小值为()A.2B.C.4D.8、小张同学去展览馆看展览,该展览馆有2个验票口A、B(可进出),另外还有2个出口C、D(不许进).小张不从同一个验票口进出的概率是多少()A. B. C. D.9、下列说法中,正确的是()A.生活中,如果一个事件不是不可能事件,那么它就必然发生B.生活中,如果一个事件可能发生,那么它就是必然事件C.生活中,如果一个事件发生的可能性很大,那么它也可能不发生D.生活中,如果一个事件不是必然事件,那么它就不可能发生10、图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是()A.甲先到B点B.乙先到B点C.甲、乙同时到BD.无法确定11、如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是()A. B. C.D.12、如图,一张半径为1的圆形纸片在边长为的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是()A. B.4-π C.π D.13、有长24m的篱笆,一面利用围墙围成如图中间隔有一道篱笆的矩形花圃,设花圃的垂直于墙的一边长为x m,面积是s m2,则s与x的关系式是()A.s=﹣3x 2+24xB.s=﹣2x 2﹣24xC.s=﹣3x 2﹣24x D.s=﹣2x 2+24x14、一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为()A.6厘米B.12厘米C. 厘米D. 厘米15、如图,二次函数的图象如图所示,下列结论:①;②;③一元二次方程有两个不相等的实数根;④当或时,.上述结论中正确的个数是()A.1个B.2个C.3个D.4个二、填空题(共10题,共计30分)16、如图,从一个直径为1m的圆形铁片中剪出一个圆心角为90°的扇形,再将剪下的扇形围成一个圆锥,则圆锥的底面半径为________m.17、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P在⊙A________.18、已知抛物线y=x2﹣k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是________.19、已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC=________.20、如图,利用成直角的墙角(墙足够长),用10m长的栅栏围成一个矩形的小花园,花园的面积S(m2)与它一边长a(m)的函数关系式是________,面积S的最大值是________.21、AB是半圆O的直径,AB=8,点C为半圈上的一点将此半圆沿BC所在的直线折叠,若配给好过圆心O,则图中阴影部分的面积是________.22、如图是二次函数y=ax2+bx+c的部分图像,在下列四个结论中正确的是________.①不等式ax2+bx+c>0的解集是-1<x<5;②a-b+c>0;③b2-4ac>0;④4a+b <0.23、如图,AB是⊙O的直径,点C,D都在⊙O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是________.24、将二次函数化为的形式,则________.25、如图,AB为☉O的切线,切点为B,连接AO,AO与☉O交于点C,BD为☉O的直径,连接CD.若∠A=30°,☉O的半径为2,则图中阴影部分的面积为________.三、解答题(共5题,共计25分)26、篮球课上,朱老师向学生详细地讲解传球的要领时,叫甲、乙、丙、丁四位同学配合朱老师进行传球训练,朱老师把球传给甲同学后,让四位同学相互传球,其他人观看体会,当甲同学第一个传球时,求甲同学传给下一个同学后,这个同学再传给甲同学的概率27、如图,直线y= 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,求横坐标为整数的点P的个数.28、”4.20芦山地震”发生后,各地积极展开抗震救援工作,一支救援车队经过如图1所示的一座拱桥,拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m,将抛物线放在所给的直角坐标系中(如图2所示),拱桥的拱顶在y轴上.(1)求拱桥所在抛物线的解析式;(2)求支柱MN的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2m、高2.4m的三辆汽车(隔离带与内侧汽车的间隔、汽车间的间隔、外侧汽车与拱桥的间隔均为0.5m)?请说说你的理由.29、珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.30、已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).(1)求b、c的值;(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;(3)该函数的图像经过怎样的平移得到y=x2的图像?参考答案一、单选题(共15题,共计45分)1、B2、A3、B4、C5、C6、D7、D8、D9、C10、C11、C12、B13、A14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、30、。
湘教版九年级下册数学期末测试卷【参考答案】

湘教版九年级下册数学期末测试卷一、单选题(共15题,共计45分)1、如图,AB为⊙O的直径,点C在⊙O上,∠A=24°,则BC弧的度数为()A.66°B.48°C.33°D.24°2、一个袋子中装有6个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率为()A. B. C. D.3、如图,摆放的几何体的俯视图是()A. B. C. D.4、从下列四张卡片中任取一张,卡片上的图形是中心对称图形的概率为()A.0B.C.D.5、如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则关于x的一元二次方程ax2+bx+c=0(a≠0)的解x1, x2的值分别是()A.﹣2,1B.﹣3,1C.﹣1,1D.不能确定6、下列命题正确的个数是()①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.A.1个B.2个C.3个D.4个7、下列函数中,不是二次函数的是()A.y=B.y=3﹣x+x 2C.y=﹣2x+3x 2D.y=(x﹣2)(x+2)﹣x 28、某一型号飞机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)之间的函数解析式是S=﹣1.5t2+60t,则该型号飞机着陆后滑行()秒才能停下来.A.600B.300C.40D.209、给出下列4个命题:①相似三角形的周长之比等于其相似比;②方程x2-3x+5=0的两根之积为5;③在同一个圆中,同一条弦所对的圆周角都相等;④圆的内接四边形对角互补.其中,真命题为()A.①②④B.①③④C.①④D.①②③④10、如图,将边长相等的正方形、正五边形和正六边形摆放在平面上,则为A. B. C. D.11、如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A 处,则平移后的抛物线解析式是()A.y=(x+1)2-1B.y=(x+1)2+1C.y=(x-1)2+1 D.y=(x-1)2-112、如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为()A.-2B.6C.D.213、如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于()A.20°B.40°C.50°D.60°14、已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是()A.相交B.相切C.相离D.无法确定15、已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x …-1 0 1 2 3 …y …10 5 2 1 2则当y≥5时,x的取值范围是( )A.x≤0B.0≤x≤4C.x≥4D.x≤0或x≥ 4二、填空题(共10题,共计30分)16、若二次函数的图象与x轴有且只有一个公共点,则m=________.17、在一个不透明的口袋中,有3个完全相同的小球,他们的标号分别是2,3,4,从袋中随机地摸取一个小球然后放回,再随机的摸取一个小球,则两次摸取的小球标号之和为5的概率是________.18、如图,△AOB和△ACD均为正三角形,顶点B,D在双曲线y= (x>0)上,则=________.19、如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,D为边AB的中点,以点A为圆心,以AD的长为半径画弧与腰AC相交于点E,以点B为圆心,以BD的长为半径画弧与腰BC相交于点F,则图中的阴影部分图形的面积为________.(结果保留π).20、如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,若用阴影部分围成一个圆锥,则该圆锥的底面半径为________.21、如图,有一块直角三角形土地,它两条直边米,米,某单位要沿着斜边修一座底面是矩形的大楼,、分别在边、上,这个矩形的面积最大值是________.22、二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确的结论有________.23、若△ABC的三边长为3、4、5,则△ABC的外接圆半径R与内切圆半径r的差为________.24、已知函数y= (m+3)x2+2x+1的图象与x轴只有一个公共点,则m的值为________.25、如图,坐标平面上,二次函数y=﹣x2+4x﹣k的图形与x轴交于A、B两点,与y轴交于C点,其顶点为D,且k>0.若△ABC与△ABD的面积比为1:3,则k值为________.三、解答题(共5题,共计25分)26、有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,从口袋中随机摸出一个小球,记下标号后放回,再从口袋中随机摸出一个小球,记下标号.用画树状图(或列表)的方法,求两次摸出的小球号码恰好都大于1的概率.27、已知,二次函数的表达式为y=4x2+8x.写出这个函数图象的对称轴和顶点坐标,并求图象与x轴的交点的坐标.28、如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2.求y与x的函数关系式,并写出自变量x的取值.29、如图,圆心角120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM 交AB于H,ON交CD于K,OM>OA.(1)证明:△AOH≌△COK;(2)若AB=2,求正六边形ABCDEF与扇形OMN重叠部分的面积.30、已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.参考答案一、单选题(共15题,共计45分)1、B2、B3、B4、D5、B6、B7、D8、D9、C10、D11、C12、B13、B14、C15、D二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、。
湘教版九年级数学下册期末综合检测试卷(有答案)

【期末专题复习】湘教版九年级数学下册期末综合检测试卷一、单选题(共10题;共30分)1.如图,1,2,3,4,T是五个完全相同的正方体,将两部分构成一个新的几何体得到其正视图,则应将几何体T放在()A.几何体1的上方B.几何体2的左方C.几何体3的上方 D.几何体4的上方2.把抛物线y=﹣2x2向上平移1个单位,再向右平移1个单位,得到的抛物线是()A.y=﹣2(x+1)2+1B.y=﹣2(x﹣1)2+1C.y=﹣2(x﹣1)2﹣1D.y=﹣2(x+1)2﹣13.从1~9这九个自然数中任取一个,是2的倍数的概率是()A. B. C. D.4.抛物线y=﹣x2向左平移1个单位长度得到抛物线的解析式为()A.y=﹣(x+1)2B.y=﹣(x﹣1)2C.y=﹣x2+1D.y=﹣x2﹣15.有长度分别为3cm,5cm,7cm,9cm的四条线段,从中任取三条线段能够组成三角形的概率是()A. B. C. D.6.(2017•青岛)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为()A.100°B.110°C.115°D.120°7.下列说法中正确的是()A.“任意画出一个等边三角形,它是轴对称图形”是随机事件B.“概率为0.001的事件”是不可能事件C.“任意画出一个平行四边形,它是中心对称图形”是必然事件D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次8.如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°9.抛物线y=x2﹣8x+m的顶点在x轴上,则m等于()A. -16B. -4C.8D.1610.如图所示,二次函数的图象经过点和,下列结论中:①;②;③④;⑤;其中正确的结论有()个BA. 2B. 3C. 4D. 5二、填空题(共 10 题;共 30 分)11.在不透明口袋内有形状.大小.质地完全一样的 5 个小球,其中红球 3 个,白球 2 个,随机抽取一个小球是红球的概率是________.12.用 12m 长的木材做窗框(如图所示),要使透过窗户的光线最多,窗框的长应为________ m ,宽应为________ m .13.如图,一边靠墙,其它三边用 12 米的篱笆围成一个矩形(ABCD )花圃,则这个花圃的面积 S (平方米)与 AB 的长 x (米)之间的函数关系式为________.14.如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点 A 、 ,并使 AB 与车轮内圆相切于点 D ,做 CD ⊥AB 交外圆于点 C .测得 CD=10cm ,AB=60cm ,则这个车轮的外圆半径为________cm .15.将抛物线先向下平移 2 个单位,再向右平移 3 个单位后所得抛物线的解析式为________.16.当点 A (1,2),B (3,﹣3),C (m ,n )三点可以确定一个圆时,m ,n需要满足的条件 ________.17.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=________.18.如图,是二次函数y=3x2的图象,把该图象向左平移1个单位,再向下平移2个单位,所得的抛物线的函数关系式为________.19.如图,ABCD是⊙O的内接四边形,点E在AB的延长线上,BF是∠CBE的平分线,∠ADC=110°,则∠FBE=________.20.如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为________.三、解答题(共10题;共60分)21.小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.22.已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,3).(1)求该函数的关系式;(2)求该抛物线与x轴的交点A,B的坐标.23.下面是由些棱长的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).24.已知直线 L 1∥L 2 , 点 A ,B ,C 在直线 L 1 上,点 E ,F ,G 在直线 L 2 上,任取三个点连成一个三角形,求:(1)连成△ABE 的概率;(2)连成的三角形的两个顶点在直线 L 2 上的概率.25.如图,AB 是半圆 O 的直径,过点 O 作弦 AD 的垂线交切线 AC 于点 C ,OC 与半圆 O 交于点 E ,连接 BE ,DE .(1)求证:∠BED=∠C ;(2)若 OA=5,AD=8,求 AC 的长.26.如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.27.(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O 上一动点,求PA的最大值和最小值.(2)如图:=,D、E分别是半径OA和OB的中点.求证:CD=CE.28.株洲五桥主桥主孔为拱梁钢构组合体系(如图 1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着 9 根支柱,他回家上网查到了拱梁是抛物线,其跨度为 20 米,拱高(中柱)10 米,于是他建立如图 2 的坐标系,发现可以将余下的 8 根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD 的高度.29.为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为 1000m 2 的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为 x(m 2),种草所需费用 y 1(元)与 x (m 2)的函数关系式为,其图象如图所示:栽花所需费用 y 2(元)与x (m 2)的函数关系式为 y 2=﹣0.01x 2﹣20x+30000(0≤x≤1000).(1)请直接写出 k 1、k 2 和 b 的值;B(2)设这块 1000m 2 空地的绿化总费用为 W (元),请利用 W 与 x 的函数关系式,求出绿化总费用 W 的最大值;(3)若种草部分的面积不少于 700m 2, 栽花部分的面积不少于 100m 2 , 请求出绿化总费用 W 的最小值.30.如图,平面直角坐标系中,抛物线 y=x 2﹣2x 与 x 轴交于 O 、 两点,顶点为 P ,连接 OP 、BP ,直线 y=x ﹣4 与 y 轴交于点 C ,与 x 轴交于点 D .(Ⅰ)直接写出点 B 坐标 ;判断△ OBP 的形状 ;(Ⅱ)将抛物线沿对称轴平移 m 个单位长度,平移的过程中交 y 轴于点 A ,分别连接 CP 、DP ;(i )若抛物线向下平移 m 个单位长度,当 △SPCD =S △ POC 时,求平移后的抛物线的顶点坐标;(ii )在平移过程中,试探究△SPCD和 △SPOD之间的数量关系,直接写出它们之间的数量关系及对应的 m 的取值范围.答案解析部分一、单选题1.【答案】D2.【答案】B3.【答案】B4.【答案】A5.【答案】A6.【答案】B7.【答案】C8.【答案】C9.【答案】D10.【答案】A二、填空题11.【答案】12.【答案】3;213.【答案】S=﹣2x2+12x14.【答案】5015.【答案】16.【答案】5m+2n≠917.【答案】4﹣18.【答案】y=3(x+1)2﹣219.【答案】55°20.【答案】三、解答题21.【答案】解:这个游戏规则对双方公平.理由如下:画树状图为:共有9种等可能的结果数,其中摸出的两张卡片的正面数字之积小于10的结果数为4;摸出的两张卡片的正面数字之积超过10的结果数为4,所以小明获胜的概率=,小亮获胜的概率=.所以这个游戏规则对双方公平22.【答案】解:(1)∵抛物线的顶点D的坐标为(1,−4),∴设抛物线的函数关系式为y=a(x−1)2−4,又∵抛物线过点C(0,3),∴3=a(0−1)2−4,解得a=1,∴抛物线的函数关系式为y=(x−1)2−4,即y=x2−2x−3;(2)令y=0,得:x2,解得,.所以坐标为A(3,0),B(-1,0).23.【答案】解:①∵俯视图中有个正方形,∴最底层有个正方体小木块,由主视图和左视图可得第二层有个正方体小木块,第三层有个正方体小木块,∴共有个正方体小木块组成.②根据①得:③表面积为:24.【答案】解:由l1上选一个点,在l2上选两个点可以得到3×3=9个三角形,由l1上选两个点,在l2上选一个点可以得到3×3=9个三角形,即任取三个点连成一个三角形总个数为18个,(1)连成△ABE的概率为;(2)连成的三角形的两个顶点在直线l2上的概率为.25.【答案】(1)证明:∵AC是⊙O的切线,AB是⊙O直径,∴AB⊥AC.则∠1+∠2=90°,又∵OC⊥AD,∴∠1+∠C=90°,∴∠C=∠2,而∠BED=∠2,∴∠BED=∠C;t(2)解:连接 BD ,∵AB 是⊙O 直径,∴∠ADB=90°,∴BD===6,∴△OAC ∽△BDA ,∴OA :BD=AC :DA ,即 5:6=AC :8,∴AC= .26.【答案】△解: PBQ 的面积 S 随出发时间 t (s )成二次函数关系变化, ∵△在 ABC 中,∠B=90°,AB=12,BC=24,动点 P 从点 A 开始沿边 AB 向终点 B 以每秒 2 个单位长度的速度移动,动点 Q 从点 B 开始沿边 BC 以每秒 4 个单位长度的速度向终点 C 移动,∴BP=12﹣2t ,BQ=4t ,∴△PBQ 的面积 S 随出发时间 (s )的解析式为:y= (12﹣2t )×4t=﹣4t 2+24t ,(0<t <6)27.【答案】(1)解:∵⊙O 的直径为 10cm ,∴⊙O 的半径为 10÷2=5(cm ),当点 P 在线段 OA 的延长线上时,PA 取得最大值,当点 P 在线段 OA 上时,PA取得最小值∵OA=12cm,∴PA的最大值为12+5=17cm,PA的最小值为12﹣5=7cm;(2)证明:连接CO,如图所示,∵OA=OB,且D、E分别是半径OA和OB的中点,∴OD=OE,又∵=,∴∠COD=∠COE,△在COD△和COE中,,∴△COD≌△COE(SAS),∴CD=CE.28.【答案】解:设抛物线的解析式为:y=ax2,∵A的坐标是(-10,10),∴100a=−10,∴a=−0.1,∴抛物线的解析式为:y=−0.1x2,又∵x=−4,∴y=−0.1×16=−1.6,∴点 C 坐标为(-4,-1.6),又∵点 D 坐标为(-4,-10)∴CD=10-1.6=8.4(米),答:中柱左边第二根支柱 CD 的高度为 8.4 米.29.【答案】(1)解:将 x=600、y=18000 代入 y 1=k 1x ,得:18000=600k 1 , 解得:k 1=30;将 x=600、y=18000 和 x=1000、y=26000 代入 y 2=k 2x+b ,得:,解得:(2)解:当 0≤x <600 时,W=30x+(﹣0.01x 2﹣20x+30000)=﹣0.01x 2+10x+30000,∵﹣0.01<0,W=﹣0.01(x ﹣500)2+32500,∴当 x=500 时,W 取得最大值为 32500 元;当 600≤x≤1000 时,W=20x+6000+(﹣0.01x 2﹣20x+30000)=﹣0.01x 2+36000,∵﹣0.01<0,∴当 600≤x≤1000 时,W 随 x 的增大而减小,∴当 x=600 时,W 取最大值为 32400,∵32400<32500,∴W 取最大值为 32500 元(3)解:由题意得:1000﹣x≥100,解得:x≤900,由 x≥700,则 700≤x≤900,=∵当 700≤x≤900 时,W 随 x 的增大而减小,∴当 x=900 时,W 取得最小值。
湘教版九年级数学下册期末综合检测试卷(有答案)

湘教版九年级数学下册期末综合检测试卷一、单选题(共10题;共30分)1.下图是某个几何体的三视图,该几何体是()A. 长方体B. 正方体 C. 圆柱 D. 三棱柱2.一个口袋里有5个红球,5个黄球,每个球除颜色外都相同,任意摸1个,则下列说法正确的是()A. 只摸到1个红球B. 一定摸到1个黄球C. 可能摸到1个黑球D. 不可能摸到1个白球3.如图所示的四个几何体中,主视图与其他几何体的主视图不同的是()A.B.C.D.4.如图,已知⊙O的直径AB为10,弦CD=8,CD⊥AB于点E,则sin∠OCE的值为()A. 45B. 35C. 34D. 435.AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠BAC=25°,则∠ADC等于()A. 20°B . 30° C.40° D.50°6.若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为()A. -2B. -1C. 0D. 17.如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为()A. 12 √3B. 15√3−6π C. 30√3−12π D. 48√3−36π8.将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为()A. y=2(x+1)2+3B. y=2(x-1)2-3C. y=2(x+1)2-3 D. y=2(x-1)2+39.一个点到圆的最大距离为9cm,最小距离为4cm,则圆的半径是()A. 5cm或13cmB. 2.5cmC. 6.5cmD. 2.5cm或6.5cm10.如图二次函数y=ax2+bx+c的图象与x轴交于(– 1,0),(3,0);下列说法正确的是()A. abc<0B. 当x>1时,y随x值的增大而增大C. a+b+c>0 D. 当y>0时,−1<x<3二、填空题(共10题;共39分)11.正八边形的中心角等于________度.12.“明天的太阳从西方升起”这个事件属于________事件(用“必然”、“不可能”、“不确定”填空).13.将抛物线y=x2-2向上平移一个单位后,得一新的抛物线,那么新的抛物线的表达式是________.14.我们把两个三角形的外心之间的距离叫做外心距.如图,在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90°,点D在边BC的延长线上,如果BC=DC=3,那么△ABC和△ACD的外心距是________.15.抛物线y=﹣x2﹣2x+3用配方法化成y=a(x﹣h)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.16.抛物线y=2x2+8x+m与x轴只有一个公共点,则m的值为________.17.在⊙O中,弦AB=2cm,圆心角∠AOB=60°,则⊙O的直径为________ cm.18.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB=10,则AC=________.19.若扇形的半径为3cm,扇形的面积为2πcm2,则该扇形的圆心角为________ °,弧长为________ cm.20.如图,PA、PB分别切圆O于A、B两点,并与圆O的切线分别相交于C、D两点,•已知PA=7cm,则△PCD的周长等于________ .三、解答题(共8题;共64分)21.某鞋店有A、B、C、D四款运动鞋,元旦期间搞“买一送一”促销活动,用树状图或表格求随机选取两款不同的运动鞋,恰好选中A、C两款的概率.22.已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
湘教版九年级下册数学期末测试卷及含答案(典型题)

湘教版九年级下册数学期末测试卷及含答案一、单选题(共15题,共计45分)1、下面所给几何体的俯视图是()A. B. C. D.2、已知锐角∠AOB如图,①在射线OA上取一点C,以点O为圆心,OC长为半径作,交射线OB于点D,连接CD;②分别以点C,D为圆心,CD长为半径作弧,交于点M,N;③连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠CODB.若OM=MN,则∠AOB=20°C.MN∥CD D.MN=3CD3、如图,AB是⊙O的直径,,∠COD=34°,则∠AEO的度数是()A.51°B.56°C.68°D.78°4、左下图是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是()A. B. C. D.5、下列说法中,正确的是()A.长度相等的弧是等弧B.平分弦的直径垂直于弦,并且平分弦所对的两条弧C.圆的切线垂直于这个圆的半径D.90°的圆周角所对的弦是圆的直径6、已知二次函数y=(x﹣1)2﹣4,当y<0时,x的取值范围是()A.﹣3<x<1B.x<﹣1或x>3C.﹣1<x<3D.x<﹣3或x>17、《九章算术》中有这样一个问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“直角三角形中,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”。
则该圆的直径为()A.3步B.5步C.6步D.8步8、在一个布袋内有大小、质量都相等的球20个,其中红球6个,从中任取1个,取到红球的概率为()A. B. C. D.9、抛物线的顶点为()A. B. C. D.10、下列说法正确的是()A.要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法 B.4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100 C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62 D.某次抽奖活动中,中奖的概率为表示每抽奖50次就有一次中奖11、已知三角形ABC,若过点A、点B作圆,那么下面说法正确的是()A.这样的圆只能作出一个B.这样的圆只能作出两个C.点C不在该圆的外部,就在该圆的内部D.圆心分布在AB的中垂线上12、如图,AB是的直径,点C,D在上,,则的大小是()A. B. C. D.13、如图是某几何体的三视图,则该几何体的全面积等于()A.112B.136C.124D.8414、如图,,是的直径,,若,则的度数是()A.32°B.60°C.68°D.64°15、如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A.18 ﹣9πB.18﹣3πC.9 ﹣D.18 ﹣3π二、填空题(共10题,共计30分)16、如图,大圆半径为6,小圆半径为2,在如图所示的圆形区域中,随机撒一把豆子,多次重复这个实验,若把“豆子落在小圆区域A中”记作事件W ,请估计事件W的概率P(W)的值________.17、如图,在平面直角坐标系xOy中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P 是△ABC的外心,则点C的坐标为________.18、已知,当________时,;________时,.19、在中,弧的度数为60°,则弧所对的圆心角的度数为________.20、某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是________元.21、如图,的外接圆O的半径为3,,则劣弧的长是________(结果保留)22、如图,点A、B、C、D、E、F均在⊙O上.若∠ADF=20°,∠FEC=35°,则∠ABC的大小为________度.23、如图,二次函数的图象经过x轴上的二点,它们的坐标分别是:(-4,0),(2,0).当x的取值范围是________ 时,y随x的增大而减小.24、已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC=________.25、如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为________ 度.三、解答题(共5题,共计25分)26、已知:如图,在⊙O中,弦AB,CD交于点E,AD=CB.求证:AE=CE.27、在一个不透明的袋子中装有三个小球,分别标有数字﹣2、2、3,这些小球除数字不同外其余均相同,现从袋子中随机摸出一个小球记下数字后放回,搅匀后再随机摸出一个小球,用画树状图或列表的方法,求两次摸出的小球上数字之和是正数的概率.28、如图,用长为的铝合金条制成“日”字形窗框,若窗框的宽为,窗户的透光面积为(铝合金条的宽度不计).(Ⅰ)求出与的函数关系式;(Ⅱ)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.29、如图,一块矩形草地的长为100m,宽为80m,欲在中间修筑两条互相垂直的宽为x(m)的小路,这时草坪的面积为y(m2).求y与x的函数关系式,并求出x的取值范围.30、如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).参考答案一、单选题(共15题,共计45分)1、A2、D4、A5、D6、C7、C8、A9、C10、A11、D12、B13、B14、D15、A二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省祁阳县2014年下学期期末教学质量检测九年级数学(试题卷)(时量120分钟,满分120分)温馨提示:1.本试卷包括试题卷和答题卡。
考生作答时,选择题和非选择题均须作答在答题卡上,在本试题卷上作答无效。
考生在答题卡上按答题卡中注意事项的要求答题。
2.考试结束后,将本试题卷和答题卡一并交回。
一、选择题(本大题共8小题,每小题3分,共计24分.)1.下列各点中,在函数xy 3-=的图象上的点是( )A. )621(-,B. )6,21(-- C. )62(-,D. )62(,- 2.一元二次方程042=-y 的实数根是( )A. 2B. 2C.2±D.2±3.已知⊙O 的半径r=5,圆心O 到直线l 的距离为( )时,圆与直线l 相交A. 7B. 6C. 5D. 4 4.若点)(3,1-,)(3,3是二次函数c bx ax y ++=2图象上的两点,则此二次函数的对称轴是( ) A. 直线x=-1B. 直线0=xC. 直线x=1D. 直线2=x5.点M 、N 、P 是ABC ∆三边的中点,下列说法正确的是( )A. MNP ABC ∆∆与的面积之比为2:1B. MNP ABC ∆∆与的周长之比是2:1C. MNP ABC ∆∆与的高之比是1:1D. MNP ABC ∆∆与的中线之比是4:16.在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m.如果在坡度为0.75的山坡上种树,也要求株距为4 m ,那么相邻两树间的坡面距离为( )A. 4B. 5C. 7D. 87.下列命题中:①所有的等腰三角形都相似;②在三角形内不存在到三条边的距离相等的点;③圆的内接正多边形是轴对称图形;④三角形的外心不会在该三角形的边上.其中正确命题的个数为( )A. 1个B. 2个C. 3个D. 4个 8.已知二次函数c bx ax y ++=2的图象如图所示,其对称轴为1-=x ,给出下列结论: ①0>abc ②02=+b a ③0>++c b a ④0<+-c b a ,其中正确的结论是( )A. ①②B. ①④C. ②③D. ③④二、填空题(本大题共8小题,每小题3分,共计24分.)9.某工厂生产了一批零件,从中随机抽取了100件来检查,发现有20件次品.试估计这批产品的次品率是 . 10.已知5:2:=b a ,且14=+b a ,则b= .11.点A ),(m 1,B ),(n 2-在反比例函数x y 3-=的图象上,则m n (填“>”“<”或“=”)12.已知圆的半径为4,圆心为O ,︒=∠60AOB ,则扇形OAB 的面积是 . 13.函数342++-=x x y 有 值(填“最大”或“最小”),所求最值是 .14.在ABC Rt ∆中,︒=∠90C ,AB AC 21=,则=∠ABC tan . 15.当m= 时,关于x 的方程5)3(72=---x x m m是一元二次方程.16.将二次函数342+-=x x y 的图象向左平移2个单位,再向上平移3个第8题图单位,则两次平移后的图象的表达式是 . 三、解答题(本大题共9小题,共计72分,请你写出必要的解题步骤.) 17.(本题6分)解下列方程(1)022=+-x x (2)05322=--x x18.(本题6分)已知反比例函数xy 2-=.(1)画出该函数的大致图象。
(2)这个函数的大致图象位于哪些象限?函数值y 随自变量x 的增大如何变化?19.(本题6分)如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB 和矩形的三边AE ,ED ,DB 组成,已知河底ED 是水平的,ED =16m ,AE =8m ,抛物线的顶点C 到ED 的距离是11m 。
试以ED 所在的直线为x 轴,抛物线的对称轴为y 轴建立平面直角坐标系,求题中抛物线的函数表达式.20.(本题8分)如图,是⊙O的一条弦,,垂足为C,交⊙O于点D,点E在⊙O上.(1)若,求的度数;(2)若,,求的长.21.(本题8分)甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:吨/公顷):为使水稻品种的产量比较稳定,根据题中所给的数据,你选择哪种水稻品种?请说明理由.22.(本题8分)小薇将一副三角尺如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD =2,求AC 的长.23.(本题9分)如图,在正方形ABCD 中,E 、F 分别是边AD 、CD 上的点,DC DF ED AE 41,==,连接EF 并延长交BC 的延长线于点G.(1)求证:ABE ∆∽DEF ∆; (2)若正方形的边长为4,求BG 的长.24.(本题9分)已知二次函数的表达式为m m x m x y -+--=22)12( (1)试判断该二次函数的图象与x 轴交点的个数?并说明理由. (2)此二次函数的图象与函数42++=m x y 的图象的一个交点在y 轴上,求m 的值.A E D FB CG 第23题图25.(本题12分)如图,有一边长为5的正方形ABCD 和一等腰∆PQR ,PQ=PR=5,QR=8,点B 、Q 、C 、R 在同一直线l 上,当Q 、C 两点重合时,等腰∆PQR 以每秒1cm 的速度沿直线l 按箭头所示的方向开始匀速运动,t 秒后正方形ABCD 和等腰∆PQR 重叠部分的面积为S 。
(1)当t=3秒时,PQ 与CD 相交于点F ,点E 为QR 的中点,连结PE ,求证:∆QCF ∽∆QEP. (2)当t=5秒时,求S 的值.(3)当8≤t<9时,求S 关于t 的函数表达式. (4)当9≤t≤13时,求S 关于t 的函数表达式.(1) (2)(3) (4)EFD祁阳县2014年下学期期末教学质量检测九 年 级 数 学 (参考答案)一、选择题(本大题共8小题,每小题3分,共计24分)二、填空题(本大题共8小题,每小题3分,共计24分)9. 51; 10. 10; 11. <; 12. π38;13. 大,7; 14.33; 15. -3; 16. 22+=x y三.解答题(本大题共9小题,共计69分) 17.解:(1)0742<-=-=∆ac b∴原方程没有实数根. ----------3分(2)将原方程左边因式分解得0)1)(52=+-x x ( 由此得052=-x 或01=+x解得1,2521-==x x --------------6分18.解:(1)(图略) ---------------2分(2)该函数的大致图象位于第二、四象限; ---------------4分 在每个象限内,y 随x 的增大而增大. ----------------6分19.解:如图所示. -----------------------2分 由题知抛物线的顶点坐标为(0,11),B (8,8)------------4分 设抛物线的表达式为112+=ax y --------------------6分 将点B 的坐标(8,8)代入抛物线的表达式,得643-=a -----7分 所以抛物线的表达式为116432+-=x y ------------------8分20.解:(1)连接OB ,∵AB OD ⊥ ,∴ AC=BC ,弧AD =弧BD ,-----2分 ∴BOD AOD ∠=∠又DOB DEB ∠=∠21, -------------------3分 ∴︒=︒⨯=∠=∠26522121AOD DEB . -------------------- 4分(2)∵OC=3,OA=5,在ACO R ∆t 中, ∴ AC=4. ------------6分 又AB BC AC 21==,∴8422=⨯==AC AB . --------------8分21.解:根据表格中的数据求得1010==乙甲,x x , --------------------2分02.02=甲S ,245.02=乙S --------------------------------------------4分 22乙甲S S < ------------------------------------------------------------6分 所以应选择甲种水稻品种. -----------------------------------------8分22.解:在Rt △BCD 中,∠BCD =45°,CD =2,cos ∠BCD =BCCD, ∴BC =BCD CD ∠cos =︒45cos 2=22. -----------------------------------------4分在Rt △ABC 中,∠BAC =60°,sin ∠BAC =AC BC ,∴AC =BAC BC ∠sin =︒60sin 22=2322=364 ∴AC 的长为364. ---------------------------8分23.(1)证明:在正方形ABCD 中, -------------1分CD AD AB == DC DF ED AE 41,== ,∴AB ED AE 21==,AB DF 41=,∴DFAEDE AB = ,--------2分又∵∠A=∠D=90° ---------------------------------------3分 ∴ ABE DEF △∽△. ---------------------------------------4分 (2)解:∵4=AB ,2=AE ,∴522422=+=BE ,∴ DEF ABE ∠=∠,︒=∠+∠=∠+∠90DEF AEB ABE AEB , ∴ ︒=∠90BEG .由AD ∥BC ,得EBG AEB ∠=∠,∴ △AEB ∽△BEG ,----------6分∴ BG BE BE AE =,∴ 102==AEBE BG . ---------------------------9分24.(1)01)(4)]12([4222>=----=-=∆m m m ac b0)12(22=-+--∴m m x m x 方程有两个不相等的实数根. ----------2分 m m x m x y -+--=∴22)12(二次函数与x 轴有两个交点. ---------4分 (2)令0=x ,则42+=-m m m , -----------------------------------6分 解得511+=m ,512-=m . ---------------------------------9分25.解:(1)如图(1), PQ=PR ,E 为QR 的中点,QR PE ⊥∴ 又F 为CD 与PQ 的交点,BC CF ⊥∴∴CF //PE ∴∆QCF ∽∆QEP. -------------------------3分 (2)如图(2),当t=5时,CR=3,设PR 与CD 相交于G 点, 由RCG ∆∽REP ∆,求得CG=49. --------------4分 827=∴∆RCG S ,86982712=-=-=∴∆∆RCG PQR S S S ---6分(3)如图(3),当9t 8<≤时,设PQ 与AB 相交于H , BQ=t-5,由QBH ∆∽PEQ ∆,求得BH=4)53-t ( 2)5(83-=∆t S QBH ,82141583-)5(831222++=--=-=∆∆t t t S S S QBH PRQ ------8分(4)如图(4),当139≤≤t 时,设PR 与CD 相交于M ,BQ=13-t ,BRM ∆∽PRE ∆,求得BM=213(43)t -850743983)13(8322+-=-==∆t t t S S BRM ------------12分。
