《数学模型》(第四版)第二章初等模型(2.3 划艇比赛的成绩 2.7 核军备竞赛)
建模3 划艇比赛的成绩
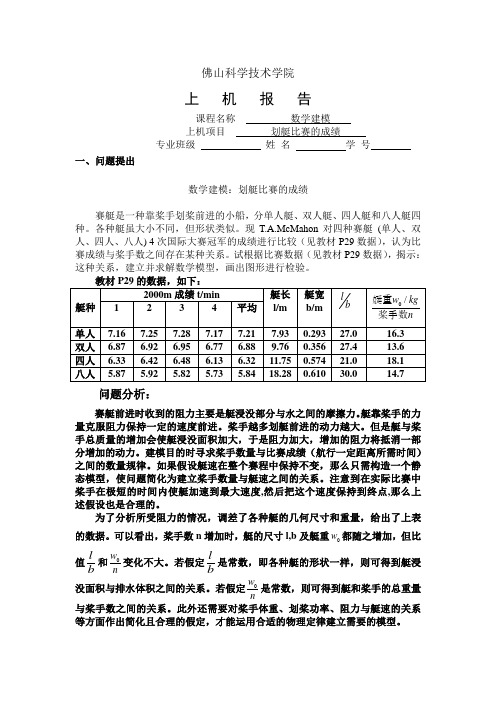
佛山科学技术学院上 机 报 告课程名称 数学建模 上机项目 划艇比赛的成绩专业班级 姓 名 学 号一、问题提出数学建模:划艇比赛的成绩赛艇是一种靠桨手划桨前进的小船,分单人艇、双人艇、四人艇和八人艇四种。
各种艇虽大小不同,但形状类似。
现T.A.McMahon 对四种赛艇 (单人、双人、四人、八人) 4次国际大赛冠军的成绩进行比较(见教材P29数据),认为比赛成绩与桨手数之间存在某种关系。
试根据比赛数据(见教材P29数据),揭示:这种关系,建立并求解数学模型,画出图形进行检验。
问题分析:赛艇前进时收到的阻力主要是艇浸没部分与水之间的摩擦力。
艇靠桨手的力量克服阻力保持一定的速度前进。
桨手越多划艇前进的动力越大。
但是艇与桨手总质量的增加会使艇浸没面积加大,于是阻力加大,增加的阻力将抵消一部分增加的动力。
建模目的时寻求桨手数量与比赛成绩(航行一定距离所需时间)之间的数量规律。
如果假设艇速在整个赛程中保持不变,那么只需构造一个静态模型,使问题简化为建立桨手数量与艇速之间的关系。
注意到在实际比赛中桨手在极短的时间内使艇加速到最大速度,然后把这个速度保持到终点,那么上述假设也是合理的。
为了分析所受阻力的情况,调差了各种艇的几何尺寸和重量,给出了上表的数据。
可以看出,桨手数n 增加时,艇的尺寸l,b 及艇重0w 都随之增加,但比值l b 和0w n 变化不大。
若假定lb是常数,即各种艇的形状一样,则可得到艇浸没面积与排水体积之间的关系。
若假定0wn是常数,则可得到艇和桨手的总重量与桨手数之间的关系。
此外还需要对桨手体重、划桨功率、阻力与艇速的关系等方面作出简化且合理的假定,才能运用合适的物理定律建立需要的模型。
模型假设:1. 各种艇的几何形状相同,lb为常数;艇重0w 与桨手数n 成正比。
这是艇的静态特性。
2. 艇速v 是常数,前进时受的阻力f 与2sv 成正比(s 是艇浸没部分面积)。
这是艇的动态特性。
3. 所有桨手的体重都相同,记住w;在比赛中每个桨手功率p 保持不变,且p 与w 成正比。
数学模型-初等模型

原则:使 rA , rB 尽可能小。
确定分配方案 利用 rA 和 rB 讨论,当增加1席时,应该分 配给A还是B。 不失一般性可设 p1 n1 > p2 n2,即对A不公 平。当再增加1席时,关于 pi ni (i = 1, 2)的不等 式有以下可能: 1. p1 (n1 + 1) > p2 n2, ,这说明即使A方增加 1席仍然对A不公平,所以这一席显然应该分 给A方;
模型构成
记第 k 次渡河前此岸的商人数 x k ,随从数为 y k . 将二维向量 s k = ( x k , y k ) 定义为状态。 安全渡河条件下的状态集合成为允许状态集合, 记做 . S x k , y k = 0,1,2,3.
x = 0 , y = 0 ,1 , 2 , 3 ; S = ( x , y ) x = 3 , y = 0 ,1 , 2 , 3 ; x = y = 1, 2
数学模型的特点
折衷 渐近 强健 可转移 非预制 条理 技艺 局限
可转移性
一个模型时现实对象抽象化、 一个模型时现实对象抽象化、理想化的产 物,它不为对象的所属领域所独有,可以转移 它不为对象的所属领域所独有, 到另外的领域。在生态、经济、 到另外的领域。在生态、经济、社会等领域内 建模就常常借用物理领域中的模型。 建模就常常借用物理领域中的模型。
开设目的
对数学教育而言,既应该让学生掌握 准确快捷的计算方法和严密的逻辑推理, 也需要培养学生用数学工具分析解决实际 问题的意识和能力。传统的数学教学体系 和内容偏重于前者,开设数学建模课程则 是加强后者的一种尝试。 另外,开设本课也是为了一年一度的 “全国大学生数学建模大赛”做一些准备 工作。
建
又设(2) p1 = 1020, p2 = 1000, n1 = n2 = 10, p1 n1 − p2 n2 = 102 − 100 = 2 。 则
数学建模培训初等模型

最后英军战胜了法军,而且双方伤亡情况与历史事实也很 相近。当年,英军在战役A和战役B中战胜法军,但法军没有增 援C,而是选择了撤退,大约有13艘战舰退回法国海港。
点评:数学建模以解决某现实问题为目的,从问题中抽象 并归结出来的数学问题。从现象到模型,数学建模必须反映现 实,既然是一种模型,它就不是现实问题的全部复制,常常会 忽略一些次要因素,作一些必要的简化,但本质上必须反映现 实问题的数量规律。
Bn Fn
0.1Fn 0.1Bn
B1 27, F1 33
但是,尼尔森将军成功的运用了逐个击破的策略,扭转劣 势转败为胜,还差一点全歼法军。经此一战,英国大大巩固了 它在海上的霸权。
当时法军舰队分在三处,分别为A处(3艘)、B处(17艘)、 C处(13艘),彼此相距很远。尼尔森将军收集了丰富的情报 以后,当机立断,制定以下作战方案:先派13艘战舰进攻法军 A队,胜利后尽快与留守港口的14艘战舰汇合,一起进攻法军B 队,最后,乘胜追击,集中所有剩余兵力,围攻法军C队。
Fra 18.0 16.7 15.4 14.2 … 4.7 3.8 2.8 1.9
战役C情况(法军剩余兵力全部参加战斗)
n
1
2
3
4 … 14 15 16 17
Bri 19.0 18.3 17.6 17.0 … 13.2 13.0 12.8 12.7
Fra 14.0 13.1 12.1 11.3 … 3.8 3.1 2.4 1.8
乙地 7000 4900 4270 4081 4024.3 4007.29 4002.187 4000.656
经过模拟(表2-表5),可以知道无论车辆如何分配,经 过有限天数后,最终都将达到平衡状态。{Jn}的极限是3000, {Yn}的极限是4000。其中,(J,Y)=(3000,4000)为该 动态系统的平衡点,而且是稳定的平衡点(不动电)!
数学建模作业3划艇比赛的成绩

四模型建立显示模型函数的构造过程有n名桨手的艇的总功率np与阻力和速度v的乘积成正比即fvnp由假设1各种艇的几何形状相同若艇浸没面积s与艇的某特征尺寸c的平方成正比与桨手数n成正比所以艇和桨手的总质量而由阿基米德定律艇排水体积a与总质量因为比赛成绩t时间与v成反比所以8式就是根据模型假设和几条物理规律得到的各种艇的比赛成绩与桨手数之间的关系
(3)
又根据艇重 与桨手数 成正比,所以艇和桨手的总质量 也与 成正比,即
(4)
而由阿基米德定律,艇排水体积 与总质量 成正比,即
(5)
(3)、(4)、(5)式给出
(6)
将(6)式代入(2)式,当 时常数时得到
(7)
因为比赛成绩 (时间)与 成反比,所以
(8)
(8)式就是根据模型假设和几条物理规律得到的各种艇的比赛成绩与桨手数之间的关系。
结果:
a =
7.2146
b =
-0.1114
a1 =
7.2842
b1 =
-0.1035
假设3中 , 为常数属于必要的简化,而 与 成正比可解释为: 与肌肉体积,肺的体积成正比,对于身体匀称的运动员,肌肉,肺的体积与体重 成正比。
四、模型建立
(显示模型函数的构造过程)
数学模型题集(二)
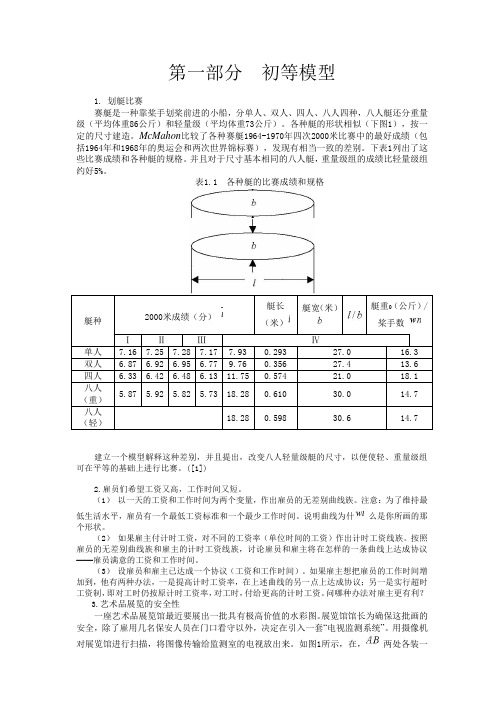
第一部分初等模型1. 划艇比赛赛艇是一种靠桨手划桨前进的小船,分单人、双人、四人、八人四种,八人艇还分重量级(平均体重86公斤)和轻量级(平均体重73公斤)。
各种艇的形状相似(下图1),按一定的尺寸建造。
McMahon比较了各种赛艇1964-1970年四次2000米比赛中的最好成绩(包括1964年和1968年的奥运会和两次世界锦标赛),发现有相当一致的差别。
下表1列出了这些比赛成绩和各种艇的规格。
并且对于尺寸基本相同的八人艇,重量级组的成绩比轻量级组约好5%。
表1.1 各种艇的比赛成绩和规格Ⅳ建立一个模型解释这种差别,并且提出,改变八人轻量级艇的尺寸,以便使轻、重量级组可在平等的基础上进行比赛。
([1])2.雇员们希望工资又高,工作时间又短。
(1)以一天的工资和工作时间为两个变量,作出雇员的无差别曲线族。
注意:为了维持最低生活水平,雇员有一个最低工资标准和一个最少工作时间。
说明曲线为什么是你所画的那个形状。
(2)如果雇主付计时工资,对不同的工资率(单位时间的工资)作出计时工资线族。
按照雇员的无差别曲线族和雇主的计时工资线族,讨论雇员和雇主将在怎样的一条曲线上达成协议——雇员满意的工资和工作时间。
(3)设雇员和雇主已达成一个协议(工资和工作时间)。
如果雇主想把雇员的工作时间增加到,他有两种办法,一是提高计时工资率,在上述曲线的另一点上达成协议;另一是实行超时工资制,即对工时仍按原计时工资率,对工时,付给更高的计时工资。
问哪种办法对雇主更有利?3.艺术品展览的安全性一座艺术品展览馆最近要展出一批具有极高价值的水彩图。
展览馆馆长为确保这批画的安全,除了雇用几名保安人员在门口看守以外,决定在引入一套“电视监测系统”。
用摄像机对展览馆进行扫描,将图像传输给监测室的电视放出来。
如图1所示,在,两处各装一台摄像机。
在展览馆的展墙上,每隔挂一幅画。
两个摄像机镜头的视角为,完成一次来回扫描。
但是,在监测室的工作人员只有的时间在观察电视画面。
《数学模型》(第四版)第二章初等模型(2.3 划艇比赛的成绩 2.7 核军备竞赛)

第二章 初等模型
2.1 光盘的数据容量 2.2 双层玻璃窗的功效 2.3 划艇比赛的成绩 2.4 实物交换 2.5 污水均流池的设计 2.6 交通流与道路通行能力 2.7 核军备竞赛 2.8 扬帆远航 2.9 天气预报的评价
初等模型
• 研究对象的机理比较简单 • 用静态、线性、确定性模型即可达到建模目的 可以利用初等数学方法来构造和求解模型 如果用初等和高等的方法建立的模型,其应用效果 差不多,那么初等模型更高明,也更受欢迎.
其全部核导弹攻击己方的核导弹基地;
• 己方在经受第一次核打击后,应保存足够的 核导弹,给对方重要目标以毁灭性的打击.
在任一方实施第一次核打击时,假定一枚核 导弹只能攻击对方的一个核导弹基地.
摧毁这个基地的可能性是常数,它由一方的 攻击精度和另一方的防御能力决定.
图 y=f(x)~甲有x枚导弹,乙所需的最少导弹数(乙安全线) 的 x=g(y)~乙有y枚导弹,甲所需的最少导弹数(甲安全线) 模 当 x=0时 y=y0,y0~乙方的威慑值 型 y0~甲方实行第一次打击后已经没有导弹,乙方
v (n/s)1/3
建立 s1/2 A1/3, A W(=w0+nw) n
s n2/3
v n1/9
比赛成绩 t n – 1/9
模型检验
nt 1 7.21 2 6.88 4 6.32 8 5.84
t anb
利用4次国际大赛冠军的平均
成绩对模型 t n – 1/ 9 进行检验.
x<y 甲方以 x枚导弹攻击乙方 y个基地中的 x个, sx个基地未被摧毁,y–x个基地未被攻击.
x=y y<x<2y
数学建模第二章 初等模型

第二章 初等模型如果研究对象的机理比较简单,一般用静态、线性、确定性模型描述就能达到建模的目的时,我们基本上可以用初等数学的方法来构造和求解模型。
通过下面的几个实例我们能够看到,用很简单的数学方法就可以解决一些有趣的实际问题。
需要强调的是,衡量一个模型的优劣完全在于它的应用效果,而不是它看它采用了多么高深的数学方法。
进一步说,对于某个实际问题我们如果能够用初等方法和所谓的高等方法建立了两个模型,而它们的应用效果相差无几的话,那么受人们欢迎并采用的,一定是前者而非后者。
§2.1公平的席位分配设有A 、B 两个单位,各有人数1p 、2p 个,现在要求按人数选出q 个代表召开一次代表会议。
那么怎样分配这q 个席位呢?一般的方法是令:q p p p q 211*1+= q p p p q 212*2+= (2.1)若*1q ,*2q 恰好是两个整数,就以*1q ,*2q 分别作为A ,B 两个单位的席位数,即可以获得一个完全合理的分配方案。
当*1q ,*2q 不是两个整数时,那么怎样分配才合理呢?下面我们就来讨论这个问题。
首先给出一种自然的想法,也就是通常所执行的方法。
即由(2.1)式计算出的*1q ,*2q ,用][*i i q q =表示*i q 的整数部分。
当*1q -1q >*2q -2q 时,则用1q +1与2q 分别作为A ,B 两个单位的席位数;当*2q -2q >*1q -1q 时,则用1q 与2q +1分别作为A ,B 两个单位的席位数;而当*2q -2q =*1q -1q 时,就只能由A ,B 两个单位协商来确定那多余的一个席位了。
这个方法的优点是简单、方便,并被很多人所接受,同时也容易推广到m (m >2)个单位的席位分配问题。
但是这个分配方案是存在弊病的,它有明显的不合理性。
例1 某学校有3个系共200名学生,其中甲系100名,乙系60名,丙系40名。
若学生代表会议设20个席位,公平而又简单的席位分配办法是按学生人数的比例分配,显然甲乙丙三系分别应占有10、6、4个席位。
第二章初等模型

模型2(幂函数模型)
线性模型并未得到广泛的接受,要改进结果,能够 想到的自然首先是幂函数模型,即令L=kBa,对此式 取对数,得 到lnL=lnk+a lnB。将原始数据也取对数, 问题即转化了线性模型,可用最小二乘法求出参数。 几十年前英国和爱尔兰采用的比较举重成绩优劣 的 Austin公式:L′=L/B3/4就是用这一方法求得的。
块下落时间 t1≈t-t2将t1代入式①再算一次,得出 崖高的近似值。例如, 若h=69.9米,则 t2≈0.21 秒,故 t1≈3.69秒,求得 h≈62.3米。
2
§2.4 经验模型
当问题的机理非常不清楚难以直接利用其他知 识来建模时,一个较为自然的方法是利用数据 进行曲线拟合,找出变量之间的近似依赖关系 即函数关系。
最小二乘法
插值方法
最小二乘法
设经实际测量已得 到n组数据(xi , yi),i=1,…, n。将数据 画在平面直角坐标系中,见 图。如果建模者判断 这n个点很 象是分布在某条直线附近,令 该直线方程 为y=ax+b,进而 利用数据来求参 数a和b。由于该直线只是数据近似满足的 关系式,故 yi-(axi+b)=0一般不成立,但我们希望 如果建模者判断变量间的关系并非线性关系而是其他类型的函数, n 则可作 变量替换使之转化为线性关系或用类似方 2法拟合。 [ yi (axi b)] 最小 y=ax+b y i 1 此式对a和b的偏导数均 为0,
(3)O’ Carroll公式:
75 4 L L B 2 75 3 L L B 1 40 3 L L B 35
29250( B ) L L 75 B(465 B )
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xm xm , ym ym
y
y0 y=f(x)
O
x0
P(xm , ym )
P(xm,ym) x=g(y)
x
甲方的被动防御也会使双方军备竞赛升级.
模型解释
• 甲方将固定核导弹基地改进为可移动发射架.
乙安全线y=f(x)不变 甲方残存率变大
威慑值x 0不变
x减小,甲安全线 x=g(y)向y轴靠近
y0= s2(x–y)+ s(2y– x )
y y0 1 s x s(2 s) 2 s
y0=s2y
y=y0/s2
分析 模型 x<y, y= y0+(1–s)x
y<x<2y, y y0 1 s x s(2 s) 2 s
x=y, y=y0/s x=2y, y=y0/s2
v (n/s)1/3
建立 s1/2 A1/3, A W(=w0+nw) n
s n2/3
v n1/9
比赛成绩 t n – 1/9
模型检验
nt 1 7.21 2 6.88 4 6.32 8 5.84
t anb
利用4次国际大赛冠军的平均
成绩对模型 t n – 1/ 9 进行检验.
双人 6.87 6.92 6.95 6.77 6.88 9.76 0.356 27.4
四人 6.33 6.42 6.48 6.13 6.32 11.75 0.574 21.0
八人 5.87 5.92 5.82 5.73 5.84 18.28 0.610 30.0
空艇重w0(kg) 桨手数n 16.3 13.6 18.1 14.7
第二章 初等模型
2.1 光盘的数据容量 2.2 双层玻璃窗的功效 2.3 划艇比赛的成绩 2.4 实物交换 2.5 污水均流池的设计 2.6 交通流与道路通行能力 2.7 核军备竞赛 2.8 扬帆远航 2.9 天气预报的评价
初等模型
• 研究对象的机理比较简单 • 用静态、线性、确定性模型即可达到建模目的 可以利用初等数学方法来构造和求解模型 如果用初等和高等的方法建立的模型,其应用效果 差不多,那么初等模型更高明,也更受欢迎.
而存在暂时的平衡状态.
• 估计平衡状态下双方拥有的最少的核武器数量, 这个数量受哪些因素影响.
• 当一方采取加强防御、提高武器精度、发展多 弹头导弹等措施时, 平衡状态会发生什么变化.
模 以双方(战略)核导弹数量描述核军备的大小.
型 假
假定双方采取如下同样的核威慑战略:
设 • 认为对方可能发起所谓第一次核打击,即倾
y P(xm,ym)
P(xm , ym )
y0 y=f(x) x=g(y)
O
x0
x
PP´ xm xm , ym ym
甲方这种单独行为,会使双方的核导弹减少.
模型解释
• 双方发展多弹头导弹,每个弹头可以独立地摧毁目标.
(x , y仍为双方核导弹的数量)
双方威慑值x 0, y0和残存率s均减小.
乙安全线 y=f(x)
y
P
y0减小 y下移且变平 s变小 y增加且变陡
P P? P P?
y=f(x)
y0
O
x0
P(xm,ym)
P
x=g(y)
x
双方导弹增加还是减少,需要更多信息及更详细的分析.
核军备竞赛
• 对“核威慑战略”做一些合理、简化假设,用图 的模型描述双方核武器相互制约、达到平衡的过程. • 提出安全曲线概念,给出它的一般形式. • 通过更精细的分析找到影响安全线的参数:威慑值 和残存率,给出安全线的分析表达式.
准 调查赛艇的尺寸和质量 备
l /b, w0/n 基本不变
问题分析 分析赛艇速度与桨手数量之间的关系
赛艇速度由前进动力和前进阻力决定: • 前进动力 ~ 桨手的划桨功率 • 前进阻力 ~ 浸没部分与水的摩擦力
桨手 数量
划桨 功率
艇 重
前进 动力
浸没 面积
前进 阻力
赛艇 速度
赛艇 速度
• 对桨手体重、功率、阻力与艇速的关系等作出假定. • 运用合适的物理定律建立模型.
划艇比赛的成绩
• 对实际数据做比较、分析,发现并提出问题. • 利用物理基本知识分析问题. • 模型假设比较粗糙. • 利用合适的物理定律及简单的比例 方法建模(只考虑各种艇的相对速度).
• 模型结果与实际数据十分吻合 (巧合!)
2.7 核军备竞赛
背 • 冷战时期美苏声称为了保卫自己的安全, 实行 景 “核威慑战略”, 核军备竞赛不断升级. 与 • 随着前苏联的解体和冷战的结束, 双方通过了 问 一系列核裁军协议. 题 • 在什么情况下双方的核军备竞赛不会无限扩张,
x<y 甲方以 x枚导弹攻击乙方 y个基地中的 x个, sx个基地未被摧毁,y–x个基地未被攻击.
x=y y<x<2y
x=2y
y0=sxLeabharlann y–x y0=syy= y0+(1–s)x y=y0/s
乙的x–y个基地被攻击2次, s2(x–y)个未被摧毁;
y –(x–y)=2y– x个被攻击1次, s(2y– x )个未被摧毁.
t
7.21 •
6.88
•
6.32 5.84
•
•
O 12 4
8n
logt a blogn
线性最小二乘法 t 7.21n0.11 与模型吻合!
建立的m文件 JQ31.m 如下:
n=[1,2,4,8]; t=[7.21,6.88,6.32,5.84]; x=log(n); y=log(t); a=polyfit(x,y,1) B=a(1) A=exp(a(2))
其全部核导弹攻击己方的核导弹基地;
• 己方在经受第一次核打击后,应保存足够的 核导弹,给对方重要目标以毁灭性的打击.
在任一方实施第一次核打击时,假定一枚核 导弹只能攻击对方的一个核导弹基地.
摧毁这个基地的可能性是常数,它由一方的 攻击精度和另一方的防御能力决定.
图 y=f(x)~甲有x枚导弹,乙所需的最少导弹数(乙安全线) 的 x=g(y)~乙有y枚导弹,甲所需的最少导弹数(甲安全线) 模 当 x=0时 y=y0,y0~乙方的威慑值 型 y0~甲方实行第一次打击后已经没有导弹,乙方
为毁灭甲方工业、交通中心等目标所需导弹数.
y y y0 x
y 乙安全区
双方 安全区
y=f(x) 乙安全线 y0
O y0 y f (x) y0 x
y1
y=f(x)
P(xm,ym)甲 安
x=g(y) 全
y0
区
xO
x0 x1
x
P~平衡点(双方最少导弹数)
分析 乙方残存率 s ~甲方一枚导弹攻击乙方一个 模型 基地,基地未被摧毁的概率.
尽量采用简单的数学工具来建模
2.3 划艇比赛的成绩
对四种赛艇 (单人、双人、四人、八人) 4次国际
问 大赛冠军的成绩进行比较,发现与桨手数有某 题 种关系. 试建立数学模型揭示这种关系.
赛艇
2000m成绩 t (min) 艇长l 艇宽b l/b
种类 1 2 3 4 平均 (m) (m)
单人 7.16 7.25 7.28 7.17 7.21 7.93 0.293 27.0
x=a y,
y
y0 sa
y0 sx/ y
y
x=y
x=2y
y0~威慑值 s~残存率
利用微积分知识可知 y是一条上凸的曲线,且
y=f(x)
y0 O
• y0变大,曲线上移、变陡. • s变大,y减小,曲线变平.
x
模型解释
• 甲方增加经费保护及疏散工业、交通中心等目标.
乙方威慑值 y0变大 (其他因素不变) 乙安全线 y=f(x)上移
模型假设
符号:艇速 v, 浸没面积 s, 浸没体积 A, 空艇重 w0, 阻力 f, 桨手数 n, 桨手功率 p, 桨手体重 w, 艇重 W.
1)艇形状相同(l/b为常数), w0与n成正比 艇的静态特性
2)v是常数,阻力 f与 sv2成正比
艇的动态特性
3)w相同,p不变,p与w成正比
桨手的特征
模型 np fv, f sv2, p w
• 利用模型对核军备竞赛中的一些现象作出合理解释.
注:在Matlab 中的线性最小二乘拟合,用的较多的是多项式拟合,其命令为: A=polyfit(x,y,m), 其中
x (x1, x2 ,L , xn ), y ( y1, y2,L , yn ), A (a1, a2,L , am1)
得到拟合的m次多项式,
f (x) a1xm a2xm1 L amx am1.
