中考数学求阴影部分面积的几种常见方法
四种方法求阴影部分面积

四种方法求阴影部分面积首先,我们可以使用几何方法来求解阴影部分的面积。
设阴影部分的形状为矩形,其底边的长度为a,高度为h。
阴影的边界可以用两条直线来表示,设直线1与x轴的交点为A,直线2与x轴的交点为B。
两条直线与x轴的交点之间的距离为b。
则阴影部分的面积可以用以下公式表示:A=(a+b)*h/2第二种方法是通过将阴影部分分割成多个小矩形来求解。
首先,我们将阴影部分分割成n个小矩形,每个小矩形的底边长度为ai,高度为hi。
则阴影部分的面积可以表示为以下公式的和:A = ∑(ai * hi)其中i的范围从1到n。
第三种方法是使用积分来求解。
假设阴影部分的形状可以用函数y=f(x)来表示。
要求阴影部分的面积,我们需要找到函数f(x)的定义域上的积分区间[a,b]。
A = ∫[a, b] f(x) dx最后一种方法是使用统计学方法来求解。
假设我们已经获得了一组阴影部分的随机样本,符合一定的分布规律。
我们可以使用这组样本数据来进行统计分析,得出阴影部分的面积的估计值。
首先,我们可以计算出这组样本数据的平均值和标准差。
然后,使用均值加减一个标准差的方法,来计算阴影部分的上下边界。
根据阴影部分的上下边界和样本数据的分布,我们可以得到阴影部分面积的估计值。
需要注意的是,这种方法求得的阴影部分面积只是一个估计值,可能存在一定的误差。
综上所述,我们可以用几何法、分割法、积分法和统计法来求解阴影部分的面积。
每种方法都有自己的优缺点和适用范围,选择合适的方法取决于具体情况和问题要求。
广西省北部湾经济区2020届中考数学大一轮新素养突破 教师课件:微专题 四种方法求阴影部分面积
2. (2019枣庄)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,
交对角线BD于点E,则图中阴影部分的面积是(结果保留π)( C ) A. 8-π
B. 16-2π
C. 8-2π
D.
8-12π源自第2题图3. 如图,在扇形AOB 中,∠AOB=90°,正方形CDEF的顶点C是AB的中点,点D 在OB上,点E在OB的延长线上.当正方形CDEF的边长为2 2 时,则阴影部分的 面积为2_π__-__4___.
第9题图
10. (2019重庆B卷)如图,四边形ABCD是矩形,AB=4,AD=2 2,以点A为圆 心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的 面积是________.
第10题图
第3题图
第4题图
4. 如图,在Rt△ABC中,BC=1,AB= 3 ,将△ABC绕点A顺时针旋转90°得到 △AFE,线段AE与 BF 交于点G,连接CG,则图中阴影部分的面积为__π2_-___23__.
方法3 等积转化法 通过图形的等面积、平移、对称或者旋转转化,将所求部分面积转化为可用公式法或 者和差法求解的图形面积. 5. 如图,在半径为4的⊙O 中,CD 是直径,AB是弦,且CD⊥AB,垂足为点E, ∠AOB =90°,则阴影部分的面积是____2_π___.
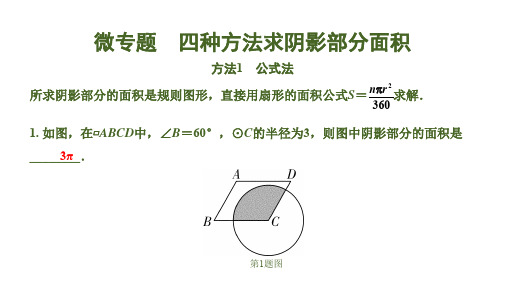
微专题 四种方法求阴影部分面积
方法1 公式法 所求阴影部分的面积是规则图形,直接用扇形的面积公式S= nr 2 求解.
360
1. 如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是 _____3_π__.
第1题图
方法2 和差法 将不规则图形分割或者与其他部分图形结合构造规则图形,再进行面积和差;或 者将不规则图形看成规则图形的一部分,通过整体作差求解.
专题8 巧求圆中阴影部分的面积(含答案)

专题8 巧求圆中阴影部分的面积【知识解读】求与圆有关的阴影部分的面积,能考查同学们的观察能力、随机应变能力和综合运用数学知识的能力,解答此类问题要注意观察和分析图形的形成,学会分解和组合图形,消除思路中的“阴影”,明确要计算图形的面积,可以通过哪些图形的和或差得到,就能给解决问题带来一片光明,切勿盲目计算;下面介绍几种常用的解法.培优学案【典例示范】等积变换法:是在不改变图形面积的前提下,利用“等底、等高的两个三角形的面积相等”,将不规则图形转化为规则图形的面积来求解的方法.例1 如图1-8-1,点P 是半径为1的⊙O 外一点,OP =2,P A 切⊙O 于点A ,弦AB ∥OP ,连接PB ,则图中阴影部分的面积是.图181AB OP图182ABCDEMNO【跟踪训练】如图1-8-2,AB 是⊙O 的直径,MN 是⊙O 的切线,C 为切点,过点A 作AD ⊥MN 于点D ,交⊙O 于点E .已知AB =6,BC =3,求图中阴影部分的面积.【解答】和差法:是指将阴影部分看作两个规则图形的和或差.例2 如图1-8-3,扇形OAB 中,∠AOB =60°,扇形半径为4,点C 在BC 上,CD ⊥OA ,垂足为点D ,当CD =OD 时,图中阴影部分的面积为.图183BCD图184CEF【跟踪训练】如图1-8-4,在等腰直角三角形ABC 中,∠C =90°,点D 为AB 的中点,已知扇形EAD 和扇形FBD 的圆心分别为点A 、点B ,且AC =2,则图中阴影部分的面积为(结果不取近似值).割补法:是在不改变图形面积的前提下,通过割补,将发散的图形面积集中在一起,把不规则的图形凑合成规则图形的方法.例3 如图1-8-5,半径为2cm ,圆心角为90°的扇形OAB 中,分别以OA ,OB 为直径作半圆,则图中阴影部分的面积为cm 2.图185ABO图186A 'O 'O ABC【跟踪训练】如图1-8-6,将半圆O 绕直径AB 的端点B 逆时针旋转30°,得到半圆O ′,A ′B 交直径AB 于点C ,若BC =23,则图中阴影部分的面积为 .【提示】连接O ′C ,A ′C ,将阴影部分的面积通过割补,转化为△BO ′C 的面积加上扇形O ′AC 的面积.特殊位置法:是在不改变题意的前提下,通过取特殊位置,将图形特殊化,以方便求解.例4 如图1-8-7,一个半径为r 的圆形纸片在边长为a (a >3r )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“接触不到的部分”的面积是()A .23r πB 233π- C .()233r πD .2r π【提示】解答本题的关键是搞清楚圆形纸片“不能接触到的部分”的面积,即圆形纸片与正三角形的相邻两边都相切时,两切点与正三角形的一个顶点形成的曲边三角形的面积.图187图188【跟踪训练】如图1-8-8,一张半径为1的圆形纸片在边长为a (a ≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触到的部分”的面积是() A .2a π-B .()24a π-C .πD .4π-整体代换法:是指在解答过程中,可将某些不易求的且不发生变化的量看作整体处理. 例5 如图1-8-9,在Rt △ABC 中,∠C =90°,CA =CB =4,分别以A ,B ,C 为圆心,以12AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是.图189CBA【提示】直接求阴影部分的面积是不可能的,根据题意结合图形,知阴影部分的面积等于直角三角形的面积减去三个扇形的面积,其中A ,B 两个扇形的面积无法直接求出,但若把它们看作一个“整体”,则问题易求.【跟踪训练】1.如图1-8-10,正方形的边长a ,以各边为直径在正方形内画半圆,则图中阴影部分的面积为 . 【提示】图中阴影部分的面积可以看作四个半圆的面积之和与正方形的面积之差.CBAOFEDCBA2.如图1-8-11,⊙A ,⊙B ,⊙C 两两不相交,且半径都是2cm ,则图中三个扇形(即阴影部分)面积之和是 cm 2.【提示】图中3个扇形正好拼成一个圆心角为180°的大扇形。
专题17 圆中阴影部分的面积七种计算方法-2023年中考数学二轮复习核心考点拓展训练(解析版)

专题17 圆中阴影部分的面积七种计算方法(解析版)第一部分典例剖析+针对训练方法一公式法典例1 (2022•凉山州)家具厂利用如图所示直径为1米的圆形材料加工成一种扇形家具部件,已知扇形的圆心角∠BAC=90°,则扇形部件的面积为( )A.12π米2B.14π米2C.18π米2D.116π米2思路引领:连结BC,AO,90°所对的弦是直径,根据⊙O的直径为1米,得到AO=BO=12米,根据勾股定理得到AB的长,根据扇形面积公式即可得出答案.解:连结BC,AO,如图所示,∵∠BAC=90°,∴BC是⊙O的直径,∵⊙O的直径为1米,∴AO=BO=12(米),∴AB=AO2+BO2=22(米),∴扇形部件的面积=90360π×(22)2=π8(米2),故选:C.总结提升:本题考查了扇形面积的计算,掌握设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=n360πR2是解题的关键.针对训练1.(2021•卧龙区二模)如图,△ABC中,D为BC的中点,以点D为圆心,BD长为半径画弧,交边BC 于点B,交边AC于点E,若∠A=60°,∠B=100°,BC=6,则扇形BDE的面积为 .思路引领:求出扇形的圆心角以及半径即可解决问题.解:∵∠A=60°,∠B=100°,∴∠C=180°﹣60°﹣100°=20°,∵DE=DC,∴∠C=∠DEC=20°,∴∠BDE=∠C+∠DEC=40°,∴S扇形DBE=40π×32360=π.故答案为:π.总结提升:本题考查扇形的面积公式、三角形内角和定理等知识,解题的关键是记住扇形的面积公式.方法二和差法典例2(2022•荆州)如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )A.3―π4B.23―πC.(6―π)33D.3―π2思路引领:作AF⊥BC,由勾股定理求出AF,然后根据S阴影=S△ABC﹣S扇形ADE得出答案.解:由题意,以A为圆心、一定的长为半径画弧,恰好与BC边相切,设切点为F,连接AF,则AF⊥BC.在等边△ABC中,AB=AC=BC=2,∠BAC=60°,∴CF=BF=1.在Rt△ACF中,AF=AB2―AF2=3,∴S阴影=S△ABC﹣S扇形ADE=12×2×3―60π×(3)2360=3―π2,故选:D.总结提升:本题主要考查了等边三角形的性质,求扇形面积,理解切线的性质,将阴影部分的面积转化为三角形的面积﹣扇形的面积是解题的关键.针对训练1.(2022•玉树市校级一模)如图,在扇形OAB中,已知∠AOB=90°,OA=2,过AB的中点C作CD⊥OA,CE⊥OB,垂足分别为点D,E,则图中阴影部分的面积为( )A.π﹣1B.π﹣2C.π﹣4D.π2―1思路引领:连接OC,求出∠AOC=∠BOC=45°,求出∠DCO=∠AOC=∠ECO=∠COE=45°,求出CD=OD,CE=OE,根据勾股定理求出CD=OD=OE=CE=2,再求出阴影部分的面积即可.解:连接OC,∵OA=2,∴OC=0A=2,∵∠AOB=90°,C为AB的中点,∴∠AOC=∠BOC=45°,∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°,∴∠DCO=∠AOC=∠ECO=∠COE=45°,∴CD=OD,CE=OE,∴2CD2=22,2OE2=22,即CD=OD=OE=CE=2,∴阴影部分的面积S=S扇形AOB﹣S△CDO﹣S△CEO=90π×22360―2×12×2×2=π﹣2,故选:B.总结提升:本题考查了等腰直角三角形的性质和判定,圆心角、弧、弦之间的关系,扇形面积的计算等知识点,把求不规则图形的面积转化成求规则图形的面积是解此题的关键,注意:如果扇形的圆心角为n°,半径为r,那么该扇形的面积为nπr2360.方法三等积变形法典例3(2020•朝阳)如图,点A,B,C是⊙O上的点,连接AB,AC,BC,且∠ACB=15°,过点O作OD ∥AB交⊙O于点D,连接AD,BD,已知⊙O半径为2,则图中阴影面积为 .思路引领:由圆周角定理可得∠AOB的度数,由OD∥AB可得S△ABD=S△ABO,进而可得S阴影=S扇形AOB,然后根据扇形面积公式计算即可.解:∵∠ACB=15°,∴∠AOB=30°,∵OD∥AB,∴S△ABD=S△ABO,∴S阴影=S扇形AOB=30π×22360=π3.故答案为:π3.总结提升:本题考查了圆周角定理、扇形面积公式和同底等高的两个三角形的面积相等等知识,属于常考题型,熟练掌握上述基本知识是解题的关键.针对训练1.(2022秋•天桥区期末)如图,菱形OABC的三个顶点A,B,C在⊙O上,对角线AC,OB交于点D,若⊙O的半径是23,则图中阴影部分的面积是( )A.2πB.6πC.33πD.3π思路引领:根据四边形OABC是菱形,得BC=OC=OB,即△COB是等边三角形,根据S△ADB=S△OCD,所以图中阴影部分的面积=S扇形COB.解:∵四边形OABC是菱形,∴BC=OC=OB,∴△COB是等边三角形,∴∠COB=60°,∵S△ADB=S△OCD,∴图中阴影部分的面积=S扇形COB=60π×(23)2360=2π.故选:A.总结提升:本题考查的是扇形面积的计算和菱形的性质,掌握扇形的面积公式是解题的关键.方法四化零为整法(整体法)典例4(2021•天桥区二模)如图,已知正六边形的边长为4,分别以正六边形的6个顶点为圆心作半径是2的圆,则图中阴影部分的面积为 .思路引领:先求出六边形的内角和,再根据扇形的面积公式即可求出.解:∵六边形的内角和=(6﹣2)×180°=720°,∴阴影面积=6×π×22―720π×22360=16π.故答案为:16π.总结提升:本题主要考查了扇形的面积公式,学会把图中不规则图形的面积由几何关系转化为规则图形的面积.针对训练1.如图,分别以五边形的各个顶点为圆心,1cm长为半径作圆,则图中阴影部分的面积为 π cm2.思路引领:根据多边形的外角和为360°可得阴影部分的面积为半径为1的圆的面积,再利用圆的面积计算公式可得答案.解:图中阴影部分的面积为π×12=π.故答案为:π.总结提升:此题主要考查了多边形的外角,关键是掌握多边形的外角和为360°.方法五割补法(拼接法)典例5(2022•铜仁市)如图,在边长为6的正方形ABCD中,以BC为直径画半圆,则阴影部分的面积是( )A.9B.6C.3D.12思路引领:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,证明BE=CE,得到弓形BE的面积=弓形CE的面积,则S阴影=S△ABE=S△ABC―S△BCE=12×6×6―12×6×3=9.解:设AC与半圆交于点E,半圆的圆心为O,连接BE,OE,∵四边形ABCD是正方形,∴∠OCE=45°,∵OE=OC,∴∠OEC=∠OCE=45°,∴∠EOC=90°,∴OE垂直平分BC,∴BE=CE,∴弓形BE的面积=弓形CE的面积,∴S阴影=S△ABE=S△ABC―S△BCE=12×6×6―12×6×3=9,故选:A.总结提升:本题主要考查了求不规则图形的面积,正方形的性质,等腰直角三角形的性质,圆的性质,熟知相关知识是解题的关键.针对训练1.(2021•郑州模拟)如图,在扇形CBA中,∠ACB=90°,连接AB,以BC为直径作半圆,交AB于点D.若阴影部分的面积为(π﹣1),则阴影部分的周长为 .思路引领:根据BC为直径可知∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,设AC=BC=m,则AB=2m,CD=AD=BD=22m,阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差,据此求得直角三角形的边长,进而求得AB和CD的长,进一步求得阴影部分的周长.解:设BC的中点为O,连接OD,连接CD,∵以BC为直径作半圆,交AB于点D.∴CD⊥AB,∵AC=BC,∠ACB=90°,∴AD=BD,CD=12 AB,∴CD=BD,∴CD=BD,∵AD=BD,CO=BO,∴OD∥AC,∴∠BOD=90°,设AC=BC=m,则AB=2m,CD=AD=BD=22 m,∵阴影部分的面积为(π﹣1),∴S阴影部分=S扇形ACB﹣S△ADC=14π•m2―12×(22m)2=π﹣1.∴14πm2―14m2=π﹣1,∴14m2=1,∴m=2,∴AC=BC=2,AB=22,OC=OB=1,∴AB的长为:90⋅π×2180=π,BD的长为:90⋅π×1180=12π,∴阴影部分的周长为:π+2×12π+22+2=2π+22+2故答案为:2π+22+2.总结提升:本题考查了扇形的面积和弧长的计算,等腰直角三角形的性质,正确的作出辅助线是解题的关键.方法6 图形变化法(旋转、平移、翻折)典例6(2022•武威模拟)在△ABC中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC 绕点A按逆时针方向旋转90°后得到△AB'C'.则图中阴影部分的面积为 .思路引领:解直角三角形得到AB=3BC=3,AC=2BC=2,然后根据扇形的面积公式即可得到结论.解:∵∠ABC=90°,∠BAC=30°,BC=1,∴AB=3BC=3,AC=2BC=2,∴图中阴影部分面积=S扇形ACC′﹣S扇形ADB′﹣S△AB′C′=90⋅π⋅22360―60⋅π⋅(3)2360―12×1×3=π―32,故答案为:π―32;总结提升:本题主要考查了图形的旋转,扇形的面积公式,解直角三角形,熟练掌握扇形的面积公式是解决问题的关键.针对训练1.(2022•西宁)如图,等边三角形ABC内接于⊙O,BC=23,则图中阴影部分的面积是 4π3 .思路引领:根据内接于圆O的等边三角形的性质可得S△AOB=S△AOC,∠AOC=120°,将阴影部分的面积转化为扇形AOC的面积,利用扇形面积的公式计算可求解.解:∵△ABC为等边三角形,∴S△BOC=S△AOC,∠AOC=120°,在△OBC中,OB=OC,∠BOC=120°,BC=23,∴OB=OC=2,∴S阴影=S扇形AOC=120π×22360=4π3,故答案为:4π3.总结提升:本题主要考查扇形面积的计算,等边三角形的性质,掌握扇形面积公式是解题的关键.典例7(2022•九龙坡区自主招生)如图,正方形ABCD的边长为4,O为对角线的交点,点E,F分别为BC,AD的中点,以C为圆心,4为半径作圆弧BD,再分别以E,F为圆心,2为半径作圆弧BO,OD,则图中阴影部分的面积为 .(结果保留π)思路引领:连接BD,根据在同圆或等圆中,相等的圆心角所对的弧,所对的弦分别相等,利用面积割补法可得阴影部分的面积等于弓形面积,即等于扇形CBD减去直角三角形CBD的面积之差.解:连接BD,EF,如图,∵正方形ABCD的边长为4,O为对角线的交点,由题意可得:EF,BD经过点O,且EF⊥AD,EF⊥CB.∵点E,F分别为BC,AD的中点,∴FD=FO=EO=EB=2,∴OB=OD,OB=OD.∴弓形OB=弓形OD.∴阴影部分的面积等于弓形BD的面积.∴S阴影=S扇形CBD﹣S△CBD=90π×42360―12×4×4=4π﹣8.故答案为:4π﹣8.总结提升:本题主要考查了正方形的性质,扇形面积的计算.通过添加适当的辅助线将不规则的阴影部分的面积转化成规则图形的面积的差是解题的关键.针对训练1.(2021•重庆模拟)如图,在正方形ABCD中,扇形BAD的半径AB=4,以AB为直径的圆与正方形的对角线BD相交于O,连接AO.则图中阴影部分的面积为 .(结果保留π)思路引领:理由圆周角定理得出AO⊥BD,利用正方形的性质性质和等腰直角三角形的性质得出OD=OA =OB,结合转化思想得出阴影部分面积=S扇形ABD﹣S△ADC,进而得出答案.解:如图,∵AB是直径,∴∠AOB=90°,∴AO⊥BD,∵AB=AD=4,∠BAD=90°,∴OD=OA=OB,∴S弓形OA=S弓形OB,∴阴影部分面积=S扇形ABD﹣S△ADC=14π×42―12×4×4=4π﹣8,故答案为4π﹣8.总结提升:本题考查正方形的性质,扇形的面积等知识,解题的关键是学会把不规则图形转化为规则图形,属于中考常考题型.典例8(2019•招远市一模)如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将CE沿弦CE翻折,交CD于点F,图中阴影部分的面积= .思路引领:根据AB⊥CD,垂足为G,OG:OC=3:5,AB=8,可以求得⊙O的半径;要求阴影部分的面积只要做出合适的辅助线,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.解:如图,连接AO,将阴影部分沿CE翻折,点F的对应点为M,过点M作MN⊥CD于点N,∵CD为⊙O的直径,AB⊥CD,AB=8,∴AG=12AB=4,∵OG:OC=3:5,AB⊥CD,垂足为G,∴设⊙O的半径为5k,则OG=3k,∴(3k)2+42=(5k)2,解得,k=1或k=﹣1(舍去),∴5k=5,即⊙O的半径是5;∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,连接OM,则∠MOD=60°,∴∠MOC=120°,过点M作MN⊥CD于点N,∴MN=MO•sin60°=5×3 2,∴S阴影=S扇形OMC﹣S△OMC=120×π×25360―2534=25π3―2534,即图中阴影部分的面积是:25π3―2534.总结提升:本题考查翻折变换、扇形的面积、垂径定理,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.针对训练1.(如图,将半径为4cm的圆形纸片折叠后,圆弧恰好经过圆心O,折痕为AB,则图中阴影部分的面积为 .思路引领:作OC⊥AB于C,交AB于点D,连接AO,BO,AD,BD,根据轴对称的性质可以得出CO=CD,由三角函数值就可以求出∠AOB的度数,由扇形的面积﹣三角形AOB的面积就可以得出结论.解:作OC⊥AB于C,交AB于点D,连接AO,BO,AD,BD,∴∠ACO=90°.∵△AOB与△ADB关于AB对称,∴△AOB≌△ADB∴AO=AD,∠ACO=∠ACD=90°,∴CO=CD.∵OD=AO=4,∴OC=2.在Rt△AOC中,由勾股定理,得AC=23.∵cos∠AOC=COAO=12,∴∠AOC=60°.∵AO=BO,OC⊥AB,∴∠AOB=2∠AOC=120°.AB=2AC=43.∴S扇形AOBD=120π×16360=163π.∵S△AOB=43×22=43.阴影部分的面积为:(163π―43)cm2.故答案为:(163π―43)cm2.总结提升:本题考查了轴对称的性质的运用,勾股定理的运用,三角函数值的运用,扇形的面积公式的运用,三角形的面积公式的运用,解答时运用轴对称的性质求解是关键.方法七重叠求余法例七(2022•鄂尔多斯二模)如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .思路引领:根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积,即可求解.解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,则阴影部分的面积是:60π×62360=6π,故答案为:6π.总结提升:本题主要考查了扇形的面积的计算,正确理解阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积是解题的关键.针对训练1.(2022•市南区校级一模)如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=2,将三角形绕着BC的中点O逆时针旋转60°,点A的对应点为E,则图中阴影部分的面积为 .思路引领:如图,连接OE,OA.根据S阴=S扇形EOA+S△EOF﹣S△BOF﹣S△AOB﹣S△PBE,求解即可.解:如图,连接OE,OA.由题意可知△BOF为等边三角形.∴OB=OF=BF=1,∴S△BOF=3 4,在Rt△ABC中,∵BC=2,∠CAB=30°,∴AB=2BC=4,AC=DE=23,∴S△EOF=12•OF•DE=3,∵OF=OD,∴S△EOF=S△DEO=3,∵∠AOE=60°,AO=AC2+OC2=(23)2+12=13,∴S扇形EOA=60⋅π⋅(13)2360=13π6,由题意,△BPE为直角三角形,BE=EF﹣BF=4﹣1=3,∴BP=12BE=32,PE=32―(32)2=332,∴S△PBE=12×32×332=938,∴S阴=S扇形EOA+S△EOF﹣S△BOF﹣S△AOB﹣S△PBE=13π6+3―34―3―938=13π6―1138.解法二:可以根据S阴=S△APE+(S扇形AOE﹣S△AOE)计算.总结提升:本题考查扇形的面积,旋转变换,解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.第二部分专题提优训练一.选择题(共15小题)1.(2022•兰州)如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为( )A.4.25πm2B.3.25πm2C.3πm2D.2.25πm2思路引领:根据S阴=S扇形DOA﹣S扇形BOC,计算即可.解:S阴=S扇形DOA﹣S扇形BOC=120π×9360―120π×94360=2.25πm2.故选:D.总结提升:本题考查的是扇形面积的计算,掌握扇形的面积公式S=nπR2360是解题的关键.2.(2022秋•西华县期末)如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,则图中阴影部分的面积是( )A.π﹣1B.π﹣2C.12π﹣1D.12π+1思路引领:已知BC为直径,则∠CDB=90°,在等腰直角三角形ABC中,CD垂直平分AB,CD=DB,D为半圆的中点,阴影部分的面积可以看作是扇形ACB的面积与△ADC的面积之差.解:在Rt△ACB中,AB=22+22=22,∵BC是半圆的直径,∴∠CDB=90°,在等腰Rt△ACB中,CD垂直平分AB,CD=BD=2,∴D为半圆的中点,∴S阴影部分=S扇形ACB﹣S△ADC=12π×22―12×(2)2=π﹣1.故选:A.总结提升:本题主要考查扇形面积的计算,在解答此题时要注意不规则图形面积的求法.3.(2022•泰安)如图,四边形ABCD中,∠A=60°,AB∥CD,DE⊥AD交AB于点E,以点E为圆心,DE为半径,且DE=6的圆交CD于点F,则阴影部分的面积为( )A.6π﹣93B.12π﹣93C.6π―932D.12π―932思路引领:根据平行线的性质,扇形的面积公式,三角形面积公式解答即可.解:过点E作EG⊥DF交DF于点G,∵∠A=60°,AB∥CD,DE⊥AD交AB于点E,∴∠GDE=∠DEA=30°,∵DE=EF,∴∠EDF=∠EFD=30°,∴∠DEF=120°,∵∠GDE=30°,DE=6,∴GE=3,DG=33,∴DF=63,阴影部分的面积=120π×36360―12×63×3=12π﹣93,故选:B.总结提升:本题主要考查了扇形面积和平行线的性质,熟练掌握扇形面积公式是解决本题的关键.4.(2022•达州)如图所示的曲边三角形可按下述方法作出:作等边△ABC,分别以点A,B,C为圆心,以AB长为半径作BC,AC,AB,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为2π,则此曲边三角形的面积为( )A.2π﹣23B.2π―3C.2πD.π―3思路引领:此三角形是由三段弧组成,如果周长为2π,则其中的一段弧长为2π3,所以根据弧长公式可得60πr 180=2π3,解得r=2,即正三角形的边长为2.那么曲边三角形的面积就=三角形的面积+三个弓形的面积.解:设等边三角形ABC的边长为r,∴60πr180=2π3,解得r=2,即正三角形的边长为2,∴这个曲边三角形的面积=2×3×12+(60π×4360―3)×3=2π﹣23,故选:A.总结提升:本题考查了扇形面积的计算.此题的关键是明确曲边三角形的面积就=三角形的面积+三个弓形的面积,然后再根据所给的曲边三角形的周长求出三角形的边长,从而求值.5.现在很多家庭都使用折叠型餐桌来节省空间,两边翻开后成圆形桌面(如图①),餐桌两边AB和CD 平行且相等(如图②),小华用皮尺量出BD=1米,BC=0.5米,则阴影部分的面积为( )A.(π12―38)平方米B.(π6―38)平方米C.(π12―34)平方米D.(π6―34)平方米思路引领:设圆心为O,连接CO,过点O作OE⊥CD于点E,进而得出CD,EO的长以及∠COD的度数,进而由S弓形CD面积=S扇形COD﹣S△COD得出弓形CD的面积,进一步即可求得阴影部分的面积.解:设圆心为O,连接CO,过点O作OE⊥CD于点E,由题意可得出:∠BCD=90°,∴BD是⊙O的直径,∵BD=1米,BC=0.5米,∴BC=12BD,CD=BD2―CD2=32米,∴∠BDC=30°,∴OE=12OD=14米,∵OC=OD,∴∠OCD=∠BDC=30°,∴∠COD=120°,∴S弓形CD面积=S扇形COD﹣S△COD=120π×(12)2360―12×14×32,=(π12―316)平方米,∴阴影部分的面积为:2×(π12―316)=(π6―38)平方米.∴故选:B.总结提升:此题主要考查了勾股定理以及扇形面积计算以及三角形面积求法等知识,熟练掌握特殊角的三角函数关系是解题关键.6.(2022•鞍山)如图,在矩形ABCD中,AB=2,BC=3,以点B为圆心,BA长为半径画弧,交CD于点E,连接BE,则扇形BAE的面积为( )A.π3B.3π5C.2π3D.3π4思路引领:解直角三角形求出∠CBE=30°,推出∠ABE=60°,再利用扇形的面积公式求解.解:∵四边形ABCD是矩形,∴∠ABC=∠C=90°,∵BA=BE=2,BC=3,∴cos∠CBE=CBBE=32,∴∠CBE=30°,∴∠ABE=90°﹣30°=60°,∴S扇形BAE=60⋅π⋅22360=2π3,故选:C.总结提升:本题考查扇形的面积,矩形的性质等知识,解题的关键是求出∠CBE的度数.7.(2022•赤峰)如图,AB是⊙O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D 落在AB上,延长CD,交⊙O于点E,若CE=4,则图中阴影部分的面积为( )A.2πB.22C.2π﹣4D.2π﹣22思路引领:连接OE,OC,BC,推出△EOC是等腰直角三角形,根据扇形面积减三角形面积计算即可.解:连接OE,OC,BC,由旋转知AC=AD,∠CAD=30°,∴∠BOC=60°,∠ACE=(180°﹣30°)÷2=75°,∴∠BCE=90°﹣∠ACE=15°,∴∠BOE=2∠BCE=30°,∴∠EOC=90°,即△EOC为等腰直角三角形,∵CE=4,∴OE=OC=22,∴S阴影=S扇形OEC﹣S△OEC=90π×(22)2360―12×22×22=2π﹣4,故选:C.总结提升:本题主要考查旋转的性质及扇形面积的计算,熟练掌握扇形面积的计算是解题的关键.8.(2022•毕节市)如图,一件扇形艺术品完全打开后,AB,AC夹角为120°,AB的长为45cm,扇面BD 的长为30cm,则扇面的面积是( )A.375πcm2B.450πcm2C.600πcm2D.750πcm2思路引领:先求出AD的长,再根据扇形的面积公式求出扇形BAC和扇形DAE的面积即可.解:∵AB的长是45cm,扇面BD的长为30cm,∴AD=AB﹣BD=15cm,∵∠BAC=120°,∴扇面的面积S=S扇形BAC﹣S扇形DAE=120π×452360―120π×152360=600π(cm2),故选:C.总结提升:本题考查了扇形的面积计算,能熟记扇形的面积公式是解此题的关键,注意:圆心角为n°,半径为r的扇形的面积S=nπr2 360.9.(2022•山西)如图,扇形纸片AOB的半径为3,沿AB折叠扇形纸片,点O恰好落在AB上的点C处,图中阴影部分的面积为( )A.3π﹣33B.3π―932C.2π﹣33D.6π―932思路引领:根据折叠的想找得到AC=AO,BC=BO,推出四边形AOBC是菱形,连接OC交AB于D,根据等边三角形的性质得到∠CAO=∠AOC=60°,求得∠AOB=120°,根据菱形和扇形的面积公式即可得到结论.解:沿AB折叠扇形纸片,点O恰好落在AB上的点C处,∴AC=AO,BC=BO,∵AO=BO,∴四边形AOBC是菱形,连接OC交AB于D,∵OC=OA,∴△AOC是等边三角形,∴∠CAO=∠AOC=60°,∴∠AOB=120°,∵AC=3,∴OC=3,AD=32AC=332,∴AB=2AD=33,∴图中阴影部分的面积=S扇形AOB﹣S菱形AOBC=120π×32360―12×3×33=3π―932,故选:B.总结提升:本题考查了扇形面积的计算,菱形的判定和性质,等边三角形的判定和性质,正确地作出辅助线是解题的关键.10.(2022•连云港)如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )A.23π―32B.23π―3C.43π﹣23D.43π―3思路引领:连接OA、OB,过点O作OC⊥AB,根据等边三角形的判定得出△AOB为等边三角形,再根据扇形面积公式求出S扇形AOB=23π,再根据三角形面积公式求出S△AOB=3,进而求出阴影部分的面积.解:连接OA、OB,过点O作OC⊥AB,由题意可知:∠AOB=60°,∵OA=OB,∴△AOB为等边三角形,∴AB=AO=BO=2∴S扇形AOB=60π×22360=23π,∵OC⊥AB,∴∠OCA=90°,AC=1,∴OC=3,∴S△AOB=12×2×3=3,∴阴影部分的面积为:23π―3;故选:B.总结提升:本题考查有关扇形面积、弧长的计算,熟练应用面积公式,其中作出辅助线是解题关键.二.填空题11.(2020•巩义市二模)如图,点A、B、C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°,则图中阴影部分的面积为 .思路引领:连接OB,交CA于E,根据圆周角定理得到∠BOA=60°,根据平行线的性质得到∠D=∠OAC =30°,即可得出∠OBD=90°,解直角三角形求出BD,分别求出△BOD的面积和扇形AOB的面积,即可得出答案.解:连接OB,交CA于E,∵∠C=30°,∠C=12∠BOA,∴∠BOA=60°,∵BD∥AC,∴∠D=∠OAC=30°,∴∠OBD=90°,∴BD=3OB=83,∴S阴影=S△BDO﹣S扇形AOB=12×8×83―60π×82360=323―32π3,故答案为323―32π3.总结提升:本题考查了平行线的性质,圆周角定理,扇形的面积,三角形的面积,解直角三角形等知识点的综合运用,题目比较好,难度适中.12.(2021•宛城区一模)如图所示,在扇形OAB中,∠AOB=90°,OA=2,长为2的线段CD的两个端点分别在线段OA、OB上滑动,E为CD的中点,点F在AB上,连接EF、BE.若AF的长是π3,则线段EF的最小值是 ,此时图中阴影部分的面积是 .思路引领:如图,连接OF,OE,BF,取OF的中点T,连接BT.根据弧长求得∠AOF=30°,jk证明△OBF是等边三角形,利用直角三角形斜边中线的性质求出OE,EF≥OF﹣OE=1,推出当O,E,F共线时,EF的值最小,此时点E与点T重合,求出BT,然后根据S阴影=S扇形BOF﹣S△BOT求得阴影的面积.解:如图,连接OF,OE,BF,取OF的中点T,连接BT.∵AF的长是π3,OA=2,∴π3=nπ×2180,∴n=30,∴∠AOF=30°,∵∠AOB=90°,∴∠BOF=60°,∵CE=DE,∴OE=12CD=12×2=1,∵OF=2,∴EF≥OF﹣OE=1,∴当O,E,F共线时,EF的值最小,此时点E与点T重合,∴此时EF=1,∵OF=OB,∠BOF=60°,∴△BOF是等边三角形,∵OT=TF,∴BT⊥OF,∴BE=BT=32OB=3,∴此时S阴影=S扇形BOF﹣S△BOT=60π×22360―12×3×1=23π―32.故答案为:1,23π―32.总结提升:本题考查了扇形的面积,等边三角形的判定,直角三角形斜边中线的性质等知识,明确当O,E,F共线时,EF的值最小是解题的关键.13.(2022•贵港)如图,在▱ABCD中,AD=23AB,∠BAD=45°,以点A为圆心、AD为半径画弧交AB于点E,连接CE,若AB=32,则图中阴影部分的面积是 .思路引领:过点D作DF⊥AB于点F,根据等腰直角三角形的性质求得DF,从而求得EB,最后由S阴影=S▱ABCD−S扇形ADE−S△EBC结合扇形面积公式、平行四边形面积公式、三角形面积公式解题即可.解:过点D作DF⊥AB于点F,∵AD=23AB,∠BAD=45°,AB=32,∴AD=23×32=22,∴DF=AD sin45°=22×22=2,∵AE=AD=22,∴EB=AB−AE=2,∴S阴影=S▱ABCD−S扇形ADE−S△EBC=32×2―45π×(22)2360―12×2×2=52―π,故答案为:52―π.总结提升:本题考查等腰直角三角形、平行四边形的性质、扇形的面积公式等知识,是重要考点,准确添加辅助线是解题关键.14.(2020春•亭湖区校级期中)如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=6,则阴影部分的面积是 .思路引领:根据扇形的面积公式计算即可.解:∵∠BOD=2∠DCB,∠DCB=30°,∴∠BOD=60°,∴S扇形OBD=60⋅π⋅62360=6π,故答案为6π.总结提升:本题考查扇形的面积,圆周角定理等知识,解题的关键是计算扇形的面积公式,属于中考常考题型.15.(2022•黔西南州)如图,边长为4的正方形ABCD的对角线交于点O,以OC为半径的扇形的圆心角∠FOH=90°.则图中阴影部分面积是 .思路引领:证明△OBE≌△OCG(SAS),推出S△OBE=S△OCG,推出S四边形OECG=S△OBC=4,再根据S 阴=S扇形OFH﹣S四边形OECG,求解即可.解:如图,∵四边形ABCD是正方形,∴AC⊥BD,OA=OC=OB=OD,∠OBE=∠OCG=45°,S△OBC=14S四边形ABCD=4,∵∠BOC=∠EOG=90°,∴∠BOE=∠COG,在△BOE和△COG中,∠BOE=∠COGOB=OC∠OBE=∠OCG,∴△OBE≌△OCG(SAS),∴S△OBE=S△OCG,∴S四边形OECG=S△OBC=4,∵△OBC是等腰直角三角形,BC=4,∴OB=OC=22,∴S阴=S扇形OFH﹣S四边形OECG=90π⋅(22)2360―4=2π﹣4,故答案为:2π﹣4.总结提升:本题考查扇形的面积,全等三角形的判定和性质,正方形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.16.(2020•康巴什一模)如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积为 .思路引领:先根据正方形的边长,求得CB1=OB1=AC﹣AB1=2―1,进而得到S△OB1C=12(2―1)2,再根据S△AB1C1=12,以及扇形的面积公式即可得出图中阴影部分的面积.解:连接DC1,∵∠CAC1=∠DCA=∠COB1=∠DOC1=45°,∴∠AC1B1=45°,∵∠ADC=90°,∴A,D,C1在一条直线上,∵四边形ABCD是正方形,∴AC=2,∠OCB1=45°,∴CB1=OB1∵AB1=1,∴CB1=OB1=AC﹣AB1=2―1,∴S△OB1C=12•OB1•CB1=12(2―1)2,∵S△AB1C1=12AB1•B1C1=12×1×1=12,∴图中阴影部分的面积=45⋅π⋅(2)2360―12(2―1)2―12=π4―2+2.故答案为π4―2+2.总结提升:本题考查了旋转的性质,正方形性质、勾股定理以及扇形面积的计算等知识点的综合应用,主要考查学生运用性质进行计算的能力.解题时注意:旋转前、后的图形全等.17.(2021秋•招远市期末)如图,在扇形OAB中,点C在AB上,∠AOB=90°,∠ABC=30°,AD⊥BC 于点D,连接AC,若OA=4,则图中阴影部分的面积为 .思路引领:连接OC,作CM⊥OB于M,根据等腰直角三角形的性质得出∠ABO=∠OAB=45°,AB=42,进而得出∠OCB=OBC=75°,即可得到∠BOC=30°,解直角三角形求得AD、BD、CM,然后根据S阴影=S△ABD+S△AOB﹣S扇形OAB+(S扇形OBC﹣S△BOC)计算即可求得.解:连接OC,作CM⊥OB于M,∵∠AOB=90°,OA=OB=2,∴∠ABO=∠OAB=45°,AB=42,∵∠ABC=30°,AD⊥BC于点D,∴AD=12AB=22,BD=32AB=26,∵∠ABO=45°,∠ABC=30°,∴∠OBC=75°,∵OB=OC,∴∠OCB=∠OBC=75°,∴∠BOC=30°,∴∠AOC=60°,CM=12OC=12×4=2,∴S阴影=S△ABD+S△AOB﹣S扇形OAB+(S扇形OBC﹣S△BOC)=S△ABD+S△AOB﹣S扇形OAC﹣S△BOC=12×22×26+12×4×4―12×4×2―60π×42360=4+43―8π3.故答案为:4+43―8π3.总结提升:此题考查了运用切割法求图形的面积.解决本题的关键是把所求的面积转化为容易算出的面积的和或差的形式.。
2024年湖南省中考数学第一轮复习课件微专题15求与圆相关阴影部分面积的四种方法

思路 结论
S大扇形=S1+S2+S3;S矩形=S2+S3+S4;S小扇形=S3+S4;S阴影=S1+S3;S阴影=S大扇形S矩形+S小扇形
【针对训练】 16.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,分别以AC,BC为直径画半圆,则图中 阴影部分的面积为( B )
A.10π-8 C.10π
B.10π-16 D.5π
π-2
18.如图,在△ABC中,AB=AC=4,∠BAC=120°,以点A为圆心,1为半径作弧,分别交 AB,AC于点D,E,以点C为圆心,4为半径作弧,分别交AC,BC于点A,F.若图中阴影部 分的面积分别为S1,S2,则S1-S2的值为____________.
本课结束
湖南2024年数学中考第一轮复习
微专题15 求与圆相关阴影 部分面积的四种方法
方法1 公式法
图形 示例
方法 解读 思路 结论
所求阴影部分面积是规则图形的面积,如圆形、扇形等,可以直接利用 公式进行计算
S阴影=(常常结合勾股定理)
【针对训练】 1.(2023·湘西古丈一模)如图,某数学兴趣小组将边长为2的正六边形铁丝框 ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形 AFB(阴影部分)的面积为( A )
4.(2022·重庆中考B卷)如图,在矩形ABCD中,AB=1,BC=2,以B为圆心,BC的长为半 径画弧,交AD于点E.则图中阴影部分的面积为______.(结果保留π)
5.如图,从一个边长是a的正五边形纸片上剪出一个扇形,这个扇形的面积为______ (用含π的代数式表示);如果将剪下来的扇形围成一个圆锥,圆锥的底面圆直径 为______.
初三数学圆阴影部分面积10种解题方法

初三数学圆阴影部分面积10种解题方法01和差法对于不规则图形实施分割、叠合后,把所求的图形面积用规则图形面积的和、差表示,再求面积.贵港中考如图1,在扇形OAB中,C是OA的中点,CD⊥OA,CD与弧AB交于点D,以O为圆心,OC的长为半径作弧CE交OB于点E,若OA= 4,∠AOB=120°,则图中阴影部分的面积为( 结果保留π) .图1解析: 图形中的阴影部分是不规则图形,较难直接计算.注意到阴影部分是环形BECA的一部分,因此阴影部分面积等于环形BECA的面积减去图形DCA的面积,又图形DCA的面积等于扇形DOA 的面积减去△ODC的面积.图2如图2,连接OD交弧CE于M.因为OA=4,C是OA的中点,CD⊥OA,所以OD=4,OC=2,DC=2√3,所以∠ODC=30°,∠DOC=60°02割补法对图形合理分割,把不规则图形补、拼成规则图形会,再求面积.吉林中考如图3,将半径为3的圆形纸片,按下列顺序折叠,若弧AB和弧BC都经过圆心O,则阴影部分的面积是( 结果保留π) .图3解析: 观察图形可以发现: 下方树叶形阴影部分的面积分成左右两块后,可以补到上方两个空白的新月形的位置.是否能够完全重合,通过计算验证即可.图4如图4,过点O作OD⊥AB于D,连接OA、OC、OB.由折叠性质知OD=1/2r=1/2AO,03等积变形法运用平行线性质或其他几何图形性质把不规则图形面积转化为与它等面积的规则图形来进行计算.天水中考如图5,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E 是半圆弧的三等分点,弧BE的长为2π/3,则阴影部分的面积为图5解析: 阴影部分是Rt△ABC的一部分,运用平行线的性质可将图形ABE面积转化成扇形BOE面积.连接BD、BE、BO、OE,如图6.图6因为点E、B是半圆弧的三等分点,所以∠DOB=∠BOE=∠EOA=60°,所以∠BAD=∠EBA=∠BAE=30°,所以BE∥AD.04平移法一些图形看似不规则,将某一个图形进行平移变换后,利用平移的性质,把不规则的图形的面积转化为规则图形的面积来计算.2019年黄石中考模拟如图7,从大半圆中剪去一个小半圆( 小半圆的直径在大半圆的直径MN上),点O为大半圆的圆心,AB是大半圆的弦,且与小半圆相切,AB∥MN,已知AB=12cm,则阴影部分的面积是.图7解析: 因为AB∥MN,由平行线间的距离处处相等,可以平移小半圆,使小半圆的圆心与大半圆的圆心重合,这样不规则的阴影图形就变成一个环形.图8如图8.过点O作OC⊥AB,垂足为C,连接OB,设大半圆的半径为R,小半圆的半径为r.05旋转法一些图形看似不规则,把某个图形进行旋转变换后,利用旋转的性质,把不规则图形的面积转化为规则图形的面积,再进行计算.安顺中考如图9,矩形ABCD中,BC=2,DC=4,以AB 为直径的⊙O与DC相切于点E,则阴影部分的面积为图9解析: 若直接利用弓形面积公式求解相当繁琐,根据已知条件及圆的旋转不变性,利用图形的旋转可实现解题.图10如图10,连接OE 交BD于M.因为CD 是⊙O 的切线,所以OE⊥CD,又AB∥CD,则OE⊥AB,而OE=OB,易知△OBM ≌△EDM,把△OBM绕点M旋转180°就会转到△EDM,阴影部分就转化为扇形BOE,恰好是半径为2的圆的四分之一,06对称法一些图形看似不规则,利用轴对称和中心对称的性质,把不规则图形进行轴对称和中心对称变换,转化为规则图形的面积,再进行计算.赤峰中考如图11,反比例函数y=k/x( k>0) 的图象与以原点(0,0)为圆心的圆交A、B两点,且A( 1,√3) ,图中阴影部分的面积等于 (结果保留π) .图11解析: 根据反比例函数图象及圆的对称性———既是轴对称图形,又是中心对称图形,可知图中两个阴影面积的和等于扇形AOB的面积.过点A作AD⊥x轴于D,如图12.图12因为A( 1,√3) ,所以∠AOD=60°,OA=2,又因为点A、B关于直线y=x对称,所以∠AOB=2×( 60°-45°)=30°.07整体法当已知条件不能或不足以直接求解时,可整体思考,化单一、分散为整体,把所求的未知量整体转换为已知量,再将问题整体化求解.安徽中考如图13,半径均为1的⊙A、⊙B、⊙C、⊙D、⊙E两两外离,A、B、C、D、E分别为五边形的五个顶点,则图中阴影部分的面积是图13解析: 由已知条件,分别求阴影部分的圆心角不易求得,但将五个扇形的圆心角合为一整体,它们的圆心角的和也是五边形的外角之和360°,所以阴影部分面积是一个整圆的面积,所以S阴影=π.08方程法有些图形的局部可以看成某个规则图形,或某些图形具有等面积的性质,这时可以把它们的关系用方程( 组) 来表示,再解方程( 组) ,求出图形的面积.2019年武汉模拟如图14,在边长为2的正方形ABCD 中,分别以2为半径,A、B、C、D 为圆心作弧,则阴影部分的面积是 ( 结果保留π) .图14解析: 仔细观察图形,有两种相同特征的图形在正方形内部,一起围成所求的阴影部分.设弧AC与弧BD交于点G,连接BE、EC,如图15.图15设形如AED 图形的面积为x,形如DEG 图形的面积为y,那么S阴影= S正-4 ( x+y) ,只需求出(x+y)的结果即可.09推算法某些题目运用已知条件,和图形的性质或定理进行推理,可把阴影部分面积用某个式子表示,从而求得不规则图形的面积.南宁中考如图16,Rt△ABC 中,AC=8,BC=6,∠C=90°,分别以AB、BC、AC 为直径作三个半圆,那么阴影部分的面积为平方单位.图16解析: 设左边阴影部分面积为S1,右边阴影部分面积为S2,整个图形的面积可以表示成: 以AC 为直径的半圆+ 以BC为直径的半圆+△ABC.也可以表示成: S1+S2+以AB为直径的半圆。
四种方法求阴影部分面积

四种方法求阴影部分面积计算阴影面积是在几何学和物理学中的一个常见问题。
在这个问题中,我们需要找到两个或多个图形之间的重叠部分的面积。
这些图形可以是任何形状,包括圆形、矩形、三角形等。
在本文中,我将介绍四种不同的方法来计算阴影面积。
这些方法分别是几何法、分割法、积分法和数值法。
每种方法都有其优点和局限性,适用于不同类型的图形和场景。
1.几何法:几何法是最常见和直观的方法之一,适用于简单的图形。
它的基本思想是将图形转化为几何体,然后计算这些几何体的体积或面积。
对于平面图形,可以使用面积公式来计算。
例如,对于矩形,可以直接计算两个方向上的长度乘积;对于圆形,可以使用圆的半径和π来计算面积。
然后,通过找到两个图形的重叠部分,并计算其面积,可以得到阴影面积。
2.分割法:分割法是一种基于图形分割的方法,适用于复杂的图形。
它的思想是将图形分割成简单的几何体,然后计算这些几何体的面积,并将它们加在一起。
这种方法一般使用数学建模软件来进行计算。
例如,对于一个复杂的图形,可以将其分割成多个矩形或三角形,并计算它们的面积,然后将它们加在一起来得到阴影面积。
3.积分法:积分法是一种基于微积分的方法,适用于连续变化的图形。
它的基本思想是使用积分来计算曲线下面积。
对于阴影面积的计算,可以将两个图形的边界曲线表示为一个函数的形式,并计算它们之间的积分。
这种方法需要具备一定的数学知识和计算能力,但可以得到更准确的结果。
4.数值法:数值法是一种通过数值逼近的方法,适用于复杂的图形和场景。
它的思想是将图形离散化成有限个点或网格,并计算每个点或网格的面积,并将它们加在一起。
这种方法可以使用计算机程序进行计算,但结果的准确性依赖于离散化的精度。
通常情况下,离散化的精度越高,计算结果越准确。
综上所述,四种方法分别是几何法、分割法、积分法和数值法。
它们适用于不同类型的图形和场景,并具有不同的优点和局限性。
在实际应用中,我们可以根据具体情况选择合适的方法来计算阴影面积。
【重点突击】2020中考数学选填题型专项专题三 求阴影部分的面积

栏目索引
5.(2019郑州模拟)如图,在正方形ABCD中,AB=4,分别以B,C为圆心,AB长为半径
4π
画弧,则图中阴影部分的面积为 4 3- 3 .
解析 如图,连接BG,CG. ∵BG=BC=CG, ∴△BCG是等边三角形, ∴∠CBG=∠BCG=60°. ∵在正方形ABCD中,AB=4, ∴BC=4,∠BCD=90°, ∴∠DCG=30°, ∴S阴影=S扇形CDG-S弓形CG =S扇形CDG-(S扇形BCG-S△CBG)
= 30 π 22 - 1 ×(4-2 3 )×1
360 2
= π -2+ 3.
3
栏目索引
栏目索引
7.(2019河南一模)如图,在△ABC中,∠BAC=120°,AB=AC=4,现将△ABC绕点C顺 时针旋转60°得到△A'B'C,其中点B的运动路径为B︵B' ,点A的运动路径为A︵A' ,则图
16π
连接BC,则图中阴影部分的面积是 8 - 4 .
解析 如图,连接OC,过点C作CD⊥AB于点D,
︵
︵
∵BC =3 AC ,
∴∠BOC=135°,∠AOC=45°,
则CD=OC·sin∠AOC= 2 ,
2
∴S阴影=135π 12 -1 ×1× 2 =3π - 2 .
360 2 2 8 4
栏目索引
栏目索引
栏目索引
=
30 π
360
42
-
60 π
360
42
-
1 2
4
2
=4 3 - 4π .
3
栏目索引
栏目索引
6.(2019新乡一模)如图,在等腰三角形ABC中,AB=AC=2,∠B=75°,以点C为旋转 中心将△ABC顺时针旋转,当点B落在AB上的点D处时,点A的对应点为E,则图中
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学求阴影部分面积的几种常见方法
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
阴影部分面积的几种常见方法
在初中数学中,求阴影部分的面积问题是一个重要内容,在近年来的各地中考试题中屡见不鲜.这类试题大多数都是求不规则图形的面积,具有一定的难度,因此,正确把握求阴影部分面积问题的解题方法,显得尤为重要.本文举例介绍解决这类问题的常见方法.
一、直接求解法
例1如图1,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在
AB边上,AD变到AD
1位置,折痕为AE.再将△AED
1
以D
1
E为折痕,向右折叠,
AE变到A
1E位置,且A
1
E交BC于点F.求图中阴影部分的面积.
分析因为阴影部分是一个规则的几何图形Rt△CEF,故根据已知条件可以直接计算阴影部分面积.
解如图1,根据对称性可得
AD=AD
1=A
1
D
1
=6.
由已知条件易知:
EC=D
1
B=4,BC=6;
Rt△FBA
1
∽Rt△FCE.设FC为x,则FB=6-x.二、间接求解法
例2如图2,⊙O
1与⊙O
2
外切于点C,且两圆分别和直线l相切于A、B两
点,若⊙O
1半径为3cm;⊙O
2
半径为1cm,求阴影部分面积.
分析这是求一个不规则图形的面积,没有现成的面积公式,因此应采用间接的方法,设法转化为规则图形的面积的和或差去计算.
三、整体合并法
例3如图3,⊙A、⊙B、⊙C两两不相交,且半径都是0.5cm,求三个阴影部分面积之和.
分析所求的阴影部分面积是三个扇形面积之和,因为三个扇形圆心角度数不知道,所以无法单独求解,但仔细观察发现,三个扇形的圆心角分别是△ABC的三个内角,其和为180°,而扇形半径都相等,所以三个扇形能合并成一个半圆.于是问题获解.
解如图3,因为三个圆的半径相等,三个扇形圆心角之和是180°,所以其面积就是半圆面积.
四、等积变换法
例4如图4,A是半径为R的⊙O外一点,弦BC为3R,OA∥BC,求阴影部分
面积.
分析本题的阴影部分是不规则的图形,求其面积较困难,
但灵活运用等积变换,就可以把它的面积转化为扇形OBC的面
积,从而获解.
解连接OC,OB,
五、分割法
例5如图5,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,求阴影部分面积.
分析阴影部分图形不规则,不能直接求面积,可以把它分割成几个部分求面积的和.
解如图5,连接CD.
∵AC、BC是直径,
∴∠ADC=∠BDC=90°,
∴A、D、B三点共线.
设阴影部分面积被分割为S
1、S
2
、S
3
、S
4
四部分.
则
六、转化法
例6如图(1),大半圆O与小半圆O
1
相切于点C,大半圆的弦AB与小半圆相切于点F,且AB∥CD,AB=4cm,求阴影部分面积.
分析如果想直接求阴影部分面积,无法求解,因为它不是规则图形.但要采取转化思想,把小半圆平移到与大半圆的圆心重合的位置,作OE⊥AB于点E.连接OB,可知BE=2cm,阴影部分面积等于大半圆面积减去小半圆的面积.
解如图(2),将小半圆O
1
移至与大半圆圆心重合,作OE⊥AB于点E,则
BE=1
2
AB=2cm.
设大圆半径为R,小圆半径为x,在Rt△OEB中,有
七、割补法
例7如图7,点P(3a,a)是反比例函数y=12
x
与⊙O在第一象限内的一个交点,求阴影部分的面积.
分析阴影部分分两部分,难于逐一求解,但考虑反比例函数的对称性,结合割补原理,问题变得特别简单.
解如图7,把右上角的S
1部分分割下来,移到左下方补在S
3
处,与S
2
就组成了
一个扇形OAB.
易知:
∵P(3a,a)在反比例函数y=12
x
的图象上,
∴3a=12
a
.
解得:a1=2,a2=-2(舍去).
∴P坐标为(6,2).
连接OP,作PC⊥x轴于点C,得:
八、方程建模法
例8如图8,正方形边长为a,以每边为直径在正方形内画四个半圆,求阴影部分的面积.
分析本题直接求阴影部分面积较复杂,但观察图形特点引入方程的思想,问题变得非常简单.
解正方形由四个阴影花瓣和四个空白图形组成,如图8,设一个阴影花瓣面积为x,一个空白图形面积为y.
根据题意得:
因此阴影部分面积为.
2
2
2
a
a
π
-.。
