小学阴影部分面积计算方法归类
小学数学图形求阴影部分面积十大方法总结(附例题)

小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题,为了很好地帮助孩子系统地掌握小学阶段的数学知识,老师把小学求图形面积的十大方法给大家做了总结,各位家长,快给孩子收藏起来吧!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例题分析例1、如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2、如下图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF 的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米。
解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3、两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
小学“阴影面积计算”的数学策略和方法

小学“阴影面积计算”的数学策略和方法小学阴影面积计算的数学策略和方法如下:
1. 理解阴影的概念:阴影是指物体在阳光或光源下面被遮挡形
成的暗影部分。
在面积计算中,这部分面积也需要被计算进去。
2. 观察图形:首先要观察图形,了解图形的大小、形状、位置
等信息,并且根据题目中的要求标出重点,比如标记需要求的面积、已知面积或边长等。
3. 分析图形:认真分析图形的性质和特征,如果是复杂图形,
可以将其分解成简单图形,然后求出每个简单图形的阴影面积,最
后将它们加起来即可得到总的阴影面积。
4. 运用公式计算:面积计算常用的公式有正方形、矩形、三角形、圆等。
如果题目中已经给出了公式,则只需代入数值计算即可。
如果没有给出公式,可以根据题目中的信息自己推导出公式。
5. 记得转换单位:在计算阴影面积时,有可能需要将单位进行
转换。
比如,从厘米换算成米、从平方米换算成平方公分等。
转换
单位时,要注意保证计算的精度和正确性。
6. 检查计算结果:计算结束后,一定要仔细检查计算结果是否
正确,并且根据题目的要求进行单位转换,最后再把答案写在答题
纸上。
四种方法求阴影部分面积

四种方法求阴影部分面积首先,我们可以使用几何方法来求解阴影部分的面积。
设阴影部分的形状为矩形,其底边的长度为a,高度为h。
阴影的边界可以用两条直线来表示,设直线1与x轴的交点为A,直线2与x轴的交点为B。
两条直线与x轴的交点之间的距离为b。
则阴影部分的面积可以用以下公式表示:A=(a+b)*h/2第二种方法是通过将阴影部分分割成多个小矩形来求解。
首先,我们将阴影部分分割成n个小矩形,每个小矩形的底边长度为ai,高度为hi。
则阴影部分的面积可以表示为以下公式的和:A = ∑(ai * hi)其中i的范围从1到n。
第三种方法是使用积分来求解。
假设阴影部分的形状可以用函数y=f(x)来表示。
要求阴影部分的面积,我们需要找到函数f(x)的定义域上的积分区间[a,b]。
A = ∫[a, b] f(x) dx最后一种方法是使用统计学方法来求解。
假设我们已经获得了一组阴影部分的随机样本,符合一定的分布规律。
我们可以使用这组样本数据来进行统计分析,得出阴影部分的面积的估计值。
首先,我们可以计算出这组样本数据的平均值和标准差。
然后,使用均值加减一个标准差的方法,来计算阴影部分的上下边界。
根据阴影部分的上下边界和样本数据的分布,我们可以得到阴影部分面积的估计值。
需要注意的是,这种方法求得的阴影部分面积只是一个估计值,可能存在一定的误差。
综上所述,我们可以用几何法、分割法、积分法和统计法来求解阴影部分的面积。
每种方法都有自己的优缺点和适用范围,选择合适的方法取决于具体情况和问题要求。
小学数学图形求阴影部分面积十大方法情况总结(附例题)

小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题,为了很好地帮助孩子系统地掌握小学阶段的数学知识,老师把小学求图形面积的十大方法给大家做了总结,各位家长,快给孩子收藏起来吧!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例题分析例1、如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2、如下图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF 的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米。
解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3、两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
小学阴影部分面积计算方法归类
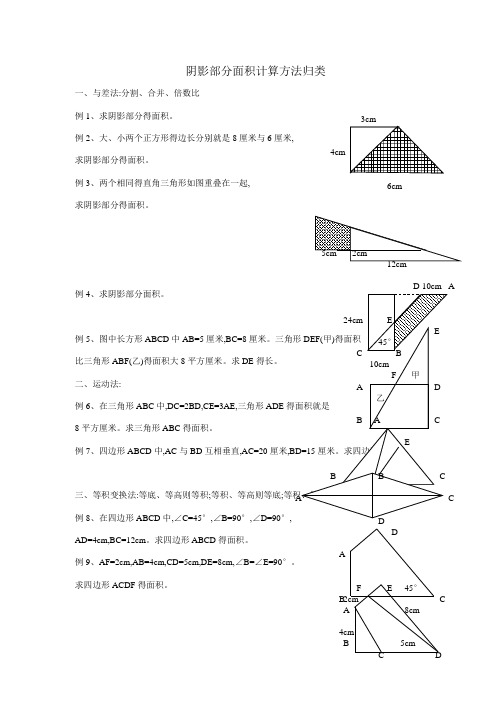
5cm阴影部分面积计算方法归类一、与差法:分割、合并、倍数比 例1、求阴影部分得面积。
例2、大、小两个正方形得边长分别就是8厘米与6厘米, 求阴影部分得面积。
例3、两个相同得直角三角形如图重叠在一起, 求阴影部分得面积。
例4、求阴影部分面积。
例5、图中长方形ABCD 中AB=5厘米,BC=8比三角形ABF(乙)得面积大8平方厘米。
求DE 得长。
二、运动法:例6、在三角形ABC 中,DC=2BD,CE=3AE,三角形ADE 8平方厘米。
求三角形ABC 得面积。
例7、四边形ABCD 中,AC 与BD 互相垂直,AC=20厘米三、等积变换法:等底、等高则等积;等积、等高则等底;例8、在四边形ABCD 中,∠C=45°,∠B=90°,∠D=90°, AD=4cm,BC=12cm 。
求四边形ABCD 得面积。
例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。
求四边形ACDF 得面积。
3cm4cm6cmAD 10cm 45°AB CDA BCDE F4cm 8cm2cm例10、已知大正方形比小正方形边长多2厘米,大正方形比小正方形得面积大10平方厘米。
求大、小正方形得面积各数多少平方厘米。
练习1、图中两个正方形得边长就是10厘米与7厘米, 求阴影部分得面积(如图)练习2、如下图,在三角形ABC 中,AD=BD,CE=3BE 。
若三角形BED 得面积 就是1平方厘米,则三角形ABC 得面积就是多少平方厘米?练习3、三角形ABC 就是直角三角形,阴影部分①得面积比阴影部分②得面积小28平方厘米、 AB 长40厘米, BC 长多少厘米、 练习4、在右图中(单位:厘米),两个阴影部分面积得与 就是 平方厘米、练习5、ABC 就是等腰直角三角形、 D 就是半圆周得中点, BC 就是半圆 得直径,已知:AB=BC=10,那么阴影部分得面积就是多少? 练习6、已知右图中大正方形边长就是6厘米,中间小正方形边长 就是4厘米、求阴影部分得面积、 练习7、右图中三角形就是等腰直角三角形, 阴影部分得面积就是 (平方厘米)、练习8、如右图,阴影部分得面积就是 、练习9、如图所求,圆得周长就是16、4厘米,圆得面积与长方形得面积正好相等、图中阴影部分得周长就是 厘米、练习10、ABC 就是等腰直角三角形、 D 就是半圆周得中点, BC 就是半圆得直径,已知: AB=BC=10,那么阴影部分得面积就是多少?练习11、在四边形ABCD 中,∠C=135°,∠D=90°。
小学数学图形求阴影部分面积十大方法总结(附例题)

小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题,为了很好地帮助孩子系统地掌握小学阶段的数学知识,老师把小学求图形面积的十大方法给大家做了总结,各位家长,快给孩子收藏起来吧!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例题分析例1、如下图,甲、乙两图形都是正方形,它们的边长分别是10 厘米和12 厘米. 求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2、如下图,正方形ABCD 的边长为 6 厘米,△ABE、△ADF 与四边形AECF 的面积彼此相等,求三角形AEF 的面积。
一句话:因为△ABE、△ADF 与四边形AECF 的面积彼此相等,都等于正方形ABCD 面积的三分之一,也就是12 厘米。
解:S△ABE=S △ADF=S 四边形AECF=12在△ABE 中,因为AB=6. 所以BE=4,同理DF=4,因此CE=CF=2 ,∴△ECF 的面积为2×2÷2=2 。
所以S△AEF=S 四边形AECF-S △ECF=12-2=10 (平方厘米)。
例3、两块等腰直角三角形的三角板,直角边分别是10 厘米和 6 厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S △BEF,S△ABG 和S△BEF 都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
4.微专题 三种方法求阴影部分面积
综合训练
1. 如图,在半径为4的⊙O 中,CD 是直径,AB是弦,且CD⊥AB,垂足为点E, ∠AOB=90°,则阴影部分的面积是___2_π____. 2. 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E.若∠AOC=60°,OC=2,则 阴影部分的面积是__2__- __2___3_c_m__2__.
针对训练 2. 如图,正方形ABCD的边长为4,以BC为直径的半圆O交对角线线BD于点E, 则阴影部分的面积为__8_-__π___.
第2题图
二、构造和差法 先设法将不规则阴影部分与空白部分组合或将阴影部分进行分割,构造规则图形, 再进行面积和差计算.如图:
针对训练 3. 如图,在扇形AOB 中,∠AOB=90°,正方形CDEF的顶点C是 »AB 的中点, 点D在OB上,点E在OB的延长线上.当正方形CDEF的边长为2 2 时,则图中 阴影部分的面积为_2_π__-__4__.第1题图第2题图
3. 如图,菱形ABCD的边长为2,∠A=60°,B»D是以点A为圆心,AB长为半径的 弧,C»D 是以点B为圆心,BC长为半径的弧,则阴影部分的面积为___3_____cm2. 4. 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4 2 ,O是AB的中点, 以O为圆心,线段OC的长为半径画圆心角为90°的扇形EOF,E¼F 经过点C,则阴 影部分的面积为__2_π_-__4__.
第3题图
第4题图
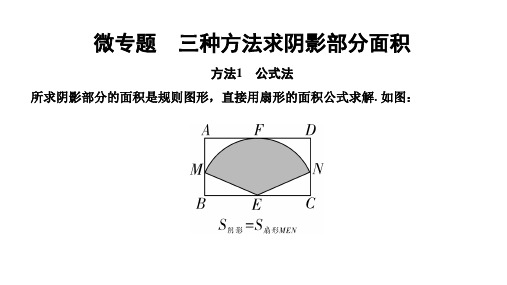
微专题 三种方法求阴影部分面积
方法1 公式法 所求阴影部分的面积是规则图形,直接用扇形的面积公式求解. 如图:
针对训练 1. 如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是 ___3_π____.
第1题图
小学数学图形求阴影部分面积十大方法总结(附例题)

小学数学图形求阴影部分面积十大方法总结(附例题)_2023.9小学阶段的学生通常在学习上存在着总结归纳能力欠缺等问题,为了很好地帮助孩子系统地掌握小学阶段的数学知识,老师把小学求图形面积的十大方法给大家做了总结,各位家长,快给孩子收藏起来吧!我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算。
如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例题分析例1、如下图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2、如下图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF 的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米。
解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3、两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决求面积十大方法01相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积02相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差. 例如:下图,求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阴影部分面积计算方法归类
一、和差法:分割、合并、倍数比
例1、求阴影部分的面积。
;
例2、大、小两个正方形的边长分别是8厘米和6厘米, 求阴影部分的面积。
例3、两个相同的直角三角形如图重叠在一起, 求阴影部分的面积。
例4、求阴影部分面积。
例5、图中长方形ABCD 中AB=5厘米,BC=8厘米。
三角形DEF (甲)的面积比三角形ABF (乙)的面积大8平方厘米。
求DE 的长。
3cm
4cm
6cm
/
2cm
12cm
甲
A
B
C
(
E
F
乙
A
D B
C 10cm 10cm
24cm
{
E
二、运动法:
$
例6、在三角形ABC 中,DC=2BD ,CE=3AE ,三角形ADE 的面积是 8平方厘米。
求三角形ABC 的面积。
(
例7、四边形ABCD 中,AC 和BD 互相垂直,AC=20厘米,BD=15厘米。
求四边形的面积。
三、等积变换法:等底、等高则等积;等积、等高则等底;等积、等底则等高。
例8、在四边形ABCD 中,∠C=45°,∠B=90°,∠D=90°, AD=4cm ,BC=12cm 。
求四边形ABCD 的面积。
&
例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。
A
B
C
D
A C
45°
A
B
C
D
5cm
求四边形ACDF 的面积。
例10、已知大正方形比小正方形边长多2厘米,大正方形比小正方形的面积大10平方厘米。
求大、小正方形的面积各数多少平方厘米。
、
练习1、图中两个正方形的边长是10厘米和7厘米, 求阴影部分的面积(如图)
练习2、如下图,在三角形ABC 中,AD=BD,CE=3BE 。
若三角形BED 的面积 是1平方厘米,则三角形ABC 的面积是多少平方厘米
<
练习3、三角形ABC 是直角三角形,阴影部分①的面积比阴影部分 ②的面积小28平方厘米. AB 长40厘米, BC 长多少厘米.
)
A
B C
D
《
F 4cm
8cm
2cm C
②
①
A
B
练习4、在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.
练习5、ABC是等腰直角三角形. D是半圆周的中点, BC是半圆
的直径,已知:AB=BC=10,那么阴影部分的面积是多少
练习6、已知右图中大正方形边长是6厘米,中间小正方形边长
是4厘米.求阴影部分的面积.
练习7、右图中三角形是等腰直角三角形,
阴影部分的面积是(平方厘米).
练习8、如右图,阴影部分的面积是.
练习9、如图所求,圆的周长是厘米,圆的面积与长方形的面积正好
12
15
20
A
10
,
C
B
21
相等.图中阴影部分的周长是 厘米.)14.3(=π
练习10、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知:
!
AB=BC=10,那么阴影部分的面积是多少
练习11、在四边形ABCD 中,∠C=135°,∠D=90°。
AD=5cm
BE=6cm 。
四边形ABCD 的面积是多少平方厘米
练习12、校园里有两块三角形空地,计划分别种上玫瑰和牡丹,玫瑰园和牡丹园一共占地多少平方米
方法归类
和差法:分割、合并、倍数比 运动法:
等积变换法:等底、等高则等积;等积、等高则等底;等积、等底则等高。
A 、
C
D
E 60。
