圆柱体侧、底、表面积计算公式及例题
圆柱、圆锥常用表格面积、体积公式

刘老师圆柱与圆锥圆柱的侧面积=底面圆周长×高字母表示:S侧=C底h 2.底面圆周长 =圆周率×直径 =圆周率×2×半径字母表示:C底=πd=2πr.3求圆柱的表面积三步:(1)圆柱的底面积 =S 底 =πr2=(πd÷2) 2=πd2÷4(2)圆柱侧面积 =S 侧 =h×C底(底面圆周长) =2πrh= πdh(3)圆柱表面积 =S 表 =S侧 +2S 底圆柱体积的公式圆柱的体积 =底面积×高字母表示:V柱=S底h圆锥体积的公式( 1)圆锥的体积等于与它等底等高圆柱体积的1/3V 锥 =V 柱÷3=S底 h÷3(2)已知圆锥底面积( S)和高( h),求体积的公式: V 锥 =S底 h÷3(3)已知圆锥体积( V)和高( h),求底面积的公式: S 底 =3V 锥÷h(4)已知圆锥体积( V)和底面积( S),求高的公式: h=3V 锥÷S底例题精讲圆柱、圆锥常用的表面积、体积公式立体图形表面积体积S圆柱侧面积个底面积2πrh 2 πr2V圆柱πr2h2 hr圆柱hr 圆锥S圆锥侧面积底面积n πl2πr2V圆锥体1πr2 h3603注: l 是母线,即从极点终究面圆上的线段长板块一圆柱与圆锥【例 1】如图,用高都是 1 米,底面半径分别为 1.5 米、1米和 0.5 米的 3 个圆柱组成一个物体.问这个物体的表面积是多少平方米( π取 )1111【例 2】有一个圆柱体的零件,高10 厘米,底面直径是 6 厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是 4 厘米,孔深 5 厘米(见右图).若是将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米)圆柱体的侧面张开,放平,是边长分别为10 厘米和12 厘米的长方形,那【例3】 (第四届希望杯 2 试一试题么这个圆柱体的体积是________立方厘米. (结果用π表示 )(接头处忽略不计),求这【例4】如右图,是一个长方形铁皮,利用图中的阴影部分,恰好能做成一个油桶个油桶的容积.( π )【牢固】如图,有一张长方形铁皮,剪以下图中两个圆及一块长方形,正好可以做成 1 个圆柱体,这个圆柱体的底面半径为10 厘米,那么本来长方形铁皮的面积是多少平方厘米( π 3.14 )10cm【例 5】把一个高是8 厘米的圆柱体,沿水平方向锯去 2 厘米后,剩下的圆柱体的表面积比本来的圆柱体表面积减少平方厘米.本来的圆柱体的体积是多少立方厘米【牢固】一个圆柱体底面周长和高相等.若是高缩短 4 厘米,表面积就减少平方厘米.求这个圆柱体的表面积是多少4cm【例 6】 (2008 年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大2008cm2,则这个圆柱体木棒的侧面积是 ________ cm2. ( π取 )第 2题【牢固】已知圆柱体的高是10 厘米,由底面圆心垂直切开,把圆柱分成相等的两半,表面积增加了40 平方厘米,求圆柱体的体积.( π3 )【例 7】一个圆柱体的体积是立方厘米,底面半径是 2 厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米( π )【例 8】右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.【例 9】输液 100 毫升,每分钟输 2.5 毫升.如图,请你观察第12 分钟时图中的数据,问:整个吊瓶的容积是多少毫升【例 10】(2008 年”希望杯” 五年级第 2 试 )一个拧紧瓶盖的瓶子里面装着一些水(如图 ),由图中的数据可推知瓶子的容积是_______ 立方厘米. ( π取 )10684( 单位:厘米)【牢固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为π立方厘米.当瓶子正放时,瓶内的酒精的液面高为 6 厘米;瓶子倒放时,空余部分的高为 2 厘米.问:瓶内酒精的体积是多少立方厘米合多少升26【牢固】一个酒瓶里面深30cm ,底面内直径是10cm ,瓶里酒深 15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深 25cm.酒瓶的容积是多少( π取 3)302515【牢固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(以以下图所示),请你依照图中注明的数据,计算瓶子的容积是______.7cm5cm4cm【牢固】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部圆柱体的底面直径和高都是12 厘米.其5 厘米,那么这个容器的容积是多少立方厘米( π 3 )5cm11cm【例 11】(第四届希望杯2)如,底面50 平方厘米的柱形容器中装有水,水面上飘扬着一棱 5 厘米的正方体木,木浮出水面的高度是 2 厘米.若将木沉着器中取出,水面将下降 ________厘米.2厘米【例12】有两个棱8厘米的正方体盒子, A 盒中放入直径8 厘米、高8 厘米的柱体一个,B 盒中放入直径 4 厘米、高8 厘米的柱体 4 个,在 A 盒注水,把 A 盒的水倒入 B 盒,使 B 盒也注水, A 盒余下的水是多少立方厘米【例 13】州来的傅擅做拉面,拉出的面条很很,他每次做拉面的步是的:将一个面先搓成柱形面棍, 1.6 米.尔后折,拉到 1.6 米;再折,拉到 1.6 米⋯⋯照此行下去,最后拉出的面条粗(直径 )有本来面棍的 1 .:最后傅拉出的些面条的64有多少米 (假傅拉面的程中.面条始保持粗平均的柱形,而且没有任何浪)【例14】一个柱形容器内放有一个方形.打开水往容器中灌水. 3 分水面恰好没方体的面.再18 分水灌容器.已知容器的高50 厘米,方体的高20 厘米,求方体底面面与容器底面面之比.【例 15】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深8 厘米.现将一个底面积是 16 平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米【牢固】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深 10 厘米.现将一个底面积是 16 平方厘米,高为12 厘米的长方体铁块竖放在水中后.现在水深多少厘米【牢固】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深 13 厘米.现将一个底面积是 16 平方厘米,高为12 厘米的长方体铁块竖放在水中后.现在水深多少厘米【例 16】一个圆柱形玻璃杯内盛有水,水面高 2.5 厘米,玻璃杯内侧的底面积是72 平方厘米.在这个杯中放进棱长 6 厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米【例 17】一个盛有水的圆柱形容器,底面内半径为 5 厘米,深20 厘米,水深15 厘米.今将一个底面半径为 2 厘米,高为17 厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米【例18】有甲、乙两只圆柱形玻璃杯,其内直径依次是淹没着一铁块,当取出此铁块后,甲杯中的水位下降了的水未外溢.问:这时乙杯中的水位上升了多少厘米10 厘米、 20 厘米,杯中盛有适合的水.甲杯中2 厘米;尔后将铁块淹没于乙杯,且乙杯中【牢固】有一只底面半径是20 厘米的圆柱形水桶,里面有一段半径是 5 厘米的圆柱体钢材浸在水中.钢材从水桶里取出后,桶里的水下降了 6 厘米.这段钢材有多长【例19】一个圆锥形容器高中,水面高多少厘米24 厘米,其中装满水,若是把这些水倒入和圆锥底面直径相等的圆柱形容器【例20】(2009 年”希望杯” 一试六年级)如图,圆锥形容器中装有水50 升,水面高度是圆锥高度的一半,这个容器最多能装水升.r1r2h12h【例 21】如图,甲、乙两容器相同,甲容器中水的高度是锥高的1 ,乙容器中水的高度是锥高的2 ,比33较甲、乙两容器,哪一只容器中盛的水多多的是少的的几倍乙甲【例22】(2008 年仁华考题 )如图,有一卷紧紧围绕在一起的塑料薄膜,薄膜的直径为直径为 8 厘米的卷轴,已知薄膜的厚度为0.04 厘米,则薄膜张开后的面积是20 厘米,中间有一平方米.20cm8cm100cm【牢固】图为一卷紧绕成的牛皮纸,纸卷直径为20 厘米,中间有素来径为 6 厘米的卷轴.已知纸的厚度为毫米,问:这卷纸张开后大体有多长【牢固】如图,厚度为0.25 毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50 厘米.这卷铜版纸的总长是多少米【例23】(人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10 厘米,侧面上的洞口是边长为 4 厘米的正方形,上下底面的洞口是直径为 4 厘米的圆,求此立体图形的表面积和体积.板块二旋转问题【例 24】如图,ABC是直角三角形,AB 、 AC 的长分别是 3 和 4.将ABC 绕 AC 旋转一周,求ABC 扫出的立体图形的体积.( π )CB A 【例 25】已知直角三角形的三条边长分别为3cm , 4cm , 5cm ,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米( π取 )【牢固】如图,直角三角形若是以BC 边为轴旋转一周,那么所形成的圆锥的体积为,以AC边为轴旋转16π一周,那么所形成的圆锥的体积为,那么若是以AB 为轴旋转一周,那么所形成的几何体的体积12π是多少BC A【例 26】如图,ABCD是矩形,BC6cm , AB10cm ,对角线 AC 、 BD 订交 O . E 、 F 分别是 AD 与BC 的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米 ( π取 3)A E DOB FC 【牢固】 (2006 年第十一届华杯赛决赛试题)如图,ABCD是矩形,BC6cm , AB10cm ,对角线 AC 、 BD圆柱、圆锥常用表格面积、体积公式订交 O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米A DOB C11 / 11。
圆柱体的认识与计算

圆柱体的认识与计算圆柱体是几何学中常见的一种立体图形,由一个圆形的底面和与底面平行的一条曲线(侧面)组成,形状类似于一个筒子。
在我们的日常生活中,圆柱体的应用非常广泛,比如瓶子、柱子、罐子等等,因此了解和计算圆柱体的相关知识具有重要的意义。
1. 圆柱体的定义与特性圆柱体是由两个平行且相等的圆面以及这两个圆面之间的侧面组成。
其中,两个圆面称为底面,侧面则是由底面上所有点与另一个底面上对应点垂直于底面的线段组成。
圆柱体的特性包括:- 圆柱体的底面是圆形,具有固定半径r;- 圆柱体的高度h是底面之间的距离,也是侧面的长度;- 圆柱体的体积V是指圆柱体所包围的三维空间大小;- 圆柱体的表面积S是指圆柱体外部所有面积的总和。
2. 圆柱体的计算公式圆柱体的计算主要涉及体积和表面积的计算。
下面是圆柱体的计算公式:- 圆柱体的体积V计算公式为:V = πr²h,其中π取近似值3.14;- 圆柱体的表面积S计算公式为:S = 2πr² + 2πrh。
3. 实际问题的圆柱体计算现在我们通过几个实际问题来应用圆柱体的计算公式。
例题1:某饮料瓶的底面半径为5厘米,高度为15厘米,求该瓶子的体积和表面积。
解答:根据公式,我们可以先计算出该瓶子的体积:V = πr²h = 3.14 × 5² × 15 ≈ 1178.5立方厘米然后,计算该瓶子的表面积:S = 2πr² + 2πrh = 2 × 3.14 × 5² + 2 × 3.14 × 5 × 15 ≈ 471平方厘米所以,该饮料瓶的体积约为1178.5立方厘米,表面积约为471平方厘米。
例题2:某水管的底面半径为8厘米,高度为25厘米,求该水管的体积和表面积。
解答:同样地,我们先计算该水管的体积:V = πr²h = 3.14 × 8² × 25 ≈ 5024立方厘米然后,计算该水管的表面积:S = 2πr² + 2πrh = 2 × 3.14 × 8² + 2 × 3.14 × 8 × 25 ≈ 1005.6平方厘米因此,该水管的体积约为5024立方厘米,表面积约为1005.6平方厘米。
圆柱、圆锥常用的表面积、体积公式

刘老师圆柱的侧面积=底面圆周长×高 字母表示:S 侧=C 底h 2. 底面圆周长=圆周率×直径=圆周率×2×半径 字母表示:C 底=πd=2πr 3. 求圆柱的表面积三步:(1)圆柱的底面积=S 底=πr²=π(d÷2)²=πd²÷4(2)圆柱侧面积=S 侧=h×C 底(底面圆周长)=2πrh=πdh (3)圆柱表面积=S 表=S 侧+2S 底圆柱体积的公式 圆柱的体积=底面积×高 字母表示:V 柱=S 底h 圆锥体积的公式(1) 圆锥的体积等于与它等底等高圆柱体积的1/3 V 锥=V 柱÷3=S 底h÷3 (2) 已知圆锥底面积(S )和高(h ),求体积的公式:V 锥=S 底h÷3 (3) 已知圆锥体积(V )和高(h ),求底面积的公式:S 底=3V 锥÷h (4) 已知圆锥体积(V )和底面积(S ),求高的公式:h=3V 锥÷S 底板块一 圆柱与圆锥【例 1】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5例题精讲圆柱与圆锥【例 2】有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【例 3】(第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【例 4】如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【例 5】把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【巩固】一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?【例 6】(2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大22008cm,则这个圆柱体木棒的侧面积是________2cm.(π取3.14)第2题【巩固】已知圆柱体的高是10厘米,由底面圆心垂直切开,把圆柱分成相等的两半,表面积增加了40平方厘米,求圆柱体的体积.(π3=)【例 7】一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【例 8】右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.【例 9】输液100毫升,每分钟输2.5毫升.如图,请你观察第12分钟时图中的数据,问:整个吊瓶的容积是多少毫升?【例 10】(2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)(单位:厘米)【巩固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?【巩固】一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)253015【巩固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是______.【巩固】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm【例 11】(第四届希望杯2试试题)如图,底面积为50平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为5厘米的正方体木块,木块浮出水面的高度是2厘米.若将木块从容器中取出,水面将下降________厘米.【例 12】有两个棱长为8厘米的正方体盒子,A盒中放入直径为8厘米、高为8厘米的圆柱体铁块一个,B盒中放入直径为4厘米、高为8厘米的圆柱体铁块4个,现在A盒注满水,把A盒的水倒入B盒,使B盒也注满水,问A盒余下的水是多少立方厘米?【例 13】兰州来的马师傅擅长做拉面,拉出的面条很细很细,他每次做拉面的步骤是这样的:将一个面团先搓成圆柱形面棍,长1.6米.然后对折,拉长到1.6米;再对折,拉长到1.6米……照此继续进行下去,最后拉出的面条粗细(直径)仅有原先面棍的164.问:最后马师傅拉出的这些细面条的总长有多少米?(假设马师傅拉面的过程中.面条始终保持为粗细均匀的圆柱形,而且没有任何浪费)【例 14】一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水灌满容器.已知容器的高为50厘米,长方体的高为20厘米,求长方体底面面积与容器底面面积之比.【例 15】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深8厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【巩固】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【巩固】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深13厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【例16】一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?【例17】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?【例18】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【巩固】有一只底面半径是20厘米的圆柱形水桶,里面有一段半径是5厘米的圆柱体钢材浸在水中.钢材从水桶里取出后,桶里的水下降了6厘米.这段钢材有多长?【例19】一个圆锥形容器高24厘米,其中装满水,如果把这些水倒入和圆锥底面直径相等的圆柱形容器中,水面高多少厘米?【例20】(2009年”希望杯”一试六年级)如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水升.【例21】如图,甲、乙两容器相同,甲容器中水的高度是锥高的13,乙容器中水的高度是锥高的23,比较甲、乙两容器,哪一只容器中盛的水多?多的是少的的几倍?甲乙【例 22】(2008年仁华考题)如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是平方米.【巩固】图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?【巩固】如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50厘米.这卷铜版纸的总长是多少米?【例23】(人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下底面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积.板块二旋转问题【例 24】如图,ABC是直角三角形,AB、AC的长分别是3和4.将ABC∆∆绕AC旋转一周,求ABC 扫出的立体图形的体积.(π 3.14=)CB A 【例 25】已知直角三角形的三条边长分别为3cm,4cm,5cm,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米?(π取3.14)【巩固】如图,直角三角形如果以BC边为轴旋转一周,那么所形成的圆锥的体积为16π,以AC边为轴旋转一周,那么所形成的圆锥的体积为12π,那么如果以AB为轴旋转一周,那么所形成的几何体的体积是多少?ABC【例 26】 如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .E 、F 分别是AD 与BC 的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)AB【巩固】(2006年第十一届华杯赛决赛试题)如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD相交O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?BA。
圆柱侧面积与表面积公式

圆柱侧面积与表面积公式
圆柱的侧面积是指圆柱体侧面的总面积,表面积是指整个圆柱体的表面总面积。
圆柱的侧面积公式为,周长乘以高,即2πrh,其中r为圆柱的底面半径,h为圆柱的高。
圆柱的表面积公式为,两个底面积加上侧面积,即2πr² + 2πrh,其中r为圆柱的底面半径,h为圆柱的高。
这两个公式是计算圆柱侧面积和表面积的基本公式,可以用于解决相关的计算和问题。
在实际问题中,这些公式可以帮助我们计算圆柱的侧面积和表面积,从而更好地理解和解决与圆柱相关的实际问题。
圆柱体侧底表面积计算公式及例题word精品
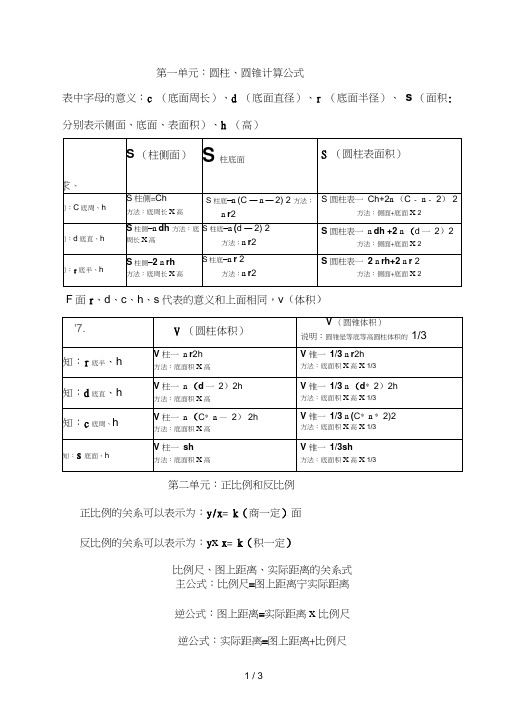
第一单元:圆柱、圆锥计算公式表中字母的意义:c (底面周长)、d (底面直径)、r (底面半径)、s (面积:分别表示侧面、底面、表面积)、h (高)v(体积)F面r、d、c、h、s代表的意义和上面相同,正比例的关系可以表示为:y/x= k(商一定)面反比例的关系可以表示为:y x x= k(积一定)比例尺、图上距离、实际距离的关系式主公式:比例尺=图上距离宁实际距离逆公式:图上距离=实际距离x比例尺逆公式:实际距离=图上距离+比例尺圆柱体的侧面、底面、表面积例题c周长d直径r半径s面积h高v体积1、一个圆柱形底面周长是6.28 厘米,高是5厘米,它的侧面、底面、表面各是多少平方厘米?①6. 28X 5 (公式:s = ch )②3 . 14X(6. 28- 3. 14 - 2)2 (公式:s = n r2 )③ 6 . 28 X 5 + 3. 14X(6 . 28 - 3. 14 - 2)2X 2 (公式:s = ch + n r2X 2)2、一个圆柱形底面直径是2 厘米,高是5厘米,它的侧面、底面、表面各是多少平方厘米?①3 . 14 X 2 X 5 (公式:s = ch )②3. 14 X(2 —2)2 (公式:s= n r2 )③3 . 14X 2X 5 + 3. 14 X(2 - 2)2X 2 (公式:s= ch +n r2 X 2)3、一个圆柱形底面半径是1 厘米,高是5 厘米,它的侧面、底面、表面各是多少平方厘米?①2 X 3. 14 X 1 X 5 (公式:s = ch )②3. 14 X 12 (公式:s= n r2 )③2 X 3. 14X 1 X 5 + 3. 14 X 12X 2 (公式:s = ch +n r2 X 2)圆柱体的体积、圆锥体的体积1、一个圆柱体的底面半径是3 厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?①3.14X 32X 10 (公式v= sh)②3.14X 32X 10X 1/3 (公式v= 1/3sh)2、一个圆柱体的底面直径是6 厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?①3. 14X(6-2)2X 10 (公式v= sh)②3. 14X(6- 2)2X 10 X 1/3 (公式v= 1/3sh)3、一个圆柱体的底面周长是18.84 厘米,高是10 厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?①3. 14(18. 84- 3. 14- 2)2X 10 (公式v= sh)②3. 14 X(18. 84- 3. 14 - 2)2X 10X 1/3 (公式v = 1/3sh)4、一个圆柱体的底面积是28.26 平方厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?① 28. 26 X 10 (公式v = sh)② 28 . 26 X 10 X 1/3 (公式v= 1/3sh)申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
圆柱公式知识点归纳总结

圆柱公式知识点归纳总结圆柱是几何学中的一个重要概念,是一个有两个平行且相等的底面、以及一个侧面由底面上的所有点到顶面的所有点都垂直于底面的点所组成的几何体。
而圆柱体的体积和表面积是我们在数学中经常需要计算的内容,下面就来对圆柱的相关公式进行归纳总结。
1. 圆柱的体积公式圆柱的体积是指圆柱内能够装下的空间容积,通常用V表示。
圆柱的体积公式为:V = πr²h其中,r为圆柱的底面半径,h为圆柱的高度。
2. 圆柱的侧面积公式圆柱的侧面积是指圆柱侧面的总表面积,通常用S表示。
圆柱的侧面积公式为:S = 2πrh其中,r为圆柱的底面半径,h为圆柱的高度。
3. 圆柱的表面积公式圆柱的表面积是指圆柱的所有表面(包括底面和侧面)的总面积,通常用S表示。
圆柱的表面积公式为:S = 2πr² + 2πrh其中,r为圆柱的底面半径,h为圆柱的高度。
4. 圆柱求体积的综合例题:若圆柱的底面半径为5cm,高度为10cm,则其体积为:V = πr²h= π×5²×10= 250π≈ 785.4cm³5. 圆柱求表面积的综合例题:若圆柱的底面半径为5cm,高度为10cm,则其表面积为:S = 2πr² + 2πrh= 2π×5² + 2π×5×10= 2π×25 + 2π×50= 50π + 100π= 150π≈ 471.2cm²另外,对于圆柱的相关计算还有一些特殊情况,比如当圆柱的侧面展开后呈矩形时,可以使用矩形的相关计算方法进行处理;当圆柱的底面或侧面不是圆或矩形时,需根据具体形状和条件来进行计算。
总之,圆柱的体积和表面积是我们在数学中常见的计算内容,掌握了圆柱的相关公式和计算方法,就能够轻松解决相关问题。
当然,对于更复杂的圆柱体积和表面积的计算,还需要灵活运用数学知识进行分析和解决。
圆柱侧面积和底面积的公式
圆柱侧面积和底面积的公式圆柱侧面积和底面积的公式是数学中常见的概念,我们可以通过这两个公式来计算圆柱的表面积和体积。
在这篇文章中,我们将深入探讨圆柱的侧面积和底面积的公式及其应用。
让我们来看看圆柱的底面积公式。
圆柱的底面是一个圆形,其面积可以通过圆的半径来计算。
底面积公式为:底面积= πr^2,其中r 表示圆柱底面的半径,π是一个固定的数值,约等于 3.14159。
通过这个公式,我们可以很容易地计算圆柱的底面积。
接下来,我们来讨论圆柱的侧面积公式。
圆柱的侧面是一个矩形,其面积可以通过圆周长和高度来计算。
侧面积公式为:侧面积= 周长× 高度,而圆周长可以通过圆的直径或半径乘以π来计算。
因此,侧面积也可以表示为侧面积= 2πrh,其中r表示圆柱的底面半径,h 表示圆柱的高度。
通过上述两个公式,我们可以计算出圆柱的表面积。
圆柱的表面积包括底面积和侧面积两部分,可以表示为表面积= 2πr(r + h),其中r表示底面半径,h表示圆柱的高度。
通过这个公式,我们可以很容易地计算出圆柱的表面积。
除了计算圆柱的表面积,底面积和侧面积的公式还可以在实际生活中的许多领域应用。
比如,在工程领域,我们可以通过这些公式来计算圆柱形的容器的容积,从而确定容器可以容纳的物体数量。
在建筑领域,我们可以通过这些公式来计算圆柱形的柱子的表面积,从而确定需要多少涂料来涂刷柱子。
总的来说,圆柱侧面积和底面积的公式是数学中非常重要的概念,通过这些公式我们可以计算圆柱的表面积和体积,并在实际生活中应用到各个领域。
希望通过这篇文章的介绍,读者能更加深入地了解圆柱的侧面积和底面积的公式及其应用。
圆柱体的侧面积计算
圆柱体的侧面积计算
圆柱体(Cylinder)是一种几何体,它由两个平行且相等的圆面以及连接两个圆面的侧面组成。
对于一个给定的圆柱体,我们可以通过一定的公式来计算其侧面积。
侧面积是指圆柱体的侧面的表面积,不包括两个圆面的面积。
为了计算圆柱体的侧面积,我们需要知道圆柱体的半径和高度。
下面是计算圆柱体侧面积的公式:
侧面积= 2 * π * 半径 * 高度
其中,π是圆周率,约等于3.14159。
半径是指圆柱体底面的半径,高度是指圆柱体两个底面之间的距离。
举个例子,假设我们要计算一个圆柱体的侧面积,该圆柱体的半径为5 cm,高度为10 cm。
我们可以使用上述公式进行计算:侧面积 = 2 * 3.14159 * 5 cm * 10 cm
= 314.159 cm²
因此,该圆柱体的侧面积为314.159平方厘米。
需要注意的是,在进行计算时,确保半径和高度的单位相同。
若半径和高度的单位不一致,需要将其转换为相同的单位后再进行计算。
此外,如果需要计算整个圆柱体的表面积,需要将侧面积加上两个圆面的面积。
圆面的面积计算公式为:
圆面的面积= π * 半径²
最后,希望通过上述公式和解释,你可以准确计算圆柱体的侧面积,提高对圆柱体的理解。
圆柱底面积公式怎么算
圆柱底面积公式怎么算圆柱的底面积是一个圆形.
那么圆柱的底面积公式就是圆形的计算公式.
已知底面直径求底面积:(直径÷2)²×3.14
已知底面半径求底面积:半径²×3.14
a²=a×a
扩展资料:
1.圆柱体的两个圆形面称为底面,周围的面称为侧面。
圆
柱体由两个底面和一个侧面组成。
2.圆柱体的两个底面是两个相同的圆形表面。
两个底面之间的距离就是圆柱体的高度。
3.圆柱体的侧面是曲面,圆柱体的侧面展开图是长方形、正方形或平行四边形(斜切)。
圆柱的侧面积=底面周长x高,即:
S侧面积=Ch=2πrh
底面周长C=2πr=πd
圆柱的表面积=侧面积+底面积x2=Ch+2πr^2=2πr(r+h)
4.圆柱的体积=底面积x高
即 V=S底面积×h=(π×r×r)h
5.等底等高的圆柱的体积是圆锥的3倍
6.圆柱体可以用一个平行四边形围成
7.圆柱的表面积=侧面积+底面积x2
8.把圆柱沿底面直径分成两个同样的部分,每一个部分叫半圆柱。
这时与原来的圆柱比较,表面积=πr(r+h)+2rh、体积是原来的一半。
9.圆柱的轴截面是直径x高的长方形,横截面是与底面相同的圆。
圆柱侧面积和底面积的公式
圆柱侧面积和底面积的公式圆柱是一种常见的几何体,由一个圆形的底面和一个平行于底面的侧面组成。
在学习圆柱的相关知识时,我们经常会涉及到圆柱的侧面积和底面积的计算公式。
下面将详细介绍这两个公式以及它们的应用。
我们来看一下圆柱的底面积。
圆柱的底面是一个圆形,其面积可以通过圆的半径来计算。
假设圆的半径为r,那么圆的面积就是πr²,其中π是一个常数,约等于3.14。
所以圆柱的底面积就是两个圆的面积之和,即2πr²。
接下来,我们来讨论圆柱的侧面积。
圆柱的侧面是一个矩形,其长度等于圆的周长,宽度等于圆柱的高度。
圆的周长可以通过圆的直径乘以π来计算,即2πr。
所以圆柱的侧面积就是矩形的周长乘以矩形的宽度,即2πrh,其中h表示圆柱的高度。
现在我们已经了解了圆柱的底面积和侧面积的计算公式,接下来我们来看一些实际应用。
我们可以通过底面积和侧面积的公式来计算圆柱的表面积。
圆柱的表面积等于底面积和侧面积之和。
所以圆柱的表面积就是2πr² + 2πrh,或者可以简化为2πr(r+h)。
我们可以通过圆柱的底面积和高度来计算体积。
圆柱的体积就是底面积乘以高度。
所以圆柱的体积就是πr²h。
圆柱的底面积和侧面积的公式也可以应用到实际生活中的问题中。
比如,如果我们知道一个圆柱的底面积和侧面积,可以通过这些信息来计算圆柱的高度。
同样地,如果我们知道一个圆柱的底面积和高度,可以通过这些信息来计算圆柱的侧面积。
除了上述的应用,圆柱的底面积和侧面积的公式还可以在建筑、制造业、物流等领域得到广泛应用。
比如,在建筑设计中,设计师需要计算圆柱形的柱子或者管道的表面积和体积,以确定所需材料的数量和成本。
在制造业中,工程师需要计算圆柱形的零件的底面积和侧面积,以确定机器加工的参数和工艺。
在物流领域,运输公司需要计算圆柱形的容器的底面积和侧面积,以确定货物的最佳装载方式和容量。
圆柱的侧面积和底面积的公式是2πr²和2πrh。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一单元:圆柱、圆锥计算公式
第二单元:正比例和反比例
正比例的关系可以表示为:y/x=k(商一定)面
反比例的关系可以表示为:y×x=k(积一定)
比例尺、图上距离、实际距离的关系式
主公式:比例尺=图上距离÷实际距离
逆公式:图上距离=实际距离×比例尺
逆公式:实际距离=图上距离÷比例尺
圆柱体的侧面、底面、表面积例题c周长d直径r半径s面积h高v体积
1、一个圆柱形底面周长是6.28厘米,高是5厘米,它的侧面、底面、表面各是多少平方厘米?
①6.28×5(公式:s=ch ) ②3.14×(6.28÷3.14÷2)²(公式:s=πr²)
③6.28×5+3.14×(6.28÷3.14÷2)²×2 (公式:s=ch+πr²×2)
2、一个圆柱形底面直径是2厘米,高是5厘米,它的侧面、底面、表面各是多少平方厘米?
①3.14×2×5(公式:s=ch ) ②3.14×(2÷2)²(公式:s=πr²)
③3.14×2×5+3.14×(2÷2)²×2 (公式:s=ch+πr²×2)
3、一个圆柱形底面半径是1厘米,高是5厘米,它的侧面、底面、表面各是多少平方厘米?
①2×3.14×1×5(公式:s=ch ) ②3.14×1²(公式:s=πr²)③2×3.14×1×5+3.14×1²×2 (公式:s=ch+πr²×2)
圆柱体的体积、圆锥体的体积
1、一个圆柱体的底面半径是3厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?
①3.14×3²×10 ( 公式v=sh)
②3.14×3²×10×1/3(公式v=1/3sh)
2、一个圆柱体的底面直径是6厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?
①3.14×(6÷2)²×10( 公式v=sh)
②3.14×(6÷2)²×10×1/3 (公式v=1/3sh)
3、一个圆柱体的底面周长是18.84厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?
①3.14×(18.84÷3.14÷2)²×10( 公式v=sh)
②3.14×(18.84÷3.14÷2)²×10×1/3 (公式v=1/3sh)
4、一个圆柱体的底面积是28.26平方厘米,高是10厘米,这个圆柱体的体积是多少立方厘米?与它等底等高的圆锥体的体积是多少立方厘米?
①28.26×10( 公式v=sh)②28.26×10×1/3 (公式v=1/3sh)。
