《运筹学》第3章习题
《运筹学教程》第三章习题答案

《运筹学教程》第三章习题答案1.影子价格是根据资源在生产中作出的贡献而做的估价。
它是一种边际价格,其值相当于在资源得到最有效利用的生产条件下,资源每变化一个单位时目标函数的增量变化。
又称效率价格。
影子价格是指社会处于某种最优状态下,能够反映社会劳动消耗、资源稀缺程度和最终产品需求状况的价格,是社会对货物真实价值的度量。
只有在完善的市场条件下才会出现,然而这种完善的市场条件是不存在的,因此现成的影子价格也是不存在的。
市场价格是物品和服务在市场上销售的实际价格,是由供求关系决定的。
2.证明:当原问题约束条件右端变为b i′时,原问题变为: maxz=∑C i X js.t. ∑a ij X i≤b i′(i=1,2,3,……,m)X j≥0 (j=1,2,3,……,n)对偶问题为: minp=∑b i′y is.t. ∑a ij y i≥C iy i≥0(i=1,2,3,……,m) (j=1,2,3,……,n) 设,当b i变为b i′原问题有最优解(X1′X2′X3′……X n-1′X n′)时,对偶问题的最优解为(y1′y2′y3′……y n-1′y n′),则有:又因为当原问题有最优解时,对偶问题也有最优解,且相等,则有:所以3(1).minp=6y1 + 2y2s.t. -y1+2y2≥-33y1+3y2≥4y1,y2≥0(2)解:令X2=X2′-X2〞,X4= X4′-X4〞,X2′,X2〞,X4′,X4〞≥0 ,原式化为:maxz=2X1 +2X2′-2X2〞-5X3 +2X4′-2X4〞s.t. 2X1 -X2′+X2〞+3X3 +3X4′-3X4〞≤-5-2X1 +X2′-X2〞-3X3 -3X4′+3X4〞≤5-6X1 -5X2′+5X2〞+X3 -5X4′+5X4〞≤-610X1 -9X2′+9X2〞+6X3 +4X4′-4X4〞≤12X1, X2′,X2〞,X3, X4′,X4〞≥0则对偶规划为:.minp= -5y1′+ 5y1〞-6y2 + 12y3s.t. 2y1′-2y1〞-6y2 + 10y3≥2-y1′+y1〞-5y2 -9y3≥2y1′-y1〞+5y2 + 9y3≥-23y1′-3y1〞+y2 + 6y3≥-53y1′-3y1〞-5y2 + 4y3≥2-3y1′+3y1〞+5y2 -4y3≥-2即:minp= -5y1′+ 5y1〞-6y2 + 12y3s.t. 2y1′-2y1〞-6y2 + 10y3≥2-y1′+y1〞-5y2 -9y3=23y1′-3y1〞+y2 + 6y3≥-53y1′-3y1〞+5y2 + 4y3=2令 y1〞- y1′= y1,得:minp= 5y1 -6y2 + 12y3s.t. -2y1-6y2 + 10y3≥2y1-5y2 -9y3=2-3y1+y2 + 6y3≥-5-3y1-5y2 + 4y3=24、试用对偶理论讨论下列原问题与他们的对偶问题是否有最优解。
《运筹学》课后习题答案 第3章 运输问题

一、选择题1. 2. 3. 4. 5. 6. 7.二、判断题1. 2. 3. 4. 5. 6. 7. 8. 9.三、表上作业法 3. 解:可知,有初始基本可行解1112132122230,10,20,10,35,0x x x x x x ======用闭回路法计算非基变量的检验数:1123(56)(84)10(98)(67)40σσ=+-+=-<=+-+=>因为110σ<,该解并不是最优解。
进行换基迭代,让11x 进基,考虑上述闭回路,调整量min(10,10)10θ==,调整后得到新的调运方案:A2 4 0645945销量10 45 20计算非基变量的检验数得:1223(84)(56)10(95)(47)30σσ=+-+=>=+-+=>故此方案为最优方案,最优解为:11121321222310,0,20,0,45,0x x x x x x ======最优值min 105207456460Z =⨯+⨯+⨯=用电子表格模型求解进行验算:4. 解:用西北角法求得初始基本可行解:1112131421222324313233344,0,0,0;1,2,4,2;0,0,0,4;x x x x x x x x x x x x ============ 用位势法计算检验数:1111212121131322214142233131324323243433333106()210167()861012()9455()12194()731010()47u u v u v v u v u v u u v u v v u v u v v u v u v v u v u v u σσσσσσ=⎧+==-+=⎧⎧⎪=⎪⎪⎪+==-+=⎪⎪⎪=⎪⎪++=-+=⎪⎪⇒=⇒⎨⎨⎨+==-+=-⎪⎪=-⎪⎪+==-+=-=⎪⎪+==-+=⎪⎪⎩=⎩⎪⎪⎪⎪⎪⎩因为3132,σσ小于0,该解不是最优解。
运筹学(机械工业出版社)教材习题答案(第一章-第三章)

教材习题答案部分有图形的答案附在各章PPT文档的后面,请留意。
第1章线性规划第2章线性规划的对偶理论第3章整数规划第4章目标规划第5章运输与指派问题第6章网络模型第7章网络计划第8章动态规划第9章排队论第10章存储论第11章决策论第12章对策论习题一1.1 讨论下列问题:(1)在例1.1中,假定企业一周内工作5天,每天8小时,企业设备A有5台,利用率为0.8,设备B有7台,利用率为0.85,其它条件不变,数学模型怎样变化.(2)在例1.2中,如果设x j(j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.(3)在例1.3中,能否将约束条件改为等式;如果要求余料最少,数学模型如何变化;简述板材下料的思路.(4)在例1.4中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.(5)在例1.6中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,模型如何变化.1.2 工厂每月生产A、B、C三种产品,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-22所示.310和130.试建立该问题的数学模型,使每月利润最大.【解】设x1、x2、x3分别为产品A、B、C的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.3 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:【解】设x j (j =1,2,…,14)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为14112342567891036891112132347910121314min 2300322450232400232346000,1,2,,14jj j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩∑ 用单纯形法求解得到两个基本最优解X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 (2)余料最少数学模型为134131412342567891036891112132347910121314min 0.60.30.70.40.82300322450232400232346000,1,2,,14j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩ 用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料650根 显然用料最少的方案最优。
运筹学(胡运权版)第三章运输问题课后习题答案
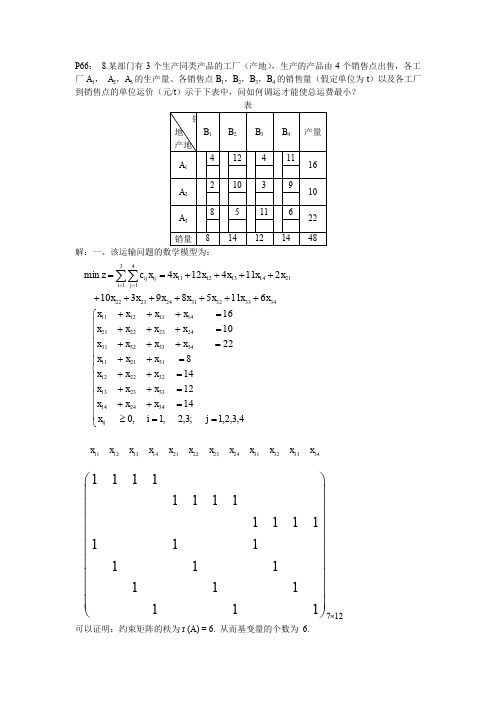
P66: 8.某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点出售,各工厂A 1, A 2,A 3的生产量、各销售点B 1,B 2,B 3,B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中,问如何调运才能使总运费最小?表解:一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想:优先满足运价(或运距)最小的供销业务。
其余(非基)变量全等于零。
此解满足所有约束条件,且基变量(非零变量)的个数为6(等于m+n-1=3+4-1=6).总运费为(目标函数值) ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔(Vogel)法伏格尔法的基本思想:运输表中各行各列的最小运价与次小运价之差值(罚数)应尽可能地小。
或者说:优先供应罚数最大行(或列)中最小运费的方格,以避免将运量分配到该行(或该列)次小运距的方格中。
运筹学:第3-4章后答案

第P命散线性規划I•设A. B产品的生产域0别为斗M •该何J8的数学M为,max Z s c l x l-¥c2x2 sj. a li x l +硼七£b、OjiX, .%无£g5X代小Sb、x,纠心2忍•为於数2.«0-l敛皿叽衣示」插派鉤i个人完成第j项任务x< = 'o.不描诫第i个人完成瀟项任务RttrHSV 为,■ ■min A工工讥■$」・工% =丨< = 1.2•・・・•n: 何■工斗=1 / = l,X..../t齐=0或1・为協数h 7 = 1.2・・•・・n3•吋仃解集介为{(4.0代(5・0)=6.0代(7・0)「・(8・0/.(5・1)『・(6」)『}・Mft*^ = (5J)r. 垃优tfl为剖半面Mu 51•求出松胞何建的峨优尬纯形黑如卜检工人勺・/• 乂||打“+》仇勺=勺•网式mwfj:5•计明:山329式闪刘:$ =》几勺-/;w内+® =工(人■呻®-(力-b〃・Xf由j 所以令*0 = TbM广T%J・结论成“•第四章2•设产A 1:产耐产.MB生产壬(Fim). 为:Jft优解为彳=—.x»・6 123.<1)«M**4优解为x^ = (!.2)r.対优ffl为/(x*) = -|:(2)於休垃优第为L M(0・2)「・域优(Tl为/(L2-2:⑶©体巖优解为卅・(2丄八協优们为/X)■右2 2 24•捉也必耍性,一次欣数/a)= *FAx + bU + c•的HzcG阵为A・故山定理4.2.4 nJ 知・肖A为正定矩阵时.二次崗敷为严格卄函效:充分山曲丁二次fifi数览产格凸函数・则山址歼4.2・3呵如:5.<1) 的;”诳册阵.故此帝8[为严格凸函8(.<2)rf«airjHesM:fl-w| ~2 0]为ftiirwR・故此厲救为严格MVI.{ 0 -10丿2 0 0'(3)rfitt的Hbw购阵0 6 0为IF定卸外・故此恳数为严格“恳救.<0 0 18.6.UHU1改r为fFj&nJtfM・对満足条fl的二°・対任盘正玫£・1+£严为吋行解・因为A(x^e:°)^Ax°^eAz0ib. ILihJ g/(x)为可版小函数.M VQQrOYfxaOMT-rWVgto + Twf"©。
管理运筹学(第四版)第三章习题答案

3.1(1)解:, 53351042..715min 212112121≥≥+≥≥++=y y y y y y y t s y y ω(2)解:无限制32132131323213121,0,0 2520474235323..86max y y y y y y y y y y y y y y y t s y y ≤≥=++≤-=+≥+--≤++=ω3.4解:例3原问题6,,1,0603020506070..min 166554433221654321 =≥≥+≥+≥+≥+≥+≥++++++=j x x x x x x x x x x x x x t s x x x x x x z j对偶问题:6,,1,0111111..603020506070max 655443322161654321 =≥≤+≤+≤+≤+≤+≤++++++=j y y y x y y y y y y y y y t s y y y y y y j ω3.5解:(1)由最优单纯形表可以知道原问题求max ,其初始基变量为54,x x ,最优基的逆阵为⎪⎪⎪⎪⎭⎫ ⎝⎛-=-31610211B 。
由P32式(2.16)(2.17)(2.18)可知b B b 1-=',5,,1,,1 ='-=='-j P C c P B P j B j j j j σ,其中b 和j P 都是初始数据。
设⎪⎪⎭⎫ ⎝⎛=21b b b ,5,,1,21 =⎪⎪⎭⎫⎝⎛=j a a P j j j ,()321,,c c c C =,则⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-⇒='-25253161021211b b b B b ,即⎪⎩⎪⎨⎧=+-=2531612521211b b b ,解得⎩⎨⎧==10521b b ⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-⇒='-0211121031610212322211312111a a a a a a P B P j j ,即 ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=+-=-=+-==+-=03161121213161212113161021231313221212211111a a a a a a a a a ,解得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-====121130231322122111a a a a a a()()()⎪⎪⎪⎪⎭⎫⎝⎛---=---⇒'-=31612102121,0,0,2,4,4132c c c P C c j B j j σ,即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=+--=+-2314612142121113132c c c c c c ,解得⎪⎩⎪⎨⎧==-=6102132c c c所以原问题为:,, 10352..1026max 32132132321≥≤+-≤++-=x x x x x x x x t s x x x z 对偶问题为:, 102263..105min 212121221≥≥+-≥-≥+=y y y y y y y t s y y ω(2)由于对偶问题的最优解为()()()2,4,,5454*=-=-=σσσc c C Y IB IB3.6解:(1)因为3x 的检验数0353≤⨯-c ,所以3c 的可变范围是153≤c 。
(典型例题)《运筹学》运输问题

xj0,yij0,zij0,(i=1,┈,4;j=1,┈,5)
2008/11
--22--
--《Ⅵ 产量
新购 1 第一天 M 第二天 M 第三天 M
第四天 M
1 1 1 1 0 5200
0.2 0.1 0.1 0.1 0 1000
2008/11
--21--
建立模型:
--《运筹学》 运输问题--
设 xj—第j天使用新毛巾的数量;yij—第i天送第j天使用快洗 餐巾的数量;zij—第i天送第j天使用慢洗餐巾的数量;
Min z=∑xj+∑∑0.2yij+∑∑0.1zij
第一天:x1=1000
需 第二天:x2+y12=700
求 约
m1
xij b j (j 1,2,...,n)
i1
x 0 (i 1,...,m,m 1; j 1,...,n) ij
2008/11
--16--
--《运筹学》 运输问题--
销>产问题单位运价表
产地销地 B1 B2 ┈
A1
C11 C12 ┈
A2
C21 C22 ┈
┊ ┆┊┈
Am Cm1 Cm2 ┈
2008/11
--8--
产销平衡表
--《运筹学》 运输问题--
单位运价表
B1 B2 B3 B4 产量
A1 (1) (2) 4 3 7 A2 3 (1) 1 (-1) 4 A3 (10) 6 (12) 3 9 销量 3 6 5 6
B1 B2 B3 B4 A1 3 11 3 10 A2 1 9 2 8 A3 7 4 10 5
Ⅰ Ⅱ
示。又如果生产出来的柴
Ⅲ
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章:引论1.1 课后习题习题1a)运筹学是一门应用数学的学科,旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域,如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划,优化供应链管理,提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题,优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域,如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中,可以使用运筹学方法优化仓储和运输的布局,提高货物的运输效率。
在生产计划中,可以使用运筹学方法优化产品的生产数量和生产周期,降低生产成本。
在供应链管理中,可以使用运筹学方法优化订单配送和库存管理,提高供应链的效率。
在流程优化中,可以使用运筹学方法优化业务流程,提高整体效率。
习题2在物流管理中,可以使用运筹学方法优化车辆的调度和路线规划,以提高运输效率和降低成本。
在生产计划中,可以使用运筹学方法优化生产线的安排和产品的生产量,以降低生产成本和提高产能利用率。
在供应链管理中,可以使用运筹学方法优化供应链各个环节的协调和调度,以提高整体效率和减少库存成本。
在流程优化中,可以使用运筹学方法优化业务流程的排布和资源的分配,以提高流程效率和客户满意度。
第二章:线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法,用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为:max c^T*xs.t. Ax <= bx >= 0其中,c是目标函数的系数向量,x是决策变量向量,A是约束矩阵,b是约束向量。
习题2使用线性规划方法可以解决许多实际问题,如生产计划、供应链管理、资源分配等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章线性规划对偶理论与灵敏度分析习题
一、 思考题
1. 对偶问题和对偶变量的经济意义是什么
2.简述对偶单纯形法的计算步骤。
它与单纯形法的异同之处是什么
3.什么是资源的影子价格它和相应的市场价格之间有什么区别
4.如何根据原问题和对偶问题之间的对应关系,找出两个问题变量之间、解及检 验数之间的关系
5.利用对偶单纯形法计算时,如何判断原问题有最优解或无可行解
6.在线性规划的最优单纯形表中,松弛变量(或剩余变量)0>+k
n x ,其经济意 义是什么
7.在线性规划的最优单纯形表中,松弛变量k n x +的检验数0>+k
n σ(标准形为 求最小值),其经济意义是什么
8.将i j j i b c a ,,的变化直接反映到最优单纯形表中,表中原问题和对偶问题的解 将会出现什么变化有多少种不同情况如何去处理
二、 判断下列说法是否正确
1.任何线性规划问题都存在且有唯一的对偶问题。
2.对偶问题的对偶问题一定是原问题。
3.若线性规划的原问题和其对偶问题都有最优解,则最优解一定相等。
4.对于线性规划的原问题和其对偶问题,若其中一个有最优解,另一个也一定 有最优解。
5.若线性规划的原问题有无穷多个最优解时,其对偶问题也有无穷多个最优解。
6.已知在线性规划的对偶问题的最优解中,对偶变量0>*i
y ,说明在最优生产计 划中,第i 种资源已经完全用尽。
7.已知在线性规划的对偶问题的最优解中,对偶变量0=*i
y ,说明在最优生产计 划中,第i 种资源一定还有剩余。
8.对于i j j i b c a ,,来说,每一个都有有限的变化范围,当其改变超出了这个范围 之后,线性规划的最优解就会发生变化。
9.若某种资源的影子价格为u ,则在其它资源数量不变的情况下,该资源增加k 个单位,相应的目标函数值增加 u k 。
10.应用对偶单纯形法计算时,若单纯形表中某一基变量0<i
x ,且i x 所在行的
所有元素都大于或等于零,则其对偶问题具有无界解。
三、 写出下列线性规划的对偶问题
(1)32123max x x x Z ++= (2)4321322max x x x x z +++=
⎪⎪⎩⎪⎪⎨⎧≥≤++≤-+≤++0,,92372452321321321321x x x x x x x x x x x x ; ⎪⎪⎩⎪⎪⎨⎧≥≥+--=+-≤+++无约束
4321431
3214321,,0,313212x x x x x x x x x x x x x x ; (3)32132min x x x z --= (4)3212min x x x z ++=
⎪⎪⎩⎪⎪⎨⎧≥=++-≥--≤+-无约束321321321321,0,1042742523x x x x x x x x x x x x ; ⎪⎪⎩⎪⎪⎨⎧≥≥-+-=--≤++无约束
321321321321,0,3
453532722x x x x x x x x x x x x ;
(5)321347max x x x z +-= (6)321345min x x x z +-=
⎪⎪⎩⎪⎪⎨⎧≤≥=+≥--≤-+无约束23132321221,0,030351546324624x x x x x x x x x x x ; ⎪⎪⎩⎪⎪⎨⎧≥=+≤-+≥+无约束
1323232131,0,306415458872x x x x x x x x x x 。
四、 用对偶单纯形法求解下列线性规划问题
(1)32123min x x x Z ++= (2)321422max x x x z ++=
⎪⎪⎩⎪⎪⎨⎧≥≥-≥-≤++0
,,3463213231321x x x x x x x x x x ; ⎪⎪⎩⎪⎪⎨⎧≥≤++≤++≥++0,,5643732532321321321321x x x x x x x x x x x x ; (3)43211216812min x x x x z +++= (4)321425min x x x z ++=
⎪⎩⎪⎨⎧≥≥++≥++0,,,34222424321421321x x x x x x x x x x ; ⎪⎩⎪⎨⎧≥≥++≥++0,,125367233
21321421x x x x x x x x x ;
五、 对下列问题求最优解、相应的影子价格及保持最优解不变时j c 与i b 的变化范围。
(1)1213max x x x z ++= (2)4211935089max x x x z x +++= ⎪⎩⎪⎨⎧≥≤++≤++0,,3232223
21321321x x x x x x x x x ;
⎪⎩⎪⎨⎧≥≤+≤+++0,,,6418410234321434321x x x x x x x x x x ; (3)32134max x x x z ++= (4)432181026max x x x x z +++=
⎪⎩⎪⎨⎧≥≤++≤++0,,622422*********x x x x x x x x x ; ⎪⎪⎩⎪⎪⎨⎧≥≤++-≤++-≤--+0
,,,103242582332044654321432143214321x x x x x x x x x x x x x x x x . 六、 已知下表(表3—1)为求解某线性规划问题的最终单纯形表,表中54,x x 为松弛变量,问题的约束为 形式
表 3—1
1x 2x 3x 4x 5x
3x 5/2 0
1/2 1 1/2
0 1x 5/2 1 -1/2 0 -1/6 1/3
j j z c - 0 -4 0 -4 -2
(1) 写出原线性规划问题;
(2) 写出原问题的对偶问题;
(3) 直接由表3—1写出对偶问题的最优解。
七、 某厂利用原料A、B生产甲、乙、丙三种产品,已知生产单位产品所需原料数、单件利润及有关数据如表1—4所示,分别回答下列问题:
甲 乙 丙 原料拥有量
A B 6 3 3 4 5 5 45
30
单件利润 4 1 5
(1)建立线性规划模型,求该厂获利最大的生产计划;
(2)若产品乙、丙的单件利润不变,产品甲的利润在什么范围变化,上述最优解不变
(3)若有一种新产品丁,其原料消耗定额:A为3单位,B为2单位,单件利润为2.5单位.问该种产品是否值得安排生产,并求新的最优计划;
(4)若原材料A市场紧缺,除拥有量外一时无法购进,而原材料B如数量不足可去市场购买,单价为0.5,问该厂应否购买,以够劲多少为宜(5)由于某种原因该厂决定暂停甲产品的生产,试重新确定该厂的最优生产计划.
八、某厂生产甲、乙、丙三种产品,分别经过A、B、C三种设备加工。
已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润见表3—4。
甲乙丙设备能力(台时)
ABC
1
10
2
1
4
2
1
5
6
100
600
300
单位产品利润(元)1064
(1)建立线性规划模型,求该厂获利最大的生产计划;
(2)产品丙每件的利润增加到多大时才值得安排生产如产品丙每件的利润增加到50/6 ,求最优生产计划。
(4)产品甲的利润在多大范围内变化时,原最优计划保持不变
(5)设备A的能力如为100+10,确定保持原最优基不变的的变化范围。
(6)如有一种新产品丁,加工一件需设备A、B、C的台时各为1、4、3小时,预期每件的利润为8元,是否值得安排生产
(7)如合同规定该厂至少生产10件产品丙,试确定最优计划的变化。
