8.2非齐次振动方程和输运方程
非齐次振动方程和输运方程
ut a 2u xx f ( x，t ) u x (0，t ) u x (l，t ) 0 u ( x， 0) 0
(2)化为
(3)按原先方法求解, 只需将t换成 t ； t ( 4) u( x，t ) v( x，t； )d
vt a 2 vxx 0 vx (0，t ) vx (l，t ) 0 v( x， ) f ( x， )
§8.2 非齐次振动方程和输运方程
(齐次边界条件) 一、傅里叶级数法
由分离变量法得出的结果提示：可以直接设非齐 次方程的解为傅里叶级数的形式：
u ( x，t ) Tn (t ) X n ( x)
n
傅里叶系数不是常数， 是时间t的函数
基本函数族Xn(x)为该 定解问题相应的齐次 方程在所给齐次边界 条件下的本征函数
t (d 0)
(3)解该定解问题，与之前解的方法一致，只是将 解的结果中t换成 t 即可 (4)叠加：将持续力看成一系列前后相继作用的瞬 时力的迭加，则所有瞬时力引起的振动等效于持 续力引起的振动
u ( x，t ) u ( x，t ) v( x，t； )d
( ) t t
vtt a 2 v xx 0 v(0，t ) v(l，t ) 0 v( x， ) 0 vt ( x， ) f ( x， )
3、按t=0的初始条件求解，只需将t换成 t ； t 4、叠加 u( x，t ) v( x，t； )d
0
对于输运问题 (1)定解问题为
(二)冲量定理法步骤：初始条件均为零 1、定解问题：
utt a 2u xx f ( x，t ) u (0，t ) u (l，t ) 0 u ( x， 0) ut ( x， 0) 0
机械动力学与振动学讲义_8
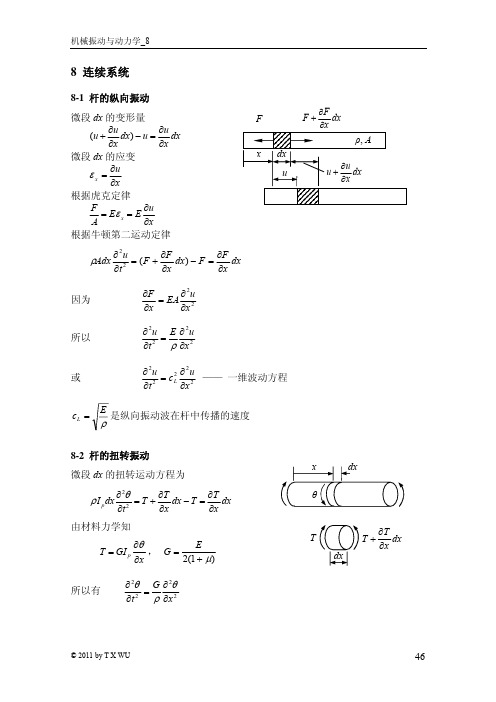
8-5 杆振动的固有频率和振型 设 代入杆运动方程得
u ( x, t ) = U ( x)φ (t )
U ( x)
2 d 2φ (t ) 2 d U ( x) c = φ (t ) dt 2 dx 2
改写成
1 d 2φ (t ) 1 d 2U ( x ) 2 c = = −ω 2 2 2 U ( x ) dx φ (t ) dt
解得 固有频率 振型
B = 0，和 sin kl = 0 => kl = nπ
ωn = kn2
EI n 2π 2 = 2 l ρA
EI ρA nπ x l
Yn ( x ) = Dn sin kn x = Dn sin
各种边界条件梁的振型：
8-7 连续系统振型函数的正交性 杆的振型函数的正交性： 杆振动的第 i 阶与第 j 阶振型函数 Ui(x)和 Uj(x)分别满足下列微分方程
Y
x =0
=0 = 0 =>
x =0
=>
A+C = 0
d 2Y dx 2
Y
x =l
A−C = 0， ∴A = C = 0
=0 =0
x =l
=> =>
B sinh kl + D sin kl = 0
B sinh kl − D sin kl = 0
d 2Y dx 2
© 2011 by T X WU
52
机械振动与动力学_8
y = Y ( X )e iωt = Ce i (ωt + kx ) − ρAω 2 + EIk 4 = 0 ⎛ρA 2⎞ ⎛ ρA 2⎞ k1−4 = ± ⎜ ω ⎟ 和 ±i ⎜ ω ⎟ ⎝ EI ⎠ ⎝ EI ⎠
齐次方程的自由振动与输运问题
u ( x, t ) X ( x)T (t ) 并代入方程得
a 2 X T 0 XT
X (0)T (t ) 0 X (l )T (t ) 0
X (l ) 0
X (0) 0
2 现用 a XT 遍除各项即得
T X 2 aT X X "X 0 X (0) 0 X (l ) 0
2n 1 l l 3l 5l x , , , , 2n 2n 2n 2n
0
l
0
l /2
l
点数为2，3，4的驻波形状
于是我们也可以说,解u ( x, t ) 是由一系列频率不同 （成倍增长）、位相不同、振幅不同的驻波叠加 而成的． 所以分离变量法又称驻波法．各驻波振幅的大小 和位相
n πa 的差异，由初始条件决定，而圆频率 n l
如果
0则
X ( x) C1 cos x C2 sin x
(C1 sin l C 2 cos l ) 0
现确定积分常数 C2 0
0 C2 0
C1 sin l 0 因此 C1 0 否则方程无解，只有
2
n 2 sin x 0 x n l n
本征值问题。虽然我们是从驻波引出解题的线索,其实
整个求解过程跟驻波并没有特殊的联系，从数学上讲，
完全可以推广应用于线性齐次方程和线性齐次边界条
件的多种定解问题。这个方法，按照它的特点，叫作 分离变数法。
用分离变数法得到的定解问题的解一
般是无穷级数,不过,在具体问题中,级数 里常常只有前若干项较为重要,后面的项
2 u ( x, t ) A cos x cos t T
数学物理方程复习
一、填空题1、物理规律反映同一类物理现象的共同规律，称为___________。
2、在给定条件下求解数学物理方程，叫作____________________。
3、方程20tt xx u a u -=称为_________方程4、方程20t xx u a u -=称为_________方程5、静电场的电场强度E是无旋的，可用数学表示为_____________。
6、方程0j Ñ×=称为_____________的连续性方程。
7、第二类边界条件，就是______________________________________。
8、第一类边界条件，就是______________________________________。
9、00(0,)(0,)x x u x t u x t -=+称为所研究物理量u 的_____________。
10、00(0,)(0,)u x t u x t -=+称为所研究物理量u 的_____________。
11、对于两个自变量的偏微分方程，可分为双曲型、________和椭圆型。
12、对于两个自变量的偏微分方程，可分为双曲型、抛物线型和________。
13、分离变数过程中所引入的常数l 不能为_____________。
14、方程中，特定的数值l 叫作本征值，相应的解叫作_____________。
15、分离变数法的关键是________________________代入微分方程。
16、非齐次振动方程可采用______________和冲量定理法求解。
17、处理非齐次边界条件时，处理非齐次边界条件时，可利用叠加原理，可利用叠加原理，可利用叠加原理，把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
18、处理非齐次边界条件时，处理非齐次边界条件时，可利用叠加原理，可利用叠加原理，可利用叠加原理，把非齐次边界条件问题转化另一把非齐次边界条件问题转化另一_________的齐次边界条件问题。
8.2非齐次振动方程和输运方程解析
对于y '' P 1 ( x) y ' P 2 ( x) y q ( x) 特解为：Y(x) y1
下面求特解Tn* (t ), 令T1n (t ) cos
y2 y1 q( x)dx y2 q( x)dx w( y1 , y2 ) w( y1 , y2 )
n at n at , T2 n (t ) sin l l t T ( ) t T ( ) * 2n Tn (t ) T1n (t ) f n ( )d T2 n (t ) 1n f ( ) d 0 w( ) 0 w( ) n n a n a sin T1n ( ) T2 n ( ) n a l l w( ) T1n '( ) T2 n '( ) n a n a n a n a l sin cos l l l l n a n a sin cos n at t l f ( )d sin n at t l f ( ) d Tn* (t ) cos n n l 0 n a l 0 n a l l l t n a sin[ (t )] f n ( ) d 0 n a l cos
(二)介绍用两种方法求解非齐次振动方程：傅里叶级数法、冲量定理法 A.首先讨论弦在外力作用下的强迫振动问题 utt a 2u xx f ( x, t ) (0 x l , t 0) (1) (2) u ( x, t ) x 0 0, u ( x, t ) x l 0 (t 0) u ( x, t ) ( x), u ( x, t ) ( x) (0 x l ) (3) t t 0 t 0 1.傅里叶级数法 根据边界条件(2)可设u ( x, t )的试探解为：u ( x, t ) Tn (t ) sin
《 数学物理方法 》课程教学大纲
《数学物理方法》课程教学大纲（供物理专业试用）课程编码：140612090学时：64 学分：4开课学期：第五学期课程类型：专业必修课先修课程：《力学》、《热学》、《电磁学》、《光学》、《高等数学》教学手段：（板演）一、课程性质、任务1．《数学物理方法》是物理教育专业本科的一门重要的基础课，它是前期课程《高等数学》的延伸，为后继开设的《电动力学》、《量子力学》和《电子技术》等课程提供必需的数学理论知识和计算工具。
本课程在本科物理教育专业中占有重要的地位，本专业学生必须掌握它们的基本内容，否则对后继课的学习将会带来很大困难。
在物理教育专业的所有课程中，本课程是相对难学的一门课，学生应以认真的态度来学好本课程。
2．本课程的主要内容包括复变函数、傅立叶级数、数学物理方程、特殊函数等。
理论力学中常用的变分法，量子力学中用到的群论以及现代物理中用到的非线性微分方程理论等，虽然也属于《数学物理方法》的内容，但在本大纲中不作要求。
可以在后续的选修课中加以介绍。
3．《数学物理方法》既是一门数学课程，又是一门物理课程。
注重逻辑推理和具有一定的系统性和严谨性。
但是，它与其它的数学课有所不同。
本课程内容有很深广的物理背景，实用性很强。
因此，在这门课的教学过程中，不能单纯地追求理论上的完美、严谨，而忽视其应用。
学生在学习时，不必过分地追求一些定理的严格证明、复杂公式的精确推导，更不能死记硬背，而应重视其应用技巧和处理方法。
4．本课程的内容是几代数学家与物理学家进行长期创造性研究的成果，几乎处处都闪耀创新精神的光芒。
教师应当提示学生注意在概念建立、定理提出的过程中所用的创新思维方法，在课堂教学中应尽可能地体现历史上的创造过程，提高学生的创造性思维能力。
二、课程基本内容及课时分配第一篇复数函数论第一章复变函数（10）教学内容：§1.1．复数与复数运算。
复平面，复数的表示式，共轭复数，无穷远点，复数的四则运算，复数的幂和根式运算，复数的极限运算。
梁昆淼 数学物理方法教学大纲
本篇还要讨论有关的特殊函数，特别是勒让得函数的理论。特殊函 数的内容十分丰富，在数学中已成为一个独立分支，它在物理学和工程 技术中有着广泛的应用。例如静电势的球坐标解将会出现勒让得函数， 而在柱坐标下的解将会出现贝塞尔函数，量子力学中谐振子本征解为厄 密多项式，中心势的角向函数可由球谐函数构成，而库伦势的径向函数 由连带拉盖尔多项式构成等等。本大纲只较详细地涉及一类常见的特殊 函数，即勒让德函数。
本章重点：
留数定理及其计算方法。
习 题：
§4.1．（第71页）：1（1）（3）（5）（7）（9），2（1）（2） （3），3。
§4.2．（第81—82页）1（1）（2）（5）（6），2（3）（4） （6），3（2）（4）（6）（8）。
第五章 傅立叶变换（2+1）
基本要求：
1．了解非周期函数的傅里叶积分表达式和傅立叶变换的概念。 2．掌握傅立叶变换的基本性质与方法。 3．了解提出狄拉克函数过程中的创造性思想。 4．掌握狄拉克函数的定义、基本性质和常用表达式。
本篇的教学时间为20课时，另安排1课时作为机动（可以用来复习 傅立叶级数以及学习其他需要的扩展内容）。
第一章 复变函数（6）
基本要求：
1．熟悉复数的基本概念和基本运算； 2．了解复变函数的定义，连续性； 3．了解多值函数的概念；
4．掌握复变函数的求导方法及柯西—黎曼方程； 5．了解解析函数的概念，熟悉一些简单的解析函数的表示式。 6．了解从实变函数到复变函数的推广过程中的创新思想与方法。
非齐次方程的冲量定理法求解
于是
lA π a(t −τ ) nπ v= sin ωτ sin cos x l l πa
于是
u = ∫ v(x, t;τ )dτ
0
t
lA π a(t −τ ) nπ =∫ sin ωτ sin cos x dτ 0π a l l π at π a ω sin − sin ω t lA nπ l l cos x = 2 2 π a πa l 2 ω − 2 l
Tn ' (0) = 0
nπ a 2 Tn"(t) + ( ) Tn (t) = fn (t) l Tn (0) = 0 2 l nπξ fn (t) = ∫ f (ξ , t) sin dξ Tn ' (0) = 0 l 0 l
nπ a Tn (t) = ∫0 fn (τ )sin l (t −τ ) dτ nπ a l
t
T0 ' (t) = Asin ω t
n=0
T0 ' (t) = Asin ω t T0 (0) = 0
nπ a 2 Tn ' (t) + ( ) Tn (t) = 0 l
n≠0
Tn (0) = 0
T0 (t) = A
ω
(1− cosω t)
u(x, t) =
Tn (t) = 0
A
ω
(1− cosω t)
τ τ +∆τ t
t
f(x,t)
τ τ +∆τ t
u
(τ ) tt (τ )
t
−a u
x=0 x=l t =τ
2 (τ ) xx
=0
u
=0 =0
u u
(τ )
(τ )
山东大学工科研究生数学物理方法class14第2节非齐次振动方程和输运方程.ppt
na(t
l
)
cos
nx
l
系数 An ( ), Bn ( ) 由初始条件确定，把上式代入初始条件：
A0 (
)
n1
An (
) cos
nx
l
0
17
B0 (
)
n1
Bn (
)
nx
l
cos
nx
l
A cos
nx
l
s in x
右边的 Acos nx sinx 也是傅里叶余弦级数，只有一个单项n＝1
l
两边比较系数可得：
系数，上述两边都是傅立叶余弦级数，由于基本函数族 cos nx
l 的正交性，等式两边对应于同一基本函数的傅立叶系数必相等：
T0 (0) 0
1 l
l
( )d
0
T0(0) 0
1 l
l
( )d
0
Tn (0) n
Tn(0) n
2 l
2 l
l ( ) cos n
0
l
l
(
)
cos
n
0
l
d
同时，量纲分析也可以侧面证明此法是正确的！
（2）冲量定理法的数学验证 即要验证通过积分得到的解u（x，t）是原非齐次振动方程定
解问题的解。
首先来验证边界条件：v |x0 0, v |xl 0 故有：
t
t
u |x0 0 v |x0 d 0, u |xl 0 v |xl d 0
边界条件
初始位移： u |t0
t
0 f (x, ) (t )d
其中 F(x, ) (t )d 为作用在很短的时间区间 ( , d ) 9
数学物理方法习题解答
习题解答
向安平
B xiangap@ xiangap@
成都信息工程学院光电技术系 2006 年 9 月 11 日
前 言
本书供电子科学与技术专业和光信息科学与技术专业《数学物理方法》课程教学使用． 本教学参考书仅供授权读者在计算机上阅读，不能编辑、拷贝和打印．经作者授权，可取消全 部限制． 在第一版中只收录了必要的试题，以后将增补习题的数量和类型，在每章增加内容小结和解题 方法讨论．欢迎读者提供建议． 作为本书的第一版，错误和排版差错在所难免，敬请读者指正．
§ 1.1 复数与复数运算
1. 下列式子在复平面上各具有怎样的意义? (1) | x |≤ 2. (2) | z − a |=| z − b | （a 、b为复常数）. (3) Rez > 1 2. (1) | x |≤ 2 解一：|z| = | x + iy| = 部． x2 + y2 ≤ 2，或 x2 + y2 ≤ 4．这是以原点为圆心而半径为2的圆及其内
z?az?bx?a12y?a22x?b12y?b22于是x?a12y?a22x?b12y?b22即2y?a2?b2b2?a22x?a1?b1a1?b1y?a2b22x?a1b12a1?b1b2?a22a2b2这是一条直线是一条过点a和点b连线的中点a1b12且与该直线垂直的直线
数 学 物 理 方 法
解二：按照模的几何意义，|z|是复数z = x + iy与原点间的距离，若此距离总是≤ 2，即表示 以原点为圆心而半径为2的圆内部． (2) |z − a| = |z − b| ( a、b为复常数)． 解一：设z = x + iy, z = a1 + ia2 , b = b1 + ib2 ； ( x − a1 )2 + (y − a2 )2 , ( x − b1 )2 + (y − b2 )2 ,
波动方程和振动方程的表达式(3篇)
第1篇一、波动方程波动方程是描述波动在连续介质中传播的偏微分方程。
常见的波动方程有弦振动方程、声波方程、光波方程等。
以下列举几种常见的波动方程及其表达式：1. 弦振动方程弦振动方程描述了弦在受到外力作用下的振动规律。
假设弦的线密度为λ，张力为T，弦上某点的位移为y(x,t)，则弦振动方程可表示为：∂²y/∂t² = (T/λ)∂²y/∂x²其中，x表示弦的长度，t表示时间，y(x,t)表示弦上某点的位移。
2. 声波方程声波方程描述了声波在介质中的传播规律。
假设介质的密度为ρ，声速为c，声波在介质中的波动函数为p(x,t)，则声波方程可表示为：∂²p/∂t² = c²∂²p/∂x²其中，x表示声波传播的距离，t表示时间，p(x,t)表示声波在介质中的波动函数。
3. 光波方程光波方程描述了光波在介质中的传播规律。
假设光波在介质中的波动函数为E(x,t)，介质的折射率为n，则光波方程可表示为：∂²E/∂t² = (n²/c²)∂²E/∂x²其中，x表示光波传播的距离，t表示时间，E(x,t)表示光波在介质中的波动函数。
二、振动方程振动方程描述了物体在受到外力作用下的振动规律。
常见的振动方程有单摆运动方程、弹簧振动方程等。
以下列举几种常见的振动方程及其表达式：1. 单摆运动方程单摆运动方程描述了单摆在重力作用下的振动规律。
假设单摆的摆长为L，摆球质量为m，摆球偏离平衡位置的角度为θ，则单摆运动方程可表示为：mL²θ'' = -mgLsinθ其中，θ'表示摆球偏离平衡位置的角度对时间的导数，θ''表示摆球偏离平衡位置的角度对时间的二阶导数。
2. 弹簧振动方程弹簧振动方程描述了弹簧在受到外力作用下的振动规律。
假设弹簧的劲度系数为k，弹簧的位移为x，则弹簧振动方程可表示为：mω²x = -kx其中，ω表示弹簧振动的角频率，m表示弹簧的质量。
武汉大学数学物理方法3_2非齐次方程—纯强迫振动
本节注意：
A 代入<4>式得： u ( x , t ) = (1 − cos ω t ) ω
(1)以上方法也适于求解带有其他齐次边界条件的非齐次 方程的定解条件，其主要精神是： <i> 先考虑对应的齐次问题，用分离变量法求得其齐次问 题的固有函数； <ii> 将未知函数按本征函数展开，其展开系数为另一变 量的系数，代入原非齐次方程和初始条件（或另一变量的 边界条件），得另一变量的常微分方程定解问题； <iii> 求常微分方程定解问题的解代入展开式得原定解问 题得解。这种分离变量的方法按其特点又叫本征函数。
而u ( x, t ) = ∫ v( x, t ;τ )dτ
0
t
所以我们可以想到，对于：
utt = a u xx + f ( x, t ) u | x =0 = 0 u | x =l = 0 u | = 0 t =0 ut |t =0 = 0
2
也可以先用冲量原理求解
根据冲量原理，先求解：
(1) 用分离变量法求得对应的齐次问题（即对应的齐次方 程连同齐次边界条件）的本征函数。 (2)将未知函数 u ( x，y )[或 u ( x，t )等]按上面求得的本征函 数展开，其展开系数为另一变量的函数，代入非齐次方程 和初始条件（或另一变量的边界条件），得到关于时间因 子的常微分方程的初值条件（或另一单元函数的常微分方 程的边值问题），用常数变易法或拉氏变换法可求得其 解。 (3)将所求得的解代入未知函数的展开式中，即得到原定解 问题的解。这种分离变量的方法按其特点又叫本征函数 （或固有函数）法。
3、有界弦（杆）的纯强迫振动的解：
将<8>代入<4>，得定解问题<1>~<3>的解为：
8.2非齐次振动方程和输运方程
Tn (t ) Tn (0) cos
n at l n at l t n a Tn '(0) sin sin[ (t )] f n ( )d 0 l n a l n a l
( B)书P204例1
x 2 解：根据(2)式，可设 u a u A cos sin t (1) xx tt l n x u ( x , t ) T ( t ) cos (2) n u x x 0 0, u x x l 0 l n 0 u ( x), u (3) t t 0 ( x) t 0 代入(1)式得： n2 2 a 2 n x x [ T ''( t ) T ( t )]cos A cos sin t (5) n n 2 l l l n 0 2a2 比较法：T1 ''(t ) 2 T1 (t ) A sin t (6) l n 2 2 a 2 Tn ''(t ) Tn (t ) 0 (n 1)(7) 2 l 对(7)式：n 0, T0 (t ) A0 B0t , 且T0 (0) A0，T0 '(0) B0
n 1
n x l
n 2 2 a 2 n x 代入(1)式得： [ T ''( t ) T ( t )]sin f ( x, t ) n n 2 l l n 1
将f ( x, t )展为傅氏级数：f ( x, t )
n 1
n x 2 l n x f n (t ) sin , f n (t ) f ( x, t ) sin dx 0 l l l
(二)介绍用两种方法求解非齐次振动方程：傅里叶级数法、冲量定理法 A.首先讨论弦在外力作用下的强迫振动问题 utt a 2u xx f ( x, t ) (0 x l , t 0) (1) (2) u ( x, t ) x 0 0, u ( x, t ) x l 0 (t 0) u ( x, t ) ( x), u ( x, t ) ( x) (0 x l ) (3) t t 0 t 0 1.傅里叶级数法 根据边界条件(2)可设u ( x, t )的试探解为：u ( x, t ) Tn (t ) sin
第八章第二节 非齐次振动方程和输运方程
例2 将例1中的初始条件改为零值，用冲量定理法求解，
即求定解问题
utt a2uxx
Acos x
l
s in t;
ux x0 0, ux xl 0; u t0 0, ut t0 0.
解：用冲量定理法先求解定解问题
vtt a2vxx 0; 变为齐次
vx x0 0, vx xl 0;
v t 0
d ,...n
0...8.2.7
Tn(t)的常微分方程的解是
n 0:
Tn
n2 2a2
l2
Tn
0...n
1
T0t 0 T0t A Bt
用初始条件： T00 A 08.2.7 T00 B 0
T0t 0 0t...8.2.8
n 1:
T1
2a2
l2
T1
A s in t...n
1
T1t
Al
a
1
2 2a2
l2
sin at
l
a sint
l
1
cos
at
l
l
a
1
sin
at
l
,... 8.2.9
详细求解过程
Hale Waihona Puke n 0,1:Tnn2 2a2
l2
Tn
0...n
1
Tn
t
n
cos
nat
l
l
na
n
sin
nat
l
....8.2.10
把Tn(t)的解代入u(x,t)得出
ux,t Al
0... n
1
3、求解Tn(t)的常微分方程后，代入1即可。
把u(x,t)的傅里叶余弦级数代入初始条件,得
分离变数傅里叶级数法
第八章平面坐标下的分离变量本征值问题（一）通过上一章的讨论，我们知道，在研究物理（场）量的变化时，不仅要考虑物理（场）量随时间的变化规律，有时候还需要考虑其在空间变化规律，由此便导致了反映物理规律的“偏微分方程”。
偏微分方程泛指同一类的物理规律，因此称为泛定方程。
偏微分方程若附加上边界条件、初始条件的限制，则物理过程（解）就唯一确定，此时便构成了定解问题。
对于偏微分方程用高等数学中介绍的一些方法，无法求解。
因此必须引进分离变量法。
分离变量法是把偏微分方程分解为几个常微分方程，从而达到求解之目的一个数学过程。
分离变数法的可行性问题：上一章推导出了三类偏微分方程，波动方程、输运方程和泊松方程。
第一类、第二类方程都是时间和空间的函数，我们在普通物理中曾对驻波问题进行过研究，其空间周期性和时间周期性彼此独立，由此受到启发，其解应具(,)()()的形式。
对于第三种情况——u x t X x T t泊松方程，反映的是“有源”情况下的一种作用，其效果相当于简单叠加。
由此看来，变量是可以分离的。
实际情况如何？我们可以通过实例进行验证。
§8.1 齐次方程的分离变数法一、分离变数法简介以两端固定的均匀弦的自由振动为例。
其定解问题为2000000(0)()()tt xx x x l t t t u a u u u x l u x u x ϕψ====⎧-=⎪⎪==<<⎨⎪==⎪⎩ (8.1.1) 这里研究的弦是有限长的，它有两个端点，波就在这两端点之间往复反射。
这样,驻波解的一般表示式应当为设 (,)()()u x t X x T t = (8.1.2)在(8.1.2)中，自变数x 只能出现于X 之中，自变数t 只出现于T 之中，驻波的一般表示式具有分离变数的形式。
那么，在两端固定的弦上究竟有哪些驻波呢？把驻波的一般表示式(8.1.2)代入弦振动方程(8.1.1)和相应的边界条件，得：20(0)()0()()0XT a X T X T t X l T t ''''⎧-=⎪=⎨⎪=⎩(8.1.3) 条件(8.1.3)表示，在时刻t ，)()0(t T X 和)()(t T l X 总是零。
非齐次方程的求解问题
x l
0
t 0 0
0
时刻以前，瞬时热源不起作用， t 0 0 时刻瞬时热源起作用。瞬时热源发出的热量使 系统温度升高。
d
c ( t 0 t 0 ) cf ( x, )
2
0时刻瞬时热源已经作用完， t a u xx 0
可以齐次化。
一、两端固定弦的受迫振动问题：
由于边界条件已是齐次的， 如果能将泛定方程也化成齐次 的，便可以求解。所以用叠加 原理，令
u u
(1)
u
( 2)
utt a 2u xx f ( x, t ) u x 0 0, u x l 0 u t 0 ( x), ut t 0 ( x)
f ( x, )
从时刻 t 0 时刻开始，瞬时力不再起作用，
方程转化为齐次方程。
【例题一】
utt a u xx Acon
2
x
ux
x 0
0 ux
x l
l 0
sin t
u t 0 0 ut
【解】应用冲量定理求解
t 0
0
tt a 2 xx 0 x
从物理学的角度理解，受迫振动是由受迫力引起的振
动与初始状态下引起振动的合成。其中：
u (1)为受迫振动引起的位移， u ( 2 )为初始条件下引起的位移。
第一组方程（关于 u
()
的方程）就是曾经讨论过的，
可以直接求解。方程二（关于 u ( 2 ) 的方程）是非齐次， 但边界条件、初始条件都为齐次的。现关键是如何求解方
定解问题转化为：
t 0 f ( x, )（或采用方程两边积分的形式得到该式）
数学物理方法教学大纲
《数学物理方法》课程教学大纲一、课程性质、地位和作用《数学物理方法》是光信息科学与技术、应用物理学、电子科学与技术本科专业的必修专业基础课程。
它是继高等数学后的一门数学基础课程。
通过该课程的学习，使学生掌握复变函数、数学物理方程和特殊函数的基本理论、建模方法和计算方法，培养学生用数学方法和物理规律解决各类物理、工程技术实际问题的能力，为后续课程的学习打下良好的基础。
二、课程教学对象、目的和要求本课程适用于光信息科学与技术，应用物理，电子科学与技术等专业。
课程教学目的、要求：（一）从内容上，使学生掌握复变函数、解析函数的概念；掌握柯西定理、积分变换、留数定理的应用；理解三种类型数学物理方程的建模思想、掌握分离变数法、傅里叶级数法；掌握轴对称球函数、一般球函数的性质。
（二）从能力方面，培养学生严密的逻辑思维能力、数学建模能力；帮助学生树立科学严谨的学习观，使学生初步具备解决简单常见物理和工程实际问题的素养。
（三）从教学方法上，结合该课程理论性强，数学推导过程复杂等特点，合理采用启发式，案例式和探究式等多种教学方法；充分结合板书，ppt，动画，matlab仿真等多种教学手段将教学内容形象直观化，以激发学生兴趣，提高教学效果。
三、相关课程及关系本课程的先修课程包括《高等数学》、《大学物理》等，为后续的《统计物理》、《量子力学》、《电动力学》、《固体物理》、《激光原理与激光技术》等课程打下必要的理论基础。
四、课程内容及学时分配总学时：64学时（一）复变函数：4学时1、复数与复数运算2、复变函数3、导数4、解析函数5、平面标量场6、多值函数要求学生：(1) 掌握复数的三种表示方式，复数的运算规则。
(2) 理解复变函数的导数和解析函数。
(3) 能应用柯西-里曼条件判断函数的解析性以及求解解析函数。
(4) 了解应用解析函数处理平面标量场的方法。
(5) 了解多值函数。
（二）复变函数的积分：4学时1、复变函数的积分2、柯西定理3、不定积分4、柯西公式要求学生：(1) 掌握复变函数的积分。
第八章第三节 非齐次边界条件的处理
0 vtt a 2vxx
t t x2 tx a2 t t
2l
l
wx x0 0, wx xl 0
w x 0 0 x2 0x
t0
2l
wt
t0
x
0 0
2l
x2
0x
2009年5月7日
补充练习：
将下面非齐次边界条件的问题转变为齐次边界条件的定解问题
ut a2uxx 0 x l,t 0 ux 0,t w1t,ux l,t w2t ux,0 x
l l
xdx 2 A
n
Tn
n2 2a2
l2
Tn
Fn
2A
n
根据
dy Pxy Qx
dx
y Ce Pxdx e Pxdx Q x e Pxdxdx
得:
Tn t
B e
n2 2a
l2
2
t
n
2Al2
n3 3a2
代入w(x,t)得
w x,t
Bne
n
2 2a2
l2
t
n1
2 Al2
由此确定 X x A sinl asinx a,从而
vx, t
A
sin l
sin
x
a
sin t....8.3.17
a
令ux,t vx,t wx,t....... 8.3.18
将(8.3.17),(8.3.18)代入(8.3.11)~(8.3.13)
wtt a 2 wxx vtt a 2 vxx 0...8.3.19
w 60 t 0
应用傅里叶级数法求解w(x,t)—非齐次项不含t，不宜用冲量定
理法。
wx,t
Tn tsin
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n 2 2 a 2 比较系数：Tn ''(t ) Tn (t ) f n (t ) ~ 二阶线性常系数非齐次微分方程 2 l 该非齐次方程的通解为对应齐次方程的通解与本身一特解之和构成。 n at n at Tn (t ) Tn 0 (t ) Tn *(t ), Tn 0 (t ) An cos Bn sin l l
1.冲量定理法的基本物理思想：把持续作用力看成许许多多前后相继 的“瞬时力”，把持续作用引起的振动看作所有“瞬时”力引起的振动 的叠加。 根据P107，持续作用力F ( x, t )可表为： F ( x, t ) F ( x, ) (t )d
0 t
f ( x, t ) f ( x, ) (t )d
n 0,1, Tn (t ) An cos
(4)
n a n a n a t Bn sin t , 且Tn (0) An , Tn '(0) Bn l l l
由初始条件(3)可得： u ( x, 0) ( x) Tn (0) cos
n 0
n x 1 l T0 (0) 0 ( )d A0 l l 0 2 l n Tn (0) n ( ) cos d An (n 0) 0 l l
T1*(t )
lA t a(t ) [ sin sin d ] 0 a l lA 1 t a(t ) a(t ) ( ) {cos[ ] cos[ ]}d 0 a 2 l l lA 1 at a [ sin sin t ] 2 2 2 2 a a / l l l
对于y '' P 1 ( x) y ' P 2 ( x) y q ( x) 特解为：Y(x) y1
下面求特解Tn* (t ), 令T1n (t ) cos
y2 y1 q( x)dx y2 q( x)dx w( y1 , y2 ) w( y1 , y2 )
n at n at , T2 n (t ) sin l l t T ( ) t T ( ) * 2n Tn (t ) T1n (t ) f n ( )d T2 n (t ) 1n f ( ) d 0 w( ) 0 w( ) n n a n a sin T1n ( ) T2 n ( ) n a l l w( ) T1n '( ) T2 n '( ) n a n a n a n a l sin cos l l l l n a n a sin cos n at t l f ( )d sin n at t l f ( ) d Tn* (t ) cos n n l 0 n a l 0 n a l l l t n a sin[ (t )] f n ( ) d 0 n a l cos
0
t
其中：F ( x, ) (t )d 为作用在很短的时间区间[ , d ]上 冲量为F ( x, )d 的“瞬时”力，设该瞬时力引起的振动为u ( ) ( x, t ) 则u ( ) ( x, t )的定解问题为： F ( x, t ) ( ) 2 ( ) u a u (t )d f ( x, ) (t )d xx tt （A） u ( ) 0, u ( ) 0 持续力用瞬时力代替 x 0 x l u ( ) 0, ut ( ) 0 t 0 t 0
对第一组定解问题可按齐次方程的求解办法进行， 而第二组定解问题初始条件已经化为零值，可用冲量定理法来求解。 非齐次泛定方程表明：作用在每单位长弦上的外力F ( x, t ) f ( x, t )， 从t=0时刻持续作用到t时刻，要求解的是F ( x, t )作用下，在时刻t的 各处位移u ( x, t )。
见P207分析，由于瞬时力F ( x, ) (t )d 作用在时间区间[ , d ]上， 从0～时刻－0，瞬时力尚未起作用，弦是静止的，即： u ( )
对(6)式：T1 ''(t )
2a2
2
T1 (t ) A sin t
a
t B1 sin
a
l
t , 令T1 cos
a
l
t , T2 sin
a
l
t
w(cos
a
l
,sin
a
l
cos )
a
l
sin
a
l
a
l
则非齐次方程特解为： T2 T1 T1*(t ) T1 f ( )d T2 f ( )d w(T1 , T2 ) w(T1 , T2 ) cos
(二)介绍用两种方法求解非齐次振动方程：傅里叶级数法、冲量定理法 A.首先讨论弦在外力作用下的强迫振动问题 utt a 2u xx f ( x, t ) (0 x l , t 0) (1) (2) u ( x, t ) x 0 0, u ( x, t ) x l 0 (t 0) u ( x, t ) ( x), u ( x, t ) ( x) (0 x l ) (3) t t 0 t 0 1.傅里叶级数法 根据边界条件(2)可设u ( x, t )的试探解为：u ( x, t ) Tn (t ) sin
T1 (t ) 1 cos
a
l
t
l a lA 1 at a 1 sin t [ sin sin t ] 2 2 2 2 a l a a / l l l
(二)冲量定理法 前提：初始条件取零值。若初始条件为非零值，可先用叠加原理 把一个定解问题分成两个定解问题 utt a 2u xx f ( x, t ) (1) (2) u x 0 0, u x l 0 可设u ( x, t ) u ( x, t ) u ( x, t ) u ( x), u t t 0 ( x) t 0 (1) 2 (1) u a u xx 0 tt (1) (1) u x 0 0, u x l 0 (1) (1) u t 0 ( x), ut t 0 ( x) u (2 ) a 2u (2) f ( x, t ) xx tt (2) (2) u x 0 0, u x l 0 (2) u 0, ut (2) 0 t 0 t 0
其中y1、y2是齐次方程y '' P 1 ( x ) y ' P 2 ( x ) y 0的两个线性无关的特解。 线性无关：指C1 y1 C2 y2 0, 当且仅当C1 C2 0 w( y1 , y2 ) y1 y1 ' y2 y2 ' （朗斯基行列式） 0 ,w 0则y1、y2线性无关。
n x 1 l T0 '(0) 0 ( )d B0 l l 0 2 l n n a Tn '(0) n ( ) cos d Bn (n 0) 0 l l l
ut ( x, 0) ( x) Tn '(0) cos
0
Tn (0)和Tn '(0)由初始条件定： n x 2 l n x u ( x, t ) t 0 ( x) Tn (0)sin Tn (0) ( x)sin dx n 0 l l l n 1 n x 2 l n x ut ( x, t ) t 0 ( x) Tn '(0)sin Tn '(0) ( x)sin dx n 0 l l l n 1
Tn (t ) Tn (0) cos
n at l n at l t n a Tn '(0) sin sin[ (t )] f n ( )d 0 l n a l n a l
( B)书P204例1
x 2 解：根据(2)式，可设 u a u A cos sin t (1) xx tt l n x u ( x , t ) T ( t ) cos (2) n u x x 0 0, u x x l 0 l n 0 u ( x), u (3) t t 0 ( x) t 0 代入(1)式得： n2 2 a 2 n x x [ T ''( t ) T ( t )]cos A cos sin t (5) n n 2 l l l n 0 2a2 比较法：T1 ''(t ) 2 T1 (t ) A sin t (6) l n 2 2 a 2 Tn ''(t ) Tn (t ) 0 (n 1)(7) 2 l 对(7)式：n 0, T0 (t ) A0 B0t , 且T0 (0) A0，T0 '(0) B0
n 1
n x l
n 2 2 a 2 n x 代入(1)式得： [ T ''( t ) T ( t )]sin f ( x, t ) n n 2 l l n 1
将f ( x, t )展为傅氏级数：f ( x, t )
n 1
n x 2 l n x f n (t ) sin , f n (t ) f ( x, t ) sin dx 0 l l l
n n (t ) n cos n a l n a t n sin t l n a l
l 非齐次方程通解为：T1 (t ) T10 (t ) T1* (t ) l T1 , T2是对应齐次方程两个线性无关的特解。 A1 1 , B1 l 1 a 对应齐次方程通解为：T10 (t ) A1 cos
n at n at l t n a Tn (t ) Tn (t ) Tn *(t ) An cos Bn sin sin[ (t )] f n ( )d 0 l l n a l 确定系数An , Bn . n a l 令t 0, 得Tn (0) An , Tn '(0) Bn Bn Tn '(0) l n a