第三章波动方程
3 第三章 地震波动方程wan

第三章 地震波动方程现在,我们用前一章提出的应力和应变理论来建立和解在均匀全空间里弹性波传播的地震波动方程。
这章涉及矢量运算和复数,附录2对一些数学问题进行了复习。
3.1 运动方程(Equation of Motion )前一章考虑了在静力平衡和不随时间变化情况下的应力、应变和位移场。
然而,因为地震波动是速度和加速度随时间变化的现象,因此,我们必须考虑动力学效应,为此,我们把牛顿定律(ma F =)用于连续介质。
3.1.1一维空间之振动方程式质点面上由于应力差的存在而使质点产生振动。
如图1-3所示,考虑一横截面为A ∆薄棒向x1轴延伸,任取以微元,沿x1的长度为1x ∆,其左端的应力为11σ,方向逆x1的方向,右端的应力为11111x σσ∂+∂,方向与x1方向相同,其位移量为u :1D caseFigure 2.8x 1111111x ∂则其作用力为“应力” “其所在的质点面积”,所以其两边的作用力差为()()()()()111111111111111111111A x x x A x x x x Ax x σσσσσσ⎛⎫∂∂∆+∆-=∆+∆-=∆∆ ⎪∂∂⎝⎭惯量﹙inertia ﹚为212ux A tρ∂∆∆∂所以得出21121u t x σρ∂∂=∂∂ ……………………………………………………... (3-1)其中ρ为密度﹙density ﹚。
3-1式表示,物体因介质中的应力梯度﹙stress gradient ﹚而得到加速度。
如果ρ与E 为常数,1111uEx x σ∂∂=∂∂,这里考虑一维情况,将x 的角标去掉,则3-1式可写为 222221tu c x u ∂∂=∂∂ …………………………………………………… (3-2)其中ρEc =运用分离变量法求解(3-2)式,设u=X(x)T(t),(3-2)式可以变为T X cT X ''=''21设22ω-=''=''TT X X c 求解20T T ω''+=,其特征方程为220r ω+=,特征根为1,2r i ω=±,所以微分方程的解为:12i t i t T C e C e ωω-=+ 同理得到,220X X c ω''+=的解为12i xi x ccX D eD eωω-=+。
数学物理方程:第3章 波动问题的行波法

第3章 波动问题的行波法§3.1 二阶线性方程的分类与化简本节讨论:①两个自变量方程的分类与化简,②多个自变量方程的分类与化简⒈ 两个自变量方程的分类与化简二阶方程的一般形式 二阶变系数方程可写为1112220(,)2(,,,,)(,)xx xy yy x y Lu x y a u a u a u x y u u u f x y =+++Φ= (3.1.1)式中:11a 、12a 、22a 为x 、y 的函数,0(,,,,)x y x y u u u Φ为低阶导数项。
公式关于二阶导数项为线性的,即称方程为准线性的。
若0(,,,,)x y x y u u u Φ关于u 及其x u 、y u 为线性的,则称方程为线性的。
方程的变换 为了简化上述方程,作可逆变换:(,)(,)x y x y ξξηη=⎧⎨=⎩, (,)0(,)J x y ξη∂=≠∂, (,)(,)x x y y ξηξη=⎧⎨=⎩(3.1.2) 代入方程中,不难得到:11122212(,,,,)(,)Lu A u A u A u u u u f ξξξηηηξηξηξη=+++Φ= (3.1.3)式中: 22111112222x x y yA a a a ξξξξ=++ (3.1.4) 12111222()x x x y y x y y A a a a ξηξηξηξη=+++ (3.1.5)22221112222x x y yA a a a ηηηη=++ (3.1.6) 我们化简的目的是使得二次项的项数尽量少,并且值尽量为简单(如0ij A =或1ij A =±)。
顾及ij A 的表达式,取关于z 的一阶非线性偏微分方程2211122220x x y y a z a z z a z ++= (3.1.7)若该方程有解),(1y x z ϕ=、),(2y x z ψ=,则110A =及220A =;公式大大简化了。
波动方程_精品文档
l
=
=
12
50
600
s
=
1
(
)
υ
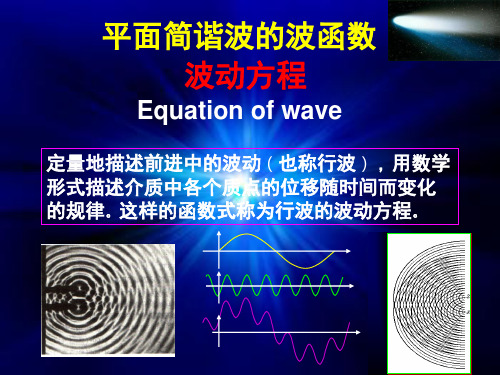
例题:有一列向x 轴正方向传播的平面简谐波,
它在t = 0 时刻的波形如图所示其波速为:
u = 600m/s 。试写出波动方程。
=
5m
A
24m
l
=
从波形图中可知:
ω
=
π
2
=
π
50
(
)
rad.
s
1
υ
原点处质点的振动方程为:
波动方程为:
y
0
2
π
由旋转矢量法:
u
l
=
=
=
t
+
cos
(
)
y
A
ω
0
1.时间推迟方法
x
x
u
y
o
P
·
A
已知振源(波源)的振动方程为:
振源的振动状态从0点以传播速度u传送到P 点,显然时间要落后:
´
u
x
=
t
u
x
j
=
t
+
cos
(
)
A
ω
-
j
=
t
+
cos
(
)
y
A
ω
0
´
t
j
=
t
+
cos
(
)
y
A
ω
-
P
介质中任一质点(坐标为 x)相对其平衡位
置的位移(坐标为 y)随时间t 的变化关系。
=
0
第三章波动方程

拉普拉斯算子: 拉普拉斯算子: 1 ∂ 1 ∂ 1 ∂u ∂u ) + (sin α ∇ 2u = 2 ( r 2 r ∂r r ∂α ∂r r ⋅ sin α ∂α ∂u ∂ u ↓← = =0 ∂ α ∂β
2 1 ∂u ∂ 2 u 2 ∂u 2 ∂ u )= 2 + = 2 ( 2r +r 2 r ∂r r ∂r ∂r ∂r
13
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解 、
已知球面纵波传播波动方程如下: 已知球面纵波传播波动方程如下: ∂ 2ϕ − VP2 ∇ 2ϕ = 0 ∂t 2 此式是直角坐标系中的波动方程, 此式是直角坐标系中的波动方程,需转换到球 坐标系中, 坐标系中,即
为了定量地描述微观粒子的状态,量子力学中引入了 为了定量地描述微观粒子的状态, 波函数,并用ψ表示。一般来讲,波函数是空间和时间 波函数, 表示。一般来讲, 的函数,并且是复函数,即ψ=ψ(x,y,z,t)。 的函数,并且是复函数,
7
无限大、 3.1 无限大、均匀各向同性介质中的平面波
一、沿任意方向传播的平面波
如果使 t −
播的波,即向震源方向传播的波,称为聚会波。聚会波只存在于t 播的波,即向震源方向传播的波,称为聚会波。聚会波只存在于t为 负值的情况,这与实际不合,则该波是不存在的。 负值的情况,这与实际不合,则该波是不存在的。
16
因此,上式又可写为: 因此,上式又可写为:
ϕ=
ϕ
1 r ) = c1 ( t − r r VP
10
无限大、均匀各向同性介质中的波动方程的解有两组。 无限大、均匀各向同性介质中的波动方程的解有两组。 第一组解: 第一组解:当 V = V p = ( λ + 2 µ ) / ρ 时,
波动理论波动方程知识点总结

波动理论波动方程知识点总结波动方程是波动理论中的重要内容,研究波的传播和特性具有重要意义。
本文对波动方程的相关知识点进行总结,以帮助读者更好地理解和应用波动理论。
一、波动方程的基本概念波动方程是描述波的传播过程中波动量随时间和空间的变化关系的数学表达式。
一般形式为:∂²u/∂t² = v²∇²u其中,u表示波动量,t表示时间,v表示波速,∇²表示拉普拉斯算子。
二、波动方程的解法1. 分离变量法:将波动量u表示为时间和空间两个变量的乘积,将波动方程转化为两个偏微分方程,分别对时间和空间变量求解。
2. 化简为常微分方程:将波动方程应用于特定情境,通过适当的变换,将波动方程化简为常微分方程,再进行求解。
3. 利用傅里叶变换:将波动方程通过傅里叶变换或拉普拉斯变换转化为频域或复频域的代数方程,再进行求解。
三、波动方程的应用1. 声波传播:声波是由介质中的分子振动引起的机械波,通过波动方程可以描述声波在空气、水等介质中传播的特性,如声速、声强等。
2. 光波传播:光波是电磁波的一种,通过波动方程可以研究光的干涉、衍射、反射等现象,解释光的传播规律和光学器件的性质。
3. 地震波传播:地震波是地震过程中的弹性波,通过波动方程可以描述地震波在地球内部传播的规律,有助于地震监测和震害预测。
4. 电磁波传播:电磁波是由电场和磁场耦合产生的波动现象,在电磁学中应用波动方程可以研究电磁波在空间中传播的特性和应用于通信、雷达等领域。
5. 水波传播:水波是液体表面的波动现象,通过波动方程可以研究水波的传播和液面形态的变化,解释液体中的波浪、涌浪、潮汐等现象。
四、波动方程的性质和定解问题1. 唯一性:波动方程的解具有唯一性,即满足初值和边值问题的解是唯一的。
2. 叠加原理:波动方程具有线性叠加性质,一系统的波动解可以通过各个部分的波动解线性叠加而得到。
3. 边界条件:波动方程的求解需要给定适当的边界条件,例如固定端、自由端、吸收边界等,以确保解满足实际问题的物理要求。
大学物理-波动方程

通过将波动方程中的空间和时间变量分离,简化求解过程。
傅里叶分析
利用傅里叶变换将时域信号转换为频域信号,便于分析波的频率 和振幅。
数值解法
对于复杂边界条件和初始条件,采用数值方法求解波动方程。
三维波动方程的应用
声波传播
研究声波在介质中的传播规律,如声呐、超声成像等。
光学研究
解释光波在介质中的传播规律,如折射、干涉、衍射等现象。
波动方程在声学中的应用
声波传播规律
波动方程可以用来描述 声波在空气、固体等介 质中的传播规律,如声 速、声压、声强等。
声学仪器设计
在声学仪器设计中,如 超声波探伤仪、声呐等, 需要利用波动方程来计 算和优化仪器的性能。
声音信号处理
在声音信号处理中,如 音频压缩、降噪等,可 以利用波动方程对声音 信号进行分析和变换。
数值解法
对于一些复杂的问题,可以通过 数值计算方法求解二维波动方程, 如有限差分法、有限元法等。
二维波动方程的应用
声波传播
在声学领域,二维波动方程可以用来描述声波在 固体、液体或气体中的传播规律。
地震波传播
在地球物理学中,二维波动方程可以用来模拟地 震波在地壳中的传播和散射。
电磁波传播
在电磁学领域,二维波动方程可以用来描述电磁 波在介质中的传播特性。
物理背景
波动方程基于物理原理,如牛顿第二定律和弹性力学 等,用于描述波在空间中的传播和变化。
建立过程
通过将物理原理和数学方法相结合,可以建立二维波 动方程的数学表达式。
二维波动方程的解法
分离变量法
通过将二维波动方程中的空间和 时间变量分离,将问题简化为求 解一系列一维方程。
傅里叶分析
利用傅里叶变换将时间和空间域 的函数转换为频率域的函数,从 而简化求解过程。
3-波动方程

统一了电磁理论后,Maxwell认识到: 1、波动是方程的解 2、光也是电r J = σE r r D = εE r r B = μH
对第三个方程取旋度,有:
r r r 或D = ε 0 E + P r r r 或B = μ 0 H + M
r r ∂ ∇ × (∇ × E ) = − (∇ × B ) Maxwell第 ∂t 4个方程 r r ∂D r r ∂ ∂ ∂ )] = [μ ( J + (∇ × B ) = ( μ∇ × H ) ∂t ∂t ∂t ∂t r r r ∂D ∂ ∂ r ∂D ) μ + μ (J + ) = (J + ∂ t ∂t r ∂t ∂t 对磁性时 不变材料 ∂ r ∂D ∂ r ∂2 r )= μ J +μ 2 D = μ (J + 代入物质 ∂t ∂t ∂t ∂t 方程 ∂ r ∂2 r = μ (σE ) + μ 2 (εE ) 对电导、介电常 ∂t ∂t 数时不变材料 ∂ r ∂2 r = μσ E + με 2 E ∂t ∂t
r r r ∇ × (∇ × E ) = ∇ (∇ ⋅ E ) − ∇ 2 E r r r r 因为: ⋅ D = ∇ ⋅ (εE ) = ∇ ε ⋅ E + ε∇ ⋅ E ∇ r 且: ∇ ⋅ D = ρ Maxwell方程的第一个方程 r r 所以,⇒ ∇ ε ⋅ E + ε∇ ⋅ E = ρ r r ∇ε ⋅ E ⇒ ∇⋅E = − +ρ
—频域内的波动方程 同样有:
r r r r ∇ 2 H (r ) + n2 k 2 H (r ) = 0
问题: 1、电磁场在介质中传输的波 动方程通式? 2、为什么说赫姆霍兹方程是 频域内的波动方程?
第三章波动方程培训课件

2 U ( )gr a F d 2 tU 2
两边分别取散度和旋度,并且令
V P 2(2)/
VS2 /
则可得纵波方程和横波方程
2t2 VP22
2t2 VS2
5
3 波动方程的解及地震波的特点
波动方程反映了物体波动过程的普遍规律。 波动方程的求解通常是和定解问题联系起来 考虑。波动方程的解就是波函数。
12
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解
已知球面纵波传播波动方程如下:
2t2 VP220
此式是直角坐标系中的波动方程,需转换到球 坐标系中,即
x rsic nos y rs in s in(0 r ,0 ,0 2 ) z rcos
前面是平行的。
▪ k1,k2,k3 是平面的法线方向数。有 k12k2 2k3 21
▪ 取负号时,表示随时间t的增加,波沿k方向前进,即延 迟一个时间。
▪ 取正号时,表示随时间t的增加,波沿-k方向前进,即 提前一个时间
▪ 当K是任意矢量的,则平面法向量为任意方向的。即表 示沿任意方向传播的平面简谐波。
8
二、沿X轴方向传播的平面波(即
kx
)
U Aex 2 p ik1xk2yk3zV td AieA co sisin
k1 1 ,k 2
U A exp
u A 1 exp
0 ,k 3 0
2i
x
Vt
2i
x
Vt
d
v
A 2 exp
2i
x
Vt
w
A 3 exp
2i
u rer u rr r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
wt (t, x; τ )dτ,
于是,再利用(1.4)可知 ut |t=0 = w(0, x; 0) = 0. (1.7)和(1.8)两式表明初始条件(1.2)式成立。 下面我们证明由(1.6)式定义的函数u = u(t, x)满足方程(1.1)。 由(1.6)及(1.4)易知
0
wxx (t, x; τ )dτ.
t
(1.10)
于是, utt − c2 uxx =
0
t
wtt (t, x; τ )dτ + f (t, x) − c2
0
wxx (t, x; τ )dτ (1.11)
t
=
0
wtt (t, x; τ ) − c2 wxx (t, x; τ ) dτ + f (t, x)
(1.1) (1.2)
其中c > 0是一常数,表示波的传播速度,f (t, x)是一给定的函数,表示 t 时刻在 x 处单 位质点所受的外力。方程(1.1) 可用来描述强迫振动的弹性弦的微小振动。 为了求解Cauchy问题(1.1)-(1.2),我们引入 wtt − c2 wxx = 0, t = τ : w = 0, wt = f (τ, x). 记Cauchy问题(1.3)-(1.4)的解为 w = w(t, x; τ ), 则我们有 定理 1.1 如果w = w(t, x; τ )是Cauchy问题(1.3)-(1.4)的解(其中τ 是参数),则Cauchy问 题(1.1)-(1.2) 的解可以表示为
0
[f (τ, x + c(t − τ )) − f (τ, x − c(t − τ ))] dτ, [fx (τ, x + c(t − τ )) − fx (τ, x − c(t − τ ))] dτ.
0
utt − c2 uxx = f (t, x), 即u(t, x)满足方程(1.1)。再由(1.19)式和(1.20)式可知 u|t=0 = 0, ut |t=0 = 0,
§ 1.
一维波动方程Cauchy问题
本节我们讨论一维波动方程的Cauchy问题,着重介绍一维波动方程的叠加原理和齐 次化原理(或称为Duhamel原理)。 1.1 叠加原理 在物理学的研究中经常会出现这样的现象:几种不同的原因的综合所产生的效果 等于这些不同原因单独产生的效果的叠加。例如,几个外力同时作用在一个物体上 所产生的加速度可以用单个外力各自单独作用在该物体上所产生的加速度相加而得 出。这个原理被称为 叠 加 原 理。叠加原理的适用范围很广泛,譬如,叠加原理对于 ::::::::::: 用线 .程 .方 .定 . 和线 .解 .条 .性 .性 . 件 . 描述的物理现象来说,都是成立的。下面我们利用一个具 体例子说明之。对于弦振动方程,如果u1 (t, x)是方程 utt − c2 uxx = f1 (t, x) 的解,而u2 是方程 utt − c2 uxx = f2 (t, x) 1
其中F, G为任意的具有二阶连续导数的单变量函数,并由此求解它的初值问题: t = 0 : u = ϕ(x), ∂u = ψ (x). ∂t
2. 问初始条件ϕ(x)与ψ (x)满足怎样的条件时,齐次波动方程初值问题的解仅由右传 播波组成? 3. 利用传播波法,求解波动方程的古沙(Goursat)问题 2 2 ∂ u 2∂ u = a , ∂t2 ∂x2 u|x−at=0 = ϕ(x), u|x+at=0 = ψ (x) (其中ϕ(0) = ψ (0)). 4. 对非齐次波动方程的初值问题(1.24),证明:当f (x, t)不变时, (1)如果初始条件在x轴的区间[x1 , x2 ]上发生变化,那么对应的解在区间[x1 , x2 ]的 影响区域以外不发生变化; (2)在x轴区间[x1 , x2 ]上所给的初始条件唯一地确定区间[x1 , x2 ]的决定区域中解的 数值。 6
再利用(1.6)式就可得到Cauchy问题(1.1)-(1.2)的解为 u(t, x) = 1 2c
t 0 x+c(t−τ )
f (τ, ξ )dξdτ =
x−c(t−τ )
1 2c
f (τ, ξ )dξdτ,
Ω
(1.19)
4
其中区域Ω为(τ, ξ )−平面上过点(t, x)向下做两特征线与ξ −轴所围成的三角形区域(见 图1.1)。 τ 6 ξ − x = c(τ − t) Ω
的解,那么对于任意的常数C1 和C2 ,函数 u(t, x) = C1 u1 (t, x) + C2 u2 (t, x) 是方程 utt − c2 uxx = C1 f1 (t, x) + C2 f2 (t, x) 的解。关于叠加原理的一个典型的例子就是声学中把弦线振动时所发生的复杂的声音 分解成各种单音的叠加。事实上,早在十八世纪Bernoulli以及以后的Fourier就利用这 个原理来研究弦振动方程的问题。 1.2 齐次化原理 考虑下述Cauchy问题 utt − c2 uxx = f (t, x), t = 0 : u = 0, ut = 0,
t
(1.3) (1.4)
(1.5)
u(t, x) =
0
w(t, x; τ )dτ.
(1.6)
定理1.1被称为齐次化原理或Duhamel原理。 证明 首先我们验证由(1.6)式定义的函数u(t, x)满足初始条件(1.2)式。 2
由(1.6)式,显然有 u(0, x) = 0. 另一方面,从(1.6)式可得
i=1 0
w(t, x; τ )dτ.
这样,我们从另外一个角度重新得到定理1.1。 ˜= 下 面 我 们 给 出w(t, x; τ )的 具 体 表 达 式 。 为 此 , 在Cauchy问 题(1.15)中 作 变 换t t − τ ,于是(1.15)便化为 w − c2 w = 0 (t ˜ > 0), xx ˜t ˜ t t ˜ = 0 : w = 0, w˜ = f (τ, x)
第三章
波动方程
波动方程是最典型的一类双曲型方程,它可以用来描述自然界以及工程技术中的 波动现象,例如在研究波的传播以及弹性体振动时经常会遇到这类方程。本章我们 将介绍波动方程的一些基本概念,方法和结果。在第一节中我们介绍一维波动方程 的Cauchy问题,着重介绍线形方程的叠加原理和齐次化原理(或称Duhamel原理)。 在第二节中我们介绍一维波动方程的初边值问题,着重介绍一种常见的解法—分离变 量法。第三节中介绍高维波动方程的Cauchy问题,特别地,用球平均法导出三维波动 方程Cauchy问题的解的表达式,即Poisson 公式,进而用Hadamard 的降维方法导出了 二维波动方程相应的解的公式。在第三节的基础上,在第四节中我们研究了波动方程 解的一些性质,譬如波的传播方式、衰减性及其正则性等,进而发现不同维数的波动 方程的解的性质有着巨大差别。在第五节中,我们介绍了高维波动方程的具有一般初 始条件的一般的Cauchy问题以及高维波动方程的混合初边值问题。在第六节中,我们 利用能量估计(或称能量积分)的方法,讨论了波动方程Cauchy问题以及初边值问题 解的唯一性和稳定性。这种方法的基础是能量守恒原理。
(1.15)
的解,则有 w(t, x; ti , ∆ti ) = ∆ti w(t, x; ti ). 于是,Cauchy问题(1.1)-(1.2)的解可以表示为
n n t
(1.16)
u(t, x) = lim
∆ti →0
w(t, x; ti , ∆ti ) = lim
i=1
∆ti →0
w(t, x; ti )∆ti =
t t
(1.8)
ut (t, x) = w(t, x; t) +
0 t
wt (t, x; τ )dτ =
0 t
wt (t, x; τ )dτ. (1.9)
utt = wt (t, x; t) +
0
wtt (t, x; τ )dτ =
0 t
wtt (t, x; τ )dτ + f (t, x).
另一方面,有 uxx =
= f (t, x). 在上式中的第三个等式中我们利用了方程(1.3)。(1.11)表明u(t, x)确实满足方程(1.1)。 这样我们就证明了定理1.1。 齐次化原理也可以用下述方法得到。 我们知道,非齐次项f (t, x)表示时刻 t在 x处的单位质量所受的外力,而ut 表示 质 点 的 速 度 。 把 时 间 段[0, t]分 成 若 干 个 小 时 段∆ti = ti+1 − ti (i = 1, 2, · · · , n),在 每 个 小 时 段∆ti 中 , 非 齐 次 项f (t, x)可 以 看 作 与 时 间t无 关 , 并 以f (ti , x)来 表 示 。 由 F (ti , x) (这里F (ti , x)表示外力,而ρ是密度函数),所以在时间段∆ti 内非齐 于f (ti , x) = ρ 次项所产生的速度改变是为f (ti , x)∆ti 。我们把这个速度改变量看作是在时刻ti 时的初 3
t
(1.24)
的解。 注记1.2 齐次化原理不仅可以应用于非齐次波动方程的Cauchy问题,而且也能应用 于初边值问题以及其它方程(譬如热传导方程)的定解问题,以后我们将多次用到这 一原理。
习 题
1. 证明方程 ∂ x ∂u 1 x ∂2u (1 − )2 = 2 (1 − )2 2 ∂x h ∂x a h ∂t 的通解可以写成 u= F (x − at) + G(x + at) , h−x (h > 0为常数)
t
[f (τ, x + c(t − τ )) + f (τ, x − c(t − τ ))] dτ,
0
(1.20) (1.21) (1.22) (1.23)
