五年级数学下册分解质因数练习(附答案)
小学数学解题方法解题技巧之分解质因数法

第一章小学数学解题方法解题技巧之分解质因数法通过把一个合数分解为两个或两个以上质因数,来解答应用题的解题方法叫做分解质因数法。
分解质因数的方法在求最大公约数和最小公倍数时有用,在学习有理数的运算、因式分解、解方程等方面也有广泛的应用。
分解质因数的方法还可为一些数学问题提供新颖的解法,有益于开辟解题思路,启迪创造性思维。
例1 一块正方体木块,体积是1331立方厘米。
这块正方体木块的棱长是多少厘米?(适于六年级程度)解:把1331分解质因数:1331=11×11×11答:这块正方体木块的棱长是11厘米。
例2 一个数的平方等于324,求这个数。
(适于六年级程度)解:把324分解质因数:324= 2×2×3×3×3×3=(2×3×3)×(2×3×3)=18×18答:这个数是18。
例3 相邻两个自然数的最小公倍数是462,求这两个数。
(适于六年级程度)解:把462分解质因数:462=2×3×7×11=(3×7)×(2×11)=21×22答:这两个数是21和22。
*例4 ABC×D=1673,在这个乘法算式中,A、B、C、D代表不同的数字,ABC是一个三位数。
求ABC代表什么数?(适于六年级程度)解:因为ABC×D=1673,ABC是一个三位数,所以可把1673分解质因数,然后把质因数组合成一个三位数与另一个数相乘的形式,这个三位数就是ABC所代表的数。
1673=239×7答:ABC代表239。
例5 一块正方形田地,面积是2304平方米,这块田地的周长是多少米?(适于六年级程度)解:先把2304分解质因数,并把分解后所得的质因数分成积相同的两组质因数,每组质因数的积就是正方形的边长。
五年级下册数学教案-分解质因数解答应用题-人教新课标(2014)

分解质因数解答应用题A 经典题型例1、把9、15、28、30、34、55、77、85这8个数平均分成两组,使每组4个数的乘积相等。
【思路导航】把8个数平均分成两组,每组4个数,要使两组数的乘积相等,这两组数的乘积中所含有的质因数必须完全相同。
因此,可以先将这8个数分解质因数,再按照每组中各个质因数的个数进行分组。
【解答示范】9=3×3 15=3×528=2×2×7 30=2×3×534=2×17 55=5×1177=7×11 85=5×17从上面18个质因数中可以看出,每组的4个数的乘积中,必须有2个2、2个3、2个5、1个7、1个11和1个17 答:这两组数分别是(9,28,55,85)和(15,30,34,77)【题后反思】要充分理解分解质因数的作用模仿提升11、把2、5、14、24、27、55、56、99这8个数平均分成两组,使每组4个数的乘积相等。
2.把40、44、45、63、65、78、99、105这8个数平均分成两组,使每组4个数的乘积相等。
例2 一个长方体木块,它的长、宽、高的厘米数正好是3个连续自然数,这个长方体的体积是720立方厘米。
这个长方体的表面积是多少平方厘米?【思路导航】长方体的体积=长x宽x高,因此,长、宽、高都是体积数720的约数。
又根据长、宽、高的厘米数正好是3个连续自然数,因此可以先把720分解质因数,然后将它的质因数重新分组,组合成3个连续自然数的乘积,得出这个长方体的长、宽、高,进而再求出它的表面积。
【解答示范】720=2×2×2×2×3×3×5=(2×2×2)×(3×3)×(2×5)=8×9×10(8×9+8×10+9×10)×2=484(平方厘米)答:这个长方体的表面积是484平方厘米。
【五年级】质数合数分解质因数练习题

质数、合数、分解质因数练习题1. 下面的数中,哪些是合数,哪些是质数。
1、13、24、29、41、57、63、79、87合数有:质数有:2. 写出两个都是质数的连续自然数。
3. 写出两个既是奇数,又是合数的数。
4. 判断:(1)任何一个自然数,不是质数就是合数。
()(2)偶数都是合数,奇数都是质数。
()(3)7的倍数都是合数。
()(4)20以内最大的质数乘以10以内最大的奇数,积是171。
()(5)只有两个约数的数,一定是质数。
()(6)两个质数的积,一定是质数。
()(7)2是偶数也是合数。
()(8)1是最小的自然数,也是最小的质数。
()(9)除2以外,所有的偶数都是合数。
()(10)最小的自然数,最小的质数,最小的合数的和是7。
()5. 在()内填入适当的质数。
10=()+()10=()×()20=()+()+()8=()×()×()6. 分解质因数。
65 56 94 76 135 105 87 93质数,合数1、在50以内的自然数中,最大的质数是(),最小的合数是()。
2、既是质数又是奇数的最小的一位数是()。
3、在20以内的质数中,()加上2还是质数。
4、如果有两个质数的和等于24,可以是()+(),()+()或()+()。
11、在自然数中,最小的奇数是( ),最小的偶数是( ),最小的质数是( ),最小的合数是( )。
14、质数只有( )个因数,它们分别是( )和( )。
15、一个合数至少有( )个因数,( )既不是质数,也不是合数。
16、自然数中,既是质数又是偶数的是( )。
17、在20至30中,不能分解质因数的数是( )。
29、在27、68、44、72、587、602、431、800中。
(共4分)奇数是:偶数是:30、在2、3、45、10、22、17、51、91、93、97中。
(共5分)质数是:合数是:15、两个质数相乘的积还是质数。
()16、一个合数至少得有三个因数。
五年级下册数学试题-2.2分解质因数-人教版(含答案)
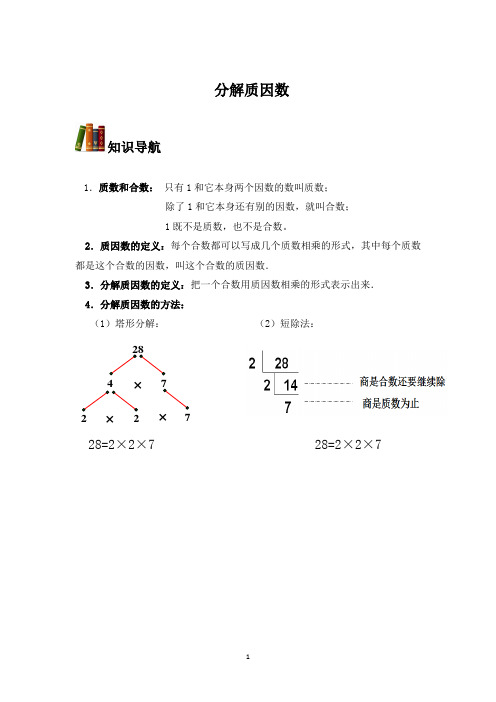
分解质因数知识导航1.质数和合数: 只有1和它本身两个因数的数叫质数;除了1和它本身还有别的因数,就叫合数; 1既不是质数,也不是合数。
2.质因数的定义:每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,叫这个合数的质因数.3.分解质因数的定义:把一个合数用质因数相乘的形式表示出来. 4.分解质因数的方法:(1)塔形分解: (2)短除法:28=2×2×7 28=2×2×7×××7227428例题分析【理解一】质数和合数.1.找出1-20各数的因数,看看有什么规律:2.质数:只有1和它本身两个因数的数。
3.合数:除了1和它本身还有别的因数的数。
4.在自然数里,1既不是质数也不是合数。
5.找出100以内的质数,做一个质数表。
例1.在括号里填上适当的质数。
18=()+()+()24=()+()=()+()=()+()例2.A、B、C是三个不同的质数,且A-B=C,若得数最小,请写出一组符合要求的数:A=()、B=()、C=()。
例3.一个四位数,千位上是最小的质数,百位上是最小的合数,十位上既不是质数也不是合数,个位上是10以内最大的质数,这个数是多少?例4.两个质数的和是 40,这两个质数分别是多少?它们的乘积最大是多少?巩固练习1.一个长方形的边长是以厘米为单位的质数,那么周长是以厘米为单位的().A.质数B.合数C.无法确定2.如果两个不同的质数相加还得到质数,其中一个质数必定是()。
3.在括号里填上适当的数.①11与()的积是合数②97与()的积是质数③23与()的积是偶数④17与()的积能被3整除⑤13与()的积能被5整除⑥29与()的积能被2、3整除⑦37与()的积能被3、5整除⑧41与()的积能被2、3、5整除4.当a分别是1、2、3、4、5时,6a+1是质数,还是合数?5.20以内的质数a和b的和是5的倍数,且a比b小4,这两个质数分别是多少?6.两个质数和为18,积是65,这两个质数是多少?【理解二】质因数和分解质因数.1.分解质因数:把一个合数用质因数相乘的形式表示出来。
小学五年级奥数第2课质数、合数和分解质因数试题附答案-精品

小学五年级上册数学奥数知识点讲解第2课《质数、合数和分解质因数》试题附答案一.基本慨念和知识L质数与合数一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数)。
一个数除了1和它本身,还有别的约数,这个数叫做合数。
要特别记住:1不是质数,也不是合数。
2.质因数与分解质因数如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
例:把30分解质因数。
解:30=2X3X5。
其中2、3、5叫做30的质因数。
又如12=2X2X3=22X3,2、3都叫做12的质因数。
二.例题例1三个连续自然数的乘积是210,求这三个数.例2两个质数的和是40,求这两个质数的乘积的最大值是多少?例3自然数123456789是质数,还是合数?为什么?例4连续九个自然数中至多有几个质数?为什么?例5把5、6、7、14、15这五个数分成两组,使每组数的乘积相等。
例6有三个自然数,最大的比最小的大6,另一个是它们的平均数,且三数的乘积是42560.求这三个自然数。
例7有3个自然数a、b、&己知aXb=6,bX c=15,例8一个整数a与1080的乘积是一个完全平方数.求a的最小值与这个平方数。
例9问36洪有多少个约数?例10求240的约数的个数。
答案二,例题例1三个连续自然数的乘积是210,求这三个数.7210=2X3X5X7・•・可知这三个数是5、6和7。
例2两个质数的和是40,求这两个质数的乘积的最大值是多少?解:把40表示为两个质数的和,共有三种形式:40=17+23=11+29=3+37。
V17X23=391>11X29=319>3X37=111O,所求的最大值是391。
答:这两个质数的最大乘积是391。
例3自然数123456789是质数,还是合数?为什么?解:123456789是合数。
因为它除了有约数1和它本身外,至少还有约数3,所以它是一个合数。
五年级下册数学一课一练质数和合数_人教新课标(含答案)

《质数和合数》同步练习一、单选题1.最小的质数与最小的合数的和是()A. 6B. 5C. 32.既是奇数又是质数的数是()A. 9B. 21C. 293.一个合数至少有()个因数。
A. 2B. 3C. 4D. 14.13的倍数是()A. 合数B. 质数C. 可能是合数,也可能是质数5.2是()。
A. 合数B. 质数C. 因数6.一个正方形的边长是一个质数,这个正方形的周长一定是()。
A. 合数B. 奇数C. 质数7.下面三个连续自然数都是合数的是()A. 4、5、6B. 7、8、9C. 14、15、16D. 18、19、208.比10小的质数有()个。
A. 3B. 4C. 个数是无限的9.71和2都是( )。
A. 合数B. 偶数C. 质数10.两个质数的积一定是()A. 奇数B. 偶数C. 质数D. 合数11.两个奇数的和()。
A. 一定是奇数B. 一定是偶数C. 可能是奇数也可能是偶数12.1是()。
A. 质数B. 合数C. 奇数13.自然数(0除外)按因数的个数分,可以分为()。
A. 奇数和偶数B. 质数和合数C. 质数、合数和114.一个质数的因数有()个。
A. 1B. 2C. 315.下列数中,是质数的有()A. 12B. 35C. 4716.下列数中,是合数的有()A. 7B. 23C. 9117.一个合数至少有()个因数。
A. 1B. 2C. 318.把66分解质因数是()。
A. 66=1×2×3×11B. 66=6×11C. 66=2×3×1119.自然数按是不是2的倍数来分,可以分为()。
A. 奇数和偶数B. 质数和合数C. 质数、合数、0和120.有两个不同质数的和是22,他们的积是()A. 105B. 121C. 85D. 14321.最小的质数和最小的合数的积是()A. 6B. 4C. 822.8和9都是()A. 奇数B. 合数C. 偶数23.两个质数的和是12,积是35,这两个质数是()A. 3和8B. 2和9C. 5和7二、填空题24.一个两位数,十位上既不是质数也不是合数,个位上既是奇数又是合数,这个数是________。
五年级数学下册试题因数和倍数重难点讲解(质数和合数、分解质因数)+答案
数学学科专属辅导讲义学员姓名教师姓名班主任上课日期上课时间年级课时教学内容因数与倍数2教学目标1、理解掌握质数和合数2、学会分解质因数教学重难点1、理解掌握质数和合数2、学会分解质因数教学内容1、理解掌握2、3、5的倍数的特征1、把55个橘子分给甲、乙、丙三人,甲得到的橘子数是乙的2 倍,且甲、乙得到的橘子数都比丙多,丙得到的橘子数比10 多,则甲、乙、丙三人各得多少个?2、一个数加3是5的倍数,减去3是6的倍数,这个数最小是多少?【课前导入1】写出3、5、7、8、10、12、13、15这7个数的所有因数观察以上数的因数,他们有什么特点。
总结:像2、3、5这几个数,只有1和它本身两个因数,这样的数叫作质数,也称为素数;像6,8、9这几个数,除了1和它本身还有别的因数,也就是有两个以上因数,这样的数叫作合数。
练习1:(1)质数只有( )个因数,合数至少有( )个因数。
(2) 自然数中,最小的质数是( ),最小的合数是( )。
(3) 比10小的数里,质数有( )个,合数有( )个。
(4) 20的因数有( ),其中是质数的有( )。
问题1:1是质数还是合数?说说想法。
问题2:可以将大于O的自然数还可以按什么分类,分成几类?问题3:按质数和合数的分类和偶数、奇数的分类比较,有什么不同?总结:20以内的质数是:2、3、5、7、1 1、1 3、1 7、19。
质数不都是奇数,因为2是质数。
【课前导入2】请把5和28分别写成两个数相乘的形式。
77=53+17+7再任取一个奇数461,那么461=449+7+5也是三个素数之和.461还可以写成257+199+5仍然是三个素数之和.这样,我就发现:任何大于5的奇数都是三个素数之和.1、30的所有因数有( )A.1、2、3、5和10B. 2、3、5、10和15C. 1、2、3、5、6、10、15和302、当两个数互质时,它们的最大公因数是( )。
A. 1B. 2C. 无法确定3、把20分解质因数应该写成()A. 20=1×2×2×5B. 2×2×5=20C. 20=2×2×54、14和28的公倍数()。
苏教版数学五年级下册 质因数和分解质因数
质因数和分解质因数
情境导入
举例说一说一个数的 因数可能有几个?
最少有1个,也可能 2个、3个及以上。
如1的因数只有1,2的 因数有1和2,4的因数 有1、2、4,10的因数 有1、2、5、10。
探究新知
在5=1×5、28=4×7中,哪些数是5的因数?哪些 例 7 数是28的因数?在这些因数中,哪几个数是质数? 5=1×5,1和 28=4×7,4和 在1、5、4、7中, 5是5的因数。 7是28的因数。 5和7是质数。
人们经常用短除法来分解质因数。
把每个除数和最后的商写成连乘的形式: 30=2×3×5。
课堂小结
这节课你们都学会了哪些知识?
1.我认识了质因数,如果一个数的因数是质数,这 个因数就是它的质因数。
2.把一个合数用质数相乘的形式表示出来,叫作分 解质因数。
试一试:是不是任何一个大于4的偶数都可以表示 成两个奇质数之和。
6.下面哪几个班的学生可以分成人数相同的几个小组? 哪几个班不可以?为什么?
班级 一班 二班 三班 四班 人数 39 41 40 43
一班和三班的学生可以分成人数相同的几 个小组,二班和四班的学生不可以分成人 数相同的几个小组,因为41和43是质数, 39和40是合数 。
如果一个数的因数是质数,这个因数就是它的质因数。
5=1×5,1和 28=4×7,4和 在1、5、4、7中, 5是5的因数。 7是28的因数。 5和7是质数。
上面的算式中,哪个数是哪个数的质因数?
5是5的质因数,7是28的质因数。
把30用几个质数相乘的形式表示出来。
例8
15
3
5
2
3
5
把一个合数用质数相乘的形式表示出来,叫作分解 质因数。
(完整版)分解质因数练习题答案
以看出,这八个数中,共含有八个 2,六个 3,二个 5,二个
7 和二个 11,如果要把
这八个数分成两组且积相等,那么,每组数中应含有
四个 2,三个 3,一个 5,一个 7,一个 11。经排列为和
:把 40、44、 45、63、 65、78、 99、105 这八个数平
2016 全新精品资料 - 全新公文范文 -全程指导写作 –独家原创 5 / 12
精品文档 数平均分成三组,每组的数相乘积相等,写出这三组数。
解:将这几个数分解质因数得: 30 = × ×
3= × 11 4= × × 5= × × 13 6= × 13 6= × × 11 7= × 11 7= × × 13 105= 个质因数 11, × 从上可知:共总有 6 个质因数 2,6 个质因数 3,,3 个 质因数 5,3 个质因数 7,3 个质因数 11,3 个质因数 13,这 些质因数平均分成 3 组,每组就有 2 个 2,2 个 3,1 个 5,1 个 7, 1 个 11, 1 个 13. 即: 30、 7、8,33、2、 105 ,42、、66。 6 、甲数比乙数大 9,两个数的积是 792,求甲、乙数 分别是多少? 解: 792=2×2×2×3×3×11=24×33 所以:甲数是 33,乙数是 24 7 、四个连续奇数的积是 19305,这四个奇数各是多 少?
2016 全新精品资料 - 全新公文范文 -全程指导写作 –独家原创 6 / 12
精品文档 解: 19305=3×3×3×5×11×13=9×15×11×13 答:这四个奇数各是 9、15、 11、13。 8 、有四个孩子,恰好一个比一个大 1 岁,4 人的年龄 积是 5040,问这四个孩子中最大的几岁? 解: 5040=2×2×2×2×2×3×3×5×7 =2×2×2×2×2×5×3×3×7 =8×10×9×7 答:这四个孩子中最大的是 10 岁。 9 、有三个自然数 a、 b、 c,已知 a×b= 30,b×c= 35,c×a= 42,求 a×b×c 的积是多少? 解:因为 a×b= 30,b×c= 35,c×a= 42,所以: a×b×b×c×c×a=30×42×35 =2×3×5×2×3×7×5×7 =2×2×3×3×5×5×7×7 则: a×b×c=5×6×7=210 答: a×b×c 的乘积是 210. 10 、两个两位整数的积是 6232,这两个数中较大的数 是多少? 解: 6232=2×2×2×19×41=76×82 所以,这两数中较大数是 82 11 、小明问小强:你射击三枪,共中几环?小强:一 二枪的环数乘积是 48;二三枪的环数乘积是 72;一三枪的
小学数学五年级 分解质因数 PPT+作业(带答案)
因数个数为:6×1=6(个)
求限制条件的因数个数 ①先满足条件 ②求符合条件的因数个数
例5
因数个数公式
一个整数有六个因数,将其分解质因数的结果写成乘方的形式,发现只含有2和3两种质因
数。这个整数可能是多少?
底数只有2和3,指数为大于或等于1的整数
总结:求有限制条件的因数个数:①先满足条件;②求符合条件的因数个数
练习4
在 96 的因数中,是 2 的倍数的有多少个?含有因数 3 的有多少个?(利用公式法求解。)
96 25 31 是2的倍数的情况: 2的指数有1、2、3、4、5五种选择。 3的指数有0、1两种选择。
因数个数为:5×2=10(个)
例2
请分别写出 12、24、36 的所有因数。
配对法找因数,按照从小到大的顺序
(1)12=1×12=2×6=3×4 12的因数有:1、2、3、4、6、12
(2)24=1×24=2×12=3×8=4×6 24的因数有:1、2、3、4、6、8、12、24
(3)36=1×36=2×18=3×12=4×9=6×6 36的因数有:1、2、3、4、6、9、12、18、36
120分解质因数为: 120=23 31 51
2 120
2 60 2 30 3 15
5
120的因数个数为: (3+1)×(1+1)×(1+1)=16(个)
总结:短除法分解质因数步骤: (1)写出短除符号;(2)写质因数(写在左侧,一般从最小质因数开始写);(3) 做除法求商(写在下方)重复(1)(2),直到商是质数为止;(4)写出乘积的形式
求有限制条件的因数个数:①先满足条件;②求符合条件的因数个数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分解质因数练习
一、填空。
1、把一合数用几个()的形式表示出来,叫做()。
2、84的质因数有()。
3、有三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是210,这三个小朋友的年龄分别是()岁、()岁、()岁。
4、A、B、C是三个不同的质数,且A-B=C,若得数最小,那么A=()B=()C=()
3、26、 1.1这几个数中,自然数有(),5、在0、3、140、17、
11
偶数有(),奇数有(),质数有(),合数有()。
6、48的因数有(),它的质因数有()。
7、最小的质数是(),在一位数中,既不是奇数又不是合数的数是()。
8、只有()的数,叫质数,也叫()数。
9、分解质因数的方法有:()分解质因数,用()法分解质因数。
10、非0自然数按因数的个数可以分为()、()和()三类。
11、一个质数,它的最大的因数就是()。
12、一个正方形的边长是质数,它的周长一定是()数。
二、判断题。
(对的在括号里画“√”,错的画“×”)
1、一个数的因数一定比这个数的倍数小。
()
2、因为2.4÷0.6=4,所以0.6是2.4的倍数。
()
3、一个数的最小倍数与最大因数都是26,这个数一定是26.()
4、只要两个整数相除没有余数(0除外),就说被除数是除数的倍数。
()
三、用短除法分解质因数。
48 51 132
1110 129 91
分解质因数练习(答案)
一、填空。
1、把一合数用几个(质数)的形式表示出来,叫做(分解质因数)。
2、84的质因数有(2、
3、7 )。
3、有三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是210,这三个小朋友的年龄分别是(5)岁、(6)岁、(7)岁。
4、A、B、C是三个不同的质数,且A-B=C,若得数最小,那么A=(5)B=(3)C=( 2 )75
3、26、 1.1、15这几个数中,自然数有(0、3、140、5、在0、3、140、17、
11
17、26、15 ),偶数有(0、140、26),奇数有(3、17、15),质数有(3、17),合数有(140、26、15 )。
6、48的因数有(1、2、3、4、6、8、12、16、24、48),它的质因数有(2、3)。
7、最小的质数是(2),在一位数中,既不是奇数又不是合数的数是(2)。
8、只有(1和它本身两个因数)的数,叫质数,也叫(素)数。
9、分解质因数的方法有:(相乘法)分解质因数,用(短除法)法分解质因数。
10、非0自然数按因数的个数可以分为( 1 )、(质数)和(合数)三类。
11、一个质数,它的最大的因数就是(它本身)。
12、一个正方形的边长是质数,它的周长一定是(合)数。
二、判断题。
(对的在括号里画“√”,错的画“×”)
1、一个数的因数一定比这个数的倍数小。
(×)
2、因为2.4÷0.6=4,所以0.6是2.4的倍数。
(×)
3、一个数的最小倍数与最大因数都是26,这个数一定是26.(√)
4、只要两个整数相除没有余数(0除外),就说被除数是除数的倍数。
(×)
三、用短除法分解质因数。
48=2×2×2×2×351=3×17132 =2×2×3×11
1110=2×3×5×37129 =3×4391 =7×13。
