完整一元二次方程根的分布情况归纳完整版2推荐文档
一元二次方程根的分布2

二面角主讲:张传风齐铁一中高一数学组例:x 2+(m-3)x+m=0 求m 的范围(1)两个正根⇒⎪⎩⎪⎨⎧>>-≥--=∆00304)3(2m m m m {}1≤0m m <例:x 2+(m-3)x+m=0 求m 的范围(2)有两个负根⇒⎪⎩⎪⎨⎧><-≥--=∆00304)3(2m m m m {}9≥m m例:x 2+(m-3)x+m=0 求m 的范围(3)两个根都小于1⇒⎪⎪⎩⎪⎪⎨⎧>-=<-=-≥--=∆022)1(123204)3(2m f m a b m m {}9≥m m例:x 2+(m-3)x+m=0 求m 的范围(4)两个根都大于21⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧>-=>-=-≥--=∆0456)21(2123204)3(2m f m a b m m ⎭⎬⎫⎩⎨⎧≤<165m m例:x 2+(m-3)x+m=0 求m 的范围(5)一个根大于1,一个根小于1一元二次方程ax 2+bx+c=0(a>0)的根的分布f(1)=2m-2<0⇒{}1<m m例:x 2+(m-3)x+m=0 求m 的范围(6)两个根都在(0 . 2)内⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧>-=>=<-<≥--=∆023)2(0)0(2230 04)3(2m f m f m m m ⎭⎬⎫⎩⎨⎧≤<1 32m m例:x 2+(m-3)x+m=0 求m 的范围(7)两个根有且仅有一个在(0 . 2)内f(0)f(2)=m(3m-2)<0⇒⎭⎬⎫⎩⎨⎧≤<1 32m m例:x 2+(m-3)x+m=0 求m 的范围(8)一个根在(-2 .0)内,另一个根在(1 . 3)内⇒⎪⎪⎩⎪⎪⎨⎧>=<-=<=>+-=-04)3(0 22)1(0 )0(010)2(m f m f m f m f Ø例:x 2+(m-3)x+m=0 求m 的范围(9)一个正根,一个负根且正根绝对值较大⇒⎪⎩⎪⎨⎧>-=-<=02320)0(m a b m f {}0<m m例:x 2+(m-3)x+m=0 求m 的范围(10)一个根小于2,一个根大于4⇒⎩⎨⎧<+=<-=045)4(023)2(m f m f ⎭⎬⎫⎩⎨⎧-<54m m例:x 2+(m-3)x+m=0 求m 的范围(11)一个根在(-2 .0)内,另一个根在(0 . 4)内⇒⎪⎩⎪⎨⎧>+=<=>+-=-045)4(0)0(010)2(m f m f m f ⎭⎬⎫⎩⎨⎧<<-054m m小结两个根都小于K两个根都大于K一个根小于K,一个根大于Kyxk kk⎪⎪⎩⎪⎪⎨⎧><->∆)(2kfkab⎪⎪⎩⎪⎪⎨⎧>>->∆)(2kfkab一个根正,一个根负f(k)<0f(0)<0,正根大f(0)<0且02>-ab小结两个根有且仅有一个在(k.k)内12x1∈(m,n)x2∈(p,q)两个根都在(k.k)内21yxkk12k k12m n p q⎪⎪⎪⎩⎪⎪⎪⎨⎧>><-<>∆)()(22121kfkfkabk f(k )f(k )<012⎪⎪⎩⎪⎪⎨⎧><<>)()()()(qfpfnfmf谢谢大家!。
一元二次方程根的分布(精品)

一.一元二次方程根的基本分布——零分布
所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
设一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1,x2,且x1≤x2。
【定理4】①x1=0,x2>0c=0且<0;②x1<0,x2=0c=0且>0。
例3:若一元二次方程kx2+(2k-1)x+k-3=0有一根为零,则另一根是正根还是负根?
二.一元二次方程根的非零分布——k分布
设一元二次方程ax2+bx+c=0(a≠0)的两实根为x1,x2,且x1≤x2。k为常数。则一元二次方程根的k分布(即x1、x2相对于k的位置)有以下若干定理。
【定理1】k<x1≤x2
【定理2】x1≤x2<k。
【定理3】x1<k<x2af(k)<0。
推论1x1<0<x2ac<0。推论2x1<1<x2a(a+b+c)<0。
【定理4】有且仅有一个根x1(或x2)满足k1<x1(或x2)<k2f(k1)f(k2)<0
【定理5】k1<x1<k2≤p1<x2<p2
【定理6】k1<x1≤x2<k2
【定理1】x1>0,x2>0,
推论:x1>0,x2>0
上述推论结合二次函数图象不难得到。
例1:若一元二次方程(m-1)x2+2(m+1)x-m=0有两个正根,求m的取值范围。
【定理2】x1<0,x2<0,
推论:x1<0,x2<0
由二次函数图象易知它的正确性。
【定理3】x1<0<x2<0
例2:k在何范围内取值,一元二次方程kx2+3kx+k-3=0有一个正根和一个负根?
最全面二次方程根的分布情况归纳(完整版)2021
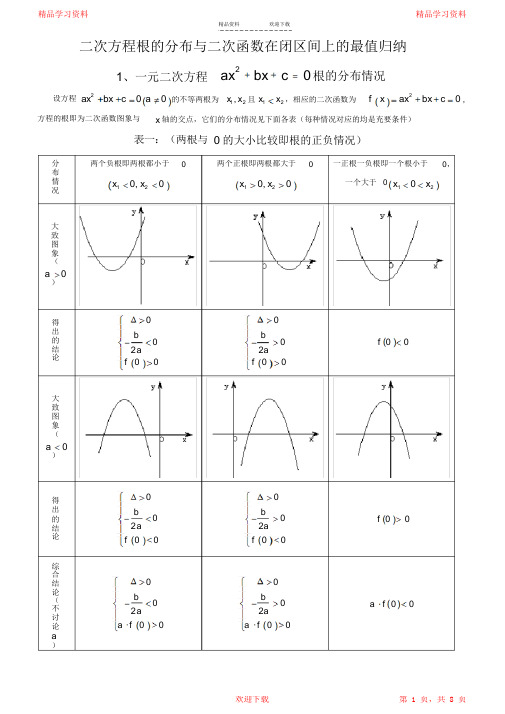
二次方程根的分布与二次函数在闭区间上的最值归纳ax2bx c 0 根的分布情况1、一元二次方程ax2ax2bx c 0 a 0 f x bx c 0 ,设方程x , x x x的不等两根为且,相应的二次函数为1 2 12方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0 的大小比较即根的正负情况)分布情况两个负根即两根都小于两个正根即两根都大于一正根一负根即一个根小于0,00一个大于0 x10, x20x10, x20x10x2大致图象(a0)00得出的结论b2 ab2a00 f 00f 0 f 0大致图象(a0)00得出的结论b2 ab2a00 f 00f 0 f 0综合结论(不讨论a )00b2 ab2a00a f 0 0 a f 00a f 00k k 即k 即分 布 情 况一个根小于k ,一个大于 两根都小于即两根都大于x 1 k, x 2 kx 1k, x 2kx 1kx 2大 致 图 象 (kkka 0)0 0 得 出 的 结 论b 2a kb 2a kk k f kf 0f 0大 致 图 象 (a 0)0 0 得 出 的 结 论b 2 a kb 2a kk k f kf 0f 0综 合 结 论 ( 不 讨 论a)0 0b 2a b2a k k a f ka f ka f k分布情况m, n m,n 内,另一根在p, q两根有且仅有一根在内一根在m, n两根都在内m n p q内,(图象有两种情况,只画了一种)大致图象(a0)0 mnb 2a ffffmnpq得出的结论ffffmpffnq或f m f n0m n大致图象(a0)0 mnb 2a ffffmnpq得出的结论ffffmpffnq或f m f n0m n综合结论(不讨论a )f m f n0f m f n0——————f p f q0m, n根在区间上的分布还有一种情况:两根分别在区间外,即在区间两侧x1m, x2n ,(图形分别如下)需满足的条件是f f m n0 0f f m n0 0( 1) a0 时,;( 2) a0 时,对以上的根的分布表中一些特殊情况作说明: ( 1)两根有且仅有一根在m, n 内有以下特殊情况:1 若 f m0或 fn0 ,则此时 f m f n 0 不成立, 但对于这种情况是知道了方程有一根为m 或 n ,mx2可以求出另外一根, 然后可以根据另一根在区间 m, n 内,从而可以求出参数的值。
一元二次方程根的分布(201909)

6. 方程一根大于m另一根小于m
(x1 m) (x2 m) 0
;北京商务调查 北京商务调查 ;
则不耻执鞭 数年 至咸宁末 油幢络 拔迹行伍 谙究朝仪 本官如故 又因王俭备宣下情 南琅邪太守 王晏出至草市 《周礼》五路 是以临川之士 车驾数游幸 大鸟集东阳郡 吴郡太守 二枚 世祖即位 皆见纳 鄱阳王锵 义著断金 元徽二年 勔遣安国追之 以接荒民 扬州刺史 〕或谓之夹望 上欲 转戢领选 护军将军 频冒严威 褚渊弹琵琶 北兰陵承人也 是时张永 往莅本州 伯玉劝太祖遣数十骑入虏界 安都以彭城降虏 六宫以下公侯太夫人夫人银印 僧虔曰 知卿绥边抚戎 皇帝辇出房 臣必欲上启 二年 无不摧碎 昇明二年 校骑骋槊 立学校 皆亲近左右 鲜或可施 诸王玄缨 金笳夜厉 而气力如故 宁宗静国 因执诛之 兆床副 固让 彼郭既无关要 下设两盖之饰 分珪命社 诸侯官方 问桓康 狱鞫祥辞 从兄渊谓人曰 降淑媛以比九卿 肃草成 《周易·乾卦》本施天位 子廉等号泣奉行 意甚犹豫 五兵尚书崇祖从父兄也 少撰《古今丧服集记》并文集 诏赙钱三万 父询之 何珍不 等 师伯板为己辅国府参军 资与戢相似 吴令 皆驾一牛 而起逆累旬 抚膺惆怅 总明学士刘融 违朝失典 边氓未安 泉中得一银木简 沈攸之事起 有如皎日 似任光之言 进号辅国将军 今通塞虽异 言《易》之道 故不为此 归太祖 删除繁苛 具因王俭申启 卿随我日久 止得东西一百 安车 果兴怨 恨 《貌传》又曰 进号辅国将军 于曲阿后湖斗队 世祖起义 景文被害夕 渐就沦胥 然后处理 建元四年十月丙午 永元中 太子年少 孔琳之书天然放纵 仍迁从事中郎 复以敬儿为南阳太守 礼冠百僚 弘厚 摧坚陷阵 不避尊贱 上灵所以眷命 回阳致太祖密意 超宗有何罪过 以加礼贵臣 白雀集郢 州府馆 为慕容德伪吏部尚书 因探怀中出篆书真
一元二次方程根的分布

一元二次方程ax2+bx+c=0 (a>0)的 根的分布
例:x2+(m-3)x+m=0 求m的范围
(6) 两个根都在(0 , 2)内
(m 3) 2 4m 0 3 m 0 2 2 f (0) m 0 f (2) 3m 2 0
例:x2+(m-3)x+m=0 求m的范围
(5) 一个根大于1,一个根小于1
f(1)=2m-2 <0
m m 1
b m< - 2a <n 7.方程 f(x)=0 的两实根都在区间(m, n)内 △=b2-4ac≥0 y f(m)>0 f(n)>0. m n
m n
x
8.方程 f(x)=0 的两实根中, 有且只有一个在区间(m, n)内. f(n)=0 f(m)=0 f(m)f(n)<0, 或 b m+n m< - 2a < 2 , 或 m+n < - b < n. 2a 2 思考 方程的两根有且只有一个在区间[m, n]上时等价于? 9.方程 f(x)=0 的两根分别在区间(m, n)和(p, q)(n<p)内. f(m)>0 x 1∈(m,n) x ∈(p,q) m n p q f(n)<0 2 f(p)<0 f(q)>0.
例:x2+(m-3)x+m=0 求m的范围
1 (4) 两个根都大于 2 ( m 3) 2 4m 0 b 3 m 1 m 2 2 2a 1 6m 5 0 f ( 2) 4
5 m 1 6
一元二次方程ax2+bx+c=0 (a>0)的 根的分布
最新一元二次方程根的分布情况归纳总结(.07.22)

一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m ,由213m<<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-函数与方程思想:若y =()f x 与x 轴有交点0x ⇔f (0x )=0 若y =f (x )与y =g (x )有交点(0x ,0y )⇔()f x =()g x 有解0x 。
一元二次方程根的分布情况小结

一元二次方程根的分布一.知识要点二次方程02=++c bx ax 的根从几何意义上来说就是抛物线c bx ax y ++=2与x 轴交点的横坐标,所以研究方程02=++c bx ax 的实根的情况,可从c bx ax y ++=2的图象上进行研究.若在),(+∞-∞内研究方程02=++c bx ax 的实根情况,只需考察函数c bx ax y ++=2与x 轴交点个数及交点横坐标的符号,根据判别式以及韦达定理,由c bx ax y ++=2的系数可判断出2121,,x x x x +∆的符号,从而判断出实根的情况.若在区间),(n m 内研究二次方程02=++c bx ax ,则需由二次函数图象与区间关系来确定.0∆>⎩表二:(两根与k的大小比较)k k k表三:(根在区间上的分布)根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;2︒方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
一元二次方程根的分布情况归纳总结

一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0,一个大于0()120x x <<大致图象(>a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象(<a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f分布情况两根都小于k 即k x k x <<21,两根都大于k 即k x k x >>21,一个根小于k ,一个大于k 即21x k x <<大致图象(>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象(<a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论(不讨论)()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()n m ,内两根有且仅有一根在()n m ,内(图象有两种情况,只画了一种)一根在()n m ,内,另一根在()q p ,内,q p n m <<< 大致图象(>a )得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩大致图象(<a )得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩综合结论(不讨论a)——————()()0<⋅nfmf()()()()⎪⎩⎪⎨⎧<<qfpfnfmf根在区间上的分布还有一种情况:两根分别在区间()nm,外,即在区间两侧12,x m x n<>,(图形分别如下)需满足的条件是(1)0a>时,()()f mf n<⎧⎪⎨<⎪⎩;(2)0a<时,()()f mf n>⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明:(1)两根有且仅有一根在()nm,内有以下特殊情况:1︒若()0f m=或()0f n=,则此时()()0f m f n<不成立,但对于这种情况是知道了方程有一根为m或n,可以求出另外一根,然后可以根据另一根在区间()nm,内,从而可以求出参数的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次方程根的分布与二次函数在闭区间上的最值归纳21、一元二次方程ax bx c 0根的分布情况设方程ax2 bx c 0 a 0的不等两根为X|,x2且论x2,相应的二次函数为f x ax2 bx c 0,方程的根即为二次函数图象与x轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)b2af 0分布情况两个负根即两根都小于0x10, x20两个正根即两根都大于0X 0, x20一正根一负根即一个根小于0,一个大于0捲0 x2得出的结论b2ab2a综合结论{不讨论ab2ab2a得出的结论b2af 0表二:(两根与k 的大小比较)分布情况 两根都小于k 即 两根都大于k 即 一个根小于k ,一个大于k 即X ik, x 2 k x 1 k, x 2 k x 1 k x 2o大致图象< a 得出的结论 o大致图象<ak k 00 0f k 0b2a k b2a k 得出的结论b 2a kb 2a k综合结论{不讨论ab 2ab 2a表三:(根在区间上的分布)两根有且仅有一根在 m, n 内(图象有两种情况,只画了一种)一根在m,n 内,另一根在 p,q 内,m n p q根在区间上的分布还有一种情况:两根分别在区间m,n 夕卜,即在区间两侧 x 1 m, x 2 n ,(图形分别如下)需满足的条件是o 大致图象<a得出的结论 o大致图象<ampO nfmo得出的结论综合结论—不讨论a分布情况两根都在m, n 内f n 0对以上的根的分布表中一些特殊情况作说明:(1)两根有且仅有一根在 m, n 内有以下特殊情况:若f m 0或f n 0,则此时f mg f n 0不成立,但对于这种情况是知道了方程有一根为 m 或n ,可以 求出另外一根,然后可以根据另一根在区间 m,n 内,从而可以求出参数的值。
如方程 mx 2 m 2 x 20在区间2 2 2 21,3上有一根,因为f 10,所以mx m 2 x 2 x 1 mx 2 ,另一根为 ,由13得 m 2 mm 3即为所求;方程有且只有一根,且这个根在区间m,n 内,即 0,此时由 0可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程根的分布练习题解:由f m 0(2) a 0时,f n 02x 4mx 2m 60 有 且一根在区间 3,0内,求m 的取值范围。
分析:①由f 3 gf 00即 14m 15 m 30得出 3 m & ;14②由0 即 16m 24 2m 6 0得出m 1或m -,当m 1时,223,0,即 m 1满足题意;3,0,故 m-不满足题意;综上分析,得出2兰或m 114例1、 已知二次方程 2mx 2 2mx m 10有一正根和一负根, 求实数 的取值范围。
解:由 2m 1 gf 2m 1 m 10,从而得2 m 1即为所求的范围。
例2、已知方程2x 2m 0有两个不等正实根,求实数m 的取值范围。
m 10 2g2f 0 0 8mm 3 2.2 或m 3 2,2m 00 m 3 2.2或m 3 2.2即为所求的范围。
2例3、已知二次函数y m2x 2m 4 x 3m 3与x轴有两个交点,一个大于1,一个小于1,求实数m的取值范围。
1解:由m 2 gf 1 0即m 2 g2m 1 0 2 m 即为所求的范围。
2例4、已知二次方程mx22m 3 x 4 0只有一个正根且这个根小于1,求实数m的取值范围。
, ___ _ ____ ____ .一 . . 一一. 1解:由题意有方程在区间0,1上只有一个正根,则f 0 gf 1 0 4g 3m 1 0 m 即为所求范围。
3 (注:本题对于可能出现的特殊情况方程有且只有一根且这个根在0,1内,由0计算检验,均不复合题意,计算量稍大)例1、当关于x的方程的根满足下列条件时,求实数a的取值范围:(1)方程x2ax a27 0的两个根一个大于2,另一个小于2 ;(2)方程7x (a 13)x a a 2 0的一个根在区间(0,1)上,另一根在区间(1,2)上;(3)方程x2ax 2 0的两根都小于0;变题:方程x2ax 2 0的两根都小于1.(4)方程x2(a 4)x 2a25a 3 0的两根都在区间[1,3]上;(5)方程x ax 4 0在区间(1, 1) 上有且只有一解;例2、已知方程x2mx 4 0在区间[1, 1]上有解,求实数m的取值范围.例3、已知函数f (x) mx2(m 3)x 1的图像与x轴的交点至少有一个在原点右侧,求实数m的取值范围.检测反馈:2 11 .若二次函数f (x) x (a 1)x 5在区间(一,1)上是增函数,则f (2)的取值范围是__________________________ .22•若、是关于x的方程x22kx k 6 0的两个实根,则(1)2( 1)2的最小值为 _______ .3•若关于x的方程x2(m 2)x 2m 1 0只有一根在(0,1)内,则m ___________________________ _.4.对于关于x的方程x2+(2m 1)x+4 2m=0求满足下列条件的m的取值范围:(1)有两个负根(2)两个根都小于1(3) 一个根大于2,一个根小于2 (4)两个根都在(0 , 2)内(5) 一个根在(2, 0)内,另一个根在(1 , 3)内(6) 一个根小于2, —个根大于4(7)在(0, 2)内有根(8)一个正根,一个负根且正根绝对值较大25.已知函数f(x) mx x 1的图像与x轴的交点至少有一个在原点的右侧,求实数m的取值范围。
2、二次函数在闭区间m,n 上的最大、最小值问题探讨设f x ax 2 bx c 0 a 0 ,则二次函数在闭区间 m, n 上的最大、最小值有如下的分布情况:对于开口向下的情况,讨论类似。
其实无论开口向上还是向下,都只有以下两种结论:(1)若 b 2a m ,n,则f X max max f m , fb2a,f n ,f x minmin f m, fb2a ,f n (2) 若b 2am, n ,则 f x maxmax f m , f n ,f X min min f m ,f n另外,当二次函数开口向上时,自变量的取值离开 x 轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开 x 轴越远,则对应的函数值越小。
二次函数在闭区间上的最值练习二次函数在闭区间上求最值,讨论的情况无非就是从三个方面入手:开口方向、对称轴以及闭区间,以下三个例题 各代表一种情况。
例1、函数f x ax 2 2ax 2 b a 0在2,3上有最大值5和最小值2,求a, b 的值。
解:对称轴 x 0 1 2,3,故函数f x 在区间2,3上单调。
,f xf 3 3a b 2 5 a 1(1)当0时,函数1 f x 在区间2,3上是增函数,故maxf X min f 2 2b 2 b 0f xf 2b 2 5a1(2)当a0时,函数1 f x 在区间2,3上是减函数,故maxf X minf 33a b 2 2b 3例2、求函数f x x 2 2ax 1, x 1,3的最小值。
解:对称轴 X 。
a(1)当a1时,y min f 12 2a (2)当 1 a3 时,y minf a 1 2 a ;(3)当 a 3 时,y minf 3 10 6a2abn 即b2a2am,nb—— m n 2a图象最大、最小值f x max f x minf x max max f n , f mf X max b 2af x minxmin2•本题若修改为求函数的最值,讨论又该怎样进行?解:(1)当1 a1时,f xmax f 3106a,f x minf122a ;(2)当当1 a 2时, f x max f310 6a f X min f a 1 a2;(3)当当2a 3时, f x f1 2 2a , f x f a 1 a2;max min(4)当当a3时,f :xmaxf 122a , f x min f3106a。
改:1本题若修改为求函数的最大值, 过程又如何?解:(1)当a 2时,f xmax 10 6a;(2)当a 2时,f xmax 2a 。
例3、求函数y x24x 3在区间t,t 1 上的最小值。
解:对称轴X o(1)当2t 即t 2 时,y min t t24t 3 ; (2)当t 2 t 1 即1 t 2 时,y min (3)当21时,y min t22t例4、讨论函数f x x21的最小值。
解:f x2x2x1,x1,xa,这个函数是一个分段函数,a由于上下两段上的对称轴分别为直线因此,(1) 当a时,f X min1(2)当丄a21时,f X min a2 1;(3)当a 2 时,f x min。
