人口预测方法(总结)
人口预测的几种方法

人口预测的几种方法附录A 重要技术方法附表A1 土地需求预测的步骤与方法一、人口预测在调查分析规划期间人口数量、构成及动态变化趋势的基础上,测算总人口、城镇人口、农村居民点人口增长变化规模。
(一)总人口预测1、人口变动比较稳定地区的人口预测法在人口变动比较稳定的地区,可采用自然平均增长法预测。
计算公式如下:PN=P0(1+K)n±ΔP式中:PN──规划目标年总人口(人)P0──规划基期年总人口(人)K──规划期间人口自然增长率(%)N ──规划年限(年)ΔP──规划期间人口机械增长数(人)人口自然增长率应根据计划生育指标,分析人口年龄与性别构成状况予以确定。
人口机械增长,宜按平均增长法计算,依公安部门统计的多年人口净迁入(出)量计算平均值,并分析影响机械增长的因素予以确定。
2、人口变动不稳定地区的人口预测法在人口变动不稳定的地区,应分析人口变动因素,采用适当方法测算。
计算公式如下:ΔP=A〔W c(1- W双/2)〕C + W单式中:ΔP──新建项目人口机械增长数A ──新建项目迁入职工总数W c──带眷职工占职工总数的比例(%)W双──双职工占带眷职工的比例(%)C──带眷系数W单──单身职工人数3、受资源、生态条件严重制约地区的人口预测方法应按环境容量法确定适宜的人口规模。
计算公式如下:P MAX=MIN{P1max,P2max,P3max,…,P imax,…}式中:P MAX──城市的极限人口P imax──自然资源、生态条件供给能力和某项基础设施支持能力的最大值(二)城镇与乡村人口预测1、一般预测方法城镇人口是指城市、建制镇建成区范围内常住人口。
常住人口指实际居住在某地区一定时间(指半年以上)的人口,包括:除离开本地半年以上(不包括在国外工作或学习的人)的全部常住本地的户籍人口;户口在外地,但在本地居住半年以上者,或离开户口地半年以上而调查时在本地居住的人口;调查时居住在本地,但在任何地方都没有登记常住户口,如手持户口迁移证、出生证、退伍证、劳改劳教释放证等尚未办理常住户口的人。
人口预测方法

人口预测方法人口预测是指通过各种统计方法和模型来预测未来其中一地区或全球的人口规模及其结构的变化趋势。
人口预测对于制定政府的经济、社会和城市规划等方面具有重要意义。
下面将综述几种常用的人口预测方法。
1.经验法(目测法)经验法是最简单的人口预测方法,通常是通过从过去的数据中观察到的趋势来推测未来的人口变化。
这种方法主要是基于历史数据和经验知识,没有复杂的统计和推理模型。
往往被用于近期短期的人口预测。
2.简单线性回归法简单线性回归法是基于线性回归模型的一种方法。
这种方法认为人口和时间是呈线性关系的,通过拟合历史数据的线性回归方程来进行预测。
然而,这种方法并未考虑到时间序列数据的非线性特征。
3.复杂线性回归法与简单线性回归法类似,复杂线性回归法采用更多的变量来构建回归模型。
这些变量可以是经济指标、社会指标、环境指标等。
通过考虑更多的因素,人口预测的准确性可以得到一定提高。
4.ARIMA模型ARIMA模型是一种基于时间序列分析的方法,其模型包括自回归(AR)、差分(I)和滑动平均(MA)三个部分。
这种方法相对来说更为复杂,但可以更好地处理时间序列数据中的趋势、季节性和随机性。
5.灰色关联度预测模型灰色关联度预测模型是一种非线性、非统计的预测方法。
它通过建立灰色模型,将历史数据和未知因素进行内部关联和外部关联计算,得到一个相对准确的预测结果。
这种方法适用于样本数据不多,变化规律较为复杂的情况。
6.基于机器学习的方法随着机器学习的发展,越来越多的人口预测方法开始采用机器学习的算法。
例如,支持向量机(SVM)、人工神经网络(ANN)和决策树等。
这些方法可以通过更大规模的数据和更多的特征来进行预测,提高预测的准确性。
总结起来,人口预测方法可以分为经验法、线性回归法、ARIMA模型、灰色关联度预测模型和基于机器学习的方法等。
每种方法都有其适用的场景和局限性,需要根据具体情况选择合适的预测方法。
随着数据的增多和技术的发展,人口预测的准确性也将不断提高,这对于社会经济的发展和规划具有重要意义。
土地利用规划中的人口预测方法综述

河北农业科学,2010,14(3):121-123,128Journal of Hebei Agricultural Sciences 编辑 蔡海燕土地利用规划中的人口预测方法综述万 庆 (华中师范大学城市与环境科学学院,湖北武汉 430079)摘要:人口预测是土地利用规划的重要环节,其预测精度直接关系到土地利用规划方案的合理性。
本文在全面、系统梳理人口预测方法研究成果的基础上,对土地利用规划中人口预测常用方法进行了概述,并运用多种方法对潜江市规划期间人口规模进行了预测,同时对其预测精度进行了检验,最后结合预测精度,对人口预测方法进行了全面分析。
关键词:土地利用规划;人口预测;精度检验;潜江市中图分类号:F30112 文献标识码:A 文章编号:100821631(2010)0320121203Rev iew of Popul a tion Pred iction M ethods i n Land Use Plann i n g WAN Q ing (College of U rban and Environmental Sciences,Huazhong Nor mal University,W uhan 430079,China )Abstract:Population p rediction is an i mportant part of land use p lanning,whose accuracy is directly related t o the rati onality of land use p lanning p r ogram 1Based on hackling the research achievements in populati on p redicti on methods,the common population p rediction methods in land use p lanning are briefly intr oduced 1The populati on scale in the p lanning period of Q ianjiang is p redicted using various methods,and the p redicti on accuracy is tested 1The population p rediction methods are comp rehensively analyzed combining with the p redicti on accuracy 1Key words:Land use p lanning;Populati on p rediction;Accuracy test;Q ianjiang收稿日期:2010203208作者简介:万 庆(1989-),男,湖北应城人,主要从事土地规划研究。
人口预测方法比较研究

人口预测方法比较研究随着全球人口的不断增长,人口预测成为了一个备受的话题。
准确的人口预测对于社会规划、经济发展和政策制定都具有重要意义。
本文将采用比较研究的方法,对常用的人口预测方法进行评估和分析,旨在为相关领域的研究和实践提供有益的参考。
人口预测的方法多种多样,其中常见的有以下四种:简单外推法、时间序列分析法、概率模型法和机器学习方法。
这些方法在不同的预测场景和需求下各有优劣。
简单外推法是最基本的人口预测方法,其基本原理是根据历史人口数据,采用线性或非线性模型进行外推。
简单外推法的优点是简单易行,适用于短期预测。
然而,该方法忽略了人口变化的复杂性和不确定性,因此在长期预测或复杂情景下的表现不佳。
时间序列分析法是一种基于时间序列数据的预测方法,其基本思想是利用时间序列数据的自相关性和季节性等进行预测。
在人口预测中,时间序列分析法可以考虑人口发展的趋势和周期性变化。
然而,该方法对数据质量和预处理要求较高,且在人口结构变化较大或未来政策影响不确定的情况下,预测结果可能不准确。
概率模型法是一种基于概率论的人口预测方法,其基本思想是建立人口变化的概率模型,并利用历史数据进行参数估计。
概率模型法能够考虑各种不确定因素对人口预测的影响,并提供置信区间。
然而,该方法需要大量的历史数据,且计算复杂度较高,对数据质量和算法要求较高。
机器学习方法是一种基于人工智能的人口预测方法,其基本思想是利用机器学习算法对历史数据进行学习,并建立预测模型。
机器学习方法具有强大的自适应能力和非线性拟合能力,可以处理复杂的和非线性的人口变化趋势。
然而,该方法需要大量的历史数据和计算资源,且对算法的选择和参数调整具有较高的要求。
比较这四种方法可以得到,每种方法都有其优点和局限性,适用于不同的预测场景和需求。
简单外推法适用于短期和简单情境下的预测,时间序列分析法适用于具有时间相关性的数据预测,概率模型法考虑了不确定性和置信区间,适用于长期和复杂情景下的预测,而机器学习方法则适用于处理复杂和非线性趋势的数据预测。
人口预测方法

现状需安置人口109552人。
本次规划,居住用地面积1339.24公顷规划用地指标表上位总体规划工业用地面积4144.76公顷总体规划中人口规模预测二、人口规模古雷港口经济区的人口包括就业人口和居住人口两大类。
1、就业人口规模本规划区内的就业人口主要是工业用地的就业人口。
(1)就业人口密度指标的分类确定通过国内工业用地的经验数据类比分析,考虑到石油炼化工业的特殊性,其就业人口密度偏低,其中上游产业的自动化程度较高,占地规模大,所能提供的就业岗位相对较少,经验数据表明,一般石化产业就业人口密度为6-20人/公顷,本规划石油炼化产业就业人口密度取7人/公顷,中下游产业用地就业人口密度取20人/公顷。
经验数据表明,综合类工业用地就业人口密度一般为80人/公顷;高新工业园用地就业密度为120人/公顷。
(2)工业用地的就业人口规模本次规划的石油炼化产业用地(即三类工业用地)约为478公顷;石化中下游产业用地约为2536公顷;二类工业用地约为987公顷;一类工业用地约为12公顷。
综上,计算可得,规划期末东海岛新区可容纳的工业用地就业人口数量约为:478公顷×7人/公顷+2536公顷×20人/公顷+987公顷×80人/公顷+12公顷×120人/公顷=136886人,约为13.4万人。
(3)仓储、港口用地等就业人口规模考虑到仓储、港口用地的集约紧凑,仓储、港口用地均按10人/公顷用地指标计算。
仓储、港口用地297+1130=1427公顷,就业岗位约1.4万人。
(4)就业相关人口规模经济区内总就业人口还包括公共服务设施用地的就业人口,约占总就业人口的20%,因此,计算可得,经济区总就业人口数量约为:(13.4+1.4万人/(1-20%)=18.5万人。
考虑到新区内就业人口部分带眷,取平均带眷系数为1.5,因此,可估算,就业相关人口为18.5万人×1.5=27.8万人。
多种人口预测方法汇总

人口预测模型的适用性,是决定预测结果的科学性和是否符合人口发展的趋势的先决条件。
人口预测作为人口研究中的重要方面,近年来其预测方法的发展很快,主要的预测方法分为用微分方程方法预测的 Logistic 模型,用数理统计方法预测的线性回归模型,用矩阵方法预测的 Leslie 模型,具体又包括了人口增长率法、 Logistic 模型、 Leslie 模型、一元线性回归预测、多元回归预测、自回归法、指数函数法、幂函数法、系统动力学以及适用更为广泛的灰色系统 GM(1,1)模型预测等主要方法。
(1) 人口增长率法人口增长率法是利用所选定的人口增长数学公式,根据基数人口总数,按照一定的人口增长速度推算未来时期人口总数的方法。
该法要求人口增长符合算数增长规律,还要求未来人口净增长量或增长速度大小方向均不变(至少相对稳定) ,其常用的推算公式为:p n = p0 (1+ r0n) 或p n = p0 + mn 。
(2) Logistic 模型Logistic 模型增长公式为:p t = p m (1+ e a+bt ) ,其中p t 为时刻的人口总数,p m 为人口极限规模, e 为自然对数的底,t 为时刻长度,a 、b 为待定参数。
Logistic 模型考虑到人口总数增长的有限性,提出了人口总数增长的规律即随着人口总数的增长,人口增长率逐渐下降,但对于在短期内如 30-50 年内人口增长可能呈上升趋势如人口生育率上升、死亡率下降等原因而导致人口呈上升趋势。
Logistic 模型在应用中对时间长,人口数据变化大,因此误差较大且不稳定。
而小城镇人口的变化就存在人口数据变化较大的特点,所以 Logistic 模型对小城镇人口的预测并不适合。
(3) Leslie 模型Leslie 模型不受短期外界因素的影响,对于中长期预测中具有很大的优势,尤其对人口转折时期的预测具有较高的精度,其模型为: P (k ) = LP (k 1) 。
人口预测方法(总结)
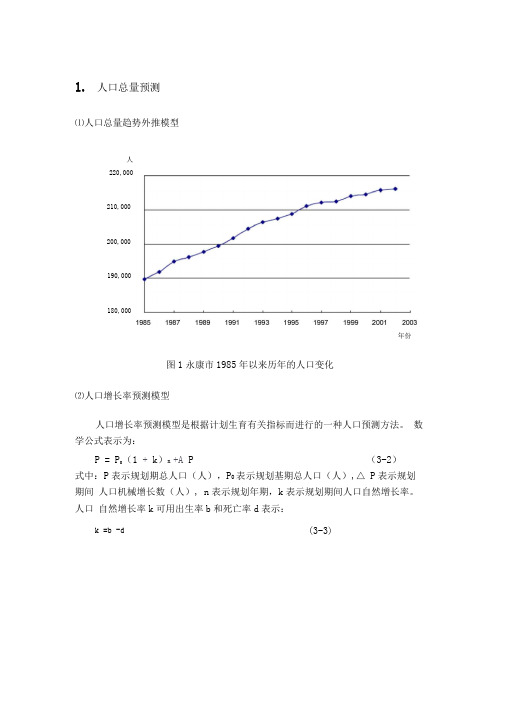
1. 人口总量预测⑴人口总量趋势外推模型图1永康市1985年以来历年的人口变化⑵人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:P = P 0(1 + k )n +A P (3-2)式中:P 表示规划期总人口(人),P 0表示规划基期总人口(人),△ P 表示规划期间 人口机械增长数(人), n 表示规划年期,k 表示规划期间人口自然增长率。
人口 自然增长率k 可用出生率b 和死亡率d 表示:(3-3)人 220,000k =b -d210,000200,000190,000180,000年份年份永康市1989年以来历年的人口出生率、死亡率和自然增长率%图3永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:r2X o(t)=[1-4oo(t)] ^(t)送h i(t) k i(t) X(t) (3_6)XF(t +1)=[1-B(t)] "Xe + fe i =0,12..,m—1式中:X o(t)为t年代O岁出生婴儿数,X i(t)为t年代之年龄组人口数,卩oo(t)为t 年出生婴儿当年死亡率,P(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(「2, r1即为生育年龄的上下限),h i(t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i(t)为t年代之年龄组女性性别比,M(t)为t年代之年龄组人口死亡率,f i(t)为t年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i(t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t年代之年龄组女性性别比k i(t)用常量k表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据P(t)= 0.8795;④模型中出生婴儿当年死亡率Moo(t)假定与2000年出生婴儿当年死亡率的80%,即采用4OO=3.88%O。
预测10年后人口数量的多元回归模型

预测10年后人口数量的多元回归模型人口预测模型1.人口预测需要考虑因素人口预测也就是某区域某段时间内的人数的预测。
往大的方面通常需要考虑“生”、“死”、“迁”。
往小的方面通常需要考虑“年龄段”,再细究可能要考虑更多因素,需要具体问题具体分析。
2.人口预测方法人口预测方法主要有四大类:推算法、队列法、线性回归法、非线性模拟法。
2.1推算法这类方法可以对人口变动的基本趋势进行判断,但对于比较复杂的情况无法进行准确的预测。
2.2队列法队列法:也称为要素预测法,主要是将未来人口数据看作一个随时间变化的队列,根据此建立一个离散的时间模型,主要是考虑人口年龄分布效应的一种预测方法。
常见的方法有:莱斯利矩阵模型( L e s l i e Leslie Leslie 矩阵模型)、凯菲茨矩阵模型等。
这类方法可以对人口变动有较好的预测,也是现在比较常见的,但对于数据的要求比较高,需要分年龄人口数据、生育率、死亡率、迁移率等多方面的数据。
(需要根据自己的情况选择需要的数据)2.3线性回归法线性回归法:根据影响因素建立回归模型,进行线性回归预测,主要是在控制其他条件不变的情况下,考察因变量与自变量之间的关系。
常见的方法有:ARMA模型(时间序列模型)、多元回归模型等。
这类方法预测效果相较于队列法会差些,而且由于人口变动不是线性的,所以长期效果并不理想,适合短期的预测。
2.4非线性模拟法非线性模拟法:通过建立非线性模型来模拟人口数量在未来的变化,主要是解决变量之间无法建立线性模型,或者是变量之间的关系无法完全确定,或面临“小样本”、“贫信息”的情况。
常见的方法有:神经网络、灰色预测等。
这类方法适用于数据不完整,或者影响因素无法确定的情况,预测结果可能不会很理想,但有较好发展前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 人口总量预测
(1)人口总量趋势外推模型
图 1 永康市1985年以来历年的人口变化
(2)人口增长率预测模型
人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:
+
1(
=)
+
P
P n∆
k
P
(3-2)0
式中: P表示规划期总人口(人),P0表示规划基期总人口(人),ΔP表示规划期间人口机械增长数(人),n表示规划年期,k表示规划期间人口自然增长率。
人口自然增长率k可用出生率b和死亡率d表示:
=(3-3)
k-
d
b
图 2 永康市1989年以来历年的人口出生率、死亡率和自然增长率
图3 永康市1989年以来历年的户籍人口迁移数量
(3)人口离散预测模型
人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:
1
,...,2,1,0)
()()](1[)1()()()()()](1[)(10002
1-=+⋅-=+⋅⋅⋅⋅-=+∑m i t f t X t t X t X t k t h t t t X i i i i r r i i i μβμ (3-6)
式中:X 0(t)为t 年代0岁出生婴儿数,X i (t)为t 年代之年龄组人口数,μ00(t)为t 年出生婴儿当年死亡率,β(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(r 2,r 1即为生育年龄的上下限),h i (t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i (t)为t 年代之年龄组女性性别比,μi (t)为t 年代之年龄组人口死亡率,f i (t)为t 年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i (t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t 年代之年龄组女性性别比k i (t)用常量 k 表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据β(t)= 0.8795;④模型中出生婴儿当年死亡率μ00(t)假定与2000年出生婴儿当年死亡率的80%,即采用μ00=3.88‰。
⑤从第五次人口普查资料看来,2000年分龄死亡率的数据波动较大,课题组结合1990第四次人口普查资料,对2000年分龄死亡率的数据进行移动平均处理,并采用死亡修正80%后作为死亡模式μi (t)1;⑥以第五次人口普查资料分龄生育率为生育模式h i (t);⑦第五次人口普查统计2000年迁入人口2 032人,迁出人口5 777人,当年人口机械增长呈负增长,而根据统计年鉴数据(图6),2000年人口机械增长接近于零,故在本模型预测中先按封闭模型进行预测。
将上述确定的参数代入模型3-6,进行计算机模拟预测,得到如下结果:2007年人口总数为212 648人,2020年为200 600人。
另人口机械按增长率预测模型取2000~2007年间的人口机械增长数为ΔP =1 000 7=7 000,取2008~2020年间为ΔP=2 000 13=26 000。
则有2007年人口总数为219 648人,2020年为233 600人。
1
移动平均采用公式:μi =0.25μi-1+0.5μi +0.25μi+1
020000
40000
6000080000100000
1200001400001999
2000200120022003
年份
暂住人口(人)
图 4 1999年以来永康市暂住人口情况
城镇人口的计算
1、线性回归法
分析历年统计资料,发现人口与年份之间有较明显的线性关系,因此我们选用1985年至1996年12年间的各年总人口数减去乡村人口数与时间(年份)进行回归分析,方程为y=a+bx 。
其中:
相关系数:
计算过程和结果见表2-4
2、经济指标回归法
城镇人口的聚集主要是工业化进展的结果,由于工业生产的发展
带来城市相关行业的发展,导致城镇人口的不断增长。
经分析发现工业总产值与城镇人口之间也呈线性相关。
因此,我们可选用1990-1996年全市及各县(市、区)的工业总产值(1990年不变价)与城镇人口作单元线性回归,拟合方程同前,即y=a+bx。
以全市及各县(市、区)政府“九五”计划及2010年远景目标纲要中2000年及2010年达到的工业总产值作为预测年依据,预测过程和结果见表2-5。
3、非农业人口预测推算法
(1)非农业人口的预测
选用1978—1996年19年间的非农业人口资料,作回归预测,方法同上。
全市及各县(市、区)预测模型和结果如下:
某某市:y=17.929+2.6289x
r=0.95555
y2000=77.97(万人)
y2010=103.99(万人)
咸安市:y=4.1402+0.7418x
r=0.960194
y2000=21.20(万人)
y2010=28.62(万人)
赤壁市:y=6.0095+0.4774x
r=0.971267
y2000=16.99(万人)
y2010=21.77(万人)
六县(市、区)合计:y2000=77.95(万人)
y2010=103.97(万人)
全市非农业总数预测结果与各县(市、区)预测结果之和相当接近,且七个相关系数均较高,说明此种方法较为可信。
(2)城镇非农人口计算
非农业人口中有少量居住在农村,根据调查和城建有关统计资料计算,全市城镇非农人口约占总非农业人口的67.13%,若保持此比例不变,全市城镇非农业人口2000年为52.34万人,2010年为69.81万人。
1978—1996年某某市非农业人口统计表
表2-6 单位:万人
(3)城镇人口的推算
城镇规模等级不同,非农人口所占比例就不同。
城镇规模越小,其自理口粮人口和其他常住人口越多,城镇非农人口所占比例越小。
根据湖北省城镇建设统计资料,某某市城镇非农人口占城镇人口的56.285%。
若照此比例推算,全市城镇人口2000年为92.99万人,2010年为124.03万人。
4、政府目标预测
根据原《某某地区国民经济和社会发展的“九五”计划及2010年远景目标纲要》,确定全市人口自然增长率控制指标2000年和2010年分别为10‰和8‰。
统计分析全市1976—1996年21年间的机械增长情况取平均数为14376人/年,则2000年和2010年全市总人口可按以下公式计算:
P=P0(1+K)n±△P
式中:P—规划期总人口
P0—规划基期总人口
K—规划期间人口自然增长率
n—规划年限
△P—规划期间人口机械增长数
则:y2000=269.51((1+10‰)4+1.4376(4=286.20(万人)y2010=286.20((1+8‰)10+1.4376(10=324.32(万人)该纲要中提出,到2000年城镇化水平提高到30%以上,另据原《某某地区国土规划》,我市城镇化水平2000年要达到30%以上,到2010年提高到35%(一说要达到近40%)。
据此计算:
286.20×30%=85.86(万人)
324.32×35%=113.51(万人)
324.32×40%=129.73(万人)
则全市城镇人口的发展目标为:
y2000≥85.86(万人)
113.51(万人)≤y2010≤129.73(万人)
5、县(市、区)预测汇总法
由各县(市、区)根据本地的经济发展水平和目标收集相关部门资料,分别预测2000年和2010年各县(市、区)城镇人口数,汇总后得出全市城镇人口2000年为88.23万人,2010年为118.99万人。
综合分析以上各种方法,最终确定全市城镇人口1996年为72.63万人,2000年为89.54万人,2010年为122.31万人。
