苏教版七上数学找规律题库(一)
苏科版数学七年级上册第二章有理数有理数加法运算律(习题)

1.3.2有理数加法运算律【夯实基础】1.数6,-1,15,-3中,任取三个不同的数相加,其中和最小的是 ( )A.-3B.-1C.3D.22.下表是一位女生记录自己8个周进行百米跑训练的8次测验成绩,达标成绩为18秒,表中“+”号表示成绩大于18秒,“-”表示成绩小于18秒.请问这8次百米跑测验的平均成绩为 ( ) A.17.9 B.17.8 C.17.2 D.18.13.你知道“少年高斯速算”的故事吧!那么请你快速算一算1+2+3+…+48+49+50的结果( ) A.1274 B.1276 C.1275 D.12704.(1)绝对值小于4的所有整数的和是________;(2)绝对值大于2且小于5的所有负整数的和是________。
5.计算:(1)23+(-17)+6+(-22)(2)(-2)+3+1+(-3)+2+(-4)(3)(−413)+(−417)+413+(−1317)(4)(−423)+(−313)+612+(−214)6.下表为某公司股票在本周内每日的涨跌情况(单位:元)-0.25计算这一周后该公司股票股价变化是上涨还是下跌,上涨或下跌的值是多少?7.有一批味精,标准质量为每袋100g,现抽取10袋样品进行检测,其结果是:99,102,101,101,98,99,100,97,99,103(单位:g),用简便方法求这10袋味精的总质量是多少?【能力提升】8.对于正整数a,b规定一种新运算※,用a※b表示由a开始的连续b个整数之和,如2※3=2+3+4=9,则(-3)※6=_____9.巧算:(1)−556+(−923)+(−312)+1734(2)89+899+8999+89999+899999(3)(+1)+(-2)+(+3)+(-4)+…+(+99)+(-100)【思维挑战】10.如图,把一个面积为1的正方形等分成两个面积为21的长方形,接着把面积为21的长方形等分成两个面积为41的正方形,再把面积为41的正方形等分成两个面积为81的长方形,如此进行下去,试利用图形揭示的规律计算+++++++24816326412825611111111=__________.。
苏教版七上数学找规律题库(三)
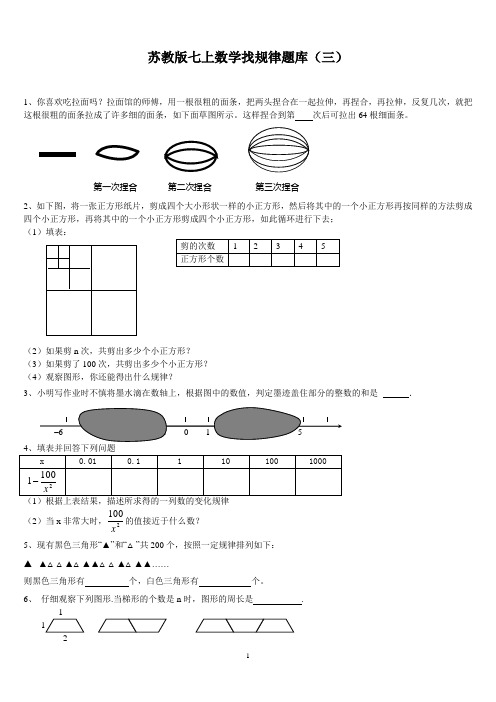
苏教版七上数学找规律题库(三)1、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示。
这样捏合到第 次后可拉出64根细面条。
第一次捏合 第二次捏合 第三次捏合2、如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去; (1)填表:(2)如果剪n 次,共剪出多少个小正方形? (3)如果剪了100次,共剪出多少个小正方形? (4)观察图形,你还能得出什么规律?3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是 .(1)根据上表结果,描述所求得的一列数的变化规律 (2)当x 非常大时,2100x的值接近于什么数? 5、现有黑色三角形“▲”和“△”共200个,按照一定规律排列如下: ▲ ▲△△▲△▲▲△△▲△▲▲……则黑色三角形有 个,白色三角形有 个。
6、 仔细观察下列图形.当梯形的个数是n 时,图形的周长是 .27、用火柴棒按如下方式搭三角形:(1) 填写下表:(2) 照这样的规律搭下去,搭n 个这样的三角形需要______根火柴棒8、把编号为1,2,3,4,…的若干盆花按右图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为___________色.9、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10第5行 11 -12 13 -14 15 … …按照上述规律排下去,那么第10行从左边数第5个数等于 . 10、观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在察规律之后并用你得到的规律填空:250___________=+⨯, 第n 个式子呢? ___________________11、一张长方形桌子可坐6人,按下列方式讲桌子拼在一起。
苏教版七年级上册数学知识点总结

七年级数学(上)知识点总结第一章数学与我们同行知识点1 数字与生活生活中我们所遇到的很多数字都蕴含着很多的数学问题,数学已成为人们表达与交流的工具。
例如,身份证号码、学生的学籍号、火车的列次等。
知识点2 图形与生活生活中充满了图形,多姿多彩的图形不仅美化了我们的生活,还包含着丰富的信息和数学知识。
知识点3 动手操作动手操作主要是让学生在实际操作的基础上设计相关的图形及制作相关图案。
这类题病根是培养学生的创新能力和实践能力。
动手操作包括折叠、裁剪、拼图等各种活动。
知识点4 找规律这类问题主要是通过一些数字或图形信息,寻求其内在的共同之处,也就是具有规律性的问题。
知识点5 统计知识在进行生产、生活和科学研究时,往往需要收集数据,并把数据加以分类、整理,需要求出数据的平均数,或者制成统计表、统计图,用来反应所了解的情况,这样的工作就是统计。
第二章有理数2.1正数与负数正数:大于零的数,正数前面可以放“+”来表示(通常省略不写)。
正数可分为正整数和正分数。
负数:小于零的数,负数前面放上“-”来表示。
负数可分为负整数和负分数。
注意:0既不是正数,也不是负数。
同时,0属于偶数、整数、非正数、非负数、非正整数、非负整数。
我们把正整数、零和负整数统称为整数,正分数、负分数统称分数。
2.2 有理数与无理数整数和分数统称为有理数。
我们把能够写成分数形式mn(m、n是整数,n≠0)的数叫做有理数。
实际上,有限小数和循环小数都可以化为分数,它们都是有理数。
无限不循环小数叫做无理数。
有理数有理数知识点提示: (1)有理数可按不同标准分类,标准不同,分类也不同。
(2)在分类时,要注意0的地位和意义。
(3)有理数的分类方法有很多,不论采取哪种分类方法,在对有理数分类时,都要做到不重不漏。
(4)习惯上,把正整数、0统称为非负整数(也叫自然数);把负整数、0统称为非正整数,正有理数、0统称为非负有理数,负有理数、0统称为非正有理数。
苏教版七上数学找规律题库

苏教版七上数学找规律题库(三)2、如以下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成 四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;(2)如果剪n 次,共剪出多少个小正方形? (3)如果剪了 100次,共剪出多少个小正方形? (4)观察图形,你还能得出什么规律?3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住局部的整数的和是4、填表并答复以下问题x1101001000d 100 12x(1)根据上表结果,描述所求得的一列数的变化规律(2)当x 非常大时, 吟 的值接近于什么数?x5、现有黑色三角形 “▲和△〞共200个,根据一定规律排列如下:▲ …… \ /那么黑色三角形有 ■个,白色三角形有 \ 个./6、 仔细观察以下图形.当梯形的个数是 n 时,图形的周长是一1 1/\ /\7/\\剪的次数12345止方形个数1、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把 这根很粗的面条拉成了许多细的面条,如下面草图所示.这样捏合到第 次后可拉出64根细面条.第一次捏合第二次捏合 第三次捏合7、用火柴棒按如下方式搭三角形:⑴填写下表:(2)照这样的规律搭下去,搭 n 个这样的三角形需要'根火柴棒8、把编号为1, 2, 3, 4,…的假设干盆花按右图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,那么第 行从左边数第6盆花的颜色为色.9、一列数:1 , -2 , 3, -4 , 5, -6 , 7,第1行 1 / 第2行 —2// 311、一张长方形桌子可坐 6①张桌子拼在一起可坐 人.3张桌子拼在一起可坐 人,n 张桌子拼在一起可坐 人. ②一家餐厅有\40张这样的长方形桌子,根据上图方式每 5张桌子拼成1张大桌子,那么40张桌子可拼成8张大桌子,共可坐 人.③假设在②中,改成每飞8张桌子拼成1张大桌子,那么共可坐 ____________________ 人. /12、用计算器计算以下各式,并将结果填写在横线上./① 1X7X15873= ______________ ② 2 X7 X15873= _____________ ③ 3X7X15873= ______________ ④4X7X15873= ______________你发现了什么规律?把你发现的规律用简练的语言写出来;13、观察以下顺序排列的等式:9 >0+1=19X1+2=11 9X2+3=21 9 X3+4=31 \ /9 >4+5=41\/猜测:第n 个等式(n 为正整数)应为14、一个两位数的个位数是a,十位数字是b,请用代数式表示这个两位数是第3行 一 45 一 6第4行 7一 8 9 —10 第5行 11 -12 13 -14根据上述规律排下去,那么第10行从左边数第5个数等于10、观察以下算式:2 _ 23 ,2 64 4,3 724 5,4 8 4 62 ,请你在察规律之后并用你得到的规律填空:一 2 一 .. 一50 ,第n 个式子呢?将这列数排成以下形式:人,按以下方式讲桌子拼在一起.O O规律吗?根据你发现的规律答复:3 2004的个位数字是、16、观察以下各式,你会发现什么规律?/\23X5= 15,而 15= 4 1.2/5X7=35,而 35= 61211 M3= 143,而 143= 121将你猜测到的规律用只含一个字母的式子表示出来:.17、问题:你能比拟和的大小吗?\为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比拟 n n+1和(n+1)n 的大小(n 为正整数),我们从n=1,n=2,n=3……这些简单的情况入手,从中发现规律,经过归纳,猜出结论.\(1)通过计算,比拟以下各组数字大小① 12 22 ② 23 32 ③ 34 43 、④ 45 54⑤ 54 65⑥ 67 76(2)把第(1)题的结果经过归纳,你能得出什么结论?你能用只含有一个字母的式子表示吗? (3)根据上面的归纳猜测得到的结论,试比拟两个数的大小(1分)(填〞 >;'<"),“=〞18、为了美化城市,某商场在门前的空地上用花盆按如下图的方式搭正方形,(1) 填写下表止方形的层数 12345花盆的个数4 \15、观察以下各式:31 =3, 32=9, 33=27, 3 4 =81, 35=243, 3 6=729 …你能从中发现底数为3的哥的个位数有什么19、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为 10.(1)1 5 5 9 =10 ;⑵ 3 3 3 3 =10 ;(3) 1 1 9 9 =1020、小红和小花在玩一种计算的游戏,计算的规那么是算得缰少?a b =ad- bco 现在轮到小红计算c d1 2 的值,请你帮助算3 421、黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比.黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处.两只蚂蚁同时起跑,说也奇怪,两只蚂蚁同时到达了乙处.(1) 两只蚂蚁请你帮助判断:谁跑得快?(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?22 . (1) 3个球队进行单循环赛 (参赛的每一个队都与其它所有各队比赛一场) ,总的比赛场数是多少?4个球队呢?m个球队呢?(代数式表示出来)(2)当m=12时,总共比赛几场?\23 .按一定规律排列的一串数:\1 123 1 2 345 1 2 3一,一,一,一,一,一,一,一,一,一,一,一,…中,第98 个数是1 3 3 3 5 5 5 5 5 7 7 714.下面的算式里,符号.、△、和口分别代表三个不同的自然数,这三个数的和是\1111———— 1"/824. 一群整数朋友根据一定的规律排成一排,可排在口位置的数跑掉了,请帮它们把跑掉的朋友找回来. \(1) 5, 8, 11, 14, 口,20;(2) 1, 3, 7, 15, 31, 63, 口;(3) 1, 1 , 2, 3, 5, 8, 口,2125.以下两列数:2, 4, 6, 8, 10, 12,……1994;6, 13, 20, 27, 34, (1994)这两列数中,相同的数的个数是〔〕A、142B、143 \C、284D、28526 . 一串数字的排列规律是:第一个数是20,从第二个数起,每一个数比前一个数小8(1)第10个数是多少? ( 2)第n个数是多少? ( 3)第几个数是一6027 .某仓库堆放一批圆木,一共、\20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根?28 .在如下图的2003年1月份的日历中,用一个方框圈出任意3X3个数/(1)从左下角到右上角的三个数字之和为那么这个数的和是多少?这个日期中最后一天是月几日?(2)用这样的方框能否圈出总和为162的9个数?\/B29.观察以下数据,按某种规律在横线上填上适当的数:57 9 916' 2530.如图,△ F 是线段CDABC 中,D 是边BC 上的中点,的中点,E 是边AC 的中点,那么 图中有条线段,有.个角,假设^ DEF 的面积是2,那么4ABC 的面积是31.平面内两两相交的 6条直线/其交点个数最少为 m 个,最多为n 个,那么m+n 等于(A 、12B 、16C 、20D 、以上都不对请你用尽可能多的不同方法把它分成形状、大小完全相同的四块,要求不把正方形糖块划破(至少五种方法)这五个数是33. 34. 35. 如果这个月的5号是星期三,那么20号是星期 36. 这三个数的和为 个个C. 9 至少找出以下几何体的4个共同点39、观祭公式:40、 公式1:(x a) 3xa公式2:4xa37. 38. 32.如图,可以看成是边长为4的小正方形的巧克力糖,三个连续偶数中,n 是最小的一个, 以下图形中三角形的个徽 ((x a)4x 3x a)个 (1)这两个公式有什么特点?在某月日历上一个竖列相邻的五个数之和为 80, 某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是 今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是 43x 4x a -226x a36,那么第三个日期是个91,那么李老师是(2) 利用公式计算:_ 4 _ 3 1 __2 1 2 _ 1 3 12 4 2 (-) 6 2 ( -) 4 2 (-)(-)2 2 2 241、下面有三组数,请你填上适宜的运算符号,使每一组数的结果都为10.(1) 1 5 5 9 =10 ; (2) 3 3 3 3 =10 ; (3) 1、1 9 9 =1042 .造一个含有字母p和q的代数式,使得不管p、q取何值,代数式的值永远不是正的.43 .图是2002年6月份的日历,现用一矩形在日历中任意框出4个数a b ,请用一个等式表示,a、b、c、d之间的关系. / c d日一一三四五六1234567891011121314151617118_ _J9_202122232425262728293044 .右图,是用火柴棒摆成的一个大三角形,它是由九个小三角形组成的,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形哪(每个小三角形内只填一个数) ,要求靠近大三角形每条边的每五个数相加的和相等,请想一想,怎样填这些数才能使五个数的和尽可能大一些,这五个数的和最大是多少?45.王容许了大臣的一个要求:即在国际象棋棋盘上2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到64格〞.但是不久国王九发现国库里没有这么多米,然而国王的话不能不算数,国王又不好意思向别人借,怎么办呢?请你帮国王想一个好方法来解决这个问题. (方法必须符合情理,有创意者可适当多加分.方法多者亦可多加分)46.如果连结多边形的一边上一点与其余各顶点可将某多边形分割成2004个三角形,求该多边形的边数47.如图1-26,在ABC中,点D,E,F分别是AB,BC,AC三边中点,图中与BOD面积相等的三角形有几个?48.观察图1-27中有几个三角形?由此你发现三角形的个数有什么规律呢个三角形(n个点) 49.求个数(1)图1-28(1)中有多少个三角形?50.如图1-29所示,图①是一个三点(将这条边分为相等的两局部的小三角形三边的中点 ,得到图③,请你根据图中三角形个数的规律, (2)图1-28(2)中有多少个四边形角形,分别连结这个三角形三边的中点)得到图②;再分别连结图②中间的按此方法继续下去完成以下问题图1-29(1)将下表填写完整.图形符号12345..三角形个数159..(2)在第n个图形中有几个三角形?(用含n的代数式表示)51、如图,哪些图形经过折叠可以围成一个长方体?/(1) ( 2) (3) / (4) (5)52、以下图形经过折叠能否围成一个正方体?55、以下图〔1〕表示1张餐桌和6张椅子〔每个小半圆代表1张椅子〕,假设按这种方式摆放20张餐桌需要的椅子张数O观察以下算式:56、⑴⑵根据上述算式中的规律,256,21 2, 22 4,23 8, 24 16,25 32,26 64, 27 128, 2你认为220的末位数字是57、某种细菌在培养过程中,每半小时分裂1次,每次一分为二.假设这种细菌由 1个分裂到 16个,那么这个过程要经)A.小时 B \ . 2小时 C58、计算:1 —2+3—4+……+2001 -2002+2003= 27, 64, 59、61、当下面这个图案被折起来组成一个正方体,数字 (2) 1 , 8, -3, _ 根据规律填上适宜的数:〔1〕—9, —6,,216 ; (3) 2 , 5, 10,会在与数字2所在的平面相对的平面上.(1) (2) / (3) (4)53、某种细胞每过30分便由1个分裂成2个,经过5小时,这种细胞由1个能分裂成 54、有一张厚度是/0 .1毫米的纸,将它对折 1次后,厚度为2X 毫米.个.〔1〕、对折2次后,厚度为 〔3〕对折n 次后,厚度为毫米. 毫米.〔2〕对折20次后,厚度为毫米.62、 在下面的图形中〔 〕是正方体的展开图.观察以下数据, 63、 66、 67、在下面的图形中,CA B D68、探索规律:用棋子按下面的方式摆出正方形 (A) (B) (C) (D)按某种规律在横线上填上适当的数: 7 一,16 一列数71, 72, 73…7 2003,其中末位数是 3的有 64、 个.指出以下平面图形是什么几何体的展开图〔 6分〕:〕是正方体的外表展开图①按图本规律填写下表:69、,13 1 - 12 22, 413 23 9 1 22 32, 4 13 23 33 36132 42,4(1)猜测填空:13 23 33 n 31( ) 2( )24(2)假设 13 23 33n 312402,试求 n 的值. 470、用火柴棒按下面方式搭图形,那么第20个图形需要的火柴棒是 根.图形编号(1)⑵(3)(4)⑸(6)棋子个数n 个正方形需要多少个棋子?②根据这种方式摆下去,摆第 ③根据这种方式摆下去,第第20个正方形需要多少个棋子?。
苏教版小升初数学专项训练+典型例题分析-找规律篇(新审定)

名校真题 测试卷 找规律篇时间:15分钟 满分5分 姓名_________ 测试成绩_________1 (12年清华附中考题)如果将八个数14,30,33,35,39,75,143,169平均分成两组,使得这两组数的乘积相等,那么分组的情况是什么?2 (13年三帆中学考题)观察1+3=4 ; 4+5=9 ; 9+7=16 ; 16+9=25 ; 25+11=36 这五道算式,找出规律,然后填写20012+( )=200223 (12年西城实验考题) 一串分数:12123412345612812,,,,,,,,,,,,.....,,,......,33,55557777779991111其中的第2000个分数是 .4 (12年东城二中考题)在2、3两数之间,第一次写上5,第二次在2、5和5、3之间分别写上7、8(如下所示),每次都在已写上的两个相邻数之间写上这两个相邻数之和.这样的过程共重复了六次,问所有数之和是多少?2......7......5......8 (3)5 (04年人大附中考题)请你从01、02、03、…、98、99中选取一些数,使得对于任何由0~9当中的某些数字组成的无穷长的一串数当中,都有某两个相邻的数字,是你所选出的那些数中当中的一个。
为了达到这些目的。
(1)请你说明:11这个数必须选出来;(2)请你说明:37和73这两个数当中至少要选出一个;(3)你能选出55个数满足要求吗?【附答案】1 【解】分解质因数,找出质因数再分开,所以分组为33、35、30、169和14、39、75、143。
2 【解】上面的规律是:右边的数和左边第一个数的差正好是奇数数列3、5、7、9、11……,所以下面括号中填的数字为奇数列中的第2001个,即4003。
3 【解】分母为3的有2个,分母为4个,分母为7的为6个,这样个数2+4+6+8…88=1980<2000,这样2000个分数的分母为89,所以分数为20/89。
小升初找规律专项巩固练习(试题)-六年级下册数学苏教版

小升初数学找规律专项巩固练习姓名:___________一、选择题1.将一些小圆球如下图摆放,第六幅图中共有( )个小圆球。
A .25B .30C .36D .422.将一根粗细均匀的长方体木料锯成6段,锯下1段的时间是锯成6段所用时间的( )。
A .14B .15C .16D .173.已知22222233445522,33,44,55338815152424+=⨯+=⨯+=⨯+=⨯,若21010b ba a+=⨯,则a b +=( )。
A .19B .21C .99D .1094.如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第2次输出的结果为12,……第20次输出的结果为( )。
A .24B .12C .6D .3二、填空题5.探索规律:用同样长的小棒按下图方式摆图形。
摆1个八边形需要8根小棒;摆2个八边形需要( )根小棒;摆3个八边形需要( )根小棒;摆n 个八边形,需要( )根小棒。
有2010根小棒,可以摆( )个这样的八边形。
6.阅览室摆放了一些长桌用于阅读课外书(如图),每张长桌单独摆放时,最多可供6人同时阅读;两张长桌连接摆放时,最多可供10人同时阅读;三张长桌连接摆放时,最多可供14人同时阅读。
(1)按照这种摆法,完成下表。
(2)按这种摆法,摆放8张长桌,最多可供( )人同时阅读。
(3)按这种摆法,摆放n张长桌,最多可供( )人同时阅读。
7.用黑白两种颜色的正六边形地面砖按如下所示的规律拼成若干个图案:则第⑥个图案中有白色地面砖( )块;第个图案中有白色地面砖( )块。
8.每一个多边形都可以按下图的方法分割成若干个三角形,那么用同样的方法,n边形又能分割成( )个三角形。
9.现有若干个圆环,它们的外直径都是5厘米,环宽5毫米,将它们扣在一起(如图所示)拉紧后测量总长度。
圆环个数1234…总长度591317…(cm)像这样,10个圆环拉紧后的长度是( )厘米。
苏教版三年级数学上册区级公开课《找规律(一一间隔排列)》说课稿

苏教版三年级数学上册区级公开课《找规律(一一间隔排列)》说课稿一. 教材分析苏教版三年级数学上册《找规律(一一间隔排列)》这一章节,主要让学生通过观察、操作、归纳等方法,发现并掌握一一间隔排列的物体的规律。
教材通过生活中的实际例子,引导学生发现规律,并运用规律解决实际问题。
本节课的内容与学生的生活紧密相连,能够激发学生的学习兴趣,培养学生的观察能力、操作能力和归纳能力。
二. 学情分析三年级的学生已经具备了一定的观察和操作能力,他们对生活中的一些规律已经有了一定的认识。
但在本节课中,学生需要通过抽象的方式来理解一一间隔排列的规律,这对他们来说是一个挑战。
此外,学生可能对规律的表述还不够清晰,需要在教学中进行引导和培养。
三. 说教学目标1.知识与技能:学生能够通过观察和操作,发现一一间隔排列的物体的规律,并能运用规律解决实际问题。
2.过程与方法:学生通过观察、操作、归纳等方法,培养观察能力、操作能力和归纳能力。
3.情感态度与价值观:学生体验数学与生活的紧密联系,培养对数学的兴趣。
四. 说教学重难点1.重点:学生能够发现并掌握一一间隔排列的物体的规律。
2.难点:学生能够通过抽象的方式来理解一一间隔排列的规律,并运用规律解决实际问题。
五. 说教学方法与手段本节课采用观察法、操作法、归纳法等教学方法,通过实物、图片等教学手段,引导学生发现规律,并运用规律解决实际问题。
六. 说教学过程1.导入:通过展示生活中的实例,引导学生发现一一间隔排列的现象,激发学生的学习兴趣。
2.新课导入:引导学生观察、操作,发现一一间隔排列的物体的规律。
3.巩固练习:学生运用规律解决实际问题,教师进行指导和评价。
4.课堂小结:学生总结一一间隔排列的规律,并分享自己的学习心得。
5.课后作业:学生运用规律解决生活中的问题,培养学生的应用能力。
七. 说板书设计板书设计以一一间隔排列的物体图片为主,配以关键的文字描述,帮助学生理解和记忆规律。
七年级苏教版数学复习要点考点专题二:整式化简求值及应用(教师用,附答案分析)

七年级苏教版数学复习要点考点专题二:整式化简求值及应用知识点一 整式化简求值1.求代数式的值的一般方法(1)直接代入法:直接将字母的值代入代数式进行计算.(2)间接代入法:先计算出对应的字母的值,再把求得的值代入代数式进行计算.(3)整体代入法:先求出含一个字母或多个字母的整体值,然后将代数式变形为含有此整体的代数式并进行计算.注意:化简求值的扩充方法 ①设k 法遇到连等式、连续比例式的题,解决这类题型的最佳方法是设k 法. ②赋值法在解题过程中,对于难以化简求值问题,我们也可以通过给未知数赋一些特殊值来解决问题. 例1(玄武区期中)已知223A x mx x =+-,21B x mx =-++,其中m 为常数,若2A B +的值与x 的取值无关,则m 的值为( ) A .0B .5C .15D .15-【解答】解:已知223A x mx x =+-,21B x mx =-++,222232(1)A B x mx x x mx +=+-+-++, 2223222x mx x x mx =+--++,52mx x =-+因为2A B +的值与x 的取值无关,所以510m -=解得15m =.故选:C . 例2(溧水区期中)已知代数式2x y +的值是2,则代数式124x y --的值是( ) A .1- B .3- C .5- D .8-【解答】解:根据题意得:22x y +=, 方程两边同时乘以2-得:244x y --=-,方程两边同时加上1得:124143x y --=-=-,故选:B .知识点二 整式运算应用一、常见找规律基本类型 1.等差型规律相邻两项之差(后减前)等于定值的数列.例如:4,10,16,22,28…,增幅是6,第一位数是4,所以,第n 位数为:()41662n n +-⨯=-. 2.等比型规律相邻两项之比(后比前)等于定值的数列.例如:3,6,12,24,48…,比值是2,第一位数是3,所以,第n 位数为:132n -⨯. 3.符号型规律符号型数列的特点是,正数与负数交替出现;解决方法:先不考虑符号,找到数列的规律,并用含n 的式子表示,然后再乘以()1n-或()11n +-.补充:①平方型规律;②求和型规律;③周期型规律二、定义新运算:是用某些特殊的符号,表示特定的意义,从而解答某些特殊算式的运算. 在定义新运算中的※,,∆……与+、-、⨯、÷是有严格区别的.解答定义新运算问题,必须先理解新定义的含义,遵循新定义的关系式把问题转化为一般的 +、-、⨯、÷运算问题.注意:①新的运算不一定符合运算规律,特别注意运算顺序.②每个新定义的运算符号只能在本题中使用.三、程序框图运算:程序框图运算是定义新运算中的一种特殊类型,解题的关键是要准确理解新程序的数学意义,进而转化为数学问题. 注意:程序框图中的运算是由前到后....依次进行的,不存在先乘除后加减的问题.例1(建邺区期中)一组有规律排列的数:1、3、7、______、31⋯⋯,在下列四个数中,填在横线上最合理的是( )A .9B .11C .13D .15 【解答】解:3121=⨯+,7321=⨯+,15721=⨯+,311521=⨯+, ∴后一个数是它前一个数的2倍加上1,故选:D . 例2(鼓楼区期末)小红在计算2320201111()()()4444+++⋯+时,拿出1张等边三角形纸片按如图所示方式进行操作.①如图1,把1个等边三角形等分成4个完全相同的等边三角形,完成第1次操作;②如图2,再把①中最上面的三角形等分成4个完全相同的等边三角形,完成第2次操作;③如图3,再把②中最上面的三角形等分成4个完全相同的等边三角形,⋯依次重复上述操作.可得2320201111()()()4444+++⋯+的值最接近的数是( )A .13B .12C .23D .1【解答】解:设2320201111()()()4444S =+++⋯+,则232019111141()()()4444S =++++⋯+, 2020141()4S S -=-,2020131()4S =-,202011()1433S -=≈,故选:A . 例3(建邺区期中)有一列数1a ,2a ,3a ,4a ,5a ,n a ⋯,从第二个数开始,等于1与它前面的那个数的差的倒数,若13a =,则2019a 为( )A.2019B.23C.12-D.3【解答】解:依题意得:13a=,211132a==--,3121312a==+,413213a==-;∴周期为3;20193673÷=所以2019323a a==.故选:B.例4(溧水区期中)如图,一个长方形运动场被分隔成A、B、A、B、C共5个区,A区是边长为am的正方形,C区是4个边长为bm的小正方形组成的正方形.(1)列式表示每个B区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;(3)如果40a m=,20b m=,求整个长方形运动场的面积.【解答】解:(1)2[()()]2()4()a b a b a b a b a m++-=++-=(2)2[()()]2()8()a ab a a b a a b a a b a m++++-=++++-=(3)解:(22)(22)4()()S a b a b a b a b=-⨯+=+-m,当40a=,20b=时原式4(4020)(4020)4800=+-=m,答:整个长方形运动场的面积为4800 m.【提优训练】一、单选题(共6小题)1.(苍溪县期末)已知一个多项式与239x x+的和等于2341x x+-,则此多项式是() A.2651x x---B.51x--C.2651x x-++D.51x-+【解答】解:由题意得:22341(39)x x x x+--+,2234139x x x x=+---,51x=--.故选:B.2.(常熟市期中)已知代数式2245x x-+的值为9,则272x x-+的值为()A.5B.6C.7D.8【解答】解:根据题意得:22459x x-+=,方程两边同时减去5得:2244x x-=,方程两边同时乘以12-得:222x x-+=-,方程两边同时加上7得:272725x x-+=-=,故选:A.3.(江阴市期中)已知2a b-=,2d b-=-,则2()a d-的值为()A.2B.4C.9D.16【解答】解:2a b-=,2d b-=-,()()4a b d b∴---=,则4a b d b--+=,4a d-=,2()16a d∴-=.故选:D.4.(姑苏区期末)如果a 和14b -互为相反数,那么多项式2(210)7(23)b a a b -++--的值是( ) A .4- B .2- C .2 D .4【解答】解:由题意可知:140a b +-=,41a b ∴-=-,∴原式242071421b a a b =-++-- 3121a b =--3(4)1a b =--31=--4=-,故选:A .5.(路北区三模)完全相同的6个小矩形如图所示放置,形成了一个长、宽分别为n 、m 的大矩形,则图中阴影部分的周长是( )A .6()m n -B .3()m n +C .4nD .4m 【解答】解:设小矩形的长为a ,宽为()b a b >,则3a b n +=,阴影部分的周长为22()2(3)222264224n m a m b n m a m b m n n m +-+-=+-+-=+-=,故选:D . 6.(宿豫区期中)下列图形都是由同样大小〇的按一定的规律组成的,其中第1个图形一共有4个〇,第2个图形一共有9个〇,第3个图形一共有15个〇,⋯则第70个图形中〇的个数为( )A .280B .349C .2485D .2695【解答】解:第①个图形中基本图形的个数1(11)4312⨯+=⨯+, 第②个图形中基本图形的个数2(21)8322⨯+=⨯+, 第③个图形中基本图形的个数3(31)11332⨯+=⨯+, ⋯∴第n 个图形中基本图形的个数为(1)32n n n ++当70n =时,707137026952⨯⨯+=,故选:D .二、填空题(共5小题)7.(海州区期中)如果23x x -的值是1-,则代数式2396x x -+-的值是 . 【解答】解:根据题意得:231x x -=-, 方程两边同时乘以3-得:393x x -+=,方程两边同时减去6得:396363x x -+-=-=-,故答案为:3-. 8.(邗江区一模)若1m n -=-,则2()22m n m n --+= .【解答】解:1m n -=-,2()22m n m n ∴--+2()2()m n m n =---2(1)2(1)=--⨯-12=+3=.9.(无锡期末)若代数式22x x -的值为5,则代数式2363x x --的值为 . 【解答】解:2363x x --23(2)3x x =--225x x -=,∴原式353=⨯-12=.故答案为:1210.(凤山县期末)如图所示的运算程序中,若开始输入的x 值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,⋯,则第2019次输出的结果为 .【解答】解:由设计的程序,知依次输出的结果是50,25,32,16,8,4,2,1,8,4,2,1⋯,发现从8开始循环.则201942015-=,201545033÷=⋯,故第2019次输出的结果是2.故答案为:2 11.(秦淮区期中)如图所示的数表是由从1开始的连续自然数组成的.观察数表特征,第n 行最中间的数可以表示为 .(用含n 的代数式表示)【解答】解:由图中的数字可知,第n 行第一个数字是2(1)1n -+,最后一个数字是2n ,则第n 行最中间的数可以表示为:222(1)112n n n n -++=-+,故答案为:21n n -+.三、解答题(共2小题)12.(海州区期中)化简或求值 (1)化简:3(2)2(3)a b a b --+(2)先化简,再求值:22225(3)4(3)a b ab ab a b --+;其中1a =,12b =-.【解答】解:(1)原式(63)(26)632649a b a b a b a b a b =--+=---=-;(2)原式22222215541239a b ab ab a b a b ab =---=-,当1a =,12b =-时,原式3915244=--=-.13.(玄武区期中)如图是小江家的住房户型结构图.根据结构图提供的信息,解答下列问题: (1)用含a 、b 的代数式表示小江家的住房总面积S ;(2)小江家准备给房间重新铺设地砖.若卧室所用的地砖价格为每平方米50元;卫生间、厨房和客厅所用的地砖价格为每平方米40元.请用含a 、b 的代数式表示铺设地砖的总费用W ; (3)在(2)的条件下,当6a =,4b =时,求W 的值.【解答】解:(1)小江家的住房总面积:83S a b =-;(2)3(8)508(3)40W b a =-⨯+-⨯1200150320960b a =-+-320150240a b =-+; (3)当6a =,4b =时32061504240W =⨯-⨯+1920600240=-+1560=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版七上数学找规律题库(一)
一、数字找规律
1.观察下列式子:
326241⨯==+⨯;4312252⨯==+⨯;5420263⨯==+⨯;6530274⨯==+⨯…… 请你将猜想得到的式子用含正整数n 的式子表示来__________。
2.观察下列顺序排列的等式:9×0+1=1 9×1+2=11 9×2+3=21 9×3+4=31 9×4+5=41……
猜想:第n 个等式(n 为正整数)应为 .
3.观察下列各式,你会发现什么规律?
3×5=15,而15=241-。
5×7=35,而35=261- ……
11×13=143,而143=2121-
将你猜想到的规律用只含一个字母的式子表示出来: .
4..观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在察规律之后并用你得到的规律填空:250___________=+⨯, 第n 个式子呢? ___________________
5.给出下列算式:1881322⨯==-,28163522⨯==-,38245722⨯==-,
48327922⨯==-,…,观察上面的一系列等式,你能发现什么规律?用代数式表示这个规律
是 。
6.研究下列算式,你会发现有什么规律?
224131==+⨯;239142==+⨯;2416153==+⨯;2525164==+⨯……
请将你找出的规律用公式表示出来: 。
8.(2009年龙岩)观察下列一组数:2
1,4
3,6
5,8
7,…… ,它们是按一定规律排列的. 那么这一组数的第k 个数是 .
10. 观察下面一列有规律的数
,48
6
,355,244,153,82,31 根据这个规律可知第n 个数是 (n 是正整数) 11. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,
4!=4×3×2×1,…,则
100!
98!
的值为 12.计算20082007654321-++-+-+- 的结果是( ) A. -2008 B. -1004 C. -1 D. 0 13下列几个算式,找出规律:
1+2+1=4
1+2+3+2+1=9
1+2+3+4+3+2+1=16
1+2+3+4+5+4+3+2+1=25
利用上面规律,请你迅速算出:
①1+2+3+…+99+100+99+…+3+2+1= ②据①你会算出1+2+3+…+100是多少吗? ③据上你能推导出1+2+3+…+n 的计算公式吗?
二.图形找规律
1.下图中①是一个三角形,分别连接这个三角形三边的中点,得到②;再分别连结②中间的小三角形三边的中点,得到图③,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下列问题。
(1)
将下表填写完整
(2
)在第n 个图形中有____________________
个三角形(用含n 的式子表示)。
2.
①张桌子拼在一起可坐______人。
3张桌子拼在一起可坐____人,n 张桌子拼在一起可坐______
①
②
③
人。
②一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
③若在②中,改成每8张桌子拼成1张大桌子,则共可坐_________人。
3,下图(1)表示1张餐桌和6张椅子(每个小半圆代表1张椅子),若按这种方式摆放20张餐桌需要的椅子张
数
是 。
4.用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案:
(1)第4个图案中有白色地面砖 块; (2)第n 个图案中有白色地面砖 块。
5.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有
)2( n n 个棋子,每个图案棋子总数为S ,按下图的排列规律推断,S 与n 之间的关系可以用式
第三个
第一个
第二个
子 来表示。
6.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆n 个“金鱼”需用火柴棒的根数为( )
A .26n +
B .86n +
C .44n +
D .8n
7. (2011•日照)观察图中正方形四个顶点所标的数字规律,可知数2011应标在( )
A 、第502个正方形的左下角
B 、第502个正方形的右下角
C 、第503个正方形的左上角
D 、第503个正方形的右下角
8. 、(2011•南平)观察下列各图形中小正方形的个数,依此规律,第(11)个图形中小正方形的个数为( )
4
2
==s n
8
3
==s n
12
4
==s n
16
5
==s n
……
①
②
③
第3个
第2个
第1个
9.下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形
组成,……,第
)个基础图形组成10.下面是用棋子摆成的“
T”字,按这样的规律摆下去,摆成第10个“T”字需要___ 个棋子;第n个需要____ 个。
①②③
●●●●●●●●●●●●●●●
●●●
●●●
●●
●
11.用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:
(1)第4个图案中有白色纸片______________张;
(2)第n个图案中有白色纸片______________张.
(3)
(2)
(1)。
