acm大学生程序设计试题
山东科技大学第二届ACM程序设计大赛试题

山东科技大学第二届ACM程序设计大赛试题册试题共14页,题目共计12道山东科技大学第二届ACM 程序设计大赛试题册Problem A 简单计算Description给出n 个十进制的数,找出这n 个数的二进制表示中1的个数最少的数。
Input输入的第一行为一个正整数T (1≤T ≤20),代表测试数据组数。
对于每组测试数据,输入的第一行为一个正整数n (1≤n ≤10000),第二行为n个正整数A 1、A 2、…、A n (1≤A i ≤109),每个数之间以空格分隔。
Output每组数据输出一行,先输出数据组数,再输出二进制中含1最少的数,如果存在多个数符合条件,输出最小的那个。
具体输出格式见样例输出。
Sample Input Sample Output山东科技大学第二届ACM 程序设计大赛试题册Problem B 关键字搜索Description我们的新网站具有了全新的搜索功能,使用了2个通配符“*”和“?”,其中“*”表示0或者多个小写字母,“?”代表1个字母。
当我们输入一个关键字的时候,我们在不确定的地方就使用通配符。
我们在数据库里面有多条记录,每条记录都是由小写字母组成,现在给出一个关键字,你能告诉我数据库里面有多少条与关键字相匹配的记录吗?例如: 如果关键字是j*y*m*y?,那么jiyanmoyu ,jyanmoyu ,jymyu 都是相匹配的记录。
Input第一行输入一个T (T ≤20),表示有T 组测试数据。
对于每组测试数据,第一行是输入的关键字,接下是数据库里面的所有记录的条数n ,1≤n ≤10000,每条记录的长度不超过50个小写字母。
Output对于每组测试数据,输出与关键字相匹配的总记录条数,占一行。
Sample Input Sample Output山东科技大学第二届ACM 程序设计大赛试题册Problem C 正方形Description在二维坐标轴内给出四个点,这四个点能否构成一个正方形。
ACM题库完整版

#include<stdio.h> int type(int); char week[7][10]={"saturday","sunday","monday","tuesday","wednesday","thursday","friday"}; int year[2]={365,366}; int month[2][12]={31,28,31,30,31,30,31,31,30,31,30,31,31,29,31,30,31,30,31,31,30,31,30,31}; int main(void) { int days,dayofweek; int i=0,j=0; while(scanf("%d",&days)&&days!=-1) { dayofweek=days%7; for(i=2000;days>=year[type(i)];i++) days-=year[type(i)]; for(j=0;days>=month[type(i)][j];j++) days-=month[type(i)][j]; printf("%d-%02d-%02d%s\n",i,j+1,days+1,week[dayofweek]); } return 0; } int type(int m) { if(m%4!=0||(m%100==0&&m%400!=0)) return 0; else return 1; }
登山
1.题目描述 五一到了,NUIST-ACM队组织大家去登 山观光,队员们发现山上一个有N个景点, 并且决定按照顺序来浏览这些景点,即 每次所浏览景点的编号都要大于前一个 浏览景点的编号。同时队员们还有另一 个登山习惯,就是不连续浏览海拔相同 的两个景点,并且一旦开始下山,就不 再向上走了。队员们希望在满足上面条 件的同时,尽可能多的浏览景点,你能 帮他们找出最多可能浏览的景点数么? 2.输入 Line 1: N (2 <= N <= 1000) 景点数 Line 2: N个整数,每个景点的海拔 3.输出 最多能浏览的景点数 4.样例输入 8 186 186 150 200 160 130 197 220 5.样例输出 4
计算机acm试题及答案

计算机acm试题及答案一、选择题1. 在计算机科学中,ACM代表什么?A. 人工智能与机器学习B. 计算机辅助制造C. 计算机辅助设计D. 国际计算机学会答案:D2. 下列哪个不是计算机程序设计语言?A. PythonB. JavaC. C++D. HTML答案:D3. 在计算机系统中,CPU代表什么?A. 中央处理单元B. 计算机辅助设计C. 计算机辅助制造D. 计算机辅助教学答案:A二、填空题1. 计算机的内存分为__________和__________。
答案:RAM;ROM2. 在编程中,__________是一种用于存储和操作数据的数据结构。
答案:数组3. 计算机病毒是一种__________,它能够自我复制并传播到其他计算机系统。
答案:恶意软件三、简答题1. 请简述计算机操作系统的主要功能。
答案:计算机操作系统的主要功能包括管理计算机硬件资源,提供用户界面,运行应用程序,以及控制其他系统软件和应用软件的运行。
2. 什么是云计算,它与传统的本地计算有何不同?答案:云计算是一种通过互联网提供计算资源(如服务器、存储、数据库、网络、软件等)的服务模式。
与传统的本地计算相比,云计算允许用户按需获取资源,无需购买和维护物理硬件,具有更高的灵活性和可扩展性。
四、编程题1. 编写一个程序,计算并输出从1到100(包括1和100)之间所有偶数的和。
答案:```pythonsum = 0for i in range(1, 101):if i % 2 == 0:sum += iprint(sum)```2. 给定一个字符串,编写一个函数,将字符串中的所有字符按ASCII 码值排序并返回。
答案:```pythondef sort_string(s):return ''.join(sorted(s))```五、论述题1. 论述计算机硬件和软件之间的关系及其对计算机系统性能的影响。
答案:计算机硬件是计算机系统的物质基础,包括CPU、内存、硬盘等,而软件则是运行在硬件上的程序和数据。
ACM试题及参考答案
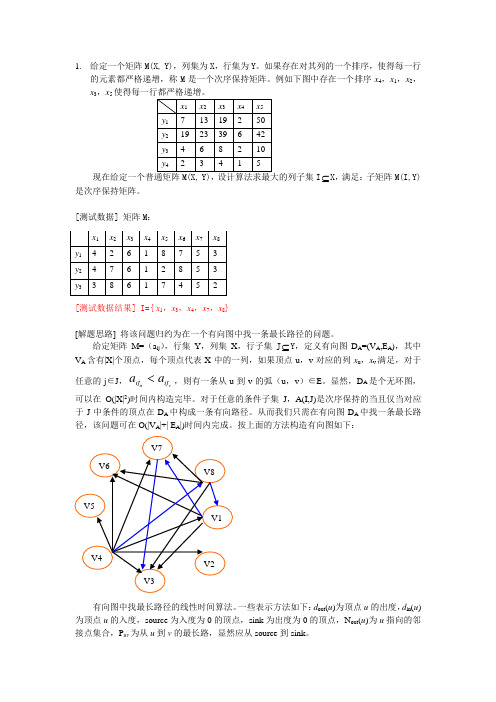
1. 给定一个矩阵M(X, Y),列集为X ,行集为Y 。
如果存在对其列的一个排序,使得每一行的元素都严格递增,称M 是一个次序保持矩阵。
例如下图中存在一个排序x 4,x 1,x 2,x 3,x 5I ⊆X ,满足:子矩阵M(I,Y)是次序保持矩阵。
[测试数据] 矩阵M :[测试数据结果] I={ x 1,x 3,x 4,x 7,x 8}[解题思路] 将该问题归约为在一个有向图中找一条最长路径的问题。
给定矩阵M=(a ij ),行集Y ,列集X ,行子集J ⊆Y ,定义有向图D A =(V A ,E A ),其中V A 含有|X|个顶点,每个顶点代表X 中的一列,如果顶点u ,v 对应的列x u ,x v 满足,对于任意的j ∈J ,u v ij ij a a <,则有一条从u 到v 的弧(u ,v )∈E 。
显然,D A 是个无环图,可以在O(|X|2)时间内构造完毕。
对于任意的条件子集J ,A(I,J)是次序保持的当且仅当对应于J 中条件的顶点在D A 中构成一条有向路径。
从而我们只需在有向图D A 中找一条最长路径,该问题可在O(|V A |+| E A |)时间内完成。
按上面的方法构造有向图如下:有向图中找最长路径的线性时间算法。
一些表示方法如下:d out (u )为顶点u 的出度,d in (u )为顶点u 的入度,source 为入度为0的顶点,sink 为出度为0的顶点,N out (u )为u 指向的邻接点集合,P uv 为从u 到v 的最长路,显然应从source 到sink 。
在每一步为每个顶点关联一个永久的或临时的标签。
v被赋了一个临时标签(v’,i v)表明在当前步,算法找出的最长的从source到v的有向路长度为i v,且经由v’而来。
v被赋了一个永久标签[v’,i v]表明从source到v的最长有向路长度为i v,且经由v’而来,通过回溯每个顶点的永久标签就可以找出最长有向路。
大学ACM考试题目及作业答案整理

ACM作业与答案整理1、平面分割方法:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
#include <iostream.h>int f(int n){if(n==1) return 2;else return f(n-1)+2*(n-1);}void main(){int n;while(1){cin>>n;cout<<f(n)<<endl;}}2、LELE的RPG难题:有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.编程全部的满足要求的涂法.#include<iostream.h>int f(int n){if(n==1) return 3;else if(n==2) return 6;else return f(n-1)+f(n-2)*2;}void main(){int n;while(1){cin>>n;cout<<f(n)<<endl;}}3、北大ACM(1942)Paths on a GridTime Limit: 1000MS Memory Limit: 30000K DescriptionImagine you are attending your math lesson at school. Once again, you are bored because your teacher tells things that you already mastered years ago (this time he's explaining that (a+b)2=a2+2ab+b2). So you decide to waste your time with drawing modern art instead.Fortunately you have a piece of squared paper and you choose a rectangle of size n*m on the paper. Let's call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner, taking care that it stays on the lines and moves only to the right or up. The result is shown on the left:Really a masterpiece, isn't it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?InputThe input contains several testcases. Each is specified by two unsigned 32-bit integers n and m, denoting the size of the rectangle. As you can observe, the number of lines of the corresponding grid is one more in each dimension. Input is terminated by n=m=0.OutputFor each test case output on a line the number of different art works that can be generated using the procedure described above. That is, how many paths are there on a grid where each step of the path consists of moving one unit to the right orone unit up? You may safely assume that this number fits into a 32-bit unsigned integer.Sample Input5 41 10 0Sample Output1262#include<iostream>using namespace std;long long f(long long m, long long n){if(n==0) return 1;else return f(m-1,n-1)*m/n;}int main(){long long m,n;while(scanf("%I64d %I64d",&n,&m) && n+m){printf("%I64d\n",f(m+n,min(m,n)));}return 0;}1、北大ACM(1012)JosephTime Limit: 1000MS Memory Limit: 10000KTotal Submissions: 31213 Accepted: 11700 DescriptionThe Joseph's problem is notoriously known. For those who are not familiar with the original problem: from among n people, numbered 1, 2, . . ., n, standing in circle every mth is going to be executed and only the life of the last remaining person will be saved. Joseph was smart enough to choose the position of the last remaining person, thus saving his life to give us the message about the incident. For example when n = 6 and m = 5 then the people will be executed in the order 5, 4, 6, 2, 3 and 1 will be saved.Suppose that there are k good guys and k bad guys. In the circle the first k are good guys and the last k bad guys. You have to determine such minimal m that all the bad guys will be executed before the first good guy.题目大意:编号为1,2…, n的n个人排成一圈,从第一个人开始,去掉后面的第m个人,在从第m+1个人开始去掉后面第m个人,以此类推。
杭电acm练习题100例(删减版)

杭电acm练习题100例(删减版)【程序1】题目:有1、2、3、4个数字,能组成多少个互不相同且无重复数字的三位数?都是多少?1.程序分析:可填在百位、十位、个位的数字都是1、2、3、4。
组成所有的排列后再去掉不满足条件的排列。
#include "stdio.h"#include "conio.h"main(){ int i,j,k;printf("\n");for(i=1;i<5;i++) /*以下为三重循环*/for(j=1;j<5;j++)for (k=1;k<5;k++){ if (i!=k&&i!=j&&j!=k) /*确保i、j、k三位互不相同*/printf("%d,%d,%d\n",i,j,k); }getch(); }==============================================================【程序2】题目:企业发放的奖金根据利润提成。
利润(I)低于或等于10万元时,奖金可提10%;利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部分,可可提成7.5%;20万到40万之间时,高于20万元的部分,可提成5%;40万到60万之间时高于40万元的部分,可提成3%;60万到100万之间时,高于60万元的部分,可提成1.5%,高于100万元时,超过100万元的部分按1%提成,从键盘输入当月利润I,求应发放奖金总数?#include "stdio.h" #include "conio.h"main(){ long int i;int bonus1,bonus2,bonus4,bonus6,bonus10,bonus;scanf("%ld",&i);bonus1=100000*0. 1;bonus2=bonus1+100000*0.75;bonus4=bonus2+200000*0.5;bonus6=bonus4+200000*0.3;bonus10=bonus6+400000*0.15;if(i<=100000)bonus=i*0.1;else if(i<=200000)bonus=bonus1+(i-100000)*0.075;else if(i<=400000)bonus=bonus2+(i-200000)*0.05;else if(i<=600000)bonus=bonus4+(i-400000)*0.03;else if(i<=1000000)bonus=bonus6+(i-600000)*0.015;elsebonus=bonus10+(i-1000000)*0.01;printf("bonus=%d",bonus);getch(); }====================================== ========================【程序3】题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?#include "math.h"#include "stdio.h"#include "conio.h"main(){ long int i,x,y,z;for (i=1;i<100000;i++){ x=sqrt(i+100); /*x为加上100后开方后的结果*/y=sqrt(i+268); /*y为再加上168后开方后的结果*/if(x*x==i+100&&y*y==i+268)printf("\n%ld\n",i); }getch(); }====================================== ========================【程序4】题目:输入某年某月某日,判断这一天是这一年的第几天?#include "stdio.h" #include "conio.h"main(){ int day,month,year,sum,leap;printf("\nplease input year,month,day\n");scanf("%d,%d,%d",&year,&month,&day);switch(month) /*先计算某月以前月份的总天数*/{ case 1:sum=0;break;case 2:sum=31;break;case 3:sum=59;break;case 4:sum=90;break;case 5:sum=120;break;case 6:sum=151;break;case 7:sum=181;break;case 8:sum=212;break;case 9:sum=243;break;case 10:sum=273;break;case 11:sum=304;break;case 12:sum=334;break;default:printf("data error");break; }sum=sum+day; /*再加上某天的天数*/if(year%400==0||(year%4==0&&year%100!=0)) /*判断是不是闰年*/leap=1;elseleap=0;if(leap==1&&month>2) /*如果是闰年且月份大于2,总天数应该加一天*/sum++;printf("It is the %dth day.",sum);getch(); }====================================== ======================== 【程序5】题目:输入三个整数x,y,z,请把这三个数由小到大输出。
acm编程练习题

acm编程练习题ACM(即:美国计算机协会)编程练习题是指ACM国际大学生程序设计竞赛中的一些编程题目,旨在考察参赛选手在算法和数据结构等方面的能力。
这些题目常常要求选手设计和实现一个算法,在规定的时间和空间限制下解决实际问题。
ACM编程练习题具有一定的难度和挑战性,它的解题过程有时需要选手在理论基础上进行创新思维和灵活运用。
相比于传统的笔试或面试形式,ACM编程练习题更加贴近实际应用场景,能够真实地展现参赛选手的编程能力和逻辑思维能力。
为了更好地完成ACM编程练习题,选手需要熟练掌握常用的数据结构和算法,比如数组、链表、栈、队列、树、图等。
此外,对于一些经典的算法,如贪心算法、动态规划、分治法等,也有必要进行深入学习和理解。
在真实的竞赛环境中,选手还需要熟悉特定的编程语言和开发环境,比如C++、Java或Python等。
解决ACM编程练习题有着多种方法和思路。
选手需要熟悉各种问题的特点,根据问题所给条件进行合理的算法设计。
对于一些复杂的问题,可以利用数学方法进行简化和转化,从而找到更高效的解决方案。
在编程实现的过程中,要注重代码的可读性和可维护性,合理地使用注释和命名,避免代码冗余和错误。
ACM编程练习题的解题过程中,选手不仅需要具备扎实的编程基础和算法知识,还需要具备压力下的良好心态和团队合作精神。
在竞赛中,选手可能面临时间紧迫、出题者的陷阱、复杂场景等挑战,因此,选手们需要保持冷静、灵活应对,不断提升自己的解题能力和竞赛技巧。
总之,ACM编程练习题是一种非常有挑战性的编程竞赛形式,对选手的编程能力、算法思维和团队协作能力都提出了较高的要求。
通过积极参与练习和实战,选手们可以不断提升自己,在ACM竞赛中取得更好的成绩,并在实际工作中具备更强的编程能力。
(字数:413)。
ACM比赛试题

The 35th ACM-ICPC Asia Regional Contest (Hangzhou)Contest SectionOctober 24, 2010Sponsored by IBM & AlibabaZhejiang Sci-Tech UniversityThis problem set should contain 10 problems on numbered 24 pages. Please inform a runner immediately if something is missing from your problem set.Problem A. Naughty fairiesDescriptionOnce upon a time, there lived a kind of fairy in the world. Those fairies could hear the voice of fruit trees, and helped people with a harvest. But people did n’t know that fruits are also those fairies’ favorite food. After the fairies ate people’s fruits, they always did something to cover it up.One day a little fairy named Lily flew into an orchard and found a large peach tree. Hungry as Lily was, she started eating without thinking until her stomach was full. In the fairy world, when a fairy ate the fruits in a fruit tree, sometimes the fruit tree would feel honored and bore more fruits immediately. That’s why sometimes the number of fruits in a tree got increased after a fairy ate fruits of that tree.But the fairies didn’t want people to find out weird things such as fruits become more or less suddenly. Lily decided to use a magic spell so that the orchard owner couldn’t find the change of the number of p eaches.Suppose there were N peaches on a tree originally and there were M peaches left after Lily was full. M may be greater than, less than or equal to N. All M peaches were visible at first, and Lily wanted to make an illusion so that exactly N peaches are visible.Lily can do 3 kinds of spell to change the total visible number of peaches:1) “PAPADOLA”:This spell would increase the number of visible peaches by one.2) “EXPETO POTRONUM”:This spell would double the number of visible peaches.3) “SAVIDA LOHA”:This spell would decrease the number of visible peaches by one. Each spell would take one minute and Lily wanted to finish as fast as possible. Now please tell Lily the least time she needs to change the number of visible peaches to N.InputThere are several test cases, ended by “0 0”.For each test case, there are only one line containing two numbers separated by a blank, N and M, the original numbers of peaches and the numbers of peaches left(0<N,M<10500).There is no leading zero.OutputFor each test case, you should output just a number K indicating the minimum time (in minutes) Lily needed to finish her illusion magic.Sample Input5 21 9986 320 0Sample Output29812Problem B. Prison BreakDescriptionRompire is a robot kingdom and a lot of robots live there peacefully. But one day, the king of Rompire was captured by human beings. His thinking circuit was changed by human and thus became a tyrant. All those who are against him were put into jail, including our clever Micheal#1. Now it’s time to escape, but Micheal#1 needs an optimal plan and he contacts you, one of his human friends, for help.The jail area is a rectangle contains n×m little grids, each grid might be one of the following:1) Empty area, represented by a capital letter ‘S’.2) The starting position of Micheal#1, represented by a capital letter ‘F’.3) Energy pool, represented by a capital letter ‘G’. When entering a n energy pool, Micheal#1 can use it to charge his battery ONLY ONCE. After the charging, Micheal#1’s batt ery will become FULL and the energy pool will become an empty area. Of course, passing an energy pool without using it is allowed.4) Laser sensor, represented by a capital letter ‘D’. Since it is extremely sensitive, Micheal#1 cannot step into a grid with a laser sensor.5) Power switch, represented by a capital letter ‘Y’. Once Micheal#1 steps into a grid with a Power switch, he will certainly turn it off.In order to escape from the jail, Micheal#1 need to turn off all the power switches to stop the electric web on the roof—then he can just fly away. Moving to an adjacent grid (directly up, down, left or right) will cost 1 unit of energy and only moving operation costs energy. Of course, Micheal#1 cannot move when his battery contains no energy.The larger the battery is, the more energy it can save. But larger battery means more weight and higher probability of being found by the weight sensor. So Micheal#1 needs to make his battery as small as possible, and still large enough to hold all energy he need. Assuming that the size of the battery equals to maximum units of energy that can be saved in the battery, and Micheal#1 is fully charged at the beginning, Please tell him the minimum size of the battery needed for his Prison break.InputInput contains multiple test cases, ended by 0 0. For each test case, the first line contains two integer numbers n and m showing the size of the jail. Next n lines consist of m capital letters each, which stands for the description of the jail.You can assume that 1<=n,m<=15, and the sum of energy pools and power switches is less than 15.OutputFor each test case, output one integer in a line, representing the minimum size of the battery Micheal#1 needs. If Micheal#1 can’t escape, output -1.Sample Input5 5GDDSSSSSFSSYGYSSGSYSSSYSS0 0Sample Output4Problem C. To Be an Dream Architect DescriptionThe “dream architect” is the key role in a team of “dream extractors” who enter other’s dreams to steal secrets. A dream architect is responsible for crafting the virtual world that the team and the target will dream into. To avoid the target noticing the world is artificial, a dream architect must have powerful 3D imagination.Cobb uses a simple 3D imagination game to test whether a candidate has the potential to be an dream architect. He lets the candidate imagine a cube consisting of n×n×n blocks in a 3D coordinate system as Figure 1. The block at bottom left front corner is marked (1, 1, 1) and the diagonally opposite block is marked (n, n, n). Then he tells the candidate that the blocks on a certain line are eliminated. The line is always parallel to an axis. After m such block eliminations, the candidate is asked to tell how many blocks are eliminated. Note that one block can only be eliminated once even if it is on multiple lines.Here is a sample graph according to the first test case in the sample input:InputThe first line is the number of test cases.In each test case, the first line contains two integers n and m( 1 <= n <= 1000, 0 <= m <= 1000).,meaning that the cube is n x n x n and there are m eliminations.Each of the following m lines represents an elimination in the following format:axis_1=a, axis_2=bwhere axis_i (i=1, 2) is ‘X’ or ‘Y’, or ‘Z’ and axis_1 is not equal to axis_2. a and b ar e 32-bit signed integers.OutputFor each test case output the number of eliminated blocks.Sample Input23 2Y=1,Z=3X=3,Y=110 2X=3,Y=3Y=3,Z=3Sample Output519Problem D. GomokuDescriptionYou are probably not familiar with the title, “Gomoku”, but you must have played it a lot. Gomoku is an abstract strategy board game and is also called Five in a Row, or GoBang. It is traditionally played with go pieces (black and white stones) on a go board (19x19 intersections). Nowadays, standard chessboard of Gomoku has 15x15 intersections. Black plays first, and players alternate in placing a stone of their color on an empty intersection. The winner is the first player to get an unbroken row of five or more stones horizontally, vertically, or diagonally.For convenience, we coordinate the chessboard as illustrated above. The left-bottom intersection is (0,0). And the bottom horizontal edge is x-axis, while the left vertical line is y-axis.I am a fan of this game, actually. However, I have to admit t hat I don’t have a sharp mind. So I need a computer program to help me. What I want is quite simple. Given a chess layout, I want to know whether someone can win within 3 moves, assuming both players are clever enough. Take the picture above for example. There are 31 stones on it already, 16 black ones and 15 white ones. Then we know it is white turn. The white player must place a white stone at (5,8). Otherwise, the black player will win next turn. After that, however, the white player also gets a perfect situation that no matter how his opponent moves, he will win at the 3rd move.So I want a program to do similar things for me. Given the number of stones and positions of them, the program should tell me whose turn it is, and what will happen within 3 moves.InputThe input contains no more than 20 cases.Each case contains n+1 lines which are formatted as follows.nx1 y1 c1x2 y2 c2......x n y n c nThe first integer n indicates the number of all stones. n<=222 which means players have enough space to place stones. Then n lines follow. Each line contains three integers: x i and y i and c i. x i and y i are coordinates of the stone, and ci means the color of the stone. If c i=0 the stone is white. If c i=1 the stone is black. It is guaranteed that 0<=x i,y i<=14, and c i=0 or 1. No two stones are placed at the same position. It is also guaranteed that there is no five in a row already, in the given cases.The input is ended by n=0.OutputFor each test case:First of all, the program should check whose turn next. Le t’s call the player who will move next “Mr. Lucky”. Obviously, if the number of the black stone equals to the number of white, Mr. Lucky is the black player. If the number of the black stone equals to one plus the numbers of white, Mr. Lucky is the white player. If it is not the first situation or the second, print “Invalid.”A valid chess layout leads to four situations below:1)Mr. Lucky wins at the 1st move. In this situation, print :Place TURN at (x,y) to win in 1 move.“TURN” must be replaced by “black” or “white” according to the situation and (x,y) is the position of the move. If there are different moves to win, choose theone where x is the smallest. If there are still different moves, choose the one where y is the smallest.2)Mr. Lucky’s opp onent wins at the 2nd move. In this situation, print:Lose in 2 moves.3)Mr. Lucky wins at the 3rd move. If so, print:Place TURN at (x,y) to win in 3 moves.“TURN” should replaced by “black” or “white”, (x,y) is the position where the Mr.Lucky should place a stone at the 1st move. After he place a stone at (x,y), no matter what his opponent does, Mr. Lucky will win at the 3rd step. If there are multiple choices, do the same thing as described in situation 1.4)Nobody wins within 3 moves. If so, print:Cannot win in 3 moves.Sample Input313 3 13 4 03 5 03 6 04 4 14 5 14 7 05 3 05 4 05 5 15 6 15 7 15 9 16 4 16 5 16 6 06 7 16 8 06 9 07 5 17 6 07 7 17 8 17 9 08 5 08 6 18 7 08 8 18 9 09 7 110 8 017 7 117 7 0Sample OutputPlace white at (5,8) to win in 3 moves. Cannot win in 3 moves.Invalid.Problem E. GunshotsDescriptionPresident Bartlet was shot! A group of terrorists shot to the crowd when President Bartlet waved to cheering people after his address. Many people were shot by the irrational bullets. Senior FBI agent Don Epps takes responsibility for this case. According to a series of crime scene investigation, including analyzing shot shells, replaying video from closed-circle television and collecting testimony by witnesses, Don keeps all the information about where and how the terrorists shot to crowd, as well as the location of every single person when the gun shoot happened. Now he wants to know how many gunshot victims are there in this case.Imagine that each target person can be regarded as a polygon (can be concave or self-intersecting) and each gunshot can be regarded as a half-line. The bullet will be stopped by the first person it shoots. A person can be shot in three ways:To simplify the problem, we assume that any two polygons can be completely separated by a line. Also each start point of the gunshot can be separated from each polygon by a line. Now given M people and N gunshots, please work out which person has been shot by each bullet.InputThere are multiple test cases in the input. The first line of the input file is an integer T demonstrating the number of test cases. (T<=10).For each test case, the first line is an integer N, representing the number of people (polygons). Following lines demonstrates the polygons. For the i th polygon (0<=i<N), the first line is an integer Q i , representing the number of edges of this polygon. In each of the following Q i lines, there are two real numbers x i and y i representing a point. Every pair of adjacent points demonstrate an edge of this polygon (i.e. (x i , y i ) to (x i+1, y i+1) is an edge, in which 0<=i<Q i -1), and (x Qi-1, y Qi-1) to (x 0, y 0) also demonstrates an edge of this polygon.PersonPerson Person 1. Normal shot 2. The bullet’s path isparallel to an edge 3. The bullet’s path is tangent to an vertexThen there is a line contains an integer M representing the number of gunshots. In the following M lines, each line contains four real numbers x, y, dx and dy, representing the start point (x, y) and direction vector (dx, dy) of that gunshot.In all test cases, we assume that 0< N<=100, 0<Q i<=1000, 0<M<=10000.OutputFor each test case, output contains M lines and the i th line demonstrates the result of the i th gunshot.If the i th gunshot shoots the j th polygon, the i th line contains “HIT j”, otherwise it contains a word “MISS” (means that it does not shoot any target). The polygons are numbered in the order of their appearance in the input file, and the numbers start from 0.At the end of each test case, please output a single line with “*****”.Sample Input1140 01 10 11 02-1 0 1 0-2 0 -1 0Sample OutputHIT 0MISS*****HintThe figure of the first case in the samples is as follows:Problem F. Rotational PaintingDescriptionJosh Lyman is a gifted painter. One of his great works is a glass painting. He creates some well-designed lines on one side of a thick and polygonal glass, and renders it by some special dyes. The most fantastic thing is that it can generate different meaningful paintings by rotating the glass. This method of design is called “Rotatio nal Painting (RP)” which is created by Josh himself.You are a fan of Josh and you bought this glass at the astronomical sum of money. Since the glass is thick enough to put erectly on the table, you want to know in total how many ways you can put it so that you can enjoy as many as possible different paintings hiding on the glass. We assume that material of the glass is uniformly distributed. If you can put it erectly and stably in any ways on the table, you can enjoy it.More specifically, if the polygonal glass is like the polygon in Figure 1, you have just two ways to put it on the table, since all the other ways are not stable. However, the glass like the polygon in Figure 2 has three ways to be appreciated.Pay attention to the cases in Figure 3. We consider that those glasses are not stable.InputThe input file contains several test cases. The first line of the file contains an integer T representing the number of test cases.For each test case, the first line is an integer n representing the number of lines of the polygon. (3<=n<=50000). Then n lines follow. The i th line contains two real number x i and y i representing a point of the polygon. (x i, y i) to (x i+1, y i+1) represents a edge of the polygon (1<=i<n), and (x n,y n) to (x1, y1) also represents a edge of the polygon. The input data insures that the polygon is not self-crossed.OutputFor each test case, output a single integer number in a line representing the number of ways to put the polygonal glass stably on the table.Sample Input240 0100 099 11 160 00 101 101 110 110 0Sample Output23HintThe sample test cases can be demonstrated by Figure 1 and Figure 2 in Description part.Problem G. Traffic Real Time Query System DescriptionCity C is really a nightmare of all drivers for its traffic jams. To solve the traffic problem, the mayor plans to build a RTQS (Real Time Query System) to monitor all traffic situations. City C is made up of N crossings and M roads, and each road connects two crossings. All roads are bidirectional. One of the important tasks of RTQS is to answer some queries about route-choice problem. Specifically, the task is to find the crossings which a driver MUST pass when he is driving from one given road to another given road.InputThere are multiple test cases.For each test case:The first line contains two integers N and M, representing the number of the crossings and roads.The next M lines describe the roads. In those M lines, the i th line (i starts from 1)contains two integers X i and Y i, representing that road i connects crossing X i and Y i (X i≠Y i).The following line contains a single integer Q, representing the number of RTQs. Then Q lines follows, each describing a RTQ by two integers S and T(S≠T) meaning that a driver is now driving on the road s and he wants to reach road t . It will be always at least one way from road s to road t.The input ends with a line of “0 0”.Please note that: 0<N<=10000, 0<M<=100000, 0<Q<=10000, 0<X i,Y i<=N, 0<S,T<=M OutputFor each RTQ prints a line containing a single integer representing the number of crossings which the driver MUST pass.Sample Input5 61 22 33 44 53 522 32 40 0Sample Output 01Problem H. National Day ParadeDescriptionThere are n×n students preparing for the National Day parade on the playground. The playground can be considered as a n×m grid. The coordinate of the west north corner is (1,1) , and the coordinate of the east south corner is (n,m).When training, every students must stand on a line intersection and all students must form a n×n square. The figure above shows a 3×8 playground with 9 students training on it. The thick black dots stand for the students. You can see that 9 students form a 3×3 square.After training, the students will get a time to relax and move away as they like. To make it easy for their masters to control the training, the students are only allowed to move in the east-west direction. When the next training begins, the master would gather them to form a n×n square again, and the position of the square doesn’t matter. Of course, no student is allowed to stand outside the playground.You are given the coordinates of each student when they are having a rest. Your task is to figure out the minimum sum of distance that all students should move to form a n×n square.InputThere are at most 100 test cases.For each test case:The first line of one test case contain two integers n,m. (n<=56,m<=200)Then there are n×n lines. Each line contains two integers, 1<=X i<=n,1<= Y i<=m indicating that the coordinate of the i th student is (X i , Y i ). It is possible for more than one student to stand at the same grid point.The input is ended with 0 0.OutputYou should output one line for each test case. The line contains one integer indicating the minimum sum of distance that all students should move to form a n×n square. Sample Input2 1682 1011 1271 1052 900 0Sample Output41Problem I. SearchlightsDescriptionThere is a piece of grids land of size n×m. Chandler and his team take responsibility to guard it. There are some searchlights on some pieces and each of them has a capability to lighten a distance towards four directions: north, south, east and west. Different searchlight has different lightening capability shown in levels. Searchlight with level k means that it can lighten k grids (including the gird that the searchlight stands in) along any of the four directions. Shown in following figure, there is a searchlight of level 3 and the shadow grids are ones that can be lightened by it. Particularly, searchlight of level 1 means that it can only lighten the grid in which the searchlight stands.Figure: A searchlight of Level 3Each searchlight has a maximum level. You can decrease a searchlight’s level to save the energy. A searchlight whose maximum level is k can be turned to level k, k-1, k-2, …, 1 and 0. Level 0 means turning off the searchlight.A grid is well-guarded if and only if at least one of the following two conditions is satisfied:1.There is a searchlight in this grid, and it is not switched to level 0 (the light is on).2.The grid is lightened by at least two searchlights. One lightens it in horizontaldirection (east or west), and another lightens it in vertical direction (north or south).Chandler asks you to help finding a solution that he can turn on some of the searchlights so that:1.All the grids are well-guarded.2.All the searchlights turned on are in a same level.3.That same level mentioned above is as small as possible.More specifically, if you choose a same level Q, then all the searchlights whose maximum level are less than Q have to be turned off. Please help him to find a solution with the minimum same level.InputThe input file contains several test cases.For each test case, the first line is two integers n and m, representing a grids land of size n×m. (0<n<=100, 0<m<=10000). Following n lines describe an n×m matrix in which a i,j means the maximum level of the searchlight in grid (i, j). a i,j can be zero, which means there is no searchlight on that grid. For all the cases, a i, j<=10000.The input file ends with a line containing two zeros.OutputFor each test case, output a single line with an integer, representing the minimum level you have found. If there is no such a solution, output “NO ANSWER!”Sampl e Input2 20 23 02 20 21 00 0Sampl e Output2NO ANSWER!Problem J. Infinite monkey theorem DescriptionCould you imaging a monkey writing computer programs? Surely monkeys are smart among animals. But their limited intelligence is no match for our human beings. However, there is a theorem about monkeys, and it states that monkeys can write everything if given enough time.The theorem is called “Infinite monkey theorem”. It states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, which of course includes the programs you are about to write (All computer programs can be represented as text, right?).It’s very easy to prove this theorem. A little calculation will show you that if the monkey types for an infinite length of time the probability that the output contains a given text will approach 100%.However, the time used is too long to be physically reasonable. The monkey will not be able to produce any useful programs even if it types until the death of the universe. To verify this and ensure that our human beings are not replaceable by monkeys, you are to calculate the probability that a monkey will get things right.InputThere will be several test cases.Each test case begins with a line containing two integers n and m separated by a whitespace (2<=n<=26, 1<=m<=1000). n is the number of keys on the typewriter and the monkey will hit these keys m times. Thus the typewriter will finally produce an output of m characters.The following n lines describe keys on the typewriter. Each line has a lower case letter and a real number separated by a whitespace. The letter indicates what the typewriter will produce if the monkey hits that key and the real number indicates the probability that the monkey will hit this key. Two hits of the monkey are independent of each other (Two different hits have the same probability for a same key), and sum of all the probabilities for each key is ensured to be 1.The last line of the test case contains a word composed of lower case letters. The length of the word will be less than or equal to 10.The input will end with a line of two zeros separated by a whitespace. This line should not be processed.OutputFor each test case, output one line containing the probability that the given word will appear in the typewriter’s output. The output should be in percentage format and numbers should be rounded to two digits after the decimal point.Sampl e Input4 10w 0.25o 0.25r 0.25d 0.25word2 10a 1.0b 0.0abc2 100a 0.312345b 0.687655abab0 0Sampl e Output2.73%0.00%98.54%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
acm大学生程序设计试题
题目一:最大公约数(GCD)
题目描述:
给定两个正整数,求它们的最大公约数(GCD)。
输入两个正整数a和b(1 <= a, b <= 10^9),求它们的最大公约数。
输入格式:
两个正整数,以空格分隔。
输出格式:
输出一个整数,表示输入两个正整数的最大公约数。
示例:
输入:
14 21
输出:
7
思路和分析:
最大公约数(GCD)可以使用欧几里得算法来求解,即辗转相除法。
具体的步骤如下:
1. 用较大的数除以较小的数,将得到的余数作为新的较大数。
2. 再用新的较大数除以较小数,将得到的余数作为新的较大数。
3. 如此重复,直到两个数可以整除,此时较小的数就是最大公约数。
代码实现:
```cpp
#include <iostream>
using namespace std;
int gcd(int a, int b) {
if (b == 0)
return a;
return gcd(b, a % b);
}
int main() {
int a, b;
cin >> a >> b;
int result = gcd(a, b);
cout << result << endl;
return 0;
}
```
题目二:字符串反转
题目描述:
给定一个字符串,要求将其反转并输出。
输入一个字符串s(1 <= |s| <= 1000),输出该字符串的反转结果。
输入格式:
一个字符串s,只包含大小写字母和数字。
输出格式:
一个字符串,表示输入字符串的反转结果。
示例:
输入:
HelloWorld123
输出:
321dlroWolleH
思路和分析:
字符串反转可以使用双指针的方法来实现。
初始时,左指针指向字符串的开头,右指针指向字符串的末尾,然后交换左右指针所指向的字符,并向中间移动,直到左指针不小于右指针。
代码实现:
```cpp
#include <iostream>
using namespace std;
string reverseString(string s) {
int left = 0, right = s.length() - 1; while (left < right) {
swap(s[left], s[right]);
left++;
right--;
}
return s;
}
int main() {
string s;
cin >> s;
string result = reverseString(s); cout << result << endl;
return 0;
}
```
题目三:字符串匹配
题目描述:
给定一个字符串s和一个模式串p,判断s中是否存在与p相匹配的子串。
输入一个字符串s和一个模式串p,输出是否存在匹配的子串。
输入格式:
两个字符串s和p,以空格分隔。
输出格式:
如果存在匹配的子串,则输出"Yes",否则输出"No"。
示例:
输入:
HelloWorld Hello
输出:
Yes
思路和分析:
字符串匹配可以使用双指针的方法来实现。
初始时,左指针指向字符串s的开头,右指针指向模式串p的开头,然后逐个字符进行比较,
如果相同则同时向后移动两个指针,如果不同则将左指针回溯到初始位置的下一个字符,右指针重新指向模式串的开头。
代码实现:
```cpp
#include <iostream>
using namespace std;
bool stringMatch(string s, string p) {
int n = s.length(), m = p.length();
for (int i = 0; i < n - m + 1; i++) {
int j;
for (j = 0; j < m; j++) {
if (s[i + j] != p[j])
break;
}
if (j == m)
return true;
}
return false;
}
int main() {
string s, p;
cin >> s >> p;
bool result = stringMatch(s, p);
if (result)
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
```
以上是三道ACM大学生程序设计试题的解答,分别涉及最大公约数(GCD)、字符串反转和字符串匹配。
希望对你有帮助!。
