人工神经网络例题
人工智能与神经网络考试试题

人工智能与神经网络考试试题一、选择题(每题 5 分,共 30 分)1、以下哪个不是人工智能的应用领域?()A 医疗诊断B 金融投资C 艺术创作D 传统手工制造业2、神经网络中的神经元通过什么方式进行连接?()A 随机连接B 全连接C 部分连接D 以上都不对3、在训练神经网络时,常用的优化算法是()A 随机梯度下降B 牛顿法C 二分法D 以上都是4、下列关于人工智能和神经网络的说法,错误的是()A 人工智能包括神经网络B 神经网络是实现人工智能的一种方法C 人工智能就是神经网络D 神经网络具有学习能力5、下面哪种激活函数常用于神经网络?()A 线性函数B 阶跃函数C Sigmoid 函数D 以上都是6、神经网络的层数越多,其性能一定越好吗?()A 一定B 不一定C 肯定不好D 以上都不对二、填空题(每题 5 分,共 30 分)1、人工智能的英文缩写是_____。
2、神经网络中的“学习”是指通过调整_____来优化模型性能。
3、常见的神经网络架构有_____、_____等。
4、训练神经网络时,为了防止过拟合,可以采用_____、_____等方法。
5、深度学习是基于_____的一种机器学习方法。
6、神经网络中的损失函数用于衡量_____与_____之间的差异。
三、简答题(每题 10 分,共 20 分)1、请简要说明人工智能和机器学习的关系。
答:人工智能是一个广泛的概念,旨在让计算机能够像人类一样思考和行动,实现智能的表现。
机器学习则是实现人工智能的重要手段之一。
机器学习专注于让计算机通过数据和算法进行学习,自动发现数据中的模式和规律,从而能够对新的数据进行预测和决策。
机器学习为人工智能提供了技术支持,使计算机能够从大量数据中获取知识和技能,不断提升智能水平。
可以说机器学习是人工智能的核心组成部分,但人工智能不仅仅局限于机器学习,还包括其他技术和方法,如知识表示、推理、规划等。
2、简述神经网络中反向传播算法的原理。
人工神经网络原理第8章习题参考答案

1.人工神经网络适合于解决哪些问题?试举例说明。
人工神经网络技术在处理对内部规律不甚了解,也不能用一组规则和方程等数学表达式描述的较为复杂的问题时具有一定的优越性,尤其对容错性有一定要求的任务,例如图形的检测与识别、诊断、特征提取、推论等,人工神经网络都是比较合适的处理手段,对于上述任务,即使输入数据是模糊的或不完善的,人工神经网络仍然能够对其进行处理。
示例略。
2.一个人工神经网络应用的开发要经过哪些阶段?明确需求、选取模型、设计神经网络节点、设计神经网络结构、设计神经网络训练算法、选择训练和测试样本、网络训练与测试、实现神经网络。
3.若要用神经网络实现对0~9十个数字字符的识别,应当如何选取适当的人工神经网络模型?参见表8-1,可以选择BP、Hopfield等神经网络模型。
4.若要实现一个简单的交通标志识别系统,应当如何选取适当的人工神经网络模型?参见表8-1,可以选择BP、Hopfield等神经网络模型。
5.若有一个私人医生,每天可接受10个预约病人的上门服务。
若要为该医生设计一条当天的巡诊路线,以使该医生的巡诊距离最短,应当如何选取适当的人工神经网络模型?这是一个优化问题,可以选择Hopfield神经网络。
6.试述对习题2、3、4中选取的人工神经网络模型进行设计开发的全过程。
略。
7.有如下几种模型,其特性如表8-4所示。
表8-4 人工神经网络模型的基本性能若要开发一个贷款评估人工神经网络,要求能够根据借贷申请人的月收入、生活费用支出、房租、水、电、交通费用支出及其他费用支出来实时地分析这一贷款申请是否合格。
如合格,则批准申请给予贷款,否则给予拒绝。
请从表8-4列出的人工神经网络模型中选择一个适合该贷款评估应用的模型,并阐明原因。
可根据输出类型(例如,此题是一个分类问题,而不是优化问题)、训练方法、要求的训练时间和执行时间等选取各项指标都符合具体需求的模型。
此题只是一个示例,让读者掌握如何选取适当的人工神经网络模型,具体选取过程略。
人工智能神经网络例题

神经网络例题1. 简介1.1 背景信息1.2 目的和范围2. 概述在本文档中,我们将讨论领域中使用的神经网络模型,并提供一些实际应用案例。
该模板旨在帮助读者理解如何构建、训练和优化神经网络。
3. 前置知识与概念解释在阅读本文之前,请确保您对以下术语有基本了解: - 神经元:一个计算单元,接收输入并输出。
- 权重:连接不同层次或节点间传递信号时所赋予的权值。
4. 示例问题描述及数据集准备我们选择了一个分类问题作为示例来说明如何使用神经网络进行预测。
具体而言,在给定鸢尾花(Iris)数据集下,我们要根据萼片长度、宽度以及花瓣长度等特征来判断其品种是Setosa, Versicolor还是Virginica。
5 . 数据处理与特征选择这个步骤包括加载原始数据文件、清洗缺失值、标准化数值变量以及转换类别变量到数字表示形式等操作。
6. 神经网络模型构建6.1 模型选择:我们将使用多层感知器(Multilayer Perceptron)作为神经网络的基本架构。
6.2 构建输入和输出层:根据问题描述,确定输入特征数目以及输出类别数目。
6.3 隐藏层数量与节点设置: 根据实际需求,在隐藏层中添加适当数量的节点,并考虑避免过拟合等问题。
7 . 训练与优化在这一阶段,我们需要定义损失函数、选择梯度下降算法并进行超参数调整。
同时还要划分训练集和测试集,并对模型进行迭代训练直至收敛或达到最大迭代次数。
8 . 结果评估我们通过计算准确率、查全率、查准率等指标来评估所得结果,并可视化展示预测效果。
9 . 实例应用案例这里了其他领域常见的神经网络应用案例:- 图像识别- 自然语言处理10 . 总结11.参考文献12.致谢13.附件说明:相关数据文件请参见“data.csv”;代码实现详见GitHub:“”。
14.法律名词及注释:- 神经网络:一种模拟人脑神经元工作方式的计算模型。
- 多层感知器(Multilayer Perceptron):由多个输入、隐藏和输出层组成的前馈神经网络。
人工神经网络例题
1、什么是BP 网络的泛化能力?如何保证BP 网络具有较好的泛化能力?(5分)解:(1)BP网络训练后将所提取的样本对中的非线性映射关系存储在权值矩阵中,在其后的工作阶段,当向网络输入训练时未曾见过的非样本数据时,网络也能完成由输入空间向输出空间的正确映射。
这种能力称为多层感知器的泛化能力,它是衡量多层感知器性能优劣的一个重要方面。
(2)网络的性能好坏主要看其是否具有很好的泛化能力,而对泛化能力的测试不能用训练集的数据进行,要用训练集以外的测试数据来进行检验。
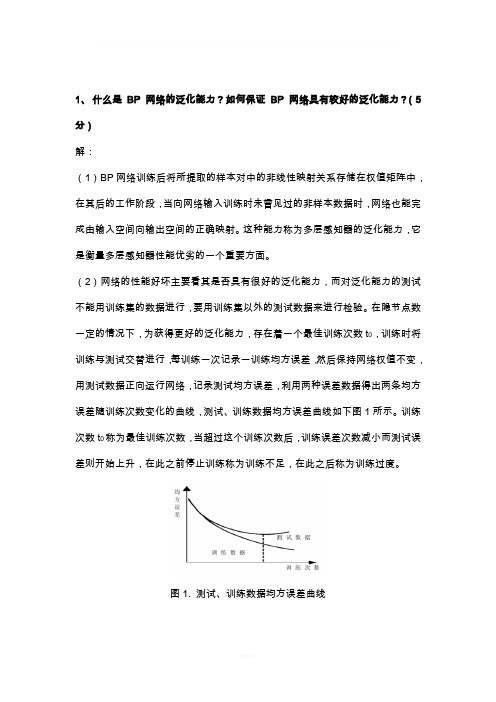
在隐节点数一定的情况下,为获得更好的泛化能力,存在着一个最佳训练次数t0,训练时将训练与测试交替进行,每训练一次记录一训练均方误差,然后保持网络权值不变,用测试数据正向运行网络,记录测试均方误差,利用两种误差数据得出两条均方误差随训练次数变化的曲线,测试、训练数据均方误差曲线如下图1所示。
训练次数t0称为最佳训练次数,当超过这个训练次数后,训练误差次数减小而测试误差则开始上升,在此之前停止训练称为训练不足,在此之后称为训练过度。
图1. 测试、训练数据均方误差曲线2、什么是LVQ 网络?它与SOM 网络有什么区别和联系?(10 分)解:(1)学习向量量化(learning vector quantization,LVQ)网络是在竞争网络结构的基础上提出的,LVQ将竞争学习思想和监督学习算法相结合,减少计算量和储存量,其特点是网络的输出层采用监督学习算法而隐层采用竞争学习策略,结构是由输入层、竞争层、输出层组成。
(2)在LVQ网络学习过程中通过教师信号对输入样本的分配类别进行规定,从而克服了自组织网络采用无监督学习算法带来的缺乏分类信息的弱点。
自组织映射可以起到聚类的作用,但还不能直接分类和识别,因此这只是自适应解决模式分类问题中的第一步,第二步是学习向量量化,采用有监督方法,在训练中加入教师信号作为分类信息对权值进行细调,并对输出神经元预先指定其类别。
人工神经网络试卷

一、填空题1、人工神经网络是生理学上的真实人脑神经网络的结构和功能,以及若干基本特性的某种理论抽象、简化和模拟而构成的一种信息处理系统。
从系统的观点看,人工神经网络是由大量神经元通过及其丰富和完善的连接而构成的自适应非线性动态系统。
2、神经元(即神经细胞)是由细胞体、树突、轴突和突触四部分组成。
3、NN的特点:信息的分布存储、大规模并行协同处理、自学习、自组织、自适应性、NN大量神经元的集体行为。
4、膜电位:以外部电位作为参考电位的内部电位。
5、神经元的兴奋:产生膜电位约为100mv,时宽约为1ms,分为四个过程:输入信号期、兴奋期、绝对不应期、相对不应期。
6、神经元的动作特征:空间性相加、时间性相加、阀值作用、不应期、疲劳、可塑性。
7、阀值作用:膜电位上升不超过一定值55mv,神经元不兴奋。
8、学习形式按照输出y划分为:二分割学习、输出值学习、无教师学习。
9、权重改变方式:训练期的学习方式、模式学习方式。
10、稳定的平稳状态指当由于某些随机因素的干扰,使平衡状态发生偏移,随着时间的推移,偏移越来越小,系统最后回到平衡状态。
二、简答题1、学习规则可以分为那几类?答:(1)相关规则:仅根据连接间的激活水平改变权系;(2)纠错规则:基于或等效于梯度下降方法,通过在局部最大改善的方向上,按照小步逐次进行修正,力图达到表示函数功能问题的全局解;(3)无导师学习规则:学习表现为自适应与输入空间的检测规则。
2、简述神经网络按照不同标准分类。
答:按网络结构分为前馈型和反馈型;按网络的性能分为连续性和离散性、确定性和随机性网络;按照学习方式分为有导师(指导)和无导师(自组织学习包括在内)学习;按照突触连接性质分为一阶线性关联与高阶非线性关联网络。
3、误差反传算法的主要思想?答:误差反传算法把学习过程分为两个阶段:第一阶段(正向传播过程),给出输入信息通过输入层经隐含层逐层处理并计算每个单元的实际输出值;第二阶段(反向过程),若在输出层未能得到期望的输出值,则逐层递归的计算实际输出与期望输出之差值(即误差),以便根据此差调节权值。
人工神经网络单选练习题

人工神经网络单选练习题一、基本概念1. 下列关于人工神经网络的描述,正确的是:A. 人工神经网络是一种静态的计算模型B. 人工神经网络可以模拟人脑的神经元连接方式C. 人工神经网络只能处理线性问题D. 人工神经网络的学习过程是监督式的2. 下列哪种算法不属于人工神经网络?A. 感知机算法B. 支持向量机算法C. BP算法D. Hopfield网络3. 人工神经网络的基本组成单元是:A. 神经元B. 节点C. 权重D. 阈值二、前向传播与反向传播4. 在前向传播过程中,下列哪个参数是固定的?A. 输入值B. 权重C. 阈值D. 输出值5. 反向传播算法的主要目的是:A. 更新输入值B. 更新权重和阈值C. 计算输出值D. 初始化网络参数6. 下列关于BP算法的描述,错误的是:A. BP算法是一种监督学习算法B. BP算法可以用于多层前馈神经网络C. BP算法的目标是最小化输出误差D. BP算法只能用于解决分类问题三、激活函数7. 下列哪种激活函数是非线性的?A. 步进函数B. Sigmoid函数C. 线性函数D. 常数函数8. ReLU激活函数的优点不包括:A. 计算简单B. 避免梯度消失C. 提高训练速度D. 减少过拟合9. 下列哪种激活函数会出现梯度饱和现象?A. Sigmoid函数B. ReLU函数C. Tanh函数D. Leaky ReLU函数四、网络结构与优化10. 关于深层神经网络,下列描述正确的是:A. 深层神经网络一定比浅层神经网络效果好B. 深层神经网络更容易过拟合C. 深层神经网络可以减少参数数量D. 深层神经网络训练速度更快11. 下列哪种方法可以降低神经网络的过拟合?A. 增加训练数据B. 减少网络层数C. 增加网络参数D. 使用固定的学习率12. 关于卷积神经网络(CNN),下列描述错误的是:A. CNN具有局部感知能力B. CNN具有参数共享特点C. CNN可以用于图像识别D. CNN无法处理序列数据五、应用场景13. 下列哪种问题不适合使用人工神经网络解决?A. 图像识别B. 自然语言处理C. 股票预测D. 线性规划14. 下列哪个领域不属于人工神经网络的应用范畴?A. 医学诊断B. 金融预测C. 智能家居D. 数值计算15. 关于循环神经网络(RNN),下列描述正确的是:A. RNN无法处理长距离依赖问题B. RNN具有短期记忆能力C. RNN训练过程中容易出现梯度消失D. RNN只能处理序列长度相同的数据六、训练技巧与正则化16. 下列哪种方法可以用来防止神经网络训练过程中的过拟合?A. 提前停止B. 增加更多神经元C. 减少训练数据D. 使用更大的学习率17. 关于Dropout正则化,下列描述错误的是:A. Dropout可以减少神经网络中的参数数量B. Dropout在训练过程中随机丢弃一些神经元C. Dropout可以提高模型的泛化能力D. Dropout在测试阶段不使用18. L1正则化和L2正则化的主要区别是:A. L1正则化倾向于产生稀疏解,L2正则化倾向于产生平滑解B. L1正则化比L2正则化更容易计算C. L2正则化可以防止过拟合,L1正则化不能D. L1正则化适用于大规模数据集,L2正则化适用于小规模数据集七、优化算法19. 关于梯度下降法,下列描述正确的是:A. 梯度下降法一定会找到全局最小值B. 梯度下降法在鞍点处无法继续优化C. 梯度下降法包括批量梯度下降、随机梯度下降和小批量梯度下降D. 梯度下降法的学习率在整个训练过程中保持不变20. 下列哪种优化算法可以自动调整学习率?A. 随机梯度下降(SGD)B. Adam优化算法C. Momentum优化算法D. 牛顿法21. 关于Adam优化算法,下列描述错误的是:A. Adam结合了Momentum和RMSprop算法的优点B. Adam算法可以自动调整学习率C. Adam算法对每个参数都使用相同的学习率D. Adam算法在训练初期可能会不稳定八、损失函数22. 在分类问题中,下列哪种损失函数适用于二分类问题?A. 均方误差(MSE)B. 交叉熵损失函数C. Hinge损失函数D. 对数损失函数23. 关于均方误差(MSE)损失函数,下列描述错误的是:A. MSE适用于回归问题B. MSE对异常值敏感C. MSE的输出范围是[0, +∞)D. MSE损失函数的梯度在接近最小值时趋近于024. 下列哪种损失函数适用于多分类问题?A. 交叉熵损失函数B. Hinge损失函数C. 对数损失函数D. 均方误差(MSE)九、模型评估与超参数调优25. 下列哪种方法可以用来评估神经网络的性能?A. 训练误差B. 测试误差C. 学习率D. 隐层神经元数量26. 关于超参数,下列描述正确的是:A. 超参数是在模型训练过程中自动学习的B. 超参数的值通常由经验丰富的专家设定C. 超参数的调整对模型性能没有影响D. 超参数包括学习率、批量大小和损失函数27. 关于交叉验证,下列描述错误的是:A. 交叉验证可以减少过拟合的风险B. 交叉验证可以提高模型的泛化能力C. 交叉验证会降低模型的训练速度D. 交叉验证适用于小规模数据集十、发展趋势与挑战28. 下列哪种技术是近年来人工神经网络的一个重要发展方向?A. 深度学习B. 线性回归C. 决策树D. K最近邻29. 关于深度学习,下列描述错误的是:A. 深度学习需要大量标注数据B. 深度学习模型通常包含多层神经网络C. 深度学习可以处理复杂的非线性问题D. 深度学习不适用于小规模数据集30. 下列哪种现象是训练深度神经网络时可能遇到的挑战?A. 梯度消失B. 参数过多C. 数据不平衡D. 所有上述选项都是挑战答案一、基本概念1. B2. B二、前向传播与反向传播4. B5. B6. D三、激活函数7. B8. D9. A四、网络结构与优化10. B11. A12. D五、应用场景13. D14. D15. C六、训练技巧与正则化16. A17. A18. A七、优化算法19. C20. B八、损失函数22. B23. D24. A九、模型评估与超参数调优25. B26. B27. D十、发展趋势与挑战28. A29. D30. D。
《人工神经网络:模型、算法及应用》习题参考答案

习题2.1什么是感知机?感知机的基本结构是什么样的?解答:感知机是Frank Rosenblatt在1957年就职于Cornell航空实验室时发明的一种人工神经网络。
它可以被视为一种最简单形式的前馈人工神经网络,是一种二元线性分类器。
感知机结构:2.2单层感知机与多层感知机之间的差异是什么?请举例说明。
解答:单层感知机与多层感知机的区别:1. 单层感知机只有输入层和输出层,多层感知机在输入与输出层之间还有若干隐藏层;2. 单层感知机只能解决线性可分问题,多层感知机还可以解决非线性可分问题。
2.3证明定理:样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集构成的凸壳互不相交.解答:首先给出凸壳与线性可分的定义凸壳定义1:设集合S⊂R n,是由R n中的k个点所组成的集合,即S={x1,x2,⋯,x k}。
定义S的凸壳为conv(S)为:conv(S)={x=∑λi x iki=1|∑λi=1,λi≥0,i=1,2,⋯,k ki=1}线性可分定义2:给定一个数据集T={(x1,y1),(x2,y2),⋯,(x n,y n)}其中x i∈X=R n , y i∈Y={+1,−1} , i=1,2,⋯,n ,如果存在在某个超平面S:w∙x+b=0能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有的正例点即y i=+1的实例i,有w∙x+b>0,对所有负实例点即y i=−1的实例i,有w∙x+b<0,则称数据集T为线性可分数据集;否则,称数据集T线性不可分。
必要性:线性可分→凸壳不相交设数据集T中的正例点集为S+,S+的凸壳为conv(S+),负实例点集为S−,S−的凸壳为conv(S−),若T是线性可分的,则存在一个超平面:w ∙x +b =0能够将S +和S −完全分离。
假设对于所有的正例点x i ,有:w ∙x i +b =εi易知εi >0,i =1,2,⋯,|S +|。
人工神经网络 试题

1、简要说明误差反向传播的BP算法的基本原理,讨论BP基本算法的优缺点。
并采用BP神经网络进行模式识别。
设计一个BP网络对附图中的英文字母进行分类。
输入向量含16个分量,输出向量分别用[1,-1,-1]T,[-1,1,-1]T,[-1,-1,1]T代表字符A,I,O。
采用不同的学习算法(traingd,traingdm,traingdx,trainlm)进行比较。
并测试施加5%噪声与输入时的测试结果。
要求:给出matlab的源程序(可调用matlab NN工具箱),网络结构,初始权值,训练结果,测试结果。
2、简要说明误差反向传播的BP算法的基本原理,讨论BP基本算法的优缺点。
并采用BP神经网络设计实现一个9*9表。
采用不同的学习算法(traingd,traingdm,traingdx,trainlm)进行比较。
要求:给出matlab的源程序(可调用matlab NN工具箱),网络结构,初始权值,训练结果,测试结果。
(考虑将其中的数改为二进制)3、简要说明误差反向传播的BP算法的基本原理,讨论BP基本算法的优缺点。
表1中给出了某结构在多种状态下的特征向量,表2给出了某时刻结构的特征向量,请使用人工神经网络根据表2中的特征向量判断其所属状态。
表1表2网络结构设计输入个数为10,输出个数为1,故神经元个数为1,结构如下图。
本题是一个模式识别问题,采用自组织竞争人工神经网络。
图1-1 网络结构图画出6个状态在坐标系中如图1-2所示。
%创建输入向量X=[0 1;0 1]clusters=6;points=10;std_dev=0.05;P=nngenc(X,clusters,points,std_dev);plot(P(1,:),P(2,:),'+r')title('Input Vectors');xlabel('p(1)');ylabel('p(2)');%创建自组织竞争神经网络net=newc([0 1;0 1],6,.1);net=init(net);w=net.IW{1};hold off;plot(P(1,:),P(2,:),'+r');hold on; plot(w(:,1),w(:,2),'ob');xlabel('p(1)');ylabel('p(2)');hold off;net.trainParam.epochs=7;hold on;net=init(net);more off;net=train(net,P);TRAINR, Epoch 0/7TRAINR, Epoch 7/7TRAINR, Maximum epoch reached. %训练该网络hold on ;net=init(net); more off;w=net.IW{1};delete(findobj(gcf,'color',[0 0 1])); hold offplot(P(1,:),P(2,:),'+r');hold off;hold on; plot(w(:,1),w(:,2),'ob'); xlabel('p(1)');ylabel('p(2)');hold off;%仿真该网络p=[0.794;0.271];a=sim(net,p);ac=vec2ind(a)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人工神经网络例题 Document serial number【LGGKGB-LGG98YT-LGGT8CB-LGUT-1、 什么是 BP 网络的泛化能力如何保证 BP 网络具有较好的泛化能力(5分)解:(1)BP 网络训练后将所提取的样本对中的非线性映射关系存储在权值矩阵中,在其后的工作阶段,当向网络输入训练时未曾见过的非样本数据时,网络也能完成由输入空间向输出空间的正确映射。
这种能力称为多层感知器的泛化能力,它是衡量多层感知器性能优劣的一个重要方面。
(2)网络的性能好坏主要看其是否具有很好的泛化能力,而对泛化能力的测试不能用训练集的数据进行,要用训练集以外的测试数据来进行检验。
在隐节点数一定的情况下,为获得更好的泛化能力,存在着一个最佳训练次数t 0,训练时将训练与测试交替进行,每训练一次记录一训练均方误差,然后保持网络权值不变,用测试数据正向运行网络,记录测试均方误差,利用两种误差数据得出两条均方误差随训练次数变化的曲线,测试、训练数据均方误差曲线如下图1所示。
训练次数t 0称为最佳训练次数,当超过这个训练次数后,训练误差次数减小而测试误差则开始上升,在此之前停止训练称为训练不足,在此之后称为训练过度。
图1. 测试、训练数据均方误差曲线2、什么是 LVQ 网络它与 SOM 网络有什么区别和联系(10 分)解:(1)学习向量量化(learning vector quantization ,LVQ )网络是在竞争网络结构的基础上提出的,LVQ 将竞争学习思想和监督学习算法相结合,减少计算量和储存量,其特点是网络的输出层采用监督学习算法而隐层采用竞争学习策略,结构是由输入层、竞争层、输出层组成。
(2)在LVQ 网络学习过程中通过教师信号对输入样本的分配类别进行规定,从而克服了自组织网络采用无监督学习算法带来的缺乏分类信息的弱点。
自组织映射可以起到聚类的作用,但还不能直接分类和识别,因此这只是自适应解决模式分类问题中的第一步,第二步是学习向量量化,采用有监督方法,在训练中加入教师信号作为分类信息对权值进行细调,并对输出神经元预先指定其类别。
3、设计一个神经网络对图一中的三类线性不可分模式进行分类,期望输出向量分别用(1, -1, -1)T 、 (-1, 1, -1) T 、 (-1, -1, 1) T 代表三类,输入用样本坐标。
要求:(1) 选择合适的隐节点数;(2)用 BP 算法训练网络,对图中的 9 个样本进行正确分类。
(15 分)分析:对于一个BP 神经网络,首先要明确输入,输出, 隐层节点个数。
对于本题,输入是点坐标组成的2*9的矩阵,输入节点个数为2,期望输出向量分别用(1, -1, -1)T 、 (-1, 1, -1)T 、 (-1, -1, 1)T 表示,至于隐层节点的个数并没有确切的方法, 根据经验公式α++=l n m (m 为隐层节点数;n 为输入层节点数;l 为输出节点数;α为1~10之间的常数),首先确定隐层节点数为5,逐渐增加隐层节点数量,然后观察其对训练误差的影响,最终选出最合适的隐层节点数量。
况下达到相同的训练精度所需要的训练次数,当隐层节点数为M=5时,在训练次数为66491时,结果达到训练精度;当隐层节点数M=7时,在训练次数到达31981时,结果达到训练精度;当隐层节点数M=9时时,在训练次数达到25338时,结果达到训练精度;当隐层节点数M=10时,在训练次数达到20770时,结果达到训练精度;当隐层节点数M=12时,在训练次数达到14052时,结果达到训练精度;当隐层节点数M=14时,在训练次数达到11622时,结果达到训练精度,由此可见,在一定范围内,隐层节点数越多,达到训练精度时所用的训练次数越少,所用训练时间则越少。
因此选择隐层节点数为14。
学习率,误差精度在以下,输出结果和导师信号对比,输出结果都为正确,正确率达到100%。
具体程序见附件一或者。
4、试设计一个吸引子为X a=(0110) T,X b=(1001)T的离散Hopfield人工神经网络。
其权值和阈值在 [-1,1]区间取值,试求权值和阈值。
(10 分)解:吸引子的分布是由网络的权值(包括阈值)决定的,设计吸引子的核心就是如何设计一组合适的权值。
为了使所设计的权值满足要求,权值矩阵应符合以下要求:(a) 为保证异步方式工作时网络收敛,W 应为对称阵。
(b) 为保证同步方式工作时网络收敛,W 应为非负定对称阵。
(c) 保证给定的样本是网络的吸引子,并且要有一定的吸引域。
具体设计时,这里采用了联立方程法:以 4 节点 DHNN为例,说明权值设计的联立方程法。
考虑到wij = wji,wii= 0,对稳态x(t +1) = x(t)。
对于状态 X a = (1001)T,各节点净输入应满足:net1=w12×0+w13×0+w14×1?T1=w14?T1>0 (1)net2=w12×1+w23×0+w24×1?T2=w12+w24?T2<0 (2)net3=w13×1+w23×0+w34×1?T3=w13+w34?T3<0 (3)net4=w14×1+w24×0+w34×0–T4=w14–T4>0 (4)对于 X b = (0110)T状态,各节点净输入应满足:net1=w12×1+w13×1+w14×0?T1=w12+w13?T1<0 (5)net2=w12×0+w23×1+w24×0?T2=w23?T2>0 (6)net3=w13×0+w23×1+w34×0?T3=w23?T3>0 (7)net4=w14×0+w24×1+w34×1–T4=w24+w34–T4<0 (8)联立以上8项不等式,可求出未知量的允许取值范围。
如取w14=,则由式(1)有 -1≤T1<,取T1= ;则由式(4)有 -1≤T4<,取T4= ;取w12=,由式(5),有 -1≤w13< ,取w 13 = ;取w24=由式(2),有<T2≤1,取T2= ;由式(6),有 < w23≤1,取w23= ;由式(7),有?1 ≤ T3 < ,取T3= ;由式(3,8),有-1 < w34≤,取w34=。
可以验证,利用这组参数构成的 DHNN网对于任何初态最终都将演变到两吸引子 X a=(1001)T和X b=(0110)T。
整理权值与阈值为:5、下面给出的训练集由玩具兔和玩具熊组成。
输入样本向量的第一个分量代表玩具的重量,第二个分量代表玩具耳朵的长度,教师信号为-1表示玩具兔,教师信号为1表示玩具熊。
(1)用 matlab 训练一个感知器,求解此分类问题。
(需附上 matlab 程序)(2)用输入样本对所训练的感知器进行验证。
(15 分)分析:对于本题,输入是样本组成的2*8的矩阵,输入节点个数为2,输出由导师信号可知分为两类。
两个输入分量在几何上构成一个二维平面,输入样本可以用该平面上的一个点表示,玩具重量和长度在坐标中标出,可以看出明显分布在两个区域,可以用一条线分开分为两类,在线上方的输出结果应大于0,在线下方的输出结果应小于0。
权向量为2*9的矩阵,输入的第一个权向量权值赋予较小的非零随机数,每一个新的权向量都由上一个权向量调整,下一次循环第1个权向量由第9个权向量来调整。
对于这样的样本线性可分,经过几次调整后就稳定到一个权向量,将样本正确分类的权向量不是唯一的。
具体程序见附件二或者。
输出分类结果如下图所示。
附件一:第三题程序clear all;%%BP算法初始化D=[1,-1,-1; 1,-1,-1; 1,-1,-1; -1,1,-1; -1,1,-1; -1,1,-1; -1,-1,1; -1,-1,1; -1,-1,1]';X=[,; ,; ,; ,; ,; ,; ,; ,; ,]';[N,n]=size(X);[L,Pd]=size(D);%M=ceil(sqrt(N*L))+7;ceil函数为正无穷方向取整m=14; %隐层节点数%初始化权矩阵%输入层到隐层权矩阵V=rand(N,m);%隐层到输出层权矩阵W=rand(m,L);%开始训练,转移函数选择双极性Sigmoid函数Q=100000;%训练次数计数器E=zeros(Q,1);%误差Emin=; %训练要求精度learnr=; %学习率q=1;%训练次数计数,批训练%%权值调整while q<Qnetj=V.'*X;Y=(1-exp(-netj))./(1+exp(-netj));netk=W.'*Y;O=(1-exp(-netk))./(1+exp(-netk));E(q)=sqrt(sum(sum((D-O).^2))/2); %计算总误差if E(q)<Eminbreak;endDelta_o=(D-O).*(1-O.^2)./2;W=W+learnr*(Delta_o*Y.').'; %隐层和输出层间的权矩阵调整 Delta_y=(W*Delta_o).*(1-Y.^2)./2;V=V+learnr*(Delta_y*X.').'; %输入层和隐层间的权矩阵调整 q=q+1;end%%输出结果qO=sign(O) %符号函数取整A=find(O~=D); %和计算输出和导师信号不同的个数length(A) %分类结果错误的个数附件二:第五题程序clc;clear%%单层感知器初始化X=[1,4;1,5;2,4;2,5;3,1;3,2;4,1;4,2]; %输入信号d=[-1;-1;-1;-1;1;1;1;1]; %输入导师信号w=zeros(2,9);w(:,1)=rand(2,1); %第一组权值赋予较小的非零随机数o=zeros(8,1); %输出结果net=zeros(8,1); %净输入netlearnr=; %学习率为n=0; %循环次数%%调整权值while n<100 %训练次数最大设为100次for i=1:8net(i)=X(i,:)*w(:,i); %计算净输入neto(i)=sign(net(i)); %计算输出,转移函数为符号函数w(:,i+1)=w(:,i)+learnr*(d(i)-o(i))*X(i,:)'; %调整权值w(:,1)=w(:,9); %最后一组权值赋值给第一组权endn=n+1if d==o %如果输出等于导师信号,那么训练停止breakendend%%结果输出x1=[1,1,2,2]; %将两组数据在图中标出y1=[4,5,4,5];x2=[3,3,4,4];y2=[1,2,1,2];scatter(x1,y1,'r')%画点hold on;scatter(x2,y2,'b')x=-1::5;y=-w(1,1)/w(2,1)*x;%得到训练过后的权都一样,取出第一组权确定直线,将两组数据分开hold on;plot(x,y)。
