弧齿锥齿轮三维实体模型的构建方法
弧齿锥齿轮展成齿面的几何建模

弧齿锥齿轮展成齿面的几何建模
弧齿锥齿轮展成齿面的几何建模可以通过以下步骤实现:
1.确定齿数和压力角:齿数和压力角是设计弧齿锥齿轮的重要参数,需要根据实际需求确定。
2.计算基圆半径:基圆半径是弧齿锥齿轮展成齿面时的关键参数,需要根据齿数和压力角进行计算。
3.绘制母齿轮:根据齿数和压力角绘制母齿轮的齿形,可以使用CAD 软件或手动绘制。
4.绘制弧齿小齿轮:根据基圆半径和母齿轮的齿形,绘制弧齿小齿轮的齿形。
5.展成齿面:将弧齿小齿轮沿着母齿轮的斜齿轮轴方向展开,得到弧齿锥齿轮的展成齿面。
6.修整齿面:根据实际生产需求,对展成齿面进行修整和优化,以确保齿轮能够正常运转。
弧齿螺旋锥齿轮副的设计及三维建模
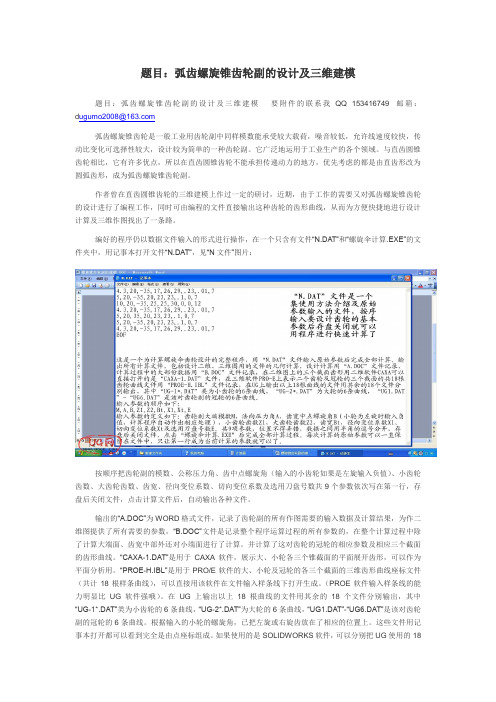
题目:弧齿螺旋锥齿轮副的设计及三维建模题目:弧齿螺旋锥齿轮副的设计及三维建模要附件的联系我QQ 153416749 邮箱:d ugumo2008@弧齿螺旋锥齿轮是一般工业用齿轮副中同样模数能承受较大载荷,噪音较低,允许线速度较快,传动比变化可选择性较大,设计较为简单的一种齿轮副。
它广泛地运用于工业生产的各个领域。
与直齿圆锥齿轮相比,它有许多优点,所以在直齿圆锥齿轮不能承担传递动力的地方,优先考虑的都是由直齿形改为圆弧齿形,成为弧齿螺旋锥齿轮副。
作者曾在直齿圆锥齿轮的三维建模上作过一定的研讨,近期,由于工作的需要又对弧齿螺旋锥齿轮的设计进行了编程工作,同时可由编程的文件直接输出这种齿轮的齿形曲线,从而为方便快捷地进行设计计算及三维作图找出了一条路。
编好的程序仍以数据文件输入的形式进行操作,在一个只含有文件“N.DA T”和“螺旋伞计算.EXE”的文件夹中,用记事本打开文件“N.DA T”,见“N文件”图片:按顺序把齿轮副的模数、公称压力角、齿中点螺旋角(输入的小齿轮如果是左旋输入负值)、小齿轮齿数、大齿轮齿数、齿宽、径向变位系数、切向变位系数及选用刀盘号数共9个参数依次写在第一行,存盘后关闭文件,点击计算文件后,自动输出各种文件。
输出的“A.DOC”为WORD格式文件,记录了齿轮副的所有作图需要的输入数据及计算结果,为作二维图提供了所有需要的参数,“B.DOC”文件是记录整个程序运算过程的所有参数的,在整个计算过程中除了计算大端面、齿宽中部外还对小端面进行了计算。
并计算了这对齿轮的冠轮的相应参数及相应三个截面的齿形曲线。
“CAXA-1.DA T”是用于CAXA软件,展示大、小轮各三个锥截面的平面展开齿形,可以作为平面分析用。
“PROE-H.IBL”是用于PRO/E软件的大、小轮及冠轮的各三个截面的三维齿形曲线座标文件(共计18根样条曲线),可以直接用该软件在文件输入样条线下打开生成。
(PROE软件输入样条线的能力明显比UG软件强哦)。
基于Pro_E的渐开线弧齿锥齿轮的三维建模_冉兆波

机械 2007年第1期 总第34卷 计算机应用技术 ·35·——————————————— 收稿日期:2006-08-22作者简介:冉兆波,在读研究生,研究方向为机械CAD/CAE ;万朝燕,教授,硕士生导师。
基于Pro/E 的渐开线弧齿锥齿轮的三维建模冉兆波,万朝燕(大连交通大学 机械工程学院,辽宁 大连 116028)摘要:介绍了在Pro/E 环境下,实现标准渐开线弧齿锥齿轮的造型方法和步骤,从原理出发,利用方程建立渐开线,从而保证齿形的准确性。
通过建立齿轮中各变量与模数m 、齿数z 等基本参数的关系,实现了不同模数、齿数齿轮的快速造型,提高了设计效率。
关键词:渐开线;弧齿锥齿轮;Pro/E中图分类号:TH122 文献标识码:A 文章编号:1006-0316(2007)01-0035-03Study on the method of molding for the standard involute spiral cone gear based on Pro/EngineerRAN Zhao-bo ,WAN Chao-yan(Dalian Jiaotong University ,Dalian 116028,China )Abstract :Introduces the methodologies and steps of exact modeling for the standard involute spiral cone gear in environment of Pro/ Engineer. Based on principle, using equation build up the involute .Consequently we can ensure the accuracy of the involute gear shape. Carry out quick modeling of various modulus and teeth number by set up relations between variable and basic parameters. t raised the design efficiency. Key words :Involute ;spiral cone gear ;Pro/E弧齿锥齿轮作为基础传动件,用于传递相交轴之间的运动和动力,广泛应用于航空、航海、汽车、拖拉机、机床等行业中。
锥形齿轮三维建模步骤

锥形齿轮三维建模步骤
锥形齿轮三维建模步骤
在绘制锥形齿轮之前,首先要知道扇形齿轮关键参数。
如下图要知道:R节锥距:节圆锥的母线长,
节锥角δ:大端分度圆与X轴夹角。
模数:m
齿数:Z
压力角:?
α
=20
分度圆直径d=mz
齿顶高h a= m
齿根高h f=1.2m
全齿高h=h f+h a=2.2m
齿宽b=RφRφR:齿宽系数φR=0.3(一般值,有实物可参照实物)。
注意:在圆锥齿轮有齿顶圆锥,分度圆锥,齿根圆锥,基圆锥等。
圆锥齿轮的大端和小端参数不同,为计算和检测方便,取大端参数为标准值。
圆锥齿轮传动的几何尺寸以大端为准,大端模数为标准模数。
画一个模数:4 ,齿数:15,圆锥角45的锥形齿轮。
1.根据锥形齿轮关键参数,在CAD中绘制平面侧视图
1.1计算出R值=4
2.426 画出分度圆锥线。
1.2根据齿根高,齿顶高,和齿宽分别画出,锥形齿轮齿的侧视图如下图:
2.使用三维画图命令绘制锥形齿轮外形2.1齿轮斜面组成为面域
2.2旋转成体
3.绘制齿形
3.1 绘制大端面齿轮齿形状
3.2扫掠命令形成齿轮齿形
3.3使用阵列命令,阵列出15个齿形
4.差集形成完整齿轮。
第七部分:UG画齿轮-04弧齿锥齿轮

第七部分:齿轮---弧齿锥齿轮关于弧齿锥齿轮(格里森gleason)的创建方法,NX 8.0自带的方法放在最后介绍。
这种齿轮的几何计算法几乎和直齿锥齿的算法相同。
所以就不解释了。
请参照《UG NX5.0工程师习题集》。
(1)采用参数的方法作。
①画出草图,②做出相关的圆,③画出渐开线,④画出渐开线轮廓。
新的坐标系1绕Z轴转过了b度⑤作出齿坯基体,⑥制作一个草图平面,并做出草图。
直线1草图平面要过直线1,垂直于直线2谁帮我解释一下,这个半径是怎么确定的。
直线2按标准,螺旋角度应为βm=35°⑦旋转“分度面”,将上步所作草图投影到这个“分度面上”。
(这种方法类似与圆柱斜齿轮的做法)我们可以看出,两个齿廓的几何中心都没有在投影线的端点上。
尤其是小端的齿廓非常明显。
⑧测量两个齿廓的偏移角度,将两齿廓旋转至曲线的端点上。
大端齿廓偏移的角度小端齿廓偏移的角度旋转后的结果如图:⑨扫掠出第一个齿体。
⑩阵列后,最终结果如图:(2)再一种方法。
自己在“ug网”的齿轮模块中讨教的一种方法。
使用作者所开发的程序:HCZCL1P.EXE。
①使用上一种方法的结果,利用公式反推出一些结论:大端模数M=3.5,小齿轮数Z1=12,径向变位系数X2=0.3276把9个参数:大端模数M=3.5,法向压力角α=20,齿宽中点螺旋角β=-35,小齿轮数Z1=12,大齿轮齿数Z2=30, 齿宽B=20,径向变位系数X2=0.03276,切向变位系数X t=0.01,选用刀盘号数E=4。
依次写入记事本中,并将记事本的名称改为:N.DA T。
结果如下:选中这两个图标,双击HCZCL1P.EXE图标在生成的所有文件中,打开A.DOC文档,即:弧齿锥齿轮副设计表第一部分输入参数计算日期:12-31-2011模数: M= 3.5齿数: Z= 12 30法向齿形角: A= 20 齿宽中点螺旋角:B= 35螺旋线旋向: 小轮左旋大轮右旋径向变位系数 X= .328 -.328切向变位系数 Xt= 0 0齿高系数: Ha= .85 (系统默认值)顶隙系数: c = .188 (系统默认值)轴交角系统默认两轴夹角为90度刀具直径Do= 101.6 刀盘号数: 4 刀尖圆弧 r= .875第二部分计算参数输出表(作图部分)节圆直径 d= 42 105节锥角 E= 21.801411 68.198592节锥距 R= 56.54423齿宽 b= 20齿顶高 Ha= 4.123 1.827齿根高 Hf= 2.485 4.781全齿高 H= 6.608齿顶圆直径 D= 49.65622 106.3571顶锥角 Ea= 26.63446 70.715根锥角 Ef= 19.285 63.36554轮冠距 Ak= 50.96875 19.30367中点模数 Mm= 2.881016中点法向模数 Mfm= 2.35999中点弧齿厚 Sfm= 4.394948 3.019179中点分度圆弦齿厚sm= 4.390353 3.019141中点分度圆弦齿高hm= 3.364488 1.394092大端分度圆螺旋角B大= 40.66094941216469大端分度圆周节Ps= 10.99557大端分度圆弧齿厚Sf= 6.599421 4.396153大端分度圆弦齿厚S大= 6.576035 4.395976大端分度圆弦齿高h大= 4.363272 1.844092第三部分计算参数输出表(非作图部分)齿数比 U= 2.5齿宽系数 F= .3537054齿根角 Of= 2.51641 4.83305齿顶角 Oa= 4.83305 2.51641当量齿数Z当= 23.51347 146.9592 冠轮齿数Z冠= 32.31099中点端面重合度Et= 1.153703 中点轴向重合度En= 1.547253中点总重合度 E总= 1.930032中点法面当量齿轮重合度Env= 1.626092小端面端面模数Ms= 2.262031小端面分度圆弧齿厚Sx= 4.26517 2.84121 计算时间:09:43:49生成的所有文件:其中,后缀名为:.DAT的文件为点文件。
格里森弧齿锥齿轮建模

格里森弧齿锥齿轮建模
格里森弧齿锥齿轮是一种用于调节行星齿轮系统和机械传动系统的齿轮系统。
它能有
效地变换行星齿轮系统中两个轴之间的动力传递比率。
格里森弧齿锥齿轮主要包括两个锥齿轮和半节圆环,正反两个锥齿轮是几何同心,通
常支承轴的外表面上安装半节圆环,用于连接两个锥齿轮,以达到调整轴之间扭矩传递比
率的作用。
我们以中心点为参考,首先确定锥齿轮上的螺旋线的方向,然后对锥齿轮的数
量进行确定和计算,并在根据螺旋线方向将一齿宽绘制成弧齿形状。
设计一个高效率的格里森弧齿锥齿轮要考虑几个方面的因素。
首先,正反两个锥齿轮
之间的节圆环和锥齿轮之间的精度要高,以便把几何同心的特性发挥出来,减少传动系统
的损耗;其次,对螺旋线参数的角度来变化,这样可以调整齿轮减速效率;第三,齿面的
精度和材料硬度也很重要,齿面精度高可以减少噪音及损耗;最后,设计格里森弧齿锥齿
轮时也要注意重力影响,将重力影响因素考虑在设计之中。
建模可以采用三维CAD/CAE软件进行建模,利用软件表达出各个零件几何尺寸、材料
特性等重要因素。
首先,利用软件的三维建模功能,建立出正向和反向的锥齿轮,结合其
精度要求,确定其螺旋线参数;接下来,将其与轴结合,将节圆环以紧定螺丝连接;最后,根据重力影响、材料特性等其他参数,对总体的齿轮参数进行规划,以满足齿轮的精度及
高效的减速效果。
总之,格里森弧齿锥齿轮是一款具有调节性能好、减振阻尼好、损耗小、质量轻的齿轮,具有重要的应用价值,在行星齿轮传动系统和机械传动系统中具有很大的发挥空间,
但要想达到最佳性能,就必须要正确设计并进行精确建模,以满足传动系统效率、精度和
损耗的要求。
基于MATLAB和Pro/E的弧齿锥齿轮三维造型
在 刀 盘 坐
式 中 : 、z : y和 为 被 加 工 大 齿 轮 齿 面 点 在 坐 标 系 中
坐 标值 的分 量表达 。
( G 0 )= S,c
( c ±5 s G sn氏 r 2 Gi n )i
一 5GOO S G
2 齿面 网格划分
图 3 大 齿 轮 齿 面 在 轴 截 面 坐 标 系 ( , , 。 为 D: R)
示 灯 HL 7由输 入 端 子 YO 5 制 。 0控
S 扳 向“ 加 料 ” 置 , S 触 头 复 位 ,O 7 通 , A5 后 位 即 A5 X0 接
定 时 器 T 得 电 同 时 , 部 辅 助 继 电 器 M1 也 得 电 , O 内 2 使
电 磁 阀 YV2 Y 得 电 吸 合 , 座 整 体 后 退 。 时 常 闭 、 v6 注 同 触 头 M1 断 开 KM2 路 , 定 时 器 T 延 时 到 时 , 会 2 电 使 O 不
参 考 文 献
1 廖 常初. L P C编程及应用[ . M]北京 : 机械工业 出版社 ,0 3 20 . 2 吴宏歧. 6 卧式镗床的 P C控制系统设计[]组合机床与 T8 L J_
自动化 加 工 ,0 4 ( ) 2 0 ,4 .
已 经 通 电 吸 合 , 已 经 将 常 开 触 点 M1 接 通 , 电 路 先 1 故
T 仍成通路 。 2
全 自动 控 制 : 半 自动 基 本 一 致 , 是 将 万 能 转 换 与 只 开 关 S 扳 到 “ 自动 ” 置 即 可 。 A4 全 位 上 述 几 种 操 作 方 式 各 动 作 进 行 时 , 应 指 示 灯 显 相
示 各 动 作 。 模 指 示 灯 HL 由 输 入 端 子  ̄ o  ̄ 制 , 闭 1 oo 起
基于Matlab和UG的弧齿锥齿轮三维造型技术
Thr e d m e i na o ei g t c o o y f r s ia e e e i nso lm d ln e hn l g o p r lb v l
e tb ih d a tra ry n r cs n eib e,w ih ly a o a l o n ain frf i lme ts t n sa l e f ra i g i p e ie a d r l l s e s a h c sa fv r be fu d t n t ee n t i a d a o o i e ac d n mi n lsso p rlb v lg a a e n ANS . y a c a ay i fs i e e e b s d o a r YS Ke r s s i e e g a ;Malb; U O e I y wo d : pr b v l e r l a t a G/ p n GR P;t re dme s n d l g h e i n i a mo e i ol n
g a a e n a l b a e r b s d o M ta nd UG
L U G a g 1 i , T AN Y e J n , F N Ho g w i , W AN Ma . a I u n . e I u .u A n . e G o y n ( . S h o o e h t nc ,N r w s r o t h i l nvri ,X ’ 1 0 2 hn 1 c o l f c ar i M o s o h et nP l e ne i s y i n7 0 7 ,C ia t e y e aU e t a
UG GRIP的弧齿锥齿轮参数化建模方法
资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载UG GRIP的弧齿锥齿轮参数化建模方法地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容UG GRIP的弧齿锥齿轮参数化建模方法基于UG GRIP,本文针对弧齿锥齿轮建模方法进行了深入细致的研究。
首先介绍了弧齿锥齿轮建模的总体方案。
其次详细说明了大轮的展成法建模原理;对于小轮的造型,基于共轭理论,提出了一种用工具大轮与小轮坯体进行展成布尔运算的实体建模的创新方法,从而得到小轮模型。
采用此方法造型弧齿锥齿轮小轮比其它造型方法简便,是弧齿锥齿轮参数化建模和加工的一种实用的新方法。
接着以一对齿数为21-35、模数为13的齿轮副为例,详细图解说明了整个建模过程。
最终还对建立的模型进行了数控加工试验以验证上述方法的正确性。
1 前言弧齿锥齿轮是一种节锥齿线为曲线、用来传递在一个平面内的两相交轴之间的定传动比回转运动的齿轮[1]。
由于其承载能力大、传动平稳、噪声小、结构紧凑等优点,是航空、造船、汽车、能源、装备、国防等部门产品的关键零件,因此弧齿锥齿轮生产在现代化机械制造业中占有十分重要的地位 [1-3]。
其制造主要使用专用的齿轮加工机床。
目前国内使用的齿轮加工机床主要有美国格里森公司生产的No.116铣齿机、No.609拉齿机、No.463磨齿机和国产的Y2280铣齿机等[1]。
随着科技的进步、技术的创新,数控化的切齿加工机床纷纷涌现。
但是由于机床结构、机床尺寸等因素的制约,每一种机床都有对应的技术规格,如最大加工模数、最大加工锥距、最大加工直径等,因此无法加工一些尺寸超过其技术规格的齿轮副(如大模数的油田、煤矿机械使用的大型弧齿锥齿轮副)。
而且弧齿锥齿轮加工中仍然存在着众多问题,如:加工过程烦琐、加工周期长、人力和资金投入大等[4]。
高重合度弧齿锥齿轮的三维建模及加工试验
高重合度弧齿锥齿轮的三维建模及加工试验张华;吉宝峰;李天兴;杨建军【摘要】When the contact ratio is bigger,logarithm of tooth meshed increase,and the gear transmission is more stable.At the same time,the force that each gear tooth loaded decrease,which is very beneficial to reduce noise.According to the theory of Non-zero modification in this paper,negative transmission design was adopted to improve the meshing performance.Based on thelocal synthesis method and TCA technology,a new approach to the gear design for increasing the contact ratio is proposed by means of sloping the contact path in the paper. Comparative analysis on geometrical parameters and milling parameters between conventional design and new design has been carried out.The milling experiment results prove that the tooth contact area is standard and easy to control,Which have proved that spiral bevel gears with high contact ratio designed by local synthesis method and the non-zero modification technology can be implemented.%重合度较大时,参与啮合齿的对数增多,齿轮传动就越平稳,每齿承载的力也减小,这对于降低噪声是非常有利的.根据螺旋锥齿轮的非零变位原理,进行负传动设计,改善其啮合性能.在此基础上,借助于局部综合法、TCA技术等仿真方法,通过改变接触路径的倾斜角度,以获得具有较大重合度的弧齿锥齿轮.对新型设计和常规设计两种方案的几何参数和加工参数进行了对比,并创建齿轮副的精确三维模型,基于UG运动仿真功能模拟大小轮接触区状况.铣齿试验表明,接触区良好,易于调整,验证了利用局部综合法与非零变位技术设计的高重合度弧齿锥齿轮的可实施性.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)004【总页数】4页(P186-189)【关键词】重合度;弧齿锥齿轮;非零变位;局部综合法;铣齿实验【作者】张华;吉宝峰;李天兴;杨建军【作者单位】河南科技大学机电工程学院,河南洛阳471003;江苏大学汽车与交通工程学院,江苏镇江212013;河南科技大学机电工程学院,河南洛阳471003;河南科技大学机电工程学院,河南洛阳471003;河南科技大学机电工程学院,河南洛阳471003【正文语种】中文【中图分类】TH16;TH132.4221 引言弧齿锥齿轮振动噪声和重合度的大小是紧密相关的,重合度达到2或接近2时,啮合在两对齿之间啮合的时间大大延长,相对于齿轮副大部分时间单对齿啮合,运转更加平稳,因而振动噪声较小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
g a a a
下标 g 换为 m ,同时加上产形轮标志 F 即可得切制小齿轮 1
( F) ( F) 时 ,在坐标系 ∑ m 中产形面的方程 r m 及法线单位矢量 e m .
_ _
x m = rFctg a F - uFcos a F
_( r mF)
( F) ( F)
ym zm
= u F sin aF sin (θ F - qF + ψ F) - bF sin ( q F - ψ F) = u F sin aFcos (θ F - qF + ψ F) - bFcos ( qF - ψ F)
1 问题的提出
弧齿锥齿轮传动平稳 、 噪音小 , 承载能力高 , 现已被广泛 应用到各种高速重载的相交轴传动中 . 然而弧齿锥齿轮加工 的高质高效始终难以实现 . 虚拟制造技术的出现为解决这一 难题带来了希望 ,产品和过程的建模与仿真技术则是实现虚 拟制造的核心技术 . 因此探讨建立弧齿锥齿轮三维实体模型 的方法有助于进一步实现虚拟制造技术在弧齿锥齿轮加工中 的应用 ,使啮合接触 、 切削切制等实际工作情况通过计算机屏 幕展现在人们眼前 .
2、 3、 4 ,分别标识背锥面 、 根锥面 、 前 方程为 ri = M1 ai ・r , i = 1 、
锥面 、 面锥面 . 求交线 l1 、 l2 、 l3 、 l4 时 ,可将齿面方程分别与各锥面方程联
37
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
(2)
将式 (1) 写成直角坐标形式 ,即为产形面在固定坐标系 的方程 :
xg = rHctg a - ucos a
_
中 ∑g
rg : yg = u sin a sin ( θ - q + ψ) - bHsin ( q - ψ ) zg = u sin a cos ( θ - q + ψ) + bHcos ( q - ψ)
_ _ _ _ _
∑ 中 ,产形面径矢
y
_
ry 和法线单位矢量 ey 可由 ry = Myd ・
_
_
rd 和 ey = Lyd・ ed 确定 ; 同样 ,在坐标系
_ _ _
_
_
∑ 中 ,产形面径矢 rg
d
和法线单位矢量 eg 可由 rg = Mgy ・ ry 和 eg = L gy ・ ey 确定 , Mgy 为坐标系 ∑ y 到坐标系 ∑ g 的变换矩阵 ,Lgy 为矢量变换矩阵 . 从而可得在固定坐标系中 ,产形面径矢方程和法线单位矢量 :
_ (F1) vm _
_
_
_
图3 坐标示意图 如图 3 ,以各锥顶点为原点 ,轴线为 z 轴分别建立坐标系 ∑ a1 、 ∑ a2 、 ∑ a3 、 ∑ a4 , ∑ a 是以节锥顶点 O 为原点建立的坐标 系 ,下标 1 、 2、 3、 4 分别表示背锥 、 根锥 、 前锥 、 面锥 . 各坐标系原点 Oai ( i = 1 、 2、 3、 4 ) 至原点 Oa 的距离 Li ( i
(8)
z = u・ cos a 为使各锥面方程进行坐标变换后形式统一 , 对于前锥面和背
锥面 ,式中 y 取负值 ; a 为圆锥的半锥角 , 当 a 分别用背锥角 、 根锥角 、 前锥角 、 面锥角代入后便得到各锥面在各自坐标系下
(8) 可得各锥面在 的方程 . 由坐标变换矩阵及式 (7) 、
中的 ∑ 1
齿面方程的求解可知 ,轮齿齿面是一个双参数曲面 ,参数为 θ P、 ψP) x = x (θ P、 ψP) ψP ,为了便于分析 ,将齿面方程简单表示为 : y = y (θ P、 ψ z = z (θ P、 P)
图4 下面求四锥面方程 . 如图 4 所示 ,设锥面上任一动点 N 的 θ确定 ,u 为动点 N 沿圆锥母线方向距锥顶的 位置由参数 u 、 距离 , θ为沿圆周方向的角度 . 则锥面方程可用坐标形式表示 为: θ x = u・ sin a・ cos θ r : y = ±u・ sin a・ sin 图2 单个轮齿示意图 因此可以固定第一个参数 ,另一个参数间隔变化 ,描出一系列 点 ,连接成线 ; 再对第一个参数给以增量 , 仍使另一个参数间 隔变化 ,再描出一系列点 ,连接成线 … 这样就可以画出曲面的 网格表示 . 在此有一个问题需要考虑 , 即边界问题 , 这必须通 过进行面面求交以及面线求交解决 . 要通过面面求交的方法确定齿面边界 , 不仅需已知各面
(6)
Δ 式中 δ L 1 分别为机床调整参数 . 在坐标系 b1为根锥角 , ΔE1 、 ∑m 中 ,产形面 F 与小齿轮 1 的啮合公式为 啮合方程 . 产形面与被切齿面的接触线在和齿轮相固连的坐标系 ∑ 1 中的轨迹就是被切齿轮的齿面 . 对式 ( 6) 进行坐标变换再联立 啮合方程可得小齿轮的齿面方程 ,同理得大齿轮齿面方程 .
eg = sin a i g + cos a [sin ( θ 2q + ψ) j g + cos ( θ 2q + ψ) kg ]
_ _
_
_
ห้องสมุดไป่ตู้
_
(1)
rg = ( rHctg a 2 ucos a
) i g + [ usin asin ( θ 2q + ψ)2 bHsin ( q - ψ) ]
_
_
ψ) ] kg j g + [ usin acos ( θ 2q + ψ) + bHcos ( q2
_
_
_
2 齿面方程
将齿轮切削过程表示为示意图 1 ,同时引入坐标系 ∑ d (与 机床摇台相固连 ,Od 为刀盘中心 ,xd 为刀盘转动轴线 ) 、 ∑ y (与 机床摇台相固连 ,Oy 为摇台中心 ,xy 为摇台转动轴线 ) 、 ∑ g (固 定坐标系 , 与机床床身相固连 , 坐标系 ∑ y 初始位置与 ∑ g 重 合 ,在其中给出了产形轮转动的位置 ( 以ψ表示) ) .
(3)
依据假想平顶齿轮原理加工弧齿锥齿轮 , 假设用产形面
F 来加工小齿轮 1 ,并引入 : (1) 坐标系
∑
a
m
,与前述固定坐标
图1 切齿示意图 在切齿过程中 ,刀盘绕其轴线回转 ,其切削刃形成一圆锥 面即产形面 . 可以得到在 ∑ d 中其矢量方程为 : rd = ( rHctg a θj d + u sin a ・ θk d . - ucos a ) i d + u sin a ・ sin cos
_( e mF)
・
_( v mF1)
L 1 = OaOa1 = L a / cosδ 1 L 2 = OaOa2 =
d1
= 0 ,将
(6) 代入即可得啮合方程 . 同理 , 可以求出大齿轮 2 的 式 (5) 、
2
d1
δ ・ ctg 1 - (
db1
2
da1
δ ・ ctg sinδ b1 - hb1 ・ b1 )
= 1、 2、 3、 4) 为 :
(F1) (F1)
(1)
v my = Ω
(F)
(1) δ δ zm + Ω [ ( xm - L sinΔ L 1) sin 1) cos b1 - ( zm + Δ b1 ]
(F1) (F) (1) δ v mz = - Ω ym + Ω ( ym + ΔE1) sin b1
θ为确 式中 rH 为刀盘的计算半径 , a 为刀刃齿形角 , u 、 定锥面动点 N 的参数 . 产形面上点的法线单位矢量方程为 : ed θk d . 由坐标系 ∑ = sin a i d + cos a sin j d + cos a cos d 到坐标系 ∑ y 的坐标变换矩阵记为 Myd , 矢量变换矩阵记为 Lyd , 则在坐标 系
Ξ 收稿日期 :2002210215
_ _ _ _
∑ 等同 ; (2) ∑ 固定坐标系 , z 为被加工齿轮回转轴 线 ; (3) ∑ ,与被加工齿轮相固连坐标系 ,初始位置与 ∑ a 重 1 合 ,随着滚切进行 ,齿轮绕 z 转动 , 坐标系 ∑ 跟随转动 , 在 1 ( 3) 中 坐标系 ∑ 中以φ 1 表示齿轮转动的位置 . 则将式 ( 1 ) 、
(4)
作者简介 : 陈国荣 (19752) ,女 ,江苏涟水人 ,硕士研究生 .
( F)
36
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
陈国荣等 : 弧齿锥齿轮三维实体模型的构建方法
_( F) em
Ω . 式中
_ _
_
_ (1)
_ (1) rm
为 接 触 点 的 径 矢 , r (1) m = xm i
_
_
m
+ ym j
_ _
_
m
+
( 1) zm k m , R m 为 引 到 矢 量 作 用 线 上 任 意 点 径 矢 , R ( 1) m =
Ω( F) = - Ω( F) i m ,Ω(1) = - Ω(1) ( sinδ δ OmO1 , b1 i m + cos b1 k m ) . 所 以可得矢量 v (mF1) 在坐标轴上的投影为 : δ v mx = - Ω ( ym + ΔE1) cos b1
切制小齿轮 1 时 ,产形轮 F 和小齿轮本身分别以角速度 Ω( F) 和 Ω(1) 绕轴 xm 和 za 回转 ,产形面 F 与小齿轮 1 的相对运
( F1) (1) 动矢 量 用 vm 表 示 : v (mF1) = ( Ω( F) - Ω(1) ) × r (1) × m - Rm
