闭区间上连续函数的性质(详细版)
合集下载
第10节闭区间连续函数性质
至少有一个不超过 4 的 且
根据零点定理 , 在开区间
内至少存在一点
原命题得证 .
二、介值定理
定理2. ( 零点定理 ) 且
至少有一点
使
( 证明略 )
m
o a1 2 b x
y y f (x) a
o bx
定理3. ( 介值定理 ) 设 f (x) C[ a , b ] , 且 f (a) A,
f (b) B , A B , 则对 A 与 B 之间的任一数 C , 至少有
一刀剪为面积相等的两片.
y
提示: 建立坐标系如图.
则面积函数 S( ) C[ , ] 因 S() 0, S( ) A
S( )
o
x
故由介值定理可知:
0
(
,
),
使
S(0 )
A. 2
2. 设
一点
使
则提示: 令 则
易证
证明至少存在
作业
P73 题 2 ; 3; 4
备用题 证明
正根 . 证: 令 显然
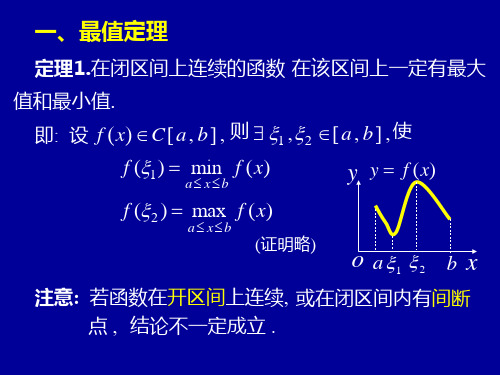
一、最值定理
定理1.在闭区间上连续的函数 在该区间上一定有最大
值和最小值.
即: 设 f (x) C[ a , b ] , 则 1 ,2 [ a , b ] , 使
f
(1)
min
a xb
f
(x)
y y f (x)
f
(2 )
max
a xb
f
(x)
(证明略)
o a1 2 b x
注意: 若函数在开区间上连续, 或在闭区间内有间断
例如,
但不一致连续 .
因为
取点
则
可以任意小
但
1.10闭区间上连续函数的性质

则称 f ( x0 )是函数 f ( x)在区间 I上的最大值 (最小值).
例如 y 1 sin x,
在[0,2]上, ymax 2, ymin 0.
2.有界性与最大值最小值定理
定理1 在闭区间上连续的函数在该区间上有界且 一定有最大值和最小值.
即:设 f (x)在[a , b] 上连续,
o
12 x
二、零点定理与介值定理
1.零点定理 定理2
即方程 f ( x) 0在(a, b)内至少存在一个实根 .
几何解释:
连续曲线弧 y f ( x)的两个端点 位于x轴两侧,则曲线弧与 x轴 至少有一个交点.
y y f (x)
a
o
bx
2.介值定理 定理3
A B,
证明 作辅助函数,
(x) f (x)C 则(x)C [a , b] ,且
证明 令 F( x) f ( x) x, 则F( x)在[a, b]上连续, 而 F (a) f (a) a 0, F (b) f (b) b 0, 由零点定理,
(a, b), 使 F ( ) f ( ) 0, 即 f ( ) .
小结
设 f ( x)在闭区间[a , b]上连续, (1) f ( x)在[a , b]上有界;
第十节 闭区间上连续函数的性质
一、有界性与最大值最小值定理 二、零点定理与介值定理
一、有界性与最大值最小值定理
1.最大值最小值定义
对于在区间 I上有定义的函数 f ( x), 若有 x0 I , 使得对于任一 x I 都有
f ( x) f ( x0 ) ( f ( x) f ( x0 ))
(2) f ( x)在[a , b]上达到最大值与最小值; (3) f ( x)在[a , b]上可取得最大值与最小值之间的任何值;
例如 y 1 sin x,
在[0,2]上, ymax 2, ymin 0.
2.有界性与最大值最小值定理
定理1 在闭区间上连续的函数在该区间上有界且 一定有最大值和最小值.
即:设 f (x)在[a , b] 上连续,
o
12 x
二、零点定理与介值定理
1.零点定理 定理2
即方程 f ( x) 0在(a, b)内至少存在一个实根 .
几何解释:
连续曲线弧 y f ( x)的两个端点 位于x轴两侧,则曲线弧与 x轴 至少有一个交点.
y y f (x)
a
o
bx
2.介值定理 定理3
A B,
证明 作辅助函数,
(x) f (x)C 则(x)C [a , b] ,且
证明 令 F( x) f ( x) x, 则F( x)在[a, b]上连续, 而 F (a) f (a) a 0, F (b) f (b) b 0, 由零点定理,
(a, b), 使 F ( ) f ( ) 0, 即 f ( ) .
小结
设 f ( x)在闭区间[a , b]上连续, (1) f ( x)在[a , b]上有界;
第十节 闭区间上连续函数的性质
一、有界性与最大值最小值定理 二、零点定理与介值定理
一、有界性与最大值最小值定理
1.最大值最小值定义
对于在区间 I上有定义的函数 f ( x), 若有 x0 I , 使得对于任一 x I 都有
f ( x) f ( x0 ) ( f ( x) f ( x0 ))
(2) f ( x)在[a , b]上达到最大值与最小值; (3) f ( x)在[a , b]上可取得最大值与最小值之间的任何值;
高数同济110闭区间上连续函数的性质

求解最值问题方法与步骤
确定函数定义域
首先明确函数f(x)的定义域,确保在求解最值问题时不会超出定义域 范围。
求导数并判断单调性
对函数f(x)求导,得到f'(x)。通过分析f'(x)的符号变化,判断函数在不 同区间的单调性。
寻找可疑点并比较函数值
可疑点包括导数为零的点、导数不存在的点和定义域的端点。将这些 可疑点代入原函数,比较函数值大小,确定最大和最小值。
判定方法与技巧
1 2 3
利用已知函数的有界性
如果已知某个函数在某个区间上是有界的,那么 可以通过这个函数来判定其他函数在该区间上是 否有界。
利用函数的单调性
如果函数在闭区间上单调增加或减少,那么可以 通过比较区间端点处的函数值来确定函数在该区 间上是否有界。
利用函数的周期性
对于周期性函数,可以通过研究其在一个周期内 的性质来判定其在整个定义域上是否有界。
03 闭区间上连续函数最值问 题
最值定理及证明过程
要点一
最值定理
若函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上必有最大 值和最小值。
要点二
证明过程
利用闭区间套定理和连续函数的局部保号性进行证明。首先, 将闭区间[a,b]等分为n个小区间,取各小区间端点处的函数 值,比较大小后得到最大和最小值。然后,不断二分有最大 (小)值的小区间,得到一个闭区间套。最后,由闭区间套 定理知,存在一个点ξ属于所有闭区间套,且f(ξ)为最大(小) 值。
性质
连续函数在定义域内的每一点都连续,且连续函数的和、差、积、商(分母不 为零)仍是连续函数。
闭区间上连续函数特点
有界性
闭区间上的连续函数一定在该区间上 有界。
高等数学闭区间上连续函数的性质

0 x 1 x =1 1 x 2
定理1(最大值和最小值定理) 在闭区间上连续的函数在该区间上 一定能取得它的最大值和最小值 定理2(有界性定理) 在闭区间上连续的函数 一定在该区间上有界 定理3(零点定理) 设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 那么在开区间 (a b)内至少存在一点x 使f(x)=0 注: 如果x0使f(x0)=0 则x0称为函数f(x)的零点
定理3(零点定理)设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异 号 那么在开区间(a b)内至少存在一点x 使f(x)=0 定理4(介值定理) 设函数 f(x)在闭区间[a b]上连 续 且f(a)f(b) 那么 对于f(a)与f(b) 之间的任意一个数C 在开区间 (a b)内至少有一点x 使得f(x)=C •推论 在闭区间上连续的函数 必取得介于最大值M与最小值 m之间的任何值
第一章 函数 极限 连续
§10 闭区间上的连续函数
一、有界性与最大值最小值定理
定理1(最大值和最小值定理)
在闭区间上连续的函数 在该区间上一定能取得它的 最大值和最小值
说明:定理说明 如果函数f(x)在闭区间[a b]上连续 那么
至少有一点x1[a b] 使f(x1)是f(x)在[a b]上的最大值 又至少有一点x2[a b] 使f(x2)是f(x)在[a b]上的最小值
定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间 上一定能取得它的最大值和最小值 应注意的问题:1、闭区间;2、连续 例如 函数f(x)=x在开区间(a b)内既无 最大值又无最小值 又如 如下函数在闭区间[0 2] 内既无最大值又无最小值
x 1 y = f (x) = 1 x 3
1.062__闭区间上连续函数的性质

即 3 4 2 1 0,
方程x 3 4 x 2 1 0在(0,1)内至少有一根 .
例2 设函数 f ( x )在区间[a , b] 上连续, 且f (a ) a ,
f (b ) b. 证明 (a , b ), 使得 f ( ) .
证 令 F ( x ) f ( x ) x, 则F ( x )在[a, b]上连续,
推论 2 零点存在定理 设函数f x 在闭区闭
a , b 上连续,且f a 与f b 异号,即 f a f b 0,那么在开区间 a , b 内至少有 函数f x 的一个零点,即至少有一点 a b ,使f 0
例如, y 1 sin x , 在[0, 2 ]上, ymax 2, ymin 0;
定理 1(最大值和最小值定理) 在闭区间上连续 的函数一定存在最大值和最小值.
即
若 f ( x ) Ca, b], 有 M f (1 ) f ( x ), m f ( 2 ) f ( x ).
注意:1.若区间是开区间, 定理不一定成立;
2.若区间内有间断点,定理不一定成立.
定理2(有界性定理) 在闭区间上连续的函数一定 在该区间上有界. 证 设函数f ( x )在[a, b]上连续, x [a , b],
有 m f ( x) M ,
取 K max{ m , M },
则有 f ( x ) K . 函数f ( x )在[a, b]上有界.
即方程 f ( x ) 0在 (a, b)内至少存在一个实根.
几何解释:
连续曲线弧 y f ( x )的两个 端点位于x轴的不同侧, 则曲 线弧与 x轴至少有一个交点.
闭区间上连续函数的性质

y
y f (x)
( x) f ( x) C
则 ( x ) C [ a , b ] , 且
B C A
(a) (b) ( A C )( B C )o aFra bibliotekb x
使 故由零点定理知, 至少有一点 即 必取得介于最小值与最 推论: 在闭区间上的连续函数 大值之间的任何值 .
定理2. ( 零点定理 )
且 使 至少有一点
( 证明略 )
y
y f (x)
o
a
b x
定理3. ( 介值定理 ) 设 f ( x) C [ a , b ] , 且 f (a) A , f (b) B , A B , 则对 A 与 B 之间的任一数 C , 至少有 一点 使
证: 作辅助函数
例1、证明方程 一个根 . 证: 显然
在区间 又 使
内至少有
故据零点定理, 至少存在一点
即
*三. 一致连续性
已知函数
在区间 I 上连续, 即:
一般情形, 与 , x0 都有关 . 了一致连续的概念 . 定义: 都有 在 I 上一致连续 . 显然:
就引出 对任意的
例如、 但不一致连续 . 因为 取点 可以任意小
f (1 ) min f ( x)
a xb
y y f (x)
f ( 2 ) max f ( x)
a x b
o a 1 2 b x
注意: 若函数在开区间上连续, 或在闭区间内有间断 点 , 结论不一定成立 .
例如、
y
2
1
也无最大值和最小值
o
1
2
x
二、零点定理与介值定理
17闭区间上连续函数的性质-15页精选文档

例 一个登山运动员从早上7:00开始攀登某座山 峰,在下午7:00到达山顶;第二天早上7:00再次从 山顶沿原路下山,下午7:00到达山脚。证明这个
运动员在这两天的某一相同时刻经过登山路线的 同一地点。
C
a
o
A
1
2 3
bx
连续y曲 f(x 线 )与水平 yC 直 至线 少有一 .
设 (x)f(x)C
则 (x)在 [a,b]上连 , 续
且 (a )f(a ) C(b)f(b)C
因 C 是f介 (a )f,(b 于 )之间 (a ) , (b ) 0 故 ,
由零点定理, (a,b)使 ,
例如:y=x在开区间(a,b)内是连续的,但在 (a,b)内无最大值和最小值。
y
a o
b x
又如函数
在闭区间[0,2]上有间断点x=1,f(x)在此区间上 无最大最小值。
y
2
1
x
o
12
二 介值定理
1 ,若 x0使 f(x 得 0)0 ,x 则 0 为称 f函 (x)的 数 零点
定理(零点定理数) f(x设 )在函闭区[a间 ,b]上连续, 且f(a)与f(b)异号,则在开 (a,区 b)内间至少存在函
证 令 f(x ) x 3 4 x 2 1 ,则 f(x)在 [0,1]上连 , 续 又 f(0)10 , f(1 ) 20 , 由零点定理,
(a,b),使f()0, 即 34 210 ,
方x3 程 4x210在 (0,1)内至少 . 有一
方x程 34x210在 (0,1)内只有 . 一根
第7节 闭区间上连续函数 的性质
一、最值定理
1、定 义 : 设 函 f (x数 )在I上 有 定, x义 0 I,如 果 对 任 意 xI,都有
闭区间上连续函数的性质

y
y = f (x)
o
a
ξ2
ξ1 b
x
注意: 若区间是开区间 定理不一定成立; 若区间是开区间, 注意:1.若区间是开区间 定理不一定成立 2.若区间内有间断点 定理不一定成立 若区间内有间断点, 若区间内有间断点 定理不一定成立.
y
y = f (x)
1
y
y = f (x)
o
π 2
x
o
1
2
x
定理2(有界性定理) 在闭区间上连续的函数一定 定理2 有界性定理) 在该区间上有界. 在该区间上有界. 证 设函数 f ( x )在[a , b]上连续 , x ∈ [a , b],
三,小结
四个定理
有界性定理;最值定理 介值定理 根的存在性定理. 有界性定理 最值定理;介值定理 根的存在性定理 最值定理 介值定理;根的存在性定理 注意 1.闭区间; 2.连续函数. .闭区间; .连续函数. 这两点不满足上述定理不一定成立. 这两点不满足上述定理不一定成立.
解题思路
1.直接法 先利用最值定理 再利用介值定理; 1.直接法:先利用最值定理 再利用介值定理 直接法 先利用最值定理,再利用介值定理 2.辅助函数法:先作辅助函数 再利用零点定理; 2.辅助函数法:先作辅助函数F(x),再利用零点定理 辅助函数法 再利用零点定理
即方程 f ( x ) = 0在 (a , b )内至少存在一个实根 .
几何解释: 几何解释
y
连续曲线弧 y = f ( x )的两个 端点位于 x轴的不同侧 , 则曲 线弧与 x轴至少有一个交点 .
y = f (x)
a o
ξ1 ξ2
ξ3
b x
定理4(介值定理) 定理 4(介值定理) 4(介值定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设函数 f(x)在闭区间[a b]上连续 且f(a)f(b) 那么 对于
f(a)与f(b)之间的任意一个数C 在开区间(a b)内至少有一点x 使得f(x)=C
•推论
在闭区间上连续的函数必取得介于最大值M与最小值m 之间的任何值
14
高等数学 ● 戴本忠
设函数 f ( x)在闭区间a, b上连续,且在这区间的端点取
f(x)f(x0) (f(x)f(x0)) 则称f(x0)是函数f(x)在区间I上的最大值(最小值)
应注意的问题:
并非任何函数都有最大值和 最小值
例 如 , 函 数 f(x)=x在 开 区 间 (a b)内既无最大值又无最小值
4
高等数学 ● 戴本忠
例如, y = 1 sin x, 在[0, 2 ]上, ymax = 2, ymin = 0;
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0 ❖定理4(介值定理)
设函数 f(x)在闭区间[a b]上连续 且f(a)f(b) 那么 对于
证明 设 f(x)=x34x21 则f(x)在闭区间[0 1]上连续
并且
f(0)=1>0 f(1)=2<0
根据零点定理 在(0 1)内至少有一点x 使得 f(x)=0
即
x 34x 21=0
这说明方程x34x21=0在区间(0 1)内至少有一个根是x
12
高等数学 ● 戴本忠
第十节
第一章
闭区间上连续函数的性质
一、有界性与最大值最小值定理 二、零点定理与介值定理 *三、一致连续性
1
高等数学 ● 戴本忠
学习指导
1.教学目的:了解闭区间上连续函数的性质。 2.基本练习:了解并通过一定的练习学习最大最
小值定理、有界性定理、零点定理及介值定理在 函数值的估计和根的估计上的应用。 3.注意事项:闭区间上连续的函数有许多好的性质。 应了解在闭区间上连续函数的最大最小值定理、 有界性定理、零点定理及介值定理。了解定理的 条件和结论,并通过一定的练习学会运用它们.
三、一致连续性
定义:设函数f(x)在区间I上有定义,如果对于任意给定 的正数ε,总存在着正数δ,使得对于区间I上的任意两 点x1,x2,当|x1-x2|< δ时,就有|f(x1)-f(x2)|< ε,那么称函 数f(x)在区间I上是一致连续的。
不论在区间I的任何部分,只要自变量的两个数 值接近到一定程度,就可使对应的函数值达到 所指定的接近程度。
mf(x)M 上式表明 f(x)在[a b]上有上界M和下界m 因此函数f(x)在 [a b]上有界
9
高等数学 ● 戴本忠
有界性与最大值最小值定理:在闭区间上连续的 函数有界且一定有最大值和最小值. 注意:1.若区间是开区间, 定理不一定成立;
2.若区间内有间断点, 定理不一定成立.
f(a)与f(b)之间的任意一个数C 在开区间(a b)内至少有一点x 使得f(x)=C
13
高等数学 ● 戴本忠
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 那么
在开区间(a b)内至少一点x 使f(x)=0
❖定理4(介值定理)
高等数学 ● 戴本忠
思考题解答
不正确.
例函数
e1 , f (x) =
2,
0 x1 x=0
f ( x)在(0,1)内连续, f (0) (1) = 2e 0.
但 f ( x)在(0,1)内无零点.
20
高等数学 ● 戴本忠
五、小结
关于闭区间上连续函数整体性质的四个定理: 有界性定理、最值定理、零点定理、介值定理,
至少有一点x1[a b] 使f(x1)是f(x)在[a b]上的最大值 又至少有一点x2[a b] 使f(x2)是f(x)在[a b]上的最小值
6
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
应注意的问题:
如果函数仅在开区间内连续 或函数在闭区间上有间断 点 那么函数在该区间上就不一定有最大值或最小值
不同的函数值
f (a) = A 及 f (b) = B,
那么,对于 A与B之间的任意一个数C ,在开区间a, b内
至少有一点x,使得 f (x ) = C (a x b).
证 设( x) = f ( x) C,
y M
则( x)在[a,b]上连续, 且 (a) = f (a) C
又如 如下函数在闭区间[0 2] 内既无最大值又无最小值
y=
f
(x)
=
x 1 1
x3
0 x1 x=1 1 x2
高等数学 ●
8
戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
❖定理2(有界性定理)
在闭区间上连续的函数一定在该区间上有界 证明 设函数f(x)在闭区间[a b]上连续 根据定理1 存在f(x)在区间[a b]上的最大值M和最小值 m 使任一x[a b]满足
= A C,
B y = f (x) C
o
A m
(b) = f (b) C = B C,
高等数学 ●
x
15
戴本忠
(a) (b) 0, 由零点定理, x (a, b),使 (x ) = 0,即 (x ) = f (x ) C = 0, f (x ) = C.
10
高等数学 ● 戴本忠
二、零点定理与介值定理 ❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0
几何解释:线弧y = f (x)的两 个端点位于x轴的不同侧,则曲 线弧与x轴至少有一个交点.
4. 当 f (a) f (b) 0 时, 必存在 x (a , b), 使 f (x ) = 0.
22
高等数学 ● 戴本忠
• P74:2,3
作业
23
高等数学 ● 戴本忠
定理5(一致连续性定理)如果函数f(x)在闭区间[a,b]上连续, 那么它在该区间上一致连续.
18
高等数学 ● 戴本忠
思考题
下述命题是否正确?
如果 f ( x) 在[a,b]上有定义,在(a, b) 内连续,且 f (a) f (b) 0,那么 f ( x) 在 (a, b)内必有零点.
19
例如 函数f(x)=x在开区间(a b) 内既无最大值又无最小值
7
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
应注意的问题:
如果函数仅在开区间内连续 或函数在闭区间上有间断 点 那么函数在该区间上就不一定有最大值或最小值
注: 如果x0使f(x0)=0 则x0称为函数f(x)的零点
11
高等数学 ● 戴本忠
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0
例1 证明方程x34x21=0在区间(0 1)内至少有一个根
2
高等数学 ● 戴本忠
如果函数f(x)在开区间(a,b)内连续,在右端点b 左连续,在左端点a右连续,那么函数f(x)就是在 闭区间[a,b]上连续的。
3
高等数学 ● 戴本忠
一、有界性与最大值最小值定理
❖最大值与最小值
对于在区间I上有定义的函数f(x) 如果有x0I 使得对于 任一xI都有
y = sgn x, 在(, )上, ymax = 1, ymin = 1; 在(0, )上, ymax = ymin = 1.
5
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
说明:
定理说明 如果函数f(x)在闭区间[a b]上连续 那么
它们是研究连续函数性质的重要工具。
注意条件: 1.闭区间; 2.连续函数. 这两点不全满足时上述定理不一定成立.
21
高等数学 ● 戴本忠
内容小结
设 f (x) C[a ,b],则 1. f (x) 在 [a ,b] 上有界; 2. f (x) 在 [a ,b] 上达到最大值与最小值; 3. f (x) 在 [a ,b] 上可取最大与最小值之间的任何值;
证 令 F(x) = f (x) x, 则F(x)在[a,b]上连续,
而 F(a) = f (a) a 0, F (b) = f (b) b 0, 由零点定理, x (a,b), 使 F (x ) = f (x ) x = 0, 即 f (x ) = x.
17
高等数学 ● 戴本忠
几何解释:连续曲线弧 y = f ( x)与水平直线 y = C至少 有一个交点.
推论 在闭区间上连续的函数必取得介于最大值M与 最小值m之间的任何值.
16
高等数学 ● 戴本忠
例2 设函数 f (x)在区间[a,b]上连续, 且f (a) a,
f (b) b. 证明 x (a,b), 使得 f (x ) = x.
f(a)与f(b)之间的任意一个数C 在开区间(a b)内至少有一点x 使得f(x)=C
•推论
在闭区间上连续的函数必取得介于最大值M与最小值m 之间的任何值
14
高等数学 ● 戴本忠
设函数 f ( x)在闭区间a, b上连续,且在这区间的端点取
f(x)f(x0) (f(x)f(x0)) 则称f(x0)是函数f(x)在区间I上的最大值(最小值)
应注意的问题:
并非任何函数都有最大值和 最小值
例 如 , 函 数 f(x)=x在 开 区 间 (a b)内既无最大值又无最小值
4
高等数学 ● 戴本忠
例如, y = 1 sin x, 在[0, 2 ]上, ymax = 2, ymin = 0;
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0 ❖定理4(介值定理)
设函数 f(x)在闭区间[a b]上连续 且f(a)f(b) 那么 对于
证明 设 f(x)=x34x21 则f(x)在闭区间[0 1]上连续
并且
f(0)=1>0 f(1)=2<0
根据零点定理 在(0 1)内至少有一点x 使得 f(x)=0
即
x 34x 21=0
这说明方程x34x21=0在区间(0 1)内至少有一个根是x
12
高等数学 ● 戴本忠
第十节
第一章
闭区间上连续函数的性质
一、有界性与最大值最小值定理 二、零点定理与介值定理 *三、一致连续性
1
高等数学 ● 戴本忠
学习指导
1.教学目的:了解闭区间上连续函数的性质。 2.基本练习:了解并通过一定的练习学习最大最
小值定理、有界性定理、零点定理及介值定理在 函数值的估计和根的估计上的应用。 3.注意事项:闭区间上连续的函数有许多好的性质。 应了解在闭区间上连续函数的最大最小值定理、 有界性定理、零点定理及介值定理。了解定理的 条件和结论,并通过一定的练习学会运用它们.
三、一致连续性
定义:设函数f(x)在区间I上有定义,如果对于任意给定 的正数ε,总存在着正数δ,使得对于区间I上的任意两 点x1,x2,当|x1-x2|< δ时,就有|f(x1)-f(x2)|< ε,那么称函 数f(x)在区间I上是一致连续的。
不论在区间I的任何部分,只要自变量的两个数 值接近到一定程度,就可使对应的函数值达到 所指定的接近程度。
mf(x)M 上式表明 f(x)在[a b]上有上界M和下界m 因此函数f(x)在 [a b]上有界
9
高等数学 ● 戴本忠
有界性与最大值最小值定理:在闭区间上连续的 函数有界且一定有最大值和最小值. 注意:1.若区间是开区间, 定理不一定成立;
2.若区间内有间断点, 定理不一定成立.
f(a)与f(b)之间的任意一个数C 在开区间(a b)内至少有一点x 使得f(x)=C
13
高等数学 ● 戴本忠
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 那么
在开区间(a b)内至少一点x 使f(x)=0
❖定理4(介值定理)
高等数学 ● 戴本忠
思考题解答
不正确.
例函数
e1 , f (x) =
2,
0 x1 x=0
f ( x)在(0,1)内连续, f (0) (1) = 2e 0.
但 f ( x)在(0,1)内无零点.
20
高等数学 ● 戴本忠
五、小结
关于闭区间上连续函数整体性质的四个定理: 有界性定理、最值定理、零点定理、介值定理,
至少有一点x1[a b] 使f(x1)是f(x)在[a b]上的最大值 又至少有一点x2[a b] 使f(x2)是f(x)在[a b]上的最小值
6
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
应注意的问题:
如果函数仅在开区间内连续 或函数在闭区间上有间断 点 那么函数在该区间上就不一定有最大值或最小值
不同的函数值
f (a) = A 及 f (b) = B,
那么,对于 A与B之间的任意一个数C ,在开区间a, b内
至少有一点x,使得 f (x ) = C (a x b).
证 设( x) = f ( x) C,
y M
则( x)在[a,b]上连续, 且 (a) = f (a) C
又如 如下函数在闭区间[0 2] 内既无最大值又无最小值
y=
f
(x)
=
x 1 1
x3
0 x1 x=1 1 x2
高等数学 ●
8
戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
❖定理2(有界性定理)
在闭区间上连续的函数一定在该区间上有界 证明 设函数f(x)在闭区间[a b]上连续 根据定理1 存在f(x)在区间[a b]上的最大值M和最小值 m 使任一x[a b]满足
= A C,
B y = f (x) C
o
A m
(b) = f (b) C = B C,
高等数学 ●
x
15
戴本忠
(a) (b) 0, 由零点定理, x (a, b),使 (x ) = 0,即 (x ) = f (x ) C = 0, f (x ) = C.
10
高等数学 ● 戴本忠
二、零点定理与介值定理 ❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0
几何解释:线弧y = f (x)的两 个端点位于x轴的不同侧,则曲 线弧与x轴至少有一个交点.
4. 当 f (a) f (b) 0 时, 必存在 x (a , b), 使 f (x ) = 0.
22
高等数学 ● 戴本忠
• P74:2,3
作业
23
高等数学 ● 戴本忠
定理5(一致连续性定理)如果函数f(x)在闭区间[a,b]上连续, 那么它在该区间上一致连续.
18
高等数学 ● 戴本忠
思考题
下述命题是否正确?
如果 f ( x) 在[a,b]上有定义,在(a, b) 内连续,且 f (a) f (b) 0,那么 f ( x) 在 (a, b)内必有零点.
19
例如 函数f(x)=x在开区间(a b) 内既无最大值又无最小值
7
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
应注意的问题:
如果函数仅在开区间内连续 或函数在闭区间上有间断 点 那么函数在该区间上就不一定有最大值或最小值
注: 如果x0使f(x0)=0 则x0称为函数f(x)的零点
11
高等数学 ● 戴本忠
二、零点定理与介值定理
❖定理3(零点定理)
设函数f(x)在闭区间[a b]上连续 且f(a)与f(b)异号 即
f(a).f(b)<0,那么在开区间(a b)内至少存在一点x 使f(x)=0
例1 证明方程x34x21=0在区间(0 1)内至少有一个根
2
高等数学 ● 戴本忠
如果函数f(x)在开区间(a,b)内连续,在右端点b 左连续,在左端点a右连续,那么函数f(x)就是在 闭区间[a,b]上连续的。
3
高等数学 ● 戴本忠
一、有界性与最大值最小值定理
❖最大值与最小值
对于在区间I上有定义的函数f(x) 如果有x0I 使得对于 任一xI都有
y = sgn x, 在(, )上, ymax = 1, ymin = 1; 在(0, )上, ymax = ymin = 1.
5
高等数学 ● 戴本忠
❖定理1(最大值和最小值定理)
在闭区间上连续的函数在该区间上一定能取得它的最大 值和最小值
说明:
定理说明 如果函数f(x)在闭区间[a b]上连续 那么
它们是研究连续函数性质的重要工具。
注意条件: 1.闭区间; 2.连续函数. 这两点不全满足时上述定理不一定成立.
21
高等数学 ● 戴本忠
内容小结
设 f (x) C[a ,b],则 1. f (x) 在 [a ,b] 上有界; 2. f (x) 在 [a ,b] 上达到最大值与最小值; 3. f (x) 在 [a ,b] 上可取最大与最小值之间的任何值;
证 令 F(x) = f (x) x, 则F(x)在[a,b]上连续,
而 F(a) = f (a) a 0, F (b) = f (b) b 0, 由零点定理, x (a,b), 使 F (x ) = f (x ) x = 0, 即 f (x ) = x.
17
高等数学 ● 戴本忠
几何解释:连续曲线弧 y = f ( x)与水平直线 y = C至少 有一个交点.
推论 在闭区间上连续的函数必取得介于最大值M与 最小值m之间的任何值.
16
高等数学 ● 戴本忠
例2 设函数 f (x)在区间[a,b]上连续, 且f (a) a,
f (b) b. 证明 x (a,b), 使得 f (x ) = x.
