齿轮的齿廓曲线分享资料
斜齿圆柱齿轮齿廓曲面的形成
斜齿圆柱齿轮齿廓曲面的形成
斜齿圆柱齿轮齿廓曲面的形成是通过两个齿轮之间的啮合过程。
其中一个齿轮被称为驱动齿轮，另一个齿轮被称为从动齿轮。
首先，确定齿轮的基本参数，包括齿数、模数、压力角等。
然后，根据这些参数计算出齿轮的尺寸和齿廓曲线的形状。
齿廓曲线的形状是通过齿轮的插齿切削来制造的。
插齿切削是一种将切削刀具沿着齿轮齿廓的方向进行切削的方法。
切削刀具的形状和尺寸与所需的齿廓曲线形状相对应。
插齿切削的过程中，切削刀具的齿形会逐渐将齿轮齿廓形成，而切削刀具和齿轮之间的相对运动会导致材料的去除。
最终，通过连续的切削动作，将齿轮的齿廓逐渐形成。
需要注意的是，斜齿圆柱齿轮的齿廓曲面是斜的，而不是垂直于齿轮轴线的。
这是为了使齿轮的啮合更加平稳。
总的来说，斜齿圆柱齿轮齿廓曲面的形成是通过插齿切削将切削刀具沿着齿轮齿廓的方向进行切削，使齿轮的齿廓逐渐形成。
齿廓啮合基本定律与齿轮的齿廓曲线
7.2 齿廓啮合基本定律与齿轮的齿廓曲线7.2.1 平均传动比和瞬时传动比的概念一对齿轮的啮合传动是通过主动齿轮1的齿面依次推动从动齿轮2的齿面而实现的，在一段时间内两轮转过的周数1n 、2n 之比称为平均传动比，用i 或12i 表示，若两轮的齿数分别为1z 、2z ，则121221n z i n z == (7-1) 由此可见，两齿轮的平均传动比与其齿数成反比，当一对齿轮的齿数确定后，其平均传动比是一个常数。
但这并不能保证在一对齿廓的啮合过程中，其任一瞬时的传动比（即瞬时传动比）也是常数，因为，这取决于齿面的齿廓形状。
7.2.2 齿廓啮合基本定律如图7-2所示，设主动轮1和从动轮2分别绕O 1、O 2轴转动，角速度分别为ω1、ω2，方向相反，两齿廓在K点接触。
为保证二齿廓既不分离又不相互嵌入地连续转动，要求沿齿廓接触点K 的公法线n -n 方向上，齿廓间不能有相对运动，即二齿廓接触点公法线方向上的分速度要相等，12n n n v v v ==显然，在切线方向上二齿廓接触点的速度不相等，即齿廓沿切线方向存在相对滑动。
根据三心定理，两齿轮的相对速度瞬心在过接触点的公法线n -n 与连心线O 1O 2的交点C 上，其速度为：1122c v OC O C ωω== 由此可得齿轮机构的瞬时传动比：1221O C i O Cωω== (7-2) 从上面的分析可看出，相互啮合传动的一对齿轮，在任一位置时的传动比都与其连心线被齿廓接触点处公法线所分隔的两线段长度成反比。
这一规律称为齿廓啮合基本定律。
该定律表明齿轮的瞬时传动比与齿廓曲线之间的关系。
齿廓啮合基本定律既适用于定传动比齿轮机构，也适用于变传动比齿轮机构。
对于定传动比机构，齿廓啮合基本定律可表达为：两齿廓在任一位置啮合时，过啮合点所作两齿廓的公法线与两轮的连心线相交于一定点。
图7-2 齿廓啮合过程齿廓啮合基本定律表明：1、不同的齿廓曲线，其啮合接触点的公法线与连心线的交点不同，因此其瞬时传动比也就不同。
§10—2齿轮的齿廓曲线
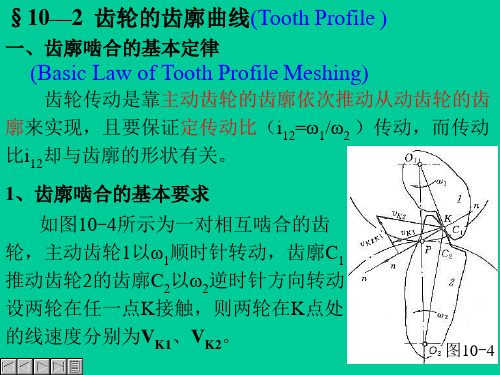
圆盘1上的已知曲线C1就会走出一 1 C 系列的轨迹，作这些轨迹的包络 线，则得到所求的齿廓曲线C2。
三、齿廓曲线的选择 理论上，只要给出一齿廓C1 ，就可以求出另一条满足 定传动比的共轭齿廓C2。但生产实际上，选择齿廓曲线时， 不仅要满足传动比要求，还必须从设计、制造、安装和使 用等方面予以考虑。 目前对定传动比传动的齿轮来说，最常用的齿廓是渐 开线(Involute) ，其次是摆线(Cycloid) 和变态摆线，近年 来出现了圆弧(Arc) 、抛物线(Parabola) 等。 由于渐开线齿廓具有良好的传动性能，便于制造、安 装、测量和互换性好等优点，所有目前绝大部分齿轮都采 用渐开线齿廓。 本章只讨论渐开线齿轮。
一、齿廓啮合的基本定律
(Basic Law of Tooth Profile Meshing)
齿轮传动是靠主动齿轮的齿廓依次推动从动齿轮的齿 廓来实现，且要保证定传动比（i12=ω1/ω2 ）传动，而传动 比i12却与齿廓的形状有关。 1、齿廓啮合的基本要求 、 如图10-4所示为一对相互啮合的齿 轮，主动齿轮1以ω1顺时针转动，齿廓C1 推动齿轮2的齿廓C2以ω2逆时针方向转动。 设两轮在任一点K接触，则两轮在K点处 的线速度分别为VK1、VK2。
目前对定传动比传动的齿轮来说最常用的齿廓是渐开线involute其次是摆线cycloid和变态摆线近年来出现了圆弧arc抛物线parabola由于渐开线齿廓具有良好的传动性能便于制造安装测量和互换性好等优点所有目前绝大部分齿轮都采用渐开线齿廓
齿轮的齿廓曲线(Tooth Profile ) §10—2 齿轮的齿廓曲线
4、节点(pitch point) 和节圆(pitch circle) 、 1）节点 节点P——过齿廓啮合点的公法线与连心线的交点。 节点 2）节圆 节圆 如要求定比传动即i12=C，则应 使O2P/ O1P= C。由于O1、O2为定点， 所以欲使 O2P/ O1P= C，则节点P在 O1O2上必须是定点。 ∴ 定比传动齿轮的齿廓啮合基本定律 可以表述为：要使两齿轮作定传动 比传动，则不论两齿廓在何处接触， 过接触点所作的公法线必须与连心 线交于一定点。
8-2 齿轮的齿廓
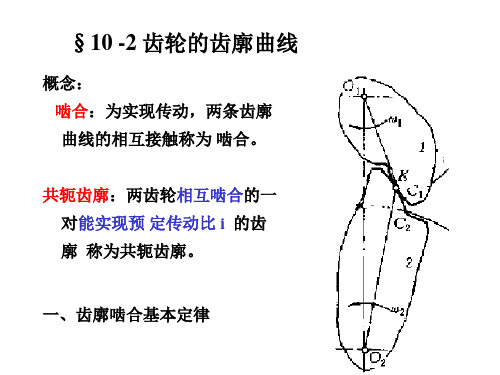
节圆
对于定比机构, 对于定比机构,O1P ,O2P 为定值 令 O1P = r1',O2P = r2' , 则:i = w1/ w2 = O2P / O1P = r2' / r1' = 常数 作纯滚时, ∵ 作纯滚时,两轮的相对瞬心在接触点 一对齿轮的传动相当于两个摩擦轮作相对纯滚动 在齿轮机构中,将这两个看不见的作相对纯滚的摩擦轮称 在齿轮机构中,将这两个看不见的作相对纯滚的摩擦轮称 纯滚 分别为两节圆的节圆半径 节圆半径. 为节圆. r2' , r1' 分别为两节圆的节圆半径. 节圆. 显然: 显然: O1O2 = r2' + r1' ------中心距 中心距 也可知, 也可知,若 i = 变量 → P为不定点 → P点的轨迹为非圆 为不定点 点的轨迹为非圆
§10 -2 齿轮的齿廓曲线
概念: 概念: 啮合:为实现传动,两条齿廓 啮合:为实现传动, 啮合. 曲线的相互接触称为 啮合. 共轭齿廓:两齿轮相互啮合的一 共轭齿廓:两齿轮相互啮合的一 相互啮合 对能实现预 定传动比 i 的齿 称为共轭齿廓. 廓 称为共轭齿廓.
一,齿廓啮合基本定律
3
已知:主动轮速 已知:主动轮速w1 ,从动轮速 w2 . P:速度瞬心 : 有:VP1 = VP2 = Vห้องสมุดไป่ตู้ ∴ O1P w1 = O2P w2 i = w1/ w2= O2P / O1P 称为两齿廓的啮合节点, 点 P-----称为两齿廓的啮合节点, 称为两齿廓的啮合节点 简称节点 简称节点 啮合基本定律: 啮合基本定律: 两齿轮的传动比(速比) 两齿轮的传动比(速比)i 等于两轮连 所分的两线段之反比. 心线上被节点 P 所分的两线段之反比.
ch10-2齿轮的齿廓曲线
Theory of machines and mechanisms
两齿廓作定传动比传动需满足
的条件是：两齿廓啮合节点P为
连心线上的一个定点。
节 圆 : 以 O1( 或 O2) 为 圆 心 、 以 O1P (或O2P)为半径的圆。
1 O2 P r2 i12 常数 2 O1P r1
Theory of machines and mechanisms
机械原理
第10章 齿轮机构及其 设计
§10-2 齿轮的齿廓曲线
一、齿廓啮合基本定律
一对齿轮的传动，是依靠主动轮的齿廓依次推动 从动轮的齿廓来实现的。两轮的瞬时角速度之比 称为传动比：
1 i12 2
传动比可以是恒定的或按某一规律变化的。在给 定传动比的条件下如何确定两轮的齿廓曲线呢？
Theory of machines and mechanisms
7
二、共轭齿廓
凡是满足齿廓啮合基本定律的一对齿廓叫 共轭齿廓。共轭齿廓的曲线叫共轭曲线。
共轭齿廓的求法：包络线法、齿廓法线法
或动瞬心线法等。
Theory of machines and mechanisms
8
齿廓法线法求共轭齿廓曲线
10
Theory of machines and mechanisms
返回目录
Theory of machines and mechanisms
机械原理
Thank you!
4
Theory of machines and mechanisms
一、齿廓啮合基本定律
两齿轮啮合传动时，节点P在两 轮各自运动平面内的轨迹分别 称为齿轮1和齿轮2的节曲线。 节曲线是齿轮的动瞬心线，齿 轮的啮合传动相当于其两节曲 线作无滑动的纯滚动。 当节曲线为圆时，称其为齿轮 的节圆。此时节点P是连心线上 的一个定点。
《机械设计原理》齿轮的齿廓曲线
§6-2 齿轮的齿廓曲线
2. 齿廓曲线的选择
共轭：按一定的规律相配的一对。
共轭齿廓：能按预
轭
定传动比规律相互啮
合传动的一对齿廓。
给定预定的传动比和 一条齿廓曲线，可根据 齿廓啮合基本定律求得 另一条齿廓曲线。
§6-2 齿轮的齿廓曲线
能满足一定传动比规律的共轭齿廓曲线有很多。
➢ 瞬时传动比为多少？
2
O2
根据速度瞬心可知，瞬时传动比：
i12 1 / 2 O2P / O1P
§6-2 齿轮的齿廓曲线
O1
1
n K
n
P C2 C1
此式表明：相互啮合传动的一对 齿轮，在任意位置时的传动比，都 与其连心线O1O2被其啮合齿廓在接 触点处的公法线所分成的两线段长 成反比。
这个规律称为齿廓啮合基本定律。
第6章 齿轮机构
§6-2 齿轮的齿廓曲线
主要内容： ➢ 齿廓啮合基本定律 ➢ 齿廓曲线的选择
平均传动比：
i12 n1 / n2 z2 / z1
§6-2 齿轮的齿廓曲线
O1
1. 齿廓啮合基本定律
1
➢ 怎样才能使一对齿廓连续接触而传
n 动？
vc1 vc2
K
n
P C2 C1
两齿廓沿接触点的公法线方向的 速度应相等；相对速度只能沿接触 点处的公切线方向。
比传动。
r2 P 点在轮1或2的运动平面上的轨迹为
一个圆，称为节圆（pitch circle）。
2
O2
传动过程中，两齿轮的节圆作纯滚 动。
§6-2 齿轮的齿廓曲线
变传动比传动：两齿廓的节点P 按其传动比
的变化规律在其连心线上移动。
齿轮的齿廓曲线--ppt课件可编辑全文
10-26
*
ppt课件
*
ppt课件
10-26、
5
50
90
*
ppt课件
260
260
250
260
460
450
260
260
235
423
260
15.7
5
7.85
7.85
*
ppt课件
0、一对渐开线轮齿的啮合过程
*
ppt课件
pn
h
N
α
s
e
ha
hf
p
B
O
rb
rf
ra
1)轮齿与齿槽正好与外齿轮相反。
2) df>d>da
三、内齿轮(internal gears)
3) 为保证齿廓全部为渐开线，
，da＝d－2ha，
df＝d＋2hf
结构特点：轮齿分布在空心圆柱体内表面上。
不同点：
要求da>db。
r
*
ppt课件
思考题
m、α、ha* 、c* 取标准值，且e=s的齿轮。
*
ppt课件
B
二、齿条(the rack)
2)齿廓是直线，各点法线和速度方向线分别平行，压力角处处相等，且等于齿形角，
3)齿距处处相等: p=πm
p
pn
z→∞的特例。齿廓曲线（渐开线）→直线
pn=pcosα
α为常数。
α
α
α
特点： 1)齿条相当于齿数无穷多的齿轮，故齿轮中的圆在齿条中都变成了直线，即齿顶线，齿根线，分度线，等等
齿轮传动对齿廓曲线的基本要求
齿轮传动对齿廓曲线的基本要求
1、齿廓曲线的几何形状必须满足齿轮传动的要求，一般要求满足螺旋线和锥齿形这两种形式。
2、曲线不能太折曲，应保持较短的半径弧线，以免使传动中心距变得太大。
3、曲线半径变化太大或太小，可能会造成齿形径向和轴向运动量改变。
因此需要保持较一致的半径变化，以防止齿轮系统不稳定问题。
4、齿面的中心角和模数等参数影响齿廓曲线的几何形状，在设计及加工中需要特别注意。
5、齿廓曲线接触不良容易导致传动功率损失、噪声增大等问题，因此齿廓曲线的接触要求及计算方法，也时刻悬在设计人员的头顶上。
6、针对于齿轮采用噪声紧凑形式，要求灵敏度大、噪声小，以降低噪声对系统正常运行的影响是很有必要的。
7、齿廓曲线也不能太平，它的精度要求也是特殊的。
精度要求太低，噪声会增加；而精度要求太高，不仅会增加加工难度，也会使齿轮受损。
8、此外，对接触必须具备损坏预防和适应性能；滚齿预留及节点清洁形状等也必须综合设计考虑。
总之，齿廓曲线是齿轮传动非常关键的组成部分，要完成有效传动，必须满足上述多种要求，才能使齿轮系统发挥出最大性能。
07-2第三十四讲 齿轮的齿廓曲线
t
ω1
n k P
vk2 vk1
n
齿廓啮合基本定律: 齿廓啮合基本定律: 互相啮合的一对齿轮在任一位置啮合时的传动比， 互相啮合的一对齿轮在任一位置啮合时的传动比， 都 与连心线O 与连心线O1O2 被其啮合齿廓在接触点的公法线所分成的两 线段成反比。 线段成反比。
ω2
o2
t
Hale Waihona Puke 分点P称为节点 分点P称为节点。P点分别在与两齿轮固定的平面内的轨迹称为节线。 显 节点。 点分别在与两齿轮固定的平面内的轨迹称为节线。 然一对齿轮的啮合相当于两齿轮的节线在作纯滚动 节线在作纯滚动。 然一对齿轮的啮合相当于两齿轮的节线在作纯滚动。 如果要求传动比为常数， 如果要求传动比为常数，则O2 P /O1P为常数，P必为一个定点。两节线为 为常数， 必为一个定点。 节圆，相切于P 两节圆作纯滚动。 节圆，相切于P点，两节圆作纯滚动。 如果传动比不恒定， 如果传动比不恒定，则O2 P /O1P为不是常数，节线为非圆曲线。 为不是常数，节线为非圆曲线。
第三十四讲 齿轮的齿廓曲线
共轭齿廓：一对能实现预定传动比( 共轭齿廓：一对能实现预定传动比(i12=ω1/ω2)规律的啮合齿廓。 规律的啮合齿廓。 1、齿廓啮合基本定律 一对齿廓在K点接触时，速度不相等： 一对齿廓在K点接触时，速度不相等： vk1≠vk2 但法向速度应相等: kn1 kn2 但法向速度应相等:vkn1=vkn2 根据三心定律， 点为相对瞬心： 根据三心定律，P点为相对瞬心： i12=ω1/ω2＝O2 P /O1P
JM
返回
2、齿廓曲线的选择 渐开线 摆线 变态摆线 圆弧 抛物线 渐开线具有很好的传动性能 而且便于制造 安装、测量和互换使用 渐开线具有很好的传动性能，而且便于制造、安装、测量和互换使用 具有很好的传动性能， 制造、 等优点。 等优点。 ——应用最广 ——应用最广
(完整版)齿轮的齿廓曲线
Fn rk
NB rb k k KA0
力方向与速度方向所夹锐角
O
为渐开线上该点之压力角
αk(pressure angle)。
基圆
rb＝rk cosαk
离中心越远，渐开线上的压力角
越大。基圆上的压力角为0。
(4)渐开线形状取决于基圆 基圆越大，渐开线越平直，
当rb→∞，变成直线。
Σ3 Σ1
Σ2
互相啮合的一对齿轮在任一位置时的传动比，
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数，则应使O2P/O1P为常数。
由于O2 、O1为定点，故P必为一个定点，称为节点
(the pitch point) 。
o1
节圆(the pitch circle)：
r’1
发生线
K
当直线沿一圆周作相切纯滚 动时，直线上任一点的轨迹 AK，称为该圆的渐开线。
B
rb
定直线
基圆
A
k
O
二、渐开线的性质
发生线
(1)BK = A B
(2) BK为渐开线在K点的法 线，又因发生线恒切于基 圆，故知渐开线上任意点 的法线切于基圆。
(3)渐开线上点Ｋ的压力角 定义：啮合时K点正压
Vk
(5)基圆内无渐开线。
B2
B1
rb1
思考：10-20
K
KO2
o2 KO1 o1
三、渐开线方程式及渐开线函数
αk
k
rk是渐开线在任意点K的向径。当渐开线与 vk
r r cos 其共轭齿廓在K点啮合时，在三角形BOK
中
A
θk
b
K
渐开线齿轮的完整齿廓曲线方程及精确建模
渐开线齿轮的完整齿廓曲线方程及精确建模一、引言在机械设计领域中，渐开线齿轮被广泛应用于传动装置中。
它具有传动平稳、传动比准确、噪音小等优点，因此备受青睐。
为了更深入地了解渐开线齿轮，我们需要探索其完整齿廓曲线方程及精确建模。
二、了解渐开线齿轮1.渐开线齿轮的概念渐开线齿轮是一种特殊的齿轮，其齿廓曲线定义为齿廓曲线上任意一点到齿轮轴线的距离，均等于该点切线方向与齿轮轴线之间的夹角的正切值乘以该点到轴线的距离。
这种设计使得渐开线齿轮在传动过程中具有更加稳定的性能。
2.渐开线齿轮的应用渐开线齿轮被广泛应用于各种机械传动装置中，如汽车变速箱、工业机械设备等。
其传动平稳、传动比准确的特点，使其在高速、大扭矩传动系统中具有重要的地位。
对其完整齿廓曲线方程及精确建模的研究具有重要意义。
三、渐开线齿轮的完整齿廓曲线方程1.齿廓曲线方程的推导渐开线齿轮的完整齿廓曲线是由渐开线和圆弧段组成的，因此其完整齿廓曲线方程可以分段推导。
在渐开线段上，齿廓曲线可以表示为直线段，而在圆弧段上，齿廓曲线可以表示为圆弧段。
将两者组合起来，即可得到渐开线齿轮的完整齿廓曲线方程。
2.完整齿廓曲线方程的数学表达根据上述推导过程，我们可以得到渐开线齿轮的完整齿廓曲线方程，该方程包含了渐开线段和圆弧段的数学表达式。
这个方程的推导过程相对复杂，但是对于深入理解渐开线齿轮的齿廓曲线具有重要意义。
四、渐开线齿轮的精确建模1.建立渐开线齿轮的三维模型在实际应用中，我们需要对渐开线齿轮进行精确建模。
建立渐开线齿轮的三维模型是一个复杂而重要的工作，需要结合完整齿廓曲线方程，使用CAD软件进行精确建模。
2.精确建模的意义精确建模能够帮助工程师更全面、准确地了解渐开线齿轮的结构和性能特点，有助于优化设计，提高传动效率和可靠性。
五、个人观点和理解对于渐开线齿轮的研究，我深刻地认识到它在机械设计中的重要性。
作为传动装置的核心部件，渐开线齿轮的完整齿廓曲线方程及精确建模对于提高机械传动系统的性能至关重要。
齿形曲线
凡是满足齿廓啮合基本定律的一对齿廓称为共轭齿廓，论上可以作为共轭齿廓的曲线有很多种，但是考虑到设计、制造、测量、安装及使用等问题，目前常用的齿廓曲线有渐开线、摆线和圆弧等。
齿轮如果要能够有效率的传输动力就应该避免接触面的滑动摩擦而使用滚动摩擦. 在这个前提之下就不是所有的共軛曲线可以达成的. 其中最佳的就是渐开线与摆线. 这也就是为什么近代的齿轮都採用这两种设计的理由。
渐开线齿轮压力角在旋转的全程都为一定值. 这意味著渐开线齿轮的主动齿轮在推动从动齿轮个时候. 推动的力量与方向始终保持不变. 所以传输动力的大小相当稳定. 可是主动齿轮虽然保持著稳定的角速度. 但传到从动齿轮时虽然接触点通过每一齿的时间相同. (也就是每一齿的角速度相同). 但是在这一齿的角度中如果再分成10段. 则每一段的角速度就有差别。
所以如果把渐开线齿轮用在天文望远镜的角度调整上. 手调的主动齿轮为10齿. 旋转角度的被动齿轮为360齿. 那么在理论上手调的主动齿轮旋过1齿. 照理说从动应该转0.1度. 但实际上因为旋转的角度已经低于1齿. 因此角度并不正确. 这也就是为什么所有必须利用齿轮系精确调整角度的各种观测仪器仍然必须维持使用摆线齿轮的原因. 但是摆线齿轮的压力角在旋转中不稳定. 如果用来做为传动系统. 在每一齿的旋转传动中力量会忽大忽小. 不但造成转动的振动. 也对轴承造成伤害. 所以动力的传动都是使用渐开线齿轮. 渐开线齿轮的角速度稳不定. 而且齿数越少越严重. 因此渐开线齿轮很少低于16齿. 大动力机械传动用最小的我见过12齿. 传动不是那么重要的玩具一般不会低于9齿. 不过这只是传动考量的次要因素. 齿数越少的齿轮齿根越薄就越容易断裂.。
齿轮分类与齿形曲线及标准直齿轮
欲使两构件的角速比恒定，就必须 保证两定轴转动构件的相对速度瞬心 位置不变。
2
C
B
3
1
A
4
D
齿轮分类与齿形曲线及标准直齿轮
o
11 齿 vC1 1O1C
廓
1
vC2 2O2C
C
2 齿 廓2
o
2
齿轮分类与齿形曲线及标准直齿轮
1 O2C 2 O1C
o
11
齿 廓
vC1 1O1C
1
C
vC2 2O2C
Vk 渐 开
K 发生线
rK
线 A
K
K
o rb
B
基
直 线 BK 沿 半 径 为 rb 的圆作纯滚动时,直线上 任意一点K的轨迹称为该 圆的渐开线。该圆称为 渐开线的基圆
rb—基圆半径； BK—渐开线发生线 θK—渐开线上K点的展角
圆
齿轮分类与齿形曲线及标准直齿轮
2.渐开线方程式及渐开线函数 极坐标方程：
240
MATLAB
90 442.8202 60
332.1152
221.4101
30
110.7051
渐用 开 线
0
330
300 270
齿轮分类与齿形曲线及标准直齿轮
生 成 的
动画按钮
把一根绳子绕在一圆（基圆）外表面上， 随后绷紧一端并展开，则绳端轨迹为渐开线。
动画按钮
齿轮分类与齿形曲线及标准直齿轮
k F
2 齿 1 O2C
o
廓2 2 O1C
2
齿轮分类与齿形曲线及标准直齿轮
vC1 1O1C vC2 2O2C
1 O2C 2 O1C
齿轮分类与齿形曲线及标准直齿轮
齿轮的齿廓曲线
o1 r
n N1N2—啮合点的轨迹线
∴传力方向不变。 传力方向不变。
3、渐开线齿廓传动具有中心距可分性 ω1 n Q O N P ~ O N P ∵
or 1
b1
1
n
N2
rb 2
P
o2
N1
∴ i12
ω1 O2P = = ω2 O1P
1
2
2
ω2
O2N 2 rb 2 = = rb 1 O1N 1
可分性： 传动比虽然不变，啮合 可分性：当实际中心距与设计中心距 注： 传动比虽然不变， 略有变化， 略有变化，也不会影响两轮的传动比 参数将发生变化。 参数将发生变化。 这一特性称为渐开线齿轮的可分性. ,1
N1 kP k o2
n
ω2
1.两齿廓在K K 1.两齿廓在K点 点 为定点。 则当两齿廓在 P为定点。 2.当两齿廓在 当两齿廓在K 2.两齿廓在 啮合时, 啮合时 b1 啮合时, , r 啮合时, rP，b2不变 ω O 常数） ∴i = = = C(常数） 常数 N1ω 2—两齿廓的 N —仍为两齿 两齿廓的 仍为两齿 OP 结论： 共法线 结论：廓的共法线 渐开线齿廓能满 NNNN与OOOO的交点 1 1 2 2与 1 1 2 2的交 足定传动比传动。 足定传动比传动。 点为P. 点为 仍为P. 仍为P.P.
o1
n
K(K1,K2 )
ω1 O2 P i12 = = ω2 OP 1
P— 称为啮合节点， 称为啮合节点， 简称节点。 简称节点。 1.若 为定点， 1.若P为定点，i12=C 点的轨迹称为节圆。 P点的轨迹称为节圆。
VP
P n o2
ω2
2.若 为动点， =C， 2.若P为动点，i12=C，P点的轨迹称为 节线。 节线。
齿轮齿廓中最常用的曲线形式
齿轮齿廓中最常用的曲线形式齿轮是机械传动中常用的零件之一，广泛应用于各种机械设备中。
齿轮的齿廓形状对于传动效果和工作性能有着至关重要的影响。
在齿轮制造中，最常用的曲线形式是圆弧形和渐开线形。
圆弧形齿廓是最早应用于齿轮设计中的曲线形式。
它的特点是曲线简单、容易加工，但是在高速传动中会产生较大的动载荷和噪声。
由于不适合用于高速齿轮传动，因此在现代机械设计中用得相对较少。
与圆弧形齿廓相比，渐开线形齿廓更加常见也更加重要。
渐开线是一条特殊的曲线，它既要满足齿轮的传动功能，又要尽量减小传动中的冲突和噪声。
与其他曲线相比，渐开线形齿廓的独特之处在于，在齿轮接触和分离时会产生渐变的速度和压力分布，从而减小了传动中的冲突。
渐开线形齿廓的优点不仅仅体现在传动效果上，还有助于提高齿轮的使用寿命和传动效率。
首先，渐开线形齿廓减小了齿轮在接触过程中的压力和应力集中，避免了齿轮齿面的过早磨损和断裂。
其次，渐开线形齿廓减小了齿面接触的冲击和滑动，减少了能量损失，提高了传动效率。
为了生成渐开线形齿廓，需要选择适当的齿廓参数，如渐开线系数和压力角。
渐开线系数是描述渐开线形状的重要参数，它决定了渐开线齿廓的弧度变化率。
渐开线系数越大，齿轮的齿廓形状越渐进，接触过程中的冲击和噪声越小。
压力角是描述齿轮传动时齿面受力的角度，它对齿轮的强度和传动效果有着重要影响。
常用的压力角有20度和14.5度两种，其中20度压力角的齿轮传动更常见。
在实际齿轮制造中，为了保证齿轮的精度和稳定性，通常采用渐开线形齿轮副。
这种齿轮副不仅能够实现稳定的传动效果，还能够减小齿轮的噪声和振动。
与此同时，渐开线形齿廓也可以通过工艺优化和制造精度的提高来进一步改善齿轮的传动性能。
综上所述，齿轮齿廓中最常用的曲线形式是渐开线形和圆弧形。
其中，渐开线形对于齿轮传动的效果和性能有着重要影响，能够减小冲突和噪声，提高使用寿命和传动效率。
在齿轮制造中，选择适当的齿廓参数和制造工艺，可以进一步优化渐开线形齿轮副的传动性能。
齿轮的分类与齿形曲线（精品）
齿轮的分类与齿形曲线（精品）
第五章齿轮机构
齿轮传动机构的特点
（1）直接接触的啮合传动；可传递空间任意两轴之间的运动和动⼒；
（2）功率范围⼤，速⽐范围⼤，效率⾼，精度⾼；（3）传动⽐稳定，⼯作可靠，结构紧凑；（4）改变运动⽅向；
（5）制造安装精度要求⾼，不适于⼤中⼼距，成本较⾼，且⾼速运转时噪声较⼤。
平⾯齿轮机构空间齿轮
齿轮的分类
1。
直齿圆柱齿轮2。
斜齿圆柱齿轮3。
⼈字齿轮
4。
蜗轮蜗杆
5。
圆锥齿轮
内齿轮
齿条
齿轮机构的作⽤
两轴平⾏
两轴相交两轴交错齿轮齿条
单击图像可播映动画
直齿⼈字齿斜齿圆柱齿轮
单击图像可播映动画
直齿圆柱齿轮内齿轮外齿轮齿轮齿条
单击图像可播映动画
圆锥齿轮传动
直齿斜齿曲线齿
单击图像可播映动画
两轴交错齿轮传动蜗轮蜗杆准双曲⾯齿轮交错轴斜齿轮单击图像可播映动画
11
112
2
z 360
1z 3602
112
2
z z 360
o 1?z z 360o
2?3
434?1?1
22
z z t t i 1
22
21121
12=??=
ωω=1122z z 360
o 1?z z 360
o
2
34
3
4?1?1?2?2
12
3 4
1
2
341
24
3A
C D A B
C D
1
2
341
24
3A
C D A B
C D。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论上，满足齿廓啮合定律的曲线有无穷多，但考虑到便于制造
和检测等因素，工程上只有极少数几种曲线可作为齿廓曲线，如渐 开线、其中应用最广的是渐开线，其次是摆线(仅用于钟表)和变态 摆线。(摆线针轮减速器)，近年来提出了圆弧和抛物线。
渐开线齿廓的提出已有近两百多年的历史，目前还没有其它曲线可以替代。
渐开线具有很好的传动性能，而且便于制造、安
§10－2 齿轮的齿廓曲线
o1
传动比：i主从=ω主/ω从
ω1
1.齿廓啮合基本定律
n
根据三心定律可知：P点为相对瞬心。 v12
k
由： v12 ＝O1P ω1 ＝O2P ω2 得： i12 ＝ω1/ω2＝O2P /O1P
P n
ω2
齿廓啮合基本定律(fundamental law
o2
of gearing):
发生线
K
当直线沿一圆周作相切纯滚 动时，直线上任一点的轨迹 AK，称为该圆的渐开线。
B
rb
定直线
基圆
A
k
O
6
7
二、渐开线的性质
发生线
(1)BK = A B
(2) BK为渐开线在K点的法 线，又因发生线恒切于基 圆，故知渐开线上任意点 的法线切于基圆。
(3)渐开线上点Ｋ的压力角 定义：啮合时K点正压
rb
K K
可得渐开线的极坐标方程式：
rKrb/cosK
K in K v t g K K
例10-21 11
例10-21
12
四 、 渐开线齿廓的啮合特性
O1
ω1
1.渐开线齿廓满足定传动比要求(the
N1
transmission ratio is constant)
K
两齿廓在任意点K啮合时，过 K点处两齿廓的公法线必然同时与
Σ2
(5)基圆内无渐开线。
B2
B1
rb1
思考：10-20
K
KO2
o2 KO1 o1
三、渐开线方程式及渐开线函数
αk
k
rk是渐开线在任意点K的向径。当渐开线与 vk
rr cos 其共轭齿廓在K点啮合时，在三角形BOK
中
A
θk
rk αk
B
பைடு நூலகம்
bK
K
rb
O
)
tan K
BK rb
AB rb
rb(K K)
Vk
k K
Fn rk
NB rb k k
KA0
力方向与速度方向所夹锐角
O
为渐开线上该点之压力角
αk(pressure angle)。
基圆
rb＝rk cosαk
离中心越远，渐开线上的压力角
越大。基圆上的压力角为0。
(4)渐开线形状取决于基圆 基圆越大，渐开线越平直，
当rb→∞，变成直线。
Σ3 Σ1
轮齿介于分度圆与齿顶圆之间的部分 称为齿顶，其径向高度称为齿顶高，
13
a a'
2、中心距的可分离性
•渐开线齿廓啮合的中心距可 变性——— 当两齿轮制成后， 基圆半径便已确定，以不同的 中心距(a或a')安装这对齿轮， 其传动比不会改变。对加工和 装配很有利。
i1 2
1 2
o2c o1c
rb 2 rb 1
i1' 2
1
' 2
o
' 2
c
'
o1c '
rb 2 rb 1
N2
3
Involutes(渐开线) gears
4
凡能按预定传动比规律相互啮合传动的一对齿廓称为共轭齿廓。一
2.齿廓曲线的选择 般说来，对于预定的传动比，只要给出一轮的齿廓曲线，就可根据 齿廓啮合基本定律求出与其啮合传动的另一轮上的共轭齿廓曲线。 渐开线(involutes) ——应用最广
摆线 圆弧 抛物线
互相啮合的一对齿轮在任一位置时的传动比，
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数，则应使O2P/O1P为常数。
由于O2 、O1为定点，故P必为一个定点，称为节点
(the pitch point) 。
o1
节圆(the pitch circle)：
r’1
N2
K’
P C2 C1
两齿廓基圆相切，又因基圆为定圆， rb2
其为定直线。
ω2
两轮中心连线也为定直线，故
O2
交点P必为定点。
i12=ω1/ω2=O2P/O1P=rb2/rb1 =const
工程意义：i12为常数可减少因速度变化所产生的附 加动载荷、振动和噪音，延长齿轮的使
用寿命，提高机器的工作精度。
N2'
1
o1
N1 N1' c
c'
ЗЗ
o2
2
o'2
'
由于上述特性，工程上广泛采用渐开线齿廓曲线。
3.齿廓间正压力方向不变
N1N2是啮合点的轨迹，称为 啮合线(the trajectory of contact) 由渐开线的性质可知：
啮 合 线 又 是 接 触 点 的 法 线 ，N2
O1 ω1
N1 α’ K K’ P C2 C1
为了便于计算齿轮各部分尺寸，在齿 轮上选择一个圆作为尺寸计算基准，
称该圆为齿轮的分度圆。
p
同一圆上
se ha h hf
齿距 (周节)—— pk= sk +ek 同侧齿廓弧长
B pk
sk
ek
pn
pb
rb
rf r ra
法向齿距(法节) —— pn = pb(基节)
齿宽(face-width)—— B
O
一、外齿轮(external gear)
1.名称与符号
分度圆（d 和 r）
齿距pk 齿厚sk 齿槽宽ek 分度圆 齿顶圆
齿顶圆（da 和 ra）
齿根圆（df 和 rf） 齿顶高ha
基圆 齿根圆
基圆（db 和 rb）
齿数 厚sk
z齿齿距槽pk宽ek齿
齿根高hf
rf rb
ra rk
o
pk sk ek
基节pb=法节pn
ω1
设想在P点放一只笔，则笔尖 节圆 在两个齿轮运动平面内所留轨迹。 a
n k
两节圆相切于P点，且两轮节 点处速度相同，故两节圆作纯滚 动(rolling without slipping)。
中心距： a=r’1+r’2
P n
ω2 r’2
o2
凡能按给定传动比规律相互啮合传动的一对齿廓称为
共轭齿廓
2
2.齿廓曲线的选择 凹凸圆弧齿轮啮合
正压力总是沿法线方向，故其传
力方向不变。这对于传动的平稳 rb2
性是有利的。
ω2
啮合线与节圆公切线之间的夹角α’ ， O2
称为啮合角(working pressure angle)
实际上α’ 就是节圆上的压力角
注意！！啮合线、啮合点的公法线和基圆的内公切
线三线合一
15
§10－4 渐开线齿轮基本参数和几何尺寸
装(manufactured and assembled easily)、测量和互换使用等 优点。因此它的应用最为广泛，故本章着重介绍渐开 线齿轮(involutes gears)。
5
§10－3 渐开线齿廓及其啮合特性
一、 渐开线的形成(Generation of Involutes)和特性
(1)渐开线的形成