图纸-A4三齿摆线齿廓
第八章齿轮机构案例

§8-1 齿轮传动的特点和基本类型
一、齿轮传动的特点
优点:1)传动效率高 2)传动比恒定 3)结构紧凑 4)工作可 靠、寿命长 缺点:1)制造、安装精度要求较高 2)不适于中心距a较大两轴 间传动 3)使用维护费用较高 )精度低时、噪音、振动较大 二、齿轮传动的主要类型 平面齿轮机构: ①外啮合;②内啮合; 直齿圆柱齿轮机构(直齿轮)—— ③齿轮齿条 平行轴斜齿轮机构(斜齿轮):①外;②内;③齿轮齿条 空间齿轮机构: 圆锥齿轮机构—— ①直齿;②斜齿;③曲线齿 交错轴斜齿轮机构 蜗杆机构:两轴垂直交错
二、标准齿轮的基本参数 1、模数m
d zp
d p
分度圆就是齿轮上 具有标准模数和标 准压力角的圆。
p
z
定义模数 m
或
p m
∴d=mz 单位:mm ; 2、分度圆压力角α
rK rb cos K
m标准化。
分度圆和节圆区别 与联系
rb r cos
mz cos (α 是决定渐开线齿廓形状的一个基本参数) 2
O P r r i12 1 2 2 b 2 常数 2 O1 P r1 rb1
Ⅰ
1 r'1
O1
rb1 g' 2
' N1 P g2 g' 1 rb2 r'2 K g1 ' t
t II N2
' 2 O2
§8-4 渐开线标准齿轮的各部分名称和几何尺寸
一、齿轮各部分名称和基本参数
GB1356-88规定标准值α=20° 某些场合:α =14.5°、15°、22.5°、25°。
3、齿数z
d mz 表明:齿轮的大小和渐开线齿轮 mz rb cos 2 形状都与齿数有关
齿轮齿形的圆弧近似画法
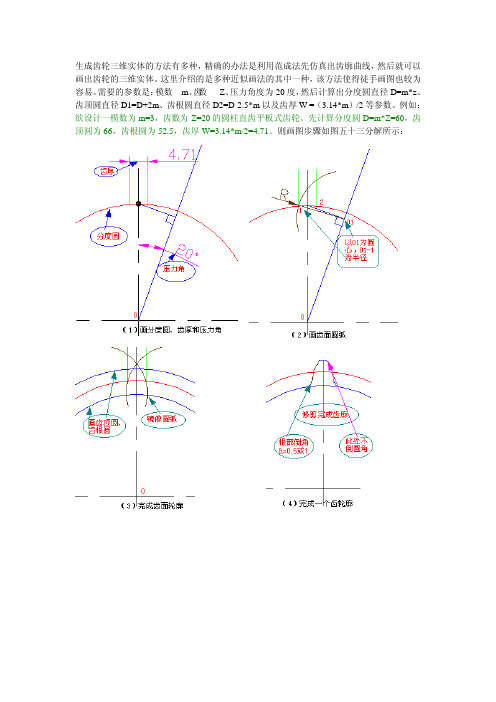
生成齿轮三维实体的方法有多种,精确的办法是利用范成法先仿真出齿廓曲线,然后就可以画出齿轮的三维实体。
这里介绍的是多种近似画法的其中一种,该方法使得徒手画图也较为容易。
需要的参数是:模数—m、齿数—Z、压力角度为20度,然后计算出分度圆直径D=m*z、齿顶圆直径D1=D+2m、齿根圆直径D2=D-2.5*m以及齿厚W =(3.14*m)/2等参数。
例如:欲设计一模数为m=3,齿数为Z=20的圆柱直齿平板式齿轮。
先计算分度圆D=m*Z=60,齿顶圆为66,齿根圆为52.5,齿厚W=3.14*m/2=4.71。
则画图步骤如图五十三分解所示:
图五十三三维齿轮的生成。
摆线轮齿廓逆向设计的仿真加工

n 次曲线拟合
i
此线性方程组求解, 得到拟合函数的系数 α k , 从而
齿廓曲线参数方程可以表示为式 (1) :
-1 / 2
ìx a = ( R z -r z ·S ) cos [ ( 1 -i H ) φ ] -
[6]
i=1
以上是关于 α 0 、 α 1 、......、 α m 的线性方程组, 对
2
(3)
如果 想 要 得 到 式 ( 2) 中 的 系 数 α k ( k = 0, 1,
2,......, n) , 那么 令 其 偏 差 平 方 和 最 小 即 可。 由 式
(2) 和式 (3) 可得, δ 是关于 α k 的函数, 想要让偏
差的平方和 δ 最小, 只要令 δ 对 α k 的偏导数为 0 即
SU Jianxin,KONG Lingju,GUO Hao. Simulation processing for reverse design of cycloid gear profile [ J] . Machine
Tool & Hydraulics,2021,49(12) :141-145.
算出来, 所以需要用曲线拟合得到一个函数 L( x) 来
描述数据 点 x i 与 之 对 应 函 数 值 y i 之 间 的 联 系, 令
L( x) 在各测量点处函数值 L( x i ) 与 f( x i ) 两者间偏差
尽可能地小。
设拟合函数为一 n 次多项式, 即
L( x) =
∑α x
m
k=0
k
(2)
E-mail:kfb@ mail haust edu cn。
· 142·
业迅速得到发展从而不再受国外制约。 利用逆向工程
机械制图课件-齿轮

齿轮
通过齿轮间的啮合可以实现:
1.传递动力
2.改变运动速度
3.改变运动方向
常见的齿轮传动的形式有:
1.圆柱齿轮传动——两齿轮轴线平行
2.圆锥齿轮传动——两齿轮轴线相交
3.蜗轮蜗杆传动——两齿轮轴线交叉
(点击图形演示动画)齿轮传动的基本知识
齿轮传动的形式还有:
1.齿轮齿条传动——将旋转运动变为直线运动
2.内啮合齿轮传动——适用于轴间距离小,结构更
紧凑的传动
(点击图形演示动画)齿轮传动的基本知识
圆柱齿轮的轮齿均匀分布在圆柱面上,有直齿、斜齿和人字齿。
(点击图形演示动画)
圆柱齿轮的轮齿有标准与变位之分,凡轮齿符合标准规定的为标准齿轮。
在标准基础上轮齿作某些改变的即为变位齿轮。
1.直齿圆柱齿轮的规定画法
⑴单个齿轮的画法
齿顶圆(齿顶线)—粗实线
分度圆(分度线)—细点画线
齿根圆—细实线(可省略)
轮齿按不剖绘制齿轮其余部分按其投影绘制
⑵啮合齿轮的画法
齿轮啮合画法同单个的画法类似,作图时只是注意以下两点:
1.两啮合齿轮的分度圆应相切
2.啮合区中有一齿轮的齿顶线为虚线
2、斜齿圆柱齿轮的画法:
斜齿轮的画法和直齿轮相同,只是用三条与齿向相同的细实线表示螺旋线的方向。
斜齿圆柱齿轮的啮合画法:。
第6章 轮系

第6章轮系本章主要介绍轮系的分类和应用,轮系传动比的计算方法。
由单对齿轮组成的齿轮机构功能单一,不能满足工程上的复杂要求,故常采用若干对齿轮,组成轮系来完成传动要求。
按轮系运动时轴线是否固定,将其分为两大类:(1)定轴轮系轮系运动时,所有齿轮轴线都固定的轮系,称为定轴轮系,如图1-1所示。
(2)行星轮系轮系运动时,至少有一个齿轮的轴线可以绕另一根齿轮的轴线转动,这样的轮系称为行星轮系。
轴线可动的齿轮称为行星轮,如图1-2中轮2,它既绕本身的轴线自转,又绕O1或O H公转。
轮1与轮3的轴线固定不动,称为太阳轮。
图1-1图1-21.1 定轴轮系定轴轮系分为两大类:一类是所有齿轮的轴线都相互平行,称为平行轴定轴轮系(亦称平面定轴轮系);另一类轮系中有相交或交错的轴线,称之为非平行轴定轴轮系(亦称空间定轴轮系)。
轮系中,输入轴与输出轴的角速度或转速之比,称为轮系传动比。
计算传动比时,不仅要计算其数值大小,还要确定输入轴与输出轴的转向关系。
对于平行轴定轴轮系,其转向关系用正、负号表示:转向相同用正号,相反用负号。
对于非平行轴定轴轮系,各轮转动方向用箭头表示。
1.1.1 平行轴定轴轮系图1-1所示为各轴线平行的定轴轮系,输入轴与主动首轮1固联,输出轴与从动末轮5固联,所以该轮系传动比,就是输入轴与输出轴的转速比,其传动比i求法如下:(1)由图1-1所示轮系机构运动简图,可知齿轮动力传递线为:(1—2)=(2′—3)=(3′—4)=(4—5)上式括号内是一对啮合齿轮,其中轮1、2′、3′、4为主动轮,2、3、4、5为从动轮;以 “—”所联两轮表示啮合,以“=”所联两轮同轴运转,它们的转速相等。
(2) 传动比i 的大小()4543321245342312354433221511i i i i z z z z z z z zn n n n n n n n n n i ⋅⋅⋅=⋅⋅⋅-=⋅⋅⋅=='''''' 上式表明,该定轴齿轮系的传动比等于各对啮合齿轮传动比的连乘积,也等于各对啮合齿轮中各从动轮齿数的连乘积与各主动轮齿数的连乘积之比,其正负号取决于轮系中外啮合齿轮的对数。
齿画法

二、圆柱齿轮规定画法1.单个圆柱齿轮的画法国家标准对齿轮画法作了统一规定。
单个圆柱齿轮的画法见图6-14。
齿顶圆和齿顶线用粗实线画出;齿根圆和齿根线用细实线画出,也可省略不画;分度圆和分度线画点画线。
但取剖视后齿根线画粗实线,轮齿部分不画剖面线,其余结构按结构真实投影画。
对于斜齿轮,在非圆外形图上用三条平行的细实线表示斜齿方向,如图6-14c所示。
图6-15为圆柱齿轮零件图。
(a)外形(b)全剖 (c)半剖(斜齿)图6-14 单个圆柱齿轮画法图6-15 圆柱齿轮零件图2.圆柱齿轮啮合的画法两模数相同的齿轮才能相互啮合。
两标准齿轮相互啮合时,它们的分度圆处于相切位置,这时分度圆又称节圆。
画齿轮啮合图时,一般采用圆的视图(端面视图)和非圆的视图(轴向视图)。
在圆的视图中,按规定分别画出齿根圆,分度圆和齿顶圆三个圆,两分度圆应相切。
采用简化画法时,允许不画齿根圆,啮合区内齿顶圆也不画,如图6-17b、c。
在非圆的视图中,如未剖切,则在分度圆的相切处画一条粗实线,如图6-17d、e。
在剖视图中,当剖切平面通过两啮合齿轮的轴线时,在啮合区内,将一个齿轮的轮齿用粗实线绘制;另一个齿轮的轮齿被遮挡的部分用虚线绘制(也可省略不画)。
由于齿顶高和齿根高不相等,故一轮齿的齿顶线与其啮合的另一轮齿的齿根线间有0.25m的径向间隙,如图6-16所示。
图6-16 齿轮啮合投影(a) (b) (c) (d) (e)图6-17 圆柱齿轮啮合图本页是2/4页三、直齿圆锥齿轮画法1.单个圆锥齿轮的画法主视图画成剖视,左视图用粗实线画大端、小端的齿顶圆;用点画线画出大端分度圆,齿根圆不必画出,见图6-18。
图6-18 单个圆锥齿轮各部分名称及画法2.圆锥齿轮啮合时的画法圆锥齿轮啮合时,两分度圆相切,锥顶交于一点。
两锥齿轮啮合画法见图6-19。
图6-19 锥齿轮啮合画法本页是3/4页四、蜗轮蜗杆画法蜗轮蜗杆用于两轴垂直交叉时的传动,蜗杆为主动件、蜗轮为从动件,蜗杆常用单头或双头(蜗杆上齿数称为头数,相当螺杆上螺纹线数),也就是说蜗杆转一圈或两圈,蜗轮转过一个齿或两个齿。
摆线齿轮展成法原理

摆线齿轮展成法原理摆线齿轮是一种独特的齿轮类型,具有非圆齿形。
其展成法原理涉及将齿形从摆线齿轮的外齿廓展成平面上的直线段。
展成步骤展成摆线齿轮的过程涉及以下步骤:1. 确定参考圆:第一个步骤是确定齿轮的参考圆,它是齿轮外齿廓上一个任意半径的圆。
2. 创建摆线:沿参考圆的圆周运动一个点,形成一个称为摆线的闭合曲线。
3. 构造外齿廓:摆线形成齿轮的外齿廓,与参考圆相切。
4. 展成平面:将摆线齿廓沿参考圆半径展成平面。
这一步将齿形从圆形转变成直线段。
展成直线段展成过程中,摆线的每个点都被展成一条从参考圆中心发出的直线段。
直线段的长度等于摆线点的弧长。
齿廓特征展开后的齿廓具有以下特征:它由一系列直线段组成。
每条直线段与齿根圆相切。
直线段的长度随参考圆半径的增加而增加。
应用摆线齿轮展成法广泛应用于各种工程应用中,包括:平面印刷机:摆线齿轮展成法用于产生均匀的油墨分布。
卧式铣床:展成齿形用于生成复杂轮廓的精密零件。
复印机和扫描仪:展成齿廓用于实现精确的纸张进纸和成像。
汽车转向系统:摆线齿轮展成法用于制造具有平稳转向性能的齿条。
优点摆线齿轮展成法提供以下优点:简单性和准确性:展成过程简单且准确,可生成精确的齿形。
均匀运动:展成齿形提供均匀的运动,消除了振动和噪音。
高强度:直线段齿廓具有高强度,使其适用于高负荷应用。
通用性:展成法适用于广泛的齿轮尺寸和材料。
总体而言,摆线齿轮展成法是一种强大的技术,用于将摆线齿形准确地展成平面直线段。
其应用广泛,生产出具有所需属性和性能的齿轮。
双摆线针齿传动的齿廓特性与啮合特性分析

2024年第48卷第2期Journal of Mechanical Transmission双摆线针齿传动的齿廓特性与啮合特性分析陆鑫浩1白国振1崔建昆2张德琪1丁佳乐1(1 上海理工大学机械工程学院,上海200093)(2 上海理工大学上海-汉堡国际工程学院,上海200093)摘要为了解决传统的摆线针齿传动输出结构易损坏、结构复杂等问题,将内、外摆线齿廓运用到NN型少齿差行星齿轮传动领域,提出了一种新型的摆线针排齿轮,并进行了其齿廓特性和啮合特性分析。
对摆线轮的齿廓方程、压力角进行公式推导,分析了齿廓参数对压力角的影响,为该新型传动系统的应用奠定基础;对不同齿廓修形方法下的内外摆线齿轮进行参数方程推导,并利用Matlab软件进行仿真分析,以解决由于润滑黏膜、制造误差等一系列原因所产生的啮合间隙问题;最后,对双摆线针齿传动进行力学特性分析,为后续的减速器设计和有限元分析提供了理论基础。
研究对开发新的传动方式具有意义和工程使用价值。
关键词摆线齿轮少齿差传动啮合特性齿廓特性Analysis of Tooth Profile Characteristics and Meshing Characteristics of DoubleCycloid Needle Tooth TransmissionLu Xinhao1Bai Guozhen1Cui Jiankun2Zhang Deqi1Ding Jiale1(1 School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)(2 Shanghai-Hamburg College, University of Shanghai for Science and Technology, Shanghai 200093, China)Abstract In order to solve the problems of the traditional output structure of the cycloid pinion transmission, such as easy damage and complex structure, a new type of cycloid pinion gear is proposed by applying the internal and external cycloid tooth profile to the field of NN-type less differential planetary gear transmission, and the analysis of its tooth profile characteristics and meshing characteristics is carried out. The equations of the tooth profile equation and pressure angle of the cycloid are derived, and the influence of the tooth profile parameters on the pressure angle is analyzed to lay the foundation for the application of this new transmission system. The parameter equations of the inner and outer cycloid gears under different tooth profile modification methods are derived, and the simulation analysis is carried out using Matlab software to solve the meshing gap problem due to a series of reasons such as lubrication mucosa and manufacturing errors. Finally, the mechanical characteristics of the double cycloid needle gear transmission are analyzed, which provides a theoretical basis for the subsequent design of the reducer and finite element analysis. This study has significance and engineering use value for the development of new transmission methods.Key words Cycloid gear Less differential gearing Meshing characteristics Tooth profile characteris⁃tics0 引言随着科学技术的发展,齿轮传动技术有了很大的进步。
