使用matlab计算长周期光纤光栅的有效折射率
光栅原理及MATLAB仿真

取样光纤光栅的原理及基于MATLAB 的反射谱仿真取样光纤光栅其实与相称光纤光栅基本上一致,不同的地方在于,相移光栅是在均匀布拉格光栅的某一点处引入相移,导致在反射谱中新开出了一个或者多个窗口,窗口的多少与光栅的相移点的多少有关,取样光栅在结构上与此相似,一段均匀布拉格光栅后接一段正常光纤,正常光纤的作用引起一定的相移,因而其反射谱呈现出梳状结构,在反射窗口中打开一个个通道。
通道的个数以及通道间隔,反射率的大小与取样的周期、光栅长度、折射率调制深度等相关。
取样光栅的结构如图:图1 取样光栅的结构图光栅长度为p ,光栅与光栅之间的间隔为q ,整个取样周期为d p q =+,取样点为:/k L d =,占空比为/p d ;取样光栅的梳状谱被sinc 函数调制,sinc 函数为:12()sin [()]2A B zf z c L=,L 指整个光栅的长度,AB 均为常数,若占空比满足一定条件时,类似于平面光栅,会出现缺级现象。
取样光栅的调制函数为:()()()s f z f z s z =(1)其中:2()[1cos()]f z n π=∆+Λ,()()p s z g z md ∞-∞=-∑ 对(1)进行付立叶变换,()s f z 的付立叶变换等于()f z 和()s z 卷积。
进行付立叶变换以后的频域上的表示可得到其取样光栅的匹配条件:22/2/0m d βππ-Λ-= (2) 用有效折射率表示为:20, 1....1eff m n m md λΛ==±Λ+ (3)由此可以得出取样光栅的反射谱由几个峰组成,而且可以计算出相邻两个峰之间的波长间隔。
对于每一个峰,所对应的传播常数以及有效折射率都不同。
设两个相邻的峰其传播常数为:1β、2β,以及其有效折射率分别为:1eff n 、2eff n , 由上式得知:12d πββ-=(4)带入得:201212022eff eff n d n d dλλλλλλλ∆Λ∆=-=≈= (5)d 为取样周期,可得,取样周期越大,波长间距越小。
关于镀膜长周期光纤光栅“模式转换”的新认识

关于镀膜长周期光纤光栅“模式转换”的新认识顾铮■;冯文斌【期刊名称】《光子学报》【年(卷),期】2018(47)6【摘要】依据包层模有效折射率的概念及包层模场的光功率密度分布,重新审视了镀膜长周期光纤光栅"模式转换"现象,对"模式转换"给出了新的物理图像.通过修正镀膜长周期光纤光栅包层模有效折射率的范围,指出有效折射率呈现的台阶式增长是各次包层模自身属性的反映,不存在高次模式替代低次模式的过程,并将"模式转换区"重命名为"模式垒区".通过分析包层模场的光功率密度分布,指出"模式转换区"较低次包层模式进入薄膜层传输说法的不合理性.研究表明,当薄膜厚度达到一定厚度时,包层模场光功率分布将愈加集中在薄膜层内部,但并非沿着薄膜层传输.讨论了镀膜长周期光纤光栅传感器薄膜参数优化的问题,在修正的包层模有效折射率范围和未修正的包层模有效折射率范围的情况下分别进行优化,并对优化结果进行比较,结果表明两种情况下的优化结果存在较大的偏差.从机理上解释了修正薄层模有效折射率范围后的优化结果的正确性,为设计高灵敏镀膜长周期光纤光栅传感器提供了新的理论指导.【总页数】9页(P66-74)【关键词】光纤光学;镀膜长周期光纤光栅;模式转换;有效折射率;功率密度分布;灵敏度【作者】顾铮■;冯文斌【作者单位】上海理工大学理学院光电功能薄膜实验室【正文语种】中文【中图分类】TN253【相关文献】1.镀膜参数对长周期光纤光栅传感特性的影响 [J], 周容卉;2.基于模式转换及双峰谐振效应的薄包层镀膜长周期光纤光栅特性研究 [J], 蓝锦龙;顾铮一先3.镀膜参数对长周期光纤光栅传感特性的影响 [J], 周容卉4.镀膜双包层螺旋长周期光纤光栅传感特性 [J], 田丹丹;刘云启5.基于长周期光栅的少模光纤模式转换器研究 [J], 靳云;陈茁因版权原因,仅展示原文概要,查看原文内容请购买。
基于长周期光纤光栅的折射率传感器

tmp rt r o p n aina d h w o i r v e s gs n i vt n e sn a g .Ad a tg sa dds d a ~ e e au ecm e s t n o t o mp o esn i e st i a ds n ig rn e n i y v n a e n i v n a
sr c u e e i e ,t e r ih y s n i v h x e n l e r c ie i d x wh c k s t eLP e y s i b e tu t r ;b s s h y a eh g l e s ie t t ee t r a fa t e ih ma e h Gsv r u t l d t o r v n a f re vr n e t r fa t e i d x s n o s o n i m n e r c i n e e s r .Th a i p i cp eo e r c ie i d x s n i g o Gsi s mma i d o v e b sc r il n r fa t n e e sn f n v LP s u rz e a d t e r c n e e r h so e r c i e i d x s n i g b s d o Gs a e r v e d n h e e tr s a c e n r fa t n e e sn a e n LP r e iwe .Cu r n e e r h f c s so v r e t r s a c o u e n
维普资讯 http://www.cqvip源自com第2 3卷第 4期
20 0 8年 8月
£乙 一臼
光 电 技 术 应 用
, OGJ AP LI A T ON ( , P C I
长周期光纤光栅折射率传感的研究概况

不断积累经验 。 对其进行补充和完善。 ( 作者单位: 门市 电信 分公 司) 厦
查: 在不同媒体上公布不同咨询号码 或有奖调查热
维普资讯
究
明 P L G对于温度的调协范围约为 F G的 7 . B 倍 而 对于外界折射率变化时的谐振峰 中心波长移动量 也明显高于布喇格光栅。由光纤场分布形式可知 . 光纤 对 于包层 模 的束 缚性 较 芯模 为 弱 . 阶模 的束 高
访 问 、 截 访 问 、 户 访 问 、 函调 查 )实 验 室 测 拦 入 回 、
试、 组合测试等多种 ; 我们可以通过与市场调查公 司长期合作 。 开展全年持续的广告效果调查 , 包括 事前调查以有效选择广告案 、 事中调查以及时调整 广告发布的计划 、事后调查以总结经验评估效果 ; 也可通过多种与客户互动的渠道开展市场调查。 例
L G的周期通常为几十到几百微米 。 P 主要特性是将 导波中某频段 的光耦合到光纤包层 中损耗掉 , 是一 种透射型光纤器件。 P L G对于温度 、 应力、 外界折射
率等 参 数 的 变化 都 有很 高 的响 应灵 敏 度 。研究 表
想和品牌态度。 因此品牌效果主要从这三方面来评 估。 品牌意识方面 , 主要包括到达率和品牌知名度 、 品牌识别率等指标 。品牌联想方面 。 主要包括品牌 形象评价和品牌理解力等指标 。品牌态度方面 , 主 要包括美誉度 、 偏好度 、 忠诚度 、 渗透率等指标。这 些指标 一般 具 有动 态 分 析 和静 态 分 析 两个 方 面 的
维普资讯
究
长周期光纤光栅
折射 率传感 的研究
李杰 由光栅 周 期 的不 同 . 纤 光栅 可 分为 布喇格 光 光 纤光栅 (B 和长 周 期光 纤光 栅 (P 。 B 的周 F G) L G) F G 期约 为几 百纳 米 . 主要特 性 是将 某 一频 段 的光 反射 回去 。形 成 以谐振 波长 为 中心 的 窄带 光学 滤波 器 ,
光纤光栅设计过程描述
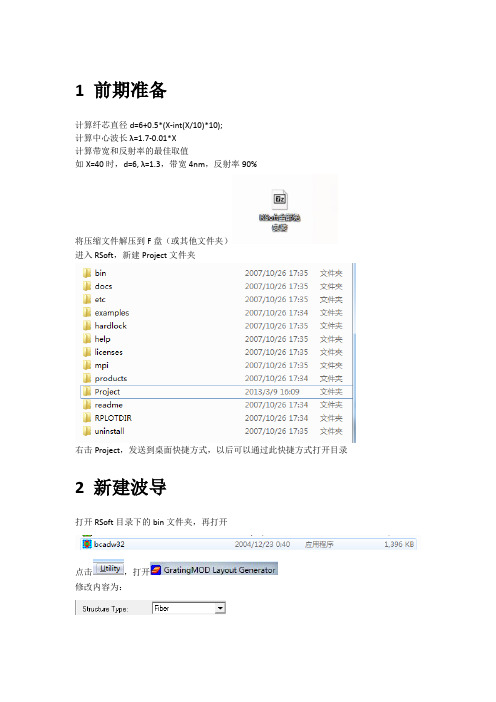
1 前期准备计算纤芯直径d=6+0.5*(X-int(X/10)*10);计算中心波长λ=1.7-0.01*X计算带宽和反射率的最佳取值如X=40时,d=6, λ=1.3,带宽4nm,反射率90%将压缩文件解压到F盘(或其他文件夹)进入RSoft,新建Project文件夹右击Project,发送到桌面快捷方式,以后可以通过此快捷方式打开目录2 新建波导打开RSoft目录下的bin文件夹,再打开点击,打开修改内容为:包层折射率为1.45修改成纤芯直径d的值这一项是输出波导文件名修改结果如下:将文件另存为至Project文件夹点击左侧的修改内容为:这一项指中心波长修改结果如下修改内容为:修改结果如下点击按照下图修改点击得到下图记下,这个是周期,以后还是要修改的重新运行修改内容为:修改结果如下运行,得到下图点击上图中的File,Export Graph,选择有BMP的一项(以后图片都这么输出,或者你也可以选择用截图工具直接截图)上图中指带宽,单位是微米,指反射率3 波导优化,主要是调制深度和波导长度的扫描变量ModDelta指调制深度变量Length指波导长度重新运行修改内容为:点击左侧按下图修改其中ModDelta是调制深度,Starting Vaule是循环初始值,Ending Value是循环结束值,Increment是循环增量,search1是输出文件名打开Project文件夹打开search.scn本文档中要寻找带宽4nm,反射率90% 的一行由于文档中的带宽都比目标值要小,需要放宽范围本文档修改范围后如下图所示(请自行修改合适的范围)更新后的search.scn如下重新扫描变量(点击)此时调制深度作为内循环变量,以0.004为中心放宽至0.003-0.005波导长度(Length)作为外循环变量,以500为初始值,3000为终值,500为循环增量循环完成后在Project文件夹中会生成以下文件依次打开scn文件其中scn文件中的格式仍然是:调制深度带宽(微米)反射率查看其中反射率最接近目标值的一行本文中找到的数据均不符合要求,放大范围本文的修改结果如下:在search1_c中找到比较接近的一行由search1_c可知,在Length循环到第三次的时候取到反射率最接近目标值由循环设置可得到Length的值为200由知,ModDelta(调制深度)取0.005时反射率最接近目标值由于带宽0.004973um与目标带宽仍有较大误差需要再次扫描本文档修改范围后如下图所示:在search1_d找到带宽和反射率较接近目标值的一行由下图可以看书,在相同长度下,ModDelta增大时,带宽、反射率可以近似看做同比例增大这里带宽和反射率都比目标值要大,可以将ModDelta向较低值修改再次修改循环范围后如下图所示:扫描结果后search1_d中的已经非常接近目标此时ModDelta取0.0039,Length取250时,最符合设计指标再进一步缩小范围,减小循环增量,能得到更加符合设计指标的一行。
光栅 衍射 matlab

光栅衍射 matlab在Matlab中进行光栅衍射模拟是通过数值方法来实现的,其中使用了光栅的传输函数和衍射公式。
以下是一个简单的Matlab示例,演示了光栅衍射的基本步骤。
% 定义常数wavelength = 0.5e-6; % 波长(米)grating_period = 2e-6; % 光栅周期(米)grating_opening_ratio = 0.5; % 光栅开口比% 定义空间参数x_max = 10e-6; % x轴范围y_max = 10e-6; % y轴范围Nx = 500; % 离散点数目Ny = 500; % 离散点数目x = linspace(-x_max, x_max, Nx);y = linspace(-y_max, y_max, Ny);% 生成光栅传输函数grating_transmission = zeros(Nx, Ny);for i = 1:Nxfor j = 1:Nyif mod(i, grating_period) < grating_opening_ratio * grating_periodgrating_transmission(i, j) = 1;endendend% 计算衍射场k = 2 * pi / wavelength;incident_wave = exp(1i * k * x');diffracted_wave = fftshift(fft(fftshift(incident_wave .* grating_transmission)));% 显示结果figure;subplot(2, 2, 1);imagesc(x, y, abs(grating_transmission));title('Grating Transmission');subplot(2, 2, 2);imagesc(x, y, abs(incident_wave));title('Incident Wave');subplot(2, 2, 3);imagesc(x, y, abs(diffracted_wave));title('Diffracted Wave');subplot(2, 2, 4);imagesc(x, y, abs(diffracted_wave).^2);title('Intensity Pattern');这个简单的示例演示了一个周期性光栅的传输函数,然后计算了入射波和衍射波的场强度。
光栅衍射matlab代码
光栅衍射matlab代码以下是一个简单的光栅衍射 MATLAB 代码,用于演示光栅衍射现象:```matlab% 初始化参数n = 1.5; % 光栅数值孔径,单位为弧度d = 10; % 光栅刻线间距,单位为波长L = 100; % 光栅长度,单位为波长theta = n * L / 2; % 入射角,单位为弧度phi = pi / 2; % 垂直于光栅平面的偏振方向% 生成光栅序列grating = zeros(L, L);for i = 1:Lfor j = 1:Lgrating(i, j) = grating(i, j) + (i - 1) * sin(j - 1); endend% 入射光束为平面波wave = 1; % 平面波频率lambda = d / wave; % 波长% 计算衍射图样dispersion = zeros(L, L);for i = 1:Lfor j = 1:Ld = diffraction(wave, lambda, i, j);dispersion(i, j) = diffract(wave, lambda, i, j) / (2 * wave);endend% 可视化结果figure;imshow(dispersion, []);title("Diffraction Pattern");xlabel("X");ylabel("Y");```该代码生成了一个长度为 L 的光栅序列,其中每个光栅刻线之间的距离为 d,入射角为 theta,垂直于光栅平面的偏振方向为 phi。
然后,该代码计算了光栅衍射图样,并将其可视化。
在代码中,我们使用了 MATLAB 的 `dispersion` 对象来存储衍射图样,并使用`imshow` 函数将其可视化。
该代码演示了光栅衍射现象,并且可以用于生成各种不同条件下的光栅衍射图样。
基于MATLAB的光纤光栅耦合模理论及其谱线特性
研究生课程论文封面课程名称光电子学论文题目基于MATLAB的光纤光栅耦合模理论及其谱线特性授课学期 2013 学年至 2014 学年第 1 学期学院物理科学与技术学院专业光学学号 2012010887 姓名王璐玮任课教师秦子雄交稿日期 2014年01月01日成绩阅读教师签名日期广西师范大学研究生学院制基于MATLAB的光纤光栅耦合模理论及其谱线特性0.前言光纤光栅是近二十几年来迅速发展的光纤器件,其应用是随着写入技术的不断改进而发展起来的,逐渐在实际中得到应用。
1978年,加拿大通信研究中心的Hill等发现纤芯参锗的光纤具有光敏性,并利用驻波干涉法制成了世界上第一根光纤光栅。
光纤的光敏性主要是指光线的折射率在收到某些波长的激光照射后,会发生永久改变的特性。
通常情况需要紫外光照射,折射率会向着增大的方向改变。
具有光敏性的光纤主要是纤芯参锗的光纤,受到紫外光照射后,纤芯折射率会增加,而包层折射率不变。
在光纤光栅的发展过程中,参锗光纤的载氢技术具有重要意义。
参锗光纤本身具有光敏性,单当要求折射率改变较大时,相应就要提高纤芯的参锗浓度,这会影响光纤本身的特性。
1993年,贝尔实验室的Lemaire等用光纤载氢技术增强了光纤的光敏性,这种发发适用于任何参锗的光纤。
通过光纤的载氢能够将在不增加参锗浓度情况下,使光纤的光敏性大大提高。
在平面介质光波导中,布拉格光栅的应用比较早,主要应用于半导体激光器中,而后出现了光纤布拉格光栅,随着光纤光栅写入技术的成熟,光纤光栅在光通信和传感中得到广泛应用,特别是在光通信领域。
光纤布拉格光栅和长周期光纤光栅的特性和应用有许多不同之处,也有类似的地方,都可用于通信和传感等领域。
光纤布拉格光栅的周期一般在微米以下,根据耦合模理论,这样的周期表现为使向前传播的纤芯模与向后传播的纤芯模之间发生耦合,结果在输出端表现为很窄的带阻滤波特性。
作为一种反射型的光纤无源器件,光纤布拉格光栅对温度,应变都有相当程度的敏感特性,其在光纤激光器,波分复用,可调谐光纤滤波器,高速光纤通信系统的色散补偿及光纤传感器等反面有许多重要应用。
光纤模式的有效折射率与波长关系仿真 matlab
光纤模式的有效折射率与波长关系仿真 matlab1. 研究背景光纤作为一种重要的光学器件,广泛应用于通信、传感器等领域。
光纤的传输特性与其折射率与波长之间的关系密切相关。
研究光纤模式的有效折射率与波长之间的关系对于深入理解光纤的特性具有重要意义。
2. 光纤模式的有效折射率光纤的有效折射率是指光在光纤中传播时所受到的等效折射率,它与光纤的结构、材料等因素息息相关。
光纤模式的有效折射率随着波长的变化而变化,这种变化对于光纤的性能具有重要影响。
3. 波长与折射率的关系波长与折射率之间存在一定的函数关系,一般来说,波长较短的光在光纤中传播时受到的折射率较大,而波长较长的光则受到的折射率较小。
研究波长与折射率之间的关系可以帮助我们更好地理解光纤的传输特性。
4. Matlab仿真Matlab作为一种强大的数学建模工具,可以通过编写程序来对光纤模式的有效折射率与波长关系进行仿真。
利用Matlab的光学工具箱可以方便地构建光纤模型,并对其进行波长与折射率的仿真计算。
5. 结论与展望通过Matlab仿真可以得到光纤模式的有效折射率与波长之间的关系,并且可以进一步研究其对光纤传输特性的影响。
未来,可以通过进一步的实验验证来验证仿真结果,并且可以结合其他因素对光纤的性能进行综合研究,为光纤在通信、传感器等领域的应用提供更加可靠的理论基础。
通过以上内容的介绍,我们可以了解到光纤模式的有效折射率与波长关系仿真在Matlab中的重要性,并且可以对其进行一定的探讨和研究。
也可以看出通过Matlab仿真可以得到丰富的研究成果,对光纤的实际应用具有一定的指导意义。
希望能够通过对光纤模式的有效折射率与波长关系的研究,推动光纤技术的发展,为其在不同领域的应用提供更加有力的支持。
光纤技术在通信、传感器等领域的应用已经成为现代社会中不可或缺的一部分。
随着科技的不断进步,人们对光纤传输特性的要求也越来越高,因此研究光纤模式的有效折射率与波长关系仿真在Matlab中的重要性也日益凸显。
不同方向和空间频率的光栅 matlab-概述说明以及解释
不同方向和空间频率的光栅matlab-概述说明以及解释1.引言1.1 概述概述部分旨在介绍本文所要探讨的主题——不同方向和空间频率的光栅,并对文章的结构和目的进行简要阐述。
光栅是一种具有周期性结构的光学元件,其作用是将入射光束分解为不同的波长成分。
在光栅研究中,光栅可以根据其周期性的方向和空间频率进行分类和分析。
本文将分为三个主要部分进行探讨。
首先,我们将介绍不同方向的光栅,包括其定义和原理、应用领域以及实验方法和结果。
其次,我们将探讨不同空间频率的光栅,包括空间频率的概念、光栅的空间频率特性以及实验验证和应用。
最后,我们将重点介绍MATLAB在光栅研究中的应用,包括MATLAB基础知识、在光栅模拟中的应用以及在光栅分析中的应用。
通过详细介绍和分析不同方向和空间频率的光栅以及MATLAB的应用,我们旨在提供一个全面而深入的了解光栅研究的现状和发展。
同时,我们也希望为光栅研究领域的学者和科研人员提供一些实用的研究工具和方法。
通过本文的研究和总结,我们期望能够对光栅研究领域的发展和未来趋势进行一些展望,并为相关研究提供一些思路和建议。
在接下来的章节中,我们将深入探讨不同方向和空间频率的光栅,并展示MATLAB在光栅研究中的重要性和应用价值。
1.2 文章结构文章结构部分主要介绍了文章的整体组织结构和各个章节的内容概要。
具体内容如下:文章结构(Article Structure)本文按照以下结构进行组织和阐述。
第一部分-引言:在引言中,我们首先对光栅的背景和研究意义进行了概述,并介绍了该文章的结构安排和目的。
第二部分-正文:正文部分是文章的核心内容,主要涵盖了不同方向和空间频率的光栅的相关研究内容。
2.1 不同方向的光栅:本节主要探讨了不同方向的光栅的定义和原理,并介绍了其在各个应用领域中的具体应用案例。
同时,我们还详细介绍了实验方法和相关结果。
2.2 不同空间频率的光栅:在本节中,我们将重点讨论空间频率的概念以及光栅的空间频率特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用matlab 计算长周期光纤光栅的有效折射率
近几年来,一种在光纤中写入光栅的技术引起了人们的极大兴趣,光纤光栅的出现,给光通信领域带来了极大的变革,尤其是在滤波和传感方面影响尤为深远。
按照光纤光栅周期的长短,通常周期把小于一微米的光纤光栅称为短周期光纤光栅,又称为布拉格光纤光栅或反射光栅,而周期为几十甚至几百微米的光纤光栅称为长周期光纤光栅,又称为透射光栅。
短周期光纤光栅的特点是传输方向相反的模式之间发生耦合,属于反射型带通滤波器,长周期光纤光栅的特点是同向传输的纤芯基模和包层模之间的耦合,没有后向反射,属于投射型带阻滤波器。
长周期光纤光栅透射谱的理论模拟
在我们研究长周期光纤光栅的各方面属性的过程中,耦合模理论提供了精确有效的解,从而被我们广泛采纳。
长周期光纤光栅的模式耦合主要是指纤芯基模和同向传播的包层模之间的耦合,由光纤的模式理论可以知道在包层中存在很多种包层模,为了方便讨论,我们在这一部分只讨论光纤光栅的纤芯基模和一个包层模之间的耦合。
首先,我们定义一下谐振波长,就是在光纤有效折射率调制无穷小的情况下的谐振波长,可以用下面的公式来表示=D eff n λ∆Λ,式子中eff n ∆表示光纤基模和包层模之间的有效折射率之差,即12eff eff eff n n n ∆=-。
第二步,我们来定义一下,直流耦合系数和交叉耦合系数,非别为
直流耦合系数 ()eff eff
eff
D n n n δσπλλ∧∆+∆=-
交流耦合系数 eff n πδκλ
= 第三步,有了上面的定义,我们接着引入直流耦合率和交叉耦合率的概念,,分别为
直流耦合率2
()222(0)||1
cos ))||1z R t R κσ
=∧==++
交叉耦合率2
()2
2(0)||1
)||1z s t R κσ⨯∧==+。
我们可以验证,直流耦合率和交叉耦合率之和等于一,这说明用直流耦合率和交叉耦合率来表示透射谱和反射谱是恰当的。
有了上面一系列的叙述,我们就可以用matlab 对长周期光纤光栅进行模仿,在这一过程中,我们对一些列的参数做如下设定,光纤有效折射率之差120.042eff eff eff n n n ∆=-=,光栅周期350m μΛ=,周期数为N=100,光栅长度35L N mm =Λ⨯=(这相当于公式中
的z ),由谐振波长计算公式我们可以得到谐振波长1470D nm λ=。
我们分别取三个不同的折射率调制分别为51.210eff n δ=⨯,52.110eff n δ=⨯,54.210eff n δ=⨯。
以下是用matlab 模拟出来的直流耦合率和交叉耦合率的图像
长周期光纤光栅有效折射率的计算
由上文的讨论我们可以看出,长周期光纤光栅谱线模拟中一个很重要的因素就是光纤光栅的有效折射率,即纤芯的有效折射率和包层的有效折射率。
分别对着两个折射率进行计算。
表征弱导光纤纤芯基模的色散方程为1100(1)()1(1)()
J V b K V b V b V b J V b K V b --=-。
其中01J J 和是0阶和1阶Bessel 函数,01K K 和是0阶和1阶修正的Bessel 函数。
22112=2/)V a n n πλ-(表示归一化频率;2222212()/co eff b n n n n =--表示模式的归一化有
效折射率。
co eff n 表示纤芯基模的有效折射率。
下面我将计算co
eff n 的程序写再下面:
首先是写出色散方程公式 接着再代入参数求得纤芯有效折射率co
eff n
最终我们得到了一系列对应于不同波长的纤芯有效折射率,保存在一个txt文本文档中。
下面是我们根据求得的结果画出的图像。
