河北省2020石家庄二中高一下期中考试
2019-2020学年河北省石家庄市第二中学高一下学期期中考试英语试题 Word版含答案
石家庄二中2019～2020 学年度高一年级下学期线上期中考试英语试卷(时间:120 分钟,分值150 分)第一部分听力（共两节，满分30 分）第一节（共5小题；每小题1.5分，满分7.5分）听下面5 段对话。
每段对话后有一个小题，从题中所给的A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。
听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the man prefer to drink?A. Tea.B. Cold water.C. Coffee.2. What does the man dislike?A. Traveling.B. Driving.C. Flying.3. What does the man think of the blouse?A. It’s of good design.B. It’s up-to-date.C. It’s old-fashioned.4. When will the man meet Mr. Smith?A. At 2:15 p.m..B. At 2:00 p.m..C. At 1:45 p.m..5. What is probably wrong with the man?A. He has caught a cold.B. He ate something bad.C. He has got an upset stomach.第二节（共15小题；每小题1.5分，满分22.5分）听下面5 段对话或独白。
每段对话或独白后有几个小题，从题中所给的A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。
听每段对话或独白前，你将有时间阅读各个小题，每小题5 秒钟；听完后，各小题将给出5 秒钟的作答时间。
每段对话或独白读两遍。
听下面一段对话，回答第6、7 题。
6. What is in the middle of Victoria Square?A. A big fountain.B. A golden statue.C. A large clock.7. How is the woman going to the square?A. On foot.B. By bus.C. By taxi.听下面一段对话，回答第8、9 题。
2019-2020学年河北省石家庄市第二中学高一下学期期中考试地理试题
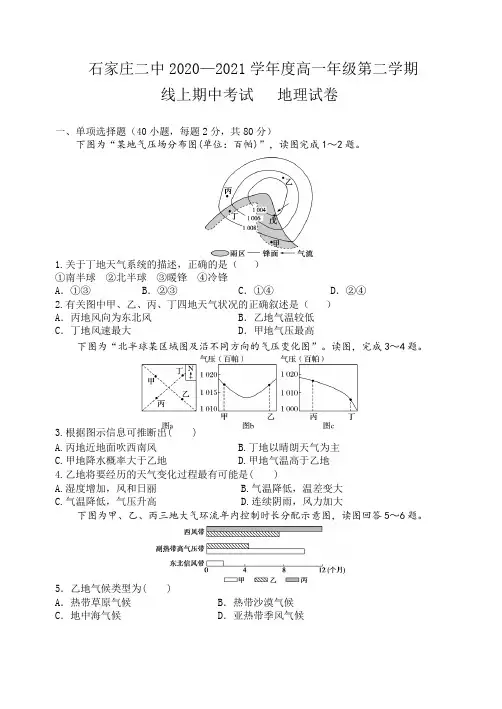
石家庄二中2020—2021学年度高一年级第二学期线上期中考试地理试卷一、单项选择题（40 小题，每题2 分，共80 分）下图为“某地气压场分布图(单位：百帕)”，读图完成1～2 题。
1.关于丁地天气系统的描述，正确的是（）①南半球②北半球③暖锋④冷锋A．①③B．②③C．①④D．②④2.有关图中甲、乙、丙、丁四地天气状况的正确叙述是（）A．丙地风向为东北风B．乙地气温较低C．丁地风速最大D．甲地气压最高下图为“北半球某区域图及沿不同方向的气压变化图”。
读图，完成3～4 题。
3.根据图示信息可推断出( )A.丙地近地面吹西南风B.丁地以晴朗天气为主C.甲地降水概率大于乙地D.甲地气温高于乙地4.乙地将要经历的天气变化过程最有可能是( )A.湿度增加，风和日丽B.气温降低，温差变大C.气温降低，气压升高D.连续阴雨，风力加大下图为甲、乙、丙三地大气环流年内控制时长分配示意图，读图回答5～6 题。
5．乙地气候类型为( )A．热带草原气候B．热带沙漠气候C．地中海气候D．亚热带季风气候6．下列关于甲、丙两地自然状况的叙述，正确的是( )A．甲地自然带是热带沙漠带B．丙地河流容易形成凌汛C．甲地气候日温差较大D．丙地冬季常有较厚积雪图1 示意咸海不同时期湖岸线的变化，图2 示意咸海流域。
据此完成7～9 题。
7．咸海流域( )A．河流参与海陆间水循环B．流水侵蚀、沉积作用强C．河流水量受气温影响小D．主要来自高山冰雪补给8．根据图中信息可以判断( )A．流域面积逐渐缩小B．湖岸的坡度西岸陡东岸缓C．流域主体位于温带草原D．全球变暖是湖泊萎缩的主因9．咸海面积不断减小产生的影响较小的是( )A．生态环境变差B．棉花种植受到极大威胁C．冬半年沙尘暴频发D．气温年较差变大黄河小北干流是指黄河禹门口至潼关河段，全长132.5 千米。
该河段左岸有汾河、涑水河，右岸有渭河等支流汇入；河道摆动频繁，冲淤变化剧烈，为典型的堆积性游荡河道。
河北省石家庄市第二中学2019-2020学年高一下学期期中考试数学试题(解析版)
期中数学试卷一、选择题1．若a ，b ，c 为实数，且a ＜b ＜0，则下列命题正确的是（ ） A ．ac 2＜bc 2B ．1a＜1bC ．a 2＞ab ＞b 2D ．b a＞ab2．设S n 为等差数列{a n }的前n 项和．若3S 3＝S 2+S 4，a 2＝﹣1，则a 4＝（ ） A ．﹣7B ．﹣10C ．10D ．123．如图，四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确的是（ ）A ．AC ⊥SBB ．AD ⊥SCC ．平面SAC ⊥平面SBDD ．BD ⊥SA4．若函数f(x)=4x +a x(x ＞0，a ＞0)当且仅当x ＝2时取得最小值，则实数a 的值为（ ） A ．12B ．24C ．16D ．365．在正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 分别为CC 1，DD 1的中点，则异面直线AF ，DE 所成角的余弦值为（ ） A ．14B ．15C ．2√65D ．√1546．在△ABC 中，cos 2B 2=a+c 2c，则△ABC 为（ ） A ．等腰直角三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形7．一直三棱柱的每条棱长都是1，且每个顶点都在球O 的表面上，则球O 的表面积为（ ）A ．283π B ．√223π C ．73πD ．√7π8．已知数列a 1，a 2a 1，a 3a 2，⋯，an a n−1是首项为4，公比为12的等比数列，则a 4等于（ ） A ．4B ．32C ．64D ．1289．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，已知B =π3，b ＝1，求a +c 的取值范围（ ） A ．(1，√3)B ．(√3，2]C ．（1，2]D ．（1，2）10．已知数列{a n }的前n 项和为S n ，S n ＝2a n ﹣2，若存在两项a m ，a n ，使得a m •a n ＝64，则1m+16n 的最小值为（ ）A ．256B ．215C ．92D ．17311．设等差数列{a n }的前n 项和为S n ，公差为d ，且满足a 1＞0，S 11＝S 18，则对S n 描述正确的有（ ） A ．S 14是唯一最小值 B ．S 15是最小值C ．S 29＝0D ．S 15是最大值12．在△ABC 中，D 在线段AB 上，且AD ＝5，BD ＝3，若CB ＝2CD ，cos ∠CDB =−√55，则（ ） A ．sin ∠CDB =310B ．△ABC 的面积为8C ．△ABC 的周长为8+4√5D ．△ABC 为锐角三角形二、填空题13．已知数列{a n }满足a 1＝1，3a n +1a n ＝a n ﹣a n +1，则通项a n ＝ ． 14．函数f(x)={−1(x ≤0)x(x ＞0)，则不等式xf （x ）﹣x ≤2的解集为 ．15．在△ABC 中，边a ，b ，c 所对的角分别为A ，B ，C ．△ABC 的面积S 满足4√33S =b 2+c 2−a 2，若a =√3，则b sinB= ．16．对于数列{a n }，定义H n =a 1+2a 2+⋯+2n−1a nn为{a n }的“优值”，现已知某数列的“优值”H n =2n ，记数列{a n }的前n 项和为S n ，则S 20202020= ．三、解答题17．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且a b=cosA 2−cosB．（Ⅰ）求ac．（Ⅱ）若b ＝4，cos C =14，求△ABC 的面积． （Ⅲ）在（Ⅱ）的条件下，求cos （2C +π3）的值．18．已知等差数列{a n }中，a 6﹣a 2＝8，且a 1，a 6，a 21依次成等比数列． （1）求数列{a n }的通项公式； （2）设b n =1a n a n+1，数列{b n }的前n 项和为S n ，若S n =111，求n 的值． 19．如图，在四棱锥P ﹣ABCD 中，底面ABCD 是直角梯形，∠ABC ≠90°，AB ∥CD ，P A ⊥平面ABCD ，AB ＝2，P A ＝AD ＝DC ＝1． （1）证明：平面P AC ⊥平面PBC ； （2）求点D 到平面PBC 的距离．20．法国数学家费马被称为业余数学之王，很多数学定理以他的名字命名．对△ABC 而言，若其内部的点P 满足∠APB ＝∠BPC ＝∠CP A ＝120°，则称P 为△ABC 的费马点．如图所示，在△ABC 中，已知∠BAC ＝45°，设P 为△ABC 的费马点，且满足∠PBA ＝45°，P A ＝2．（1）求△P AC 的面积； （2）求PB 的长度．21．等差数列{a n}的公差为2，a2，a4，a8分别等于等比数列{b n}的第2项，第3项，第4项．（1）求数列{a n}和{b n}的通项公式；（2）若数列{c n}满足c1a1+c2a2+⋯+c na n=b n+1，求数列{c n}的前2020项的和．22．如图，在三棱锥D﹣ABC中，DA＝DB＝DC，D在底面ABC上的射影E在AC上，DF ⊥AB于F．（Ⅰ）求证：BC平行平面DEF；（Ⅱ）若∠BAC=∠ADC=π3，求直线BE与平面DAB所成角的余弦值．一、选择题1．若a，b，c为实数，且a＜b＜0，则下列命题正确的是（）A．ac2＜bc2B．1a ＜1bC．a2＞ab＞b2D．ba＞ab【分析】利用不等式的基本性质即可得出．【解答】解：∵a＜b＜0，则A．c＝0时，ac2＜bc2不成立；B．由已知可得1a ＞1b，因此不成立；C．由已知可得：a2＞ab＞b2，因此正确；D．由已知可得：a2＞b2，∴a2ab＞b2ab，化为ab＞ba，因此不成立．故选：C．【点评】本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．2．设S n为等差数列{a n}的前n项和．若3S3＝S2+S4，a2＝﹣1，则a4＝（）A．﹣7B．﹣10C．10D．12【分析】设等差数列{a n}的公差为d，由3S3＝S2+S4，a2＝﹣1，利用通项公式求和公式可得：3（3a1+3d）＝6a1+7d，a1+d＝﹣1，解得a1，d，即可得出．【解答】解：设等差数列{a n}的公差为d，∵3S3＝S2+S4，a2＝﹣1，∴3（3a1+3d）＝6a1+7d，a1+d＝﹣1，解得a1＝2，d＝﹣3．则a4＝2﹣3×3＝﹣7．故选：A．【点评】本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于基础题．3．如图，四棱锥S﹣ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（）A ．AC ⊥SBB ．AD ⊥SCC ．平面SAC ⊥平面SBDD ．BD ⊥SA【分析】在A 中，推导出AC ⊥SD ，AC ⊥BD ，从而AC ⊥平面SBD ，由此得到AC ⊥SB ；在B 中，推导出AD ⊥CD ，AD ⊥SD ，从而AD ⊥平面SDC ，由此得到AD ⊥SC ；在C 中，推导出AC ⊥平面SBD ，从而平面SAC ⊥平面SBD ；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DS 为z 轴，建立空间直角坐标系，利用向量法摔倒导出BD 与SA 不垂直， 【解答】解：由四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ，知： 在A 中，∵SD ⊥底面ABCD ，∴AC ⊥SD ， ∵四棱锥S ﹣ABCD 的底面为正方形，∴AC ⊥BD ， ∵SD ∩BD ＝D ，∴AC ⊥平面SBD ， ∵SB ⊂平面SBD ，∴AC ⊥SB ，故A 正确；在B 中，∵四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ， ∴AD ⊥CD ，AD ⊥SD ，∵SD ∩CD ＝D ，∴AD ⊥平面SDC ， ∵SC ⊂平面SCD ，∴AD ⊥SC ，故B 正确； 在C 中，∵SD ⊥底面ABCD ，∴AC ⊥SD ， ∵四棱锥S ﹣ABCD 的底面为正方形，∴AC ⊥BD ， ∵SD ∩BD ＝D ，∴AC ⊥平面SBD ，∵AC ⊂平面SAC ，∴平面SAC ⊥平面SBD ，故C 正确；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DS 为z 轴，建立空间直角坐标系， 设AB ＝a ，DS ＝b ，则D （0，0，0），B （a ，a ，0），A （a ，0，0），S （0，0，b ）， DB →=（a ，a ，0），SA →=（a ，0，﹣b ），∵DB →⋅SA →=a 2≠0，∴BD 与SA 不垂直，故D 错误． 故选：D ．【点评】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．4．若函数f(x)=4x +ax (x ＞0，a ＞0)当且仅当x ＝2时取得最小值，则实数a 的值为（ ） A ．12B ．24C ．16D ．36【分析】利用基本不等式的性质即可得出．【解答】解：函数f(x)=4x +ax(x ＞0，a ＞0)当且仅当x ＝2时取得最小值， ∴f （x ）≥2√4x ⋅ax =4√a ，当且仅当x =√a2=2时取等号，解得a ＝16． 故选：C ．【点评】本题考查了基本不等式的性质，考查了推理能力与计算能力，属于基础题． 5．在正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 分别为CC 1，DD 1的中点，则异面直线AF ，DE 所成角的余弦值为（ ） A ．14B ．15C ．2√65D ．√154【分析】可画出图形，连接BE ，从而可得出∠DEB 为异面直线AF ，BE 所成的角，并连接DB ，然后可设正方体的棱长为2，从而可得出△BDE 三边的长度，根据余弦定理即可求出cos ∠DEB 的值．【解答】解：如图，连接BE ，则BE ∥AF ，则∠DEB 为异面直线AF ，DE 所成的角，连接DB ，设正方体的棱长为2，则： BE =DE =√5，BD =2√2，∴在△BDE 中，由余弦定理得，cos ∠DEB =BE 2+DE 2−BD 22BE⋅DE =2×5×5=15．故选：B ．【点评】本题考查了异面直线所成角的定义及求法，余弦定理的应用，考查了计算能力，属于基础题． 6．在△ABC 中，cos 2B 2=a+c2c，则△ABC 为（ ） A ．等腰直角三角形B ．等边三角形C ．直角三角形D ．等腰三角形或直角三角形【分析】根据二倍角的余弦公式变形、余弦定理化简已知的等式，化简后即可判断出△ABC 的形状．【解答】解：∵cos 2B2=a+c2c ， ∴12（1+cos B ）=a+c 2c， 在△ABC 中，由余弦定理得，12+12•a 2+c 2−b 22ac=a+c 2c，化简得，2ac +a 2+c 2﹣b 2＝2a （a +c ）， 则c 2＝a 2+b 2，∴△ABC 为直角三角形， 故选：C ．【点评】本题考查余弦定理以及二倍角的余弦公式变形的应用，属于基础题．7．一直三棱柱的每条棱长都是1，且每个顶点都在球O 的表面上，则球O 的表面积为（ ） A ．283π B ．√223π C ．73πD ．√7π【分析】正三棱柱的两个底面的中心的连线的中点就是球的球心，球心与顶点的连线长就是半径，求出球的半径，即可求出球的表面积．【解答】解：正三棱柱的两个底面的中心的连线的中点就是球的球心，球心与顶点的连线长就是半径，下底面三角形的外接圆半径r 满足：2r =1sin60°⇒r =√33， 所以，球半径R =√r 2+ℎ2=(√33)2+(12)2=√712， ∴球的表面积为：4πR 2＝4π（√712）2=73π； 故选：C ．【点评】本题是基础题，考查正三棱柱的外接球的表面积的求法，明确球心、球的半径与正三棱柱的关系是本题解决的关键．8．已知数列a 1，a 2a 1，a 3a 2，⋯，a na n−1是首项为4，公比为12的等比数列，则a 4等于（ ）A ．4B ．32C ．64D ．128【分析】推导出a n a n−1=4×(12)n−1=23﹣n ，从而a 4=a 1×a 2a 1×a 3a 2×a 4a 3，由此能求出a 4的值．【解答】解：∵数列a 1，a 2a 1，a3a 2，⋯，a nan−1是首项为4，公比为12的等比数列，∴a n a n−1=4×(12)n−1=23﹣n ，∴a 4=a 1×a 2a 1×a 3a 2×a4a 3＝4×2×1×12=4． 故选：A ．【点评】本题考查数列的第四项的求法，考查等比数列的性质等基础知识，考查运算求解能力，是基础题．9．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，已知B =π3，b ＝1，求a +c 的取值范围（ ） A ．(1，√3)B ．(√3，2]C ．（1，2]D ．（1，2）【分析】由已知结合余弦定理及基本不等式可求a +c 的范围，然后再结合三角形的两边之和大于第三边即可求解．【解答】解：由余弦定理可得，cos B =12=a 2+c 2−12ac， 所以（a +c ）2﹣2ac ﹣1＝ac 即（a +c ）2＝1+3ac ≤1+3×(a+c2)2，当且仅当a ＝c 时取等号，解可得，a +c ≤2， 又a +c ＞b ＝1， 综上1＜a +c ≤2． 故选：C ．【点评】本题主要考查了利用余弦定理及基本不等式求解三角形，属于基础试题． 10．已知数列{a n }的前n 项和为S n ，S n ＝2a n ﹣2，若存在两项a m ，a n ，使得a m •a n ＝64，则1m+16n 的最小值为（ ）A ．256B ．215C ．92D ．173【分析】运用数列的递推式和等比数列的定义、通项公式可得a n ＝2n ．求得m +n ＝6，1m+16n=16（m +n ）（1m+16n）=16（17+n m +16mn ），运用基本不等式，检验等号成立的条件，即可得到所求最小值．【解答】解：S n ＝2a n ﹣2，可得a 1＝S 1＝2a 1﹣2，即a 1＝2， n ≥2时，S n ﹣1＝2a n ﹣1﹣2，又S n ＝2a n ﹣2，相减可得a n ＝S n ﹣S n ﹣1＝2a n ﹣2a n ﹣1，即a n ＝2a n ﹣1， {a n }是首项为2，公比为2的等比数列． 所以a n ＝2n ．a m a n ＝64，即2m •2n ＝64， 得m +n ＝6， 所以1m+16n =16（m +n ）（1m+16n）=16（17+n m +16m n ）≥16（17+2√16）=256，当且仅当n m=16m n时取等号，即为m =65，n =245． 因为m 、n 取整数，所以均值不等式等号条件取不到，则1m+16n＞256，验证可得，当m ＝1，n ＝5时，1m+16n取得最小值为215．故选：B ．【点评】本题考查数列的通项公式的求法，注意运用数列的递推式和等比数列的定义、通项公式，考查基本不等式的运用，注意检验等号成立的条件，考查化简运算能力，属于中档题．11．设等差数列{a n}的前n项和为S n，公差为d，且满足a1＞0，S11＝S18，则对S n描述正确的有（）A．S14是唯一最小值B．S15是最小值C．S29＝0D．S15是最大值【分析】由S11＝S18，可得：11a1+11×102d＝18a1+18×172d，化为：a1+14d＝0＝a15，根据a1＞0，可得d＜0，即可判断出结论．【解答】解：由S11＝S18，可得：11a1+11×102d＝18a1+18×172d，化为：a1+14d＝0＝a15，∵a1＞0，∴d＜0，∴S14，S15是最大值，S29=29(a1+a29)2=29a15＝0．∴CD正确．故选：CD．【点评】本题考查了等差数列的通项公式与求和公式及其性质，考查了推理能力与计算能力，属于基础题．12．在△ABC中，D在线段AB上，且AD＝5，BD＝3，若CB＝2CD，cos∠CDB=−√55，则（）A．sin∠CDB=310B．△ABC的面积为8C．△ABC的周长为8+4√5D．△ABC为锐角三角形【分析】直接利用余弦定理和三角形面积公式的应用求出结果．【解答】解：在△ABC中，D在线段AB上，且AD＝5，BD＝3，若CB＝2CD，cos∠CDB=−√55，所以sin∠CDB=2√5 5．如图所示：设CD＝x，则CB＝2x，在△BCD中，利用余弦定理：cos∠CDB=−√55=x2+9−(2x)22×3×x，整理得√5x2−2x−3√5=0，解得x=√5（负值舍去）．所以CD=√5，CB＝2√5，进一步求出cos B=32+(2√5)2−(√5)22×3×25=2√55．在△ABC中，利用余弦定理：AC2＝AB2+BC2﹣2•AB•BC cos B，解得：AC＝2√5，所以：l△ABC=8+2√5+2√5=8+4√5．S△ABC=12×8×2√5×√55=8．cos∠ACB=(2√5)2+(2√5)2−642×2√5×2√50，所以△ABC为钝角三角形．故选：BC．【点评】本题考查的知识要点：正弦定理余弦定理和三角形面积公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．二、填空题13．已知数列{a n}满足a1＝1，3a n+1a n＝a n﹣a n+1，则通项a n＝13n−2．【分析】利用数列的递推关系式，推出{1a n}是等差数列，然后求解数列的通项公式．【解答】解：数列{a n}满足a1＝1，3a n+1a n＝a n﹣a n+1，可得1a n+1−1a n=3，可得数列{1a n}是等差数列，首项为1，公差为3，所以1a n=1+3（n﹣1），所以a n =13n−2． 故答案为：13n−2．【点评】本题考查数列的递推关系式的应用，考查转化思想以及计算能力，是中档题． 14．函数f(x)={−1(x ≤0)x(x ＞0)，则不等式xf （x ）﹣x ≤2的解集为 [﹣1，2] ．【分析】由已知函数解析式可把原不等式进行转化即可求解．【解答】解：当x ≤0时，由xf （x ）﹣x ≤2可得，﹣x ﹣x ≤2，解可得，x ≥﹣1，此时﹣1≤x ≤0，当x ＞0时，由xf （x ）﹣x ≤2可得，x 2﹣x ≤2，解可得，﹣1≤x ≤2，此时0＜x ≤2， 综上可得，x 的范围[﹣1，2] 故答案为：[﹣1，2]【点评】本题主要考查了利用分段函数求解不等式，体现了分类讨论思想的应用． 15．在△ABC 中，边a ，b ，c 所对的角分别为A ，B ，C ．△ABC 的面积S 满足4√33S =b 2+c 2−a 2，若a =√3，则b sinB= 2 ．【分析】由已知结合余弦定理及三角形的面积公式可求tan A ，进而可求A ，然后结合正弦定理即可求解． 【解答】解：因为4√33S =b 2+c 2−a 2，所以4√33×12bcsinA =2bc cos A ， 则tan A =√3，因为A 为三角形的内角，故A =13π， 因为a =√3， 由正弦定理可得，bsinB=a sinA=√3√32=2．故答案为：2【点评】本题主要考查了正弦定理，余弦定理及三角形的面积公式在求解三角形中的应用，属于基础试题．16．对于数列{a n }，定义H n =a 1+2a 2+⋯+2n−1a nn为{a n }的“优值”，现已知某数列的“优值”H n =2n ，记数列{a n }的前n 项和为S n ，则S 20202020=20232．【分析】先由题设条件得到a1+2a 2+⋯+2n−1a n =n •2n ，再利用a1+2a 2+⋯+2n−2a n−1=(n −1)⋅2n−1，两式相减求出a n ＝n +1（n ≥2），检验n ＝1时是否适合，然后求出S 20202020即可．【解答】解：由题意知H n =a 1+2a 2+⋯+2n−1a nn=2n ，即a1+2a 2+⋯+2n−1a n =n •2n ，又当n ≥2时，有a1+2a 2+⋯+2n−2a n−1=(n −1)⋅2n−1，两式相减得：2n ﹣1a n ＝n •2n ﹣（n ﹣1）•2n ﹣1＝（n +1）•2n ﹣1， 整理得a n ＝n +1（n ≥2），当n ＝1时，有a 1＝1×2＝2也适合， ∴a n ＝n +1， S 2020=2020(2+2021)2，∴S 20202020=20232．故答案为：20232．【点评】本题主要考查数列通项公式的求法及等差数列前n 项和公式，属于基础题． 三、解答题17．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且ab =cosA 2−cosB．（Ⅰ）求ac．（Ⅱ）若b ＝4，cos C =14，求△ABC 的面积． （Ⅲ）在（Ⅱ）的条件下，求cos （2C +π3）的值．【分析】（I ）由已知结合正弦定理先进行代换，然后结合和差角公式及正弦定理可求； （II ）由余弦定理可求a ，然后结合三角形的面积公式可求； （III ）结合二倍角公式及和角余弦公式即可求解． 【解答】解：（I ）因为ab =cosA 2−cosB=sinA sinB，所以2sin A ﹣sin A cos B ＝sin B cos A ，所以2sin A ＝sin A cos B +sin B cos A ＝sin （A +B ）＝sin C ， 由正弦定理可得，ac =sinA sinC=12；（II ）由余弦定理可得，14=a 2+16−4a 28a，整理可得，3a 2+2a ﹣16＝0， 解可得，a ＝2， 因为sin C =√154，所以S △ABC =12absinC =12×2×4×√154=√15； （III ）由于sin2C ＝2sin C cos C ＝2×√154×14=√158，cos2C ＝2cos 2C ﹣1=−78． 所以cos （2C +π3）=12cos2C −√32sin2C =12×(−78)−√32×√158=−7−3√516． 【点评】本题主要考查了正弦定理、余弦定理，以及和差角公式，二倍角公式及三角形的面积公式的综合应用，属于中档试题．18．已知等差数列{a n }中，a 6﹣a 2＝8，且a 1，a 6，a 21依次成等比数列． （1）求数列{a n }的通项公式； （2）设b n =1a n a n+1，数列{b n }的前n 项和为S n ，若S n =111，求n 的值． 【分析】（1）利用已知条件，求出数列的首项与公差，然后求解数列的通项公式． （2）化简通项公式，利用裂项相消法，求解数列的和，然后求解n 即可． 【解答】解：（1）设数列{a n }的公差为d ， 因为a 6﹣a 2＝8，所以4d ＝8，解得d ＝2，因为a 1，a 6，a 21依次成等比数列，所以a 62=a 1a 21，即(a 1+5×2)2=a 1(a 1+20×2)，解得a 1＝5， 所以a n ＝2n +3；（2）由（1）知b n =1a n a n+1=1(2n+3)(2n+5)，所以b n =12(12n+3−12n+5)，所以S n =12[(15−17)+(17−19)+⋯+(12n+3−12n+5)]=n5(2n+5)， 由n 5(2n+5)=111，得n ＝25．【点评】本题考查数列的递推关系式以及数列求和，考查转化思想以及计算能力，是中档题．19．如图，在四棱锥P ﹣ABCD 中，底面ABCD 是直角梯形，∠ABC ≠90°，AB ∥CD ，P A ⊥平面ABCD ，AB ＝2，P A ＝AD ＝DC ＝1． （1）证明：平面P AC ⊥平面PBC ； （2）求点D 到平面PBC 的距离．【分析】（1）证明BC ⊥AC ，P A ⊥BC ，推出BC ⊥平面P AC ，即可证明平面P AC ⊥平面PBC ．（2）设点D 到平面PBC 的距离为d ，利用V P ﹣BCD ＝V D ﹣PBC ，转化求解即可． 【解答】（1）证明：由已知得AC =√AD 2+CD 2=√2，BC =√AD 2+(AB −CD)2=√2，AB ＝2，∴AC 2+BC 2＝AB 2，∴BC ⊥AC ，∵P A ⊥平面ABCD ，BC ⊂平面ABCD ，∴P A ⊥BC ， ∵P A ∩AC ＝A ，∴BC ⊥平面P AC ，∵BC ⊂平面PBC ，∴平面P AC ⊥平面PBC ．（2）解：由（1）得BC ⊥平面PAC ，∴BC ⊥AC ，BC =√2，PC =√12+(√2)2=√3， 设点D 到平面PBC 的距离为d ， ∵V P ﹣BCD ＝V D ﹣PBC ， ∴13×12×DC ×AD ×PA =13×12×PC ×BC ×d ，∴13×12×1×1×1=13×12×√3×√2×d ，解得d =√66，∴点D 到平面PBC 的距离为√66．【点评】本题考查直线与平面垂直的判断定理的应用，几何体的体积的求法等体积法的应用，考查空间想象能力以及计算能力．20．法国数学家费马被称为业余数学之王，很多数学定理以他的名字命名．对△ABC而言，若其内部的点P满足∠APB＝∠BPC＝∠CP A＝120°，则称P为△ABC的费马点．如图所示，在△ABC中，已知∠BAC＝45°，设P为△ABC的费马点，且满足∠PBA＝45°，P A＝2．（1）求△P AC的面积；（2）求PB的长度．【分析】（1）由已知利用三角形的内角和定理可得∠P AB＝15°，∠P AC＝30°，可得在△P AC中，∠PCA＝30°，可得P A＝PC＝2，利用三角形的面积公式即可求解△P AC的面积．（2）利用特殊角的三角函数值，两角差的正弦函数公式可求sin45°，sin15°的值，在△P AB中，由正弦定理可得PB的值．【解答】解：（1）由已知可得∠P AB＝180°﹣120°﹣45°＝15°，∴∠P AC＝45°﹣15°＝30°，在△P AC中，∠PCA＝180°﹣120°﹣30°＝30°，∴P A＝PC＝2，∴△P AC的面积S=12P A•PC•sin∠P AC=12×2×2×√32=√3．（2）∵sin15°＝sin（45°﹣30°）=√22×√32−√22×12=√6−√24，sin45°=√22，∴在△P AB中，由正弦定理PBsin15°=PAsin45°，可得PB=2sin15°sin45°=2×√6−√2422=√3−1．【点评】本题主要考查了三角形的内角和定理，三角形的面积公式，特殊角的三角函数值，两角差的正弦函数公式，正弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于基础题．21．等差数列{a n}的公差为2，a2，a4，a8分别等于等比数列{b n}的第2项，第3项，第4项．（1）求数列{a n}和{b n}的通项公式；（2）若数列{c n}满足c1a1+c2a2+⋯+c na n=b n+1，求数列{c n}的前2020项的和．【分析】（1）由已知结合等比数列的性质及等差数列的通项公式求得a1＝2．则a n可求．设等比数列{b n}的公比为q，求得q与b2，则{b n}的通项公式可求；（2）由（1）知，a n=2n，b n=2n．代入得c1a1+c2a2+⋯+c n−1a n−1+c na n=2n+1，即可求得数列{c n}d的通项公式；数列{c n}的前2020项的和S2020=8+2×23+3×24+⋯+ 2020×22021=4+1×22+2×23+3×24+…+2020×22021．然后利用错位相减法求解．【解答】解：（1）依题意得：b32=b2b4，∴(a1+6)2=(a1+2)(a1+14)，∴a12+12a1+36=a12+16a1+28，解得a1＝2．∴a n＝2+2（n﹣1）＝2n．设等比数列{b n}的公比为q，∴q=b3b2=a4a2=84=2，又b 2＝a 2＝4，∴b n =4×2n−2=2n ； （2）由（1）知，a n =2n ，b n =2n ． ∵c 1a 1+c 2a 2+⋯+c n−1a n−1+c n a n=2n+1，①当n ≥2时，c 1a 1+c 2a 2+⋯+c n−1a n−1=2n ，②由①﹣②得，c na n=2n ，即c n =n ⋅2n+1，又当n ＝1时，c 1=a 1b 2=23不满足上式， ∴c n ={8，n =1n ⋅2n+1，n ≥2；数列{c n }的前2020项的和S 2020=8+2×23+3×24+⋯+2020×22021 ＝4+1×22+2×23+3×24+…+2020×22021．设T 2020=1×22+2×23+3×24+⋯+2019×22020+2020×22021，③ 则2T 2020=1×23+2×24+3×25+⋯+2019×22021+2020×22022，④ 由③﹣④得：−T 2020=22+23+24+⋯+22021−2020×22022=22(1−22020)1−2−2020×22022=−4﹣2019×22022．∴T 2020=2019×22022+4，∴S 2020=T 2020+4=2019×22022+8．【点评】本题考查等差数列和等比数列的通项公式、性质，错位相减法求和，考查学生的逻辑推理能力，化归与转化能力及综合运用数学知识解决问题的能力．考查的核心素养是逻辑推理与数学运算．22．如图，在三棱锥D ﹣ABC 中，DA ＝DB ＝DC ，D 在底面ABC 上的射影E 在AC 上，DF ⊥AB 于F ．（Ⅰ）求证：BC 平行平面DEF ；（Ⅱ）若∠BAC =∠ADC =π3，求直线BE 与平面DAB 所成角的余弦值．【分析】（Ⅰ）推导出EF ∥BC ，由此能证明BC ∥平面DEF ．（Ⅱ）在△DEF 中过E 作DF 的垂线，垂足H ，由EF ⊥平面DAB ，得∠EBH 即所求线面角，由此能求出直线BE 与平面DAB 所成角的余弦值． 【解答】解：（Ⅰ）证明：因为DA ＝DB ＝DC ， 所以E ，F 分别是AB ，AC 的中点，所以EF ∥BC ， 因为EF ⊂平面DEF ，BC ⊄平面DEF ， 所以BC ∥平面DEF ．（Ⅱ）解：在△DEF 中过E 作DF 的垂线，垂足H ，由（Ⅰ）知EF ⊥平面DAB ，∠EBH 即直线BE 与平面DAB 所成角， 由F 是AB 的中点，AB ⊥EF 得EA ＝EB ， 设AC ＝2，∠BAC =π3，则DE =√3， EF =√32，EF =√152EH =√155，所以直线BE 与平面DAB 所成角的正弦值为sin ∠EBF =EHEB =√155， 所以直线BE 与平面DAB 所成角的余弦值为√105．【点评】本题考查线面平行的证明，考查线面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．。
2020-2021石家庄二中高一数学下期中试卷(含答案)
公式，以及直线斜率的求法，利用了数形结合的思想，其中抓住两个关键点是解本题的关
键．
6．B
解析：B 【解析】
【分析】
【详解】
①a∥α，a⊥b⇒b 与 α 平行，相交或 b⊂α，故①错误； ②若 a∥b，a⊥α，由直线与平面垂直和判定定理得 b⊥α，故②正确； ③a⊥α，a⊥b⇒b 与 α 平行，相交或 b⊂α，故③错误； ④若 a⊥α，b⊥α，则由直线与平面垂直的性质得 a∥b，故④正确． 故选 B．
10．C
解析：C 【解析】 【分析】 由题意首先求得长方体的棱长，然后求解其外接球的表面积即可. 【详解】
ab 2
设长方体的棱长分别为
a,
b,
c
，则
bc
3
，
ac 6
a 2
所以 abc2
36 ，于是
b
1
，
c 3
设球的半径为 R ，则 4R2 a2 b2 c2 14 ，所以这个球面的表面积为 4 R2 14 ．
中档题．
8．C
解析：C 【解析】
试题分析：由三视图可知，几何体是三棱柱消去一个同底的三棱锥，如图所示，三棱柱的
高为 ，消去的三棱锥的高为 ，三棱锥与三棱柱的底面为直角边长分别为 和 的直角三角
形，所以几何体的体积为
，故选 C．
考点：几何体的三视图及体积的计算．
【方法点晴】本题主要考查了几何体的三视图的应用及体积的计算，着重考查了推理和运
19．已知 PA 垂直于平行四边形 ABCD 所在平面，若 PC BD ，则平行四边形 ABCD 一
定是___________.
20．已知直线 l1 : y x 1 上有两个点 A(x1, y1) 和 B(x2 , y2 ) , 且 x1, x2 为一元二次方程 x2 6x 1 0 的两个根, 则过点 A, B 且和直线 l2 : x 1相切的圆的方程为
河北省石家庄市第二中学2019-2020学年高一下学期（线上）期中考试语文试题 Word版含解析
【点睛】分析文章结构，把握文章思路.解答此类试题首要的就是整体阅读,把握中心论点或论题,找出文中所用论据，分析论证方法，明辨论据与论点之间的关系,不仅要明辨中心论点与论据之间的关系，更要明辨各个分论点与论据之间的关系，最后提炼整合。同时还要注意论述类试题设题常见陷阱：答非所问、以偏概全、混淆时态、因果混乱、主次颠倒、混淆是非、无中生有、张冠李戴，曲解文意等等.对于试题选项内容一定要在原文中找到对应信息区间，然后再进行判断.
【解析】
【1题详解】
本题考查学生筛选文中信息的能力。解答此类题目，应先明确题干的提问方式，然后浏览选项，到文中圈出相关的句子，再进行比对，设题的误区如下：因果关系不当、于文无据、以偏概全、说法过于绝对化、变未然为已然等.
B项，“舍弃了厚人伦、美教化、移风俗等内容”错误，最后一段中说“突破了将文学视为‘经夫妇,成孝敬，厚人伦,美教化，移风俗’的工具的‘诗教’樊篱”，是“突破……藩篱”而不是“舍弃"。
C.文章从第二段到最后一段，从不同角度论述了建安文人忧患意识的多重内涵，结构清晰。
D.文章第四段引用曹植《赠徐干》的诗句，是为了证明建安文人以建立功业为自己的人生理想。
3。根据原文内容,下列说法正确的一项是( )
A。作者否定了老庄“由自我走向自我”的忧患，认为建安文人“由自我走向社会”的忧患是社会的进步。
“这钱要是老人的养老钱呢?”
“嘁。”豆豆反问，“你看这老头的气质，像乡下老农存钱的土办法吗？”
亮亮听了点点头。突然一激灵:“这个楼是银行的楼，这个老头要是个贪官……”
豆豆一下子用小手捂住他的嘴，前后看了看，然后用手抚摸自己的胸口说:“吓死我了。”
喘息一会儿，才定定地说：“《水浒》上有一句话，不义之财，取之何碍。"
河北省石家庄市第二中学2019-2020学年高一下学期期中考试语文试题答案
石家庄二中2019～2020学年度高一年级第二学期线上期中考试语文答案1.B “舍弃了厚人伦、美教化、移风俗等内容”错，最后一段中说“突破了将文学视为‘经夫妇，成孝敬,厚人伦，美教化，移风俗’的工具的‘诗教’樊篱”。
2.D “为了证明建安文人以建立功业为自己的人生理想”错，第四段是写建安文人对人生苦短的哀叹，对无法超越生命的感叹，引用曹植《赠徐干》的诗句也是为了证明这一点。
3.D A项，“作者否定了老庄‘由自我走向自我’的忧患”错，作者并没有否定老庄的忧患，只是说建安文人突破了老庄的忧患。
B项，“使得建安时期的文学在文学史上有一席之地”错，建安文学占一席之地的原因有很多，选项以偏概全。
C项，“不能体现建安文人的忧患意识”错。
建安文人的忧患意识中包含“他们以建立功业之举激励人生”，他们有时候积极向上，自然也会在诗歌中抒发豪迈之情，所以《观沧海》《龟虽寿》两首诗也能体现建安文人的忧患意识。
4.B “这个楼是银行的楼”是在发现纸钞之后，“这个楼是银行的楼”为老人曾是银行职工埋伏笔。
5.①善良厚道：收纸箱不讲价；觉得将“钱”据为己有不合适，担心这是人家的买房钱、养老钱。
②秉公守法：发现收来的纸箱中有巨款，坚持把钱交给公安机关处理。
③品德高尚：当好几年志愿者；当老人要把那些钞票送给他时，他予以回绝，不占便宜。
6.①丰富了主人公的形象，突出了亮亮品德高尚、善良厚道的形象。
②升华主题，耐人寻味，表现了对社会文明程度提升的赞颂。
③与小说标题、开头照应，结构严谨。
7.B8.C 应是“在其兄周武王去世后”。
周公是周文王姬昌的儿子，周武王姬发的弟弟。
9.D “高肇忌其为人，欲密出之，乃言于世宗，……于是出授安北将军、定州刺史。
”10.元详趁着于忠上表辞让的时候，暗中劝世宗任命于忠为列卿，让（世宗）解除他近臣的职务，听任他辞让爵位。
（“因”、“让”、“密”、“解”、“听”，各1分）11.所以停止这一外任，把朝内事务交付给你。
河北省石家庄市第二中学2019-2020学年高一下学期期中考试化学答案(23号10点半改)
石家庄二中2019-2020学年度高一年级第二学期线上期中考试化学试卷参考答案一、单项选择题（每题2分，共54分）题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14答案 D B A B A D B C B D B C A A题号15 16 17 18 19 20 21 22 23 24 25 26 27答案 D B B C C B D A C B C C D28．（共14分）（1）第四周期第VIA族（1分）（2）F（1分）（3）KOH （1分），OH- + Al(OH)3= AlO2- +2H2O（4）HCl（1分）（5）（6）高（1分），水分子间存在氢键（不写“分子间”不给分）（7）离子（1分），29．（共12分）（1）C＋2H2SO4(浓)CO2↑＋2SO2↑＋2H2O（2）②⑤⑥①（此小问共2分，全对得2分，有错即为0分）（3）验证二氧化硫已被吸收完全（4）d（5）CuSO4（6）Ca(OH) 2 或者Ba(OH) 230．（共10分）（1）②（1分），Cu2++2e-=Cu，24（2）A（1分），CH4-8e-+10OH-=CO32-+7H2O（3）b d（b、d写出一个给1分，别的情况不给分）31．（共10分）I．（1）CH4O(l)+O2(g)＝CO2(g) + 2H2O(l) ΔH＝﹣726.4kJ/mol（CH4O也可写为CH3OH）（2）2N2H4(g)+2NO2(g)＝3N2(g) + 4H2O(g)ΔH＝（2b-a）kJ/mol〔或者ΔH=﹣（a -2b）kJ/mol〕写成N2H4(g)+NO2(g)＝N2(g) + 2H2O(g)ΔH＝kJ/mol〔或者ΔH= ﹣kJ/mol〕也可得分II．（1）偏大（1分）（2）① 4.2（1分）②﹣56.2 （数值为56.3或者56.1也可得分）③不相等（1分）；相等（1分）。
河北省2020石家庄二中高一下期中考试答案
答案
一．选择题
1．C．2.A 3．A 4．C．5．D．6．C．7．C 8．A．9．C．
10．A．11．CD．12．BC．
二．填空题
13．
1 3n
2
三．解答题
14． 1,2
2023
15.2 16.
2
17．解：（I）因为 ＝
＝，
所以 2sinA﹣sinAcosB＝sinBcosA，
＝ ﹣1．
＝．
＝
，
， 可 得 PB ＝
＝
21．解：（1）依题意得：
，
∴
，
∴
，
解得 a1＝2． ∴an＝2+2（n﹣1）＝2n．
设等比数列{bn}的公比为 q，∴
，
又 b2＝a2＝4，∴
；
（2）由（1）知，
．
∵
，①
当 n≥2 时，
，②
由①﹣②得， 又当 n＝1 时， ∴
，即
，
不满足上式，
；
数列{cn}的前 2020 项的和 ＝4+1×22+2×23+3×24+…+2020×22021． 设
，③
则
，④
由③﹣④得：
＝
＝﹣4﹣2019×22022．
∴
，
∴S2020＝
．
22．（1）证明：因为 DA＝DB＝DC，所以 E，F 分别是 AB，AC 的中点， 所以 EF∥BC，从而 BC∥平面 DEF （2）解：在△DEF 中过 E 作 DF 的垂线，垂足 H，
由（1）知 EH⊥平面 DAB，∠EBH 即所求线面角， 由 F 是 AB 中点，AB⊥EF 得 EA＝EB
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
石家庄二中2019--2020学年度高一年级第二学期期中考试
数学试卷(线上)
（时间：120分钟，分值150分，命题人梁平，朱秀华）
一．选择题（共12题，每题5分，11,12题为多选题，其余均为单选）1．若a ，b ，c 为实数，且a ＜b ＜0，则下列命题正确的是（）
A ．ac 2＜bc 2
B ．
C ．a 2＞ab ＞b 2
D ．
2．设S n 为等差数列{a n }的前n 项和．若3S 3＝S 2+S 4，a 2＝﹣1，则a 4＝（）A ．﹣7B ．﹣10C ．10D ．12
3．如图，四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确的是（）
A ．BD ⊥SA
B ．AD ⊥S
C C ．平面SAC ⊥平面SB
D D ．AC ⊥SB
4．若函数f （x ）＝x
a
x
4（x ＞0，a ＞0）当且仅当x ＝2时取得最小值，则实数a 的值为（）A ．12B ．24C ．16D ．36
5．在正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 分别为CC 1，BB 1的中点，则异面直线AF ，B E 所成角的余弦值为（）
A ．
B ．
C ．
D ．
6．在△ABC 中，c
c a B 22cos
2
+=，则△ABC 为（）
A ．等腰直角三角形
B ．等边三角形
C ．直角三角形
D ．等腰三角形或直角三角形
7．一直三棱柱的每条棱长都是1，且每个顶点都在球O 的表面上，则球O 的表面积为（）
A ．
B ．
C ．
π3
7
D ．
8．已知数列a 1，是首项为4，公比为的等比数列，则a 4等于
（）A ．4
B ．32
C ．64
D ．128
9．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，已知1,3
==b B π
，求c a +的取值范围（
）
A ．（1，）
B ．（，2]
C ．（1，2]
D ．（1，2）
10．已知数列{a n }的前n 项和为S n ，S n ＝2a n ﹣2，若存在两项a n ，a m ，使得a n •a m ＝64，
则
n m 16
1+的最小值为（）A ．521B ．
6
25C ．
2
9
D ．
3
17多选题
11．设等差数列{a n }的前n 项和为S n ，公差为d ，且满足a 1＞0，S 11＝S 18，则对S n 描述正确的有（）A ．S 14是唯一最小值B ．S 15是最小值C ．S 29＝0D ．S 15是最大值12．在△ABC 中，D 在线段AB 上，且AD ＝5，BD ＝3，若CB ＝2CD ，cos ∠CDB ＝5
5
-，则（）
A ．
B ．△AB
C 的面积为8
C ．△ABC 的周长为
D ．△ABC 为锐角三角形
二．填空题（共4题，每题5分）
13．已知数列{a n }满足a 1＝1，3a n +1a n ＝a n ﹣a n +1，则通项a n ＝．
14．函数f （x ）＝⎩⎨
⎧>≤-)
0()
0(1x x x ，则不等式xf （x ）﹣x ≤2的解集为
15.在△ABC 中，边a ，b ，c 所对的角分别为A ，B ，C ．△ABC 的面积S 满足
S ＝b 2+c 2﹣a 2，若a ＝
，则
B
b
sin ＝．
16.对于数列{a n }，定义
为{a n }的“优值”，现已知某数列的
“优值”
，记数列{a n }的前n 项和为S n ，则
2020
2020
S ＝．
三．解答题（共6题，17题10分，其余均为12分，共70分）17．已知a ，b ，c 分别是△ABC 的内角A ，B ，C 的对边，且＝．
（Ⅰ）求．
（Ⅱ）若b ＝4，cos C ＝，求△ABC 的面积．
18．已知等差数列{a n }中，826=-a a ，且a 1，a 6，a 21依次成等比数列．（1）求数列{a n }的通项公式；（2）设
，数列{b n }的前n 项和为S n ，若11
1
=
n S ，求n 的值．19．如图，在四棱锥P ﹣ABCD 中，底面ABCD 是直角梯形，∠ABC ≠90°,CD AB //，
PA ⊥平面ABCD ，AB ＝2,PA ＝AD ＝DC ＝1．（1）证明：平面PAC ⊥平面PBC ；（2）求点D 到平面PBC 的距离．
20．法国数学家费马被称为业余数学之王，很多数学定理以他的名字命名．对△ABC而言，若其内部的点P满足∠APB＝∠BPC＝∠CPA＝120°，则称P为△ABC的费马点．如图所示，在△ABC中，已知∠BAC＝45°，设P为△ABC的费马点，且满足∠PBA＝45°，PA＝2．
（1）求△PAC的面积；
（2）求PB的长度．
21．等差数列{a n}的公差为2，a2，a4，a8分别等于等比数列{b n}的第2项，第3项，第4项．
（1）求数列{a n}和{b n}的通项公式；
（2）若数列{c n}满足，求数列{c n}的前2020项的和．22.如图，在三棱锥D﹣ABC中，DA＝DB＝DC，D在底面ABC上的射影E在AC上，
DF⊥AB于F．
（Ⅰ）求证：BC平行平面DEF；
（Ⅱ）若∠BAC＝∠ADC＝，求直线BE与平面DAB所成角的余弦值．。