现代光学系统第四章习题答案
《光学教程》课后习题解答

对 的第三个次最大位
即:
9、波长为的平行光垂直地射在宽的缝上,若将焦距为的透镜紧贴于缝的后面,并使光聚焦到屏上,问衍射图样的中央到⑴第一最小值;⑵第一最大值;⑶第三最小值的距离分别为多少?
解:⑴第一最小值的方位角为:
⑵第一最大值的方位角为:
⑶第3最小值的方位角为:
10、钠光通过宽的狭缝后,投射到与缝相距的照相底片上。所得的第一最小值与第二最小值间的距离为,问钠光的波长为多少?若改用X射线()做此实验,问底片上这两个最小值之间的距离是多少?
解:
⑴
⑵级光谱对应的衍射角为:
即在单缝图样中央宽度内能看到条(级)光谱
⑶由多缝干涉最小值位置决定公式:
第3xx 几何光学的基本原理
1、证明反射定律符合费马原理
证明:
设A点坐标为,B点坐标为
入射点C的坐标为
光程ACB为:
令
即:
*2、根据费马原理可以导出近轴光线条件下,从物点发出并会聚到像点的所有光线的光程都相等。由此导出薄透镜的物像公式。
另一个气泡
, 即气泡离球心
13、直径为的球形鱼缸的中心处有一条小鱼,若玻璃缸壁的影响可忽略不计,求缸外观察者所看到的小鱼的表观位置和横向放大率。
解:由球面折射成像公式:
解得 ,在原处
14、玻璃棒一端成半球形,其曲率半径为。将它水平地浸入折射率为的水中,沿着棒的轴线离球面顶点处的水中有一物体,利用计算和作图法求像的位置及横向放大率,并作光路图。
解:
由球面折射成像公式:
15、有两块玻璃薄透镜的两表面均各为凸球面及凹球面,其曲率半径为。一物点在主轴上距镜处,若物和镜均浸入水中,分别用作图法和计算法求像点的位置。设玻璃的折射率为,水的折射率为。
现代光学基础 光的偏振习题

第四章 光的偏振(2)一.选择题:(共30分)1.在双缝干涉实验中,用单色自然光,在屏上形成干涉条纹,若在两缝后放一个偏振片,则[ ](A ) 干涉条纹的间距不变,但明纹的亮度加强。
(B ) 干涉条纹的间距不变,但明纹的亮度减弱。
(C ) 干涉条纹的间距不窄,但明纹的亮度减弱。
(D ) 无干涉条纹。
2.光强为I 0的自然光垂直通过两个偏振片,它们的偏振化方向之间的夹角α =600,设偏振片没有吸收,则出射光强I 与入射光强I 0之比为 [ ](A )1/4 (B ) 3/4 (C )1/8 (D )3/83.如果两个偏振片堆叠在一起,且偏振化方向之间夹角为600,假设二者对光无吸收,光强为I 0的自然光垂直入在偏振片上,则出射光强为 [ ](A) I 0/8 (B) 3I 0 /8 (C) I 0 /4 (D) 3 I 0/44.光强为I 0的自然光依次通过两个偏振片和,若的偏振化方向的夹角,则透射偏振光的强度是[ ](A) I 0/4 (B) √3 I 0/4 (C) √3 I 0/2 (D) I 0/8 (E) 3I 0 /85.两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过。
当其中一偏振片慢慢转动1800时透射光强度发生变化为: [ ](A) 光强单调增加。
(B) 光强先增加,后有减小至零(C) 光强先增加,后减小,再增加(D) 光强先增加,然后减小,再增加,再减小至零6.一束自然光自空气射向 一块平板玻璃(如图),设入射角等于布儒斯特角i 0 ,则在界面2的反射光 [ ](A) 是自然光(B) 是完全偏振光且光矢量的振动方向垂直入射面 (C) 是完全偏振光且光矢量的振动方向平行入射面(D) 是部分偏振光7.一束单色平面偏振光,垂直投射到一块用方解石(负晶体)制成的四分之一波片(对投射光的频率)上,如图所示,如果入射光的振动面与光轴成450角,则对着光看从波片射出的光是(A) 逆时针方向旋转的圆偏振光(B) 逆时针方向旋转的椭圆偏振光(C) 顺时针方向旋转的圆偏振光(D) 顺时针方向旋转的椭圆偏振光8(A) 线偏振光 (B) 部分偏振光(C) 和原来旋转方向相同的圆偏振光(D) 和原来旋转方向相反的圆偏振光9(对投射光的频率)上,如图所示 成300角,则对着光看从波片射出的光是(A) 逆时针方向旋转的圆偏振光(B) 逆时针方向旋转的椭圆偏振光(C) 顺时针方向旋转的圆偏振光(D) 顺时针方向旋转的椭圆偏振光10.一束单色线偏振光其偏振化方向与1/4波片的光轴夹角α =π/4。
光学系统与像差全套答案

8.有一等边折射三棱镜,其折射率为1.65,求1)光线经该棱镜的二个折射面折射后产生最小偏角时的入射角;2)最小偏角值。
解:
(1)如上图,因为仅当 时,才产生最小偏向角,由公式 ,可得I1=55.6度
(2)如上图,根据折射定律,可得最小偏向角与 , 的关系 ,把 , 带入上式,可解得最小偏向角δm=51.2度。
9.一正薄透镜将物体成像于屏幕上时,测得其放大率β=-3×, 而当透镜向物体移近180mm时,屏上像的放大率为-4×,问该透镜的焦距为多少?
解:由 ,其中 为物体移动的距离,所以该透镜的焦距 mm, mm
该系统的焦距为2160mm
11.一焦距为10cm的正薄透镜在某一共轭距时,二个成清晰像的透镜位置相距15cm; 现若将共轭距加倍,问此时能成清晰像的二个透镜位置相距多少?
解:
2.一块厚度为15mm的平凸透镜放在报纸上,当平面朝上时, 报纸上的文字的虚像在平面下10mm处;当凸面朝上时,像的放大率为β=3,求透镜的折射率和凸面的曲率半径。
解:
26.某望远镜物镜由正、负分离的二个薄透镜组组成,已知 ,求其焦距。若用此望远镜来观察前方200m处的物体时,仅用第二个负透镜组来调焦以使其像仍位于物镜的原始焦平面上,问该镜组应向什么方向移动多少距离?此时物镜的焦距为多少?
解: 由薄透镜的物象位置关系
(1)l’=-250代入 得l=-60.607mm
4.有一实物被成一实像于薄透镜后300mm处时,其放大率正好为1倍。问放大率为50倍时,实像应位于透镜后什么位置?
解:由薄透镜的物象位置关系 和 。
由 和 ,解得焦距 mm;
陈家璧版-光学信息技术原理及应用习题解答(4-7章)

第四章习题4.1 若光波的波长宽度为λΔ,频率宽度为νΔ,试证明:λλννΔΔ=。
设光波波长为nm 8632=.λ,nm 8-10⨯2=λΔ,试计算它的频宽νΔ。
若把光谱分布看成是矩形线型,那么相干长度?=c l证明:参阅苏显渝,李继陶《信息光学》P349,第4.1题答案。
421.510c λνλ∆∆==⨯赫,32010()c c cl ct m ν===⨯∆4.2 设迈克尔逊干涉仪所用的光源为nm 0589=1.λ,nm 6589=.2λ的钠双线,每一谱线的宽度为nm 010.。
(1)试求光场的复自相干度的模。
(2)当移动一臂时,可见到的条纹总数大约为多少?(3)可见度有几个变化周期?每个周期有多少条纹? 答:参阅苏显渝,李继陶《信息光学》P349,第4.2题答案。
假设每一根谱线的线型为矩形,光源的归一化功率谱为 ()^1212rect rect νννννδνδνδν⎡--⎤⎛⎫⎛⎫=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦G (1)光场的复相干度为^1()()exp(2)1sin ()exp(2)[1exp(2)]2r j d c j j τνπντνδντπντπντ∞==+∆⎰G式中12ννν-=∆,复相干度的模为ντπδνττ∆=cos )(sin )(c r 由于νδν∆,故第一个因子是τ的慢变化非周期函数,第二个因子是τ的快变化周期函数。
相干时间由第一个因子决定,它的第一个零点出现在δντ1=c 的地方,c τ为相干时间,故相干长度δλλδλλδντ22≈===cc l c c 。
(2)可见到的条纹总数589301.05893====δλλλcl N (3)复相干度的模中第二个因子的变化周期ντ∆=1,故可见度的变化周期数601.06==∆=∆==δλλδννττc n 每个周期内的条纹数9826058930===n N4.3假定气体激光器以N 个等强度的纵模振荡,其归一化功率谱密度可表示为()()()()∑21-21--=+-1=N N n n NνννδνΔgˆ 式中,νΔ是纵模间隔,ν为中心频率并假定N 为奇数。
现代光学基础课件:第四章 光学仪器的基本原理

• 放大镜放大率的公式,通常采用以下形式
M 250 f'
• 放大镜的放大率仅由放大镜的焦距f ′ 所决定,焦 距越大则放大率越小。
§4-3 目 镜
放大镜是一种通过直接放大实物达到增大视角的助视仪器。下面将介绍 一种放大像的助视仪器——目镜。 一、目镜
• 由于场镜的物为虚物,所以这种目镜无法对物镜所成的像进行测量。
• 此目镜的视角较大(可达400),在250范围内像更清晰。而且结构 紧凑,适用于生物显微镜。
2、冉斯登目镜 1
Q 'Q
2
⑴ 结构:如图示 3
⑵ 特点:
F2 F
o1
• 场镜、视镜均为同种材
3
F1' 3
o2
2
2
料的平凸透镜,二镜凸 面相向,平面朝外。
网膜 脉络膜 黄斑中心凹
前室
晶状体
盲斑
总能将像成在网膜上。
后室
角膜和晶状体之间的空间称为前室;充满1.336的水状液;
晶状体和网膜所包围的空间称为后室;充满1.336的玻状体
人眼的构造剖视图
瞳孔 虹膜 角膜
1.376
前室
1.336
晶状体
巩膜
网膜 脉络膜 黄斑中心凹
视轴
光轴
盲斑
后室 1.336
眼睛的像方节点与中心凹的连线为眼睛的视轴, 在观察物 体时眼睛本能地把物体瞄准在这根轴上。
x'
f1' f1'
• 物镜的像被目镜放大,其放大率为
Me
250 f2 '
• 式中: f2' 为目镜的焦距。由此,显微镜系统的
物理光学课后习题答案-汇总

,
两式相减,可得 ,利用折射定律和小角度近似,得 ,( 为平行平板周围介质的折射率)
对于中心点,上下表面两支反射光线的光程差为 。因此,视场中心是暗点。由上式,得 ,因此,有12条暗环,11条亮环。
解:由题意,得,波列长度 ,
由公式 ,
又由公式 ,所以频率宽度
。
某种激光的频宽 Hz,问这种激光的波列长度是多少?
解:由相干长度 ,所以波列长度 。
第二章光的干涉及其应用
在与一平行光束垂直的方向上插入一透明薄片,其厚度 ,若光波波长为500nm,试计算插入玻璃片前后光束光程和相位的变化。
解:由时间相干性的附加光程差公式
,所以
。
杨氏干涉实验中,若波长 =600nm,在观察屏上形成暗条纹的角宽度为 ,(1)试求杨氏干涉中二缝间的距离(2)若其中一个狭缝通过的能量是另一个的4倍,试求干涉条纹的对比度
解:角宽度为 ,
所以条纹间距 。
由题意,得 ,所以干涉对比度
若双狭缝间距为,以单色光平行照射狭缝时,在距双缝远的屏上,第5级暗条纹中心离中央极大中间的间隔为,问所用的光源波长为多少是何种器件的光源
解:由公式 ,所以
= 。
此光源为氦氖激光器。
在杨氏干涉实验中,照明两小孔的光源是一个直径为2mm的圆形光源。光源发光的波长为500nm,它到小孔的距离为。问两小孔可以发生干涉的最大距离是多少?
解:因为是圆形光源,由公式 ,
则 。
月球到地球表面的距离约为 km,月球的直径为3477km,若把月球看作光源,光波长取500nm,试计算地球表面上的相干面积。
物理光学第四章 习题及答案

1λ第四章 习题及答案 1。
双缝间距为1mm ,离观察屏1m ,用钠灯做光源,它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ,问两种单色光的第10级这条纹之间的间距是多少? 解:由杨氏双缝干涉公式,亮条纹时:dDm λα=(m=0, ±1, ±2···) m=10时,nm x 89.511000105891061=⨯⨯⨯=-,nm x 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆2。
在杨氏实验中,两小孔距离为1mm ,观察屏离小孔的距离为50cm ,当用一片折射率1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ,试决定试件厚度。
21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆-3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。
试求注入气室内气体的折射率。
0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ4。
垂直入射的平面波通过折射率为n 的玻璃板,透射光经透镜会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。
工程光学习题参考答案第四章-光学系统中的光束限制
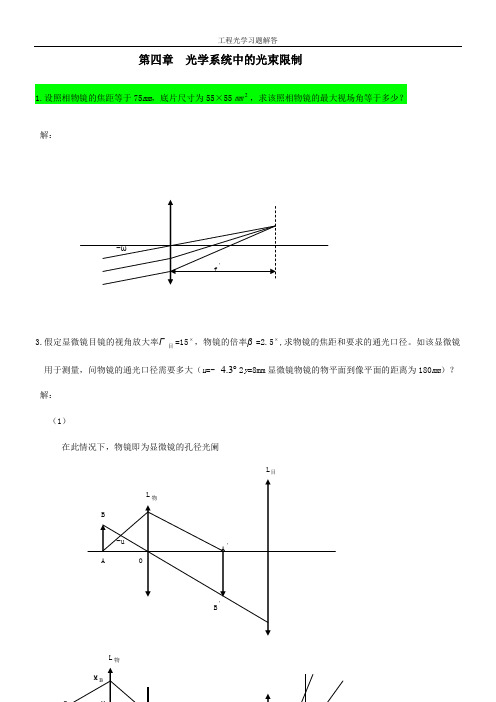
第四章 光学系统中的光束限制1.设照相物镜的焦距等于75mm ,底片尺寸为55×55㎜2,求该照相物镜的最大视场角等于多少?解:3.假定显微镜目镜的视角放大率Γ目=15⨯,物镜的倍率β=2.5⨯,求物镜的焦距和要求的通光口径。
如该显微镜用于测量,问物镜的通光口径需要多大(u =-︒3.42y =8mm 显微镜物镜的物平面到像平面的距离为180mm )? 解: (1)在此情况下,物镜即为显微镜的孔径光阑L 目(2)用于测量时,系统中加入了孔径光阑,目镜是视场光阑 由于u 已知,根据u 可确定孔径光阑的大小在中M M B B '∆ OA P AB A O M B A D B ‘‘’‘’‘孔=++21 答:物镜的焦距为36.73mm ,物镜的孔径为7.734mm ,用于测量时物镜孔径为15.726mm 。
4. 在本章第二节中的双目望远镜系统中,假定物镜的口径为30mm ,目镜的通光口径为20mm ,如果系统中没有视场光阑,问该望远镜最大的极限视场角等于多少?渐晕系数k =0.5的视场角等于多少? 解:(1)A ’F 2出瞳L 目αω'F '1f ‘物L '-目fL ‘Z-uOB‘(2)答:极限视场角等于11.33︒渐晕系数为0.5的视场角为9.08︒。
5. 如果要求上述系统的出射瞳孔离开目镜像方主面的距离为15mm,求在物镜焦面上加入的场镜焦距。
解:D 物对场镜成像,位置为mm f l 1081-=-=’物对目镜有’目f l l 1112'2=- l mm l Z 15''2== mm f 18=‘目 可得 mm l 902=对场镜‘场f l l 1111'1=- 答:场镜焦距为54mm 。
6.思考题:当物点在垂直光轴方向上下移动时,系统的孔径光阑是否改变?答:当物点在垂直光轴方向上下移动时,孔径光阑对来自不同点的成像光束 口径限制最大,所以系统的孔径光阑不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:空间相干件是指在波面上固定两空间点的位相差随时间的
变化情况。它描述在同一时刻波面上两点之间光场的相干性。 它用横向相干长度来表针。它与光源的线度或中心波长以及光
源中心对两观测点的张角有关。
[4-4] 光场的互相干函数和互相干度表针 答:光场的互相干函数和互相干度既可以表针空间相干性 也可以时间相干性。当互相干函数所指的两空间点重合, 互相干函数和互相干度就变成衡量同一空间点不同时间之 间的相干特性,即时间相干性。类似地,如果互相干函数 所指的两空间点不重合,但观测点到此两空间点等光程时, 互相干函数和互相干度就变成衡量同一时间点不同空间点
解:由
v
c
c
2
c
v
根据已知条件,可得
8 3 108 2 10 14 14 4 v 4.74 10 , 4.74 10 1.5 10 Hz 9 632.8 632.8 10
c
由于假定其光谱分布是矩形, 则
1 c c 1 c 相干长度 Lc c c 2 10 4 m
[4-2] 什么叫光源的时间相干性?由什么物理量来表针?与哪
些因素有关? 答:光源的时间相干性是指在同一空间点处,在任意相等的时间 区间t内测得该点的位相差随时间的变化情况。 用相干时间或相干长度来表针。光源的时间相干性取决于光源 的频谱宽度、中心波长等。 [4-3] 什么叫光源的空间相干性?由什么物理量来表针?与哪 些因素有关?
间光场的相干特性,即空间相干性。除此两种情况之外,
互相干函数和互相干度与光场的空间相干性和时间相干性 均有关。
