江苏高考数学一轮复习试题分类汇编14《解析几何》(苏教版)
江苏省高三数学专题专练练习:解析几何苏教版 试题

某某省2010届高三数学专题专练解析几何1.椭圆12222=+by a x (a>b>0)的两焦点为F 1F 2,连接点F1,F 2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为2.已知N (3,1),点A 、B 分别在直线y=x 和y =0上,则△ABN 的周长的最小值是。
3.双曲线C 与双曲线221916x y -=有共同的渐进线,且过点(A -,则C 的两条准线间的距离为4.一个动圆的圆心在抛物线28y x =上,且动圆恒与直线20x +=相切,则此动圆必经过点5.抛物线顶点在原点,焦点在y 轴上,其上一点(,1)M m 到焦点的距离为5,则此抛物线的方程为6.椭圆22221(0)x y a b a b +=>>22221x y a b-=的离心率为7.已知椭圆的焦点是12,,F F P 是椭圆上的一个动点,如果延长1F P 到Q ,使得2PQ PF =,那么动点Q 的轨迹是(写出曲线类型)8.椭圆221123x y +=的焦点是12,F F ,点P 在椭圆上,如果线段1F P 的中点在y 轴上,那么12:PF PF9.过点(0,1)M 且与抛物线2:4C y x =仅有一个公共点的直线方程是10.函数()()1x 1x x 21x f 2≤≤---=的图象为C,则C 与x 轴围成的封闭图形的面积为____________.11.若椭圆)0(12222>>=+b a by a x 的左、右焦点分别为21,F F ,抛物线bx y 42=的焦点为M ,若||2||21M F M F =,则此椭圆的离心率为12.已知双曲线)0(122>=-m my x 的右顶点为A ,而B 、C 是双曲线右支上两点,若三角形ABC 为等边三角形,则m 的取值X 围是。
13.经过双曲线)0,0(12222>>=-b a by a x 上任一点M ,作平行于实轴的直线,与渐近线交于Q P ,两点,则MQ MP ⋅=14.过抛物线焦点F 的直线与抛物线交于A 、B 两点,若A 、B 在抛物线准线上的射影分别为A 1、B 1,则∠A 1FB 1=。
高三数学解析几何复习材料 苏教版

高三数学解析几何复习材料一、考点回顾:1.基本曲线方程:圆,圆锥曲线3. 圆锥曲线的离心率:ae =椭圆:10<<e 双曲线:1>e 抛物线:1=e4. 圆锥曲线的焦半径公式:5. 直线与圆锥曲线之间的关系,①定直线曲线 ②动直线曲线6.高考热点题型主要有:⑴运用方程(组)求圆锥曲线的基本量 ⑵运用函数研究圆锥曲线的有关量的范围 ⑶运用直译法或参数法求动点的轨迹方程 ⑷运用“计算”的方法证明圆锥曲线的有关性质 ⑸运用一元二次方程研究直线和圆锥曲线相交的问题。
二、课前预习:1. 已知F F 12,是双曲线x y 2221-=的左右焦点,P 、Q 为右支上的两点,直线PQ 过F 2且倾斜角为α,则PF QF PQ 11+-的值为( ) A. 42B. 8C. 22D. 随α大小变化2. 已知椭圆222253n y m x +和双曲线222232ny m x -=1有公共的焦点,那么双曲线的渐近线方程是( )A.x =±y 215B.y =±x 215 C.x =±y 43D.y =±x 43 3. 定点M 3103,⎛⎝⎫⎭⎪与抛物线y x 22=上一点P 之间的距离为x P 1,到准线的距离为x 2,当x x 12+取得最小值时,点P 的坐标为___________。
4. 双曲线2x 2-y 2+6=0上的一点P 到一个焦点的距离为4,则点P 到较远的准线的距离是( )A .31264+ B .62364或 C .364 D .462+三、例题精析:5. 已知双曲线与椭圆在x 轴上有公共焦点,若椭圆焦距为52,它们的离心率是方程6x 2-55x+5 =0的两根,求双曲线和椭圆的标准方程.6. 已知双曲线2222by a x -=1(a >0,b >0)的右准线l 2与一条渐近线l 交于点P ,F 是双曲线的右焦点.(1)求证:PF ⊥l ;(2)若|PF |=3,且双曲线的离心率e =45,求该双曲线方程; (3)延长FP 交双曲线左准线l 1和左支分别为点M 、N ,若M 为PN 的中点,求双曲线的离心率.7. 已知椭圆C x a y ba b 1222210:+=>>()的一条准线方程是x =254,其左、右顶点分别是A 、B ;双曲线C x a y b222221:-=的一条渐近线方程为350x y -=。
江苏省高三数学一轮复习 考试试题精选(1)分类汇编14 解析几何

江苏省2014届高三数学一轮复习考试试题精选(1)分类汇编14:解析几何一、填空题1 .(江苏省扬州中学2014届高三开学检测数学试题)已知实数0p >,直线3420x y p -+=与抛物线22x py =和圆222()24p p x y +-=从左到右的交点依次为,A B C D 、、、则AB CD 的值为 ▲ . 【答案】1162 .(江苏省淮安市车桥中学2014届高三9月期初测试数学试题)如果圆x 2+y 2-2ax-2ay+2a 2-4=0与圆x 2+y 2=4总相交,则a 的取值范围是___.【答案】00a a -<<<<或3 .(江苏省常州市武进区2014届高三上学期期中考试数学(理)试题)若实数x 、y 满足()222x y x y +=+,则x y +的最大值是_________. 【答案】44 .(江苏省无锡市市北高中2014届高三上学期期初考试数学试题)椭圆中有如下结论:椭圆22221x y a b+=上斜率为1的弦的中点在直线0b y a x 22=+上,类比上述结论得到正确的结论为:双曲线22221x y a b-=上斜率为1的弦的中点在直线_______________上. 【答案】22x y0a b -=5 .(江苏省泰州中学2014届第一学学期高三数学摸底考试)设中心在原点的双曲线与椭圆+y 2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是__________. 【答案】2x 2﹣2y 2=1 6 .(江苏省连云港市赣榆县清华园双语学校2014届高三10月月考数学试题)我们把形如()0,0b y a b x a=>>-的函数称为“莫言函数”,并把其与y 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心,凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当1=a ,1=b 时,在所有的“莫言圆”中,面积的最小值______. ) 【答案】π3.7 .(江苏省无锡市2014届高三上学期期中调研考试数学试题)直线1y kx =+与圆22(3)(2)9x y -+-=相交于A B 、两点,若4AB >,则k 的取值范围是____________________. 【答案】1(,2)2-8 .(江苏省连云港市赣榆县清华园双语学校2014届高三10月月考数学试题)设F 是椭圆x 2a 2+y 2b2=1(a >b >0)右焦点,A 是其右准线与x 轴的交点.若在椭圆上存在一点P ,使线段PA 的垂直平分线恰好经过点F ,则椭圆离心率的取值范围是 ___________.]【答案】[12,1)9 .(江苏省南京市第五十五中学2014届高三上学期第一次月考数学试题)抛物线212y x =-的准线与双曲线22193x y -=的两条渐近线所围成的三角形的面积等于(A) (B)2【答案】A10.(江苏省苏州市2014届高三暑假自主学习测试(9月)数学试卷)已知双曲线221(0)y x m m-=>的离心率为2,则m 的值为 ______.【答案】311.(江苏省诚贤中学2014届高三上学期摸底考试数学试题)若双曲线221y x k-=的焦点到渐近线的距离为则实数k 的值是________. 【答案】812.(江苏省宿迁市2014届高三上学期第一次摸底考试数学试卷)已知双曲线22221(00)x y a b a b-=>>,的左、右焦点分别为12F F ,,以12F F 为直径的圆与双曲线在第一象限的交点为P .若1230PF F ∠=,则该双曲线的离心率为______.113.(江苏省宿迁市2014届高三上学期第一次摸底考试数学试卷)已知过点(25),的直线l 被圆22240C x y x y +--=:截得的弦长为4,则直线l 的方程为______.【答案】20x -=或4370x y -+=14.(江苏省无锡市2014届高三上学期期中调研考试数学试题)若中心在原点,以坐标轴为对称轴的圆锥曲线C ,且过点(2,3),则曲线C 的方程为________. 【答案】225x y -=15.(江苏省苏州市2014届高三暑假自主学习测试(9月)数学试卷)已知P 是直线l :40(0)kx y k ++=>上一动点,PA ,PB 是圆C :2220x y y +-=的两条切线,切点分别为A ,B .若四边形PACB 的最小面积为2,则k =______.【答案】216.(江苏省南京市2014届高三9月学情调研数学试题)如图,已知过椭圆的左顶点A(-a,0)作直线1交y 轴于点P,交椭圆于点Q.,若△AOP 是等腰三角形,且,则椭圆的离心率为____17.(江苏省扬州市扬州中学2014届高三10月月考数学试题)当且仅当m r n ≤≤时,两圆2249x y +=与22268250(0)x y x y r r +--+-=>有公共点,则n m -的值为______________.【答案】10 二、解答题18.(江苏省南京市2014届高三9月学情调研数学试题)已知椭圆C 的中心在坐标原点,右准线为x =离心率为3.若直线y=t(t>o)与椭 圆C 交于不同的两点A,B,以线段AB 为直径作圆M. (1)求椭圆C 的标准方程;(2)若圆M 与x 轴相切,求圆M 被直线10x +=截得的线段长. 【答案】19.(江苏省泰州中学2014届第一学学期高三数学摸底考试)给定圆P :222x y x +=及抛物线S :24y x =,过圆心P 作直线l ,此直线与上述两曲线的四个交点,自上而下顺次记为A B C D 、、、,如果线段AB BC CD 、、的长按此顺序构成一个等差数列,求直线l 的方程.【答案】解:圆P 的方程为()2211x y -+=,则其直径长2B C =,圆心为()1,0P ,设l 的方程为1ky x =-,即1x ky =+,代入抛物线方程得:244y ky =+,设()()1122,, ,A x y D x y ,有121244y y ky y +=⎧⎨=-⎩,则222121212()()416(1)y y y y y y k -=+-=+.故222222212121212||()()()()4y y AD y y x x y y -=-+-=-+ 22221212()[1()]16(1)4y y y y k +=-+=+,因此2||4(1)AD k =+ 据等差,2BC AB CD AD BC =+=-,所以36AD BC ==,即()2416k +=,2k =±, xyoABCDP即:l0y -0y +=20.(江苏省扬州市扬州中学2014届高三10月月考数学试题)已知椭圆:2222:1(0)x y C a b a b+=>>的离一条准线:2l x =. (1)求椭圆C 的方程;(2)设O 为坐标原点,M 是l 上的点,F 为椭圆C 的右焦点,过点F 作OM 的垂线与以OM 为直径的圆交于P Q 、两点.①若6PQ =,求圆D 的方程;②若M 是l 上的动点,求证:P 在定圆上,并求该定圆的方程. 【答案】解:(1)由题设:22c a a c⎧=⎪⎪⎨⎪=⎪⎩,1a c ⎧=⎪∴⎨=⎪⎩,2221b a c ∴=-=,椭圆C 的方程为:2212x y +=(2)①由(1)知:(1,0)F ,设(2,)M t ,则圆D 的方程:222(1)()124t t x y -+-=+, 直线PQ 的方程:220x ty +-=,PQ ∴=∴=,24t ∴=,2t ∴=±∴圆D 的方程:22(1)(1)2x y -+-=或22(1)(1)2x y -++=②解法(一):设00(,)P x y ,由①知:2220000(1)()124220t t x y x ty ⎧-+-=+⎪⎨⎪+-=⎩,即:2200000020220x y x ty x ty ⎧+--=⎪⎨+-=⎪⎩, 消去t 得:2200x y +=2,∴点P 在定圆22x y +=2上. 解法(二):设00(,)P x y ,则直线FP 的斜率为001FP y k x =-, ∵FP ⊥OM ,∴直线OM 的斜率为001OM x k y -=-,∴直线OM 的方程为:001x y x y -=-, 点M 的坐标为002(1)(2,)x M y --. ∵MP ⊥OP ,∴0OP MP ⋅=, ∴000002(1)(2)[]0x x x y y y ∂--++= ,∴2200x y +=2,∴点P 在定圆22x y +=2上. 21.(江苏省梁丰高级中学2014届第一学期阶段性检测一)如图:一个城市在城市改造中沿市内主干道国泰路修建的圆形广场圆心为O,半径为100m ,其与国泰路一边所在直线l 相切于点M,A 为上半圆弧上一点,过点A 作l 的垂线,垂足为 B.市园林局计划在ABM ∆内进行绿化,设ABM ∆的面积为S(单位:2m )(1)以θ=∠AON 为参数,将S 表示成θ的函数;(2)为绿化面积最大,试确定此时点A 的位置及面积的最大值.【答案】22.(江苏省南京市第五十五中学2014届高三上学期第一次月考数学试题)已知A 为椭圆)0(12222>>=+b a b y a x 上的一个动点,弦AB 、AC 分别过焦点F 1、F 2,当AC 垂直于x 轴时,恰好有13||||21::=.(Ⅰ)求椭圆离心率;O国 泰 路B M l AN(Ⅱ)设C F AF B F AF 222111,λλ==,试判断21λλ+是否为定值?若是定值,求出该定值并证明;若不是定值,请说明理由.【答案】解:(Ⅰ)当AC 垂直于x 轴时,a b AF 22||=,13||||21::=,∴ab AF 213||=∴a a b 242=,∴222b a =,∴22c b =,故22=e . (Ⅱ)由(Ⅰ)得椭圆的方程为22222b y x =+,焦点坐标为)0,(),0,(21b F b F -.①当弦AC 、AB 的斜率都存在时,设),(),,(),,(221100y x C y x B y x A ,则AC 所在的直线方程为)(00b x bx y y --=, 代入椭圆方程得0)(2)23(20200202=--+-y b y b x by y bx b .∴02222023bx b y b y y --=,F AF 222λ=,bx b y y 020223-=-=λ.同理b x b 0123+=λ,∴621=+λλ ②当AC 垂直于x 轴时,则bbb 23,112+==λλ,这时621=+λλ; 当AB 垂直于x 轴时,则5,121==λλ,这时621=+λλ. 综上可知21λλ+是定值 【D 】6.23.(江苏省苏州市2014届高三暑假自主学习测试(9月)数学试卷)已知椭圆22221(0)x y a b a b+=>>的长轴两端点分别为A ,B ,000(,)(0)P x y y >是椭圆上的动点,以AB 为一边在x 轴下方作矩形ABCD ,使(0)AD kb k =>,PD 交AB 于点E ,PC 交AB 于点F .(Ⅰ)如图(1),若k =1,且P 为椭圆上顶点时,PCD ∆的面积为12,点O 到直线PD 的距离为65,求椭圆的方程;(Ⅱ)如图(2),若k =2,试证明:AE ,EF ,FB 成等比数列.图(1) 图(2)【答案】解:(Ⅰ)如图,当k =1时,CD 过点(0,-b ),CD =2a ,∵PCD ∆的面积为12,∴122122a b ⨯⨯=,即6ab =.①此时D (-a ,-b ),∴直线PD 方程为20bx ay ab-+=.∴点O 到PD 的距离d =65. ② 由①②解得3,2a b ==∴所求椭圆方程为22194x y += (Ⅱ)如图,当k =2时,(,2),(,2)C a b D a b ---,设12(,0),(,0)E x F x,由D ,E ,P 三点共线,及1(,2)DE x a b =+,00(,2)DP x a y b =++ (说明:也可通过求直线方程做) 得100()(2)2()x a y b b x a ++=⋅+, ∴0102()2b x a x a y b ⋅++=+,即002()2b x a AE y b⋅+=+由C ,F ,P 三点共线,及2(,2)CF x a b =-,00(,2)CP x a y b =-+得200()(2)2()x a y b b x a -+=⋅-, ∴0202()2b a x a x y b ⋅--=+,即002()2b a x FB y b⋅-=+又2200221x y a b +=,∴222220022004()4(2)(2)b a x a y AE FB y b y b ⋅-⋅==++而00000002()2()242222222b x a b a x ay abEF a AE FB a a y b y b y b y b⋅+⋅-=--=--=-=++++∴2EF AE FB =⋅,即有AE ,EF ,FB 成等比数列24.(江苏省扬州中学2014届高三开学检测数学试题)如图,已知椭圆14:22=+y x C 的上、下顶点分别为B A 、,点P 在椭圆上,且异于点B A 、,直线BP AP 、与直线2:-=y l 分别交于点N M 、, (Ⅰ)设直线BP AP 、的斜率分别为1k 、2k ,求证:21k k ⋅为定值; (Ⅱ)求线段MN 的长的最小值;(Ⅲ)当点P 运动时,以MN 为直径的圆是否经过某定点?请证明你的结论.【答案】解(Ⅰ))1,0(A ,)1,0(-B ,令),(00y x P ,则由题设可知00≠x ,P∴ 直线AP 的斜率0011x y k -=,PB 的斜率0021x y k +=,又点P 在椭圆上,所以 142020=+y x ,(00≠x ),从而有411112020000021-=-=+⋅-=x y x y x y k k 。
苏教版 高三数学 一轮复习---压轴题型突破练——解析几何

压轴题型突破练——解析几何A 组 专项基础训练 (时间:35分钟,满分:62分)一、填空题(每小题5分,共35分)1.已知两条直线l 1:y =x ,l 2:ax -y =0,其中a 为实数,当这两条直线的夹角在⎝⎛⎭⎫0,π12内变动时,a 的取值范围是__________.答案 ⎝⎛⎭⎫33,1∪(1,3)解析 直线l 1的倾斜角为π4,依题意l 2的倾斜角的取值范围为⎝⎛⎭⎫π4-π12,π4∪⎝⎛⎭⎫π4,π4+π12,即⎝⎛⎭⎫π6,π4∪⎝⎛⎭⎫π4,π3,从而l 2的斜率a 的取值范围为⎝⎛⎭⎫33,1∪(1,3). 2.若直线3x +4y +m =0与圆x 2+y 2-2x +4y +4=0没有公共点,则实数m 的取值范围是 __________.答案 (-∞,0)∪(10,+∞)解析 将圆x 2+y 2-2x +4y +4=0化为标准方程,得(x -1)2+(y +2)2=1,圆心坐标为(1,-2),半径为1.若直线与圆无公共点,即圆心到直线的距离大于半径, 即d =|3×1+4×(-2)+m |32+42=|m -5|5>1,∴m <0或m >10.3.已知双曲线x 2a 2-y 2b 2=1 (a >0,b >0)与抛物线y 2=8x 有一个公共的焦点F ,且两曲线的一个交点为P ,若PF =5,则双曲线的渐近线方程为____________. 答案 y =±3x解析 设点P (x 0,y 0).依题意得,焦点F (2,0),⎩⎪⎨⎪⎧x 0+2=5,y 20=8x 0,于是有x 0=3,y 20=24;⎩⎪⎨⎪⎧a 2+b 2=4,9a 2-24b 2=1,由此解得a 2=1,b 2=3, 因此该双曲线的渐近线方程是y =±bax =±3x .4.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为________.答案 172解析 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 到点(0,2)的距离.因此所求的最小值等于⎝⎛⎭⎫122+22=172.5.如果x 2k -2+y 21-k =-1表示焦点在y 轴上的双曲线,那么它的半焦距c 的取值范围是________. 答案 (1,+∞)解析 将原方程化成标准方程为y 2k -1-x 2k -2=1.由题意知k -1>0且k -2>0,解得k >2.又a 2=k -1,b 2=k -2,所以c 2=a 2+b 2=2k -3>1, 所以c >1,故半焦距c 的取值范围是(1,+∞).6.若点(3,1)是抛物线y 2=2px 一条弦的中点,且这条弦所在直线的斜率为2,则p =________. 答案 2解析 设弦两端点为P 1(x 1,y 1),P 2(x 2,y 2),则⎩⎪⎨⎪⎧y 21=2px 1y 22=2px 2,两式相减得,y 1-y 2x 1-x 2=2p y 1+y 2=2.又∵y 1+y 2=2,∴p =2.7.已知抛物线x 2=4y 的焦点为F ,经过F 的直线与抛物线相交于A ,B 两点,则以AB 为直径的圆在x 轴上所截得的弦长的最小值是________. 答案 2 3解析 由抛物线定义得以AB 为直径的圆与抛物线的准线相切,利用直角三角形中勾股定理得到弦长的解析式,再求弦长的最小值.设以AB 为直径的圆的半径为r ,则AB =2r ≥4,r ≥2,且圆心到x 轴的距离是r -1,所以在x 轴上所截得的弦长为2r 2-(r -1)2=22r -1≥23,即弦长的最小值是2 3.二、解答题(共27分)8.(13分)已知椭圆C 的中心为坐标原点O ,一个长轴顶点为(0,2),它的两个短轴顶点和焦点所组成的四边形为正方形,直线l 与y 轴交于点P (0,m ),与椭圆C 交于异于椭圆顶点的两点A ,B ,且AP →=2PB →. (1)求椭圆的方程; (2)求m 的取值范围.解 (1)由题意,知椭圆的焦点在y 轴上,设椭圆方程为y 2a 2+x 2b2=1(a >b >0),由题意,知a =2,b =c ,又a 2=b 2+c 2,则b =2,所以椭圆方程为y 24+x 22=1.(2)设A (x 1,y 1),B (x 2,y 2),由题意,知直线l 的斜率存在, 设其方程为y =kx +m ,与椭圆方程联立,即⎩⎪⎨⎪⎧y 2+2x 2=4,y =kx +m ,消去y ,得(2+k 2)x 2+2mkx +m 2-4=0, Δ=(2mk )2-4(2+k 2)(m 2-4)>0,由根与系数的关系,知⎩⎪⎨⎪⎧x 1+x 2=-2mk2+k 2,x 1·x 2=m 2-42+k 2,又AP →=2PB →,即有(-x 1,m -y 1)=2(x 2,y 2-m ), 所以-x 1=2x 2.则⎩⎪⎨⎪⎧x 1+x 2=-x 2,x 1x 2=-2x 22,所以m 2-42+k 2=-2⎝ ⎛⎭⎪⎫2mk 2+k 22.整理,得(9m 2-4)k 2=8-2m 2, 又9m 2-4=0时等式不成立,所以k 2=8-2m 29m 2-4>0,得49<m 2<4,此时Δ>0.所以m 的取值范围为⎝⎛⎭⎫-2,-23∪⎝⎛⎭⎫23,2. 9.(14分)已知中心在原点的椭圆C :x 2a 2+y 2b2=1的一个焦点为F 1(0,3),M (x,4)(x >0)为椭圆C上一点,△MOF 1的面积为32.(1)求椭圆C 的方程;(2)是否存在平行于OM 的直线l ,使得直线l 与椭圆C 相交于A ,B 两点,且以线段AB 为直径的圆恰好经过原点?若存在,求出直线l 的方程;若不存在,说明理由. 解 (1)因为椭圆C 的一个焦点为F 1(0,3),所以c =3,b 2=a 2+9,则椭圆C 的方程为x 2a 2+y 2a 2+9=1,因为x >0,所以S △OMF 1=12×3×x =32,解得x =1.故点M 的坐标为(1,4).因为点M (1,4)在椭圆上,所以1a 2+16a 2+9=1,得a 4-8a 2-9=0,解得a 2=9或a 2=-1(不合题意,舍去),则b 2=9+9=18,所以椭圆C 的方程为x 29+y 218=1.(2)假设存在符合题意的直线l 与椭圆C 相交于A (x 1,y 1),B (x 2,y 2)两点,其方程为y =4x +m (因为直线OM 的斜率k =4),由⎩⎪⎨⎪⎧y =4x +m ,x 29+y 218=1,消去y 化简,得18x 2+8mx +m 2-18=0. 进而得到x 1+x 2=-8m18,x 1·x 2=m 2-1818.因为直线l 与椭圆C 相交于A ,B 两点, 所以Δ=(8m )2-4×18×(m 2-18)>0, 化简得m 2<162,解得-92<m <9 2. 因为以线段AB 为直径的圆恰好经过原点,所以OA →·OB →=0,所以x 1x 2+y 1y 2=0.又y 1y 2=(4x 1+m )(4x 2+m )=16x 1x 2+4m (x 1+x 2)+m 2, x 1x 2+y 1y 2=17x 1x 2+4m (x 1+x 2)+m 2 =17(m 2-18)18-32m 218+m 2=0.解得m =±102.由于±102∈(-92,92), 所以符合题意的直线l 存在,且所求的直线l 的方程为 y =4x +102或y =4x -102.B 组 专项能力提升 (时间:35分钟,满分:58分)一、填空题(每小题5分,共30分)1.已知椭圆E 的左、右焦点分别为F 1、F 2,过F 1且斜率为2的直线交椭圆E 于P 、Q 两点,若△PF 1F 2为直角三角形,则椭圆E 的离心率为________. 答案 53解析 由题意可知,∠F 1PF 2是直角,且tan ∠PF 1F 2=2,∴PF 2PF 1=2,又PF 1+PF 2=2a ,∴PF 1=2a 3,PF 2=4a3.根据勾股定理得⎝⎛⎭⎫2a 32+⎝⎛⎭⎫4a 32=(2c )2, 所以离心率e =c a =53.2.由直线y =x +1上的一点向圆(x -3)2+y 2=1引切线,则切线长的最小值为________. 答案7解析 如图所示, 设直线上一点P ,切点为Q ,圆心为M ,则PQ 即为切线长, MQ 为圆M 的半径,长度为1, PQ =PM 2-MQ 2=PM 2-1,要使PQ 最小,即求PM 的最小值,此题转化为求直线y =x +1上的点到圆心M 的最小距离, 设圆心到直线y =x +1的距离为d , 则d =|3-0+1|12+(-1)2=2 2.所以PM 的最小值为2 2. 所以PQ =PM 2-1≥(22)2-1=7.3.(2011·四川)在抛物线y =x 2+ax -5(a ≠0)上取横坐标为x 1=-4,x 2=2的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x 2+5y 2=36相切,则抛物线顶点的坐标为__________. 答案 (-2,-9)解析 当x 1=-4时,y 1=11-4a ;当x 2=2时,y 2=2a -1,所以割线的斜率k =11-4a -2a +1-4-2=a -2.设直线与抛物线的切点横坐标为x 0,由y ′=2x +a 得切线斜率为2x 0+a ,∴2x 0+a =a -2, ∴x 0=-1.∴直线与抛物线的切点坐标为(-1,-a -4),切线方程为y +a +4=(a -2)(x +1),即(a -2)x -y -6=0.圆5x 2+5y 2=36的圆心到切线的距离d =6(a -2)2+1.由题意得6(a -2)2+1=65,即(a-2)2+1=5.又a ≠0,∴a =4,此时,y =x 2+4x -5=(x +2)2-9,顶点坐标为(-2,-9).4.过椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点A 且斜率为1的直线与椭圆的另一个交点为M ,与y轴的交点为B ,若AM =MB ,则该椭圆的离心率为________.答案 63解析 由题意知A 点的坐标为(-a,0), 设直线的方程为y =x +a ,∴B 点的坐标为(0,a ),故M 点的坐标为⎝⎛⎭⎫-a 2,a 2, 代入椭圆方程得a 2=3b 2,∴2a 2=3c 2,∴e =63. 5.已知曲线x 2a -y 2b =1与直线x +y -1=0相交于P 、Q 两点,且OP →·OQ →=0(O 为原点),则1a-1b 的值为________. 答案 2解析 将y =1-x 代入x 2a -y 2b =1,得(b -a )x 2+2ax -(a +ab )=0.由题意,知a ≠b .设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=2aa -b ,x 1x 2=a +ab a -b .OP →·OQ →=x 1x 2+y 1y 2=x 1x 2+(1-x 1)(1-x 2) =2x 1x 2-(x 1+x 2)+1. 所以2a +2ab a -b -2a a -b+1=0,即2a +2ab -2a +a -b =0,即b -a =2ab ,所以1a -1b=2.6.设抛物线y 2=2x 的焦点为F ,过F 的直线交该抛物线于A ,B 两点,则AF +4BF 的最小值为________.答案 92解析 设A (x 1,y 1),B (x 2,y 2),则由抛物线定义可得AF +4BF =x 1+p 2+4⎝⎛⎭⎫x 2+p 2=x 1+12+4⎝⎛⎭⎫x 2+12=x 1+4x 2+52,设直线AB 的方程为ky =x -12,联立抛物线方程得方程组⎩⎪⎨⎪⎧ky =x -12,y 2=2x消元整理得y 2-2ky -1=0,由根与系数的关系可得y 1y 2=-1,又A ,B 在抛物线上,代入方程得y 21y 22=2x 1·2x 2=4x 1x 2=1,即x 1x 2=14,因此根据均值不等式AF +4BF =x 1+4x 2+52≥2x 1×4x 2+52=2+52=92,当且仅当x 1=4x 2时取得最小值92.二、解答题(共28分)7.(14分)如图,已知椭圆的中心在原点,焦点在x 轴上,长轴长是短轴长的2倍,椭圆经过点M (2,1),平行于OM 的直线l 在y 轴上的截距为m (m ≠0),l 交椭圆于A ,B 两个不同点. (1)求椭圆的方程;(2)求m 的取值范围.解 (1)设椭圆方程为x 2a 2+y 2b2=1 (a >b >0),则⎩⎪⎨⎪⎧a =2b ,4a 2+1b 2=1,解得a 2=8,b 2=2, ∴所求椭圆方程为x 28+y 22=1.(2)∵直线l 平行于OM ,且在y 轴上的截距为m ,又k OM =12,∴l 的方程为y =12x +m .由⎩⎨⎧y =12x +m ,x 28+y 22=1 得x 2+2mx +2m 2-4=0.∵直线l 与椭圆交于A ,B 两个不同点, ∴Δ=(2m )2-4(2m 2-4)>0, 解得-2<m <2且m ≠0.8.(14分)在平面直角坐标系xOy 中,如图所示,已知椭圆x 29+y 25=1的左,右顶点分别为A ,B ,右焦点为F .设过点T (t ,m )的直线TA ,TB 与此椭圆分别交于点M (x 1,y 1),N (x 2,y 2),其中m >0,y 1>0,y 2<0.(1)设动点P 满足:PF 2-PB 2=4,求点P 的轨迹;(2)设x 1=2,x 2=13,求点T 的坐标;(3)设t =9,求证:直线MN 必过x 轴上的一定点(其坐标与m 无关). (1)解 设P (x ,y ),由题知F (2,0),B (3,0),A (-3,0), 则PF 2=(x -2)2+y 2,PB 2=(x -3)2+y 2,由PF 2-PB 2=4,得(x -2)2+y 2-[(x -3)2+y 2]=4,化简,得x =92.故点P 的轨迹方程是x =92.(2)解 将x 1=2,x 2=13分别代入椭圆方程,并考虑到y 1>0,y 2<0,得M ⎝⎛⎭⎫2,53,N ⎝⎛⎭⎫13,-209. 则直线MA 的方程为y -053-0=x +32+3,即x -3y +3=0直线NB 的方程为y -0-209-0=x -313-3,即5x -6y -15=0.联立方程⎩⎪⎨⎪⎧x -3y +3=0,5x -6y -15=0,解得x =7,y =103,所以点T 的坐标为⎝⎛⎭⎫7,103. (3)证明 如图所示, 点T 的坐标为(9,m ).直线TA 的方程为y -0m -0=x +39+3,直线TB 的方程为y -0m -0=x -39-3,分别与椭圆x 29+y 25=1联立方程,解得M ⎝ ⎛⎭⎪⎫3(80-m 2)80+m 2,40m 80+m 2, N ⎝ ⎛⎭⎪⎫3(m 2-20)20+m 2,-20m 20+m 2.直线MN 的方程为y +20m20+m 240m 80+m 2+20m 20+m 2=x -3(m 2-20)20+m 23(80-m 2)80+m 2-3(m 2-20)20+m 2. 令y =0,解得x =1,所以直线MN 必过x 轴上的一定点(1,0).。
2019届江苏专版高考数学一轮复习第十四章平面解析几何初步14

解析 (1)设圆的方程为x2+y2+Dx+Ey+F=0, 将P、Q两点的坐标分别代入得 2D-4E-F=20,① 3D-E+F=-10.② 令y=0,得x2+Dx+F=0.③ 设x1,x2是方程③的两根, 由|x1-x2|=6得D2-4F=36,④ 由①②④解得D=-2,E=-4,F=-8,或D=-6,E=-8,F=0. 故所求圆的方程为x2+y2-2x-4y-8=0,或x2+y2-6x-8y=0.
3.圆的一般方程
方程x2+y2+Dx+Ey+F=0可变形为
x
D 2
2
+
y
E 2
2
=
D2
E2 4
4F
.
(1)当D2+E2-4F>0时,方程表示以④
D 2
,
E 2
为圆心,⑤
D2 E2 4F
2
为半径的圆;
(2)当D2+E2-4F=0时,方程表示D2+E2-4F<0时,方程不表示任何图形. (4)圆的标准方程的优点在于明确地指出了圆心和半径,而一般方程突 出了方程形式的特点: (i)x2和y2系数相等且不为0.
高考数学
§14.2 圆的方程
知识清单
1.圆的定义
平面内到定点的距离等于定长的点的集合(轨迹)叫做圆.定点就是①
圆心 ,定长就是② 半径 .
2.圆的标准方程
(1)方程(x-a)2+(y-b)2=r2(r>0)表示圆心为③ (a,b) ,半径为r的圆的标准
方程;
(2)特别地,以原点为圆心,r(r>0)为半径的圆的标准方程为x2+y2=r2.
高三数学专题复 习-解析几何苏教版

高三数学专题复习-解析几何苏教版【本讲教育信息】一. 教学内容: 专题复习-解析几何【高考要求】二、基本内容:(二)圆的方程(1)圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆(2)圆的标准方程 :222)()(r b y a x =-+- 圆心为),(b a C ,半径为r , (3)圆的一般方程:只有当0422>-+F E D 时,022=++++F Ey Dx y x ①表示的曲线才是圆,把形如①的方程称为圆的一般方程(1)当0422>-+F E D 时,①表示以(-2D ,-2E )为圆心,F E D 42122-+为半径的圆;(2)当0422=-+F E D 时,方程①只有实数解2D x -=,2Ey -=,即只表示一个点(-2D ,-2E ); (3)当0422<-+F E D 时,方程①没有实数解,因而它不表示任何图形。
【典型例题】例1、过点P (2,1)的直线分别与x 轴和y 轴的正半轴交于A 、B 两点.求OA OB ⋅取得最小值时直线的方程.解:设直线的方程为1,(0,0),x y a b a b +=>>211a b+=. ∴28ab b a ab =+≥≥, ∴8OA OB ab ∙=≥,即OA OB ⋅的最小值为8 当且仅当a=2b ,即a =4,b =2时取得等号。
故所求直线的方程为:x +2y -4=0. 变式:过点P (2,1)的直线分别与x 轴和y 轴的正半轴交于A 、B 两点.求PA PB ⋅取得最小值时直线的方程.解:显然直线的斜率存在,设其方程为:y -1=k (x -2),则A 1(2,0),(0,12)B k k--由1201200k k k->-><及得,∴PA PB ⋅4=当且仅当2211k k k ==-即时取等号,∴PA PB ⋅的最小值为4时直线的方程为x+y -3=0.例2、已知甲、乙、丙三种食物的维生素A 、B 含量及成本如下表,若用甲、乙、丙三种食物各x 千克,y 千克,z 千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A 和(Ⅰ)用x ,y 表示混合食物成本c 元;(Ⅱ)确定x ,y ,z 的值,使混合物的成本最低.解:(Ⅰ)由题,1194c x y z =++,又100x y z ++=,所以40075c x y =++.(Ⅱ)由60070040056000, 10080040050063000x y z z x y x y z ++≥⎧=--⎨++≥⎩及得,46320 3130x y x y +≥⎧⎨-≥⎩,所以75450.x y +≥所以当且仅当⎩⎨⎧=-=+130y x 3320y 6x 4,即⎩⎨⎧==20y 50x 时等号成立.所以,当x =50千克,y =20千克,z =30千克时,混合物成本最低,为850元.点评:本题为线性规划问题,用解析几何的观点看,问题的解实际上是由四条直线所围成的区域00463203130xy x y x y ≥⎧⎪≥⎪⎨+≥⎪⎪-≥⎩上使得40075c x y =++最大的点.不难发现,应在点M (50,20)处取得.例3、如图,一列载着危重病人的火车从O 地出发,沿射线OA 的方向行驶,其中sin α=.在距离O 地a 5(a 为正常数)千米、北偏东β角的N 处住有一位医学专家,其中3sin 5β=.现120指挥中心紧急调离O 地正东p 千米B 处的救护车,先到N 处载上医学专家,再全速赶往载有危重病人的火车,并在C 处相遇。
2021年高考数学一轮总复习 能力提升练 解析几何 理 苏教版

2021年高考数学一轮总复习能力提升练解析几何理苏教版一、填空题1.(xx·山东省实验中学诊断)已知两条直线y=ax-2和3x-(a+2)y+1=0互相平行,则a等于________.解析因为直线y=ax-2的斜率存在且为a,所以-(a+2)≠0,所以3x-(a+2)y+1=0的斜截式方程为y=3a+2x+1a+2,由两直线平行,得3a+2=a且1a+2≠-2,解得a=1或a=-3.答案1或-32.(xx·洛阳模拟)椭圆x216+y29=1的焦距为________.解析由题意知a2=16,b2=9,所以c2=a2-b2=16-9=7,所以c=7,即焦距为2c=27.答案273.(xx·长沙模拟)在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于________.解析圆心到直线的距离d=|-5|32+42=1,弦AB的长l=2r2-d2=24-1=2 3.答案2 34.(xx·武汉一模)已知圆C经过A(5,2),B(-1,4)两点,圆心在x轴上,则圆C的方程是________________.解析设圆心坐标为C(a,0),则|AC|=|BC|,即a-52+22=a+12+42,解得a=1,所以半径r=1+12+42=20=25,所以圆C的方程是(x-1)2+y2=20.答案 (x -1)2+y 2=205.(xx·湖州模拟)设双曲线x 2a 2-y 29=1(a >0)的焦点为(5,0),则该双曲线的离心率等于________.解析 因为双曲线的焦点为(5,0),所以c =5,又a 2+9=c 2=25,所以a 2=16,a =4,所以离心率为e =c a =54.答案546.(xx·济南一模)若抛物线y 2=2px (p >0)的焦点在直线x -2y -2=0上,则该抛物线的准线方程为________.解析 抛物线的焦点坐标为⎝ ⎛⎭⎪⎫p2,0,代入直线x -2y -2=0方程,得p2-2=0,即p =4,所以抛物线的准线方程为x =-p 2=-42=-2.答案 x =-27.(xx·郑州模拟)以双曲线x 26-y 23=1的右焦点为圆心且与双曲线的渐近线相切的圆的方程是______________.解析 双曲线的右焦点为(3,0),双曲线的渐近线为y =±22x ,不妨取渐近线y =22x ,即2x -2y =0,所以圆心到渐近线的距离等于圆的半径,即r =|32|22+22=326=33= 3.所以圆的方程为(x -3)2+y 2=3.答案 (x -3)2+y 2=38.(xx·汕头一模)若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为________.解析 抛物线的焦点坐标为⎝ ⎛⎭⎪⎫p2,0,椭圆的右焦点为(2,0),所以由p2=2,得p =4.答案 49.(xx·杭州模拟)已知两点M (-5,0)和N (5,0),若直线上存在点P ,使|PM |-|PN |=6,则称该直线为“R 型直线”.给出下列直线:①y =x +1;②y =2;③y =43x ;④y =2x+1,其中为“R 型直线”的是________.解析 由题意可知,点P 的轨迹是在双曲线的右支上,其中2a =6,a =3,c =5,所以b 2=c 2-a 2=16.所以双曲线方程为x 29-y 216=1(x >0).显然当直线y =x +1与y =2和双曲线的右支有交点,所以为“R 型直线”的是①②. 答案 ①②10.(xx·湖州一模)已知抛物线y 2=4px (p >0)与双曲线x 2a 2-y 2b2=1(a >0,b >0)有相同的焦点F ,点A 是两曲线的交点,且AF ⊥x 轴,则双曲线的离心率为________.解析 依题意,得F (p,0),因为AF ⊥x 轴,设A (p ,y ),y >0,y 2=4p 2,所以y =2p .所以A (p,2p ).又点A 在双曲线上,所以p 2a 2-4p 2b 2=1.又因为c =p ,所以c 2a 2-4c2c 2-a2=1,化简,得c 4-6a 2c 2+a 4=0,即⎝ ⎛⎭⎪⎫c a 4-6⎝ ⎛⎭⎪⎫c a 2+1=0.所以e 2=3+22,e =2+1.答案2+111.(xx·兰州一模)已知抛物线x 2=4y 上一点P 到焦点F 的距离是5,则点P 的横坐标是________.解析 由抛物线定义知,y P +1=5,即y P =4,所以有x 2P =16,解得x P =±4. 答案 ±412.(xx·上海卷)设AB 是椭圆Γ的长轴,点C 在Γ上,且∠CBA =π4.若AB =4,BC =2,则Γ的两个焦点之间的距离为________.解析 设D 在AB 上,且CD ⊥AB ,AB =4,BC =2,∠CBA =45°,所以有CD =1,DB =1,AD =3,所以有C (1,1),把C (1,1)代入椭圆的标准方程得1a 2+1b2=1,a 2=b 2+c 2且2a=4,解得,b 2=43,c 2=83,则2c =43 6.答案436 13.已知双曲线x 2-y 22=1的焦点为F 1,F 2,点M 在双曲线上且MF 1→·MF 2→=0,则M 到x 轴的距离为________.解析 设|MF 1|=m ,|MF 2|=n ,则⎩⎪⎨⎪⎧|m -n |=2,m 2+n 2=12,可得mn =4.由△MF 1F 2的面积可得M 到x 轴的距离为423=233.答案23314.(xx·淄博二模)若双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1和F 2,线段F 1F 2被抛物线y 2=2bx 的焦点分成5∶3两段,则此双曲线的离心率为________. 解析 抛物线的焦点坐标为⎝ ⎛⎭⎪⎫b2,0,由题意知b2--cc -b2=53,c =2b ,所以c 2=4b 2=4(c 2-a 2),即4a 2=3c 2,所以2a =3c ,所以e =c a=23=233. 答案233二、解答题15.(xx·广东卷改编)已知抛物线C 的顶点为原点,其焦点F (0,c )(c >0)到直线l :x -y -2=0的距离为322.设P 为直线l 上的点,过点P 作抛物线C 的两条切线PA ,PB ,其中A ,B 为切点. (1)求抛物线C 的方程;(2)当点P (x 0,y 0)为直线l 上的定点时,求直线AB 的方程. 解 (1)依题意,设抛物线C 的方程为x 2=4cy , 则|c +2|2=322,c >0,解得c =1.所以抛物线C 的方程为x 2=4y . (2)抛物线C 的方程为x 2=4y , 即y =14x 2,求导得y ′=12x ,设A (x 1,y 1),B (x 2,y 2),则切线PA ,PB 的斜率分别为12x 1,12x 2,所以切线PA 的方程为y -y 1=x 12(x -x 1), 即y =x 12x -x 212+y 1,即x 1x -2y -2y 1=0.同理可得切线PB 的方程为x 2x -2y -2y 2=0, 又点P (x 0,y 0)在切线PA 和PB 上,所以x 1x 0-2y 0-2y 1=0,x 2x 0-2y 0-2y 2=0,所以(x 1,y 1),(x 2,y 2)为方程x 0x -2y 0-2y =0 的两组解, 所以直线AB 的方程为x 0x -2y -2y 0=0.16.已知圆M :(x +1)2+y 2=1,圆N :(x -1)2+y 2=9,动圆P 与圆M 外切并且与圆N 内切,圆心P 的轨迹为曲线C . (1)求C 的方程;(2)l 是与圆P ,圆M 都相切的一条直线,l 与曲线C 交于A ,B 两点,当圆P 的半径最长时,求|AB |.解 (1) 设圆P 的半径为r ,则|PM |=1+r ,|PN |=3-r ,∴|PM |+|PN |=4>|MN |,∴P 的轨迹是以M ,N 为焦点的椭圆(左顶点除外),且2a =4,2c =2,∴a =2,c =1,∴b 2=a 2-c 2=3.∴P 的轨迹曲线C 的方程为x 24+y 23=1(x ≠-2).(2)由(1)知2r =(|PM |-|PN |)+2≤|MN |+2=4, ∴圆P 的最大半径为r =2.此时P 的坐标为(2,0). 圆P 的方程为(x -2)2+y 2=4.①当l 的倾斜角为90°,方程为x =0时,|AB |=23, ②当l 的倾斜角不为90°, 设l 的方程为y =kx +b (k ∈R ),⎩⎪⎨⎪⎧|-k +b |1+k 2=1,|2k +b |1+k 2=2,解得⎩⎪⎨⎪⎧k =24,b =2或⎩⎪⎨⎪⎧k =-24,b =- 2.∴l 的方程为y =24x +2,y =-24x - 2.联立方程⎩⎪⎨⎪⎧x 24+y 23=1,y =24x +2,化简得7x 2+8x -8=0,∴x 1+x 2=-87,x 1x 2=-87,∴|AB |=1+k 2x 1+x 22-4x 1x 2=187. 当k =-24时,由图形的对称性可知|AB |=187. 综上,|AB |=23或187. 17.(xx·东北三校联考)如图,已知点E (m,0)(m >0)为抛物线y 2=4x 内一个定点,过E 作斜率分别为k 1,k 2的两条直线交抛物线于点A ,B ,C ,D ,且M ,N 分别是AB ,CD 的中点.(1)若m =1,k 1k 2=-1,求△EMN 面积的最小值; (2)若k 1+k 2=1,求证:直线MN 过定点. 解 (1)当m =1时,E 为抛物线y 2=4x 的焦点, ∵k 1k 2=-1,∴AB ⊥CD .设直线AB 的方程为y =k 1(x -1),A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧y =k 1x -1,y 2=4x ,得k 1y 2-4y -4k 1=0,y 1+y 2=4k 1,y 1y 2=-4.∵M ⎝⎛⎭⎪⎫x 1+x 22,y 1+y 22,∴M ⎝ ⎛⎭⎪⎫2k 21+1,2k 1,同理,点N (2k 21+1,-2k 1), ∴S △EMN =12|EM |·|EN |=12⎝ ⎛⎭⎪⎫2k 212+⎝ ⎛⎭⎪⎫2k 12·2k 212+-2k 12=2k 21+1k 21+2≥22+2=4,当且仅当k 21=1k 21,即k 1=±1时,△EMN 的面积取得最小值4. (2)设直线AB 的方程为y =k 1(x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k 1x -m ,y 2=4x 得k 1y 2-4y -4k 1m =0,y 1+y 2=4k 1,y 1y 2=-4m ,∵M ⎝⎛⎭⎪⎫x 1+x 22,y 1+y 22,∴M ⎝ ⎛⎭⎪⎫2k 21+m ,2k 1,同理,点N ⎝ ⎛⎭⎪⎫2k 22+m ,2k 2, ∴k MN =k 1k 2k 1+k 2=k 1k 2.∴直线MN 的方程为y -2k 1=k 1k 2⎣⎢⎡⎦⎥⎤x -⎝ ⎛⎭⎪⎫2k 21+m ,即y =k 1k 2(x -m )+2,∴直线MN 恒过定点(m,2).18.(xx·重庆卷)如图,椭圆的中心为原点O ,长轴在x 轴上,离心率e =22,过左焦点F 1作x 轴的垂线交椭圆于A ,A ′两点,|AA ′|=4.(1)求该椭圆的标准方程;(2)取垂直于x 轴的直线与椭圆相交于不同的两点P ,P ′,过P ,P ′作圆心为Q 的圆,使椭圆上的其余点均在圆Q 外.若PQ ⊥P ′Q ,求圆Q 的标准方程. 解 (1)由题意知点A (-c,2)在椭圆上,则-c2a2+22b 2=1,从而e 2+4b2=1.由e =22,得b 2=41-e 2=8,从而a 2=b 21-e 2=16.故该椭圆的标准方程为x 216+y 28=1.(2)由椭圆的对称性,可设Q (x 0,0). 又设M (x ,y )是椭圆上任意一点,则|QM |2=(x -x 0)2+y 2=x 2-2x 0x +x 20+8⎝ ⎛⎭⎪⎫1-x 216=12(x -2x 0)2-x 20+8(x ∈[-4,4]).设P (x 1,y 1),由题意知,P 是椭圆上到Q 的距离最小的点,因此,上式当x =x 1时取最小值,又因x 1∈(-4,4),所以上式当x =2x 0时取最小值,从而x 1=2x 0,且|QP |2=8-x 20.因为PQ ⊥P ′Q ,且P ′(x 1,-y 1),所以QP →·QP ′→=(x 1-x 0,y 1)·(x 1-x 0,-y 1)=0, 即(x 1-x 0)2-y 21=0. 由椭圆方程及x 1=2x 0, 得14x 21-8⎝ ⎛⎭⎪⎫1-x 2116=0, 解得x 1=±463,x 0=x 12=±263. 从而|QP |2=8-x 20=163. 故这样的圆有两个,其标准方程分别为 ⎝ ⎛⎭⎪⎫x +2632+y 2=163,⎝⎛⎭⎪⎫x -2632+y 2=163.]122203 56BB 嚻34259 85D3 藓28454 6F26 漦+Y &\K.24882 6132 愲\=。
高三数学专题复习-解析几何苏教版知识精讲
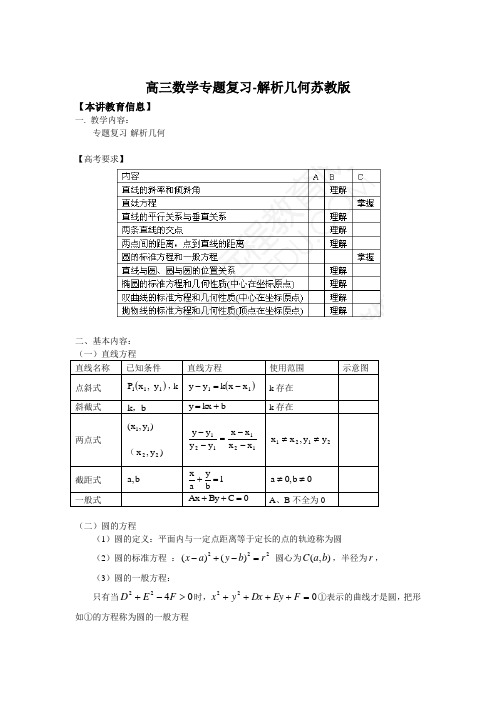
高三数学专题复习-解析几何苏教版【本讲教育信息】一. 教学内容: 专题复习-解析几何【高考要求】二、基本内容: 直线名称 已知条件直线方程使用范围 示意图 点斜式 ()111y ,x P ,k ()11x x k y y -=- k 存在 斜截式b k , b kx y += k 存在两点式)y ,x (11()y ,x 22121121x x x x y y y y --=-- 2121y y ,x x ≠≠截距式 b ,a1by a x =+ 0b ,0a ≠≠一般式0C By Ax =++A 、B 不全为0(二)圆的方程(1)圆的定义:平面内与一定点距离等于定长的点的轨迹称为圆(2)圆的标准方程 :222)()(r b y a x =-+- 圆心为),(b a C ,半径为r , (3)圆的一般方程:只有当0422>-+F E D 时,022=++++F Ey Dx y x ①表示的曲线才是圆,把形如①的方程称为圆的一般方程(1)当0422>-+F E D 时,①表示以(-2D ,-2E )为圆心,F E D 42122-+为半径的圆;(2)当0422=-+F E D 时,方程①只有实数解2D x -=,2Ey -=,即只表示一个点(-2D ,-2E); (3)当0422<-+F E D 时,方程①没有实数解,因而它不表示任何图形。
渐 近 线焦点在x 轴上时:0=-bya x 焦点在y 轴上时: 0=-bxa y 图形xyO FlxyO Fl方程)0(22>=p px y )0(22>-=p px y )0(22>=p py x )0(22>-=p py x焦点 )0,2(p )0,2(p-)2,0(p)2,0(p -准线 2p x -= 2p x =2p y -=2p y =【典型例题】例1、过点P (2,1)的直线分别与x 轴和y 轴的正半轴交于A 、B 两点.求OA OB ⋅取得最小值时直线的方程.解:设直线的方程为1,(0,0),x y a b a b +=>>211a b+=. ∴2228ab b a ab ab =+≥≥于是, ∴8OA OB ab •=≥,即OA OB ⋅的最小值为8 当且仅当a =2b ,即a =4,b =2时取得等号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 y2 2 x y ,则 x y 的最大值是_________.
【答案】4
4 .(江苏省无锡市市北高中 20XX 届高三上学期期初考试数学试题)椭圆中有如下结论:椭圆
x2 a2
y2 b2
1
上斜率为
1
的弦的中点在直线
x a2
y b2
0 上,类比上述结论得到正确的结论为:双
曲线 x2 y2 1上斜率为 1 的弦的中点在直线_______________上. a2 b2
线为 x 3 2 ,离心率为 6 学科网.若直线 y=t(t>o)与椭 3
圆 C 交于不同的两点 A,B,以线段 AB 为直径作圆 M. (1)求椭圆 C 的标准方程;
(2)若圆 M 与 x 轴相切,求圆 M 被直线 x 3y 1 0 截得的线段长.
=1(a>b>0)右焦点,A 是其右准线与 x 轴的交点.若在椭圆上存在一点 P,使线段 PA 的垂直
平分线恰好经过点 F,则椭圆离心率的取值范围是 ___________.]
【答案】[12,1)
9 .(江苏省南京市第五十五中学 20XX 届高三上学期第一次月考数学试题)抛物线 y2 12x
的准线与双曲线 x2 y2 1的两条渐近线所围成的三角形的面积等于 93
别为 A,B.若四边形 PACB 的最小面积为 2,则 k=______. 【答案】2
16.(江苏省南京市 20XX 届高三 9 月学情调研数学试题)如图,已知过椭圆
的
左顶点 A(-a,0)作直线 1 交 y 轴于点 P,交椭圆于点 Q.,若△AOP 是等腰三角形,且
,则椭圆的离心率为____
【答案】 2 5 5
【答案】 x y 0 a2 b2
5 .(江苏省泰州中学 20XX 届第一学学期高三数学摸底考试)设中心在原点的双曲线该双曲线的方程是__________. 【答案】2x2﹣2y2=1
6 .(江苏省连云港市赣榆县清华园双语学校 20XX 届高三 10 月月考数学试题)我们把形如
y b a 0,b 0 的函数称为“莫言函数”,并把其与 y 轴的交点关于原点的对称
x a 点称为“莫言点”,以“莫言点”为圆心,凡是与“莫言函数”图象有公共点的圆,皆称
之为“莫言圆”.当 a 1 , b 1时,在所有的“莫言圆”中,面积的最小值______. ) 【答案】 3 .
7 .( 江 苏 省 无 锡 市 20XX 届 高 三 上 学 期 期 中 调 研 考 试 数 学 试 题 ) 直 线 y kx 1 与 圆
(A) 3 3 (B) 2 3
【答案】A
(C) 2
(D) 3
10 .( 江 苏 省 苏 州 市 20XX 届 高 三 暑 假 自 主 学 习 测 试 ( 9 月 ) 数 学 试 卷 ) 已 知 双 曲 线
x2 y2 1 (m 0) 的离心率为 2,则 m 的值为 ______. m
【答案】3 11.(江苏省诚贤中学 20XX 届高三上学期摸底考试数学试题)若双曲线 x2 y2 1 的焦点到渐
k
近线的距离为 2 2 ,则实数 k 的值是________. 【答案】8
12 .( 江 苏 省 宿 迁 市 20XX 届 高 三 上 学 期 第 一 次 摸 底 考 试 数 学 试 卷 ) 已 知 双 曲 线
x2 a2
y2 b2
1(a>0 ,b>0) 的左、右焦点分别为 F1 ,F2 ,以 F1F2 为直径的圆与双曲线在第一
称轴的圆锥曲线 C ,离心率为 2 ,且过点 (2, 3) ,则曲线 C 的方程为________.
【答案】 x2 y2 5
15.(江苏省苏州市 20XX 届高三暑假自主学习测试(9 月)数学试卷)已知 P 是直线
l: kx y 4 0(k 0) 上一动点,PA,PB 是圆 C: x2 y2 2 y 0 的两条切线,切点分
象限的交点为 P .若 PF1F2 30 ,则该双曲线的离心率为______.
【答案】 3 1
13.(江苏省宿迁市 20XX 届高三上学期第一次摸底考试数学试卷)已知过点 (2 ,5) 的直线 l 被
圆 C :x2 y2 2x 4 y 0 截得的弦长为 4,则直线 l 的方程为______. 【答案】 x 2 0 或 4x 3y 7 0 14.(江苏省无锡市 20XX 届高三上学期期中调研考试数学试题)若中心在原点,以坐标轴为对
(x 3)2 ( y 2)2 9 相 交 于 A、B 两 点 , 若 AB 4 , 则 k 的 取 值 范 围 是
____________________.
【答案】 ( 1 , 2) 2
8
. (江苏省连云港市赣榆县清华园双语学校
20XX
届高三
10
月月考数学试题)设
F
x2 y2 是椭圆a2+b2
解析几何
一、填空题
1 .( 江 苏 省 扬 州 中 学 20XX 届 高 三 开 学 检 测 数 学 试 题 ) 已 知 实 数 p 0 , 直 线
3x 4 y 2 p 0 与抛物线 x2 2 py 和圆 x2 ( y p )2 p2 从左到右的交点依次为 24
A、B、C、D, 则 AB 的值为 ▲ . CD
17.(江苏省扬州市扬州中学 20XX 届高三 10 月月考数学试题)当且仅当 m r n 时,两圆
x2 y2 49 与 x2 y2 6x 8y 25 r2 0(r 0) 有 公 共 点 , 则 n m 的 值 为
______________. 【答案】10 二、解答题 18.(江苏省南京市 20XX 届高三 9 月学情调研数学试题)已知椭圆 C 的中心在坐标原点,右准
【答案】 1 16
2 .( 江 苏 省 淮 安 市 车 桥 中 学 20XX 届 高 三 9 月 期 初 测 试 数 学 试 题 ) 如 果 圆 x2+y2-2ax-2ay+2a2-4=0 与圆 x2+y2=4 总相交,则 a 的取值范围是___.
【答案】 2 2 a 0或0 a 2 2
3 .(江苏省常州市武进区 20XX 届高三上学期期中考试数学(理)试题)若实数 x 、 y 满足
