09-10年度第一学期《自动控制原理》考卷A卷答案
自动控制原理考试试卷及答案30套
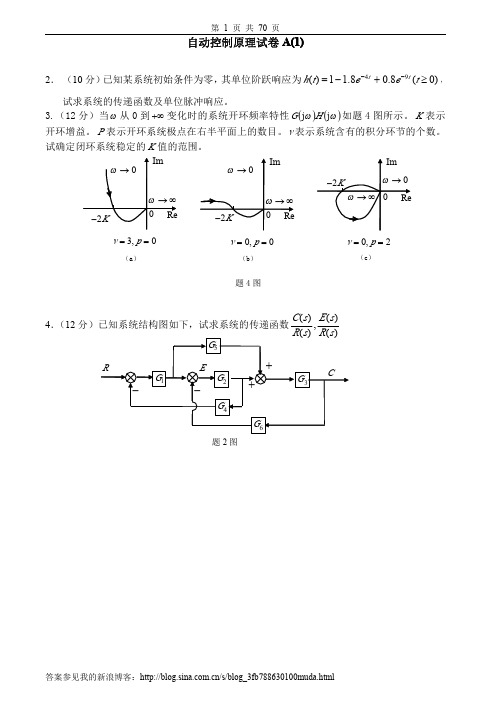
7. (15 分)已知系统结构图如下图所示,试求传递函数
C ( s) E ( s ) 。 , R ( s ) R( s )
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 6 页 共 70 页
自动控制原理试卷 A(4)
第 1 页 共 70 页
自动控制原理试卷 A(1)
2. (10 分) 已知某系统初始条件为零, 其单位阶跃响应为 h(t ) = 1 − 1.8e −4t + 0.8e −9t (t ≥ 0) , 试求系统的传递函数及单位脉冲响应。 3.(12 分)当 ω 从 0 到 +∞ 变化时的系统开环频率特性 G ( jω )H ( jω ) 如题 4 图所示。 K 表示 开环增益。 P 表示开环系统极点在右半平面上的数目。 v 表示系统含有的积分环节的个数。 试确定闭环系统稳定的 K 值的范围。 Im Im Im ω →0 ω →0 ω →0 −2 K ω → ∞ 0 Re ω →∞ ω →∞
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 7 页 共 70 页
类型的校正。 7. (15 分)题 6 图示采样系统的结构框图。已知采样周期 T=1 秒。
R T
1 − e −Ts s
k s
C
题6图
(1)求使系统稳定的 k 值; (2)当 k=1 时,求系统的单位阶跃响应 (3)求单位阶跃扰动下的稳态误差。 8. (12 分)已知系统结构图如下,试求系统的传递函数
1. (9 分)设单位负反馈系统开环零极点分布如图所示,试绘制其一般根轨迹图。 (其中-P 为开环极点,-Z 为开环零点)
3. (10 分) 已知某系统初始条件为零, 其单位阶跃响应为 h(t ) = 1 − 1.8e −4t + 0.8e −9t (t ≥ 0) , 试求系统的传递函数及单位脉冲响应。 4. (8 分)已知一单位负反馈系统的开环传递函数为 G ( s ) =
自动控制原理试题库(含答案)

课程名称: 自动控制理论 (A/B 卷 闭卷)一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
自动控制原理试卷、习题及答案2套
第 7 页 共 32 页
2-5 求图示运算放大器构成的网络的传递函数。
题 2-5 图
2-6 已知系统方框图如图所示,试根据方框图简化规则,求闭环传递函数。
题 2-6 图
2-7
分别求图示系统的传递函数 C1 (s) 、 C2 (s) 、 C1 (s) 、 C2 (s) R1 (s) R1 (s) R2 (s) R2 (s)
第 1 页 共 32 页
自动控制 (A )试卷
一、系统结构如图所示,u1 为输入, u2 为输出,试求
1.求网络的传递函数 G(s)=U1(s)/U2(s)
2. 讨论元件 R1,R2,C1,C2 参数的选择对系统的稳定性是否有影响。(15 分)
i2
i1
C1
R1
U1
R2
U2
C2
二、图示系统,试求,
(1) 当输入 r(t)=0,n(t)=1(t)时,系统的稳态误差 ess; (2) 当输入 r(t)=1(t),n(t)=1(t)时,系统的稳态误差 ess; (3) 若要减小稳态误差,则应如何调整 K1,K2?(15 分)
(2) 三阶系数的一对主导极点为 s1,2 1 j2 ,求同时满足上述条件的开环传递函 数G(s) 。
3 – 10 系统结构图如图所示,试求当 0 时,系统的 和
n 之值,如要求 =0.7,试确定参数 。
题 3-10 图
3 – 11 设单位反馈系统的开环传递函数如下,试确定系统稳定时 K 的取值范围。
输入信号 r(t)=1 作用下,能使给定系统成为最少拍系统的数字控制器的
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 4 页 共 32 页
安徽大学期末试卷09-10年度第一学期《自动控制原理》考卷B卷答案
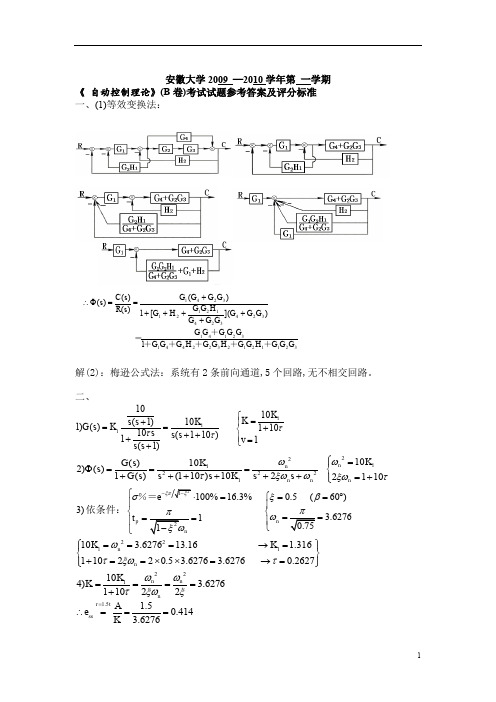
安徽大学2009 —2010学年第 一学期《 自动控制理论》(B 卷)考试试题参考答案及评分标准 一、(1)等效变换法:解(2):梅逊公式法:系统有2条前向通道,5个回路,无不相交回路。
二、111101010(1)1)() 11010(110)11(1)K K K s s G s K s s s v s s τττ⎧=+⎪==+⎨++⎪+=⎩+221122211010()2)() 1()(110)1022110n n n n n K K G s s G s s s K s s ωωτξωωξωτ⎧=⎪Φ===⎨++++++=+⎪⎩ 3)依条件:0.5 (60)100%16.3% 3.62761n p e t ξβσω-⎧==︒=⎧⎪⎪⎨⎨====⎪⎪⎩⎩%= 221110 3.627613.16 1.316110220.5 3.6276 3.6276 0.2627n n K K ωτξωτ⎧⎫===→=⎪⎪⎨⎬+==⨯⨯=→=⎪⎪⎩⎭221104) 3.627611022n n n K K ωωτξωξ====+1.5 1.50.4143.6276r t ss A e K =∴===3211212322441321413243241212132411)]([1)()()()(G G G H G G H G G H G G G G G G G G G G G G G G H G G H G G G G G s R s C s ++++++ =++++++==Φ∴三、(1)特征方程为()10(1)10(2)(1)10(2)(1)1(2)D s GH K s s s K s s s K s s s =+=-+=+-=+-=+换算成首一多项式,为:-根轨迹方程为: 由此可知,需要绘制零度根轨迹。
分离点的计算:12()()02.732,0.732dG sH s dss s ===- (2)由特征方程求取根轨迹与虚轴的交点,1,2s =±此时闭环系统临界稳定,出现等幅振荡,所对应的K =2。
08-09年度第一学期《自动控制原理》考卷A卷
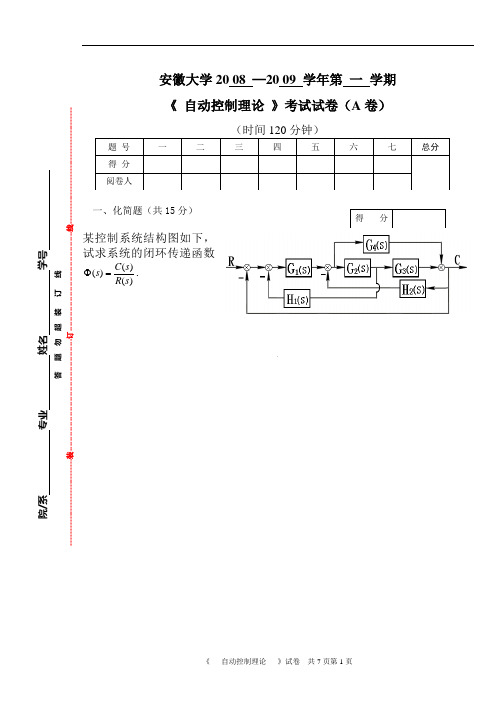
安徽大学20 08 —20 09 学年第 一 学期《 自动控制理论 》考试试卷(A 卷)(时间120分钟)一、化简题(共15分)某控制系统结构图如下,试求系统的闭环传递函数)()()(s R s C s =Φ.院/系 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------二、简答题(共15分)已知一控制系统的结构图如下(1) 求使系统稳定时K 的取值范围;(2) 如果要求闭环系统的极点全部位于1s =-垂线之左,求K 的取值范围。
三、绘图题(共10分)已知单位负反馈系统的开环传递函数为:()(1)(0.51)KG s s s s =++(1)绘制该系统的根轨迹图;(2)为保证该系统稳定,试确定K 的取值范围。
四、判断题(共15分)已知单位负反馈系统,开环传递函数4(1)3(),0(1)k sG s ks s+=>-。
(1)绘制k=6时的乃氏曲线,并用乃氏判据判断系统的稳定性;(2)给出系统稳定时k的范围。
五、设计题(共15分)已知单位负反馈系统开环传递函数为)2()(+=s s Ks G o ,试设计串联校正装置,使t t r =)(时,稳态误差为05.0=ss e ,系统的相角裕度050≥γ。
六、分析题(共15分)设复合校正系统的结构如下图所示,试确定前馈校正装置的 结构参数1λ和2λ,使复合校正后控制系统具有Ⅲ型控制精度。
(2121,,,T T K K 已知且均大于0)七、计算题(共15分)某含有零阶保持器的采样系统结构如图所示,试求: (1) 当采样周期s T 1=时系统的临界开环增益c K ; (2) 求1,1==K s T 时系统单位阶跃响应)(kT C ; (3) 求系统在阶跃输入信号作用下的稳态误差。
自动控制原理考试试卷及答案30套

−b
Im
Re
B2 ω B1
A
−1 N ( A)
0
K
−
b
K = 1, b = 1
题 7 图 (a)
4 s(s + 1)(s + 2)
G ( jω )
题 7 图(b)
8. (15 分)某离散控制系统如下图,采样周期 T=0.2 秒,试求闭环稳定的 K1、K2 的取值 范围。
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
7. (15 分)已知系统结构图如下图所示,试求传递函数
C ( s) E ( s ) 。 , R ( s ) R( s )
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 6 页 共 70 页
自动控制原理试卷 A(4)
第 5 页 共 70 页
自动控制原理试卷 A(3)
1、 . (10 分)已知某单位负反馈系统的开环传递函数为 G ( s ) =
6 ,试求系统的单位脉 s ( s + 5)
冲响应和单位阶跃响应。 2、 (10 分)已知单位负反馈系统的闭环零点为 -1,闭环根轨迹起点为 0,-2,-3,试确定系 统稳定时开环增益的取值范围。 3、 (10 分)已知系统的结构图如下,试求: (1)闭环的幅相特性曲线; (2)开环的对数幅频和相频特性曲线; (3)单位阶跃响应的超调量σ%,调节时间 ts; (4)相位裕量γ,幅值裕量 h。
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 4 页 共 70 页
(1)试写出系统的传递函数 G(s); (2)画出对应的对数相频特性的大致 形状; (3)在图上标出相位裕量Υ。 7. (15 分)题 7 图(a)所示为一个具有间隙非线性的系统,非线性环节的负倒幅相特性与 线性环节的频率特性如题 6 图(b)所示。这两条曲线相交于 B1 和 B 2 两点,判断两个交点处 是否存在稳定的自持振荡。
第一学期《自动控制原理》考卷A卷答案
安徽大学2009 —2010学年第 一学期《 自动控制理论》(A 卷)考试试题参考答案及评分标准一、系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
解:图中有2条前向通路,5个回路,,,,112321211=∆==∆=G P G G P,,,,,22135342132212121H G H G L G L G G L H G G L H G L =-=-=-=-=,)(154321L L L L L ++++-=∆则有∆∆+∆=2211)()(P P s R s C 2213321221123211H G H G G G G H G G H G G G G -+++++=二、(1)闭环传递函数为 21132223211()75007500()234.675007500n n n n s K s K s s s s K s s s K ωζωωω++Φ==++++++ 特征方程为321()34.6750075000D s s s s K =+++= 列劳斯表如下:321s s s s 11134.634.67500750034.67500K K ⨯- 1750075000K 根据劳斯判据得到:1034.6K <<时,系统稳定。
(2)令s=s 1-1代入到原特征方程,得到新的特征方程:321111()(1)34.6(1)7500(1)75000D s s s s K =-+-+-+=整理得:321111()34.67433.875007466.40D s s s s K =+++-=()列劳斯表如下:321s s s s 11131.631.67433.875007466.431.675007466.4K K ⨯---() 17433.875007466.40K - 根据劳斯判据得到:1032.3K <<时,闭环系统的极点全部位于s=-1垂线之左。
(3)31()R s s =, 单位反馈系统的误差传递函数()1()e s s Φ=-Φ故2321(34.6)()34.675007500s s e s s s s K +Φ=+++2332001320111(34.6)()lim ()()lim 34.675007500(34.6)34.61lim 7500375034.675007500s s s s s E s sR s e s s s s s s K s K s s s K →→→+=Φ=++++===+++三、1.绘制根轨迹的典型步骤如下:(1) 开环极点为0,-1,-2,见图,它们是根轨迹各分支上的起点。
自动控制原理考试试卷及答案30套
1.(10分)设系统开环极点(×)、零点(○)分布如题1图所示。试画出相应的根轨迹图。
2、(10分)已知系统开环幅相频率特性如下图所示,试根据奈氏判据判别系统的稳定性,并说明闭环右半平面的极点个数。其中 为开环传递函数在s右半平面极点数, 为开环系统积分环节的个数。
3、(15分)某系统方框图如下图所示,
8、(14分)试绘制 方程所描述系统的根轨迹。
自动控制原理试卷A(10)
一、(12分)典型二阶系统的开环传递函数为
当取 时,系统的稳态输出为 ,试确定系统参数
二、(12分)试求下图所示无源校正网络的的传递函数,画出其伯德图并说明其特性(是超前还是滞后)。
三、(12分)某闭环系统的特征方程为 ,试求系统产生等幅振荡的k值。
6. (15分)已知最小相位系统的对数幅频特性曲线如下图所示(分段直线近似表示)
7.(15分)题7图(a)所示为一个具有间隙非线性的系统,非线性环节的负倒幅相特性与线性环节的频率特性如题6图(b)所示。这两条曲线相交于 和 两点,判断两个交点处是否存在稳定的自持振荡。
8.(15分)某离散控制系统如下图,采样周期T=0.2秒,试求闭环稳定的K1、K2的取值范围。
自动控制原理试卷A(3)
1、.(10分)已知某单位负反馈系统的开环传递函数为 ,试求系统的单位脉冲响应和单位阶跃响应。
2、(10分)已知单位负反馈系统的闭环零点为-1,闭环根轨迹起点为0,-2,-3,试确定系统稳定时开环增益的取值范围。
3、(10分)已知系统的结构图如下,试求:
(1)闭环的幅相特性曲线;
1.(9分)设单位负反馈系统开环零极点分布如图所示,试绘制其一般根轨迹图。
(其中-P为开环极点,-Z为开环零点)
10级(A)卷参考答案及评分标准
自动控制原理10级试卷(A )参考答案及评分标准一、(15分)已知系统的结构图如图1所示,图中R(s)为输入信号,N(s)为干扰信号。
(1)画出系统对应的信号流图;(5分)(2)利用(1)中的信号流图(或结构图等效化简法),求出传递函数)()(s R s C ,)()(s N s C 。
(10分)二、(15分)单位负反馈控制系统如图2所示。
(1)求二阶系统特征参数ωn 、ζ与本系统实际参数的关系;(7分)(2)若K=16,T=0.25s ,计算系统的各动态性能指标t r 、t p 、t s 和σ%。
(8分)三、(20分)系统结构如图3所示。
(1)求系统稳定时,参数a 、T 、K 1需要满足什么条件;(10分)(2)当r(t)=2t+4t 2时,系统的稳态误差e ss 是多少。
(10分)四、(20分)已知某单位负反馈系统的闭环根轨迹图如图4所示。
(1)该根轨迹属于180度根轨迹还是零度根轨迹?(2分)(2)写出该系统以根轨迹增益K*为变量的开环传递函数;(6分)(3)求出分离点坐标,并写出该系统临界阻尼时的闭环传递函数;(8分)(4)求出系统为欠阻尼状态时,根轨迹增益K*的取值范围。
(4分)五、(10分)某系统的开环传递函数为12)()(-=s s H s G 。
(1)试证明当ω由0→+∞变化时,系统的开环幅相曲线是一个半圆;(6分)(2)根据(1)中的证明结果,画出系统的开环幅相曲线,并利用奈氏判据判断闭环系统的稳定性。
(4分)六、(15分)已知某单位反馈的最小相位系统,有开环极点-40和-10,并且当开环增益K=25时,系统的开环幅相频率特性G (j ω)曲线如图所示。
(1)试写出开环传递函数G(s)的表达式;(5分)(2)作出其近似对数幅频特性曲线(要计算出各个转折频率处的幅值分贝数,并在曲线上标出);(6分)(3)求系统开环截止频率ωc 。
(4分)七、(10分)设离散控制系统结构如图所示。
自动控制原理试卷含答案4套完整(免费)
课程名称: 自动控制理论 (A/B 卷 闭卷)试卷A一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽大学2009 —2010学年第 一学期
《 自动控制理论》(A 卷)考试试题参考答案及评分标准 一、系统的结构图如图所示,试求该系统的闭环传递函数)
()
(s R s C 。
解:图中有2条前向通路,5个回路
,
221H G 则有
二、(1)3210
s s s s (2)令s=s ()(D s =3210
s s s s 1131.6
31.67433.875007466.431.6
75007466.4
K K ⨯---()
175007466.4
K -
根据劳斯判据得到:1032.3K <<时,闭环系统的极点全部位于s=-1垂线之左。
(3)3
1()R s s =
,
单位反馈系统的误差传递函数()1()e s s Φ=-Φ
故2321
(34.6)
()34.675007500s s e s s s s K +Φ=+++
233
200132011
1(34.6)
()lim ()()lim 34.675007500(34.6)34.61lim 7500375034.675007500s s s s s E s sR s e s s s s s s K s K s s s K →→→+=Φ=++++===+++
三、1.绘制根轨迹的典型步骤如下:
(1) 开环极点为0,-1,-2,见图,它们是根轨迹各分支上的起点。
由于开环无有限零点,故根轨迹各分支都将趋向无穷。
(2) 一共有三个分支。
且根轨迹是对称实轴的。
(3) 定根轨迹的渐近线。
三根分支的渐近线方向,可按式(4-9)来求,即
3
)12()12(π
πϕ+±=
-+±=
k m n k a ( ,2,1=k )
因为当k 值变化时,相角值是重复出现的,所以渐近线不相同的相角值只有60o ,-60o 和180o 。
因此,
该系统有三条渐近线,其中相角等于1800的一条是负实轴。
(4) (5) 解得 因为0>>s 577
.1-(6) 式为:
使第一列中s 1 可求得根轨迹与虚轴的交点 2j s ±=
虚轴上交点的频率为2±=ω
,与交点相应的增益值为3*=K 。
2.系统稳定时满足:30*
<<K
5.0=ζ
四、(1)奈奎斯特曲线
系统开环频率特性为:222
[()(1)]
()()(1)
K T j T G j H j T τωτωωωωω-+--=+ 开环幅相曲线的起点:(0),(0)90A ϕ++=∞=-︒
终点:()0,()270A ϕ∞=∞=-︒
与实轴的交点:令虚部为零,解得
x ω⎧
=
⎪⎨
⎪
因为(ϕ
︒的圆弧,(21K τ<;K 五、(1数为:
(2)校正前:14.14c
ω==
900.20.062522c c arctg arctg γωω=︒--=-︒
可知系统不稳定。
若选超前校正,可知校正后系统的''c ω会大于14.14,而原系统在16ω=之后相
角下降很快,因此,可选滞后校正一试。
(3)选择''c ω:考虑''50555γ=︒+︒=︒,其中5︒为考虑滞后校正的滞后角度。
由:''900.20.062555c c arctg arctg γωω=︒--=︒,可计算在 2.4c ω=处有(2.4)55.83γ=︒,
因此,可取:
'' 2.4c ω=
(4)确定滞后校正的参数b 和T 。
由:20lg ('')0c b L ω+=,可求得 2.4
0.0640
b =
= 由:
1
0.1''c bT
ω=,可求得69.44T =,由此可得: 1/0.241
()1/0.0141
c bTs s G s Ts s ++==
++ (5)经验算,相角裕度满足要求。
六、由系统的结构以及已知参量)()()
(t c t r t e -=得
)(
)
1)(1()
()1()()()()(2122121s R s T s T s bs as k s T s k k s R s C s R s E ++++
+-=-=
)(s E ==即:
e ss 要使ss e
七、1. 系统开环脉冲传递函数为
⎥⎦
⎤⎢⎣⎡------=⎥⎦⎤⎢⎣⎡+-=----))(1()1()1()1()1(1)1()(2121
T T e z z z e z Tz z s s Z z z G 将1.0=T
代入并整理得
[]11110.005(0.9)
()(1)(0.905)
0.005(0.9)lim 1()lim 1(1)(0.905)0.005(0.9)
lim(1)()lim(1)0.1
(1)(0.905)0
p z z v z z a z G z z z z K G z z z z K z G z z z z K →→→→+=
--⎡⎤
+=+=+=∞⎢⎥--⎣⎦
+=-=-=--=
2.待求稳态误差()1v
T
e K ∞=
= 3.)905.0)(1()
9667.0(00484.011)1(1)1()
(1
1.021+-+=⎥⎦
⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡+⋅-===---z z z e z e z T K s s Z K z z G K T T T
901
.09.1)
9667.0(00484.0)(1)()(21
1
.0+-+=
+=
Φ==z z z z G z G z K T
901.0801.29.2)
9667.0(00484.01901.09.1)9667.0(00484.0)()()(2322-+-+=
-⋅+-+=⋅Φ=z z z z z z z z z z z R z z C 123456
0.004840.01870.04070.070.1060.148z z z z z z Λ------=++++++
*()0.00484()0.0187(2)0.0407(3)0.07(4)
0.106(5)0.148(6)c t t T t T t T t T t T t T δδδδδδΛ
=-+-+-+-+-+-+。
